1 Introduction

The first mathematical model of an artificial neural network (NN) was developed in 1943 [13]. The use of NN methodology in various engineering and science fields has increased because the networks can efficiently integrate information and extract important features from information. The NNs have been broadly applied in pattern recognition, image recognition [8, 14], voice recognition and machine translation [6, 7, 17], medicine [1, 4], weather prediction, computational finance, and applied mathematics. In spite of the progress in the field of NN techniques, there has been limited literature that has applied the NNs to multiscale modeling for simulation of a physical phenomenon.

In 2010, Hambli et al. constructed a multiscale hierarchical model of bone structures using NN technique [10]. Hambli et al. stated “among the various multiscale modeling approaches, hierarchical multiscale modeling methods are more advantageous than homogenization methods for determining the interactions of the various levels.” The approach incorporated an NN regression model and finite element simulation to analyze multilevel bone adaptation. The NN was used to predict and update bone material properties and factors referring to a set of boundary conditions, stress applied to the bone structure, and the previous bone parameters. Subsequently, Barkaoui et al. [3] presented a hierarchical multiscale approach using NN computation and a homogenization method and employed the approach to estimate elastic properties of human cortical bone structures.

Asproulis and Drikakis developed a neural network-based multiscale approach that couples a continuum fluid dynamics and molecular dynamics [2]. In this article the entire simulation field was analyzed using a macroscopic numerical scheme and a microscopic simulation was employed to obtain detailed information on its local field. The NNs helped to transfer analytical results bi-directionally between the macroscopic and microscopic analyses. A similar NN-based coupling method is addressed in [16].

The NN approaches can be used to link different scales quickly and easily [12, 15] and, therefore, are beneficial especially when a target model is complicated and time consuming to analyze [9, 19, 20].

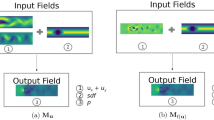
The main difference between the above approaches and my current work lies in usage of the NNs. Unlike the other manuscripts, this study does not perform the NN calculations to estimate material properties, structural parameters, boundary conditions, governing equations, or constitutive laws. I present a spatial discretization scheme employing the NNs for nonlinear governing equations. Instead of the conventional “direct and mathematical” discretization, the presented scheme “indirectly and statistically” constructs the discretized equation (Fig. 1b). The NN is employed as a substitute for a discretized nonlinear equation itself.

Fig. 1
figure 1

Schematic illustration of discretization of general solvers such as finite difference method (FDM), finite element method, and finite volume method in (a) and that of the presented scheme using regression analysis in (b)

Full size image

In general numerical analyses such as finite difference method (FDM), finite element method, and finite volume method, I spatially discretize a target simulated field into grids, elements, and cells (Fig. 1a). The discretized field is represented by a finite number of points: grid points and nodes. Each point is endowed with dependent-variable values (and variable gradients). To compute all unknown values for the points, I discretize differential equation(s) governing the field and construct discrete equations that contain the unknown values. By solving the discrete equations, I can determine the unknown values.

For instance, the spatial discretization of many finite element solvers is done on the basis of weighted-residual methods. In the discretization process of standard FDMs, the governing differential equation is approximated as a difference equation. In other words, the discrete equation is “directly and mathematically” derived from the governing equation in the conventional schemes. Conversely, the presented scheme “indirectly and statistically” constructs the discretized nonlinear equation using a machine learning approach including NNs.

In [18], the authors applied a neural network to a fluid simulation. They solved incompressible Euler equations using a marker-and-cell (MAC) scheme [11]. In the MAC scheme, large-scale linear Poisson’s equations must be solved to compute a pressure field at each time step. They employed a convolutional neural network to solve the equations. The network estimated a pressure profile, i.e., the network performed a role as the discretized equations of pressure. Therefore, the main contribution of their work is similar to that of this work. However, there are the following differences between their and my studies.

  • Although Tompson et al. employed a neural network to solve linear algebraic equations (linear Poisson’s equations), my approach can solve nonlinear equations.

  • Their target simulated field was homogeneous, but my approach is applicable to both homogeneous fields (Sects. 3.1 and 3.2) and heterogeneous fields (Sect. 3.3).

  • They applied the NN technique only to the pressure calculation, i.e., one of the simulation processes. Conversely, I replace the whole simulation processes with the NN-based approach in this article.

Procedure of the presented scheme The presented approach can be summarized by the below steps (the detailed procedure is given in Sect. 2.2):

  1. 1.

    Acquire training data

    Training data contain dependent-variable values (and variable gradients in some cases) at neighboring discrete points in the target field. I then construct a regression model that expresses the relation among variable values at the points and train the model based on the data. The data can be obtained from either a pre-analysis or experiment.

    • Training data obtained from numerical analyses of local fields

      I can employ conventional numerical solvers such as FDMs, finite element methods, and finite volume methods to simulate local fields. The local fields are extracted from the entire simulated field (global field) and contain several discrete points in themselves. I conduct the local analysis for various boundary conditions and acquire a variety of sets of variable values at the neighboring points in the local field. From a numerical point of view, the presented modeling is regarded as multiscale when the training data are obtained from pre-analysis of local fields.

    • Training data obtained from an experiment

      Experimental data can be used as substitutes for the numerical training data.

  2. 2.

    Train regression models

    I train each regression model using the training data so that the model returns a variable for a discrete point referring to the variables for its neighboring discrete points. Therefore, the regression models function as discretized equations for the governing equation of the field.

  3. 3.

    Construct simultaneous equations by assembling the regression functions

    This process constructs simultaneous nonlinear equations by assembling the discretized equations obtained in step (2). The simultaneous equations include all unknown dependent-variable values (and variable gradients) for the discrete points in the entire field.

  4. 4.

    Solve the simultaneous equations

    By solving the simultaneous equations constructed in step (3), all the unknown variable values can be determined.

  5. 5.

    If necessary, interpolate the variable distribution between the discrete points

    I can interpolate detailed information on the microscopic (local) variable distributions by conducting the local analysis again. I impose the local boundary conditions (e.g., the variable profiles on the local boundaries that are obtained in step (4)) on each local field. The local analysis gives detailed variable profile between the discrete points. After obtaining the variable profiles in all local fields, I connect them to construct the global profile.

Advantages of the presented scheme

  1. 1.

    Efficient modeling of a heterogeneous field

    As with many multiscale modeling approaches, the presented scheme can construct an efficient numerical model of a heterogeneous structure. The entire model is represented by only coarse-grained discrete points. I need not, respectively, model all constituents when simulating the whole structure. Therefore, the entire model is computationally inexpensive.

  2. 2.

    No necessity of iterative multiscale computations

    Many multiscale nonlinear solvers conduct repeated multiscale computations that couple local and global simulations. I need to repeat the two analyses until the microscopic solution converges onto the macroscopic solution, which is time consuming. In the presented approach, once valid regression models for each discrete point are constructed, I can quickly reveal the behavior the whole field without repeated multiscale simulation for every convergence computation. In other words, I need not conduct additional local analysis while conducting the global analysis.

  3. 3.

    Possibility of analyzing a field even if there is unknown information about the field

    The presented scheme can accurately simulate a nonlinear field as long as a sufficient amount of valid observed data can be obtained, even if the following information is unknown, unclear, or unavailable:

    • Material property,

    • Governing equation, and

    • Detailed morphological feature of a microstructure in a heterogeneous field.

      When I have no information on the above items, the regression analysis can construct a discretized equation that determines relation between neighboring discrete points in the field.

2 Computational procedure

This section illustrates the presented computational procedure to solve a nonlinear problem. Let me consider stationary heat conduction in a one-dimensional homogeneous rod as an example. Although the problem discussed in this section is specific, the presented solver is applicable to many other kinds of nonlinear problems.

In this example, the dependent variable, its gradient, and flow are the temperature, temperature gradient, and heat flow, respectively. The rod is 1 m long. It is thermally insulated and no heat transfers through the surface. The rod is governed by

$$\frac{\text{d}}{{{\text{d}}x}}\left( {k\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right) = 0\quad{\text{for}}\quad0 \le x \le 1,$$
(1)

where \(u = u\left( x \right)\) and \(k\) are the temperature at point \(x\) and the thermal conductivity, respectively. Temperature values at both ends are fixed at \(u_{1}^{\text{given}}\) and \(u_{n}^{\text{given}}\); i.e.,

$$\begin{aligned} u\left( 0 \right) & = u_{1}^{\text{given}} \\ u\left( 1 \right) & = u_{n}^{\text{given}} . \\ \end{aligned}$$
(2)

The problem is linear when \(k\) is constant. However, \(k\) changes according to temperature, \(u\); the problem then has material nonlinearity.

$$k = k\left( u \right).$$
(3)

In Sect. 3, I will compare the true solution of \(u\left( x \right)\), a standard FDM, and the presented scheme in terms of accuracy when solving three nonlinear heat conduction problems.

2.1 True solution

By integrating the governing equation in Eq. (1), I get

$$\int {k\left( u \right){\text{d}}u} = \int {C_{1} {\text{d}}x} = C_{1} x + C_{0} \quad{\text{for}}\,0 \le x \le 1,$$
(4)

where \(C_{1} ,C_{0}\) are unknown constant values and determined by the boundary conditions in Eq. (2). When I can integrate the left side of Eq. (4) by \(u\) and \(u\) is expressible as a function of \(x\), the true solution of \(u\left( x \right)\) can be obtained. Otherwise, I cannot acquire the true solution. Therefore, whether the true solution is available depends on the functional form of \(k\left( u \right).\)

2.2 Presented scheme

2.2.1 Outline

To obtain an approximate temperature solution employing the presented approach, I arrange \(n\) discrete points as depicted in Fig. 2a. Note that the intervals between the points need not necessarily be equal. Each discrete point is endowed with a temperature value. The temperature at point \(i\) is denoted \(u_{i}\). To compute all unknown temperatures, \(u_{2} , \, \ldots , \, u_{n - 1}\), I need to obtain each local relation among neighboring points (Fig. 2b). Figure 3a shows the true relationship among temperature values at three neighboring points, \(u_{i - 1} , \, u_{i} , \, u_{i + 1}\). Unfortunately, the true relation cannot be derived in many general cases.

Fig. 2
figure 2

Example of a one-dimensional stationary heat conduction problem: an entire global field (a) and a local field that is partially extracted from the global field (b)

Full size image
Fig. 3
figure 3

Relationship between dependent-variable values at points i–1, i, and i + 1: the curved surface of the true relation (a) and a regression model that is statistically identified from the training data, i.e., the observed values of ui–1, ui, and ui+1 (b)

Full size image

Hence, in the presented approach, I express the relation between \(u_{i}\) and \(u_{i - 1} , \, u_{i + 1}\) using a regression model, \(f\):

$$u_{i} = f\left( {u_{i - 1} ,u_{i + 1} } \right) + \varepsilon ,$$
(5)

where \(\varepsilon\) is the error of \(u_{i}\). The function \(f\) is trained so that \(f\) fits the observed values of \(u_{i - 1} , \, u_{i} , \, u_{i + 1}\), which are shown as black circles in Fig. 3b, as much as possible. It is important to select \(f\) whose functional form is suitable to approximately express the true relation. In this article I prepare three kinds of regression models that are explained in Sect. 2.2.2.

The temperature values that are computed using the presented scheme are denoted

$${\mathbf{u}}^{\text{pre}} = \left( {u_{2}^{\text{pre}} \cdots u_{n - 1}^{\text{pre}} } \right)^{\text{T}} .$$
(6)

I formulate Eq. (5) for \(i = 2, \ldots ,n - 1\) and construct the below simultaneous equations:

$$\begin{array}{*{20}c} {u_{2}^{\text{pre}} = f\left( {u_{1}^{\text{given}} ,u_{3}^{\text{pre}} } \right)} \\ \vdots \\ {u_{i}^{\text{pre}} = f\left( {u_{i - 1}^{\text{pre}} ,u_{i + 1}^{\text{pre}} } \right)} \\ \vdots \\ {u_{n - 1}^{\text{pre}} = f\left( {u_{n - 2}^{\text{pre}} ,u_{n}^{\text{given}} } \right)} \\ \end{array} .$$
(7)

The above simultaneous equations are repeatedly computed to determine \({\mathbf{u}}^{\text{pre}} .\)

2.2.2 Regression models

Standard polynomial function

I prepare four kinds of full polynomial regression models: 2nd-, 3rd-, 4th-, and 5th-order polynomial functions. The lth order of full polynomial function is as follows.

$$u_{i} = f\left( {u_{i - 1} ,u_{i + 1} } \right) = \sum\limits_{0 \le m + n \le l} {a_{m,n} u_{i - 1}^{m} u_{i + 1}^{n} } ,$$
(8)

where \(a_{m,n}\) (\(m,n\) are nonnegative integers) are regression coefficients that are determined by the least squares method so that \(f\) fits training data.

Locally weighted scatterplot smoothing (LOESS)

LOESS is a nonparametric regression model that uses locally weighted linear regression to smooth data. The model divides data into multiple intervals (25 intervals in this paper) and calculates a data point in interval \(j\) referring to its surrounding data points within interval \(j\). LOESS uses a second-order polynomial interpolation for each interval. I determine regression weights in interval \(j\) by the formula,

$$v_{i,j} = \left( {1 - \left( {\frac{{s - s_{i,j} }}{d\left( s \right)}} \right)^{3} } \right)^{3} ,$$
(9)

where \(v_{i,j}\) is the \(i\)th weight, \(s\) is a predictor value related to output parameter, \(s_{i,j}\) are the adjacent data points of \(s\) as defined by interval \(j\), \(d\left( s \right)\) is the distance from \(s\) to the farthest estimator value within the interval. The weight for data points outside the interval is zero, which means no influence on the fit.

Neural network (NN)

The detailed information on the NNs used in this manuscript is shown in Table 1 and Fig. 4. I employ feed-forward hierarchical NNs that are composed of multiple layers such as input, output, and intermediate hidden layers. The layers have simple elements called neurons, which are depicted as white circles in Fig. 4. The networks are fully connected, i.e., each neuron in a layer is connected to all neurons in its adjacent layer. Input signals (\(u_{i - 1}\) and \(u_{i + 1}\) in this manuscript) are transmitted from the input layer to the output layer through the hidden layers. The output layer finally gives \(u_{i} .\)

Table 1 Configurations of neural network models used to solve numerical examples
Full size table
Fig. 4
figure 4

Example of feed-forward hierarchical neural network that has input layer, two hidden layers, and output layer

Full size image

Figure 5 describes output values of neurons and those of biases in three neighboring layers of an example NN. The \(i\)th neuron in the \(l\)th layer receives the input value, \(v_{i}^{\left( l \right)}\), which is a sum of weighted outputs of neurons in the previous layer, \(y_{j}^{{\left( {l - 1} \right)}}\), and the bias, \(b_{i}^{{\left( {l - 1} \right)}}\):

$$v_{i}^{\left( l \right)} = b_{i}^{{\left( {l - 1} \right)}} + \sum\limits_{{1 \le j \le R_{l - 1} }} {w_{i,j}^{{\left( {l - 1} \right)}} y_{j}^{{\left( {l - 1} \right)}} } ,$$
(10)

where \(w_{i,j}^{\left( l \right)}\) are the weights and \(R_{l - 1}\) is the number of neurons in the \(\left( {l - 1} \right)\)th layer. \(v_{i}^{\left( l \right)}\) is activated by an activation function \(a_{i}^{\left( l \right)}\) to produce output \(y_{i}^{\left( l \right)}\). I employ hyperbolic tangent sigmoid function that is commonly used for the activation. It is given by

$$y_{i}^{\left( l \right)} = a_{i}^{\left( l \right)} \left( {v_{i}^{\left( l \right)} } \right) = \frac{2}{{1 + \exp \left( { - 2v_{i}^{\left( l \right)} } \right)}} - 1.$$
(11)
Fig. 5
figure 5

Output values of neurons and those of biases in three neighboring layers of an example neural network

Full size image

I train the NN to perform a particular function by optimizing the weights and biases on the basis of training data, i.e., various sets of known inputs (\(u_{i - 1}\) and \(u_{i + 1}\)) and known output (\(u_{i}\)). This process is called supervised learning. Several algorithms have been proposed for the supervised learning. This article uses the gradient descent back propagation method. The method is an iterative gradient algorithm that adjusts the weight and bias values to minimize the difference between the network output and the given output according to the gradient descent. The detailed procedure of the back propagation is explained in [5].

2.3 Finite difference method (FDM)

This subsection illustrates the procedure of a standard FDM. In similar way to the presented technique explained in the previous subsection, I arrange \(n\) grid points at equal intervals in the rod. The interval is \(h\). In the FDM, I approximate the governing differential equation in Eq. (1) as the following difference equation.

$$0 = \frac{\text{d}}{{{\text{d}}x}}\left( {k\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right) \approx \frac{{\left. {k\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right|_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} - \left. {k\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right|_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{h} \approx \frac{{k\left( {u_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)\frac{{u_{i + 1} - u_{i} }}{h} - k\left( {u_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)\frac{{u_{i} - u_{i - 1} }}{h}}}{h},\,{\text{therefore}},\,u_{i} = \frac{{k\left( {u_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)u_{i + 1} + k\left( {u_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)u_{i - 1} }}{{k\left( {u_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) + k\left( {u_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)}}\quad{\text{for}}\,i = 2, \ldots ,n - 1$$
(12)

where \(u_{i}^{\text{FDM}}\) is temperature at point \(i\) computed employing the FDM. It is said that the above relational expression is derived “directly and mathematically” from the governing equation. In this paper, I use the below approximations:

$$\begin{aligned} k\left( {u_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) \approx \frac{{k\left( {u_{i + 1} } \right) + k\left( {u_{i} } \right)}}{2} \hfill \\ k\left( {u_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) \approx \frac{{k\left( {u_{i} } \right) + k\left( {u_{i - 1} } \right)}}{2}. \hfill \\ \end{aligned}$$
(13)

Finally, I formulate Eq. (12) for \(i = 2, \ldots ,n - 1\) and solve them to obtain the solution, \({\mathbf{u}}^{\text{FDM}}\),

$${\mathbf{u}}^{\text{FDM}} = \left( {u_{2}^{\text{FDM}} \cdots u_{n - 1}^{\text{FDM}} } \right)^{\text{T}} .$$
(14)

3 Numerical example problems

To compare the computational precision and robustness, I solve three nonlinear stationary heat conduction problems of one-dimensional rods using the presented scheme and the standard FDM. The 1-m-long rod is divided into \(n - 1\) parts and represented by \(n\) discrete points. The locations of the points are denoted \(x_{1} , \ldots ,x_{n}\) and the temperature at \(x_{i}\) is denoted \(u_{i}\). In all the problems, temperatures at both the ends of the rod are fixed at 0° and 1°; i.e.,

$$\begin{aligned} u_{1} & = u\left( 0 \right) = 0 \\ u_{n} & = u\left( 1 \right) = 1. \\ \end{aligned}$$
(15)

3.1 Example 1: homogeneous rod (\(k\left( u \right) = k_{0} + k_{1} u\))

3.1.1 Problem statement

Let me consider a case that the rod has 21 points (i.e., \(n = 21\)) and its thermal conductivity, \(k\), is a linear function of temperature, \(u.\)

$$k\left( u \right) = k_{0} + k_{1} u,$$
(16)

where

$$\begin{aligned} k_{0} & = 0.1 \\ k_{1} & = 1; \\ \end{aligned}$$
(17)

therefore,

$$k\left( u \right) = 0.1 + u.$$
(18)

3.1.2 Computational procedure

3.1.2.1 True solution

I can derive the true solution of \(u\left( x \right)\) for this example directly from the governing equation in Eq. (4) based on Eq. (16). Integrating the left side of Eq. (4), I get

$$k_{0} u + \frac{{k_{1} u^{2} }}{2} = C_{1} x + C_{0} '\,{\text{for}}\,0 \le x \le 1$$
(19)

when \(k_{0} , \, k_{1}\) are constant values, \(k_{1} \ne 0\), and \(k_{0} + k_{1} u > 0\) for \(0 \le u \le 1\), I obtain the below equation by substituting the boundary conditions (Eq. (15)) into Eq. (19)

$$u\left( x \right) = - \frac{{k_{0} }}{{k_{1} }} + \sqrt {\left( {1 - x} \right)\left( {u\left( 0 \right) + \frac{{k_{0} }}{{k_{1} }}} \right)^{2} + x\left( {u\left( 1 \right) + \frac{{k_{0} }}{{k_{1} }}} \right)^{2} } .$$
(20)

It follows from the above equation and Eq. (17) that

$$u\left( x \right) = - 0.1 + \sqrt {0.01 + 1.2x} .$$
(21)

Therefore, the true temperature at each point, \({\mathbf{u}}^{\text{true}}\), is computed from the above equation,

$${\mathbf{u}}^{\text{true}} = \left( {u_{2}^{\text{true}} \cdots u_{n - 1}^{\text{true}} } \right)^{\text{T}} ,$$
(22)

where

$$u_{i}^{\text{true}} = - 0.1 + \sqrt {0.06i - 0.05} \quad{\text{for}}\quad i = 2, \ldots ,n - 1.$$
(23)

I compare \({\mathbf{u}}^{\text{true}}\) with the solution of the FDM, \({\mathbf{u}}^{\text{FDM}}\) in Eq. (14), and the solution of the presented scheme, \({\mathbf{u}}^{\text{pre}}\) in Eq. (6).

In a similar way to derive the true temperature, I can obtain the true relational expression among \(u_{i - 1} , \, u_{i} , \, u_{i + 1}\) in the below form from Eqs. (4) and (17)

$$u_{i} = - 0.1 + \sqrt {0.5} \sqrt {\left( {u_{i - 1} + 0.1} \right)^{2} + \left( {u_{i + 1} + 0.1} \right)^{2} } \quad {\text{for}}\quad i = 2, \ldots ,n - 1.$$
(24)

It is noted that the functional form of Eq. (24) is different from any of the regression models illustrated in Sect. 2.2.2. The main objective of this example problem is to investigate whether a regression model can accurately express the true relation between neighboring points even if the functional form of the regression model is different from the true one.

3.1.2.2 Presented scheme

To prepare training data, I first sample various sets of \(u_{i - 1}\) and \(u_{i + 1}\). I substitute each set into Eq. (24) and obtain accurate \(u_{i}\). I use the obtained sets of \(u_{i - 1} , \, u_{i} , \, u_{i + 1}\) to train the three kinds of regression models that are illustrated in subsection Sect. 2.2.2.

In general, training data have a strong influence on the computational precision of a regression model. The detailed illustration of the sampling method is as follows.

Number of training points

First of all, you have to prepare a sufficient number of data. In this manuscript, I prepare \(m_{l}\) sets of \(u_{i - 1} , \, u_{i} , \, u_{i + 1}\) (\(m_{l} = 2 0 0 , { 400, 600}\)).

Sampling technique

I use Latin hypercube sampling to generate well-balanced sets of \(u_{i - 1}\) and \(u_{i + 1} .\)

Sampling range

I test two kinds of sampling ranges: (1) unbiased data and (2) biased data.

  1. 1.

    Unbiased data

    As shown in Fig. 6a, I sample sets of \(u_{i - 1}\) and \(u_{i + 1}\) within a range of:

    Fig. 6
    figure 6

    Sample collections of explanatory variables (ui–1 and ui+1) used to train the regression models: a unbiased sets that are uniformly sampled and b biased sets where \(u_{i - 1}\) is close to \(u_{i + 1}\)

    Full size image
    $$0 \le u_{i - 1} , \, u_{i + 1} \le 1.$$
    (25)

    Since the minimum and maximum temperatures in the rod are 0 and 1 degree, Inequality (25) covers the entire range of possible values of \(u_{i - 1}\) and \(u_{i + 1}\). The inequality indicates that I uniformly sample sets of \(u_{i - 1}\) and \(u_{i + 1}\) so that

    $$- 1 \le u_{i + 1} - u_{i - 1} \le 1.$$
    (26)

    Although samples collections of explanatory variables where \(u_{1}\) is close to \(u_{3}\) (markers in the white area near the straight line \(u_{i - 1} = u_{i + 1}\) in Fig. 6a) are meaningful, samples where \(u_{i - 1}\) is far from \(u_{i + 1}\) are worthless to the accuracy of the regression model. This is because point \(i - 1\) is located near point \(i + 1\); therefore, \(u_{i - 1}\) would be close to \(u_{i + 1}\) in general. The regression model does not have to learn the worthless samples.

  2. 2.

    Biased data

    As depicted in Fig. 6b, I sample sets of \(u_{i - 1}\) and \(u_{i + 1}\) within a range of:

    $$\begin{array}{ll} 0 &\le u_{i - 1} , \, u_{i + 1} \le 1 \hfill \\ 0 \le u_{i + 1} - u_{i - 1} &\le \alpha \frac{{u_{n} - u_{1} }}{n - 1}, \hfill \\ \end{array}$$
    (27)

    where \(\alpha\) is a constant value and set to 5 in this article (\(\alpha = 5\)). The right side of the second inequality is the product of \(\alpha\) and the average temperature difference between two neighboring points in the rod. Inequalities (27) enable me to sample only meaningful sets where \(u_{i - 1}\) is close to \(u_{i + 1}\) and \(u_{i - 1}\) is smaller than \(u_{i + 1} .\)

3.1.2.3 FDM

By substituting Eqs. (13) and (18) into Eq. (12), it follows that

$$u_{i} = \frac{{u_{i - 1}^{2} + u_{i + 1}^{2} + \left( {u_{i} + 0.2} \right)\left( {u_{i - 1} + u_{i + 1} } \right)}}{{u_{i - 1} + 2u_{i} + u_{i + 1} + 0.4}}.$$
(28)

To obtain the FDM solution, \({\mathbf{u}}^{\text{FDM}}\) in Eq. (14), I formulate Eq. (28) for \(i = 2, \ldots ,n - 1\) and solve them by iterative computation. Number of the iterative cycles is 500.

Solving Eq. (28) for \(u_{i}\), the relation between \(u_{i}\) and \(u_{i - 1} , \, u_{i + 1}\) is expressed in the form,

$$u_{i} = - 0.1 + \sqrt {0.5} \sqrt {\left( {u_{i - 1} + 0.1} \right)^{2} + \left( {u_{i + 1} + 0.1} \right)^{2} } \quad {\text{for}}\quad i = 2, \ldots ,n - 1.$$
(29)

The above relation is completely equivalent with the true one in Eq. (24). Therefore, in general, when stationary heat conduction in a one-dimensional rod whose thermal conductivity is linearly proportional to temperature, the standard nonlinear FDM can construct the exact relation between neighboring three grid points and solve the problem completely accurately.

3.1.3 Results

In the following, I compare the solutions of the presented scheme with the true solution in terms of a root-mean-squared error of temperature values over all discrete points.

Type of polynomial function

The five types of polynomial regression models are compared in Table 2. By and large, the higher-order polynomial models generate smaller errors than the lower-order models. However, the LOESS, which uses a second-order polynomial interpolation for each of 25 divided spans, gives the most accurate solution regardless of the number of training samples, \(m_{l}\). A similar tendency is recognized on example problems 2 and 3, in part because a regression model with a larger number of terms can represent complex relational expression of variables more flexibly in general.

Table 2 Root-mean-squared temperature error of the polynomial regression model when analyzing example 1
Full size table

Number of neurons in the single-hidden-layer NN

An overview of the errors of the single-hidden-layer NNs listed in Table 3 reveals that the NNs consisting of more neurons are superior. However, some NNs having many neurons generated large errors when the training data are insufficient. For instance, the NN, which has more than 20 neurons and is trained by 200 biased sample sets, causes a larger error than the NN with 20 neurons. Therefore, an increase in the number of neurons does not necessarily improve the precision, which makes it difficult to optimize the number of the neurons.

Table 3 Root-mean-squared temperature error of the neural networks with a single hidden layer when analyzing example problem 1
Full size table

Number of hidden layers of the NN regression models

In general, addition of hidden layer(s) into an NN structure is often effective to express complex nonlinear relation, but an unnecessary hidden layer would lead to a reduction in the generalization performance of the NN.

The NNs with one hidden layer and those with two hidden layers are compared in Table 4. All the NNs are trained by 600 unbiased samples. For the two-hidden-layer NNs, I test three cases that the number of neurons in the second hidden layer is 50, 75, and 100% of that of the first layer (round-up after the decimal point). However, the number of neurons in the second layer does not have a significant effect on the temperature error.

Table 4 Comparison of root-mean-squared temperature error between the neural networks with a single hidden layer and the neural networks with two hidden layers when analyzing example problem 1. 600 UNBIASED sample sets are used to train the networks (\(m_{l} = 600\))
Full size table

Interestingly, the fewer the number of neurons in the first layer is, the more accurate all the two-hidden-layer NNs become except for a case that the first layer has only five neurons. Conversely, the error of the single-hidden-layer NN decreases with an increase of neurons. When the total number of parameters in an NN architecture including weights and biases in all layers is too large, the NN would not be able to allow for a good description of nonlinear relation between input and output parameters in general.

Training and test errors of the NN regression models during training process

Figure 7 shows example learning curves, i.e., training and test errors of two example neural networks during the training process. The two networks have a single hidden layer that consists of 25 neurons. The left figure presents the case where 200 biased sample sets are used to train the network (\(m_{l} = 200\)) and the right figure gives another case where \(m_{l} = 600\). The vertical and horizontal axes show the mean-squared error of the network response and the number of epochs, respectively.

Fig. 7
figure 7

Example learning curves, i.e., training and test errors of two example neural networks during the training process. The two networks have a single hidden layer that consists of 25 neurons

Full size image

Two hundred sample sets would be insufficient and there is a large difference between the training and test errors, which is called the overfitting problem (left figure of Fig. 7). There is almost no reduction in the test error since approximately 50 epochs. Conversely, both the training and test errors decrease simultaneously in the case where \(m_{l} = 600\) (right figure of Fig. 7). Therefore, 600 sample sets are regarded as sufficient to train the network and to prevent overfitting.

Number of training data, \(m_{l}\)

Tables 2 and 3 show that the regression models trained by a larger number of sample sets generate a temperature error equal to or smaller than those trained by a smaller number of sets. Note that additional training data are not highly effective in cases where a sufficient amount of data is already provided. For instance, Table 2 indicates that the polynomial models trained by 200 sets are almost full grown and the additional data are not so effective to enhance the accuracy. Conversely, the NN models trained by 200 sets require more training data to be completely sophisticated as shown in Table 3. By and large, 200 sample sets are necessary to sufficiently train the polynomial models and 400 sets are required for the single-hidden-layer NN models.

Comparison between unbiased and biased training data

As expected, Tables 2 and 3 indicate that the biased training data greatly improve the precisions of all the regression models including the polynomials and NNs in comparison with the unbiased data. The biased data have many meaningful sets where \(u_{i - 1}\) is close to \(u_{i + 1}\), which are important to construct valid regression models having a high generalization performance.

Let me illustrate the \(K\)-fold cross-validation that evaluates generalization performance of a regression model. In the validation method, \(m_{l}\) samples sets are divided into \(K\)-folds equally. Each of folds \(1, \ldots ,K\) has \({{m_{l} } \mathord{\left/ {\vphantom {{m_{l} } K}} \right. \kern-0pt} K}\) sets. For \(i = 1, \ldots ,K\):

  • Fold \(i\) forms a validation set and the other \(K - 1\)-folds form a training set.

  • I train a regression model using the \(K - 1\)-folds and test the model on fold \(i.\)

  • Difference between the true and estimated output parameters is computed.

Subsequently, I calculate the root-mean-squared difference, which could be an index of the generalization ability.

The results of the \(K\)-fold cross-validation (\(K = 10\)) for the regression models are depicted in Fig. 8. In all the regression models, the biased data are more helpful to enhance the generalization ability than the unbiased data.

Fig. 8
figure 8

\(K\)-fold cross-validation results in the case where \(K = 10\) and \(m_{l} = 600\). The NN model has a single hidden layer consisting of 25 neurons

Full size image
Fig. 9
figure 9

Root-mean-squared temperature errors compared with the true solution when solving example problem 1. 600 sample sets are used to train each regression model (\(m_{l} = 600\))

Full size image

Temperature profiles

Figure 10 depicts the true and estimated temperature profiles for example problem 1 when 600 sample sets are used to train each regression model. The red curve shows the true temperature profile and the circles show the estimated temperature values. As stated above, the biased training data greatly reduce the temperature error. In addition, the higher-order polynomial models generate more accurate solutions than the lower-order models for both the biased and unbiased data.

Fig. 10
figure 10

True and estimated temperature profiles for example problem 1. 600 sample sets are used to train each regression model (\(m_{l} = 600\))

Full size image

Summary of subsection 3.1.3

The calculation accuracies for example 1 are summarized in Fig. 9. The following findings are taken from the obtained results.

  • When comparing Figs. 8 and 9, the generalization performance of the regression models has a lot in common with their ability to solve the nonlinear problem.

  • The biased training data (\(u_{i - 1}\) is close to \(u_{i + 1}\)) greatly enhance the generalization performance of many regression models and reduce the temperature errors.

  • Figure 9 indicates that the FDM solution is the most accurate of all the results because the FDM’s discretized equation is exactly precise as illustrated in Sect. 3.1.2.3.

  • The high-order polynomial models are superior to low-order polynomial models in terms of precision.

  • The LOESS model is the most accurate of all the polynomial models.

  • The single-hidden-layer NN models with 20 or more neurons give solutions at the same or higher level of accuracy as the solution obtained from the LOESS model.

  • Additional training data are often effective to improve the regression accuracy but would be worthless if a sufficient amount of data is already provided.

  • The NN models require more training data to be fully grown than the polynomial models.

    The above results demonstrates that the following regression models can sufficiently correctly solve example problem 1 and generate a root-mean-squared temperature error smaller than 0.005 degrees even if the functional form of the true relation is different from those of the regression models.

  • The fourth- and fifth-order polynomial models and the LOESS model trained by 200 or more biased sample sets, and

  • The single-hidden-layer NNs with 20 or more neurons that are trained by 600 unbiased sets, 400 biased sets, or 600 biased sets.

3.2 Example 2: Homogeneous rod (\(k\left( u \right) = k_{0} + k_{1} u + k_{2} u^{2}\))

3.2.1 Problem statement

Let me consider a homogeneous rod having 21 points (\(n = 21\)). The thermal conductivity is expressed in the below quadratic function of \(u\).

$$k\left( u \right) = k_{0} + k_{1} u + k_{2} u^{2} ,$$
(30)

where

$$\begin{aligned} k_{0} &= 0.1 \hfill \\ k_{1} = k_{2} &= 1, \hfill \\ \end{aligned}$$
(31)

therefore,

$$k\left( u \right) = 0.1 + u + u^{2} .$$
(32)

3.2.2 Computational procedure

3.2.2.1 True solution

In a similar way to example problem 1, the analytical solution of \(u\left( x \right)\) for example 2 can be obtained in the below form,

$$\begin{aligned} u\left( x \right) & = \left( {1.4x - 0.05 + \sqrt {\left( {1.4x - 0.05} \right)^{2} - 0.15^{3} } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} \\ & \quad + \left( {1.4x - 0.05 - \sqrt {\left( {1.4x -\, 0.05} \right)^{2} - 0.15^{3} } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} - 0.5. \\ \end{aligned}$$
(33)

The true temperature for point \(i\), \(u_{i}^{\text{true}}\), is computed from the above equation,

$$\begin{array}{*{20}l} {u_{i}^{\text{true}} = \left( {0.07i - 0.12 + \sqrt {\left( {0.07i - 0.12} \right)^{2} - 0.15^{3} } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} } \hfill \\ {\quad + \left( {0.07i - 0.12 - \sqrt {\left( {0.07i - 0.12} \right)^{2} - 0.15^{3} } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} - 0.5,} \hfill \\ \end{array} \,{\text{for}}\quad i = 2, \ldots ,n - 1.$$
(34)

Additionally, from Eq. (30) and the governing equation in Eq. (4), the relational expression among \(u_{i - 1} , \, u_{i} , \, u_{i + 1}\) is derived:

$$u_{i} = \left( { - q + \sqrt {q^{2} - 0.15^{3} } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} + \left( { - q - \sqrt {q^{2} - 0.15^{3} } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} - 0.5,$$
(35)

where

$$q = - 0.25\left( {u_{i - 1}^{3} + u_{i + 1}^{3} } \right) - 0.375\left( {u_{i - 1}^{2} + u_{i + 1}^{2} } \right) - 0.075\left( {u_{i - 1} + u_{i + 1} } \right) + 0.05.$$
(36)
3.2.2.2 Presented scheme

Except for the relational expression among \(u_{i - 1} , \, u_{i} , \, u_{i + 1}\), the way to acquire training data is the same to that discussed in Sect. 3.1.2.2. I solve Eq. (35) for various sets of \(u_{i - 1}\) and \(u_{i + 1}\) to get \(u_{i}\). The thus obtained sets of \(u_{i - 1} , \, u_{i} , \, u_{i + 1}\) are used to train the regression models.

3.2.2.3 FDM

Substituting Eqs. (13) and (32) into Eq. (12), it follows that

$$u_{i} = \frac{{u_{i - 1}^{3} + u_{i + 1}^{3} + u_{i - 1}^{2} + u_{i + 1}^{2} + \left( {u_{i}^{2} + u_{i} + 0.2} \right)\left( {u_{i - 1} + u_{i + 1} } \right)}}{{u_{i - 1}^{2} + 2u_{i}^{2} + u_{i + 1}^{2} + u_{i - 1} + 2u_{i} + u_{i + 1} + 0.4}}.$$
(37)

To obtain the FDM solution, \({\mathbf{u}}^{\text{FDM}}\) in Eq. (14), I construct Eq. (37) for \(i = 2, \ldots ,n - 1\) and solve them by repeated calculation. Number of the cycles is 500.

By solving Eq. (37) for \(u_{i}\), the true relation between \(u_{i}\) and \(u_{i - 1} , \, u_{i + 1}\) is obtained in the following form

$$u_{i} = \left( { - s + \sqrt {s^{2} + r^{3} } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} + \left( { - s - \sqrt {s^{2} + r^{3} } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} + \frac{{u_{i + 1} + u_{i - 1} - 2}}{6},$$
(38)

where

$$\begin{aligned} r & = \frac{{25\left( {u_{i - 1}^{2} + u_{i + 1}^{2} } \right) + 20\left( {u_{i - 1} + u_{i + 1} } \right) - 10u_{i - 1} u_{i + 1} - 8}}{180} \\ s & = \frac{{ - 115\left( {u_{i - 1}^{3} + u_{i + 1}^{3} } \right) - 165\left( {u_{i - 1}^{2} + u_{i + 1}^{2} } \right) - 48\left( {u_{i - 1} + u_{i + 1} } \right) + 15\left( {u_{i - 1} u_{i + 1}^{2} + u_{i + 1} u_{i - 1}^{2} } \right) + 30u_{i - 1} u_{i + 1} + 2}}{540}. \\ \end{aligned}$$
(39)

The functional form of Eq. (38) is greatly different from that of the true relation in Eq. (35); there is no guarantee that the FDM can generate true solution for this problem.

The main aim of this example problem is to investigate whether the presented scheme can generate an accurate solution for a nonlinear problem that the standard FDM cannot exactly solve.

3.2.3 Results

The root-mean-squared temperature errors for example problem 2 are summarized in Fig. 11. A similar tendency is seen between Figs. 9 and 11 that shows the results for example 1. That is why I do not discuss the results for example 2 in detail.

Fig. 11
figure 11

Root-mean-squared temperature errors compared with the true solution when solving example problem 2. 600 sample sets are used to train each regression model (\(m_{l} = 600\))

Full size image

Unlike example problem 1, the FDM’s discrete equation is not perfectly the same as the true one in example 2 as explained in Sect. 3.2.2.3. Therefore, the FDM solution for example 2 generates a temperature error larger than 0.001°.

Similar to example 1, both the LOESS model trained by the biased data and the single-hidden-layer NN model can accurately solve example 2 and cause errors smaller than 0.001°.

3.3 Example 3: composite rod

3.3.1 Problem statement

Let me consider a composite rod having a periodic unit cell consisting of two materials (materials A and B) as shown in Fig. 12. The thermal conductivities of materials A and B are:

$$\begin{aligned} k_{\text{A}} & = u + 0.1 \\ k_{\text{B}} & = 0.5 \\ \end{aligned} .$$
(40)
Fig. 12
figure 12

Example problem 3: a composite rod constructing of two kinds of materials

Full size image

I simulate four types of composite rods that have 2, 5, 10, 20 unit cells and 3, 6, 11, 21 discrete points (i.e., \(n = 3 , { 6, 11, 21}\)), respectively.

Instead of the FDM analysis, I apply the homogenization method to this problem. The homogenization is one of typical multiscale modeling techniques and will be illustrated in Sect. 3.3.2.4.

The objectives of this example problem are as follows:

  • To assess the applicability of the presented scheme to a heterogeneous field,

  • To compare the presented scheme with the homogenization method when simulating various heterogeneous fields that have different numbers of unit cells, and

  • To investigate whether a regression model can approximately express the true function \(u_{i} = f\left( {u_{i - 1} ,u_{i + 1} } \right)\) for a problem whose true function in closed form does not exist (see Sect. 3.3.2.1).

3.3.2 Computational procedure

3.3.2.1 True solution

Because the analytical solution of \(u_{i}^{\text{true}}\) cannot be obtained for this example, I numerically obtain the approximate solution of \(u_{i}^{\text{true}}\). By taking equilibrium of heat flow rate at the interface between materials A and B into consideration, I derive the relational expression of \(u_{i - 1} , \, u_{i} , \, u_{i + 1}\):

$$u_{i} = \sqrt {0.35 + \left( {u_{i - 1} + 0.1} \right)^{2} + u_{i} } - \sqrt {0.35 + \left( {u_{i} + 0.1} \right)^{2} + u_{i + 1} } + u_{i + 1} .$$
(41)

\(u_{i}\) remains in both sides of the equation, which means that \(u_{i}\) is not available in closed form. Therefore, I cannot completely solve Eq. (41) for \(u_{i}\) and \(u_{i}\) is not expressible as a function of only \(u_{i - 1}\) and \(u_{i + 1}\). To determine \(u_{i}^{\text{true}}\), I formulate Eq. (41) for \(i = 2, \ldots ,n - 1\) and solve them using a nonlinear system solver (fsolve command, MATLAB software, R2014a).

3.3.2.2 Proposed scheme

Even when the rod is composed of multiple kinds of materials, I do not have to separately model the materials. In other words, I need not arrange discrete points at every material interface in the presented model. I only have to arrange points at ends of the unit cells as shown in Fig. 12. Therefore, I can decrease the total number of points in the simulated field. This is one of the main advantages of the presented scheme.

When preparing sample sets of \(u_{i - 1} , \, u_{i} , \, u_{i + 1}\), I numerically solve Eq. (41) for various kinds of sets of \(u_{i - 1}\) and \(u_{i + 1}\) to obtain \(u_{i}\). The rest of the computational procedure is excluded here because it is exactly the same as that illustrated in Sect. 3.1.2.2.

3.3.2.3 FDM

I do not apply the FDM to this numerical example.

3.3.2.4 Homogenization method

The homogenized thermal conductivity of the rod, \(k_{\text{homo}}\), can be obtained without numerical analysis. This is because \(k_{\text{homo}}\) is expressed as a harmonic mean of \(k_{\text{A}}\) and \(k_{\text{B}}\), i.e.,

$$k_{\text{homo}} = \frac{{2k_{\text{A}} k_{\text{B}} }}{{k_{\text{A}} + k_{\text{B}} }} = \frac{u + 0.1}{u + 0.6}.$$
(42)

Substituting \(k = k_{\text{homo}}\) into Eq. (4), it follows that,

$$u - 0.5\ln \left( {u + 0.6} \right) = C_{1} x + C_{0}^{''} \quad{\text{for}}\quad0 \le x \le 1.$$

By imposing the boundary conditions, Eq. (15), I obtain

$$u - 0.5\ln \left( {u + 0.6} \right) - \left( {1 + 0.5\ln 0.375} \right)x + 0.5\ln 0.6 = 0\quad{\text{for}}\quad0 \le x \le 1.$$
(43)

Subsequently, I substitute \(x = x_{i}\) (i.e., the location of discrete point \(i\)) and solve the above equation employing the nonlinear solver, the temperature at point \(i\), \(u_{i}^{\text{homo}}\), can be determined. I compare the solution of the homogenization method, \({\mathbf{u}}^{\text{homo}}\), with \({\mathbf{u}}^{\text{true}}\) and \({\mathbf{u}}^{\text{pre}}\).

$${\mathbf{u}}^{\text{homo}} = \left( {u_{2}^{\text{homo}} \cdots u_{n - 1}^{\text{homo}} } \right)^{\text{T}} .$$
(44)

3.3.3 Results

Figure 13 presents the root-mean-squared temperature errors for example problem 3. The regression models using the LOESS and the NN stably perform and provide valid solutions even though the unbiased training data are used.

Fig. 13
figure 13

Root-mean-squared temperature errors compared with the true solution when solving example problem 3. 600 unbiased sample sets are used to train each regression model (\(m_{l} = 600\)). “Homo” means the result of the homogenization method. All the NN models have a single hidden layer consisting of 25 neurons

Full size image

When the length ratio of the unit cell to the entire rod is sufficiently small (i.e., the rod has many unit cells), the composite rod is more likely to behave as a homogeneous rod. If the ratio is infinitely close to zero, it becomes a complete homogeneous rod whose conductivity is equivalent to \(k_{\text{homo}}\) in Eq. (42). That is why the error of the homogenized model increases with the reduction in the number of unit cells (i.e., \(n - 1\)). Especially when the rod is composed of only two units (i.e., \(n = 3\)), the homogenized model causes a temperature error greater than 0.01°.

Conversely, when \(n\) is smaller, the presented regression models tend to generate a smaller error. The reasons are as follows. The temperature difference between the two ends of the rod is fixed at 1°. When the rod has a small number of units, the interval between the discrete points is long and temperature difference between neighboring points is large. Additionally, all the regression models used in this problem are trained by unbiased data, which are uniformly sampled within a range of \(0 \le u_{i - 1} , \, u_{i + 1} \le 1\). Consequently, when \(n\) is small, even the unbiased data cover the wide range of temperature difference and train the regression models sufficiently thoroughly. However, when \(n\) is large, the unbiased data would include many worthless sets (\(u_{i - 1}\) is far from \(u_{i + 1}\)) and may not be effective to enhance the regression accuracy. In this case, the biased data would be more appropriate than the unbiased data. That is why all the regression models trained by the unbiased data cause non-negligible errors in the case that \(n = 21\).

Because the presented approach simulates the composite rod without homogenization, the approach does not generate error due to the size effect. Therefore, the presented model using a proper regression function would be able to generate an accurate solution as long as a sufficient amount of valid training sample sets are provided.

4 Conclusions

This manuscript proposed a rapid and low-cost nonlinear numerical solver based on a regression analysis approach. Because the solver requires no interactive and coupled multiscale computation, it can solve a nonlinear problem without iterative multiscale simulation for each convergence computation.

In the proposed solver, a simulation field is spatially discretized and represented by a finite number of points. On the basis of training data that are obtained from either pre-analyses or experiments, I construct and train regression models that express nonlinear relationships among neighboring points. Each regression model functions as a discretized equation for nonlinear differential equation(s) governing the field. This manuscript employed artificial NNs and standard polynomial functions as the regression models. By constructing the “regression discrete equations” for all points in the field and solving them, all dependent-variable values can be obtained.

I applied the presented solver to nonlinear one-dimensional steady-state heat conduction fields. As a result, as long as a sufficient amount of valid training data was prepared, the presented numerical models (which were constructed by assembling the regression functions based on the high-order polynomials, LOESS, and NNs) provided sufficiently precise solutions for the following example problems:

  • A problem where functional form of the true relation among temperature values at neighboring three points (\(u_{i - 1} , \, u_{i} , \, u_{i + 1}\)) is different from those of the regression models (Sect. 3.1),

  • A problem that the standard FDM cannot exactly solve (Sect. 3.2), and.

  • A problem where \(u_{i}\) is not expressible as a function of \(u_{i - 1}\) and \(u_{i + 1}\) (Sect. 3.3).

However, to put it the other way around, the above-presented models were invalid and generated a non-negligible computational error when training data were insufficient or included many worthless sample sets.

When analyzing a heterogeneous field having a periodic microstructure, the homogenization approach generally causes an error related to the scale size effect. However, even if the scale size ratio of the microstructure to the entire field is not negligible, the solutions of the presented scheme are not affected by the ratio. This is because the presented technique simulates the entire field without homogenization.

Note that the current work is only a first attempt at presenting neural network-based discretization scheme for nonlinear differential equations. This article focuses on only quite simple nonlinear problems; there is no guarantee that it would generate an accurate solution for any nonlinear problem.

By combining the presented scheme with deep learning techniques (i.e., a neural network consisting of many hidden layers), I may be able to solve highly complicated problems related to elastoplasticity, fracture, and multiphysics at low computational cost. Nonlinear solver using deep learning methodology can be developed as a future task.