1 Introduction

As we known, time delays inevitably exist in biological and artificial neural networks because of the finite switching speed of neurons and amplifiers [1], which can also affect the stability of neural network systems and may lead to some complex dynamic behaviors such as oscillation, chaos and instability. In reality, time delays involving in neural networks may be proportional in theory, that is to say, the proportional delay function \(\tau (t)=t- qt\) is a monotonically increasing function with the increase of time \(t > 0\), where q is a constant and satisfies \(0< q < 1\). In particular, the proportional delay is one of the many objective-existent delay types such as the proportional delay usually is required in web quality of service routing decision, which is because it is convenient to control the networks running time according to the network allowed delays [2,3,4,5,6,7]. Moreover, the systems with proportional delays have many interesting applications, for example, collection of current by the pantograph of an electric locomotive [8], electrodynamics [9], nonlinear dynamics [10, 11], and probability theory on algebraic structures [12].

On other hand, in the aspect of studying the almost periodic problems for dynamic systems and its related topics, the existence of almost periodic, asymptotically almost periodic, pseudo-almost periodic solutions become the most attractive hot issues in qualitative theory of differential equations due to their applications, especially in biology, economics and physics (see [13,14,15]). In particular, people have paid much attention to the study of existence and stability of almost periodic solutions and pseudo almost periodic solutions for shunting inhibitory cellular neural networks (SICNNs) with time-varying delays and distributed delays because of its successful applications in variety of areas such as signal processing, pattern recognition, chemical processes, nuclear reactors, biological systems, static image processing, associative memories, optimization problems and so on (see [16,17,18,19,20,21,22,23,24,25,26,27,28] and the references cited therein). However, to the best of our knowledge, there is no result on the existence of pseudo almost periodic solutions for SICNNs with proportional delays.

Motivated by the above discussions, the main purpose of this paper is to establish some sufficient conditions on the existence and exponential stability of pseudo almost periodic solutions for the following SICNNs with multi-proportional delays:

$$\begin{aligned} \left\{ \begin{array}{ll} x '_{ij}(t)=-a_{ij}(t){x}_{ij}(t)-\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(x_{kl}(q_{kl} t) )x_{ij}(t)+L_{ij}(t),\\ {x}_{ij}(s)=\varphi _{ij }(s),s\in [q_{ij}t_{0}, \ t_{0}], t_{0}>0, \end{array}\right. \end{aligned}$$
(1.1)

for \(t\ge t_{0}\) and \(ij \in J:=\{11, \ldots , 1n, 21, \ldots , 2n, \ldots , m1, \ldots , mn \}\), where \(C_{ij}\) denotes the cell at the (i, j) position of the lattice, the r-neighborhood \(N_{r}(i,j)\) of \(C_{ij}\) is

$$\begin{aligned} N_{r}(i,j)=\{C_{kl}:\max (|k-i|,|l-j|)\le r,1\le k\le m,1\le l\le n\}. \end{aligned}$$

\(x_{ij}\) is the activity of the cell \(C_{ij}, L_{ij}(t)\) is the external input to \(C_{ij}, a_{ij}(t)\) represents the passive decay rate of the cell activity, \(C_{ij}^{kl}(t)\) is the connection or coupling strength of postsynaptic activity of the cell transmitted to the cell \(C_{ij}\), and the activity function \(f(x_{kl})\) is a continuous function representing the output or firing rate of the cell \(C_{kl}, q _{ij}, i j \in J, \) are proportional delay factors and satisfy \(0 < q _{ij} \le 1\), and \(q _{ij} t=t -(1-q _{ij})t\), in which \(\tau _{ij}(t)=(1-q _{ij})t\) is the transmission delay function, and \((1-q _{ij})t \rightarrow \infty \) as \(q_{ ij}\ne 1, t \rightarrow \infty , \varphi _{ij }(s)\) denotes the initial value of \(x _{ij}(s) \) at \(s \in [q_{ij}t_{0}, \ t_{0}] ,\) and \( {\varphi }_{ij }\in C([q_{ij}t_{0}, \ t_{0}], \mathbb {R}) \). It can be shown by the method-of-steps given in Hale and Verduyn Lunel [29] that the solution of (1.1) exists and is unique.

The remaining of this paper is organized as follows. In Sect. 2, we give some basic definitions and lemmas, which play an important role in Sect. 3 to establish the existence of pseudo almost periodic of (1.1). Here we also study the global exponential stability of pseudo almost periodic solutions. The paper concludes with an example to illustrate the effectiveness of the obtained results by numerical simulation.

2 Preliminaries

In this section, we shall first recall some basic definitions, lemmas which are used in what follows.

Let l be a positive integer, we denote by \(\mathbb {R}^{l}\) \(\left( \mathbb {R}=\mathbb {R}^{1}\right) \) the set of all \(l-\)dimensional real vectors (real numbers). For any \( \{x_{ij} \}=(x_{11} , \ x_{12} , \ldots , x_{m n} ) \in \mathbb {R}^{ mn}\), we let |x| denote the absolute-value vector given by \(|x|=\{|x_{ij }|\} \), and define \(\Vert x \Vert =\max \nolimits _{ ij\in J} |x_{ij } | \). A matrix or vector \(A\ge 0\) means that all entries of A are greater than or equal to zero. \(A>0\) can be defined similarly. For matrices or vectors \(A_{1}\) and \(A_{2}, A_{1}\ge A_{2}\) (resp. \(A_{1}> A_{2}\)) means that \(A_{1}- A_{2}\ge 0\) (resp. \(A_{1}- A_{2}>0\)). \(BC\left( \mathbb {R},\mathbb {R}^{l}\right) \) denotes the set of bounded and continuous functions from \(\mathbb {R}\) to \(\mathbb {R}^{l}\), and \(BUC\left( \mathbb {R},\mathbb {R}^{l}\right) \) denotes the set of bounded and uniformly continuous functions from \(\mathbb {R}\) to \(\mathbb {R}^{l}\). Note that \(\left( BC\left( \mathbb {R},\mathbb {R}^{l}\right) , \Vert \cdot \Vert _{\infty }\right) \) is a Banach space, where \(\Vert \cdot \Vert _{\infty }\) denotes the supremum norm \(\Vert \varphi \Vert _{\infty } := \sup \nolimits _{ t\in \mathbb {R}} \Vert \varphi (t)\Vert \). For \(h\in BC(\mathbb {R},\mathbb {R} )\), let \(h^+\) and \(h^-\) be defined as

$$\begin{aligned}h^{+}=\sup \limits _{t\in \mathbb {R}}|h(t)|, ~~ h^{-}=\inf \limits _{t\in \mathbb {R}}|h(t)| .\end{aligned}$$

We denote by \(AP\left( \mathbb {R},\mathbb {R}^{l}\right) \) the set of the almost periodic functions from \(\mathbb {R}\) to \(\mathbb {R}^{l}\). Besides, define the class of functions \(PAP_{0}\left( \mathbb {R},\mathbb {R}^{l}\right) \) as follows:

$$\begin{aligned}\left\{ \varphi \in BC\left( \mathbb {R},\mathbb {R}^{l}\right) |\lim \limits _{T\rightarrow +\infty }\frac{1}{2T}\int _{-T}^{T}|\varphi (t)|dt=\mathbf {0}\right\} .\end{aligned}$$

A function \(u\in {BC\left( \mathbb {R},\mathbb {R}^{l}\right) }\) is called pseudo almost periodic if it can be expressed as

$$\begin{aligned}u=h+\varphi ,\end{aligned}$$

where \(h\in {AP\left( \mathbb {R},\mathbb {R}^{l}\right) }\) and \(\varphi \in {PAP_{0}\left( \mathbb {R},\mathbb {R}^{l}\right) }.\) The collection of such functions will be denoted by \(PAP\left( \mathbb {R},\mathbb {R}^{l}\right) .\) Then, \(\left( PAP\left( \mathbb {R},\mathbb {R}^{l}\right) ,\Vert .\Vert _{\infty }\right) \) is a Banach space and \(AP\left( \mathbb {R},\mathbb {R}^{l}\right) \) is a proper subspace of \(PAP(\mathbb {R},\mathbb {R}^{n})\) [13, 14].

For \(ij\in J,\) it will be assumed that \(c_{i} :\mathbb {R}\rightarrow \mathbb {R}\) is an almost periodic function, \( \eta _{i }: \mathbb {R}\rightarrow [0, \ +\infty ), I_{i}, \ a_{ij}, \ b_{ij} :\mathbb {R}\rightarrow \mathbb {R}\) are pseudo almost periodic functions.

We also make the following assumptions which will be used later.

  • \((\mathbf {H_{0}})\) for \(ij \in J, M[a_{ij}]=\lim \nolimits _{T\rightarrow +\infty }\frac{1}{T}\int _{t}^{t+T}a_{ij}(s)ds>0, \) and there exist a bounded continuous function \(\tilde{a}_{ij} :\mathbb {R}\rightarrow (0, \ +\infty )\) and a positive constant \(K_{ij} \) such that

    $$\begin{aligned}e ^{ -\int _{s}^{t}a_{ij}(u)du}\le K_{ij} e ^{ -\int _{s}^{t}\tilde{a} _{ij}(u)du}, \quad \ \text{ for } \text{ all } t,s\in \mathbb {R} \text{ and } t-s\ge 0.\end{aligned}$$

  • \((\mathbf {H_{1}})\) there exist constants \(M _{f} \) and \(L ^ {f} \) such that

    $$\begin{aligned} |f(u )-f(v )|\le L ^{f} |u -v |, \ |f(u ) |\le M_{f}, \quad { \ \text {for all}} \ u , v \in \mathbb {R}. \end{aligned}$$

  • \((\mathbf {H_{2}})\) there exist positive constants L and \(\kappa \) such that

    $$\begin{aligned}\{L\}\ge \left\{ \sup \limits _{t\in \mathbb {R}}\int _{-\infty }^{t}e^{-\int _{s}^{t}a_{ij}(u)du}| L_{ij}(s)| ds\right\} , \end{aligned}$$
    $$\begin{aligned}\sup \limits _{t\in \mathbb {R}}\left\{ -\frac{\kappa }{\kappa +L}\tilde{a}_{ij}(t)+K_{ij} \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl} (t)|( L^{f}(\kappa +L)+|f(0)|)\right\} <0, \end{aligned}$$

and

$$\begin{aligned}\delta _{ij}=\sup \limits _{t\in \mathbb {R}}\frac{K_{ij} \sum \nolimits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl} (t)| (M_{f} +L^{f} (\kappa +L))}{\tilde{a}_{ij}(t)}<1,\ ij \in J.\end{aligned}$$

Lemma 2.1

(see [5, Lemma 2.1]) Let \(\varphi (t)\in PAP(\mathbb {R},\mathbb {R} ) \), and \(\beta \in \mathbb {R}\) be a constant. Then, \(\varphi (\beta t)\in PAP(\mathbb {R},\mathbb {R} )\).

3 Main Results

In this section, we establish sufficient conditions on the existence and exponential stability of pseudo almost periodic solutions of (1.1).

Theorem 3.1

Let \((H_{0}), (H_{1})\) and \((H_{2})\) hold. Then, there exists a unique continuously differentiable pseudo almost periodic solution of system (1.1).

Proof

Let \( \varphi \in PAP(\mathbb {R},\mathbb {R}^{mn})\), it follows from Lemma 2.1 that

$$\begin{aligned} \varphi _{kl}(q _{kl}t )\in PAP(\mathbb {R},\mathbb {R}), kl\in J. \end{aligned}$$

In view of \((H_{1})\) and Corollary 5.4 in [14, p. 58], we have

$$\begin{aligned} f (\varphi _{kl}(q _{kl}t ))\in PAP(\mathbb {R},\mathbb {R}), kl\in J. \end{aligned}$$
(3.1)

Then, notice that \( M[a_{ij}(t) ]>0, \ ij\in J \), in view of (3.1), it follows from Theorem 2.3 in [30] that the nonlinear pseudo almost periodic differential equations,

$$\begin{aligned} x_{ij}'(t) = -a_{ij}(t) x_{ij} (t )-\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f(\varphi _{kl}(\varphi _{kl}(t ) ))\varphi _{ij}(t)+L_{ij}(t), ij\in J, \qquad \end{aligned}$$
(3.2)

has exactly one pseudo almost periodic solution:

$$\begin{aligned} x^{\varphi }(t)= & {} \left\{ x^{\varphi }_{ij}(t)\right\} \nonumber \\= & {} \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{ij}(u)du}\left[ -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)f(\varphi _{kl}(\varphi _{kl}(s ) ))\varphi _{ij}(s) +L_{ij}(s)\right] ds\right\} . \nonumber \\ \end{aligned}$$
(3.3)

Let \(\varphi ^{0}(t)=x ^{0}(t)\). Then,

$$\begin{aligned} \varphi ^{0}(t)= & {} \left\{ \varphi ^{0}_{ij}(t)\right\} =\left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}a_{ij}(u)du} L_{ij}(s) ds\right\} \\&\in PAP(\mathbb {R},\mathbb {R}^{mn}), \ L\ge \Vert \varphi ^{0}\Vert _{\infty }. \end{aligned}$$

Set

$$\begin{aligned} \ \ \ \mathbf {B} =\left\{ \varphi |\varphi \in PAP(\mathbb {R},\mathbb {R}^{mn}), \Vert \varphi -\varphi ^{0}\Vert _{\infty }\le \kappa \right\} . \end{aligned}$$

It follows that \(\mathbf {B}\) is a bounded closed subset of \(PAP(\mathbb {R},\mathbb {R}^{mn})\). If \(\varphi \in \mathbf {B} \) , then

$$\begin{aligned} \left\| \varphi \right\| _{\infty }\le \left\| \varphi -\varphi ^{0}\right\| _{\infty }+\left\| \varphi ^{0}\right\| _{\infty }\le \kappa +L. \end{aligned}$$
(3.4)

Now, we define a mapping \(T:\mathbf {B} \rightarrow PAP(\mathbb {R},\mathbb {R}^{mn})\) by setting

$$\begin{aligned} (T\varphi )(t)=x^{\varphi }(t), \ \ \ \forall \varphi \in \mathbf {B} .\end{aligned}$$

We next prove that the mapping T is a contraction mapping of the \(\mathbf {B} \).

First we show that for any \(\varphi \in \mathbf {B} , \ T(\varphi ) =x^{\varphi } \in \mathbf {B} \).

Note that

$$\begin{aligned} \left| T(\varphi )(t)- \varphi ^{0}(t)\right|\le & {} \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}\tilde{a}_{ij}(u)du} K_{ij} \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl} (s)|(|f(\varphi _{kl}(q_{kl} s ))\right. \\&\left. \quad -f(0)|+|f(0)|)\Vert \varphi \Vert _{\infty } ds \right\} \\\le & {} \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}\tilde{a}_{ij}(u)du} K_{ij} \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl} (s)|( L^{f}(\kappa +L)\right. \\&\left. \quad +\,|f(0)|) ds\Vert \varphi \Vert _{\infty }\right\} \\\le & {} \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}\tilde{a}_{ij}(u)du} \frac{\kappa }{\kappa +L}\tilde{a}_{ij}(s) ds(\kappa +L)\right\} \\\le & {} \left\{ \kappa \right\} , \end{aligned}$$

i.e., \( T(\varphi ) =x^{\varphi } \in \mathbf {B} \).

Second, we show that T is a contract operator.

In fact, in view of (3.3), (3.4), \((H_{0}), (H_{1})\) and \((H_{2})\), for \( \varphi , \psi \in \mathbf {B} \), we have

$$\begin{aligned}&|T(\varphi (t))-T(\psi (t))| \\&\quad \le \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}\tilde{a}_{ij}(u)du}K_{ij} \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl} (s)|(|f(\varphi _{kl}(q_{kl} s ))||\varphi _{ij}(s)-\psi _{ij}(s))|\right. \\&\quad \quad \quad \left. +\,|f(\varphi _{kl}(q_{kl} s )) - f(\psi _{kl}(q_{kl} s ))|| \psi _{ij}(s))|) ds \right\} \\&\quad \le \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}\tilde{a}_{ij}(u)du}K_{ij} \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl} (s)| (M_{f} +L^{f} \Vert \psi \Vert _{\infty })ds \Vert \varphi -\psi \Vert _{\infty } \right\} \\&\quad \le \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}\tilde{a}_{ij}(u)du}K_{ij} \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl} (s)| (M_{f} +L^{f} (\kappa +L))ds \Vert \varphi -\psi \Vert _{\infty } \right\} \\&\quad \le \left\{ \int _{-\infty }^{t}e^{-\int _{s}^{t}\tilde{a}_{ij}(u)du}\delta _{ij} \tilde{a}_{ij}(s) ds \Vert \varphi -\psi \Vert _{\infty } \right\} \\&\quad \le \left\{ \delta _{ij}\Vert \varphi -\psi \Vert _{\infty } \right\} , \end{aligned}$$

which yields

$$\begin{aligned} \Vert T (\varphi )-T (\psi )\Vert _{\infty } \le \max \limits _{ij\in J} \delta _{ij}\Vert \varphi -\psi \Vert _{\infty }, \end{aligned}$$

which implies that the mapping \(T :\mathbf {B} \longrightarrow \mathbf {B} \) is a contraction mapping. Therefore, the mapping T possesses a unique fixed point

$$\begin{aligned}x^{* }=\left\{ x_{ij}^{* }(t)\right\} \in B, \ Tx^{*}=x^{*}.\end{aligned}$$

By (3.2) and (3.3), \(x^{* } \) satisfies (3.2). So (1.1) has at least one pseudo almost periodic solution \(x^{* } \) . The proof of Theorem 3.1 is now completed.

Theorem 3.2

Let \((H_{0})\) and \((H_{1})\) hold. Moreover, assume that there exist positive constants \(\lambda _{0}, \ L \) and \(\kappa \) such that \((H_{2})\) holds, and

$$\begin{aligned} \delta _{ij}^{*}=\sup \limits _{t \ge t_{0}}\frac{K_{ij} \sum \nolimits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl} (t)| \left( M_{f} +L^{f} (\kappa +L)e^{ \lambda _{0} (1-q_{kl})t }\right) }{\tilde{a}_{ij}(t)}<1,\ ij \in J. \qquad \end{aligned}$$
(3.5)

Then system (1.1) has at least one pseudo almost periodic solution \(x^{*}(t)\). Moreover, \(x^{*}(t)\) is globally exponentially stable, i.e., for arbitrary solution x(t) of (1.1), there exist two positive constants \(\lambda \) and \(\bar{M}\) such that

$$\begin{aligned} |x_{ij} (t)-x_{ij}^{*}(t) | \le \bar{M} \max \limits _{ij \in J }\left\{ \max \limits _{t \in [q_{ij}t_{0} , \ t_{0}]}|\varphi _{ij} (t)-x^{*}_{ij}(t) |\right\} e^{-\lambda t} \quad { \ \text {for all} } t \ge t_{0}, \ ij\in J. \end{aligned}$$

Proof

Obviously, by Theorem 3.1, (1.1) has a pseudo almost periodic solution \(x^{*}(t)=\left\{ x^{*}_{ij}(t)\right\} \). Suppose that \( x(t)=\{x_{ij}(t)\} \) is an arbitrary solution of (1.1) associated with initial value \( \varphi (t)=\{\varphi _{ij}(t)\} \) satisfying the second equation of (1.1).

Let \( y (t) = \{y_{ij}(t)\} = \{ x_{ij}(t) -x_{ij}^{*}(t) \}.\) Then

$$\begin{aligned} y_{ij}'(t)= & {} -a_{ij}(t)y_{ij }(t )\nonumber \\&\quad -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)(f(x_{kl}(q_{kl} t ))x_{ij}(t)\nonumber \\&\quad -f(x^{*}_{kl}(q_{kl} t ))x^{*}_{ij}(t))\ ,\ ij\in J. \end{aligned}$$
(3.6)

From (3.5), we can choose a constant \(\lambda \in (0, \ \min \{ \lambda _{0}, \ \min \nolimits _{ij\in J}\inf \nolimits _{t\ge t_{0}}\tilde{a}_{ij} (t)\}) \) such that

$$\begin{aligned}&\sup \limits _{t\ge t_{0}}\left\{ \lambda -\tilde{a}_{ij}(t) + K_{ij} \left[ \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl}(t)| \left( M^{f} +L^{f} (\kappa +L)e^{ \lambda (1-q_{kl})t }\right) \right] \right\} < 0 , \nonumber \\&\quad ij\in J.\end{aligned}$$
(3.7)

Let

$$\begin{aligned} \Vert \varphi \Vert _{\xi }= \max \limits _{ij \in J }\left\{ \max \limits _{t \in [q_{ij}t_{0} , \ t_{0}]}|\varphi _{ij} (t)-x^{*}_{ij}(t) | \right\} . \end{aligned}$$
(3.8)

For any \(\varepsilon >0\), we obtain

$$\begin{aligned} |y_{ij}(t) |< (\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (t-t_{0})}<M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (t-t_{0})} \quad \text{ for } \text{ all } t \in [q_{ij}t_{0} , \ t_{0}], \end{aligned}$$

and

$$\begin{aligned} \Vert y (t) \Vert< (\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (t-t_{0})}<M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (t-t_{0})} \quad \text{ for } \text{ all } t \in \left[ \max \limits _{ij \in J }q_{ij}t_{0} , \ t_{0}\right] ,\end{aligned}$$

where \(M=\max \nolimits _{ij \in J }K_{ij}+1\).

In the following, we will show

$$\begin{aligned} \Vert y(t)\Vert <M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (t-t_{0})} \quad \ \hbox {for} \ \hbox {all} \ t > t_{0} . \end{aligned}$$
(3.9)

Otherwise, there must exist \(ij \in J\) and \(\theta >t_{0} \) such that

$$\begin{aligned} \Vert y(\theta )\Vert = |y_{ij}(\theta ) | =M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (\theta -t_{0})}, \end{aligned}$$
(3.10)

and

$$\begin{aligned} |y_{kl}(t) | < M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (t-t_{0})} \quad \text{ for } \text{ all } t \in [q_{kl}t_{0} , \theta ), \ kl\in J. \end{aligned}$$
(3.11)

Note that

$$\begin{aligned} y_{ij} (t)= & {} y_{ij} (t_{0}) e ^{-\int _{t_{0}}^{t}a_{ij}(u)du}+ \int _{t_{0}}^{t}e ^{ -\int _{s}^{t}a_{ij}(u)du}\nonumber \\&\times \bigg [ -\sum \limits _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(s)(f(x_{kl}(q_{kl} s ))x_{ij}(s)-f(x^{*}_{kl}(q_{kl} s ))x^{*}_{ij}(s))\bigg ] ds, \nonumber \\&t\in [t_{0}, \ \theta ]. \end{aligned}$$
(3.12)

With the help of (3.7), (3.8) and (3.11), we have

$$\begin{aligned} |y_{ij} (\theta )|\le & {} (\Vert \varphi \Vert _{\xi }+\varepsilon )K_{ij}e ^{-\int _{t_{0}}^{\theta }\tilde{a}_{ij}(u)du}+ \int _{t_{0}}^{\theta }e ^{ -\int _{s}^{\theta }\tilde{a}_{ij}(u)du}K_{ij}\bigg [ \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl}(s)|\\&\times (|f(x_{kl}(q_{kl} s ))||x_{ij}(s)-x^{*}_{ij}(s)|+|f(x_{kl}(q_{kl} s ))-f(x^{*}_{kl}(q_{kl} s ))||x^{*}_{ij}(s)|)\bigg ]ds \\\le & {} (\Vert \varphi \Vert _{\xi }+\varepsilon )K_{ij}e ^{-\int _{t_{0}}^{\theta }\tilde{a}_{ij}(u)du}+ \int _{t_{0}}^{\theta }e ^{ -\int _{s}^{\theta }\tilde{a}_{ij}(u)du}K_{ij}\bigg [ \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl}(s)|\\&\times (M^{f}|y_{ij}(s) |+L^{f}|y_{kl}(q_{kl} s ) ||x^{*}_{ij}(s)|)\bigg ]ds \\\le & {} (\Vert \varphi \Vert _{\xi }+\varepsilon )K_{ij}e ^{-\int _{t_{0}}^{\theta }\tilde{a}_{ij}(u)du}+ \int _{t_{0}}^{\theta }e ^{ -\int _{s}^{\theta }\tilde{a}_{ij}(u)du}K_{ij}\bigg [ \sum \limits _{C_{kl}\in N_{r}(i,j)}|C_{ij}^{kl}(s)|\\&\times (M^{f}M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (s-t_{0})}+L^{f}M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (q_{kl}s-t_{0})} (\kappa +L))\bigg ]ds \\\le & {} (\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (\theta -t_{0})}K_{ij}e ^{-\int _{t_{0}}^{\theta }(\tilde{a}_{ij}(u)-\lambda )du}\\&+ \int _{t_{0}}^{\theta }e ^{ -\int _{s}^{\theta }(\tilde{a}_{ij}(u)-\lambda )du} (\tilde{a}_{ij}(s)-\lambda )ds M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (\theta -t_{0})}\\= & {} M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (\theta -t_{0})}\bigg [\left( \frac{K_{ij}}{M}-1\right) e ^{-\int _{t_{0}}^{\theta }(\tilde{a}_{ij}(u)-\lambda )du}+ 1 \bigg ] \\< & {} M(\Vert \varphi \Vert _{\xi }+\varepsilon )e^{-\lambda (\theta -t_{0})}, \end{aligned}$$

which contradicts (3.10). Hence, (3.9) holds. Letting \(\varepsilon \longrightarrow 0^{+}\), we have from (3.9) that

$$\begin{aligned} |y_{ij}(t) | \le M\Vert \varphi -x^{*}\Vert _{\xi }e^{-\lambda (t-t_{0})} \quad \text{ for } \text{ all } t \ge t_{0} , \quad ij\in J, \end{aligned}$$

and

$$\begin{aligned} |x_{ij} (t)-x_{ij}^{*}(t) | \le \bar{M} \max \limits _{ ij\in J }\left\{ \max \limits _{t \in [q_{ij}t_{0} , \ t_{0}]}|\varphi _{ij} (t)-x_{ij}^{*}(t) |\right\} e^{-\lambda t} \text{ for } \text{ all } t \ge t_{0}, \quad ij\in J, \end{aligned}$$

where \(\bar{M}=Me^{ \lambda t_{0} }\). This completes the proof.

4 An Example

Example 4.1

Consider the following non-autonomous SICNNs with multi-proportional delays:

$$\begin{aligned} \frac{dx_{ij}}{dt}=-a_{ij}(t) x_{ij}(t)- \sum _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t) f\left( x_{kl}\left( \frac{1}{2} t \right) \right) x_{ij}(t) +L_{ij}(t), \end{aligned}$$
(4.1)

where \(t\ge 1, \ f (x) =\frac{1}{50} (|x+1|-|x-1|) , x_{ij}(s)=\varphi _{ij}(s), s\in \left[ \frac{1}{2}, \ 1\right] , \) and \( {\varphi }_{ij }\in C\left( \left[ \frac{1}{2}, \ 1\right] ,\mathbb {R}\right) \ i, j=1,2,3.\) Let

$$\begin{aligned} \left[ \begin{array}{ccc} a_{11}&{}a_{12}&{}a_{13}\\ a_{21}&{}a_{22}&{}a_{23}\\ a_{31}&{}a_{32}&{}a_{33} \end{array} \right]= & {} \frac{1}{4}\left[ \begin{array}{ccc} 1+2 \sin 400t &{}1+2 \sin 400t&{}3+4 \sin 400t\\ 3+4 \sin 400t&{}1+2 \sin 400t&{}3+4 \sin 400t\\ 3+4 \sin 400t&{}1+2 \sin 400t&{}3+4 \sin 400t \end{array} \right] , \end{aligned}$$
(4.2)
$$\begin{aligned} \left[ \begin{array}{ccc} C_{11}&{}C_{12}&{}C_{13}\\ C_{21}&{}C_{22}&{}C_{23}\\ C_{31}&{}C_{32}&{}C_{33} \end{array} \right]= & {} e^{-|t|}\left[ \begin{array}{ccc} 0.01 \sin t &{}0.02 \sin t&{}0.01 \sin t\\ 0.02 \sin t&{}0&{}0.02 \sin t\\ 0.01\sin t&{}0.02\sin t&{}0.01\sin t \end{array} \right] , \end{aligned}$$
(4.3)
$$\begin{aligned} \left[ \begin{array}{ccc} L_{11}&{}L_{12}&{}L_{13}\\ L_{21}&{}L_{22}&{}L_{23}\\ L_{31}&{}L_{32}&{}L_{33} \end{array} \right]= & {} \left[ \begin{array}{lll} \sin \sqrt{2}t &{} \cos t&{}1\\ \cos ^{2} t-\frac{1}{1+t^2}&{} \sin t&{}1\\ \cos t-\frac{1}{1+t^2}&{} \sin t&{}1 \end{array} \right] . \end{aligned}$$
(4.4)

Obviously,

$$\begin{aligned}&\left[ \begin{array}{ccc} \tilde{a}_{11}&{}\tilde{a}_{12}&{}\tilde{a}_{13}\\ \tilde{a}_{21}&{}\tilde{a}_{22}&{}\tilde{a}_{23}\\ \tilde{a}_{31}&{}\tilde{a}_{32}&{}\tilde{a}_{33} \end{array} \right] =\frac{1}{4}\left[ \begin{array}{ccc} 1 &{}1 &{}3 \\ 3 &{}1 &{}3 \\ 3 &{}1 &{}3 \end{array} \right] , \{ K_{ij}\}\le \left[ \begin{array}{ccc} e^{\frac{1}{400}} &{} e^{\frac{1}{400}} &{}2e^{\frac{1}{400}} \\ 2e^{\frac{1}{400}} &{} e^{\frac{1}{400}} &{}2e^{\frac{1}{400}} \\ 2e^{\frac{1}{400}} &{} e^{\frac{1}{400}} &{}2e^{\frac{1}{400}} \end{array} \right] , \\ M_{f}= & {} 0.04, \ q_{ij}=\frac{1}{2}, \ L_{f}= 0.04, \ \sum _{C_{kl}\in N_{1}(3.3)}|C_{33}^{kl}(t)| \le 0.05 e^{-|t|},\\&\sum _{C_{kl}\in N_{1}(1.1)}|C_{11}^{kl}(t)| \le 0.05 e^{-|t|}, \sum _{C_{kl}\in N_{1}(1.2)}| C_{12}^{kl} (t)| \le 0.08 e^{-|t|}, \\&\sum _{C_{kl}\in N_{1}(1.3)}| C_{13}^{kl} (t)| \le 0.05 e^{-|t|}, \\&\sum _{C_{kl}\in N_{1}(2.2)}|C_{22}^{kl} (t)| \le 0.12 e^{-|t|}, \ \sum _{C_{kl}\in N_{1}(2.3)}|C_{23}^{kl} (t)| \le 0.08 e^{-|t|},\\&\sum _{C_{kl}\in N_{1}(2.1)}|C_{21}^{kl}(t)| \le 0.08 e^{-|t|}, \sum _{C_{kl}\in N_{1}(3.1)}|C_{31}^{kl}(t)| \le 0.05 e^{-|t|}, \\&\sum _{C_{kl}\in N_{1}(3.2)}|C_{32}^{kl}(t)| \le 0.08 e^{-|t|}, \end{aligned}$$
Fig. 1
figure 1

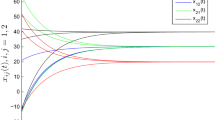
Numerical solutions to system (4.1) with three groups of different initial values

Full size image

where \( ij \in J=\{11,12,13,21,22,23,31,32,33\}.\) Let \(L=5, \lambda _{0}=2, \kappa =1, q_{ij}=\frac{1}{2}, \ L^{f}_{i}=L^{g}_{i} =\frac{1}{18},\ K_{i}=e^{3}, \tilde{a}_{ij} =1, i,j=1,2,\) one can easily check that system (4.1) satisfies \((H_{0}), (H_{1}), (H_{2})\) and (3.5). By the consequence of Theorem 3.2, it follows that system (4.1) has exactly one pseudo almost periodic solution \(x^{*}(t)\). Moreover, all solutions of solutions for (4.1) converge exponentially to \(x^{*}(t)\) . The exponential convergent rate is about 0.001. The fact is verified by the numerical simulation in Fig. 1 and there are three different initial values which are \(\varphi _{11}\equiv 2.1, \varphi _{12}\equiv -2.3\),\(\varphi _{13}\equiv 2.4, \varphi _{21}\equiv 2.2, \varphi _{22}\equiv 2.5, \varphi _{23}\equiv 2.3, \varphi _{31}\equiv -2.1, \varphi _{32}\equiv -2.2, \varphi _{33}\equiv -2.5\); \(\varphi _{11}\equiv 2.2, \varphi _{12}\equiv -2.1\),\(\varphi _{13}\equiv 2.5, \varphi _{21}\equiv 2.4, \varphi _{22}\equiv 2.2, \varphi _{23}\equiv 2.1, \varphi _{31}\equiv -2.3, \varphi _{32}\equiv -2.4, \varphi _{33}\equiv -2.3\) and \(\varphi _{11}\equiv -2.2, \varphi _{12}\equiv 2.1\),\(\varphi _{13}\equiv -2.5, \varphi _{21}\equiv -2.4, \varphi _{22}\equiv -2.2, \varphi _{23}\equiv -2.1, \varphi _{31}\equiv 2.3, \varphi _{32}\equiv 2.4, \varphi _{33}\equiv -2.3,\) respectively.

Remark 4.1

To the best of our knowledge, there is no research on the globally exponential convergence of the pseudo almost periodic solution of SICNNs with multi-proportional delays. We also mention that all results in the reference [16,17,18,19,20,21,22,23,24,25,26,27,28] cannot be applied to imply that all solutions for (4.1) converge exponentially to \(x^{*}(t)\). In particular, we employ a novel proof to establish some criteria to guarantee the existence and exponential stability of pseudo almost periodic solutions for SICNNs with multi-proportional delays. We expect to extend this work to other neural networks models with multi-proportional delays.