1 Introduction

During the past several years, dynamics of delayed neural networks have been extensively studied because of their important applications in many areas such as associative memory, pattern recognition and nonlinear optimization problems, see [1–5]. Many researchers have a lot of contributions to these subjects. However, most previous works on delayed neural networks have predominantly concentrated on stability analysis and periodic oscillations, see [6–11]. It is well known that chaos synchronization of dynamics systems has important applications in many fields including biological systems, parallel image processing, neural networks, information science, see [12–16]. Moreover, it has been shown that if the network’s parameters and time delays are appropriately chosen, the delayed neural networks can exhibit some complicated dynamics and even chaotic behaviors [17, 18]. Hence, it has attracted many scholars to study the synchronization of chaotic delayed neural networks and many excellent papers and monographs dealing with synchronization of chaotic systems have been published [19–23, 27–33, 38–41]. For instance, Cheng et al. [20] investigated the exponential synchronization problem for a class of chaotic neural networks with or without constant delays via Lyapunov stability method and the Halanay inequality. Xia et al. [22] studied the asymptotical synchronization for a class of coupled identical Yang–Yang type fuzzy cellular neural networks with time-varying delays via Lyapunov–Krasovskii functional and linear matrix inequality (LMI) approach.

It is well known that due to the finite speeds of the switching and transmission of signals [7, 35], time delays which can cause instability and oscillations in system do exist in a working network and thus should be incorporated into the models. Most of the existing works on delayed neural networks have dealt with the neural networks with discrete delays, see for example Refs. [5, 7, 9, 18] and the references therein. As we known, neural networks have a spatial nature due to the presence of parallel pathways with a variety of axon sizes and lengths [35]. So it is desirable to model them by introducing unbounded distributed delays. In other words, unbounded distributed delays should also be taken into account in the neural networks models as well as discrete delays [10, 11, 24–26]. Recently, some works dealing with synchronization phenomena in chaotic neural networks with discrete delays and distributed delays have appeared [27–33]. In [29–31], Li et al. investigated the exponential synchronization of neural networks with time-varying delays and finite distributed delays by using the drive–response concept, LMI approach and the Lyapunov stability theorem. However, the time-varying delays in [29–31] are continuously differentiable and their derivatives have finite upper bounded. In [32, 33], Song further obtained the asymptotical and exponential synchronization LMIs-based schemes for the neural networks with time-varying delays and finite distributed delays by constructing proper Lyapunov–Krasovskii functional and inequality technique, which removed those restrictions on time-varying delays. However, all the synchronization problems in [27–33] have dealt with the chaotic neural networks with time-varying delays or finite distributed delays and cannot be applied to the models with unbounded distributed delays.

On the other hand, many evolutionary processes, particularly some biological systems such as biological neural networks and bursting rhythm models in pathology, undergo abrupt changes at certain moments of time due to impulsive inputs, that is, do exhibit impulsive effects [34, 35]. Neural networks as artificial electronic systems are often subject to impulsive perturbations that in turn affect dynamical behaviors of the systems. According to Haykin [35] and Arbib [36], when stimuli from the body or the external environment are received by receptors, the electrical impulses will be conveyed to the neural net and impulsive effects arise naturally. Moreover, impulses can also be introduced as a control mechanism to stabilize some otherwise unstable neural networks, see [37]. Hence, it is very important and, in fact, necessary to investigated the dynamics of neural networks with mixed delays and impulsive effects. To date, a large number of results on dynamics of neural networks with mixed delays and impulsive effects have been derived in the literatures, see [10, 11], and the references cited therein. Recently, there are several results on synchronization problems of chaotic neural networks with delays and impulsive effects [23, 38–41]. In particular, Yang and Cao [39] investigated the exponential synchronization of neural networks with delays and impulsive effects by employing the Lyapunov stability theory. However, the time delays addressed are constants. Sheng and Yang [40] further studied the exponential synchronization for a class of neural networks with unbounded distributed delays and impulsive effects by using the Lyapunov functional method. However, the obtained results in [40] not only ignore the information of delay kernels for synchronization of chaotic neural networks but also impose certain unnecessary restrictions on impulses. In addition, it is widely known that the results based on LMIs have advantages not only in that they can be easily verified via MATLAB LMI toolbox, but also in that they take into consideration the neuron’s inhibitory and excitatory effects on neural networks [42]. Despite all this, there are some rigorous drawbacks: (a) The considered neural networks in [38–41] are not expressed in terms of LMIs; (b) some restrictive conditions are rigorous; (c) they do not allow the existence of large-scale impulsive effects. Obviously, these drawbacks restricted the availability for applications .

The purpose of this paper is to consider a class of chaotic neural networks with mixed delays and impulsive effects. By constructing suitable Lyapunov–Krasovskii functional and employing stability theory, we present some delay-dependent schemes which contain all the information in chaotic neural networks to guarantee the exponential synchronization of the addressed systems. The synchronization conditions are given in terms of LMIs, which can be easily checked via MATLAB LMI toolbox. Moreover, we not only essentially drop the requirement of traditional Lipschitz condition on the activation functions but also remove the restrictions on differentiability of time-varying delays and the boundedness of their derivatives.

The rest of the paper is organized as follows. In Sect. 2, problem formulations and some preliminaries are introduced. In Sect. 3, we present some exponential synchronization schemes for chaotic neural networks with mixed delays and impulsive effects by constructing different suitable Lyapunov–Krasovskii functionals. Two numerical examples are given to illustrate the proposed results in Sect. 4. Finally, conclusions are given in Sect. 5.

2 Problem formulations

Let \({\mathbb {R}}\) denote the set of real numbers, \({\mathbb {Z}}_+\) denote the set of positive integers and \({\mathbb {R}}^n\) the n-dimensional real space equipped with the Euclidean norm \(||\cdot ||.\) \(\mathscr {A}> 0\) or \(\mathscr {A}<0\) denotes that the matrix \(\mathscr {A}\) is a symmetric and positive definite or negative definite matrix. The notation \(\mathscr {A}^T\) and \(\mathscr {A}^{-1}\) mean the transpose of \(\mathscr {A}\) and the inverse of a square matrix. If \(\mathscr {A}, \mathscr {B}\) are symmetric matrices, \(\mathscr {A}>\mathscr {B}\) means that \(\mathscr {A}-\mathscr {B}\) is positive definite matrix. I denotes the identity matrix with appropriate dimensions and \(\Lambda =\{1,2,\ldots ,n\}\). Moreover, the notation \(\star\) always denotes the symmetric block in one symmetric matrix.

Denote \({\mathbb {PC}}_b^1((-\infty ,0], {\mathbb {R}}^{n}) =\{\psi :(-\infty ,0]\rightarrow \ {\mathbb {R}}^{n}\) is continuously differentiable bounded everywhere except at finite number of points t, at which \(\psi (t^{+}), \psi (t^{-}),\psi ^{'}(t^{+})\) and \(\psi ^{'}(t^{-})\) exist, \(\psi (t^{+})=\psi (t),\) \(\psi ^{'}(t^{+})=\psi ^{'}(t),\) where \(\psi ^{'}\) denotes the derivative of \(\psi\)}. Especially, let \({\mathbb {PC}}_b^1\doteq {\mathbb {PC}}_b^1((-\infty ,0], {\mathbb {R}}^{n}).\)

For any \(\psi \in {\mathbb {PC}}^{1}_b,\) we introduce the following norm:

$$\begin{aligned} ||\psi ||^2_{\tau }=\max \left\{ \max\limits_{\theta \le 0}\sum\limits _{i=1}^n\left| \psi ^2_i(\theta )\right| ,\,\, \max\limits_{-\tau \le \theta \le 0} \sum\limits_{i=1}^n\left| {\psi ^{'}}^2_i(\theta )\right| \right\} . \end{aligned}$$

Consider the following chaotic neural networks with mixed delays and impulsive effects:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = - C x(t)+ Af_{1}(x(t))+Bf_{2}(x(t-\tau (t)))+W\int _{-\infty }^{t}h(t-s)f_3(x(s)){\text{d}}s+I(t),\quad t\ne t_{k},\\ \Delta x(t_k) = x(t_k)-x(t^{-}_k)=-D_kx(t^{-}_k),\quad k\in {\mathbb {Z}}_+,\\x(s)=\phi (s),\quad s\in (-\infty ,0], \end{array}\right. \end{aligned}$$
(1)

where the impulse times \(t_{k}\) satisfy \(0= t_{0}<t_{1}<\ldots <t_{k}<\ldots , \lim _{k\rightarrow \infty }t_{k}=+\infty\), \(x(t)=(x_1(t),\cdots ,x_n(t))^T\) is the neuron state vector and \(f_i(x(\cdot ))=(f_{i1}(x_1(\cdot )),\cdots ,f_{in}(x_n(\cdot )))^T\), \(i=1,2,3,\) represents neuron activation functions, \(C=\hbox {diag}(c_1,\cdots ,c_n)\) is a diagonal matrix with \(c_i>0\), A, B, W are the connection weight matrix, the delayed weight matrix and the distributively delayed connection weight matrix, respectively; I(t) is a time-varying input vector, \(\tau (t)\) is the time-varying delay of the neural networks satisfying \(0\le \tau (t)\le \tau\); \(h(\cdot )=\hbox {diag}(h_1(\cdot ),\cdots ,h_n(\cdot ))\) is the delay kernel and \(D_k=\hbox {diag}(d^{(1)}_k,\cdots ,d^{(n)}_k)\) is the impulsive matrix, \(\phi (\cdot )\in {\mathbb {C}},\ {\mathbb {C}}\) is an open set in \({\mathbb {PC}}^{1}_b\).

We remark that the model formulation given above implies that the states of neuron x will meet sudden changes at the discontinuity points \(t_k\) due to some stimuli from the internal or external environment, that is, \(x(t_k)=(I-D_k)x(t^{-}_k),\) where \(x(t^{-}_k)\) denotes the state of neuron x before changes at jump points \(t_k\) and \(x(t_k)=x(t^{+}_k)\) the state after changes.

For the sake of simplicity, we give the following assumptions:

\((H_1)\) :

The neuron activation functions \(f_{1j},\,f_{2j},\,f_{3j}\) are bounded and satisfy the following conditions:

$$\begin{aligned} \sigma ^{-}_j\le & \frac{f_{1j}(u)-f_{1j}(v)}{u-v}\le \sigma ^{+}_j,\\ \zeta ^{-}_j\le & \frac{f_{2j}(u)-f_{2j}(v)}{u-v}\le \zeta ^{+}_j,\\ \rho ^{-}_j\le & \frac{f_{3j}(u)-f_{3j}(v)}{u-v}\le \rho ^{+}_j,\quad \forall \ u,v\in {\mathbb {R}},\ u\ne v,\,j\in \Lambda , \end{aligned}$$

where \(\sigma ^{-}_j,\sigma ^{+}_j,\zeta ^{-}_j,\zeta ^{+}_j,\rho ^{-}_j,\rho ^{+}_j\) are some real constants.

\((H_2)\) :

The delay kernels \(h_{j},j\in \Lambda ,\) are some real value nonnegative continuous function defined in \([0,\infty),\) and there exists a constant \(\eta >0\) such that

$$\begin{aligned} \int _{0}^{\infty }h_{j}(s){\text{d}}s\doteq {\mathbbm {h}}_{j},\quad \int _{0}^{\infty }h_{j}(s)e^{\eta s}{\text{d}}s\doteq {\mathbbm {h}}^\star _{j}<\infty ,\quad j\in \Lambda , \end{aligned}$$

where \({\mathbbm {h}}_{j},{\mathbbm {h}}^\star _{j}\) denote some positive constants.

Remark 2.1

It should be noted that as discussed in [4, 43] in many electronic circuits, the input–output functions of amplifiers may be neither monotonically increasing nor continuously differentiable, thus non-monotonic functions can be more appropriate to describe the neuron activation in designing and implementing an artificial neural network. Hence, the constants \(\sigma ^{-}_j,\sigma ^{+}_j,\zeta ^{-}_j,\zeta ^{+}_j,\rho ^{-}_j,\) \(\rho ^{+}_j\) which are allowed to be positive, negative or zero in assumption \((H_1)\) are more general than the previously used Lipschitz conditions, see, for example, [21, 39, 40]. Assumption \((H_2)\) provides the information on the delay kernels which can be used in the stability criteria, and therefore more precise synchronization conditions can be obtained in the following section.

Now we consider the system (1) as the master/drive system, and the slave/response system can be as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{y}(t) = - C y(t)+ Af_{1}(y(t))+Bf_{2}(y(t-\tau (t)))+W\int _{-\infty }^{t}h(t-s)f_3(y(s)){\text{d}}s +I(t)+u(t),\quad t\ne t_{k}, \\ \Delta y(t_k) = y(t_k)-y(t^{-}_k)=-D_ky(t^{-}_k),\quad k\in {\mathbb {Z}}_+,\\ y(s) = \varphi (s),\quad s\in (-\infty ,0], \end{array}\right. \end{aligned}$$
(2)

where \(\varphi (\cdot )\in {\mathbb {C}},\,u(t)\) is the appropriate control input that will be designed in order to obtain the synchronization of the drive system (1) and the controlled response system (2). And the other notations and conditions are the same as system (1).

For the synchronization scheme, the synchronization error is defined as

$$\begin{aligned} e(t)=(e_1(t),\cdots ,e_n(t))^T:=y(t)-x(t) \end{aligned}$$

and the control input in the response system is designed as (Inspired by the ideas in [29–33])

$$\begin{aligned} u(t)=K_1e(t)+K_2e(t-\tau (t)), \end{aligned}$$

where \(K_1,K_2\) are the gain matrices. Then the error dynamics between (1) and (2) can be expressed by

$$\begin{aligned} \left\{ \begin{array}{l} \dot{e}(t) = (-C+K_1) e(t)+K_2e(t-\tau (t))+ Ag_{1}(e(t))+Bg_{2}(e(t-\tau (t)))+W\int _{-\infty }^{t}h(t-s)g_3(e(s)){\text{d}}s,\quad t\ne t_{k},\\ \Delta e(t_k) = e(t_k)-e(t^{-}_k)=-D_ke(t^{-}_k),\quad k\in {\mathbb {Z}}_+,\\ e(s) = \varphi (s)-\phi (s),\quad \theta \in (-\infty ,0], \end{array}\right. \end{aligned}$$
(3)

where \(g_i(e(\cdot ))=f_i(e(\cdot )+x(\cdot ))-f_i(x(\cdot )).\) Obviously, \(g_i(0)=0, i=1,2,3.\) Moreover, by \((H_1)\) we note that the following conditions hold:

$$\begin{aligned} \sigma ^{-}_j\le & \frac{g_{1j}(s)}{s}\le \sigma ^{+}_j,\\ \zeta ^{-}_j\le & \frac{g_{2j}(s)}{s}\le \zeta ^{+}_j,\\ \rho ^{-}_j\le & \frac{g_{3j}(s)}{s}\le \rho ^{+}_j,\quad \forall \, s\in {\mathbb {R}},\,s\ne 0,\ j\in \Lambda . \end{aligned}$$

In addition, we give the following definitions:

$$\begin{aligned} \Sigma _1=\hbox {diag}( \sigma ^{-}_1\sigma ^{+}_1,\cdots ,\sigma ^{-}_n\sigma ^{+}_n),&\Sigma _2=\hbox {diag}\left( \frac{\sigma ^{-}_1+\sigma ^{+}_1}{2},\cdots ,\frac{\sigma ^{-}_n+\sigma ^{+}_n}{2}\right) ,\\ \Sigma _3=\hbox {diag}( \zeta ^{-}_1\zeta ^{+}_1,\cdots ,\zeta ^{-}_n\zeta ^{+}_n),& \Sigma _4=\hbox {diag}\left( \frac{\zeta ^{-}_1+\zeta ^{+}_1}{2},\cdots ,\frac{\zeta ^{-}_n+\zeta ^{+}_n}{2}\right) ,\\ \Sigma _5=\hbox {diag}( \rho ^{-}_1\rho ^{+}_1,\cdots ,\rho ^{-}_n\rho ^{+}_n),& \Sigma _6=\hbox {diag}\left( \frac{\rho ^{-}_1+\rho ^{+}_1}{2},\cdots ,\frac{\rho ^{-}_n+\rho ^{+}_n}{2}\right) .\\ \end{aligned}$$

Definition 2.1

([22]) Systems (1) and (2) are said to be exponentially synchronized if there exist constants \(\lambda >0\) and \(\mathscr {M}\ge 1\) such that \(||e(t)||\le \mathscr {M}||\varphi -\phi ||_\tau e^{-\lambda t}\) for any \(t>0.\) Constant \(\lambda\) is said to be the degree of exponential synchronization.

Definition 2.2

([23]) Systems (1) and (2) are said to be globally asymptotically synchronized if the synchronization error system (3) is globally asymptotically stable.

3 Synchronization schemes

In the section, we will investigate the exponential synchronization and global asymptotical synchronization of systems (1) and (2) with or without impulsive effects by constructing suitable Lyapunov–Krasovskii functionals.

Theorem 3.1

Assume that assumptions \((H_1)\) and \((H_2)\) hold. Then systems (1) and (2) are exponentially synchronized if there exist four constants \(\alpha \in (0,\eta ),\gamma >0,\delta \in [0,\alpha ), {\mathbb {M}}\ge 1\), an \(n\times n\) matrix \(P>0,\) an \(n\times n\) inverse matrix \(Q_1\), four \(n\times n\) diagonal matrices \(Q_2>0,U_i>0,i=1,2,3,\) and an \(2n\times 2n\) matrix \(\left( \begin{array}{ll} T_{11}&T_{12}\\ \star &T_{22} \\ \end{array}\right) >0\) such that

$$\begin{aligned} \left( \begin{array}{lllllll} \Pi _{11}&\Pi _{12}&Q_1K_2+\gamma T^T_{12}&Q_1A+U_1\Sigma _2&Q_1B&U_3\Sigma _6&Q_1W\\ \star &\Pi _{22}&Q_1K_2&Q_1A& Q_1B&0&Q_1W\\ \star &\star &\Pi _{33}&0&U_2\Sigma _4&0&0\\ \star &\star &\star &-U_1&0&0&0\\ \star &\star &\star &\star &-U_2&0&0\\ \star &\star &\star &\star &\star &Q_2\mathcal {H}-U_3&0\\ \star &\star &\star &\star &\star &\star &Q_2\\ \end{array}\right) <0 \end{aligned}$$
(4)

and

$$\begin{aligned} \prod _{k=1}^m\max \left\{ \lambda ^{k}_{\max },\ 1 \right\} \le {\mathbb {M}} e^{\delta t_m}\quad {\text{for\,\,all}}\quad m\in {\mathbb {Z}}_+\quad {\text{holds}}, \end{aligned}$$

where

$$\begin{aligned} \Pi _{11}&= \alpha P+Q_1(K_1-C)+\left( K^T_1-C\right) Q_1^T-U_1\Sigma _1-U_3\Sigma _5,\\ \Pi _{12}&= P-Q_1+\left( K_1^T-C\right) Q_1^T,\\ \Pi _{22}&= -Q_1-Q_1^T+\gamma ^2 \frac{e^{\alpha \tau }-1}{\alpha }T_{22},\\ \Pi _{33}&= \tau T_{11}-\gamma T_{12}-\gamma T^T_{12}-U_2\Sigma _3,\\ \mathcal {H}&= \hbox {diag}\left( {\mathbbm {h}}_1{\mathbbm {h}}_1^\star ,\ldots ,{\mathbbm {h}}_n{\mathbbm {h}}_n^\star \right) , \end{aligned}$$

\(\lambda ^{k}_{\max }\) denotes the maximum eigenvalue of matrix \(P^{-1}(I-D_k)P(I-D_k),k\in {\mathbb {Z}}_+\).

Proof

Consider the following Lyapunov–Krasovskii functional:

$$\begin{aligned} V(t,e(t))=V_1(t,e(t))+V_2(t,e(t))+V_3(t,e(t))+V_4(t,e(t)), \end{aligned}$$

where

$$\begin{aligned} V_1(t,e(t))&=\, e^{\alpha t}e^T(t)Pe(t),\\ V_2(t,e(t))&=\, \int _{0}^t e^{\alpha u}\int _{u-\tau (u)}^u\left( \begin{array}{ll} e(u-\tau (u))\\ \gamma \dot{e}(s)\\ \end{array}\right) ^T\left( \begin{array}{ll} T_{11}&T_{12} \\ \star &T_{22}\\ \end{array}\right) \left( \begin{array}{ll} e(u-\tau (u))\\ \gamma \dot{e}(s)\\ \end{array}\right) {\text{d}}s{\text{d}}u,\\ V_3(t,e(t))&= \, \gamma ^2\int _{-\tau }^0\int _{t+u}^t e^{\alpha (s-u)}\dot{e}^T(s)T_{22}\dot{e}(s){\text{d}}s{\text{d}}u,\\ V_4(t,e(t))&= \sum _{j=1}^n q^{(2)}_j {\mathbbm {h}}_j\int _0^\infty h_j(u)\int _{t-u}^t e^{\alpha (s+u)}g^2_{3j}(e_j(s)){\text{d}}s{\text{d}}u. \end{aligned}$$

Calculating the time derivative of \(V_1,V_2,V_3,V_4\) along the solution of (3) at the continuous interval \([t_{k-1},t_k),k\in {\mathbb {Z}}_+\), we get

$$\begin{aligned} D^{+}V_1(t,e(t))&=\, \alpha e^{\alpha t}e^T(t)Pe(t)+2e^{\alpha t}e^T(t)P\dot{e}(t)\\ &=\, \alpha e^{\alpha t}e^T(t)Pe(t)+2e^{\alpha t}e^T(t)P\dot{e}(t)+2e^{\alpha t}(e(t)+\dot{e}(t))^TQ_1 \left\{ -\dot{e}(t)+ (-C+K_1) e(t) +K_2e(t-\tau (t))+ Ag_{1}(e(t))+Bg_{2}(e(t-\tau (t)))+W\int _{-\infty }^{t}h(t-s)g_3(e(s)){\text{d}}s\right\}\\ &=\, e^{\alpha t} \left\{ e^T(t) \left[ \alpha P+2Q_1(-C+K_1) \right] e(t)+2e^T(t)\left[ P-Q_1+(K_1^T-C)Q_1^T \right] \dot{e}(t)+ 2e^T(t)Q_1K_2e(t-\tau (t))+ 2e^T(t)Q_1Ag_{1}(e(t))+ 2e^T(t)Q_1Bg_{2}(e(t-\tau (t)))+ 2e^T(t)Q_1W\int _{-\infty }^{t}h(t-s)g_3(e(s)){\text{d}}s-2\dot{e}^T(t)Q_1\dot{e}(t)+2\dot{e}^T(t)Q_1K_2e(t-\tau (t))+ 2\dot{e}^T(t)Q_1Ag_{1}(e(t))+ 2\dot{e}^T(t)Q_1Bg_{2}(e(t-\tau (t)))+ 2\dot{e}^T(t)Q_1W\int _{-\infty }^{t}h(t-s)g_3(e(s)){\text{d}}s \right\}, \end{aligned}$$
(5)
$$\begin{aligned} D^{+}V_2(t,e(t))=\, & e^{\alpha t}\int _{t-\tau (t)}^t\left( \begin{array}{ll} e(t-\tau (t)) \\ \gamma \dot{e}(s) \\ \end{array}\right) ^T\left( \begin{array}{ll} T_{11} & T_{12} \\ \star &T_{22}\\ \end{array}\right) \left( \begin{array}{ll} e(t-\tau (t)) \\ \gamma \dot{e}(s) \\ \end{array}\right) {\text{d}}s\nonumber \\=\, & e^{\alpha t}\left\{ \tau (t)e^T(t-\tau (t))T_{11}e(t-\tau (t))+2\gamma e^T(t)T^T_{12}e(t-\tau (t))- 2\gamma e^T(t-\tau (t))T^T_{12}e(t-\tau (t))+ \gamma ^2\int _{t-\tau (t)}^t\dot{e}^T(s)T_{22}\dot{e}(s){\text{d}}s\right\} \nonumber \\\le & e^{\alpha t} \left\{ e^T(t-\tau (t))[\tau T_{11}-2\gamma T^T_{12}]e(t-\tau (t)) +2\gamma e^T(t)T^T_{12}e(t-\tau (t))+ \gamma ^2\int _{t-\tau }^t\dot{e}^T(s)T_{22}\dot{e}(s){\text{d}}s \right\} , \end{aligned}$$
(6)
$$\begin{aligned} D^{+}V_3(t,e(t))&=\,\gamma ^2\int _{-\tau }^0e^{\alpha (t-u)}\dot{e}^T(t)T_{22}\dot{e}(t){\text{d}}u-\gamma ^2\int _{-\tau }^0e^{\alpha t}\dot{e}^T(t+u)T_{22}\dot{e}(t+u){\text{d}}u\nonumber \\&\,=\gamma ^2 e^{\alpha t}\left\{ \frac{e^{\alpha \tau }-1}{\alpha } \dot{e}^T(t)T_{22}\dot{e}(t)-\int _{t-\tau }^t\dot{e}^T(s)T_{22}\dot{e}(s){\text{d}}s,\right\} \end{aligned}$$
(7)

and

$$\begin{aligned} D^{+}V_4(t,e(t))= & \sum\limits_{j=1}^n q^{(2)}_j {\mathbbm {h}}_j\int _0^\infty h_j(u)e^{\alpha (t+u)}g^2_{3j}(e_j(t)){\text{d}}u- \sum\limits_{j=1}^n q^{(2)}_j {\mathbbm {h}}_j\int _0^\infty h_j(u)e^{\alpha t}g^2_{3j}(e_j(t-u)){\text{d}}u\nonumber \\\le & e^{\alpha t}\left\{ g^T_3(e(t))Q_2\mathcal {H}g_3(e(t))- \sum\limits_{j=1}^n q^{(2)}_j\int _0^\infty h_j(u){\text{d}}u\int _0^\infty h_j(u)g^2_{3j}(e_j(t-u)){\text{d}}u\right\} \nonumber \\\le & e^{\alpha t}\left\{ g^T_3(e(t))Q_2\mathcal {H}g_3(e(t))- \sum\limits_{j=1}^n q^{(2)}_j \left( \int _0^\infty h_j(u)g_{3j}(e_j(t-u)){\text{d}}u\right) ^2 \right\} \nonumber \\= & e^{\alpha t}\left\{ g^T_3(e(t))Q_2\mathcal {H}g_3(e(t))- \left( \int _{-\infty }^{t}h(t-s)g_3(e(s)){\text{d}}s \right) ^TQ_2 \left( \int _{-\infty }^{t}h(t-s)g_3(e(s)){\text{d}}s \right) \right\} . \end{aligned}$$
(8)

On the other hand, for any \(n \times n\) diagonal matrices \(U_i>0,i=1,2,3,\) it follows that

$$\begin{aligned}&e^{\alpha t}\left\{ \begin{array}{ll} \left( \begin{array}{ll} e(t) \\ g_1(e(t)) \\ \end{array}\right) ^T\left( \begin{array}{ll} -U_1\Sigma _1 & U_1\Sigma _2 \\ \star &-U_1\\ \end{array}\right) \left( \begin{array}{ll} e(t) \\ g_1(e(t)) \\ \end{array}\right) + \left( \begin{array}{ll} e(t-\tau (t))\\ g_2(e(t-\tau (t))) \\ \end{array}\right) ^T\left( \begin{array}{ll} -U_2\Sigma _3 & U_2\Sigma _4 \\ \star &-U_2\\ \end{array}\right) \end{array}\right. \nonumber \\&\quad \left. \begin{array}{ll} \cdot \left( \begin{array}{ll} e(t-\tau (t)) \\ g_2(e(t-\tau (t))) \\ \end{array}\right) + \left( \begin{array}{ll} e(t) \\ g_3(e(t)) \\ \end{array}\right) ^T\left( \begin{array}{ll} -U_3\Sigma _5 & U_3\Sigma _6 \\ \star &-U_3\\ \end{array}\right) \left( \begin{array}{ll} e(t) \\ g_3(e(t)) \\ \end{array}\right) \end{array}\right\} \ge 0. \end{aligned}$$
(9)

Thus, by (5)–(9), we can obtain

$$\begin{aligned} e^{-\alpha t}D^+V\le & e^T(t) \left[ \alpha P+2Q_1(-C+K_1)\right] e(t)+2e^T(t)\left[ P-Q_1+(K_1^T-C)Q_1^T\right] \dot{e}(t)\\&+ 2e^T(t)Q_1K_2e(t-\tau (t))+ 2e^T(t)Q_1Ag_{1}(e(t))+ 2e^T(t)Q_1Bg_{2}(e(t-\tau (t)))\\&+ 2e^T(t)Q_1W\int _{-\infty }^{t}h(t-s)g_3(e(s)){\text{d}}s-2\dot{e}^T(t)Q_1\dot{e}(t)+2\dot{e}^T(t)Q_1K_2e(t-\tau (t))\\&+ 2\dot{e}^T(t)Q_1Ag_{1}(e(t))+2\dot{e}^T(t)Q_1Bg_{2}(e(t-\tau (t)))\\&+ 2\dot{e}^T(t)Q_1W\int _{-\infty }^{t}h(t-s)g_3(e(s)){\text{d}}s + e^T(t-\tau (t))[\tau T_{11}-2\gamma T^T_{12}]e(t-\tau (t))\\&+ 2\gamma e^T(t)T^T_{12}e(t-\tau (t))+\gamma ^2 \frac{e^{\alpha \tau }-1}{\alpha } \dot{e}^T(t)T_{22}\dot{e}(t)+g^T_3(e(t))Q_2\mathcal {H}g_3(e(t))\\&-\left( \int _{-\infty }^{t}h(t-s)g_3(e(s)){\text{d}}s\right) ^TQ_2 \left( \int _{-\infty }^{t}h(t-s)g_3(e(s)){\text{d}}s\right) \\&+ \left( \begin{array}{ll} e(t) \\ g_1(e(t)) \\ \end{array}\right) ^T\left( \begin{array}{ll} -U_1\Sigma _1 & U_1\Sigma _2 \\ \star &-U_1\\ \end{array}\right) \left( \begin{array}{ll} e(t) \\ g_1(e(t)) \\ \end{array}\right) \\&+ \left( \begin{array}{ll} e(t-\tau (t)) \\ g_2(e(t-\tau (t))) \\ \end{array}\right) ^T\cdot \left( \begin{array}{ll} -U_2\Sigma _3 & U_2\Sigma _4 \\ \star &-U_2\\ \end{array}\right) \left( \begin{array}{ll} e(t-\tau (t)) \\ g_2(e(t-\tau (t))) \\ \end{array}\right) \\&+\left( \begin{array}{ll} e(t) \\ g_3(e(t)) \\ \end{array}\right) ^T\left( \begin{array}{ll} -U_3\Sigma _5 & U_3\Sigma _6 \\ \star &-U_3\\ \end{array}\right) \cdot \left( \begin{array}{ll} e(t) \\ g_3(e(t)) \\ \end{array}\right) \\\le & \xi ^T(t)\Xi \xi (t), \end{aligned}$$

where

$$\begin{aligned} \Xi= & \left( \begin{array}{lllllll} \Pi _{11}&\Pi _{12}&Q_1K_2+\gamma T^T_{12}&Q_1A+U_1\Sigma _2&Q_1B&U_3\Sigma _6&Q_1W\\ \star &\Pi _{22}&Q_1K_2&Q_1A& Q_1B&0&Q_1W\\ \star &\star &\Pi _{33}&0&U_2\Sigma _4&0&0\\ \star &\star &\star &-U_1&0&0&0\\ \star &\star &\star &\star &-U_2&0&0\\ \star &\star &\star &\star &\star &Q_2\mathcal {H}-U_3&0\\ \star &\star &\star &\star &\star &\star &-Q_2\\ \end{array}\right) ,\\ \xi (t)= & \left(e(t),\ \dot{e}(t),\ e(t-\tau (t)),\ g_1(e(t)),\ g_2(e(t-\tau (t))),\ g_3(e(t)),\ \int _{-\infty }^{t}h(t-s)g_3(e(s)){\text{d}}s\right) ^T. \end{aligned}$$

Since (4) holds, we know that matrix \(\Xi\) is a negative define matrix, then

$$\begin{aligned} D^+V\le 0, t\in [t_{k-1},t_k),k\in {\mathbb {Z}}_+. \end{aligned}$$
(10)

On the other hand, we note that for any \(k\in {\mathbb {Z}}_+\)

$$\begin{aligned} V_1(t_k,e(t_k)) =e^{\alpha t_k}e^T(t_k)Pe(t_k)&=\, e^{\alpha t_k}e^T(t^{-}_k)(I-D_k)P(I-D_k)e(t^{-}_k)\nonumber \\&\le e^{\alpha t_k} \lambda ^{k}_{\max } e^T(t^{-}_k)Pe(t^{-}_k)\nonumber \\&=\,\lambda ^{k}_{\max } V_1(t^{-}_k,e(t^{-}_k)). \end{aligned}$$
(11)

Moreover, we know

$$\begin{aligned} V_2(t_k,e(t_k))=V_2(t^{-}_k,e(t^{-}_k)),\quad V_3(t_k,e(t_k))=V_3(t^{-}_k,e(t^{-}_k)),\quad V_4(t_k,e(t_k))=V_4(t^{-}_k,e(t^{-}_k)). \end{aligned}$$

Together with (11), it follows that for any \(k\in {\mathbb {Z}}_+\)

$$\begin{aligned} V(t_k,e(t_k))\le \max \left\{ \lambda ^{k}_{\max },\ 1\right\} V(t^{-}_k,e(t^{-}_k)). \end{aligned}$$
(12)

By simple induction, from (10) and (12) we get for \(t\in [t_m,t_{m+1}),m\in {\mathbb {Z}}_+\)

$$\begin{aligned} e^{\alpha t}\lambda _{\min }\cdot ||e(t)||^2\le V(t,e(t))\le V(0,e(0))\prod _{k=1}^m\max \left\{ \lambda ^{k}_{\max },\ 1\right\} , \end{aligned}$$

which implies that

$$\begin{aligned} ||e(t)||^2\le \frac{{\mathbb {M}}}{\lambda _{\min }} V(0,e(0))e^{-\alpha t}e^{\delta t_m},\ t\in [t_m,t_{m+1}),m\in {\mathbb {Z}}_+, \end{aligned}$$

i.e.,

$$\begin{aligned} ||e(t)||^2\le \frac{{\mathbb {M}}}{\lambda _{\min }} V(0,e(0))e^{-(\alpha -\delta )t},\ t>0. \end{aligned}$$
(13)

In addition, it can be deduced that

$$\begin{aligned} V(0,e(0))&=\,e^T(0)Pe(0)+ \gamma ^2\int _{-\tau }^0\int _{u}^0 e^{\alpha (s-u)}\dot{e}^T(s)T_{22}\dot{e}(s){\text{d}}s{\text{d}}u\nonumber \\&\quad + \sum\limits_{j=1}^n q^{(2)}_j {\mathbbm {h}}_j\int _0^\infty h_j(u)\int _{-u}^0 e^{\alpha (s+u)}g^2_{3j}(e_j(s)){\text{d}}s{\text{d}}u\nonumber \\ &\le \lambda _{\max }||\varphi -\phi ||^2+\mu _{\max }\gamma ^2\left( \frac{e^{\alpha \tau }-1-\alpha \tau }{\alpha ^2}\right) ||\varphi -\phi ||_\tau ^2\nonumber \\&\quad + \frac{1}{\alpha }\sum\limits_{i=1}^n q^{(2)}_j {\mathbbm {h}}_j\rho ^2_j({\mathbbm {h}}^\star _j-{\mathbbm {h}}_j)||\varphi -\phi ||_\tau ^2\nonumber \\ &\le \left\{ \lambda _{\max }+\mu _{\max }\gamma ^2\left( \frac{e^{\alpha \tau }-1-\alpha \tau }{\alpha ^2}\right) + \frac{1}{\alpha }\sum\limits_{i=1}^n q^{(2)}_j {\mathbbm {h}}_j\rho ^2_j\left( {\mathbbm {h}}^\star _j-{\mathbbm {h}}_j\right) \right\} ||\varphi -\phi ||_\tau ^2, \end{aligned}$$
(14)

where \(\rho _j=\max \{|\rho ^{-}_j|,\ |\rho ^{+}_j|\},j\in \Lambda ,\mu _{\max }\) and \(\lambda _{\max }\) denote the maximum eigenvalues of matrix \(T_{22}\) and P, respectively.

Substituting (14) into (13), we finally obtain

$$\begin{aligned} ||e(t)||\le \mathscr {M}||\varphi -\phi ||_\tau e^{-\frac{\alpha -\delta }{2}t},\ t>0, \end{aligned}$$

where

$$\begin{aligned} \mathscr {M}= \sqrt{\frac{{\mathbb {M}}}{\lambda _{\min }}\left\{ \lambda _{\max }+\mu _{\max }\gamma ^2\left( \frac{e^{\alpha \tau }-1-\alpha \tau }{\alpha ^2}\right) + \frac{1}{\alpha }\sum\limits_{i=1}^n q^{(2)}_j {\mathbbm {h}}_j\rho ^2_j\left( {\mathbbm {h}}^\star _j-{\mathbbm {h}}_j\right) \right\} }\ge 1. \end{aligned}$$

Hence, the origin of the synchronization error system (3) is globally exponentially stable, i.e., the networks (1) and (2) achieve global exponential synchronization. This completes the proof. \(\square\)

Remark 3.1

Theorem 3.1 provides some sufficient conditions to ensure the exponential synchronization of systems (1) and (2). Although the computation process is complex, the conditions are easy to check, which are given in terms of LMI. In order to show the design of the estimate gain matrices \(K_1\) and \(K_2,\) a simple transformation is made to obtain the following result.

Corollary 3.1

Assume that assumptions \((H_1)\) and \((H_2)\) hold. Then systems (1) and (2) are exponentially synchronized if there exist four constants \(\alpha \in (0,\eta ),\gamma >0,\delta \in [0,\alpha ), {\mathbb {M}}\ge 1\), three \(n\times n\) matrices \(P>0, Y_1,Y_2\), an \(n\times n\) inverse matrix \(Q_1,\) four \(n\times n\) diagonal matrices \(Q_2>0,U_i>0,i=1,2,3,\) and an \(2n\times 2n\) matrix \(\left( \begin{array}{ll} T_{11} & T_{12} \\ \star &T_{22}\\ \end{array}\right) >0\) such that

$$\begin{aligned} \left( \begin{array}{lllllll} \Pi _{11}&\Pi _{12}&Y_2+\gamma T^T_{12}&Q_1A+U_1\Sigma _2&Q_1B&U_3\Sigma _6&Q_1W\\ \star &\Pi _{22}&Y_2&Q_1A& Q_1B&0&Q_1W\\ \star &\star &\Pi _{33}&0&U_2\Sigma _4&0&0\\ \star &\star &\star &-U_1&0&0&0\\ \star &\star &\star &\star &-U_2&0&0\\ \star &\star &\star &\star &\star &Q_2\mathcal {H}-U_3&0\\ \star &\star &\star &\star &\star &\star &-Q_2\\ \end{array}\right) <0 \end{aligned}$$

and

$$\begin{aligned} \prod _{k=1}^m\max \left\{ \lambda ^{k}_{\max },\ 1\right\} \le {\mathbb {M}} e^{\delta t_m}\quad {\text{for\,\,all}}\quad m\in {\mathbb {Z}}_+\,\,{\text{holds}}, \end{aligned}$$

where

$$\begin{aligned} \Pi _{11}&= \, \alpha P-Q_1C-CQ_1^T+Y_1+Y_1^T-U_1\Sigma _1-U_3\Sigma _5,\\ \Pi _{12}&=\, P-Q_1+Y_1^T- CQ_1^T,\\ \Pi _{22}&= -Q_1-Q_1^T+\gamma ^2 \frac{e^{\alpha \tau }-1}{\alpha }T_{22},\\ \Pi _{33}&= \tau T_{11}-\gamma T_{12}-\gamma T^T_{12}-U_2\Sigma _3,\\ \mathcal {H}&= \hbox {diag}\left( {\mathbbm {h}}_1{\mathbbm {h}}_1^\star ,\ldots ,{\mathbbm {h}}_n{\mathbbm {h}}_n^\star \right) , \end{aligned}$$

\(\lambda ^{k}_{\max }\) denotes the maximum eigenvalue of matrix \(P^{-1}(I-D_k)P(I-D_k),k\in {\mathbb {Z}}_+\).

Remark 3.2

Let \(K_i=Q_1^{-1}Y_i\) in Theorem 3.1, then we can obtain above result immediately. In particular, if P is a positive definite diagonal matrix, then by Theorem 3.1 the following result can be obtained:

Corollary 3.2

Assume that assumptions \((H_1)-(H_3)\) hold. Then systems (1) and (2) are exponentially synchronized if there exist four constants \(\alpha \in (0,\eta ),\gamma >0,\delta \in [0,\alpha ), {\mathbb {M}}\ge 1\), an \(n\times n\) inverse matrix \(Q_1\), five \(n\times n\) diagonal matrices \(P>0,Q_2>0,U_i>0,i=1,2,3,\) and an \(2n\times 2n\) matrix \(\left( \begin{array}{ll} T_{11}& T_{12} \\ \star & T_{22}\\ \end{array}\right) >0\) such that

$$\begin{aligned} \left( \begin{array}{lllllll} \Pi _{11}&\Pi _{12}&Q_1K_2+\gamma T^T_{12}&Q_1A+U_1\Sigma _2&Q_1B&U_3\Sigma _6&Q_1W\\ \star &\Pi _{22}&Q_1K_2&Q_1A& Q_1B&0&Q_1W\\ \star &\star &\Pi _{33}&0&U_2\Sigma _4&0&0\\ \star &\star &\star &-U_1&0&0&0\\ \star &\star &\star &\star &-U_2&0&0\\ \star &\star &\star &\star &\star &Q_2\mathcal {H}-U_3&0\\ \star &\star &\star &\star &\star &\star &-Q_2\\ \end{array}\right) <0 \end{aligned}$$

and

$$\begin{aligned} \prod _{k=1}^m\max \left\{ \max\limits_{j\in \Lambda }|1-d^{(j)}_k|^2,\ 1\right\} \le {\mathbb {M}} e^{\delta t_m}\quad for\,\,all\quad m\in {\mathbb {Z}}_+\,\,holds, \end{aligned}$$

where

$$\begin{aligned} \Pi _{11}&=\, \alpha P+Q_1(K_1-C)+\left( K^T_1-C\right) Q_1^T-U_1\Sigma _1-U_3\Sigma _5,\\ \Pi _{12}&=\, P-Q_1+\left( K_1^T-C\right) Q_1^T,\\ \Pi _{22}&= -Q_1-Q_1^T+\gamma ^2 \frac{e^{\alpha \tau }-1}{\alpha }T_{22},\\ \Pi _{33}&= \tau T_{11}-\gamma T_{12}-\gamma T^T_{12}-U_2\Sigma _3,\\ \mathcal {H}&= \hbox {diag}\left( {\mathbbm {h}}_1{\mathbbm {h}}_1^\star ,\ldots ,{\mathbbm {h}}_n{\mathbbm {h}}_n^\star \right) . \end{aligned}$$

To compare Corollary 3.2 with some previous results (e.g., [21, 38–40]), we derive the following remark:

Remark 3.3

In the literature [38–40], the impulsive condition is assumed to be \(d^{(j)}_k\in [0,2]\) (or (0,2)),\(j\in \Lambda ,\ k\in {\mathbb {Z}}_+.\) Obviously, it is just a special case of Corollary 3.2. Our results can be applied to neural networks with large impulses. In addition, consider a special case with \(D_k=0\) and \(W=0,\) that is, systems (1) and (2) are reduced to chaotic neural networks which have been studied in [21] with control input \(u(t)=K e(t)\). They gave some sufficient conditions that guaranteed the chaotic synchronization of neural networks under the assumption that the neuron activation functions are monotonous nondecreasing and the time-varying delay is differentiable. This implies that our development results have wider adaptive range.

Next, we consider the asymptotic synchronization of systems (1) and (2). First, condition \((H_2)\) in Sect. 2 will be properly relaxed by

\((H_2^{'})\) The delay kernels \(h_{j},j\in \Lambda ,\) are some real value nonnegative continuous function defined in \([0,\infty )\) and satisfy

$$\begin{aligned} \int _{0}^{\infty }h_{j}(s){\text{d}}s\,\doteq\, {\mathbbm {h}}_{j}<\infty ,\quad j\in \Lambda \end{aligned}$$

where \({\mathbbm {h}}_{j}\) denotes a positive constant.

Theorem 3.2

Assume that assumptions \((H_1)\) and \((H_2^{'})\) hold. Then systems (1) and (2) are asymptotically synchronized if there exist a constant \(\gamma >0,\) a \(n\times n\) matrix \(P>0\), an \(n\times n\) inverse matrix \(Q_1,\) four \(n\times n\) diagonal matrices \(Q_2>0,U_i>0,i=1,2,3,\) and an \(2n\times 2n\) matrix \(\left( \begin{array}{ll} T_{11} & T_{12} \\ \star &T_{22}\\ \end{array}\right) >0\) such that

$$\begin{aligned} \left( \begin{array}{lllllll} \Pi _{11}&\Pi _{12}&Q_1K_2+\gamma T^T_{12}&Q_1A+U_1\Sigma _2&Q_1B&U_3\Sigma _6&Q_1W\\ \star &\Pi _{22}&Q_1K_2&Q_1A& Q_1B&0&Q_1W\\ \star &\star &\Pi _{33}&0&U_2\Sigma _4&0&0\\ \star &\star &\star &-U_1&0&0&0\\ \star &\star &\star &\star &-U_2&0&0\\ \star &\star &\star &\star &\star &Q_2{\mathbb {H}}-U_3&0\\ \star &\star &\star &\star &\star &\star &-Q_2\\ \end{array}\right) <0 \end{aligned}$$

and

$$\begin{aligned} 0 \le d^{(j)}_k \le 2,\ j\in \Lambda ,\ k\in {\mathbb {Z}}_+, \end{aligned}$$

where

$$\begin{aligned} \Pi _{11}= & Q_1(K_1-C)+(K^T_1-C)Q_1^T-U_1\Sigma _1-U_3\Sigma _5,\\ \Pi _{12}= & P-Q_1+(K_1^T-C)Q_1^T,\\ \Pi _{22}= & -Q_1-Q_1^T+\gamma ^2 \tau T_{22},\\ \Pi _{33}= & \tau T_{11}-\gamma T_{12}-\gamma T^T_{12}-U_2\Sigma _3,\\ {\mathbb {H}}&= \hbox {diag}({\mathbbm {h}}^2_1,\cdots ,{\mathbbm {h}}^2_n). \end{aligned}$$

Proof

Consider the following Lyapunov–Krasovskii functional:

$$\begin{aligned} V(t,e(t))=V_1(t,e(t))+V_2(t,e(t))+V_3(t,e(t))+V_4(t,e(t)), \end{aligned}$$

where

$$\begin{aligned} V_1(t,e(t))&=\, e^T(t)Pe(t),\\ V_2(t,e(t))&= \, \int _{0}^t \int _{u-\tau (u)}^u\left( \begin{array}{ll} e(u-\tau (u)) \\ \gamma \dot{e}(s) \\ \end{array}\right) ^T\left( \begin{array}{ll} T_{11} & T_{12} \\ \star &T_{22}\\ \end{array}\right) \left( \begin{array}{ll} e(u-\tau (u)) \\ \gamma \dot{e}(s) \\ \end{array}\right) {\text{d}}s{\text{d}}u,\\ V_3(t,e(t))&=\, \gamma ^2\int _{-\tau }^0\int _{t+u}^t \dot{e}^T(s)T_{22}\dot{e}(s){\text{d}}s{\text{d}}u,\\ V_4(t,e(t))&=\, \sum\limits_{j=1}^n q^{(2)}_j {\mathbbm {h}}_j\int _0^\infty h_j(u)\int _{t-u}^t g^2_{3j}(e_j(s)){\text{d}}s{\text{d}}u. \end{aligned}$$

The rest of the proof is similar to that of Theorem 3.1. Here it is omitted.

Remark 3.4

So far, numerous synchronization schemes for chaotic neural networks have been established in the literature. We can find the recent papers [19–23, 27–33, 38–41] in this direction. However, the time-varying delays appearing in [21, 22, 29, 30] are differential and their derivatives are simultaneously required to be not greater than 1 or finite and the delay kernels need satisfy (i)—(iii) in [40]. Obviously, these requirements are relaxed in our results. Moreover, the sufficient conditions established in [40] ignore the information of delay kernels for synchronization of chaotic neural networks.

Remark 3.5

In Li and Bohner [23] investigated the exponential synchronization of chaotic neural networks with mixed delays and impulsive effects via output coupling with delay feedback. It can be applied to the case that only output signals can be measured in neural networks. In the present paper, via state coupling we investigate the synchronization problem of chaotic neural networks. For the different coupling strategies, state and output coupling, different synchronization schemes have been derived and they are complementary with each other.

4 Numerical examples

In this section, we will give two numerical examples showing the effectiveness of the results obtained. First, we consider a simple chaotic neural network with impulses, see [40].

Example 4.1

Consider a two-dimensional chaotic neural network with impulses ([40]):

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = - C x(t)+ Af_{1}(x(t))+Bf_{2}(x(t-0.85))+I(t),\quad t\ne t_{k},\\ \Delta x(t_k) = x(t_k)-x(t^{-}_k)=-D_kx(t^{-}_k),\quad k\in {\mathbb {Z}}_+,\\x(s) = \phi (s),\quad s\in [-0.85,0], \end{array}\right. \end{aligned}$$
(15)

where the initial condition \(\phi (s)=(-0.5,0.8)^T, s\in [-0.85,0],\, f_1=f_2=0.5(|x+1|-|x-1|),I(t)=(0,0)^T,\ D_k=\)diag\((0.1,0.1),\, t_k=2k,\,k\in {\mathbb {Z}}_+\), and parameter matrices C, A and B as follows:

$$\begin{aligned} C=\left( \begin{array}{ll} 1& 0\\ 0& 1\\ \end{array}\right) ,\quad A=\left( \begin{array}{ll} 1+\frac{\pi }{4} & 20\\ 0.1 & 1+\frac{\pi }{4}\\ \end{array}\right), \quad B= \left( \begin{array}{ll} -\frac{1.3\pi \sqrt{2}}{4} & 0.1\\ 0.1 & -\frac{1.3\pi \sqrt{2}}{4} \\ \end{array}\right) . \end{aligned}$$

To achieve synchronization, the response system is designed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{y}(t) = - C y(t)+ Af_{1}(y(t))+Bf_{2}(y(t-0.85)) +I(t)+u(t),\quad t\ne t_{k},\\ \Delta y(t_k) = y(t_k)-y(t^{-}_k)=-D_k y(t^{-}_k),\quad k\in {\mathbb {Z}}_+,\\ y(s) = \varphi (s),\quad s\in [-0.85,0], \end{array}\right. \end{aligned}$$
(16)

where the initial condition \(\varphi (s)=(0.3,-0.2)^T, s\in [-0.85,0], \,u(t)=K_1 e(t)+K_2e(t-0.85),\,K_1\) and \(K_2\) are the controller gain matrices.

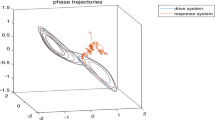
As shown in Fig. 1a–d, the state trajectories x, y and the synchronization error \(e_1,e_2\) between drive system (15) and response one (16) without control input (i.e., \(u(t)=(0,0)^T\)) does not approach to zero.

Fig. 1
figure 1

State trajectories and error trajectories of drive system (15) and response system (16) without control input

Full size image

Let \(\eta =0.5, \alpha =0.49\) and \(\gamma =2\) and using the tools of LMI toolbox, we obtain that the LMIs in Corollary 3.1 have feasible solution. Consequently, the controller gain matrices \(K_1\) and \(K_2\) are designed as follows:

$$\begin{aligned} K_1&=\,Q_1^{-1}Y_1= \left( \begin{array}{ll} -272.3592 & 1.0268\\ 8.2749& -143.8495\\ \end{array}\right) ,\nonumber \\ K_2&=\,Q_1^{-1}Y_2= \left( \begin{array}{ll} 0.7210 & -0.0494\\ -0.0498& 0.7212\\ \end{array}\right) . \end{aligned}$$
(17)

Note that

$$\begin{aligned} \lambda ^{k}_{\max }=P^{-1}(I-D_k)P(I-D_k) =0.81<1,k\in {\mathbb {Z}}_+. \end{aligned}$$

Hence, one may choose \({\mathbb {M}}=1,\delta =0\) in Corollary 3.1. Then the systems (15) and (16) are said to be exponentially synchronized. The simulation results are illustrated in Fig. 2a–d in which the controller designed in (17) is applied.

Remark 4.1

In fact, one may observe that matrices \(Q_2>0,U_3>0\) and constant \(\alpha \ge 0\) in Example 4.1 can be chosen arbitrarily since the distributed delays are not involved in system (15).

Remark 4.2

In [40], the authors have studied the chaotic synchronization between derive system (15) and response one (16) with control input \(u(t)=M(f(y(t)-f(x(t))).\) Note in Example 4.1, a different scheme is given to obtain the chaotic synchronization with control input \(u(t)=K_1 e(t)+K_2e(t-0.85).\) Moreover, when the impulsive condition \(D_k=\)diag\((-0.5,2.5), k\in {\mathbb {Z}}_+\) (abbrev. \(D^{\star }_k\)), let \({\mathbb {M}}=1,\delta =0.46(<0.49),\) by simple calculation, we get \(\lambda ^{k}_{\max } \approx 2.2957<e^{2\delta },\) which implies that systems (15) and (16) still are exponentially synchronized under control input \(u(t)=K_1 e(t)+K_2e(t-0.85)\) by Theorem 3.1 (see Figs. 3a, b, 2c, d). However, it is obvious that the sufficient conditions in [40] are not satisfied and chaotic synchronization cannot be guaranteed for the case \(D^{\star }_k\).

Remark 4.3

It should be noted that for the case \(D^{\star }_k,\) the corresponding error trajectories are the same as Fig. 2c, d since the impulsive interval \(t_k-t_{k-1}=2,k\in {\mathbb {Z}}_+\).

Example 4.2

Consider the following chaotic neural networks with mixed delays and impulsive effects:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = - C x(t)+ Af_{1}(x(t))+Bf_{2}(x(t-\tau (t)))+W\int _{-\infty }^{t}h(t-s)f_3(x(s)){\text{d}}s+I(t),\quad t\ne t_{k},\\ \Delta x(t_k) = x(t_k)-x(t^{-}_k)=-D_kx(t^{-}_k),\quad k\in {\mathbb {Z}}_+,\\ x(s) = \phi (s),\quad s\in (-\infty ,0], \end{array}\right. \end{aligned}$$
(18)

where the initial condition \(\phi (s)=(0.5,-0.5)^T, s\in (-\infty ,0], \,f_i=0.5(|x+1|-|x-1|),i=1,2,3,\,\tau (t)=0.4,\ h(s)=0.2e^{-s},\ I(t)=(0,0)^T,\ D_k=\)diag\((0.1,0.2),\,t_k=3k,\ k\in {\mathbb {Z}}_+,\) and parameter matrices C, A, B and W as follows:

$$\begin{aligned} C=\left( \begin{array}{ll} 1 & 0\\ 0 & 1\\ \end{array}\right) ,\quad A = \left( \begin{array}{ll} 2.0 & -0.1 \\ -5.0 & 3.2\\ \end{array}\right) ,\quad B= \left( \begin{array}{ll} -1.3 & -0.2\\ -0.2& -4.2 \\ \end{array}\right) ,\quad W= \left( \begin{array}{ll} -0.6 & -0.6\\ 4.6 & -3.1\\ \end{array}\right) . \end{aligned}$$

To achieve synchronization, the response system is designed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{y}(t) = - C y(t)+ Af_{1}(y(t))+Bf_{2}(y(t-\tau (t)))+W\int _{-\infty }^{t}h(t-s)f_3(y(s)){\text{d}}s+I(t)+u(t),\quad t\ne t_{k},\\ \Delta y(t_k) = y(t_k)-y(t^{-}_k)=-D_k y(t^{-}_k),\quad k\in {\mathbb {Z}}_+,\\y(s) = \varphi (s),\quad s\in (-\infty ,0], \end{array}\right. \end{aligned}$$
(19)

where the initial condition \(\varphi (s)=(-0.8,0.2)^T, s\in (-\infty ,0],\,u(t)=K_1 e(t)+K_2e(t-0.4),\,K_1\) and \(K_2\) are the controller gain matrices.

As shown in Fig. 4a–d, the state trajectories x, y and the synchronization error \(e_1,e_2\) between drive system (18) and response one (19) without control input (i.e., \(u(t)=(0,0)^T\)) does not approach to zero.

Fig. 2
figure 2

State trajectories and error trajectories of drive system (15) and response system (16) with control input (17

Full size image
Fig. 3
figure 3

State trajectories of drive system (15) and response system (16) with control input (17) under impulsive condition \(D^{\star }_k\)

Full size image
Fig. 4
figure 4

State trajectories and error trajectories of drive system (18) and response system (19) without control input

Full size image

Let \(\eta =0.5,\alpha =0.48\) and \(\gamma =3\) and using the tools of LMI toolbox, we obtain that the LMIs in Corollary 3.1 has feasible solution. The controller gain matrices \(K_1\) and \(K_2\) are designed as follows:

$$\begin{aligned} K_1=\, & Q_1^{-1}Y_1= \left( \begin{array}{ll} -24.5010 & -6.9690\\ -5.6928 &-301.1971\\ \end{array}\right) ,\nonumber \\ K_2=\,& Q_1^{-1}Y_2= \left( \begin{array}{ll} 0.6073 & 0.1014\\ 0.1125 & 2.1076\\ \end{array}\right) . \end{aligned}$$
(20)

Note that

$$\begin{aligned} \lambda ^{k}_{\max }=P^{-1}(I-D_k)P(I-D_k) =0.81<1,k\in {\mathbb {Z}}_+. \end{aligned}$$

Hence, one may choose \({\mathbb {M}}=1,\delta =0\) in Corollary 3.1. Then the systems (18) and (19) are said to be exponentially synchronized. The simulation results are illustrated in Fig. 5a–d in which the controller designed in (20) is applied.

Fig. 5
figure 5

State trajectories and error trajectories of drive system (18) and response system (19) with control input (10)

Full size image

5 Conclusions

In this paper, chaotic neural networks with mixed delays and impulsive effects have been studied. By constructing suitable Lyapunov–Krasovskii functional and employing stability theory, some delay-dependent schemes are designed to guarantee the exponential synchronization of neural networks, which are different from the existing ones and can be applied to a wider range of applications. Moreover, the obtained results are given in terms of LMIs, which can be easily checked via MATLAB LMI toolbox. Finally, two numerical examples and their simulations have been given to verify the theoretical results. The idea in this paper can be extended to the study of synchronization control of complex-value neural networks, but it is difficult to be applied to impulsive NNs with state-delay. More methods and tools should be explored and developed in this direction.