Finite-time synchronization of chaotic neural networks with mixed time-varying delays and stochastic disturbance

Abstract

This paper treats of the finite-time stochastic synchronization problem of chaotic dynamic neural networks with mixed time-varying delays and stochastic disturbance. State feedback controller and adaptive controller are designed such that the response system can be finite-timely synchronized with corresponding drive system. Some novel and useful finite-time synchronization criteria are derived based on finite-time stability theory. A numerical example presents the effectiveness of our proposed methods.

1 Introduction

In recent years, a great number of efforts have been devoted to neural networks (see [1–4]), and have been successfully applied to a variety of fields such as image and signal processing, parallel computing, optimization, pattern recognition, associative memory, automatic control, etc. Both Hopfield neural networks and cellular neural networks have become important fields of active research over the past two decades for their potential applications in modeling complex dynamics. Both of them have been successfully applied in solving various linear and nonlinear programming problems, as well as in the applications of image processing. However, stability analysis in this kind of neural networks is a very important issue, and several stability criteria have been developed in the literature [3, 4] and references cited therein.

Ever since the pioneering work of Pecora and Carroll [5], the issue of synchronization and chaos control has been extensively studied due to its potential engineering applications such as secure communication, biological systems, information processing [6–14]. In addition, it is well known that chaotic systems have complex dynamical behaviors which possess some special features, such as being extremely sensitive to tiny variations of initial conditions, having bounded trajectories in phase space, etc. Synchronization is a typical collective behavior of chaotic neural networks which has caused increasing concern because of its ubiquity in lots of neural network models. To the best of knowledge, most of the existing papers are concerned with asymptotic or exponential synchronization of networks. However, in fact, the networks might always be expected to achieve synchronization as quickly as possible, particularly in engineering fields. To obtain faster convergence rate in neural networks, it is necessary to use effective finite-time synchronization control techniques [15–18].

On the other hand, due to the network traffic congestion and the finite speed of signal transmission, time delays occur commonly in neural networks, which may lead to oscillations or instability of the networks. Hence, the study on the dynamical behavior of the delayed neural networks is an active research topic and has received considerable attention during the past few years. However, in these recent works, most papers on delayed neural networks have been restricted to simple cases of discrete delays. In general, because of the existence of a lot of parallel pathways of all kinds of axon sizes and lengths, a neural network usually has a spatial nature, which makes us model them by introducing the distributed delays. Then, both discrete and distributed time-varying delays should be taken into account when modeling some realistic neural networks [19–21].

In real world, due to random uncertainties such as stochastic forces on the physical systems and noisy measurements caused by environmental uncertainties, a system with stochastic perturbations should be produced instead of a deterministic form. There have been some works in the field of stochastic chaos synchronization of master-slave type [22–26]. In [22], exponential synchronization of stochastic perturbed chaotic delayed neural networks is considered. In [23, 24], adaptive synchronization for delayed neural networks with stochastic perturbation is investigated. In [25], the author investigates the finite-time stochastic synchronization problem for complex networks with stochastic noise perturbations, and a new kind of complex network model has been introduced, which includes not only the diffusive linear couplings, but also the unknown diffusive couplings and Wiener processes. In [26], works with non-delayed and delayed coupling has been proposed by utilizing the impulsive control and the periodically intermittent control. Hence, the novel models in [25, 26] are more practical in real world. However, there is no any kind of time delays in the model of [25] and there only has discrete time delays in the model of [26].

Motivated by the discussion above, this paper aims to treat of the stochastic finite-time synchronization of neural networks with mixed time-varying delays and stochastic disturbance via designing different controllers: feedback controller and adaptive controller.

Notations: The superscript “T” stands for matrix transposition; ${\mathbb {R}}$ denotes the real space; ${\mathbb {R}}^{n}$ denotes the n-dimensional Euclidean space; the notation $P> 0$ means that $P$ is real symmetric and positive definite; $I$ and $0$ represent identity matrix and zero matrix, respectively; ${\mathcal {E}}\{\cdot \}$ represents the mathematical expectation; ${\mathcal {L}}$ represents the diffusion operator; and matrices, if their dimensions are not explicitly stated, are assumed to be compatible for algebraic operations; For $r>0$, $C([-r,0];{\mathbb {R}}^{n})$ denotes the family of continuous function $\varphi$ from $[-r,0]$ to ${\mathbb {R}}^{n}$ with the norm $\Vert \varphi \Vert =\sup _{-r\le s\le 0}|\varphi (s)|$; $\dot{x}(t)$ denotes the derivative of $x(t)$; The Euclidean norm in ${\mathbb {R}}^{n}$ is denoted as $\Vert \cdot \Vert _{2}$, accordingly, for vector $x\in {\mathbb {R}}^{n}$, $\Vert x\Vert _{2}=\sqrt{x^{T}x}$; $A$ denotes a matrix of n-dimension, $|A|=(|a_{ij}|)_{n\times n}$, $\Vert A\Vert =\sqrt{\lambda _{max}(A^{T}A)},$ where $\lambda _{max}$ denotes the maximum eigenvalue of $A$.

The rest of this paper is organized as follows. In Sect. 2, the model formulation and some preliminaries are given. Finite-time synchronization of neural networks with mixed time-vary delays and stochastic disturbance can be achieved by designing two different controllers in Sect. 3. In Sect.  4, A numerical example is presented to demonstrate the validity of the proposed results, and in Sect. 5, this paper also demonstrates the effectiveness of application in secure communication. Some conclusions are drawn in Sect. 6.

2 Model description and preliminaries

In this paper, the manifold network is that

$$\begin{aligned} \dot{z}(t)&=-Cz(t)+Ag(z(t))+Bg(z(t-\alpha (t)))\nonumber \\&\quad +E\int _{t-\theta (t)}^{t}{g(z(s))ds}+J(t), \end{aligned}$$

(1)

where $z(t)\in {\mathbb {R}}$ is the state vector; $C=\text {diag}(c_{1},c_{2},\ldots ,c_{n})$, where $c_{i}(.)$ denotes self-inhibition of $ith$ neuron; $A=(a_{ij})_{n\times n}$, $B=(b_{ij})_{n\times n}$ and $E=(e_{ij})_{n\times n}$ are $n\times n$ real matrices representing, respectively, the neuron, the delayed neuron interconnection matrices and distributed neuron interconnection matrices; $g(x(t))=(g_{1}(x_{1}(t)), g_{2}(x_{2}(t)), \ldots ,g_{n}(x_{n}(t)))^{T}$ is a diagonal mapping, with $g_{i}(\cdot ),i=1,\ldots ,n$ modeling the non-linear input-output activation of $ith$ neuron; $J(t)=(J_{1}(t),J_{2}(t),\ldots ,J_{n}(t))^{T}$ is a constant external input; $\alpha (t)$ and $\theta (t)$ represent the discrete time delay and distribute time-delay, respectively, in the network; $z(t)=\phi _{0}(t)\in C([-\tau ,0];{\mathbb {R}}^{n})$ is the initial condition.

Consider the following stochastic neural network

$$\begin{aligned} d{x}(t)&=\left[ -Cx(t)+Ag(x(t))+Bg(x(t-\alpha (t)))\right. \nonumber \\&\quad \left. +E\int _{t-\theta (t)}^{t}{g(x(s))ds} +J(t)+u(t)\right] dt\nonumber \\&\quad +\sigma (t,e(t),e(t-\alpha (t)))dw(t), \end{aligned}$$

(2)

where $x(t)=(x_{1}(t),x_{2}(t),\ldots ,x_{n}(t))^{T}$ is the vector of neuron states at time $t$ and the system parameters $C,A,B$ and $g,\alpha (t),\theta (t),J(t)$ have the same definitions as those in (1); $e(t)=(e_{1}(t),e_{2}(t),\ldots ,e_{n}(t))=x(t)-z(t)$ denotes the error between the state variable $x(t)$ and the desired state vector $z(t)$; $w(t)\in {\mathbb {R}}$ is a Brownian motion and defined on a complete probability space $(\Omega ,{\mathcal {F}},{\mathcal {P}})$ satisfying $E\{dw(t)\}=0$ and $E\{dw^2(t)\}=dt, \ \sigma :{\mathbb {R}}^{+}\times {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}$ is the noise intensity function; $x(t)=\phi (t)\in \mathcal {L}^{2}_{{\mathcal {F}}_0}([-\tau ,0],{\mathbb {R}}^{n})$ is the initial condition with ${\mathcal {L}}^{2}_{{\mathcal {F}}_0}([-\tau ,0],{\mathbb {R}}^{n})$ denoting the set of ${\mathcal {F}}_0$-measurable $C([-\tau ,0];{\mathbb {R}}^{n})$-valued stochastic process $\xi =\{\xi (s)|-\tau \le s\le 0\}$ such that $\sup \nolimits _{-\tau \le s\le 0}E\{\Vert \xi (s)\Vert ^2\}<\infty$, $\tau =\max \nolimits _{t\in {\mathbb {R}} }\{\alpha (t),\theta (t)\}$. This type of stochastic perturbation can be regarded as a result from the occurrence of random uncertainties which affect the dynamic behavior of the controlled networks.

In this paper, we use the feedback controller and adaptive controller to achieve the synchronization of the different systems.

Then, the error system can be obtained from (1) and (2) is that

$$\begin{aligned} d{e}(t)&=\left[ -Ce(t)+A\tilde{g}(t)+B\tilde{g}(t-\alpha (t))\right. \nonumber \\&\left. \quad +E\int _{t-\theta (t)}^{t}{\tilde{g}(s)ds} +u(t)\right] dt\nonumber \\&\quad +\sigma (t,e(t),e(t-\alpha (t)))dw(t), \end{aligned}$$

(3)

where $\tilde{g}(t)=g(x(t))-g(z(t))$. The initial condition of the error system (3) on $[-\tau ,0]$ can be given by

$$\begin{aligned} e(t)=\varphi (t),\ \ t\in [-\tau ,0], \end{aligned}$$

where $\varphi (t)= \phi (t) - \phi _{0}(t)$. It is obvious that $\varphi (t) \in {\mathcal {L}}^{2}_{{\mathcal {F}}_0}([-\tau ,0],{\mathbb {R}}^{n})$.

Remark 1

In this paper, the model not only has the discrete time-varying delays, but also has the distributed time-varying delays, which means that the results of the work will be more general, better and more practical.

Throughout this paper, we make the following assumptions:

$(A_{1})$ Assume that there exists a positive definite diagonal matrix $L=diag(L_{1},L_{2},...,L_{n})>0$ such that the neuron activation function $g(\cdot )$ satisfies the following condition

$$\begin{aligned} |(g(y)-g(x)|\le |L(y-x)|,\quad \forall x,y\in {\mathbb {R}}^{n}. \end{aligned}$$

$(A_{2})$ In this paper, we assume $\sigma (\cdot )$ is locally Lipschitz continuous and satisfies the linear growth condition. Moreover, there exist positive definite matrices $U$ and $V$ such that

$$\begin{aligned}&\text {trace}\left\{ \sigma ^{T}(t,e(t),e(t-\alpha (t))) \sigma (t,e(t),e(t-\alpha (t))) \right\} \nonumber \\&\quad \le e^{T}(t)Ue(t)+e^{T}(t-\alpha (t))Ve(t-\alpha (t)). \end{aligned}$$

$(A_{3})$ Time-varying delays $\alpha (t)$ and $\theta (t)$ satisfy $0<\alpha (t)<\alpha$, $0<\theta (t)<\theta$ and $\dot{\alpha }(t)<\gamma <+\infty$ for all $t>0$, where $\alpha$ and $\theta$ are positive constants.

Definition 1

The network (1) and (2) is said to be stochastically synchronized in finite-time, if for a suitable designed controller, there exists a constant $t^{'} > 0$, such that

$$\begin{aligned} \lim _{t\rightarrow t^{'}} \mathcal {E}\Vert x(t)-z(t)\Vert _{2}=0, \end{aligned}$$

and ${\mathcal {E}}\Vert x(t)-z(t)\Vert _{2}\equiv 0,$ for $t>t^{'}$.

To obtain the main results of this paper, the following lemmas will be needed.

Lemma 1

([27]) Let $x\in {\mathbb {R}}^{n},y\in {\mathbb {R}}^{n}$ and a scalar $\varepsilon >0$. Then we have

$$\begin{aligned} x^{T}y+y^{T}x\le \varepsilon x^{T}x+\varepsilon ^{-1}y^{T}y. \end{aligned}$$

Lemma 2

([28]) If $m_{1},m_{2},\ldots ,m_{n}$ are positive number and $r>1$, then

$$\begin{aligned} \sum \limits _{i=1}^{n}m_{i}\ge \left( \sum \limits _{i=1}^{n}m_{i}^{r}\right) ^{\frac{1}{r}}. \end{aligned}$$

Lemma 3

([29]) For any positive definite matrix $M>0$, scalars $\gamma _{2}>\gamma _{1}>0$ and vector function $\omega :[\gamma _{1},\gamma _{2}]$ such that the integrations concerned are well defined, then the following inequality holds:

$$\begin{aligned}&\left( \int _{\gamma _{1}}^{\gamma _{2}}{\omega (s)ds}\right) ^{T}M\left( \int _{\gamma _{1}}^{\gamma _{2}}{\omega (s)ds}\right) \nonumber \\&\quad \le (\gamma _{2}-\gamma _{1})\int _{\gamma _{1}}^{\gamma _{2}} {\omega ^{T}(s)M\omega (s)ds}. \end{aligned}$$

Lemma 4

([30]) Assume that a continuous positive-definite function $V(t)$ satisfies the following differential inequality:

$$\begin{aligned} \dot{V}(t)\le -\alpha V^{\eta }(t),\quad \forall \ t\ge t_{0},V(t_{0})\ge 0, \end{aligned}$$

where $\alpha >0$, $0<\eta <1$ are two constants. Then, for any given $t_{0}$, $V(t)$ satisfies the following inequality:

$$\begin{aligned} V^{1-\eta }(t)\le V^{1-\eta }(t_{0})-\alpha (1-\eta )(t-t_{0}),\ \ t_{0}\le t\le t_{1}, \end{aligned}$$

and

$$\begin{aligned} V(t)\equiv 0,\quad \forall t\ge t_{1}, \end{aligned}$$

with $t_{1}$ given by

$$\begin{aligned} t_{1}=t_{0}+\frac{V^{1-\eta }(t_{0})}{\alpha (1-\eta )}. \end{aligned}$$

3 Main results

Theorem 1

Suppose the assumptions $(A_{1})$–$(A_{3})$ are satisfied, then the neural networks (1) and (2) can achieve finite-time synchronization under the following feedback controller:

$$\begin{aligned} u(t)=&-\Lambda e(t)-\eta sign(e(t))\nonumber \\&-\eta \left( \int _{t-\alpha (t)}^{t}{e^{T}(s)Pe(s)ds}\right) ^{\frac{1}{2}} \frac{e(t)}{\Vert e(t)\Vert ^{2}}\nonumber \\&-\eta \left( \int _{-\theta (t)}^{0}\int _{t+s}^{t}{\tilde{g} ^{T}(r)Q\tilde{g}(r)drds}\right) ^{\frac{1}{2}} \frac{e(t)}{\Vert e(t)\Vert ^{2}}, \end{aligned}$$

(4)

where $\Lambda =diag(\Lambda _{1},\Lambda _{2},\ldots ,\Lambda _{n})>0$ is constant diagonal matrix to be determined, $P>0$, $Q>0$, $\Lambda > -C+\Vert \bar{A}\Vert I+\frac{1}{2}|E||E|^{T} +\frac{P}{2}+\frac{\theta }{2}L^{T}QL+\frac{U}{2}+\frac{1}{2}I$, $\bar{A}=|A|L$, $P=\frac{1}{1-\gamma }(L^{T}|B|^{T}|B|L+V)$, and $\eta >0$ is a tunable constant.

Proof

Define the following Lyapunov functions candidate:

$$\begin{aligned} V(e_{t},t)&=\frac{1}{2}e^{T}(t)e(t) +\frac{1}{2}\int _{t-\alpha (t)}^{t}{e^{T}(s)Pe(s)ds}\nonumber \\&\quad +\frac{1}{2}\int _{-\theta (t)}^{0} \int _{t+s}^{t}{\tilde{g}^{T}(r)Q\tilde{g}(r)drds}, \end{aligned}$$

where $\{e_{t}=e(t+\theta )|t\ge 0,-\tau \le \theta \le 0\}$ is a stochastic process. By Itô formula, the stochastic differential $dV(e_{t},t)$ can be obtained as

$$\begin{aligned} dV(e_{t},t)\!=\!{\mathcal {L}}V(e_{t},t)+e^{T}(t)\sigma (t,e(t),e(t-\alpha (t)))dw(t), \end{aligned}$$

where

$$\begin{aligned} {\mathcal {L}}V(e_{t},t)&\le e^{T}(t)\left[ -Ce(t)+A\tilde{g}(t) +B\tilde{g}(t-\alpha (t))\right. \\&\quad \left. +E\int _{t-\theta (t)}^{t}{\tilde{g}(s)ds}+u(t)\right] \\&\quad +\frac{1}{2}e^{T}(t)Pe(t)\\&\quad -\frac{1}{2}(1-\dot{\alpha }(t))e^{T}(t-\alpha (t))Pe(t-\alpha (t))\\&\quad +\frac{\theta (t)}{2}\tilde{g}^{T}(t)Q\tilde{g}(t)-\frac{1}{2}\int _{t-\theta (t)}^{t}{\tilde{g}^{T}(s)Q\tilde{g}(s)ds}\\&\quad +\frac{1}{2}\text {trace}\left\{ \sigma ^{T}(t,e(t),e(t-\alpha (t)))\right. \\&\qquad \left. \sigma (t,e(t),e(t-\alpha (t)))\right\} \\&\le \!-e^{T}(t)Ce(t)\!+\!e^{T}(t)A\tilde{g}(t)\!+\!e^{T}(t)B\tilde{g}(t\!-\!\alpha (t))\\&\quad +e^{T}(t)E\int _{t-\theta (t)}^{t}{\tilde{g}(s)ds}\\&\quad -e^{T}(t)\Lambda e(t) -\eta e^{T}(t)sign(e(t))\\&\quad -e^{T}(t)\eta \left( \int _{t-\alpha (t)}^{t}{e^{T}(s)e(s)ds}\right) ^{\frac{1}{2}} \frac{e(t)}{\Vert e(t)\Vert ^{2}}\\&-e^{T}(t)\eta \left( \int _{-\theta (t)}^{t}\int _{t+s}^{t}{\tilde{g}^{T}(r)\tilde{g}(r)drds}\right) ^{\frac{1}{2}} \frac{e(t)}{\Vert e(t)\Vert ^{2}}\\&\quad -\frac{1}{2}(1-\dot{\alpha }(t))e^{T}(t-\alpha (t))Pe(t-\alpha (t))\\&\quad +\frac{\theta (t)}{2}\tilde{g}^{T}(t)Q\tilde{g}(t)-\frac{1}{2}\int _{t-\theta (t)}^{t}{\tilde{g}^{T}(s)Q\tilde{g}(s)ds}\\&\quad +\frac{1}{2}e^{T}(t)Pe(t)+\frac{1}{2}\text {trace}\left\{ \sigma ^{T}(t,e(t),\right. \\&\left. \quad \times e(t-\alpha (t)))\sigma (t,e(t),e(t-\alpha (t)))\right\} \\ \end{aligned}$$

$$\begin{aligned}&\le -e^{T}(t)Ce(t)+e^{T}(t)|A|Le(t)\\&\quad +e^{T}(t)|B|Le(t-\alpha (t))\\&\quad +|e^{T}(t)E\int _{t-\theta (t)}^{t}{\tilde{g}(s)ds}|-e^{T}(t)\Lambda e(t)\\&\quad -\eta e^{T}(t)sign(e(t))\\&\quad -e^{T}(t)\eta \left( \int _{t-\alpha (t)}^{t}{e^{T}(s)e(s)ds}\right) ^{\frac{1}{2}} \frac{e(t)}{\Vert e(t)\Vert ^{2}}\\&\quad -e^{T}(t)\eta \left( \int _{-\theta (t)}^{t}\int _{t+s}^{t}{\tilde{g}^{T}(r)\tilde{g}(r)drds}\right) ^{\frac{1}{2}} \frac{e(t)}{\Vert e(t)\Vert ^{2}}\\&\quad -\frac{1}{2}(1-\gamma )e^{T}(t-\alpha (t))Pe(t-\alpha (t))\\&\quad +\frac{1}{2}e^{T}(t)Pe(t)+\frac{\theta }{2}\tilde{g}^{T}(t)Q\tilde{g}(t)\\&\quad -\frac{1}{2}\int _{t-\theta (t)}^{t}{\tilde{g}^{T}(s)Q\tilde{g}(s)ds}\\&\quad +\frac{1}{2}e^{T}(t)Ue(t)+\frac{1}{2}e^{T}(t-\alpha (t))Ve(t-\alpha (t)).\\ \end{aligned}$$

On the other hand, by means of Lemma 3,

$$\begin{aligned} |e^{T}(t) E\int _{t-\theta (t)}^{t}{\tilde{g}(s)ds}|&\le \frac{1}{2}e^{T}(t)|E||E|^{T} e(t)\\&\quad +\frac{1}{2}\left( \int _{t-\theta (t)}^{t}{\tilde{g}(s)ds}\right) ^{T}\left( \int _{t-\theta (t)}^{t}{\tilde{g}(s)ds}\right) \\ \le&\frac{1}{2}e^{T}(t)|E||E|^{T} e(t)\\&\quad +\frac{\theta }{2}\left( \int _{t-\theta (t)}^{t}{\tilde{g} ^{T}(s)\tilde{g}(s)ds}\right) ,\\ e^{T}(t)|B|Le(t-\alpha (t))&\le \frac{1}{2}e^{T}(t)e(t)\\&\quad +\frac{1}{2}e^{T}(t-\alpha (t))L^{T}|B|^{T}|B|Le(t-\alpha (t)),\\ \frac{\theta }{2}\tilde{g}^{T}(t)Q\tilde{g}(t)&\le \frac{\theta }{2}e^{T}(t)L^{T}QLe(t), \end{aligned}$$

then

$$\begin{aligned} {\mathcal {L}}V(e_{t},t)&\le e^{T}(t)\left\{ -C+\Vert \bar{A}\Vert I\right. \nonumber \\&\quad +\frac{1}{2}|E||E|^{T} +\frac{P}{2}+\frac{\theta }{2}L^{T}QL\nonumber \\&\quad \left. +\frac{U}{2}+\frac{1}{2}I-\Lambda \right\} e(t)-\eta e^{T}(t)sign(e(t))\nonumber \\&\quad +e^{T}(t-\alpha (t))\left\{ \frac{1}{2}L^{T}|B|^{T}|B|L+\frac{V}{2}\right. \nonumber \\&\quad \left. -\frac{1-\gamma }{2}P\right\} e(t-\alpha (t))\nonumber \\&\quad -\eta \left( \int _{t-\alpha (t)}^{t}{e^{T}(s)Pe(s)ds}\right) ^{\frac{1}{2}}\nonumber \\&\quad -\eta \left( \int _{-\theta (t)}^{t}\int _{t+s}^{t}{\tilde{g} ^{T}(r)Q\tilde{g}(r)drds}\right) ^{\frac{1}{2}}. \end{aligned}$$

(5)

By virtue of $\Lambda > -C+\Vert \bar{A}\Vert I+\frac{1}{2}|E||E|^{T}+\frac{P}{2}+\frac{\theta }{2} L^{T}QL+\frac{U}{2}+\frac{1}{2}I$ and $P=\frac{1}{1-\gamma }(L^{T}|B|^{T}|B|L+V)$, one can get

$$\begin{aligned} {\mathcal {L}}V(e_{t},t)&\le -\eta e^{T}(t)sign(e(t))\\&\quad -\eta \left( \int _{t-\alpha (t)}^{t}{e^{T}P(s)e(s)ds}\right) ^{\frac{1}{2}}\\&\quad -\eta \left( \int _{-\theta (t)}^{t}\int _{t+s}^{t}{\tilde{g}^{T}(r)Q \tilde{g}(r)drds}\right) ^{\frac{1}{2}}.\\ \end{aligned}$$

Base on Lemma 2, one has

$$\begin{aligned} {\mathcal {L}}V(e_{t},t)&\le -\eta \left\{ \sum \limits _{i=1}^{n}|e_{i}(t)|^{2} +\int _{t-\alpha (t)}^{t}{e^{T}(s)Pe(s)ds}\right. \\&\quad \left. +\int _{-\theta (t)}^{t}\int _{t+s}^{t} {\tilde{g}^{T}(r)Q\tilde{g}(r)drds}\right\} ^{\frac{1}{2}}\\&=\! -\sqrt{2}\eta \left\{ \frac{1}{2}e^{T}(t)e(t)\!+\!\frac{1}{2} \int _{t-\alpha (t)}^{t}{e^{T}(s)Pe(s)ds}\right. \\&\quad \left. +\frac{1}{2}\int _{-\theta (t)}^{0}\int _{t+s}^{t} {\tilde{g}^{T}(r)Q\tilde{g}(r)drds}\right\} ^{\frac{1}{2}}\\&=-\sqrt{2}\eta V^{\frac{1}{2}}(t,e(t)). \end{aligned}$$

Hence,

$$\begin{aligned} {\mathcal {E}}[dV(e_{t},t)] =\,&{\mathcal {E}}[{\mathcal {L}}V(e_{t},t)dt]\\&\le {\mathcal {E}}\left\{ -\sqrt{2}\eta \left\{ \frac{1}{2}e^{T}(t)e(t)\right. \right. \\&\quad +\frac{1}{2}\int _{t-\alpha (t)}^{t}{e^{T}(s)Pe(s)ds}\\&\quad \left. \left. +\frac{1}{2}\int _{-\theta (t)}^{0}\int _{t+s}^{t}{\tilde{g} ^{T}(r)Q\tilde{g}(r)drds}\right\} ^{\frac{1}{2}}dt\right\} , \end{aligned}$$

therefore,

$$\begin{aligned} {\mathcal {E}}[\dot{V}(e_{t},t))]\le -\sqrt{2}\eta \left( {\mathcal {E}}[V(e_{t},t)]\right) ^{\frac{1}{2}}. \end{aligned}$$

By Lemma 4, ${\mathcal {E}}[V(e_{t},t)]$ converges to zero in a finite time, and the finite time is estimated by

$$\begin{aligned} t_{1}=\frac{\sqrt{2v(0)}}{\eta }. \end{aligned}$$

(6)

Hence, the error vector $e(t)$ will stochastically converge to zero within $t_{1}$. This completes the proof.$\square$

Theorem 2

Suppose the assumptions $(A_{1})$–$(A_{3})$ hold, then the neural networks (2) can finite-timely synchronize with (1) under the following adaptive controller:

$$\begin{aligned} \left\{ \begin{array}{l} u_{i}(t)=-k_{i}(t)e_{i}(t),\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \dot{k}_{i}(t)=\varepsilon _{i}\left[ e_{i}^{2}(t)-\frac{\Lambda _{i} }{k_{i}(t)}e_{i}^{2}(t)\right. \\ \ \ \ \ \ \ \ \ \ \ -\frac{e_{i}(t)}{k_{i}(t)}\eta sign(e_{i}(t))-\frac{\eta }{\sqrt{\varepsilon _{i}}}sign(k_{i}(t))\\ \ \ \ \ \ \ \ \ \ \ \ -\frac{\eta }{k_{i}(t)}\sqrt{\lambda _{max}(P)}\left( \displaystyle \int _{t-\alpha (t)} ^{t}{e^{2}_{i}(s)ds}\right) ^{\frac{1}{2}}\\ \ \ \ \ \ \ \ \ \ \ \ \left. -\frac{\eta }{k_{i}(t)}\sqrt{\lambda _{max}(Q)} \left( \displaystyle \int _{-\theta (t)}^{0}\displaystyle \int _{t+s}^{t} {\tilde{g}^{2}_{i}(r)drds}\right) ^{\frac{1}{2}}\right] ,\\ \ \ \ \ \ \ \ \ \ \ \ i =1,2,\ldots ,n, \end{array} \right. \end{aligned}$$

(7)

where $\Lambda =diag(\Lambda _{1},\Lambda _{2},...,\Lambda _{n})>0$ is constant diagonal matrix to be determined, $P>0$, $Q>0$, $\Lambda > -C+\Vert \bar{A}\Vert I+\frac{1}{2}|E||E|^{T}+\frac{P}{2} +\frac{\theta }{2}L^{T}QL+\frac{U}{2}+\frac{1}{2}I$, $\bar{A}=|A|L$, $P=\frac{1}{1-\gamma }(L^{T}|B|^{T}|B|L+V)$, and $\eta >0$ is a tunable constant.

Proof

Define the following Lyapunov function candidate:

$$\begin{aligned} V(e_{t},t)&=\frac{1}{2}e^{T}(t)e(t) +\int _{t-\alpha (t)}^{t}{e^{T}(s)Pe(s)ds}\\&\quad +\frac{1}{2}\int _{-\theta (t)}^{0}\int _{t+s}^{t}{\tilde{g} ^{T}(r)Q\tilde{g}(r)drds}\\&\quad +\frac{1}{2}\sum \limits _{i=1}^{n}\frac{1}{\varepsilon _{i}}k_{i}^{2}(t), \end{aligned}$$

where $\left\{ e_{t}=e(t+\theta )|t\ge 0,-\tau \le \theta \le 0\right\}$ is a stochastic process. By Itô formula, the stochastic differential $dV(e_{t},t)$ can be obtained as

$$\begin{aligned} dV(e_{t},t)\!=\!{\mathcal {L}}V(e_{t},t)\!+\!e^{T}(t)\sigma (t,e(t),e(t-\alpha (t)))dw(t), \end{aligned}$$

where

$$\begin{aligned} {\mathcal {L}}V(e_{t},t)\le&e^{T}(t)\Bigg [-Ce(t)+A\tilde{g}(t) +B\tilde{g}(t-\alpha (t))\\&+E\int _{t-\theta (t)}^{t}{\tilde{g}(s)ds}+u(t)\Bigg ]\\&+\frac{1}{2}e^{T}(t)Pe(t)\\&-\frac{1}{2}(1-\dot{\alpha }(t))e^{T}(t-\alpha (t))Pe(t-\alpha (t))\\&+\frac{\theta (t)}{2}\tilde{g}^{T}(t)Q\tilde{g}(t)-\frac{1}{2}\int _{t-\theta (t)}^{t}{\tilde{g}^{T}(s)Q\tilde{g}(s)ds}\\&+\frac{1}{2}\text {trace}\Big \{\sigma ^{T}(t,e(t),e(t-\alpha (t)))\\&\qquad \sigma (t,e(t),e(t-\alpha (t)))\Big \}\\ \le&\!-e^{T}(t)Ce(t)\!+\!e^{T}(t)A\tilde{g}(t)\!+\!e^{T}(t)B\tilde{g}(t\!-\!\alpha (t))\\&+e^{T}(t)E\int _{t-\theta (t)}^{t}{\tilde{g}(s)ds}\\&-e^{T}(t)\Lambda e(t) -\eta e^{T}(t)sign(e(t))\\&-e^{T}(t)\eta \Big (\int _{t-\alpha (t)}^{t}{e^{T}(s)e(s)ds}\Big )^{\frac{1}{2}} \frac{e(t)}{\Vert e(t)\Vert ^{2}}\\ {}&-e^{T}(t)\eta \Big (\int _{-\theta (t)}^{t}\int _{t+s}^{t}{\tilde{g}^{T}(r)\tilde{g}(r)drds}\Big )^{\frac{1}{2}} \frac{e(t)}{\Vert e(t)\Vert ^{2}}\\&-\frac{1}{2}(1-\dot{\alpha }(t))e^{T}(t-\alpha (t))Pe(t-\alpha (t))\\&+\frac{\theta (t)}{2}\tilde{g}^{T}(t)Q\tilde{g}(t)-\frac{1}{2}\int _{t-\theta (t)}^{t}{\tilde{g}^{T}(s)Q\tilde{g}(s)ds}\\&+\!\frac{1}{2}e^{T}(t)Pe(t)\!+\!\frac{1}{2}\text {trace}\Big \{\sigma ^{T}(t,e(t),e(t-\alpha (t)))\\&\times \sigma (t,e(t),e(t-\alpha (t)))\Big \}\\ \end{aligned}$$

$$\begin{aligned}&\le -e^{T}(t)Ce(t)+e^{T}(t)|A|Le(t)\\&\quad +e^{T}(t)|B|Le(t-\alpha (t))\\&\quad +|e^{T}(t)E\int _{t-\theta (t)}^{t}{\tilde{g}(s)ds}|-e^{T}(t)\Lambda e(t)\\&\quad -\eta e^{T}(t)sign(e(t))\\&\quad -e^{T}(t)\eta \Big (\int _{t-\alpha (t)}^{t}{e^{T}(s)e(s)ds}\Big )^{\frac{1}{2}} \frac{e(t)}{\Vert e(t)\Vert ^{2}}\\&\quad -e^{T}(t)\eta \Big (\int _{-\theta (t)}^{t}\int _{t+s}^{t}{\tilde{g}^{T}(r)\tilde{g}(r)drds}\Big )^{\frac{1}{2}} \frac{e(t)}{\Vert e(t)\Vert ^{2}}\\&\quad -\frac{1}{2}(1-\gamma )e^{T}(t-\alpha (t))Pe(t-\alpha (t))\\&\quad +\frac{1}{2}e^{T}(t)Pe(t)+\frac{\theta }{2}\tilde{g}^{T}(t)Q\tilde{g}(t)\\&\quad -\frac{1}{2}\int _{t-\theta (t)}^{t}{\tilde{g}^{T}(s)Q\tilde{g}(s)ds}\\&\quad +\frac{1}{2}e^{T}(t)Ue(t)+\frac{1}{2}e^{T}(t-\alpha (t))Ve(t-\alpha (t)).\\ \end{aligned}$$

$$\begin{aligned}&\le -e^{T}(t)Ce(t)+e^{T}(t)|A|Le(t)\\&\quad +e^{T}(t)|B|Le(t-\alpha (t))\\&\quad +|e^{T}(t)E\int _{t-\theta (t)}^{t}{\tilde{g}(s)ds}|-e^{T}(t)K(t) e(t)\\&\quad +\frac{1}{2}e^{T}(t)Pe(t)\\&\quad -\frac{1}{2}(1-\gamma )e^{T}(t-\alpha (t))Pe(t-\alpha (t))\\&\quad +\frac{\theta }{2}\tilde{g}^{T}(t)Q\tilde{g}(t)\\&\quad -\frac{1}{2}\int _{t-\theta (t)}^{t}{\tilde{g}^{T}(s)Q\tilde{g}(s)ds}\\&\quad +e^{T}(t)K(t)e(t)-e^{T}(t)\Lambda e(t)\\&\quad +\frac{1}{2}e^{T}(t)Ue(t)\\&\quad +\frac{1}{2}e^{T}(t-\alpha (t))Ve(t-\alpha (t))\\&\quad -\eta \sum \limits _{i=1}^{n}|e_{i}(t)|\\&\quad -\eta \sum \limits _{i=1}^{n} \frac{1}{\sqrt{\varepsilon _{i}}}|k_{i}(t)| -\eta \left( \int _{t-\alpha (t)}^{t}{e^{T}(s)Pe(s)ds}\right) ^{\frac{1}{2}}\\&\quad \left. -\eta \left( \int _{-\theta (t)}^{0}\int _{t+s}^{t}{\tilde{g} ^{T}(r)Q\tilde{g}(r)drds}\right) ^{\frac{1}{2}}\right] \\ \end{aligned}$$

$$\begin{aligned}&\le e^{T}(t)\left\{ -C+\Vert \bar{A}\Vert I+\frac{1}{2}|E||E|^{T}+\frac{P}{2}\right. \nonumber \\&\quad \left. +\frac{\theta }{2}L^{T}QL+\frac{U}{2}+\frac{1}{2}I-\Lambda \right\} e(t)\nonumber \\&\quad +e^{T}(t-\alpha (t))\left\{ \frac{1}{2}L^{T}|B|^{T}|B|L\right. \nonumber \\&\quad \left. +\frac{V}{2}-\frac{1-\gamma }{2}P\right\} e(t-\alpha (t))\nonumber \\&\quad -\eta \left( \int _{t-\alpha (t)}^{t}{e^{T}(s)Pe(s)ds}\right) ^{\frac{1}{2}}\nonumber \\&\quad -\eta \left( \int _{-\theta (t)}^{t}\int _{t+s}^{t}{\tilde{g}^{T}(r)Q\tilde{g}(r)drds}\right) ^{\frac{1}{2}}\nonumber \\&\quad -\eta e^{T}(t)sign(e(t)) -\eta \sum \limits _{i=1}^{n}\frac{1}{\sqrt{\varepsilon _{i}}}|k_{i}(t)|. \end{aligned}$$

(8)

By virtue of $\Lambda > -C+\Vert \bar{A}\Vert I+\frac{1}{2}|E||E|^{T}+\frac{P}{2} +\frac{\theta }{2}L^{T}QL+\frac{U}{2}+\frac{1}{2}I$, $P=\frac{1}{1-\gamma }(L^{T}|B|^{T}|B|L+V)$ and Lemma 2, one gets

$$\begin{aligned} {\mathcal {L}}V(e_{t},t)&\le -\eta \left\{ \sum \limits _{i=1}^{n}|e_{i}(t)|^{2} +\int _{t-\alpha (t)}^{t}{e^{T}(s)Pe(s)ds}\right. \\&\quad +\int _{-\theta (t)}^{t}\int _{t+s}^{t}{\tilde{g}^{T}(r)Q\tilde{g}(r)drds}\\&\quad \left. +\sum \limits _{i=1}^{n}\frac{1}{\varepsilon _{i}} |k_{i}(t)|^{2}\right\} ^{\frac{1}{2}}\\&= -\sqrt{2}\eta \left\{ \frac{1}{2}e^{T}(t)e(t)\!+\!\frac{1}{2} \int _{t-\alpha (t)}^{t}{e^{T}(s)Pe(s)ds}\right. \\&\quad +\frac{1}{2}\int _{-\theta (t)}^{0}\int _{t+s}^{t} {\tilde{g}^{T}(r)Q\tilde{g}(r)drds}\\&\quad \left. +\frac{1}{2}\sum \limits _{i=1}^{n}\frac{1}{\varepsilon _{i}}k_{i}^{2}(t)\right\} ^{\frac{1}{2}}\\&=-\sqrt{2}\eta V^{\frac{1}{2}}(t,e(t)). \end{aligned}$$

Therefore,

$$\begin{aligned} {\mathcal {E}}[\dot{V}(e_{t},t)]\le -\sqrt{2}\eta \left( {\mathcal {E}}[V(e_{t},t)]\right) ^{\frac{1}{2}}. \end{aligned}$$

By Lemma 4, ${\mathcal {E}}[V(e_{t},t)]$ converges to zero in a finite time, and the finite time is estimated by

$$\begin{aligned} t_{2}=\frac{\sqrt{2v(0)}}{\eta }. \end{aligned}$$

(9)

Hence, the error vector $e(t)$ will stochastically converge to zero within $t_{2}$. This completes the proof.$\square$

Remark 2

In this paper, one adopts feedback control and adaptive control techniques to guarantee the stochastic finite-time synchronization of chaotic neural networks with mixed time-varying delays. As far as we are concerned, although there are many papers focusing on the finite-time synchronization or stability [25, 26, 31–34], few works concerning finite-time synchronization with mixed time-varying delays and stochastic perturbation have been published. Therefore, the results have better robustness and disturbance rejection properties, which shows that they are more practical than those in [25, 26, 31–34].

Remark 3

From the proof of Theorems 1 and 2, we can see the important roles that parameters $\Lambda =diag(\Lambda _{1},\Lambda _{2},\ldots ,\Lambda _{n})$ and the tunable constant $\eta$ played in the feedback controller (4) and adaptive controllers (7). The inequalities (5) and (8) indicate that the synchronization rate increases when $\Lambda =diag(\Lambda _{1},\Lambda _{2},\ldots ,\Lambda _{n})$ and the tunable constant $\eta$ increase. On the other hand, whether the network (1) and (2) can be synchronized or not relies on the value of $\Lambda =diag(\Lambda _{1},\Lambda _{2},\ldots ,\Lambda _{n})$ and $\eta$, whereas the synchronization time depends on the value of $\eta$, and has nothing to do with the value of $\Lambda =diag(\Lambda _{1},\Lambda _{2},\ldots ,\Lambda _{n})$. If the value of $\Lambda =diag(\Lambda _{1},\Lambda _{2},\ldots ,\Lambda _{n})$ is less than some value, then stochastic chaotic networks (2) cannot synchronize with the manifold system (1).

4 Illustrative examples

In this section, a numerical example has been given to show that our theoretical results obtained above are effective.

Example 1

Consider the two-node delayed stochastic neural network mode (2) with the following parameters: $x(t)=(x_{1}(t),x_{2}(t))^{T}, z(t)=(z_{1}(t),z_{2}(t))^{T},J(t)=(0,0), \alpha (t)=\theta (t)=0.6(e^{t})/(1+e^{t})$, and

$$\begin{aligned} A&=\begin{pmatrix}1.7&{}\quad -0.12\\ -5.2&{}\quad 3.5\end{pmatrix},\, B=\begin{pmatrix}-1.7&{}\quad -0.12\\ -0.25&{}\quad -2.4\end{pmatrix},\\ C&=\begin{pmatrix}1&{}\quad 0\\ 0&{}\quad 0.5\end{pmatrix},\, E=\begin{pmatrix}0.12&{}\quad 0\\ 0&{}\quad -0.12\end{pmatrix},\ \end{aligned}$$

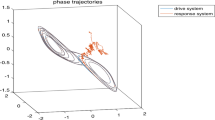
$g_{1}(t)=g_{2}(t)=tanh(t)$. Figure 1 shows the chaotic-like trajectory (2) with initial condition $x(t)=(-0.2,-0.3)^{T}, t\in [-1,0].$ The noise intensity function matrix is taken as

$$\begin{aligned} \sigma (t,e(t),e(t\!-\!\alpha (t)))&= \begin{pmatrix}0.2&{}\quad 0&{}\quad 0.01&{}\quad 0\\ 0&{}\quad 0.2&{}\quad 0&{}\quad 0.01\end{pmatrix}\\&\quad \times \begin{pmatrix}e(t)\\ e(t-\alpha (t))\end{pmatrix}. \end{aligned}$$

Here, It is straightforward to check that all the conditions in Theorem 1 hold. Obviously, neural networks (2) satisfies $(A_{1})-(A_{3})$ with $L_{i}=1,i=1,2,\alpha =\theta =0.6,\gamma =0.15,$ letting $\eta =0.15$,

$$\begin{aligned} Q=\begin{pmatrix}1&{}\quad 0\\ 0&{}\quad 1\end{pmatrix},\quad U=\begin{pmatrix}0.2&{}\quad 0\\ 0&{}\quad 0.2\end{pmatrix},\quad V=\begin{pmatrix}0.01&{}\quad 0\\ 0&{}\quad 0.01\end{pmatrix}\!. \end{aligned}$$

Consider the following manifold (1) with the initial condition $z(t)=(0.3,0.5)^{T},\ t\in [-1,0]$.

According to the conditions in Theorem 1, we get that

$$\begin{aligned} P=\begin{pmatrix}3.48&{}\quad 0.95\\ 0.95&{}\quad 6.8\end{pmatrix},\quad \Lambda =\begin{pmatrix}10&{}\quad 0\\ 0&{}\quad 12\end{pmatrix}.\ \end{aligned}$$

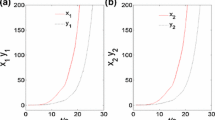
It follows from Theorem 1 that system (2) can finite-timely synchronize with the desired system (1) under the feedback controller (4) and adaptive controllers (7). We get the simulations shown in Figs. 2, 3, 4, 5 and 6. The Figs. 2, 3 show the $x_{1}(t) \ and \ z_{1}(t)$, $x_{2}(t) \ and \ z_{2}(t)$ can not achieve synchronization without any controller. Figures 4, 5 present that the system (2) and manifold system (1) can realize finite-time synchronization under feedback controller and adaptive controller, respectively. Figure 6 shows the trajectories of control parameters $k_{i}(t), i=1,2$ of adaptive controllers (7).

Fig. 1

Chaotic-like trajectory of system (2)

Fig. 2

Time-domain behavior of the state variables $x_{1}(t)$ and $z_{1}(t)$ without controller

Fig. 3

Time-domain behavior of the state variables $x_{2}(t)$ and $z_{2}(t)$ without controller

Fig. 4

Time response of synchronization error between system (1) and (2) under the feedback controller (4)

Fig. 5

Time response of synchronization error between system (1) and (2) under the adaptive controllers (7)

Fig. 6

Trajectories of control parameters $k_{i}(t), i=1,2$ of adaptive controllers (7)

5 Application in secure communication

In this section, the adaptive synchronization scheme proposed in Theorem 2 is applied to chaotic secure communications. An information signal $p(t)$ carrying the message to be transmitted can be masked by the chaotic signal $x(t)$. The finite-time chaotic synchronization discussed above can be used to extract the message at the receiver. Different strategies can be used to make the actual transmitted signal $v(t)$ as broadband as possible, so that make its detection through spectral techniques difficult. In general, three strategies are proposed in secure communications with chaos [35–37]. One is signal masking, where $v(t)= x(t)+ \delta p(t)$; another is modulation, $v(t)= x(t)p(t)$; the third is a combination of masking and modulation, such as $v(t)= x(t)[1+ \delta p(t)]$. We only focus on the first chaotic masking in this paper. Figure 7 shows the proposed communication system consisting of a transmitter and receiver. The transmitted signal is $v(t)= x(t)+ \delta p(t)$. In addition, it is also injected into the transmitter and, simultaneously, transmitted to the receiver. By the proposed adaptive synchronization scheme, a chaotic receiver is derived to recover the message signal at the receiving end. We propose the following masking technique. The transmitter is designed as

$$\begin{aligned} d{x}_{1}(t)&=\left[ -0.9x_{1}(t)+\sum _{j=1}^{2}a_{1j}g_{j}(x_{j}(t))\right. \\&\quad +\sum _{j=1}^{2}b_{1j}g_{j}(x_{j}(t-\alpha (t)))\\&\quad \left. +\sum _{j=1}^{2}e_{1j}\int _{t-\theta (t)}^{t}{g_{j}(x_{j}(s))ds}+u_{1}(t)\right] dt\\&\quad +\sigma _{1}(t,e_{1}(t),e_{1}(t-\alpha (t)))dw(t)+p_{1}(t),\\ d{x}_{2}(t)&=\left[ -0.5x_{2}(t)+\sum _{j=1}^{2}a_{2j}g_{j}(x_{j}(t))\right. \\&\quad +\sum _{j=1}^{2}b_{2j}g_{j}(x_{j}(t-\alpha (t)))\\&\quad \left. +\sum _{j=1}^{2}e_{2j}\int _{t-\theta (t)}^{t}{g_{j}(x_{j}(s))ds}+u_{2}(t)\right] dt\\&\quad +\sigma _{2}(t,e_{2}(t),e_{2}(t-\alpha (t)))dw(t),\\ \end{aligned}$$

where $p_{1}(t)=\delta p(t)$ is the information message. It should be noted that the message signal must possess low power, i.e., be small in comparison to the chaotic carrier in general [37]. To assure this, we take $\delta =0.1$. The receiver is designed as

$$\begin{aligned} d{y}_{1}(t)&=\left[ -0.9y_{1}(t)+\sum _{j=1}^{2}a_{1j}g_{j}(y_{j}(t))\right. \\&\quad +\sum _{j=1}^{2}b_{1j}g_{j}(y_{j}(t-\alpha (t)))\\&\quad \left. +\sum _{j=1}^{2}e_{1j}\int _{t-\theta (t)}^{t}{g_{j}(y_{j}(s))ds}-y_{1}(t)+l_{1}(t)\right] dt,\\ d{y}_{2}(t)&=\left[ -0.5y_{2}(t)+\sum _{j=1}^{2}a_{2j}g_{j}(y_{j}(t))\right. \\&\quad +\sum _{j=1}^{2}b_{2j}g_{j}(y_{j}(t-\alpha (t)))\\&\quad \left. +\sum _{j=1}^{2}e_{2j}\int _{t-\theta (t)}^{t}{g_{j}(y_{j}(s))ds}-y_{2}(t)+l_{2}(t)\right] dt,\\ \end{aligned}$$

where $l_{1}(t)= v(t)= x_{1}(t)+ \delta p(t)$ is the transmitted signal, $l_{2}(t)= x_{2}(t)$. The information message can be recovered by $r(t)= \delta ^{-1} [v(t)- y_{1}(t)]$. In the simulations, we take the same parameters and functions as Example 4.1 in Sect. 4, and choose the initial information message as $p(t)=0.2$. Since the eigenfrequency of the message signal $p(t)$ is much less than the oscillating frequency of the chaotic system in practice, we can get $\dot{p}(t)\approx 0$. Figure 8 depicts the error between the transmitted signal $p(t)$ and the recovered signal $r(t)$.

Fig. 7

Secure communication system based on adaptive synchronization

Fig. 8

Error between the transmitted signal $p(t)$ and the recovered signal $r(t)$

From the simulations, one can get that the signal can be exactly recovered under the adaptive controller. The developed results check the simulations perfectly.

6 Conclusion

In this paper, the finite-time synchronization between the drive-response systems in the mean square sense has been investigated for neural networks with mixed-time delays. Compared to the results in [25, 26], there have mixed time-varying delays in the model of this paper, which are more applicable in practice. Since finite-time synchronization has better robustness and disturbance rejection properties, the results of this work are of great importance. A numerical example has been given to illustrate the effectiveness of the present results. Furthermore, an application scheme for secure communication is presented in theory, and numerical simulation illustrates the effectiveness.