1 Introduction

Decision making can be defined as a process of finding a way to use one process to control another process. In multiple criteria (or attribute) decision making (MCDM/MADM) problem, a decision maker selects or ranks alternatives after qualitative and/or quantitative assessment of finite set of interdependent or independent attributes. The increasing complexity of the socio-economic environment makes it less and less possible for a single decision maker (DM) to consider all relevant aspects of a problem.

As a result, many decision making processes, in the real-world, take place in group settings. The increased interest in shared decision making derives from a number of different factors, for example, informed consent, mutual benefits, cooperative agendas, bonus, etc. Moving from a single DM setting to the group setting introduces a great deal of complexity in the MAGDM process. However, preference information in real-world situations can be assessed easily in a qualitative way which is vague possessing imprecise knowledge rather than completely known quantitative information. In such cases, ambiguity caused by vague or imprecise preference information is a big challenge for DMs. This fact was a great motivation for researchers to extend MAGDM techniques in fuzzy environment.

Thus, fuzzy set theory, introduced by Zadeh [1], has been used and adopted as a means of representing and manipulating data that was not precise, but rather fuzzy. Fuzzy MADM methods are proposed to solve problems which involve fuzzy data. Bellman and Zadeh [2] were the first to utilize fuzzy set theory concepts to decision making problems. Zimmermann [3] among others treated the fuzzy MADM method as a two-phase process. The first phase requires finding the fuzzy utilities (fuzzy final ratings) of alternatives. The second phase requires applying fuzzy ranking methods to determine the ranking order of alternatives, and thus, fuzzy MAGDM (FMAGDM) methods were developed in order to encompass shared decision making [4].

The fuzziness as well as hesitation of the expert’s subjective assessments which are not accounted for are modelled or reflected though IFS. The choice of using IFS in this study is based on the fact that, it is more capable than traditional fuzzy sets to handle vagueness and uncertain information in practice. Unlike the traditional fuzzy set theory, IFS, as introduced by Atanassov [5, 6] is characterized by membership and non-membership degree, such that the sum of membership and non-membership degree is less than or equal to one, keeping room for hesitation or uncertainty. In some cases, determining precisely the exact value of the attribute in terms of membership, non-membership and hesitation degree is difficult and as a result of this, their values are considered as intervals, thereby the coining of the term called IVIFS by Atanassov and Gargov [7].

Consider that DMs or experts usually come from different specialty fields and thus each DM has unique characteristics with respect to knowledge, skills, experience and personality, which implies that each DM may have different influence in the overall decision result. That is, the weights of DMs can be different. Also, since each attribute is different and has its own utility, every attribute also has its own grade of importance provided by the DM in the decision making process. Thus, in the process of MAGDM, attributes weights can take various forms such as completely known, subjective information, partially known or completely unknown weights depending upon the nature, psychology, expertise, state of mind, knowledge, technical know-how, topic of interest, etc., of DMs. The DM can be sure about the utility value of each attribute and hence able to impart an exact importance degree in the form of crisp weights, whether equal or unequal, depending upon the case may be. The form of attributes weights can be of subjective evaluation such as intuitionistic fuzzy number (IFN) or interval valued intuitionistic fuzzy number (IVIFN) or any other variation of fuzzy set or IFS. Due to factors like time pressure, lack of knowledge or data or the expert’s limited expertise about the problem domain, etc., the information about attributes weights can be incomplete or partially known. For instance, the DM might pay more attention to the importance of some attributes, i.e. specify some preference relation on weights of attributes according to his/her knowledge, experience and judgement. Such information of attributes weights is incomplete. Usually incomplete information of attributes weights can be obtained according to partial preference relation on weights given by the DM and has several different forms of structures [8,9,10]. These incomplete weight information structures may be expressed in the following five basic relations among attributes weights such as (i) weak ranking, (ii) strict ranking, (iii) ranking of differences, (iv) ranking with multiples and (v) interval form [11]. Also, there may exist a situation when there is no weight information available, and one of the most eminent methods is the entropy method to determine objective weights. An entropy-based object weighting scheme determines the weight for a set of attributes by quantifying the amount of information within the decision matrix and based on evaluation values. Hence, the bigger the entropy is, the smaller the weight assigned to an attribute and vice versa.

TOPSIS is a multiple criteria decision analysis method introduced by Hwang and Yoon [12], which is based upon the concept that it simultaneously considers the distance to both positive ideal solution (PIS) and negative ideal solution (NIS) to rank the alternatives. The PIS is identified with a hypothetical alternative that has the best values among all considered attributes, whereas the NIS is identified with a hypothetical alternative that has the worst attribute values. For instance, the PIS maximizes the benefit attribute and minimizes the cost attribute, whereas the NIS maximizes the cost attribute and minimizes the benefit attribute. The procedure by Hwang and Yoon [12] for implementing TOPSIS technique is as follows: After forming an initial decision matrix, the procedure starts by normalizing the decision matrix. This is followed by building the weighted normalized decision matrix and thus, determining the PIS and NIS and hence, calculating the separation measures for each alternative in the next step. The procedure ends by computing the relative closeness coefficient and thus the set of alternatives are ranked and the most preferable one is selected. Here, in our approach, the inclusion of multiple DMs is inculcated which is crucial as the state of the decision problem changes, both autonomously and as a consequence of the DMs action. Second, it suggests that even once an individual’s risk orientation is fixed, individual or group DMs can be purposefully selected on the basis of their outcome histories and risk propensity to influence the likelihood that more or less risky decisions will be made because the economic cost of a bad decision is indeed an element of risk. After aggregating over DMs weight, the aggregated matrix is normalized. Attributes weights are aggregated over DMs weights depending upon the information supplied for attributes weights. Further, advantage and disadvantage scores are found which are more realistic and reasonable instead of hypothetical ideal benchmarks which are too impractical to be achieved in the non-ideal unrealistic decision making environment. There scores are further weighted over attributes weights and hence aggregated to find closeness coefficient in order to rank the alternatives and choose the preferable one.

There is quite less research on TOPSIS taking multiple DMs under the realm of intuitionistic fuzzy (IF) environment. For instance, TOPSIS method is extended under the arena of MAGDM problems using IFS as spotted in the following literature. Su et al. [13] investigated the dynamic IF–MAGDM problem and employs IF-TOPSIS method to calculate the individual relative closeness coefficient of each alternative for each DM in order to obtain the individual ranking of alternatives. Aikhuele and Turan [14] proposed a new approach based on IF-TOPSIS model, applied using the exponential related function for the computation of the separation measures from the IF–PIS and IF–NIS, thereby finding the preferable alternative. Boran et al. [15] proposed TOPSIS method combined with IFS to select appropriate suppliers in group decision making environment. Liu et al. [16] introduced a new modified TOPSIS method, named IF hybrid TOPSIS approach to determine the risk priorities of failure modes identified in failure mode and effect analysis. Rouyendegh [17] proposed a unification of fuzzy TOPSIS and data envelopment analysis (DEA) to select the units with most efficiency and provide a full ranking in the DEA context for all units by aggregating individual opinions of DMs for rating the importance of attributes and alternatives. Yue [18] proposed the TOPSIS-based group decision making methodology under IF setting. Büyüközkan and Güleryüz [19] provided an effective MCDM approach with group decision making to evaluate different smart phone alternatives according to consumer preferences using IF-TOPSIS. Li [20] extended the TOPSIS for solving MAGDM problems under Atanassov IF environment. Furthermore, quite less research is being carried on applying IVIFS in the extended TOPSIS method as a group decision making problem. For instance, an extended TOPSIS method for group decision making with IVIFNs is proposed to solve the partner selection problem under incomplete and uncertain information environment in [21]. Park et al. [22] extended the TOPSIS method to solve MAGDM problems in interval valued intuitionistic fuzzy (IVIF) environment in which all the preference information provided by the DMs is presented as IVIF decision matrices and the information about attributes weights is partially known. Tan [23] investigated the extension of TOPSIS, a multi-criteria IVIF decision making technique to a group decision environment, where interdependent or interactive characteristics among criteria and preference of DMs are taken into account and dealt with. Zhang and Xu [24] developed a soft computing technique based on maximizing consensus and fuzzy TOPSIS in order to solve IVIF–MAGDM problems from two aspects of decision data. Izadikhah [25] proposed an extended TOPSIS method for group decision making with IVIFNs to solve the supplier selection problem under incomplete and uncertain information environment.

In a similar vein, this study is, therefore, presenting a new approach based on an IF-TOPSIS model under group decision making. That is, TOPSIS method is extended under MAGDM paradigm under the influence of both IFS and IVIFS, while taking all the four variations of attributes weights in the said approach such as completely known crisp weights, subjective evaluations in the form of IFN as well as IVIFN, incompletely known partial weights and the case of completely unknown weights.

1.1 Focus of the Paper

In this paper, we examine the IF–MAGDM problems wherein TOPSIS method has been extended under IF setting, viz. utilizing IFS as well as IVIFS. Since we are dealing under the domain of MAGDM problems, multiple DMs provide input data in the form of assessment information, attributes weights and DMs weights by the expert judges in the framework of both IFS and IVIFS. Varied possible cases for attributes weights information have been inculcated in the decision making process, viz. completely known weights, uncertain subjective evaluations in the form of IFN as well as IVIFN, incompletely known partial weights or completely unknown weights. Crisp DMs weights are obtained in order to aggregate judgement values by different DMs into a cumulative assessment decision matrix as well as composite weight matrix encompassing the grades of importance of various DMs reflecting the expertise and technical know-how in their own domains using weighted arithmetic (WA) and weighted geometric (WG) operators, respectively under the realm of IFS and IVIFS. Further, advantage and disadvantage scores are employed to analyse the performance estimation of each alternative with the rest on the given attribute. This leads to strength and weakness scores to be evaluated corresponding to each alternative as a function of the weight vector which are henceforth incorporated into the performance degrees to ascertain the ranking order of the alternatives under question.

1.2 Major Distinguishing Features of the Proposed Approach

  1. 1.

    The role of multiple DMs is being considered here, which is crucial as the state of the decision problem changes, both autonomously and as a consequence of the DMs actions. Second, it suggests that even once an individual’s risk orientation is fixed, individual or group DMs can be purposively selected on the basis of their outcome histories and risk propensity to influence the likelihood that more or less risky decisions will be made because the economic cost of a bad decision is indeed an element of risk.

  2. 2.

    In this paper, besides the membership and non-membership degrees, the hesitancy degree is also treated at its independent level of importance in the whole methodology and ranking of the alternatives is done on the basis of trade-off values of all the three parameters in the whole process. Comprehending hesitation can provide a significant universal insight into human awareness and behaviour. Whatever we do or observe others doing occurs in a temporal frame of reference and hence involves some degree of hesitation. In this paper, we take into account the triplet, viz. membership degree, non-membership degree and hesitation margin which is not yet fully considered in the research pertaining to MAGDM problems including TOPSIS as an MCDM method involving IFS as well as IVIFS.

  3. 3.

    Instead of obtaining ideal benchmarks in the form of PIS as well as NIS in MAGDM problems undertaking TOPSIS methodology [14, 16], this methodology, instead considers advantage as well as disadvantage scores which symbolize the performance evaluation (in terms of distance) of each alternative with the rest on multiple attribute assessment, where the respective scores explain how advantageous or disadvantageous an alternative in question is as compared to rest of the alternatives on given attributes taking into account all the three parameters of IF concept, viz. the membership degree, non-membership degree and hesitation degree.

  4. 4.

    To the best of our knowledge, there is hardly any literature on MAGDM employing extended TOPSIS method in the realm of both IFS as well as IVIFS that takes into consideration various cases of attributes weights such as completely known weights information, uncertain subjective evaluations in the form of IFN as well as IVIFN, incompletely known partial weights or completely unknown weights. The proposed approach is more wholesome and efficient as compared to the literature on MAGDM.

  5. 5.

    When compared with [14], the proposed approach may be considered a better contribution because of the understated reasons. In [14], idealistic benchmarks are used while finding IF–PIS as well as IF–NIS which is too impractical to be achieved in an uncertain decision making world unlike the proposed approach where advantage and disadvantage scores of alternatives are obtained signifying how much better or worse an alternative is as compared to all other alternatives on the given attribute. Also, the effect of ideal IF–PIS and IF–NIS would reflect in the separation measures used. Furthermore, the weights of DMs in [14] are considered as completely known, reflecting certainty and too much surety in any practical uncertain decision making process. The entropy formula used for the calculation of attributes weights in the proposed approach is more efficient as compared to the one listed in [14] which has its own drawbacks [26]. Also, the whole methodology doesn’t take into consideration the inclusion of the third parameter of IFS, viz. the hesitation degree in the approach listed in [14], but in some of the steps only. In the end, single variation of attribute weight information is considered in the process described in [14]. Thus, the proposed procedure can be adopted to a particular situation such as the one used in [14], however, the same is not true about the latter.

  6. 6.

    When compared with [16], the proposed approach may be considered a better contribution because of the underlying points. In [16], to start with the whole process, the weights of the DMs are taken as completely known, reflecting too much surety and conviction in a DM’s opinion which seems impractical in any practical uncertain decision making process. Also, idealistic benchmarks are used while finding IF–PIS as well as IF–NIS which are too unrealistic to be achieved mostly in an uncertain practical decision making process, unlike the proposed approach where advantage and disadvantage scores of alternatives is obtained signifying how much better or worse an alternative is as compared to all other alternatives taking multiple attribute evaluation. Also, the effect of ideal IF–PIS and IF–NIS would reflect in the separation measures used. Furthermore, the methodology listed in [16] doesn’t take into consideration the inclusion of the third parameter of IFS, viz. the hesitation degree, which brings a significant universal insight into human awareness and behaviour. In the end, just one variation of attribute weight is considered in the methodology discussed in [16]. Thus, although, the proposed approach can be adapted to a particular situation such as the one in [16], but the same is not true about the latter.

1.3 Organization of the Paper

This paper is organized as follows. Section 2 describes the prerequisites enveloping the basic definitions, arithmetic operations as well as aggregation operators over IFS and IVIFS, respectively. Section 3 discusses the extended TOPSIS-based methodology for MAGDM process using IFNs in Sect. 3.1 and IVIFNs in Sect. 3.2. Numerical illustrations of the proposed approach are demonstrated in Sect. 4 with an application of an investment decision making problem illustrated using IFNs in Sect. 4.1 and using IVIFNs in Sect. 4.2. Section 5 presents the comparison analysis with other works followed by concluding remarks in Sect. 6.

2 Prerequisites

In this section, the fundamental definitions and concepts of IFS as well as IVIFS theory are presented along with the arithmetic operations as well as aggregation operators which will be required in the subsequent sections.

Atanassov [5] introduced IFS, an extension of classical fuzzy set proposed by Zadeh [1], which is a suitable way to deal with vagueness. The IFS can be defined as follows.

Definition 1

[1] Let Z be a non-empty universe of discourse. Then an IFS a in Z is given by

$$ a=\{<z,\mu _{a}(z),\nu _{a}(z)>\mid z\in Z\}, $$

where \(\mu _{a}(z):Z\rightarrow [0,1]\) and \(\nu _{a}(z):Z\rightarrow [0,1]\) are degrees of membership and non-membership of an element \(z\in Z\), respectively, with the condition \(0\le \mu _{a}(z)+\nu _{a}(z)\le 1\). For each a in Z, \(\pi _{a}(z)=1-\mu _{a}(z)-\nu _{a}(z),z\in Z\), is called the intuitionistic index of z to a. It represents the degree of indeterminacy or hesitation of z to a. For each \(z\in Z,0\le \pi _{a}(z)\le 1\).

For an IFS, \((\mu _{a}(z),\nu _{a}(z), \pi _{a}(z))\) is called an IFN and each IFN can be simply denoted as \(a=(\mu _{a},\nu _{a},\pi _{a})\), where \(\mu _{a}\in [0,1], \nu _{a}\in [0,1], \pi _{a}\in [0,1]\), and \(\mu _{a}+\nu _{a}+\pi _{a}=1\).

Definition 2

[27] Let \(a=(\mu _{a},\nu _{a},\pi _{a})\) and \(b=(\mu _{b},\nu _{b},\pi _{b})\) be any two IFNs. The following operational laws over IFNs are stated as follows:

$$\begin{aligned}&(i)\ a+b=(\mu _{a}+\mu _{b}-\mu _{a}\mu _{b}, \nu _{a}\nu _{b}, 1-\mu _{a}-\mu _{b}-\nu _{a}\nu _{b}+\mu _{a}\mu _{b}),\\&(ii)\ a\times b=(\mu _{a}\mu _{b}, \nu _{a}+\nu _{b}-\nu _{a}\nu _{b}, 1-\nu _{a}-\nu _{b}-\mu _{a}\mu _{b}+\nu _{a}\nu _{b}),\\&(iii)\ \lambda a=(1-(1-\mu _{a})^{\lambda }, \nu _{a}^{\lambda }, (1-\mu _{a})^{\lambda }- \nu _{a}^{\lambda }), \lambda \ge 0,\\&(iv)\ a^{\lambda }=(\mu _{a}^{\lambda }, 1-(1-\nu _{a})^{\lambda },(1-\nu _{a})^{\lambda }-\mu _{a}^{\lambda }), \lambda \ge 0,\\&(v)\ \bar{a}=(\nu _{a},\mu _{a},\pi _{a}), \end{aligned}$$

where \(\bar{a}\) denotes the compliment or negation of IFN a.

Two operators, namely, intuitionistic fuzzy weighted arithmetic (IFWA) and intuitionistic fuzzy weighted geometric (IFWG) are defined for aggregating intuitionistic fuzzy information as given in [28]. Note that the obtained aggregated value using IFWA or IFWG operator is also an IFN.

Definition 3

Let \(X=\{x_{1},x_{2},\ldots ,x_{n}\}\) be a universe of discourse and \(a_{j}=(\mu _{a}(x_{j}),\nu _{a}(x_{j}),\pi _{a}(x_{j}))\) for \(j=1,2,\ldots ,n\) be a collection of IFNs. Let IFWA: \(\varOmega ^{n}\rightarrow \varOmega \), if

$$\begin{aligned}{\text {IFWA}}_{\omega }(a_{1},a_{2},\ldots ,a_{n})& =\sum _{j=1}^{n} \omega _{j}a_{j}=\omega _{1}a_{1}\oplus \omega _{2}a_{2}\oplus \cdots \oplus \omega _{n}a_{n}\\& =\left( 1-\prod _{j=1}^{n}(1-\mu _{a_{j}})^{\omega _{j}},\prod _{j=1}^{n}(\nu _{a_{j}})^{\omega _{j}},\prod _{j=1}^{n}(1-\mu _{a_{j}})^{\omega _{j}}-\prod _{j=1}^{n}(\nu _{a_{j}})^{\omega _{j}}\right) , \end{aligned}$$

where \(\varOmega \) is a set of all IFNs, \(\omega =(\omega _{1},\omega _{2},\ldots ,\omega _{n})^{T}\) is the weight vector of \(a_{j},\ j=1,2,\ldots ,n\) satisfying \(\omega _{j}\in [0,1]\) and \(\sum _{j=1}^{n}\omega _{j}=1\), then the above-defined function is called an IFWA operator.

Also, let IFWG: \(\varOmega ^{n}\rightarrow \varOmega \), if

$$\begin{aligned}{\text {IFWG}}_{\omega }(a_{1},a_{2},\ldots ,a_{n})&=\sum _{j=1}^{n}a_{j}^{\omega _{j}}=a_{1}^{\omega _{1}}\otimes a_{2}^{\omega _{2}}\otimes \cdots \otimes a_{n}^{\omega _{n}}\\& =\left( \prod _{j=1}^{n}(\mu _{a_{j}})^{\omega _{j}},1-\prod _{j=1}^{n}(1-\nu _{a_{j}})^{\omega _{j}},\prod _{j=1}^{n}(1-\nu _{a_{j}})^{\omega _{j}}-\prod _{j=1}^{n}(\mu _{a_{j}})^{\omega _{j}}\right) , \end{aligned}$$

where \(\varOmega \) is a set of all IFNs, \(\omega =(\omega _{1},\omega _{2},\ldots ,\omega _{n})^{T}\) is the weight vector of \(a_{j},\ j=1,2,\ldots ,n\) satisfying \(\omega _{j}\in [0,1]\) and \(\sum _{j=1}^{n} \omega _{j}=1\), then the above defined function or operator is termed as an IFWG operator.

Atanassov and Gargov [7] introduced the notion of IVIFS as a generalization of IFS to deal with ambiguity [27] which is characterized by membership and non-membership degree in interval form and can be defined as follows.

Definition 4

Let X be a non-empty universe of discourse and D[0, 1] denote the subset of all closed subintervals of the interval [0, 1], then an IVIFS A over X is an expression represented by

$$ A=\{ <x, {\tilde{\mu }}_{A}(x),{\tilde{\nu }}_{A}(x)>|x\in X \}, $$

where the intervals \({\tilde{\mu }}_{A}(x)\) and \({\tilde{\nu }}_{A}(x)\) denote the degree of belongingness and non-belongingness, respectively of the element x to the set A and \({{\tilde{\mu }}}_{A}(x):X\rightarrow D[0,1]\) and \({{\tilde{\nu }}}_{A}(x):X\rightarrow D[0,1]\) under the condition \(0\le {\text {sup}}({{\tilde{\mu }}}_{A}(x))+{\text {sup}}({{\tilde{\nu }}}_{A}(x))\le 1\). For each \(x\in X\), \({\tilde{\mu }}_{A}(x)\) and \({\tilde{\nu }}_{A}(x)\) are closed intervals whose lower and upper bounds can be written as \(\mu ^{L}_{A}(x), \mu ^{U}_{A}(x) {\text { and }} \nu ^{L}_{A}(x), \nu ^{U}_{A}(x)\), respectively. Thus, an IVIFS A can be re-expressed as

$$ A=\{ <x,[\mu ^{L}_{A}(x), \mu ^{U}_{A}(x)] ,[\nu ^{L}_{A}(x), \nu ^{U}_{A}(x)]>|x\in X \}, $$

where \(0\le \mu ^{L}_{A}(x)\le \mu ^{U}_{A}(x)\le 1\), \(0\le \nu ^{L}_{A}(x)\le \nu ^{U}_{A}(x)\le 1\), \(0\le \mu ^{U}_{A}(x)+\nu ^{U}_{A}(x)\le 1\).

In addition, the IVIF index \({\tilde{\pi }}_{A}(x)\) of an element x belonging to an IVIFS A is defined as an indeterminacy or hesitation degree of an IVIFS A in X. It is represented by \({\tilde{\pi }}_{A}(x)=[\pi ^{L}_{A}(x), \pi ^{U}_{A}(x)]\) where \(\pi ^{L}_{A}(x)=1-\mu ^{U}_{A}(x)-\nu ^{U}_{A}(x)\), \(\pi ^{U}_{A}(x)=1-\mu ^{L}_{A}(x)-\nu ^{L}_{A}(x)\).

For simplicity purposes, \(([\mu ^{L}_{A}(x), \mu ^{U}_{A}(x)],[\nu ^{L}_{A}(x), \nu ^{U}_{A}(x)], [\pi ^{L}_{A}(x), \pi ^{U}_{A}(x)])\) is called an IVIFN, where \([\mu ^{L}_{A}(x), \mu ^{U}_{A}(x)]\subseteq D[0,1], [\nu ^{L}_{A}(x),\nu ^{U}_{A}(x)]\subseteq D[0,1]\) and \([\pi ^{L}_{A}(x),\pi ^{U}_{A}(x)]\subseteq D[0,1]\) such that \(\mu ^{U}_{A}(x)+\nu ^{U}_{A}(x)\le 1\).

Clearly, if \({\tilde{\mu }}_{A}(x)=\mu ^{L}_{A}(x)=\mu ^{U}_{A}(x)\), \({\tilde{\nu }}_{A}(x)=\nu ^{L}_{A}(x)=\nu ^{U}_{A}(x)\) and \({\tilde{\pi }}_{A}(x)=\pi ^{L}_{A}(x)=\pi ^{U}_{A}(x)\), then the given IVIFS A is reduced to an ordinary IFS a.

Definition 5

Let \(A=([\mu ^{L}_{A}(x), \mu ^{U}_{A}(x)],[\nu ^{L}_{A}(x), \nu ^{U}_{A}(x)], [\pi ^{L}_{A}(x), \pi ^{U}_{A}(x)])\), and \(B=([\mu ^{L}_{B}(x), \mu ^{U}_{B}(x)],[\nu ^{L}_{B}(x), \nu ^{U}_{B}(x)], [\pi ^{L}_{B}(x), \pi ^{U}_{B}(x)])\) be any two IVIFNs. The following operational laws over IVIFNs are stated as follows:

$$\begin{aligned}&(i)\ A+B=([\mu _{A}^{L}+ \mu _{B}^{L}- \mu _{A}^{L} \mu _{B}^{L}, \mu _{A}^{U}+ \mu _{B}^{U}- \mu _{A}^{U} \mu _{B}^{U}], [\nu _{A}^{L}\nu _{B}^{L}, \nu _{A}^{U}\nu _{B}^{U}], [1-\mu _{A}^{U}-\\&\qquad \mu _{B}^{U}-\nu _{A}^{U}\nu _{B}^{U}+\mu _{A}^{U}\mu _{B}^{U}, 1-\mu _{A}^{L}-\mu _{B}^{L}-\nu _{A}^{L}\nu _{B}^{L}+\mu _{A}^{L}\mu _{B}^{L}]),\\&(ii)\ A\times B=([\mu _{A}^{L}\mu _{B}^{L}, \mu _{A}^{U}\mu _{B}^{U}], [\nu _{A}^{L}+\nu _{B}^{L}-\nu _{A}^{L}\nu _{B}^{L}, \nu _{A}^{U}+\nu _{B}^{U}-\nu _{A}^{U}\nu _{B}^{U}], [1-\nu _{A}^{U}-\\&\qquad \nu _{B}^{U}-\mu _{A}^{U}\mu _{B}^{U}+\nu _{A}^{U}\nu _{B}^{U}, 1-\nu _{A}^{L}-\nu _{B}^{L}-\mu _{A}^{L}\mu _{B}^{L}+\nu _{A}^{L}\nu _{B}^{L}]),\\&(iii)\ \lambda A=([1-(1-\mu _{A}^{L})^{\lambda },1-(1-\mu _{A}^{U})^{\lambda }], [(\nu _{A}^{L})^{\lambda }, (\nu _{A}^{U})^{\lambda }], [(1-\mu _{A}^{U})^{\lambda }- (\nu _{A}^{U})^{\lambda },\\&\qquad (1-\mu _{A}^{L})^{\lambda }- (\nu _{A}^{L})^{\lambda }]), \lambda \ge 0,\\&(iv)\ A^{\lambda }=([(\mu _{A}^{L})^{\lambda }, (\mu _{A}^{U})^{\lambda }], [1-(1-\nu _{A}^{L})^{\lambda },1-(1-\nu _{A}^{U})^{\lambda }],[(1-\nu _{A}^{U})^{\lambda }-(\mu _{A}^{U})^{\lambda },\\&\qquad (1-\nu _{A}^{L})^{\lambda }-(\mu _{A}^{L})^{\lambda }]), \lambda \ge 0,\\&(v)\ \bar{A}=([\nu _{A}^{L},\nu _{A}^{U}],[\mu _{A}^{L},\mu _{A}^{U}],[\pi _{A}^{L},\pi _{A}^{U}]). \end{aligned}$$

Definition 6

[29] Let \(X=\{x_{1},x_{2},\ldots ,x_{n}\}\) be a universe of discourse and \(A_{j}=([\mu ^{L}_{A}(x_{j}), \mu ^{U}_{A}(x_{j})], [\nu ^{L}_{A}(x_{j}), \nu ^{U}_{A}(x_{j})], [\pi ^{L}_{A}(x_{j}), \pi ^{U}_{A}(x_{j})])\) for \(j=1,2,\ldots ,n\) be a collection of IVIFNs. Let IVIFWA: \(\varOmega ^{n}\rightarrow \varOmega \), if

$$\begin{aligned}&{\text {IVIFWA}}_{\omega }(A_{1},A_{2},\ldots ,A_{n})\\&\quad =\sum _{j=1}^{n} \omega _{j}A_{j}=\omega _{1}A_{1}\oplus \omega _{2}A_{2}\oplus \cdots \oplus \omega _{n}A_{n}\\&\quad =\left( \left[ 1-\prod _{j=1}^{n}(1-\mu _{A_{j}}^{L})^{\omega _{j}},1-\prod _{j=1}^{n}(1-\mu _{A_{j}}^{U})^{\omega _{j}}\right] ,\right. \\&\quad\qquad \left[ \prod _{j=1}^{n}(\nu _{A_{j}}^{L})^{\omega _{j}},\prod _{j=1}^{n}(\nu _{A_{j}}^{U})^{\omega _{j}}\right] ,\\&\quad\qquad \left. \left[ \prod _{j=1}^{n}(1-\mu _{A_{j}}^{U})^{\omega _{j}}-\prod _{j=1}^{n}(\nu _{A_{j}}^{U})^{\omega _{j}},\prod _{j=1}^{n}(1-\mu _{A_{j}}^{L})^{\omega _{j}}-\prod _{j=1}^{n}(\nu _{A_{j}}^{L})^{\omega _{j}}\right] \right) , \end{aligned}$$

where \(\varOmega \) is a set of all IVIFNs, \(\omega =(\omega _{1},\omega _{2},\ldots ,\omega _{n})^{T}\) is the weight vector of \(A_{j},\ j=1,2,\ldots ,n\) satisfying \(\omega _{j}\in [0,1]\) and \(\sum _{j=1}^{n}\omega _{j}=1\), then the above defined function is called an Interval valued intuitionistic fuzzy weighted arithmetic (IVIFWA) operator.

Also, let IVIFWG: \(\varOmega ^{n}\rightarrow \varOmega \), if

$$\begin{aligned}&{\text {IVIFWG}}_{\omega }(A_{1},A_{2},\ldots ,A_{n})\\&\quad =\sum _{j=1}^{n}A_{j}^{\omega _{j}}=A_{1}^{\omega _{1}}\otimes A_{2}^{\omega _{2}}\otimes \cdots \otimes A_{n}^{\omega _{n}}\\&\quad =\left( \left[ \prod _{j=1}^{n}(\mu _{A_{j}}^{L})^{\omega _{j}},\prod _{j=1}^{n}(\mu _{A_{j}}^{U})^{\omega _{j}}\right] ,\right. \\&\quad\qquad \left[ 1-\prod _{j=1}^{n}(1-\nu _{A_{j}}^{L})^{\omega _{j}},1-\prod _{j=1}^{n}(1-\nu _{A_{j}}^{U})^{\omega _{j}}\right] ,\\&\qquad\quad \left. \left[ \prod _{j=1}^{n}(1-\nu _{A_{j}}^{U})^{\omega _{j}}-\prod _{j=1}^{n}(\mu _{A_{j}}^{U})^{\omega _{j}},\prod _{j=1}^{n}(1-\nu _{A_{j}}^{L})^{\omega _{j}}-\prod _{j=1}^{n}(\mu _{A_{j}}^{L})^{\omega _{j}}\right] \right) , \end{aligned}$$

where \(\varOmega \) is a set of all IVIFNs, \(\omega =(\omega _{1},\omega _{2},\ldots ,\omega _{n})^{T}\) is the weight vector of \(A_{j},\ j=1,2,\ldots ,n\) satisfying \(\omega _{j}\in [0,1]\) and \(\sum _{j=1}^{n} \omega _{j}=1\), then the above defined function or operator is termed as an Interval valued intuitionistic fuzzy weighted geometric (IVIFWG) operator.

The definition of an IVIFN is preserved in the aggregation results obtained after the operation of IVIFWA and IVIFWG operator over IVIFN.

3 Extended TOPSIS Methodology for MAGDM Under IF Environment

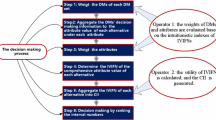
In this section, we present an extended TOPSIS method to solve MAGDM problems in which the preference information provided by DMs are expressed as IF matrices as well as IVIF matrices and the matrix elements are characterized by IFNs and IVIFNs. Four variations of attributes weights are taken, viz. completely known, subjective evaluation, incomplete partial information and completely unknown weight information under the scenario of IF as well as IVIF setting. The group decision making methodology can be described as follows:

Suppose that there exists a discrete set of alternatives \(\varLambda =\{A_{1},A_{2},\ldots ,A_{m}\}\) to be assessed on n attributes denoted by \(C=\{C_{1},C_{2},\ldots ,C_{n}\}\) and let \(\varDelta =\{D_{1},D_{2},\ldots ,D_{l}\}\) be the set of DMs. In the process of decision making, the DM usually needs to provide his/her assessment information over alternatives. Especially, in real-life situations, the DM may provide his/her preferences over alternatives to a certain degree, but it is possible that he/she is not certain about it and would be partially sure and sceptical. Thus, it is very suitable for the DM to estimate judgement under the IF environment which represents the membership degree, non-membership degree and hesitancy degree, respectively, of the alternative \(A_{i}\in \varLambda \) with respect to the attribute \(C_{j}\in C\) given by the DM \(D_{k}\in \varDelta \) for the fuzzy concept of excellence. Therefore, we can elicit a decision matrix \({\widetilde{\varOmega }}^{k}=({\alpha }_{ij}^{k})_{(m\times n)}\) provided by the DM under IF scenario. Assume that l DMs and n attributes have been given respective weights by the experts and n attributes are assigned weights by the DMs using appropriate IFNs. The MAGDM problem considered is how to choose the best alternative from the alternative set \(\varLambda \).

3.1 Extended TOPSIS for MAGDM Using IFN

The DM estimate the judgement in the form of IFN as \({\alpha }_{ij}^{k}=(\mu _{ijk},\nu _{ijk},\pi _{ijk}), i=1,2,\ldots ,m, j=1,2,\ldots ,n, k=1,2,\ldots ,l\) which represents the membership degree, non-membership degree and hesitancy degree, respectively of the alternative \(A_{i}\in \varLambda \) with respect to the attribute \(C_{j}\in C\) given by the DM \(D_{k}\in \varDelta \) for the fuzzy concept of excellence. Therefore, we can elicit an IF decision matrix \({\widetilde{\varOmega }}^{k}=({\alpha }_{ij}^{k})_{(m\times n)}\) given by the DM. Assume that l DMs have been given respective weights by the experts as \(\beta _{k}=(\mu _{k}, \nu _{k}, \pi _{k})\, {\text { for }}\, k=1,2,\ldots ,l\) and the associated attributes weights given by the kth DM \(D_{k}\) are expressed as \(w_{jk}=(\mu _{jk},\nu _{jk},\pi _{jk}) {\text { for }} j=1,2,\ldots ,n, k=1,2,\ldots ,l\).

Step 1. Determine crisp DMs weights \(\lambda _{k}\)

Set up a group of DMs to enclose decision making involving different perspectives. Suppose ratings provided to each DM by the experts are \(\beta _{k}=(\mu _{k},\nu _{k},\pi _{k}), k=1,2,\ldots ,l\). According to the voting model of IFSs, \(\mu _{k}\), \(\nu _{k}\) and \(\pi _{k}\) can be interpreted as proportions of the affirmative, dissent and abstention in a vote, respectively. Considering the possibility that in abstention group some people tend to cast affirmative votes, others are dissenters and still others tend to abstain from voting, we can divide the abstention proportion \(\pi _{k}\) into three parts: \(\mu _{k}\pi _{k}\), \(\nu _{k}\pi _{k}\) and \(\pi _{k}\pi _{k}\) which express the proportion of the affirmative, dissent and abstention in the original part of abstention [30]. Thus, the score function of IFN \(\beta _{k}=(\mu _{k},\nu _{k},\pi _{k})\) is defined as \(s_k=\mu _{k}+ \mu _{k}\pi _{k}=\mu _{k}(2-\mu _{k}-\nu _{k}), k=1,2,\ldots ,l\). Normalizing the score function \(s_{k}, k=1,2,\ldots ,l\), the weight of DM \(\lambda _{k}\) can be generated as follows:

$$ \lambda _{k}=\frac{\mu _{k}(2-\mu _{k}-\nu _{k})}{\sum _{k=1}^{l}[\mu _{k}(2-\mu _{k}-\nu _{k})]} $$
(1)

such that \(\sum _{k=1}^{l}\lambda _{k}=1\).

Step 2. Aggregation of individual assessment over DMs weights \(\lambda _{k}\)

Aggregate the individual evaluation matrices provided by the DMs in terms of IFN or linguistic variables mapped to IFNs using IFWA operator over the weight vector \(\lambda _{k}\) into an IF group assessment decision matrix as follows:

$$\begin{aligned} \alpha _{ij}&=IFWA_{\lambda _{k}}(\alpha _{ij}^{1},\alpha _{ij}^{2},\ldots ,\alpha _{ij}^{l})\nonumber \\&=\sum _{k=1}^{l} \lambda _{k}\alpha _{ij}^{k}\nonumber \\&=\left[ 1-\prod _{k=1}^{l}(1-\mu _{ij}^{k})^{\lambda _{k}}, \prod _{k=1}^{l}(\nu _{ij}^{k})^{\lambda _{k}}, \prod _{k=1}^{l}(1-\mu _{ij}^{k})^{\lambda _{k}}-\prod _{k=1}^{l}(\nu _{ij}^{k})^{\lambda _{k}}\right] \end{aligned}$$
(2)

We’ll get \(\varOmega =(\alpha _{ij})_{m\times n}\).

Step 3. Standardized IF decision matrix

The IF decision matrix is standardized into a uni-directional matrix so as to encompass both types of attributes, viz. benefit as well as cost attributes as follows:

$$ r_{ij} = {\left\{ \begin{array}{ll} \alpha _{ij}=(\mu _{ij}, \nu _{ij}, \pi _{ij}), &{}j\in C_{B},\\ {\bar{\alpha }}_{ij}=(\nu _{ij}, \mu _{ij}, \pi _{ij}), &{}j\in C_{C}. \end{array}\right. } $$
(3)

We’ll get \(R=(r_{ij})_{m\times n}=(\mu _{ij}, \nu _{ij}, \pi _{ij})\).

Step 4. Advantage and disadvantage scores

To advance further, advantage score \(a_{ij}\) and disadvantage score \(b_{ij}\) of each alternative with respect to a certain attribute considering the performance of all other alternatives over the same attribute has been defined [31]. The crisp advantage score \(a_{ij}\) of an alternative \(A_{i}\) as compared to all other alternatives \(i\ne t\) on an attribute \(C_{j}\) signifies as to how much advantageous or preferable a specific alternative is over the rest on the basis of multiple attribute evaluation, defined as follows:

$$\begin{aligned} a_{ij}&=\dfrac{1}{2}\left\{ \sum _{i\ne t}max(\mu _{ij}-\mu _{tj},0)+\sum _{i\ne t}max(\nu _{tj}-\nu _{ij},0)\right. \nonumber \\&\quad \left. +\sum _{i\ne t}max(\pi _{tj}-\pi _{ij},0)\right\} \end{aligned}$$
(4)

Similarly, disadvantage score \(b_{ij}\) of an alternative \(A_i\) as compared to all other alternatives \(i\ne t\) on an attribute \(C_j\) represents how disadvantageous in a context an alternative performance is over the rest on the basis of multiple attribute evaluation, defined as follows:

$$\begin{aligned} b_{ij}=&\dfrac{1}{2}\left\{ \sum _{i\ne t}max(\mu _{tj}-\mu _{ij},0)+\sum _{i\ne t}max(\nu _{ij}-\nu _{tj},0)\right. \nonumber \\&\left. +\sum _{i\ne t}max(\pi _{ij}-\pi _{tj},0)\right\} \end{aligned}$$
(5)

Step 5. Attributes weights

Importance weights of attributes are either provided by the DMs in the form of completely known information, subjective evaluation in the form of IFN, incomplete uncertain partial weights or completely unknown weight information. It depends upon the DMs perception and psychology and various other subjective factors. Here, four variations of attribute weight information are dealt with as follows:

(i) Completely known weights

The case where the weights of the attributes are provided as completely known values yields \(w=(w_{1},w_{2},\ldots ,w_{n})\) where \(w_{j}\) is the triplet \(w_{j}=(\mu _{j},\nu _{j},\pi _{j})\) such that \(\sum _{j=1}^{n}w_{j}=1\). Attributes weights, already provided by the DMs with certainty, whether of equal or unequal importance can be directly substituted to obtain weighted strength and weighted weakness in Step 6.

(ii) Subjective evaluation: IFN

Let \(w^k_{j}=(\mu _{j}^{k}, \nu _{j}^{k}, \pi _{j}^{k}), j=1,2,\ldots ,n, k=1,2,\ldots ,l\) be the weight vector assigned to an attribute \(C_{j}\) by DM \(D_{k}\) in the form of an IFN so as to contribute in the analysis the individual importance of each attribute. Since attributes weights provided by l DMs are subjective in nature, these are aggregated using IFWG operator over DMs weight \(\lambda _{k}\) in order to obtain unified attribute weight matrix and hence is normalized to obtain crisp form in Steps (ii)-a and (ii)-b, respectively.

(ii)-a Aggregation of attributes weights over DMs weights \(\lambda _{k}\)

Subjective evaluations of attributes weights are aggregated into collective assessments enveloping DMs importance in the form of \(w_{j}, j=1,2,\ldots ,n\) using IFWG operator as follows:

$$\begin{aligned} w_{j}&=IFWG_{\lambda _{k}}(w_{j}^{1},w_{j}^{2},\ldots ,w_{j}^{l})\nonumber \\&=\sum _{k=1}^{l}(w_{j}^{k})^{\lambda _{k}}\nonumber \\&=(w_{j}^{1})^{\lambda _1}\otimes (w_{j}^{2})^{\lambda _2}\otimes \cdots \otimes (w_{j}^{l})^{\lambda _l}\nonumber \\&=\left[ \prod _{k=1}^{l}(\mu _{j}^{k})^{\lambda _{k}},1-\prod _{k=1}^{l}(1-\nu _{j}^{k})^{\lambda _{k}},\prod _{k=1}^{l}(1-\nu _{j}^{k})^{\lambda _{k}}-\prod _{k=1}^{l}(\mu _{j}^{k})^{\lambda _{k}}\right] \end{aligned}$$
(6)

We’ll get \(w=(w_{1},w_{2},\ldots ,w_{l})\) such that \(w_{j}=(\mu _{j},\nu _{j},\pi _{j})\).

(ii)-b Normalize subjective weights

Based on the unified attributes weights \(w_{j}=(\mu _{j},\nu _{j},\pi _{j})\), the normalized subjective weights of each factor can be calculated using [30] as follows:

$$ \bar{w}_{j}=\frac{\mu _{j}(2-\mu _{j}-\nu _{j})}{\sum _{j=1}^{n}[\mu _{j}(2-\mu _{j}-\nu _{j})]} $$
(7)

such that \(\sum _{j=1}^{n}\bar{w}_{j}=1\). Normalized subjective weights can thus be used to obtain weighted strength and weighted weakness further in Step 6.

(iii) Completely unknown weights: IF entropy

It is known that entropy can measure the uncertainty degree of IFSs. \(R=(r_{ij})_{m\times n}=(\mu _{ij},\nu _{ij},\pi _{ij}), i=1,2,\ldots ,m, j=1,2,\ldots ,n\) is the standardized IF decision matrix which includes the overall assessment values of alternative \(A_{i}\) inclusive of all DMs grades of importance. When weights of the attributes are completely unknown, we can use the IF entropy weight method to determine the weights [26]. Define entropy of IFN \(r_{ij}=(\mu _{ij},\nu _{ij},\pi _{ij})\) as follows:

$$ \bar{E}_{j}=E(r_{ij})=\dfrac{1}{m}\sum _{i=1}^{m}\cos \dfrac{\mu _{ij}-\nu _{ij}}{2(1+\pi _{ij})}.\pi $$
(8)

for \(j=1,2,\ldots ,n\). \(\bar{E}_{j}\) indicates the uncertainty degree of assessment information with respect to attribute \(C_{j}\). During the group decision making process, the uncertainty degrees of the judgement evaluations by the DMs is expected to be as less as possible. Hence, the bigger \(\bar{E}_{j}\) is, the smaller the weight assigned to an attribute and vice versa. Therefore, the weights of attributes are obtained as follows:

$$ w_{j}=\dfrac{1-e_{j}}{\sum _{j=1}^{n}(1-e_{j})} $$
(9)

where \(e_{j}=\dfrac{\bar{E}_{j}}{\sum\nolimits _{j=1}^{n}\bar{E}_{j}}\) for \(j=1,2,\ldots ,n\). Therefore, completely unknown attributes weights information, deciphered through entropy method is obtained in crisp form as \(w_{j}=\lbrace w_{1},w_{2},\ldots ,w_{n}\rbrace \), in order to be used further in Step 6.

(iv) Partially known weights

Here, it is presumed that the relation of weights is given in the form of incomplete or partial uncertain information, say H, for instance, the weight of an attribute changes in an interval or an attribute is more preferable than another and so on. The incomplete information on the weights can be divided into the following five forms as follows:

$$\begin{aligned}&(i) \; {\text { Weak \, ranking}}: \lbrace w_{i}\ge w_{j}\rbrace , i\ne j.\nonumber \\&(ii)\; {\text { Strict \, ranking}}: \lbrace w_{i}-w_{j}\ge \alpha \rbrace , i\ne j.\nonumber \\&(iii)\; {\text { Ranking \, of \, differences}}: \lbrace w_{i}-w_{j}\ge w_{k}-w_{l}\rbrace , i\ne j\ne k\ne l.\nonumber \\&(iv) \; {\text { Ranking \, with \, multiples}}: \lbrace w_{i}\ge \alpha _{i}w_{j}\rbrace , i\ne j.\nonumber \\&(v)\; {\text { Interval \, form}}: \lbrace \alpha _{i}\le w_{i}\le \alpha _{i}+\epsilon _{i}\rbrace , {\text {where}}\; \alpha _{i}\; {\text { and }}\; \epsilon _{i}\; {\text {are}}\, \text{{non-negative}}\nonumber \\&\quad {\text {numbers}}. \end{aligned}$$
(10)

These five listed forms are linear inequalities, whereas in real application, relations between attributes weights might be a linear equality. So, incomplete uncertain partial weight information can be remodelled into incomplete certain information of three types, whereby it is assumed that attributes weights can be both linear inequality as well as a linear equality and can be categorized by \(H_{1}\) [32] as follows:

$$\begin{aligned}&{\text {Type 1}}: \lbrace w: Aw \ge b, w> 0, b\ge 0\rbrace \nonumber ,\\&{\text {Type 2}}: \lbrace w: Aw \le b, w> 0, b\ge 0\rbrace ,\nonumber \\&{\text {Type 3}}: \lbrace w: Aw=b, w > 0, b\ge 0\rbrace , \end{aligned}$$
(11)

where A is a \(m\times n\) matrix and \(w=\lbrace w_{1}, w_{2},\ldots ,w_{n}\rbrace \). We seek to obtain \(w=\lbrace w_{1},w_{2},\ldots ,w_{n}\rbrace \in H_{1}\) such that \(w_{j}\ge 0\) and \(\sum _{j=1}^{n} w_{j}=1\).

(iv)-a Since wj’s are not known, we find the optimal weight vector of attributes with an objective of maximizing the performance degree of each alternative on multiple attribute evaluation simultaneously by forming a multiple objective programming (MOP) problem subject to the constraints:

$$\begin{aligned} \mathbf{(MOP1) }\quad&{\text {max}}\ \lbrace z_{1},z_{2},\ldots ,z_{m}\rbrace \nonumber \\&{\hbox {subject to}}\\&w=(w_{1},w_{2},\ldots ,w_{n})\in H_{1}, \\&\sum _{j=1}^{n}w_{j}=1, \\&w_{j}\ge 0,\qquad j=1,2,\ldots ,n. \end{aligned}$$
(12)

(iv)-b Using weighted sum method (WSM) and assigning equal weights [33], the problem (MOP1) can be remodelled into a weighted sum problem (WSP1) problem as follows:

$$\begin{aligned} \mathbf{(WSP1) }\quad&{\text {max}}\ \sum _{i=1}^{m} z_{i}=\sum _{i=1}^{m}\dfrac{\sum _{j=1}^{n}w_{j}a_{ij}}{\sum _{j=1}^{n}w_{j}a_{ij}+\sum _{j=1}^{n}w_{j}b_{ij}}\nonumber \\&{\hbox{subject to}}\nonumber \\&w=(w_{1},w_{2},\ldots ,w_{n})\in H_{1},\nonumber \\&\sum _{j=1}^{n}w_{j}=1,\nonumber \\&w_{j}\ge 0,\qquad j=1,2,\ldots ,n. \end{aligned}$$
(13)

By solving the linear fractional problem (13), we’ll get the optimal weights as \(w=\{w_{1},w_{2},\ldots ,w_{n}\}\). Thus, by forming the optimization problem, the case of partially known attributes weights information is used to obtain completely known crisp values to be substituted in Step 6 to obtain weighted strength and weakness scores.

Step 6. Weighted strength and weakness scores

Next, weighted strength is computed as the sum of the multiplicatives obtained by multiplying the advantage score of the alternatives on each evaluation attribute with the aggregated weight of the corresponding attribute to obtain the strength score or the weighted advantage of each alternative as follows:

$$ S_{i}=\sum _{j=1}^{n}w_{j}a_{ij}. $$
(14)

Analogously, the sum of the multiplicatives obtained by multiplying the disadvantage score of the alternatives on each attribute with the aggregated weight of the corresponding attribute signifies the weakness score or the weighted disadvantage of each alternative as follows:

$$ W_{i}=\sum _{j=1}^{n}w_{j}b_{ij}. $$
(15)

Step 7. Performance degrees

Merging the strength and weakness score to find the total performance score \(Z_{i}\) corresponding to alternative \(A_{i}\), \(i=1,2,\ldots ,m\) which ascertains the assessment status of each alternative and determine the ranking order of the alternatives in decreasing order based on the overall assessment, obtained as follows:

$$ Z_{i}=\dfrac{S_{i}}{S_{i}+W_{i}},\ i=1,2,\ldots ,m. $$
(16)

The step-wise description of the MAGDM approach based on an extended TOPSIS method using IFNs is presented as follows.

  1. 1.

    From the IF assessment data provided by DMs, compute the numeric DMs importance weight degrees using Eq. (1).

  2. 2.

    The individual assessments of alternatives with respect to each attribute is aggregated over DMs weights using Eq. (2).

  3. 3.

    The IF decision matrix D is standardized using Eq. (3) as R.

  4. 4.

    Calculate advantage and disadvantage scores using Eqs. (4) and (5), respectively.

  5. 5.

    Variation in weight information of the attributes:

    1. (i)

      Attributes weights are completely known.

    2. (ii)

      If weight information of the attributes is given subjectively, i.e. in the form of IFNs, then calculate aggregated attributes weights over DMs weights using Eq. (6) and normalize it using Eq. (7).

    3. (iii)

      If there is no information about attributes weights, calculate entropy values using Eq. (8) and attributes weights using Eq. (9).

    4. (iv)

      Partial or incomplete information on attributes weights in the form of (10), i.e. set H can be transformed into set \(H_{1}\) using (11). Performance degree of each alternative is maximized by solving the (MOP1) problem using (12). It is then converted into a (WSP1) problem using (13). The calculated weights after solving the respective optimization problem are then used to obtain weighted strength as well as weakness scores.

  6. 6.

    Weighted strength and weighted weakness are calculated using Eqs. (14) and (15), respectively, by imparting the obtained attributes weights.

  7. 7.

    Performance degree of each alternative is calculated in order to rank the alternatives in descending order using Eq. (16).

3.2 Extended TOPSIS for MAGDM Using IVIFN

The DM estimates the judgement in the form of IVIFNs as \(\alpha _{ij}^{k}=\lbrace [t_{ijk}^L,t_{ijk}^U],\)\([f_{ijk}^L, f_{ijk}^{U}], [\pi _{ijk}^L, \pi _{ijk}^U]\rbrace _{m\times n}, i=1,2,\ldots ,m, j=1,2,\ldots ,n, k=1,2,\ldots ,l\) representing the membership degree, non-membership degree and hesitancy degree, respectively, of the alternative \(A_{i}\in \varLambda \) with respect to the attribute \(C_{j}\in C\) given by the DM \(D_{k}\in \varDelta \) for the fuzzy concept of excellence, where \([\pi _{ijk}^L,\pi _{ijk}^U]=[1-t_{ijk}^U-f_{ijk}^U, 1-t_{ijk}^L-f_{ijk}^L]\). Therefore, we can elicit an IVIF decision matrix \({\widetilde{\varOmega }}^{k}=({\alpha }_{ij}^{k})_{(m\times n)}\) given by l DMs who have been given respective weights by the experts as \(\beta _{k}=([\mu _{k}^{L},\mu _{k}^{U}],[\nu _{k}^{L},\nu _{k}^{U}], [\pi _{k}^{L},\pi _{k}^{U}]) {\text { for }} \, k=1,2,\ldots ,l\) and the associated attribute weight vector given by the kth DM \(D_{k}\) is expressed as \(w_{jk}=([\mu _{jk}^{L},\mu _{jk}^{U}],[\nu _{jk}^{L},\nu _{jk}^{U}],[\pi _{jk}^{L},\pi _{jk}^{U}])\; {\text { for }}\; j=1,2,\ldots ,n, k=1,2,\ldots ,l\).

Step 1. Determine crisp DMs weights \(\lambda _{k}\)

DMs are provided importance ratings by the experts based on their expertise as \(\beta _{k}=([\mu _{k}^L,\mu _{k}^U],[\nu _{k}^L,\nu _{k}^U],[\pi _{k}^L,\pi _{k}^U]), k=1,2,\ldots ,l\). To reflect their relative importance in the decision making process, numeric DMs weights are obtained as follows:

$$ \lambda _{k}=\dfrac{(\mu _{k}^L+\mu _{k}^U)(2+\pi _{k}^L+\pi _{k}^U)}{\sum _{k=1}^{l}(\mu _{k}^L+\mu _{k}^U)(2+\pi _{k}^L+\pi _{k}^U)} $$
(17)

such that \(\sum _{k=1}^{l}\lambda _{k}=1\) being the crisp weight of the kth DM \(D_{k}\).

Step 2. Aggregation of individual assessment over DMs weights \(\lambda _{k}\)

Employing DMs weights \(\lambda _{k}>0, k=1,2,\ldots ,l\) satisfying \(\sum _{k=1}^{l}\lambda _{k}=1\) in order to unify the individual judgements by l DMs using IVIFWA operator is defined as follows:

$$\begin{aligned} \alpha _{ij}&=IVIFWA_{\lambda _{k}}(\alpha _{ij}^{1}, \alpha _{ij}^{2},\ldots , \alpha _{ij}^{l})\nonumber \\&=\sum _{k=1}^{l} \lambda _{k}\alpha _{ij}^{k}\nonumber \\&=\left\{ \left[ 1-\prod _{k=1}^{l}(1-t_{ijk}^{L})^{\lambda _{k}},1-\prod _{k=1}^{l}(1-t_{ijk}^{U})^{\lambda _{k}}\right] , \left[ \prod _{k=1}^{l}(f_{ijk}^{L})^{\lambda _{k}},\prod _{k=1}^{l}(f_{ijk}^{U})^{\lambda _{k}}\right] ,\right. \nonumber \\&\qquad \left. \left[ \prod _{k=1}^{l}(1-t_{ijk}^{U})^{\lambda _{k}}-\prod _{k=1}^{l}(f_{ijk}^{U})^{\lambda _{k}}, \prod _{k=1}^{l}(1-t_{ijk}^{L})^{\lambda _{k}}-\prod _{k=1}^{l}(f_{ijk}^{L})^{\lambda _{k}}\right] \right\} \end{aligned}$$
(18)

We’ll get \(\varOmega =(\alpha _{ij})_{m\times n}=([t_{ij}^L,t_{ij}^U], [f_{ij}^L,f_{ij}^U], [\pi _{ij}^L,\pi _{ij}^U])\).

Step 3. Standardized IVIF decision matrix

Since the decision problems might consist of both benefit as well as cost attributes, there is a need to standardize the corresponding matrix in order to make it uni-dimensional as follows:

$$ r_{ij} = {\left\{ \begin{array}{ll} \alpha _{ij}=([t_{ij}^L,t_{ij}^U], [f_{ij}^L,f_{ij}^U], [\pi _{ij}^L,\pi _{ij}^U]), &{}j\in C_{B},\\ {\bar{\alpha }}_{ij}=([f_{ij}^L,f_{ij}^U], [t_{ij}^L,t_{ij}^U], [\pi _{ij}^L,\pi _{ij}^U]), &{}j\in C_{C}. \end{array}\right. } $$
(19)

The standardized IVIF decision matrix \(R=(r_{ij})_{m\times n}\) is obtained where \(r_{ij}=([\mu _{ij}^L,\mu _{ij}^U],[\nu _{ij}^L,\ \nu _{ij}^U],[\pi _{ij}^L,\pi _{ij}^U])\) is an element of obtained neutralized matrix R.

Step 4. Advantage and disadvantage scores

To advance further, advantage score \(a_{ij}\) and disadvantage score \(b_{ij}\) of each alternative with respect to a certain attribute considering the performance of all other alternatives over the same attribute has been defined [16] as follows:

$$\begin{aligned} a_{ij}&=\dfrac{1}{4}\left\{ \sum _{i\ne t}max(\mu _{ij}^{L}-\mu _{tj}^{L},0)+\sum _{i\ne t}max(\mu _{ij}^{U}-\mu _{tj}^{U},0)+\sum _{i\ne t}max(\nu _{tj}^{L}-\nu _{ij}^{L},0)\right. \nonumber \\&\quad \left. +\sum _{i\ne t}max(\nu _{tj}^{U}-\nu _{ij}^{U},0)+\sum _{i\ne t}max(\pi _{tj}^{L}-\pi _{ij}^{L},0)+\sum _{i\ne t}max(\pi _{tj}^{U}-\pi _{ij}^{U},0)\right\} \end{aligned}$$
(20)

and

$$\begin{aligned} b_{ij}&=\dfrac{1}{4}\left\{ \sum _{i\ne t}max(\mu _{tj}^{L}-\mu _{ij}^{L},0)+\sum _{i\ne t}max(\mu _{tj}^{U}-\mu _{ij}^{U},0)+\sum _{i\ne t}max(\nu _{ij}^{L}-\nu _{tj}^{L},0)\right. \nonumber \\&\quad \left. +\sum _{i\ne t}max(\nu _{ij}^{U}-\nu _{tj}^{U},0)+\sum _{i\ne t}max(\pi _{ij}^{L}-\pi _{tj}^{L},0)+\sum _{i\ne t}max(\pi _{ij}^{U}-\pi _{tj}^{U},0)\right\} \end{aligned}$$
(21)

Step 5. Attributes weights

Here, as described in the previous subsection, all four variations of weight information of attributes are considered, viz. completely known, subjective evaluation in the form of IVIFN, incomplete partially known or completely unknown weight information depending upon the DMs expertise and various subjective factors. The varied cases are discussed below:

(i) Completely known weights

The case where the attributes weight are provided as completely known yields \(w=(w_{1},w_{2},\ldots ,w_{n})\) where \(w_{j}=(\mu _{j},\nu _{j},\pi _{j})\) such that \(\sum _{j=1}^{n}w_{j}=1\). Attributes weight, already in crisp form provided by the DMs, whether of equal or unequal importance can be directly substituted to obtain weighted strength and weighted weakness in Step 6.

(ii) Subjective evaluation: IVIFN

Suppose the weight vector assigned to attribute \(C_{j}\) by kth DM \(D_{k}\) takes the form of an IVIFN as \(w^k_{j}=([\mu _{jk}^{L},\mu _{jk}^{U}],[\nu _{jk}^{L},\nu _{jk}^{U}],[\pi _{jk}^{L},\pi _{jk}^{U}])\) in order to inculcate the subjective utility of each attribute. Since, weights provided by l DMs are subjective in nature, these are aggregated using IVIFWG operator over DMs weights in order to obtain unified attribute weight matrix and hence is normalized to obtain crisp weights in Steps (ii)-a and (ii)-b, respectively.

(ii)-a Aggregation of attributes weights over DMs weights \(\lambda _{k}\)

Subjective evaluations of attributes weight are aggregated into a cumulative assessment matrix inculcating DMs importance as \(w_{j}, j=1,2,\ldots ,n\) using IVIFWG operator.

$$\begin{aligned} w_{j}&=IVIFWG_{\lambda _{k}}(w_{j}^{1},w_{j}^{2},\ldots ,w_{j}^{l})\nonumber \\&=\sum _{k=1}^{l}(w_{j}^{k})^{\lambda _{k}}\nonumber \\&=(w_{j}^{1})^{\lambda _{1}}\otimes (w_{j}^{2})^{\lambda _{2}}\otimes \cdots \otimes (w_{j}^{l})^{\lambda _{l}}\nonumber \\&=\left\{ \left[ \prod _{k=1}^{l}(\mu _{jk}^{L})^{\lambda _{k}},\prod _{k=1}^{l}(\mu _{jk}^{U})^{\lambda _{k}}\right] , \left[ 1-\prod _{k=1}^{l}(1-\nu _{jk}^{L})^{\lambda _{k}},1-\prod _{k=1}^{l}(1-\nu _{jk}^{U})^{\lambda _{k}}\right] ,\right. \nonumber \\&\qquad \left. \left[ \prod _{k=1}^{l}(1-\nu _{jk}^{U})^{\lambda _{k}}-\prod _{k=1}^{l}(\mu _{jk}^{U})^{\lambda _{k}}, \prod _{k=1}^{l}(1-\nu _{jk}^{L})^{\lambda _{k}}-\prod _{k=1}^{l}(\mu _{jk}^{L})^{\lambda _{k}}\right] \right\} \end{aligned}$$
(22)

Thus, we get \(w=(w_{1},w_{2},\ldots ,w_{n})\) such that \(w_{j}=([\mu _{j}^{L},\mu _{j}^{U}],[\nu _{j}^{l},\nu _{j}^{U}],[\pi _{j}^{L},\pi _{j}^{U}]),\ j=1,2,\ldots ,n\).

(ii)-b Normalized subjective weights

Based on the obtained attributes weights \(w_{j}=([\mu _{j}^{L},\mu _{j}^{U}],[\nu _{j}^{L},\nu _{j}^{U}],[\pi _{j}^{L},\pi _{j}^{U}])\), the normalized subjective weights can be calculated using the following:

$$ \bar{w}_{j}=\dfrac{(\mu _{j}^L+\mu _{j}^U)(2+\pi _{j}^L+\pi _{j}^U)}{\sum _{j=1}^{n}(\mu _{j}^L+\mu _{j}^U)(2+\pi _{j}^L+\pi _{j}^U)} $$
(23)

such that \(\sum _{j=1}^{n}\bar{w}_{j}=1\). Normalized subjective weights can thus be used to obtain weighted strength and weakness further in Step 6.

(iii) Completely unknown weights: IVIF entropy

We have the standardized IVIF decision matrix \(R= (r_{ij})m\times n=([\mu _{ij}^{L},\mu _{ij}^{U}],\)\( [\nu _{ij}^{L},\nu _{ij}^{U}],[\pi _{ij}^{L},\pi _{ij}^{U}])_{m\times n},\ i=1,2,\ldots ,m, j=1,2,\ldots ,n\) which includes the overall assessment values of alternative \(A_{i}\) inclusive of all DMs grades of importance. When attributes weights are completely unknown, we can use the IVIF entropy weight method to determine the weights [26]. Define entropy of IVIFN \(r_{ij}=([\mu _{ij}^{L},\mu _{ij}^{U}],[\nu _{ij}^{L},\nu _{ij}^{U}],[\pi _{ij}^{L},\pi _{ij}^{U}])\) as

$$ \bar{E}_{j}=E(r_{ij})=\dfrac{1}{m}\sum _{i=1}^{m}\cos \dfrac{|\mu _{ij}^{L}-\nu _{ij}^{L}|+|\mu _{ij}^{U}-\nu _{ij}^{U}|}{2[2+\pi _{ij}^{L}+\pi _{ij}^{U}]}.\pi $$
(24)

for \(j=1,2,\ldots ,n\), where \(\bar{E}_{j}\) indicates the uncertainty degree of assessment information with respect to attribute \(C_{j}\). Therefore, the weights of attributes are calculated as:

$$ w_{j}=\dfrac{1-e_{j}}{\sum _{j=1}^{n}(1-e_{j})} $$
(25)

where \(e_{j}=\dfrac{\bar{E}_{j}}{\sum\nolimits _{j=1}^{n}\bar{E}_{j}}\) for \(j=1,2,\ldots ,n\). Therefore, completely unknown attribute weight information, deciphered through entropy method is obtained in crisp form as \(w_{j}=\lbrace w_{1},w_{2},\ldots ,w_{n}\rbrace \) in order to be used further in Step 6.

(iv) Partially known weights

Here, it is presumed that the relation between weights is given in the form of incomplete or partial uncertain information, say H, listed as the following five forms:

$$\begin{aligned}&(i) \; {\text { Weak \, ranking}}: \lbrace w_{i}\ge w_{j}\rbrace , i\ne j.\nonumber \\&(ii)\; {\text { Strict \, ranking}}: \lbrace w_{i}-w_{j}\ge \alpha \rbrace , i\ne j.\nonumber \\&(iii)\; {\text { Ranking \, of \, differences}}: \lbrace w_{i}-w_{j}\ge w_{k}-w_{l}\rbrace , i\ne j\ne k\ne l.\nonumber \\&(iv) \; {\text { Ranking \, with \, multiples}}: \lbrace w_{i}\ge \alpha _{i}w_{j}\rbrace , i\ne j.\nonumber \\&(v)\; {\text { Interval \, form}}: \lbrace \alpha _{i}\le w_{i}\le \alpha _{i}+\epsilon _{i}\rbrace , {\text { where }} \, \alpha _{i} {\text { and }} \, \epsilon _{i} \ {\text { are \, non-negative}}\nonumber \\&\quad {\text {numbers}}. \end{aligned}$$
(26)

It is assumed that attributes weights can be both linear equality as well as linear inequality and these five listed forms can be remodelled into incomplete certain information of three types and thus categorized as \(H_{1}\) [32] as follows:

$$\begin{aligned}&{\text {Type 1}}: \lbrace w: Aw \ge b, w> 0, b\ge 0\rbrace \nonumber \\&{\text {Type 2}}: \lbrace w: Aw \le b, w> 0, b\ge 0\rbrace \nonumber \\&{\text {Type 3}}: \lbrace w: Aw=b, w > 0, b\ge 0\rbrace , \end{aligned}$$
(27)

where A is a \(m\times n\) matrix and \(w=\lbrace w_{1}, w_{2},\ldots ,w_{n}\rbrace \). We seek to obtain \(w=\lbrace w_{1},w_{2},\ldots ,w_{n}\rbrace \in H_{1}\) such that \(w_{j}\ge 0\) and \(\sum _{j=1}^{n} w_{j}=1\).

(iv)-a Since \(w_{j}\) is not known, we need to find the optimal weight vector of attributes while maximizing the performance degree with respect to all the alternatives by forming a (MOP2) problem subject to the constraints as follows:

$$\begin{aligned} \mathbf{(MOP2) }\quad&{\text {max}}\ \lbrace z_{1},z_{2},\ldots ,z_{m}\rbrace \nonumber \\&{\hbox {subject to}}\nonumber \\&w=(w_{1},w_{2},\ldots ,w_{n})\in H_{1},\nonumber \\&\sum _{j=1}^{n}w_{j}=1,\nonumber \\&w_{j}\ge 0,\qquad j=1,2,\ldots ,n. \end{aligned}$$
(28)

(iv)-b Using WSM and assigning equal weights [33], we have the following (WSP2) as follows:

$$\begin{aligned} \mathbf{(WSP2) }\quad&{\text {max}}\ \sum _{i=1}^{m} z_{i}=\sum _{i=1}^{m}\dfrac{\sum _{j=1}^{n}w_{j}a_{ij}}{\sum _{j=1}^{n}w_{j}a_{ij}+\sum _{j=1}^{n}w_{j}b_{ij}}\nonumber \\&{\hbox {subject to}}\nonumber \\&w=(w_{1},w_{2},\ldots ,w_{n})\in H_{1},\nonumber \\&\sum _{j=1}^{n}w_{j}=1,\nonumber \\&w_{j}\ge 0,\qquad j=1,2,\ldots ,n. \end{aligned}$$
(29)

Solving the nonlinear optimization problem (linear fractional problem), we’ll get the optimal weights as \(w=\{w_{1},w_{2},\ldots ,w_{n}\}\). Thus, by forming the optimization problem, the case of partially known weight information of attributes is used to obtain crisp attributes weight to be used further in Step 6 to find weighted strength and weakness scores.

Step 6. Weighted strength and weakness scores

Next, weighted strength as well as weighted weakness is computed as the sum of the multiplicatives obtained by multiplying the crisp advantage and the disadvantage scores, respectively, of the alternatives on each evaluation attribute with the aggregated weights of the corresponding attributes to obtain the strength score and the weakness score of each alternative as follows:

$$ S_{i}=\sum _{j=1}^{n}w_{j}a_{ij}, $$
(30)

and

$$ W_{i}=\sum _{j=1}^{n}w_{j}b_{ij}. $$
(31)

Step 7. Performance degrees

Total performance score \(Z_{i}\) corresponding to alternative \(A_{i}\), \(i=1,2,\ldots ,m\) is obtained taking into account both the strength score and weakness score to find the most preferable alternative and determining the ranking order of all the alternatives in descending order based on the overall assessment as follows:

$$ Z_{i}=\dfrac{\sum _{j=1}^{n}w_{j}a_{ij}}{\sum _{j=1}^{n}w_{j}a_{ij}+\sum _{j=1}^{n}w_{j}b_{ij}}, \ i=1,2,\ldots ,m. $$
(32)

The step-wise description of the MAGDM approach based on an extended TOPSIS method using IVIFNs is presented as follows.

  1. 1.

    From the IVIF assessment data provided by DMs, compute the crisp DMs importance weight using Eq. (17).

  2. 2.

    The individual assessment of alternatives with respect to each attribute is aggregated over DMs weights using Eq. (18).

  3. 3.

    The IVIF decision matrix D is standardized using Eq. (19) as R.

  4. 4.

    Calculate advantage and disadvantage scores using Eqs. (20) and (21), respectively.

  5. 5.

    Variation in weight information of the attributes:

    1. (i)

      Attributes weights are completely known.

    2. (ii)

      If attributes weight information is given as subjective evaluations in the form of IVIFNs, then calculate aggregated attributes weight over DMs weights using Eq. (22) and normalize it using Eq. (23).

    3. (iii)

      If there is no information about attributes weight, calculate entropy values using Eq. (24) and weights using Eq. (25).

    4. (iv)

      Partial information on attributes weight in the form of (26), i.e. set H can be transformed into set \(H_{1}\) using (27). Performance degree of each alternative is maximized by solving the (MOP2) problem using (28). It is then converted into a (WSP2) problem using (29). The calculated weights after solving the respective optimization problem are then used to obtain weighted strength as well as weakness scores.

  6. 6.

    Weighted strength and weighted weakness are calculated using Eqs. (30) and (31), respectively, by imparting the obtained attributes weights.

  7. 7.

    Performance degree of each alternative is calculated in order to rank the alternatives in descending order using Eq. (32).

In what follows next, we present the solution methodology in terms of IFNs as well as IVIFNs taking into account all the four variations of attributes weights information (Fig. 1).

Fig. 1
figure 1

Generalized TOPSIS method for MAGDM problem

Full size image

4 Numerical Illustrations

In this section, computational procedure is demonstrated with the help of numerical illustrations in terms of the proposed approach. To validate the applicability of the approach in the setting of MAGDM and IFNs, an investment decision making problem [34] is considered in Sect. 4.1, whereby the case of partial attribute weight information is exemplified. Also, an investment group decision making problem is again considered [35] to illustrate the applicability in an IVIF setting in Sect. 4.2 whereby attributes weights are taken as completely unknown.

4.1 Application Using IFNs

An investment company offers three feasible alternatives \(\varLambda =\{A_{1},A_{2},A_{3}\}\) which are evaluated by three DMs with respect to four attributes: risk (\(C_{1}\)), growth (\(C_{2}\)), social-political issues (\(C_{3}\)) and environmental impact (\(C_{4}\)). Additionally, it has been assumed that the information on attributes weights have been provided partially or incompletely by the respective DMs in the form of set H as follows:

$$\begin{aligned} H&=\left\{ w=(w_{1},w_{2},w_{3},w_{4})^{T} | \ 0.2\le w_{2}\le 0.5,\ w_{3}=0.2,\ 0.2\le w_{4} \le 0.6, \right.\\&\quad w_{4} \ge w_{1},\ w_{3}-w_{1} \le 0.1,\ w_{3}-w_{2} \ge w_{4}-w_{1},\ w_{j}\ge 0, j=1,2,3,4;\\&\left.\quad \sum _{j=1}^{4} w_{j}=1 \right\} \end{aligned}$$

Furthermore, suppose that the weights of DMs are IFNs and are expressed as

$$ \{[0.28,0.58,0.14],[0.25,0.6,0.15],[0.3,0.55,0.15]\}. $$

The IF decision matrices given by DMs \(D_{k}, k=1,2,3\) can be obtained in Table 1 in the form of \({\widetilde{\varOmega }}^{k}=(\alpha _{ij}^{k})_{3 \times 4}\) as follows:

Table 1 Assessment \((\alpha _{ij}^{k})_{3 \times 4}\) given by DMs \(D_{k}, k=1,2,3\)
Full size table

Step 1. Since DMs weights as given by the experts are given in the form of IFNs, crisp DMs weights \(\lambda _{k}, k=1,2,3\) have been obtained using Eq. (1) as \(\{\lambda _{1}=0.335,\lambda _{2}=0.302,\lambda _{3}=0.363\}\).

Step 2. Judgement provided by three DMs have been aggregated utilizing Eq. (2) into a cumulative IF decision matrix \(D=(\alpha _{ij})_{3 \times 4}\) taking into effect the importance of individual DMs and are provided in Table 2.

Table 2 Aggregation of individual assessment \((\alpha _{ij})_{3 \times 4}\) over DMs weights \(\lambda _{k}\)
Full size table

Step 3. Since attribute \(A_{2}\) being the growth factor is a benefit attribute, and rest all are cost attributes, there is a need to standardize the IF decision matrix D into R using Eq. (3) and is given in Table 3.

Table 3 Standardized IF decision matrix R
Full size table

Step 4. Next, advantage and disadvantage scores have been obtained using Eqs. (4) and (5) wherein it is calculated how advantageous an alternative is with respect to all other alternatives keeping fixed a particular attribute. On the other hand, disadvantage score analyses as to how much an alternative is disadvantageous or not preferable in comparison to the rest of the alternatives with respect to a particular attribute and is provided in Table 4.

Table 4 Advantage score matrix \((a_{ij})_{3\times 4}\) and disadvantage score matrix \((b_{ij})_{3\times 4}\)
Full size table

Step 5. Since attributes weights are provided in the form of incomplete uncertain information as H, thus, it can be transformed into incomplete certain information using (11) as \(H_{1}\) and bifurcated into three types as follows:

Type 1: \(\{w_{2}\ge 0.2, w_{4}\ge 0.2,w_{4}-w_{1}\ge 0,w_{3}-w_{2}-w_{4}+w_{1}\ge 0 \}\)

Type 2: \(\{w_{2}\le 0.5,w_{4} \le 0.6,w_{3}-w_{1} \le 0.1 \}\)

Type 3: \(\{w_{3}=0.2 \}\)

We seek to obtain \(w=\{w_{1},\ldots ,w_{4}\}\in H_{1}\) such that \(w_{j}\ge 0, j=1,\ldots ,4,\)\(\sum _{j=1}^{4}w_{j}=1\).

In order to obtain the weight vector, performance degree of each alternative is maximized subject to partial weights \(H_{1}\) and by using (12), (MOP1) problem is formed. Then, using WSM with equal weights, model (MOP1) can be transformed using (13) into a single objective (WSP1) problem. Solving the above nonlinear optimization problem (linear fractional problem) using LINGO [36], the optimal attributes weights are obtained as \(w=\{0.3,0.2,0.2,0.3\}\).

Step 6. What follows next, is the calculation of weighted strength \(S_{i}\) as well as weighted weakness \(W_{i}\) using Eqs. (14) and (15), encompassing the weight vector \(w=\{0.3,0.2,0.2,0.3\}\) obtained after solving the (WSP1) problem as listed in Table 5.

Step 7. Performance degrees \(Z_{i}\) corresponding to each alternative \(A_{i}\) are obtained using Eq. (16) as listed in Table 5.

Table 5 Weighted strength, weighted weakness and performance degree
Full size table

Thus, the investment options are ranked in descending order of preference as \(A_{1}\succ A_{3}\succ A_{2}\).

4.2 Application Using IVIFNs

An investment company wants to invest a sum of money in the best option. There is a panel with four possible alternatives to invest the money: \(A_{1}\) (car company), \(A_{2}\) (food company), \(A_{3}\) (computer company) and \(A_{4}\) (arms company). The investment company must take a decision according to the following three attributes: \(C_{1}\) (the risk analysis), \(C_{2}\) (the growth analysis) and \(C_{3}\) (the environmental impact analysis). Assume that the weight vector of DMs as given by the experts are given in the form of IVIFN as \(\lbrace \left( [0.2,0.4],[0.3,0.6], [0.2,0.6]),([0.2,0.6],[0.4,0.5],[0.6,0.8]), ([0.4,0.5],[0.6,0.8],[0.3,0.6]\right) \rbrace \). Additionally, to show the applicability of the proposed approach, attributes weights have been taken as completely unknown. Also the four possible alternatives \(A_{i}, (i=1,2,3,4)\) are to be evaluated under three mentioned attributes using IVIF information, given by three DMs \(D_{k}, (k = 1, 2, 3)\), as listed in Table 6.

Table 6 Assessment \((\alpha _{ijk})_{4 \times 3}\) given by DMs \(D_{k}, k=1,2,3\)
Full size table

Step 1. Since DMs weights as given by the experts are in the form of IVIFNs, crisp DMs weights \(\lambda _{k}, k=1,2,3\) are obtained using Eq. (17) as \(\{\lambda _{1}=0.24,\lambda _{2}=0.388, \lambda _{3}=0.372\}\).

Step 2. Assessments provided by three DMs are aggregated over their weights \(\lambda _{k}\) using Eq. (18) into a unified IVIF decision matrix \(D=(\alpha _{ij})_{4 \times 3}\) and is provided in Table 7.

Step 3. Since attributes \(A_{1}\) and \(A_{3}\) being the risk and environmental impact analysis factor are cost attributes and \(A_{2}\) being the growth factor is a benefit attribute, so, there is a need to standardize the IVIF decision matrix D into R using Eq. (19) and is given in Table 8.

Step 4. Advantage and disadvantage scores of the alternatives have been obtained using Eqs. (20) and (21) and are given in Table 9.

Table 7 Aggregation of individual assessment \((\alpha _{ij})_{4 \times 3}\) over DMs weights \(\lambda _{k}\)
Full size table
Table 8 Standardized IVIF decision matrix R
Full size table
Table 9 Advantage score matrix \((a_{ij})_{4\times 3}\) and disadvantage score matrix \((b_{ij})_{4\times 3}\)
Full size table

Step 5. Since attribute weight information is not provided by the DM, weights are obtained using the proposed entropy measures in Eqs. (24) and (25) and are listed in Table 10.

Table 10 Entropy \(\bar{E}_{j}\) and attributes weights \(w_{j}\)
Full size table

Step 6. Weighted strength as well as weighted weakness taking into effect attributes weights are obtained using Eqs. (30) and (31) in Table 11.

Step 7. Finally, performance degree is calculated corresponding to each alternative using Eq. (32) as given in Table 11, which concludes that the most preferred investment option is \(A_{3}\) followed by \(A_{1}, A_{2}\) and \(A_{4}\).

Table 11 Weighted strength, weighted weakness and performance degree
Full size table

5 Comparison with Other Works

To further exhibit the efficiency of the proposed approach, we compare the results and methodology by analysing the case with some similar computational approaches such as by Aikhuele and Turan [14] and Liu et al. [16].

  1. 1.

    Comparison with Aikhuele and Turan [14]

    We solved the MAGDM problem applying the IF-TOPSIS model for failure detection presented in [14] with appropriate modifications. Though [14] considered multiple DMs, but the weight vector of DMs were taken as completely known single numeric value which reflects too much certainty in the uncertain decision making scenario. Also, the numerical illustration considered in [14] cites DMs weights as equal which is less common and impractical because it is unlikely that the outlook of the DMs are same as far as knowledge or perspective is concerned in order to be labelled with indifference in judgement; whereas the ranking order of the alternatives obtained in the illustration presented in [14] through the proposed approach is the same as that obtained in [14] itself, that is, \(PM_2>PM_4>PM_3>PM_1\). Also in [14], idealistic benchmarks are used while finding IF–PIS as well as IF–NIS, which are too impractical to be achieved in uncertain real-world decision making and which also reflects its effect in the separation measures used unlike the proposed approach where advantage and disadvantage scores of alternatives are found. Furthermore, the entropy method listed in [14] has drawbacks as listed in [26]. Thus, the proposed procedure can be adopted to a particular situation such as the one used in [14]; however, the same is not true about the latter.

  2. 2.

    Comparison with Liu et al. [16]

    In order to compare with [16], we solved the failure mode and effect analysis approach presented therein using our methodology with appropriate modifications. In [16], DMs are assigned crisp weights to reflect their differences in performance which implies too much certainty and surety in a practical uncertain decision making process. In [16], we came across the ranking order for the first five alternatives, for instance, out of sixteen as \(FM_{10}>FM_{13}>FM_{12}>FM_{8}>FM_{3}\), whereas if the illustration is solved by the proposed approach, ranking order comes out to be \(FM_{8}>FM_{3}>FM_{10}>FM_{12}>FM_{13}\). The prospective reasons for the change in ranking order can be attributed to employing advantage and disadvantage scores rather than the application of ideal benchmarks which are too idealistic to be achieved in an unrealistic, non-idealistic decision making process, thereby affecting the calculation of separation measures used too. The proposed methodology saw the usage of all the three parameters of IFN, viz. membership degree, non-membership degree as well as hesitation degree whereas in [16], hesitation parameter is truncated in the decision making process. Although the proposed approach can be adapted to a particular situation such as the one in [16], but the same is not true about the latter.

6 Conclusions

In this paper, TOPSIS method has been generalized encompassing the MAGDM parameters into the picture with the application of intuitionistic fuzziness in the background. The paper highlights the said methodology in the presence of IFS as well as IVIFS. Multiple DMs are incorporated so as to include multiple sources of subjective influence with DMs weights taken subjectively in the form of IFN and IVIFN, reflecting a realistic assessment by the experts. Different variations of attributes weight information are considered such as completely known weight information, uncertain subjective evaluations in the form of IFN or IVIFN, incompletely known partial weights and completely unknown weights. Advantage and disadvantage scores are used for assessing the performance evaluation of alternatives. The selection of the best alternative is done based on relative comparison of performances of the alternatives among each other rather than measuring the performance of each alternative using some hypothetical benchmarks or peers. In this paper, besides the membership and non-membership degrees, the hesitancy degree is also treated at its independent level of importance and the ranking of the alternatives is done on the basis of trade-off values of all three parameters of IFN or IVIFN. Furthermore, potential applications of the proposed approach are examined and demonstrated with a numerical illustration in the realm of IFNs where the attributes weights are given incomplete or partially and another illustration with input data in the form of IVIFNs where the attributes weights are completely unknown. Examples have been employed to compare the experimental results of the proposed approach with the ones obtained by the methods presented in [14] and [16]. Also, highlights of the said approach are emphasized. Finally, it can be concluded that the procedure proposed in this study, provides a better alternative method for choosing an alternative in a MAGDM problem as it allows for the fuzziness and the hesitation of the DMs subjective assessments to be reflected and modelled in the evaluation with the consideration of variations in attributes weights information. For future research, we would like to extend the proposed MAGDM problem with all variations in DMs weights so as to further generalize it. Also, we would like to use granular computing techniques to propose simpler methods as far as computational work is concerned for dealing with MAGDM problems.