Neural identifier for unknown discrete-time nonlinear delayed systems

Abstract

This work proposes a discrete-time nonlinear neural identifier based on a recurrent high-order neural network trained with an extended Kalman filter-based algorithm for discrete-time deterministic multiple-input multiple-output systems with unknown dynamics and time-delay. To prove the semi-globally uniformly ultimately boundedness of the proposed neural identifier, the stability analysis based on the Lyapunov approach is included. Applicability of the proposed identifier is shown via simulation and experimental results, all of them performed under the presence of unknown external and internal disturbances as well as unknown time-delays.

1 Introduction

The study of time-delay systems (TDS) has become an important field of research due to its frequent presence in engineering applications [4, 7, 14, 33], and some examples of this kind of systems are: chemical processes, engine cooling systems, hydraulic systems, irrigation channels, metallurgical processing systems, network control systems and supply networks [4, 14, 33].

Delays in systems happen due to the limited capabilities of their components of processing data and transporting information and materials [18]. Therefore, the main sources of time-delay in systems are [19]:

• Nature of the process which arises when the system has to wait a process in order to continue to the next step, for example chemical reactors, diesel engines and recycled processes.

• Transport delay which occurs when systems must transport materials and the controller takes time to affect the process, for example rolling mills, cooling and heating systems.

• Communication delay can occur due to:

  • Propagation time-delay of signals among actuators, controllers, sensors, especially in networking control and fault-tolerant systems.

  • Access time-delay as a result of finite time required to access to a shared media. The data at the controller are a delayed version of the current state, and the control action suffers time-delay when is sent. It is found in network systems.

Delays can be constant or time-varying, known or unknown, deterministic or stochastic depending on the system under consideration [18]. It is well known that delay in systems is a source of instability and poor performance. A number of methodologies have been proposed to handle these problems [7, 14, 20, 21, 33], some of them based on neural networks where neural networks are used to deal with unknown dynamics [5, 7, 20, 31, 32] and most of them developed for continuous-time systems. Besides, loss of packets in network systems can happen as the result of delays which are introduced in the system due to the limited capacity of data transmission between devices [15] which can also result in instability [31, 32].

In order to control a system, a model is usually required, which is a mathematical structure knowledge about the system represented in the form of differential or difference equations. Some motives for establishing mathematical descriptions of dynamical systems are: simulation, prediction, fault detection and control system design, among them [22].

There are two ways to obtain a system model: It can be derived in a deductive manner using laws of physics, or it can be inferred from a set of data collected during a practical experiment of the system through its operating range [22]. The first method can be simple; however, in many cases, necessary time for getting the system model can be excessive; moreover, obtaining an accurate model this way would be unrealistic because of unknown dynamics and delays that cannot be modeled. The second method, which is known as system identification, could be a helpful shortcut for deriving the model. Despite the fact that system identification does not always result in an accurate model, a satisfactory one can be obtained with reasonable efforts [22].

There are a considerable number of methods to accomplish system identification, to name a few: based on neural network, based on fuzzy logic, auxiliary model identification and hierarchical identification [6]. Neural networks stand out for their characteristics, such as no need to establish the model structure of the actual system, any linear and nonlinear model can be identified, and a neural network is a model and an actual system. Neural networks allow us to identify and obtain mathematical models which are close to the actual system behaviors even in the presence of variations and disturbances [6, 22].

Recurrent neural networks (RNNs) are a special kind of neural networks which have feedback connections that have an impact on the learning capabilities and performance of the network; moreover, unit-delay elements on the feedback loops result in a nonlinear dynamical behavior [8].

Recurrent high-order neural networks (RHONNs) are an extension of first-order Hopfield network. A RHONN has more interaction among its neurons and characteristics which make them ideal for modeling complex nonlinear systems, such as: approximation capabilities, easy implementation, robustness against noise and online training, which make them ideal for modeling complex nonlinear systems [28].

Backpropagation through time learning is the most used training algorithm for RNNs; however, it is a first-order gradient descent method, that even if it gives great results in several occasions, it presents some problems such as slow convergence, high complexity, bifurcations, instability and limited applicability due to high computational costs [10, 28], and it is not able to discover contingencies spanning long temporal intervals due to the vanishing gradient [3, 12]. On the other hand, training algorithms that are based on the extended Kalman filter (EKF) improve learning convergence, reduce the epoch number and the number of required neurons. Moreover, EKF training methods for training feedforward and RNNs have proven to be reliable and practical [9, 28].

In this work, a RHONN identifier trained with a EKF-based algorithm for discrete-time nonlinear deterministic multiple-input multiple-output (MIMO) systems with unknown time-delay is presented, and simulation results of the proposed RHONN identifier are compared with the results presented in [20] for the same system. In order to prove the semi-globally uniformly ultimately boundedness (SGUUB) of the RHONN identifier trained with a EKF-based algorithm, a Lyapunov stability analysis is included.

It is important to note that the proposed discrete-time RHONN identifier does not require previous knowledge of the system model nor an estimation of the time-delay or system perturbation or their bounds. These characteristics make it ideal for devices which require of a real-time implementation. Most of the work on the field of system identification of nonlinear TDS addressed the continuous-time case [1, 24, 31, 32] and assumed that the time-delay is known, approximated or at least a bound is previously known [2]. In [13, 24], the authors present methodologies for system identification of nonlinear continuous-time-delayed systems in which an approximation of the time-delay is needed. In [24], the authors present an approach where the knowledge of the system model is necessary at least nominally. Then, all the above-explained properties allow the proposed discrete-time identifier, an excellent option for real-time implementations in digital devices.

Therefore, the main contributions of this paper are:

• 1. A RHONN identifier trained with an EKF-based algorithm for discrete-time deterministic MIMO systems with unknown dynamics and time-delay.

• 2. Results of simulation and real-time for three time-delay benchmarks. Systems are presented in order to show the performance of the identifier.

• 3. The stability proof based on the Lyapunov approach for the neural identifier without the need of previous knowledge for plant dynamics, disturbances, delays nor its bounds.

This work is organized as follows: In Sect. 2, time-delay systems are introduced, Sects. 3 and 4 give a brief explanation of RHONNs and EKF-trained algorithm, respectively, in Sect. 5, the RHONN-based neural identifier is described, in Sect. 6, results are shown, important conclusions are presented in Sect. 7, and finally, at the “Appendix”, the Lyapunov analysis is included.

2 Time-delay nonlinear system

Time-delay is the property of physical systems by which the response to an applied force is delayed as well as its effects [36]. Whenever a material, information or energy is transmitted, there is an associated delay and its value is determined by distance and speed of the transmission [36].

TDS, also known as systems with after effect or dead-time, hereditary systems, equations with deviating argument or differential-difference equations, are systems which have a significant time-delay between the application of the inputs and their effects. TDS inherit time-delay in its components or from introduction of delays for control design purposes [25, 30, 34].

In general, TDS can be classified as [18]:

• Systems with lumped delays: where a finite number of parameters can describe their delay phenomena.

• Systems with distributed delays: where it is not possible to find a finite number of parameters which described their time-delay phenomena.

The presence of delays in the systems makes system analysis and control design complex and also can degrade the performance or induce instability [34, 36], this is why it is important to understand delays in systems; otherwise, the system could become unstable [36].

Let us consider the following discrete-time-delay nonlinear MIMO system described by:

$$x \left( k+1\right)= F\left( x \left( k - l\right) ,u\left( k\right) \right)$$

(1)

$$y \left( k\right)= h\left( x\left( k\right) \right)$$

(2)

where $x\in \mathfrak {R}^{n}$, $u\in \mathfrak {R}^{m}$ , $F\in \mathfrak {R}^{n}\times \mathfrak {R}^{m}\rightarrow \mathfrak {R}^{n}$ is a nonlinear function and $l=1,2,\ldots$ is the unknown delay.

3 Recurrent high-order neural network

Recurrent neural networks are considered as good candidates for identification and control of general nonlinear and complex systems, RNNs deal with uncertainties and modeling error on the systems, and also they are attractive due to their characteristics as easy implementation, simple structure, robustness and capacity to adjust their weights online [23, 28].

RNN outputs flow in forward and backward directions, and they are feedback to the same neurons or neurons in different layers. This two-way connectivity between units distinguished RNN from feedforward neural networks, where the output of one unit is only connected to the units in the next layer [16, 23].

RNNs are mostly based on the Hopfield model [23], and their recurrent structure has a profound impact on their learning capabilities and performance [35].

Recurrent high-order neural networks are the result of including high-order interactions represented by triplets $(y_{i}y_{j}y_{k})$, quadruplets $(y_{i}y_{j}y_{k}y_{l})$, etc. to the first-order Hopfield model [16, 35]. RHONN model is very flexible, and it allows to incorporate a priori information about the system into the neural network model [28]

Consider the following discrete-time recurrent High-Order neural network:

$$\widehat{x}_{i}(k+1)=w_{i}^{\top }\left( k\right) z_{i}(x(k-l),u(k)),\ \ i=1,\ldots ,n$$

(3)

where $\widehat{x}_{i}$ ($i=1,2,\ldots ,n$) is the state of the i-th neuron, $w_{i}$ is the respective online adapted weight vector, n is the state dimension, and $z_{i}(x(k-l),u(k))$ is given by

$$z_{i}(x(k-l),\varrho (k))=\left[ \begin{array}{c} z_{i_{1}} \\ z_{i_{2}} \\ \vdots \\ z_{i_{L_{i}}} \end{array} \right] =\left[ \begin{array}{c} \varPi _{j\in I_{1}}\xi _{i_{j}}^{di_{j}(1)} \\ \varPi _{j\in I_{2}}\xi _{i_{j}}^{d_{i_{j}}\left( 2\right) } \\ \vdots \\ \varPi _{j\in I_{L_{i}}}\xi _{i_{j}}^{di_{j}(L_{i})} \end{array} \right]$$

(4)

with $L_{i}$ as the respective number of high-order connections, $\{I_{1},I_{2},\ldots,\,I_{L_{i}}\}$ is a collection of nonordered subsets of $\{1,2,\ldots,\,n+m\}$, m is the number of external inputs, $d_{i_{j}}(k)$ being nonnegative integers, and $\xi _{i}$ defined as follows:

$$\xi _{i}=\left[ \begin{array}{c} \xi _{i_{1}} \\ \vdots \\ \xi _{i_{n}} \\ \xi _{i_{n+1}} \\ \vdots \\ \xi _{i_{n+m}} \end{array} \right] =\left[ \begin{array}{c} S(x_{1}) \\ \vdots \\ S(x_{n}) \\ u_{1} \\ \vdots \\ u_{m} \end{array} \right]$$

(5)

In (5), $u =[u_{1},u_{2},\ldots ,u_{m}]^{\top }$ is the input vector to the neural network, and $S(\cdot )$ is defined by

$$S\left( \varsigma \right) = \frac{1}{{1 + \exp \left( { - \beta \varsigma } \right) }},\quad {\beta > 0}$$

(6)

where $\varsigma$ is any real value variable.

4 Kalman filter learning algorithm

There are a number of training algorithms for neural networks; however, most of them have problems such as local minimal, slow learning and high sensitivity to initial conditions. Kalman filter (KF)-based algorithms show up as an alternative which overcome these problems [9, 28].

KF estimates the state of a linear system with additive state and output white noise [28]. KF has a recursive solution; in each update, the state is estimated from the previous estimated state and the new input data. The fact that it is only necessary to store the previous estimated state in memory makes KF computationally more efficient than computing the estimated state directly from the entire past observed data of previous steps [9, 28].

For KF-based neural network training, the network weights become the states to be estimated, and for this case, the error between the neural network output and the measured plant output is considered as additive noise [9, 28].

Extended Kalman filter is used due to the fact that neural network mapping is a nonlinear problem [28]. EKF is an extension of KF obtained through a linearization procedure [9].

4.1 Extended Kalman filter training algorithm

The EKF-based training algorithm used for training the RHONN identifier on this work is:

$$\begin{aligned} {\omega _i}\left( {k + 1} \right)=\, & {\omega _i}\left( k \right) + {\eta _i}{K_i}\left( k \right) {e_i}\left( k \right) \\ {K_i}\left( k \right)=\, & {P_i}\left( k \right) {H_i}\left( k \right) {M_i}\left( k \right) \\ {P_i}\left( {k + 1} \right)=\, & {P_i}\left( k \right) - {K_i}\left( k \right) H_i^ \top \left( k \right) {P_i}\left( k \right) + {Q_i}\left( k \right) \\ i=\, & 1, \ldots ,n \end{aligned}$$

(7)

with

$$M_{i}\left( k\right)=\left[ R_{i}\left( k\right) +H_{i}^{\top }\left( k\right) P_{i}\left( k\right) H_{i}\left( k\right) \right] ^{-1}$$

(8)

$$e_{i}\left( k\right)= x_{i}\left( k\right) -\widehat{x}_{i}\left( k\right)$$

(9)

The dynamics of (9) can be expressed as

$$e_{i}\left( k+1\right)= \widetilde{w}_{i}\left( k\right) z_{i}\left( x(k-l),\,u(k)\right) +\epsilon _{z_{i}}$$

(10)

$${H_{ij}}= {\left[ {\frac{{\partial {\chi _i}(k)}}{{\partial {\omega _{ij}}(k)}}} \right] ^T}$$

(11)

where $i = 1, \ldots ,n$, ${e_i} \in \mathfrak {R}$ is the identification error, ${P_i} \in {\mathfrak {R}^{{L_i} \times {L_i}}}$ is the weight estimation error covariance matrix, ${\omega _i} \in {\mathfrak {R}^{{L_i}}}$ is the online adapted weight vector, ${\chi _i}$ is the i-th state variable of the neural network, ${K_i} \in {\mathfrak {R}^{{L_i}}}$ is the Kalman gain vector, ${Q_i} \in {\mathfrak {R}^{{L_i} \times {L_i}}}$ is the estimation noise covariance matrix, ${R_i} \in \mathfrak {R}$ is the error noise covariance matrix, ${H_i} \in {\mathfrak {R}^{{L_i}}}$ is a vector in which each entry ${H_{ij}}$ is the derivative of the neural network state $({\chi _i})$ with respect to one neural network weight $({\omega _{ij}})$, and it is given by (11), where $i = 1,...,n$ and $j = 1,...,{L_i}$. ${P_i}$ and ${Q_i}$ are initialized as diagonal matrices with entries ${P_i}(0)$ and ${Q_i}(0)$, respectively. It is important to remark that ${H_i}(k)$, ${K_i}(k)$ and ${P_i}(k)$ for the EKF are bounded [29].

5 Neural identification

Neural Identification consists in selecting a neural network model, adjusting its weights according an adaptation law in order to approximate the real system response to the same input [22].

5.1 RHONN identifier

Let us consider the problem to approximate the general discrete-time nonlinear delayed systems (1), by the following discrete-time RHONN series–parallel representation:

$$x_{i}\left( k+1\right) =w_{i}^{*\top }z_{i}\left( x(k-l),u(k)\right) +\epsilon _{z_{i}},\quad \ i=1,\ldots ,n$$

(12)

$\epsilon _{z_{i}}$ is a bounded approximation error, which can be reduced by increasing the number of the adjustable weights [27]. Assume that there exists a ideal weight vector $w_{i}^{*}$ such that $\left\| \epsilon _{z_{i}}\right\|$ can be minimized on a compact set $\varOmega _{z_{i}}\subset \mathfrak {R}^{L_{i}}$. The ideal weight vector $w_{i}^{*}$ is an artificial quantity required for analytical purpose [27]. In general, it is assumed that this vector exists and is constant but unknown. Let us define its estimate as $w_{i}$ and the estimation error as

$$\widetilde{w}_{i}\left( k\right) =w_{i}^{*}-w_{i}\left( k\right)$$

(13)

then, considering (8), the dynamics of (13) can be defined as

$$\widetilde{w}_{i}\left( k+1\right) =\widetilde{w}_{i}\left( k\right) -\eta _{i}K_{i}\left( k\right) e\left( k\right)$$

(14)

Theorem 1

The RHONN model (12) trained with the modified EKF-based algorithm (8) to identify the delayed nonlinear plant (12) ensures that the identification error (10) is SGUUB; moreover, the RHONN weights remain bounded.

Proof

Please, see the “Appendix”. $\square$

6 Results

6.1 Example 1. Simulation results

Consider the following nonlinear time-delay system:

$$\begin{aligned} {{\dot{x}}_1}\left( t \right)= &\, {x_2}\left( t \right) + 0.001{x_1}\left( t \right) u\left( t \right) \\ {{\dot{x}}_2}\left( t \right)= &\, \left( {1 - x_1^2\left( t \right) } \right) {x_2}\left( t \right) - {x_1}\left( t \right) + {x_3}\left( t \right) u\left( t \right) \\& +\, 2\cos \left( {{x_1}\left( {t - 3} \right) } \right) \\ {{\dot{x}}_3}\left( t \right)= &\, {x_4}\left( t \right) + 0.01{x_2}\left( t \right) {x_3}\left( t \right) \exp \left( {u\left( t \right) } \right) \\ {{\dot{x}}_4}\left( t \right)= &\, \left( {1 - x_3^2\left( t \right) } \right) {x_4}\left( t \right) - {x_3}\left( t \right) + \frac{u\left( t \right) }{{\left( {1 + x_2^2\left( t \right) x_4^2\left( t \right) } \right) }} \\&+\, 2\left( {x_1^2\left( {t - 3} \right) + x_2^2\left( {t - 3} \right) } \right) \sin ({x_2}\left( {t - 3} \right) ) \\ {y_1}\left( t \right)= &\, {x_1}\left( t \right) + {x_2}\left( t \right) \\ {y_2}\left( t \right)= &\, {x_3}\left( t \right) + {x_4}\left( t \right) \end{aligned}$$

(15)

System (15) is a chaotic oscillator similar to a van der Pol system [20].

To conduct the simulation tests, the system (15) is simulated using MATLAB^{® 1}\Simulink^{® 2} 2013a and its states are discretized by a zero-order hold with sampling time equals to 0.2 s and initial conditions $x(0) = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ \end{array} } \right]^{T}$.

6.1.1 High-order neural network observer

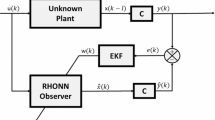
Let us consider the following high-order neural network (HONN) observer design in [20]:

$$\begin{aligned} \hat{x}\left( {k + 1} \right)= & \,A\hat{x}\left( k \right) +\, B\left[ \hat{W}_{1}^{T} \left( k \right) \varPhi _{1} \left( \hat{x}\left( k \right) ,u\left( k \right) \right) \right. \\&\left. +\, h\left( \hat{x}\left( {k - \hat{d}} \right) \right) \right] +\, K\left[ {y\left( k \right) - \hat{y}\left( k \right) } \right] + Du\left( u \right) \\ \hat{y}\left( k \right)= & \, C\hat{x}\left( k \right) \end{aligned}$$

(16)

where $\hat{x}(k)$ is the estimation of x(k), h is a known function vector with constant time-delay, ${\hat{d}}$ is the estimation of d which is the unknown time-delay, ${{\hat{W}}_1}$ is the HONN weight matrix, $\varPhi ({\hat{x},u})$ is the basis function vector, and K is the observer gain matrix [20], with

$$\begin{aligned} {{\hat{W}}_1}\left( {k + 1} \right)= & \,\left( {1 - {\sigma _1}} \right) {{\hat{W}}_1}\left( k \right) \\&+\, {\varGamma _1}{\varPhi _1}\left( {\hat{x}\left( k \right) ,\quad u\left( k \right) } \right) {{\tilde{y}}^T}\left( k \right) {F^T} \\ \end{aligned}$$

(17)

Parameter values are set as in [20]: delay functions (18) are known with estimation of the unknown time-delay $d=3\,{\rm s}$ and ${\hat{d}} = 3.2\,s$. $u(t) = \sin ({0.3t})$.

$$\begin{aligned} {h_1}\left( x \right)= &\, 0 \\ {h_2}\left( x \right)= &\, 2\cos \left( {{x_1}(t)} \right) \\ {h_3}\left( x \right)= &\, 0 \\ {h_3}\left( x \right)= & \,2\left( {x_1^2\left( t \right) + x_2^2\left( t \right) } \right) \sin \left( {{x_2}\left( t \right) } \right) \end{aligned}$$

(18)

Matrices A, C, F and K are set as:

$$\begin{aligned} A= & \left[ {\begin{array}{cccc} 1&{0.2}&0&0\\ 0&1&0&0\\ 0&0&1&{0.2}\\ 0&0&0&1 \end{array}} \right] ,\quad F = \left[ {\begin{array}{cc} 1& 1\\ 1& 1\\ 1& 1\\ 1& 1\\ \end{array}} \right] \\ C= & \left[ {\begin{array}{cc} 1&0\\ 1&0\\ 0&1\\ 0&1 \\ \end{array}} \right] ,\quad K = \left[ {\begin{array}{cc} 0.3& 0\\ 1&0\\ 0& {0.3}\\ 0& 1\\ \end{array}} \right] \end{aligned}$$

$B = {I^{4\,\times \,4}}$, $D = 0$, and as activation function:

$$\sigma \left( x \right) = \frac{{\left( {1 - {e^{ - 0.01x}}} \right) }}{{\left( {1 + {e^{ - 0.01x}}} \right) }}$$

(19)

with ${\varGamma _1} = {\text {diag}}(0.2, \ldots ,0.2)$ and ${\sigma _1} = 0.6$, ${l_1} = 16$, and initial conditions $\hat{x}\left( 0 \right) = {\left[ {\begin{array}{cccc} 0&0&0&0\end{array}} \right] ^T}$

The HONN observer (16) is used for comparison purposes against the RHONN identifier (12) for the states of the system (15). It is important to note that an identifier can be considered as an observer with $y\left( k \right) = x\left( k \right)$. Then, this comparison is a valid one.

6.1.2 RHONN identifier

The RHONN identifier (12) activation function is (19), and the values of the matrices ${{P}_{i}}\left( 0 \right)$, ${{Q}_{i}}\left( 0 \right)$ and ${R}_{i}$ of the EKF-based algorithm training (20) are:

$$\begin{aligned} {{P}_{1}}\left( 0 \right)= &\, {{P}_{2}}\left( 0 \right) ={{P}_{3}}\left( 0 \right) ={{P}_{4}}\left( 0 \right) =1{\text {x}}{{10}^{8}}\,\times \, {\text {diag}}(4) \nonumber \\ {{Q}_{1}}\left( 0 \right)= &\, {{Q}_{2}}\left( 0 \right) ={{Q}_{3}}\left( 0 \right) ={{Q}_{4}}\left( 0 \right) =5{\text {x}}{{10}^{5}}\,\times \, {\text {diag}}(4) \nonumber \\ {{R}_{1}}= &\, {{R}_{2}}={{R}_{3}}={{R}_{4}}=1\,\times \,{{10}^{4}} \end{aligned}$$

(20)

6.1.3 Simulation results

Figures 1, 2, 3, 4, 5, 6, 7 and 8 show the states $x_{i}$ versus the observed and the identified states.

Tables 1 and 2 show the root-mean-square errors (RMSE) and the absolute deviation of the HONN observer and RHONN identifier errors for the same states of system (15) for a test with sampling time equals to 0.2 s. Tables 3 and 4 show the RMSE and the absolute deviation of the errors of the HONN observer and RHONN identifier errors for a test with sampling time equals to 0.02 s.

Fig. 1

Real ${x_1}(k)$ versus observed ${\hat{x}_1}(k )$

Fig. 2

Real ${x_1}(k)$ versus identified ${\hat{x}_1}( k )$

Fig. 3

Real ${x_2}(k)$ versus observed ${\hat{x}_2}( k )$

Fig. 4

Real ${x_2}(k)$ versus identified ${\hat{x}_2}( k )$

Fig. 5

Real ${x_3}(k)$ versus observed ${\hat{x}_3}( k )$

Fig. 6

Real ${x_3}(k)$ versus identified ${\hat{x}_3}( k )$

Fig. 7

Real ${x_4}(k)$ versus observed ${\hat{x}_4}( k )$

Fig. 8

Real ${x_4}(k)$ versus identified ${\hat{x}_4}( k )$

Table 1 RMSE of simulation results with a sampling time equals to 0.2 s

Table 2 Absolute deviation of simulation results with a sampling time equals to 0.2 s

Table 3 RMSE of simulation results with a sampling time equals to 0.02 s

Table 4 Absolute deviation of simulation results with a sampling time equals to 0.02 s

The results show a similar performance between the identifier (12) and the observer (16) for the same states of the system (15); however, the errors of the identifier are in most cases smaller than the ones of the observer. Both identifier and observer improved their performance using a smaller sampling time.

6.2 Example 2. Simulation results for a differential robot

In second test for the RHONN identifier (12), a delay is added to each of the seven states of the model of a differential robot presented in [17], and such delays consist in simulating that for 0.1 s, information is not updated. Simulation is made using MATLAB^®/Simulink^® 2013a, the sampling time for the test is 0.01 s and a total time equals to 15 s and $u_{1}(t) = \sin (c(t))$ and $u_{2}(t)=\cos (c(t))$ where c(t) is a chirp signal generated by MATLAB^®.

The delays start in this test at 13, 9, 5, 8, 6, 1, 4 s, respectively, for each state.

Table 5 shows the absolute deviation of the error and RMSE of the results of the simulation test.

Figures 9, 10, 11, 12, 13, 14 and 15 show the behavior of the neural identifier before and after the delay where information cannot be updated.

Fig. 9

Identification of the position X of a differential robot. Real signal (black solid line) versus identified signal (gray dotted line)

Fig. 10

Identification of the position Y of a differential robot. Real signal (black solid line) versus identified signal (gray dotted line)

Fig. 11

Identification of theta of a differential robot. Real signal (black solid line) versus identified signal (gray dotted line)

Fig. 12

Identification of the angular velocity 1 of a differential robot. Real signal (black solid line) versus identified signal (gray dotted line)

Fig. 13

Identification of the angular velocity 2 of a differential robot. Real signal (black solid line) versus identified signal (gray dotted line)

Fig. 14

Identification of the current 1 of a differential robot. Real signal (black solid line) versus identified signal (gray dotted line)

Fig. 15

Identification of the current 2 of a differential robot. Real signal (black solid line) versus identified signal (gray dotted line)

Table 5 Absolute deviation of the error and RMSE of simulation test of a differential robot

6.3 Example 3. Linear induction motor

As third test for the neural identifier (12), simulation results and real-time result are shown in this section using a linear induction motor (LIM) model and a laboratory prototype for real-time experimental results.

6.3.1 Simulation results for a linear induction motor

A delay has been added to the position state of the model of the LIM in [11]. Such delay consists in simulating that for 1 s, it is not possible to update the information of the LIM states starting at 2.1 s, sampling time equals to 0.0001 s and $u_{\alpha }$ is and $u_{\beta }$ are defined as (21) and (22), respectively, where t is time.

$$\begin{aligned} u_{\alpha }(t)= & \, \left\{ \begin{array}{ll} 0& \quad {\text { if }}\quad t < 2s \\ 255\left( {170cos\left( {0.3t\left( {\frac{{98.6}}{6}t - \frac{{98.6}}{3}} \right) } \right) } \right) & \quad {\text { if }}\quad t \ge 2s \end{array} \right. \end{aligned}$$

(21)

$$\begin{aligned} u_{\beta }(t)= & \, \left\{ \begin{array}{ll} 0& \quad {\text { if }}\quad t < 2s \\ 255\left( {170\sin \left( {0.3t\left( {\frac{{98.6}}{6}t - \frac{{98.6}}{3}} \right) } \right) } \right) & \quad {\text { if }}\quad t \ge 2s \end{array} \right. \end{aligned}$$

(22)

Figure 16 shows LIM position and identified LIM position, and Fig. 17 shows LIM velocity and identified LIM velocity. Table 6 shows the RMSE and absolute deviation of the identification errors.

Fig. 16

Identification of LIM position. Position (black solid line) versus identified position (gray dotted line)

Fig. 17

Identification of LIM velocity. Velocity (black solid line) versus identified velocity (gray dotted line)

Table 6 Absolute deviation of the error and RMSE of LIM position and velocity at simulation test

6.3.2 Experimental Results for a LIM

Using the prototype shown in Fig. 18 for real-time test with a LIM presented in [26], the test of the previous section is made at real time.

The prototype consists mainly of a dSPACE^{® 3} DS1104 controller board and its connector panel, a Linear Induction Motor Lab-Volt^{® 4} 8228, a linear encoder SENC 50^{® 5}, a POWERSTAT^{® 6} variable transformer type 126U-3 and a power module. The prototype is operated using MATLAB^®/Simulink^® and dSPACE^® software ControlDesk^{® 7}.

The real-time test has a delay similar to that starts at 1.1 s. Figure 19 shows real LIM position and the identified LIM position, and Fig. 20 shows real LIM velocity and the identified LIM velocity, a sampling time equals to 0.0003 s and $u_{\alpha }$ is and $u_{\beta }$ are defined as (21) and (22), respectively.

Fig. 18

LIM laboratory prototype

Fig. 19

Real-time identification of LIM position. Position (black solid line) versus identified position (gray dotted line)

Fig. 20

Real-time identification of LIM velocity. Velocity (black solid line) versus identified velocity (gray dotted line)

Table 7 Absolute deviation of the error and RMSE of LIM position and velocity at real-time test

It is important to note that the high-frequency signals presented in Figures [SubEquationDirect] (18a) and (19) are due to encoder limitations. However, from Table 7, it is possible to conclude that the RHONN can identify such signals besides limitations.

7 Conclusion

In this work, the performance of a RHONN identifier (12) trained with a EKF-based training algorithm (8) is shown. Its results for the states of a discrete nonlinear time-delay system (15) are compared with the results of a HONN observer (16) design in [20], and a similar behavior is observed; however, for states $x_{2}$ and $x_{4}$ the RHONN identifier has a better performance. In order to support the simulation graphs, Table 1 and Table 2 contain the RMSE and absolute deviation of the errors of the simulation test with a sampling time equals to 0.2s. RHONN identifier performance is improved with a smaller sampling time as can be seen in Tables 3 and 4 which contain the RMSE and absolute deviation of the errors of a simulation test with a sampling time equals to 0.02s. Additionally, the identifier (12) is easier to implement in real time due to the fact that it has less parameters to be tuned.

Results of the second test for the RHONN identifier are performed by adding a delay to a LIM model showing an excellent performance.

As future work, it is a plan to extend this work to stochastic systems and loss of packets.

Appendix

Proof of Theorem 1

Step 1, for ${\mathbf {V}}\left( k\right)$. First consider, the equation for each i-th neuron $(i=1,...,n)$

$$\begin{aligned} V_{i}\left( k\right)= & \, \gamma _{i}e_{i}^{2}\left( k\right) +\widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \nonumber \\ \Delta V_{i}\left( k\right)= & \, V\left( k+1\right) -V\left( k\right) \nonumber \\= & \, \gamma _{i}e_{i}^{2}\left( k+1\right) \nonumber \\&+\,\widetilde{w}_{i}^{T}\left( k+1\right) P_{i}\left( k+1\right) \widetilde{w}_{i}\left( k+1\right) \nonumber \\&-\,\widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) -\gamma _{i}e_{i}^{2}\left( k\right) \end{aligned}$$

(23)

Using (10) and (14) in (23)

$$\begin{aligned} \Delta V_{i}\left( k\right)= & \,\left[ \widetilde{w}_{i}\left( k\right) -\eta _{i}K_{i}\left( k\right) e_{i}\left( k\right) \right] ^{T}[P_{i}\left( k\right) -A_{i}\left( k\right) ] \\ \times&\left[ \widetilde{w}_{i}\left( k\right) -\eta _{i}K_{i}\left( k\right) e_{i}\left( k\right) \right] \\&+\,\gamma _{i}\left[ \widetilde{w}_{i}\left( k\right) z_{i}\left( x(k-l),u(k)\right) +\epsilon _{z_{i}}\right] ^{2} \\&-\,\widetilde{w}_{i}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) -\gamma _{i}e_{i}^{2}\left( k\right) \end{aligned}$$

(24)

with

$$A_{i}\left( k\right) =K_{i}\left( k\right) H_{i}^{\top }\left( k\right) P_{i}\left( k\right) +Q_{i}\left( k\right)$$

(25)

then, (24) can be expressed as

$$\begin{aligned} \Delta V_{i}\left( k\right)= & \, \widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&-\,\eta _{i}e_{i}\left( k\right) K_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&-\,\widetilde{w}_{i}^{T}\left( k\right) A_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&+\,\eta _{i}e_{i}\left( k\right) K_{i}^{T}\left( k\right) A_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&-\,\eta _{i}e_{i}\left( k\right) \widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) K_{i}\left( k\right) \\&+\,\eta _{i}^{2}e_{i}^{2}\left( k\right) K_{i}^{T}\left( k\right) P_{i}\left( k\right) K_{i}\left( k\right) \\&+\,\eta _{i}e_{i}\left( k\right) \widetilde{w}_{i}^{T}\left( k\right) A_{i}\left( k\right) K_{i}\left( k\right) \\&-\,\eta _{i}^{2}e_{i}^{2}\left( k\right) K_{i}^{T}\left( k\right) A_{i}\left( k\right) K_{i}\left( k\right) \\&+\,\gamma _{i}\left( \widetilde{w}_{i}\left( k\right) z_{i}\left( x(k-l),u(k)\right) \right) ^{2} \\&+\,\gamma _{i}2\epsilon _{z_{i}}\widetilde{w}_{i}\left( k\right) z_{i}\left( x(k),u(k)\right) \\&+\,\gamma _{i}\epsilon _{z_{i}}^{2}-\widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) -\gamma _{i}e_{i}^{2}\left( k\right) \end{aligned}$$

(26)

Using the inequalities

$$\begin{aligned} X^{T}X+Y^{T}Y\ge & 2X^{T}Y \\ X^{T}X+Y^{T}Y\ge & -2X^{T}Y \\ -\lambda _{\min }\left( P\right) X^{2}\ge & -X^{T}PX\ge -\lambda _{\max }\left( P\right) X^{2} \end{aligned}$$

(27)

which are valid $\forall X,Y\in \mathfrak {R}^{n}$, $\forall P\in \mathfrak {R}^{n\times n}, P=P^{T}>0,$ then (26) can be rewritten as

$$\begin{aligned} \Delta V_{i}\left( k\right)\le & -\widetilde{w}_{i}^{T}\left( k\right) A_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&-\,\eta _{i}^{2}e_{i}^{2}\left( k\right) K_{i}^{T}\left( k\right) A_{i}\left( k\right) K_{i}\left( k\right) \\&+\,\widetilde{w}_{i}^{T}\left( k\right) \widetilde{w}_{i}\left( k\right) +e_{i}^{2}\left( k\right) \\&+\,\eta _{i}^{2}e_{i}^{2}\left( k\right) K_{i}^{T}\left( k\right) P_{i}\left( k\right) P_{i}^{T}\left( k\right) K_{i}\left( k\right) \\&+\,\eta _{i}^{2}\widetilde{w}_{i}^{T}A_{i}\left( k\right) K_{i}\left( k\right) K_{i}^{T}\left( k\right) A_{i}^{T}\left( k\right) \widetilde{w}_{i}\left( k\right) \\&+\,\eta _{i}^{2}e_{i}^{2}\left( k\right) K_{i}^{T}\left( k\right) P_{i}\left( k\right) K_{i}\left( k\right) \\&+\,2\gamma _{i}\left( \widetilde{w}_{i}\left( k\right) z_{i}\left( x(k-l),u(k)\right) \right) ^{2} \\&+\,2\gamma _{i}\epsilon _{z_{i}}^{2}-\gamma _{i}e_{i}^{2}\left( k\right) \end{aligned}$$

(28)

Then,

$$\begin{aligned} \Delta V_{i}\left( k\right)\le & -\left\| \widetilde{w}_{i}\left( k\right) \right\| ^{2}\lambda _{\min }\left( A_{i}\left( k\right) \right) \\&-\,\eta _{i}^{2}\left| e_{i}\left( k\right) \right| ^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\min }\left( A_{i}\left( k\right) \right) \\&+\,\eta _{i}^{2}\left| e_{i}\left( k\right) \right| ^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\max }^{2}\left( P_{i}\left( k\right) \right) \\&+\,2\eta _{i}^{2}\left| e_{i}\left( k\right) \right| ^{2}\left\| K_{i}\left( k\right) \right\| ^{2} \\&+\,\left\| \widetilde{w}_{i}\left( k\right) \right\| ^{2}\lambda _{\max }\left( P_{i}\left( k\right) \right) \\&+\,\left\| \widetilde{w}_{i}\left( k\right) \right\| ^{2}\lambda _{\max }^{2}\left( A_{i}\left( k\right) \right) \\&+\,2\gamma _{i}\left\| \widetilde{w}_{i}\left( k\right) \right\| ^{2}\left\| z_{i}\left( x(k-l),u(k)\right) \right\| ^{2} \\&+\,2\gamma _{i}\epsilon _{z_{i}}^{2}-\gamma _{i}\left| e_{i}\left( k\right) \right| ^{2} \end{aligned}$$

(29)

Defining

$$\begin{aligned} E_{i}\left( k\right)= & \,\lambda _{\min }\left( A_{i}\left( k\right) \right) -\lambda _{\max }^{2}\left( A_{i}\left( k\right) \right) \\&-\,2\gamma _{i}\left\| z_{i}\left( x(k-l),u(k)\right) \right\| ^{2}+\lambda _{\max }\left( P_{i}\left( k\right) \right) \\ F_{i}\left( k\right)= & \,\gamma _{i}+\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\min }\left( A_{i}\left( k\right) \right) \\&-\,\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\max }^{2}\left( P_{i}\left( k\right) \right) -2\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2} \end{aligned}$$

and selecting $\eta _{i}$, $\gamma _{i}$, $Q_{i}$ and $R_{i}$, such that $E_{i}>0$ and $F_{i}>0$, $\forall k$, then, (29) can be expressed as

$$\begin{aligned} \Delta {V_i}\left( k \right) \le- & {\left\| {{{\tilde{\omega }}_i}\left( k \right) } \right\| ^2}{E_i}\left( k \right) - {\left| {{e_i}\left( k \right) } \right| ^2}{F_i}\left( k \right) \\+ &\, 2{\gamma _i}\delta \varepsilon _{{z_i}}^2 \end{aligned}$$

(30)

Hence, $\Delta V_{i}\left( k\right) <0$ when

$$\left\| \widetilde{w}_{i}\left( k\right) \right\| >\sqrt{\frac{2\gamma _{i}\epsilon _{z_{i}}^{2}}{E_{i}\left( k\right) }}\equiv \kappa _{1}$$

(31)

or

$$\left| e_{i}\left( k\right) \right| >\sqrt{\frac{2\gamma _{i}\epsilon _{z_{i}}^{2}}{F_{i}\left( k\right) }}\equiv \kappa _{2}$$

(32)

Step 2. Now for ${\mathbf {V}}\left( k\right)$, consider the Lyapunov function candidate.

$$\begin{aligned} {\mathbf {V}}\left( k\right)= & \, \sum \limits _{i=1}^{n}\widetilde{w} _{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) +\gamma _{i}e_{i}^{2}\left( k\right) \\ \Delta {\mathbf {V}}\left( k\right)= &\, \sum \limits _{i=1}^{n}\left( \widetilde{w }_{i}^{T}\left( k+1\right) P_{i}\left( k+1\right) \widetilde{w}_{i}\left( k+1\right) \right. \\&\left. +\,\gamma _{i}e_{i}^{2}\left( k+1\right) -\widetilde{w}_{i}^{T}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) \right. \\&\left. -\,\gamma _{i}e_{i}^{2}\left( k\right) \right) \end{aligned}$$

(33)

Using (10) and (14) in (23)

$$\begin{aligned} \Delta {\mathbf {V}}\left( k\right)= &\, \sum \limits _{i=1}^{n}\left( \left[ \widetilde{w}_{i}\left( k\right) -\eta _{i}K_{i}\left( k\right) e_{i}\left( k\right) \right] ^{T}\right. \\ \times &\,[P_{i}\left( k\right) -A_{i}\left( k\right) ]\left[ \widetilde{w}_{i}\left( k\right) -\eta _{i}K_{i}\left( k\right) e_{i}\left( k\right) \right] \\&+\,\gamma _{i}\left[ \widetilde{w}_{i}\left( k\right) z_{i}\left( x(k-l),u(k)\right) +\epsilon _{z_{i}}\right] ^{2} \\&\left. -\,\widetilde{w}_{i}\left( k\right) P_{i}\left( k\right) \widetilde{w}_{i}\left( k\right) -\gamma _{i}e_{i}^{2}\left( k\right) \right) \end{aligned}$$

(34)

Defining

$$\begin{aligned} A_{i}\left( k\right)= & \,K_{i}\left( k\right) H_{i}^{\top }\left( k\right) P_{i}\left( k\right) +Q_{i}\left( k\right) \\ E_{i}\left( k\right)= & \,\lambda _{\min }\left( A_{i}\left( k\right) \right) -\lambda _{\max }^{2}\left( A_{i}\left( k\right) \right) \\&-\,2\gamma _{i}\left\| z_{i}\left( x(k-l),u(k)\right) \right\| ^{2}+\lambda _{\max }\left( P_{i}\left( k\right) \right) \\ F_{i}\left( k\right)= & \,\gamma _{i}+\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\min }\left( A_{i}\left( k\right) \right) \\&-\,\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2}\lambda _{\max }^{2}\left( P_{i}\left( k\right) \right) -2\eta _{i}^{2}\left\| K_{i}\left( k\right) \right\| ^{2} \end{aligned}$$

and selecting $\eta _{i}$, $\gamma _{i}, Q_{i}$ and $R_{i}$, such that $E_{i}>0$ and $F_{i}>0$, $\forall k$, then, (24) can be expressed as

$$\begin{aligned} \Delta {\mathbf {V}}\left( k\right)\le & \sum \limits _{i=1}^{n}(-\left\| \widetilde{w}_{i}\left( k\right) \right\| ^{2}E_{i}\left( k\right) \\&- \,\left| e_{i}\left( k\right) \right| ^{2}\left( k\right) F_{i}\left( k\right) +2\gamma _{i}\epsilon _{z_{i}}^{2}) \end{aligned}$$

Hence, $\Delta {\mathbf {V}}\left( k\right) <0$ when (31) or (32) is fulfilled

Therefore, considering Step 1 and Step 2 for (23), the solution of (10) and (14) is SGUUB. $\square$

Remark 1

Considering Theorem 1 and its proof, it can be easily shown that the result can be extended to a system (12) with multiple delays like $x\left( k-l_{i}\right)$ with $i=1,2,\ldots$, can be used instead of $x\left( k-l\right)$ in (3) and/or for time-varying delays $x\left( k-l_{i}\left( k\right) \right)$ with $l_{i}\left( k\right)$ bounded by $l_{i}\left( k\right) \le l$.