1 Introduction

The data-driven system identification has been extensively used to model systems having complex and nonlinear dynamics [1, 2]. The time delay occurs naturally in almost all industrial process models, where the material or information takes some time to travel between source and destination [3]. The problem with time delay estimation is that it produces multiple minima in the cost function, which makes global minima hard to reach [4].

In general, many industrial processes are preferred to be identified as lower order models with time delays [5,6,7,8,9,10]. There are various model-based techniques are available which uses identified lower-order (mostly first- or second-order) time delay models to design and tune regulators [11,12,13,14,15,16,17,18,19]. Therefore, an accurate model estimation plays a key role in the success of these model-based techniques.

The literature studies suggest that the identification of stable delayed dynamics is relatively easy and extensively available in various papers (see [20] and references therein). The advantage associated with the stable delayed process is that the identification can be performed in open-loop with less concern on the predictor’s stability. On the other hand, the identification of unstable delayed dynamics is a challenging task, which should be carried out in closed-loop to keep the output bounded. In general, identification with a controller in the loop is referred to as closed-loop identification [21]. More specifically, a regulator is needed to stabilize unstable dynamic systems, which also helps to ensure the safety concerns and in generating stable predictors [22]. Moreover, most of the methods that are useful for stable delayed process identification may not be suitable for unstable counterparts and hence the availability of such methods is limited.

Although neural networks have been used in various modeling and control-related tasks [23, 24] and, also, in handling time delays effectively as well [25,26,27,28,29,30], however, the existing contributions that uses neural networks for estimating system models are nonparametric due to uncertainty in selecting layers, number of neurons and type of activation functions [31, 32]. Another limitation associated with the neural networks is that it may produce overfitted models [33]. An identified model is considered to be overfitted if it captures the local features (noisy trends) present in the identification data instead of the desired global characteristics (useful system dynamics) [34]. In this work, it is demonstrated that by carefully choosing the network’s (model’s) complexity, which is suitable enough to capture the useful desired dynamics only, the problem of identifying unstable delayed systems can be performed. Furthermore, the accuracy of estimated parameters can be enhanced based on a guaranteed convergence criterion, which is demonstrated in the simulation studies.

The manuscript is organized as follows: In next Sect. 2, the related works, problems and the objectives of proposed work have been discussed. In Sect. 3, the concept, challenges, and advantages of closed-loop identification have been discussed. In Sect. 4, the formulation of proposed technique has been presented. The Sect. 5 is devoted for the detailed development of proposed identification algorithm. The results are included in Sect. 6. The manuscript is concluded with possible future directions in Sect. 7.

2 Related Works, Problems and Objectives

In recent studies, it is shown that the weights of neural networks can also be related to the actual system parameters [35,36,37]. In this context, some modeling and identification approaches are developed, where it is demonstrated that by using some reduced or simplified neural network architectures parametric identification can be performed.

The work presented by Ho et al. [38] uses artificial neural networks to identify unknown systems as first order plus time delay models. The authors demonstrated that the controller tuned based on the identified model performed better than the conventional methods. However, the limitation of this method is its limited scope where only stable delayed process dynamics can be identified. In [39], authors performed a neural network based technique for the identification of stable-FOD (first-order delayed) processes. However, the main drawbacks of this method is that only stable systems can be estimated and the identified parameters are biased in the presence of measurement noise.

Other useful contributions can be found in [40, 41], where discrete transfer function models are identified in terms of trained neural network weights. However, this method is not suitable for time delay estimation. Chon and Cohen [42] presented an approach to estimate time-series model using trained network employing polynomial activation. However, the choice of polynomial orders is critical for accurate estimation.

In [43], a linear recurrent neural is proposed for identifying delay-free systems. In this approach, they demonstrated that the distributed parallel neural structure can be used for identifying multiple transfer functions together. However, this approach cannot be used for identifying unstable systems having time delay. A simplified block-oriented RNN is designed in [44], to extract the delay-free, stable Wiener model, directly in the form of trained network weights. It is also demonstrated that a neural proportional, integral, and derivative (PID) controller designed using this identified model gives better performance on the actual system as compared to the conventional PID controller.

The above discussions shows that the neural networks are capable to interpret parametric models and can outperform the conventional techniques. However, in the existing literature the parametric identifiability of RNNs are limited to stable delayed dynamics only, where the time delay estimation is not efficient. This was the main motivation behind the proposed approach to utilize RNNs for parametric identification of unstable time delayed systems, which is more challenging and has not been reported yet. Hence, in this work, a new method is proposed to identify an unknown unstable delayed dynamics of any order to its equivalent unstable first- or second-order delayed (FOD or SOD) model for improved controller design and model analysis purposes. Also, where all the model parameters as: gain, time constants, and time delay can be derived in terms of the neural network weights.

The conventional contributions that deals with the problem of unstable delayed process identification are also reported in literature. The reaction curve based methods are developed in [45,46,47] for unstable-FOD (UFOD) process modeling, which is simple, but the time delay estimation is inaccurate. In [48], a closed-loop step response method is developed. However, a suitable choice of step length and damping factor is needed for convergence. A curve fitting approach is proposed in [49] to estimate unstable systems with delay. However, this approach is practically limited as the rational model is needed in advance.

The relay feedback methods are also found to be useful for estimating unstable models with time delay [50,51,52,53,54,55,56,57,58]. However, their success relay upon the existence of limit cycles, which is hard to get for unstable systems. Furthermore, in most of the relay-based techniques, the limit cycles corrupted by measurement noise are required to be cleaned first by using some Fourier series based curve fitting methods before applying the relay identification techniques to it [52, 54]. However, the proposed work does not impose any limiting conditions on parameters, and the noisy data can be directly used for model identification.

More literature works that deal with unstable system identification are included here. The reference [21], talks about the modified Box–Jenkins models for unstable systems. In [59, 60], a virtual control method was developed to recover model of an unstable system through closed-loop data. In [61], an impulse response approach was adapted for estimating unstable dynamics. However, in all these references, the time delays are not included in the model structure, which makes it relatively simpler problem.

From these existing contributions, one can infer that the estimation of unstable dynamics with time delay is a challenging area of research. Also, due to various issues like plant’s safety, predictor’s stability, input’s correlation and nonlinear optimization, the problem of identifying unstable delayed systems is less reported in the literature. It is also discussed that the neural network with its various attractive features can be a better alternative in solving such problems.

This work proposed a novel closed-loop identification approach, where the closed-loop data (which is uncorrelated to noise disturbance) and the controller information (which is used to ensure predictor’s stability) is utilized in proposed CLDRNN architecture, to identify the unknown unstable delayed process. The developed CLDRNN structure is fully parametric and transparent to carry out the closed-loop identification of unstable time delay models with more accuracy and guaranteed convergence.

The main objectives and contributions of this work are outlined as:

  1. 1.

    An RNN based, closed-loop identification technique is proposed to identify the unstable process models with time delay, which can also handle controller complexity and long process time delays.

  2. 2.

    The mathematical relationships are formulated to get model and time delay parameters using CLDRNN weights.

  3. 3.

    Theorems are proved to obtain the theoretical conditions on convergence and adaptive learning for the proposed algorithm, along with the Monte-Carlo experiments to show the convergence for practical examples.

  4. 4.

    The convergence and parameter initialization issues are discussed under model uncertainty and noisy datasets.

  5. 5.

    Extensive simulations are performed to demonstrate that the proposed method can produce robust and unbiased parameter estimates with excellent convergence.

Fig. 1
figure 1

Closed-loop identification system

Full size image

3 Closed-Loop Identification

Identification in closed-loop has gained a lot of attention in recent years as most of the industrial systems operate in closed-loop [22, 34, 62]. Also, the unstable systems cannot operated in open-loop because of safety issues. Further, it has been observed that, for model-based control relevant applications the closed-loop configuration is often considered to be the optimal experimental setup [59, 63]. Additionally, identifying the closed-loop behavior of the unstable systems is important as they are ultimately going to be operated in a closed-loop only [21].

A closed-loop identification system is presented in Fig. 1, where n is discrete time the reference signal r(n) and an additional signal \(r_1(n)\) act as inputs at set-point and at controller’s C output. The input, output and disturbance signals for the process \(G_p\) are defined as u(n), y(n) and d(n), respectively.

The direct, indirect and joint approaches are popular for closed-loop identification [34, 62]. In the direct approach, the open-loop identification techniques can be used directly by using input u(n) and output y(n) data. The advantage of this technique is that the knowledge of feedback mechanism and controller is not required. Still, the limitation is that the biased estimates are obtained in the presence of measurement noise due to the correlation between input u(n) and noise disturbance d(n) [60]. One more disadvantage of a direct approach is that the user has little control over input design because the controller derives the process. Therefore, it is not easy to design inputs, which can produce persistent excitation and information-rich data [34]. It is mentioned in [21] that, without ensuring the predictor’s stability the direct closed-loop identification can not be applied for unstable systems.

In the indirect approach, the overall system relating reference input r(n) to output y(n) is identified first. Then the process model for \(G_p\) is recovered from the overall closed-loop system with the knowledge of the controller C. The main benefits of this approach are uncorrelated input, stable predictor and any open-loop identification techniques can be used to identify the overall closed-loop system [22]. The major drawback of the indirect method is that the recovery of an equivalent model for process \(G_p\) becomes difficult and requires further model reductions [62].

The joint input–output approach uses the identification of two separate systems by relating set-point input r(n) with output y(n) and input u(n), respectively. Then, the equivalent process model for \(G_p\) can be recovered by dividing the first system to the second system. The advantage of this approach is that the controller is not required to be known. Still, the drawback associated with this technique is that the denominator parts (poles) of both identified systems should be identical for accurate estimation [34, 62].

The objective of this manuscript is to perform improved closed-loop identification, especially for unstable processes with time delays and to overcome the limitations associated with the closed-loop identification approaches, as pointed out in the above discussion. The proposed technique is presented in the next section, which can produce unbiased parameter estimates in a noisy environment, with an added advantage to directly recover an unknown unstable delayed dynamics in terms of UFOD and USOD models.

The proposed method has following assumptions for performing identification experiment:

A1: The data generation for identification is performed in closed-loop with a known controller.

A2: The reference input is piecewise constant and persistently exciting to get information-rich data.

A3: The initial conditions are taken as zero for both input as well as output signals.

A4: A zero mean and finite variance white noise is used as disturbance signal.

Remark 1

The above assumptions are the standard considerations which are adopted in most of the identification techniques. The assumption in A1 is essential to perform identification of unstable systems in closed-loop. Otherwise, in open-loop, the output would be unbounded resulting in safety concerns of the plants. Also, in cases where the controllers are not known the joint input–output approach can be employed. Furthermore, the applicability of proposed approach method will still be valid if the assumptions in A2, A3 & A4 are relaxed. However, in that situation it might have an impact on convergence, accuracy and consistency of the estimated parameters.

4 Proposed CLDRNN Identification Approach

This section is devoted in developing the following novel concepts of the proposed work.

  1. 1.

    A novel CLDRNN architecture is proposed to enable closed-loop identification.

  2. 2.

    The unique thing about CLDRNN is that the time delayed process model can be directly extracted from its network weights.

  3. 3.

    New mathematical formulation has been developed in Theorems 1 and 2 for computing unstable delayed model parameters.

  4. 4.

    The adaptive learning rate criterion for CLDRNN training is obtained by Lyapunov theory in Theorem 1.

  5. 5.

    An original condition has been derived for fractional delay, which ensures the guaranteed convergence of the proposed algorithm.

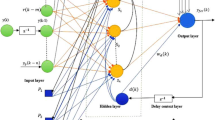
The proposed CLDRNN based closed-loop identification and modeling scheme is shown in Fig. 2, where it can be observed that the CLDRNN mimics the complete closed-loop system. The CLDRNN consists of three layers. The first layer referred to the error layer, which calculates the error signal e(n) between reference input r(n) and estimated output \(\hat{y}(n)\). The second layer is called the controller layer, whose structure and weights are selected according to a known controller, which is used to stabilize the actual unstable process. The last layer is referred to as the process layer, which is responsible for capturing the unknown unstable delayed process dynamics in terms of its optimized weights.

Fig. 2
figure 2

The proposed closed-loop identification and modeling scheme using CLDRNN

Full size image

The proposed CLDRNN is trained with closed-loop data, and during training weights of error and controller layer are kept fixed. In contrast, weights of process layer are altered to reduce the difference error \(\varepsilon (n)\) between actual output y(n) and estimated output \(\hat{y}(n)\). Finally, the process model can be recovered directly through the process layer weights of CLDRNN as suitable UFOD or USOD process models.

Fig. 3
figure 3

The proposed CLDRNN architecture for the closed-loop process identification as UFOD and USOD models. Delay represents unit sample delay. Note that, the terms with dashed lines are used for USOD system modeling

Full size image

A more detailed CLDRNN architecture, utilizing the parallel connection mode, is shown in Fig. 3, which includes three layers whose connection weights are w and activation functions denoted by \(f(\sum )\). The proposed CLDRNN contains all the components of a typical closed-loop system, i.e., error computation part, controller part, and the process identifier part within its architecture. The advantage of the CLDRNN structure is that it is trained with closed-loop data to directly identify the unknown unstable delayed dynamics in terms of UFOD and USOD model parameters. In the following subsection, a method is demonstrated, to include a PID-type controller in the controller layer of the CLDRNN.

4.1 Inclusion of the PID-Type Controller in the CLDRNN

It is clearly mentioned in the literature [22, 34, 62] that a pre-stabilizing controller of some kind is essentially required for the identification of unstable system dynamics. Also, the identification experiment for unstable processes cannot be performed, without ensuring the stability of the overall closed-loop system [21, 48]. The authors in [59, 60] recommended the use of stabilizing controller as virtual controller to demonstrate its utility in identifying unstable systems. In general, the PID-type (P, PI, PD, or PID) controllers are commonly employed to stabilize the unstable dynamics in order to generate bounded data for identification [36]. In the proposed approach, this controller information has been utilized in the CLDRNN structure as virtual controller [59, 60], to gain the following advantages:

  1. 1.

    It helps the CLDRNN structure to mimic the complete closed-loop system, from which the equivalent models (UFOD or USOD) of actual unstable delayed processes can be directly extracted in terms of the process model layer weights.

  2. 2.

    It helps in utilizing the reference (set point) input r(n) directly for identification, which is uncorrelated to the noise disturbances d(n).

  3. 3.

    It helps in keeping the CLDRNN structure stable (generates stable output \({\hat{y}}(n)\) predictions) during training, as we are identifying unstable systems.

In the CLDRNN architecture of Fig. 3, for error calculation, the reference signal r(n) is subtracted from estimated output \({\hat{y}}(n)\) by setting the weights \(w_0^e=1\) and \(w_1^e=-1\). To set the weights in the second layer of the CLDRNN, consider the parallel form of PID controller in terms of unit sample delay (USD) operator \(z^{-1}\) with uniform sampling time \(T_s\) as

$$\begin{aligned} C(z^{-1})=K_p+\frac{K_iT_sz^{-1}}{1-z^{-1}}+\frac{K_\textrm{d}\beta (1-z^{-1})}{1-(1-\beta T_s)z^{-1}}, \end{aligned}$$
(1)

where \(K_p\) is proportional gain, \(K_i\) is integral gain, \(K_\textrm{d}\) is derivative gain, and \(\beta \) represents the filter coefficient of the derivative term. The PID controller presented in (1), is popular and extensively used in various industrial applications. The reason is its simplicity and easy implementation on digital hardware in almost all computer-aided controllers, with the addition of hold device such as the zero-order hold (ZOH), to generate analog control signals for the actual process. If the error signal e(n) is the input and u(n) is the output of the CLDRNN’s controller layer then according to (1), one can have the following difference equation representation as

$$\begin{aligned} u(n) =&(2 - \beta {T_s})u(n - 1) + (\beta {T_s} - 1)u(n - 2)\nonumber \\&+ ({K_p} + {K_\textrm{d}}\beta )e(n)+ ({K_i}{T_s} - {K_p}(2 - \beta {T_s})\nonumber \\&- 2{K_\textrm{d}}\beta )e(n - 1)+ ({K_\textrm{d}}\beta + {K_p}(1 - \beta {T_s})\nonumber \\&- {K_i}{T_s}(1 - \beta {T_s}))e(n - 2), \end{aligned}$$
(2)

where the weights of the controller layer of CLDRNN are computed by using known controller parameter values in (2) as:

$$\begin{aligned} w_0^c= & {} {K_p} + {K_\textrm{d}}\beta , \end{aligned}$$
(3)
$$\begin{aligned} w_1^c= & {} {K_i}{T_s} - {K_p}(2 - \beta {T_s}) - 2{K_\textrm{d}}\beta , \end{aligned}$$
(4)
$$\begin{aligned} w_2^c= & {} {K_\textrm{d}}\beta + {K_p}(1 - \beta {T_s}) - {K_i}{T_s}(1 - \beta {T_s}), \end{aligned}$$
(5)
$$\begin{aligned} w_3^c= & {} 2 - \beta {T_s}, \end{aligned}$$
(6)
$$\begin{aligned} w_4^c= & {} \beta {T_s} - 1. \end{aligned}$$
(7)

Therefore, for any combinations like P, PI, PD, or PID, the controller layer weights of the CLDRNN can be calculated by using expressions from (3) to (7).

Remark 2

It is also possible to consider a more sophisticated PID-type controller structure that includes nonlinearities, integral windups, and saturation terms in the controller layer of the proposed CLDRNN, by incorporating separate training of controller layer with suitable activation functions [23, 44]. However, to keep the analysis fully parametric, we have restricted the proposed work to a PID controller of type (1) with a linear activation function only.

The following subsections used to develop a new methodology to obtain the parameters of UFOD and USOD system models in terms of the CLDRNN weights. The main attraction of the developed mathematical formulation is that the integer and non-integer (fractional) parts of the time delay can also be computed along with other rational parameters, directly from the process model layer of the CLDRNN.

4.2 UFOD System Identification Using CLDRNN

Let the UFOD system models G(s) to be identified is represented as:

$$\begin{aligned} {\hat{G}}\left( s \right) = \frac{{{\hat{K}}{e^{ - {\hat{\theta }} s}}}}{{\hat{\tau }s}-1}, \end{aligned}$$
(8)

where \({\hat{K}} \) is the gain, \({\hat{\theta }}\) is the time delay and \( {\hat{\tau }} \) is the time constant of the identified UFOD model. In the proposed technique the unknowns (\({\hat{K}}\), \({\hat{\theta }}\) and \( {\hat{\tau }} \)) of (8) are determined through closed-loop training of the CLDRNN. Considering that the time delay \({\hat{\theta }}\) is expressed in discrete domain as the combination of integer \(\hat{\theta }_I\) and fractional \({{\hat{\theta }} _{f}};-1<\hat{\theta }_f<1,\) delay terms as \({\hat{\theta }} = \left( {{{{\hat{\theta }} }_I} + {{\hat{\theta }}_{f}}} \right) {T_s},\) then for UFOD modeling the typical estimated output of the process model layer of the CLDRNN is given by:

$$\begin{aligned} {\hat{y}}\left( n \right)&= \mathrm{{ }}w_1^l{\hat{y}}\left( {n - 1} \right) + w_{{\hat{\theta _I}} + 1}^iu\left( {n -{\hat{\theta }}_I - 1} \right) \nonumber \\ {}&\quad + w_{{\hat{\theta _I}} + 2}^iu\left( {n - {\hat{\theta _I}} - 2} \right) , \end{aligned}$$
(9)

where the terms \(w_1^l\), \(w_{{\hat{\theta _I}} + 1}^i\) and \(w_{{\hat{\theta _I}} + 2}^i\) in (9) are the associated weights of \({\hat{y}}(n-1)\), \(u(n - {\hat{\theta _I}} - 1)\) and \(u(n - {\hat{\theta _I}} - 2)\), respectively. Now by using the USD operator \(z^{-1}\) such that \({z^{ - 1}}u(n) = u(n - 1)\) in (9), one can have an equivalent discrete-time transfer function model corresponding to the continuous-time UFOD model of (8) as:

$$\begin{aligned} {\hat{G}}({z^{ - 1}}) = \frac{{w_{{{\hat{\theta }} _I} + 1}^i{z^{ - 1}} + w_{{{\hat{\theta }} _I} + 2}^i{z^{ - 2}}}}{{1 - w_1^l{z^{ - 1}}}}{z^{ - {{\hat{\theta }} _I}}}. \end{aligned}$$
(10)

To recover the model in (8), in terms of the trained CLDRNN’s process layer weights present in (10), a ZOH based modified \({\mathcal {Z}}\)-transform [34, 64, 65] approach is utilized, which is written and proved in Theorem I outlined as:

Theorem 1

Consider the modified \({\mathcal {Z}}\)-transform of UFOD system with \(ZOH = \left( {1 - {e^{ - s{T_s}}}} \right) /s\), to have the following relations as:

$$\begin{aligned}&\mathcal {Z}\left[ \mathcal {L}^{-1}\left\{ \frac{\left( 1-e^{-sT_s} \right) }{s}\frac{\hat{K}e^{-s\left( \hat{\theta }_I+\hat{\theta }_f \right) T_s}}{\left( \hat{\tau }s-1 \right) } \right\} \right] ;-1<\hat{\theta }_f<1 \nonumber \\&\quad = \frac{{w_{{{\hat{\theta }} _I} + 1}^i{z^{ - 1}} + w_{{{\hat{\theta }} _I} + 2}^i{z^{ - 2}}}}{{1 - w_1^l{z^{ - 1}}}}{z^{ - {{\hat{\theta }} _I}}}, where\nonumber \\&\begin{matrix} {\hat{K}} = \left( {w_{{{\hat{\theta }} _I} + 1}^i + w_{{{\hat{\theta }} _I} + 2}^i} \right) /(w_1^l-1),&{\hat{\tau }} = {T_s}/{\log }\left( {w_1^l} \right) , \end{matrix} \nonumber \\&\begin{matrix} {{{\hat{\theta }} }_{f}} = 1 - {\log }\left( {\frac{{w_{{{{\hat{\theta }} }_I} + 2}^i + w_{{{\hat{\theta }}_I} + 1}^iw_1^l}}{{w_{{{\hat{\theta }}_I} + 1}^i + w_{{{\hat{\theta }}_I} + 2}^i}}} \right) /{\log }(w_1^l),&{\hat{\theta }} = ({{\hat{\theta }} _I} + {{\hat{\theta }} _{f}}){T_s}. \end{matrix} \end{aligned}$$
(11)

Proof

Let us consider the left hand side term of the Theorem, with substitution \(z^{-1}=e^{-sT_s}\) as

$$\begin{aligned} {\hat{G}}({z^{ - 1}}) = (1 - {z^{ - 1}}){z^{ - {{\hat{\theta }}_I}}}\mathcal {Z}\left[ {{\mathcal {L}^{ - 1}}\left\{ {\frac{{{\hat{K}}}}{{s(\hat{\tau }s - 1)}}{e^{ - s{{\hat{\theta }}_{f}}{T_s}}}} \right\} } \right] ,\nonumber \\ \end{aligned}$$
(12)

where denoted by \({\mathcal {L}}^{-1}\) is the inverse Laplace transform. Now by using partial fraction computation in (12), to get

$$\begin{aligned} {\hat{G}}({z^{ - 1}})&= (1 - {z^{ - 1}}){z^{ - {{\hat{\theta }}_I}}}\times \nonumber \\ {}&\mathcal {Z}\left[ \mathcal {L}^{-1}\left\{ \frac{\hat{K}\hat{\tau }e^{-s\hat{\theta }_fT_s}}{\hat{\tau }s-1} \right\} -\mathcal {L}^{-1}\left\{ \frac{\hat{K}e^{-s\hat{\theta }_fT_s}}{s} \right\} \right] . \end{aligned}$$
(13)

The subsequent Lemma and Corollary are proved to simplify the expression in (13) as:

Lemma 1

For the following unstable transfer function the modified \(\mathcal Z\)-transform is computed as:

$$\begin{aligned} \mathcal {Z}\left[ \mathcal {L}^{-1}\left\{ \frac{\hat{\tau }e^{-s\hat{\theta }_fT_s}}{\hat{\tau }s-1} \right\} \right] ;-1<\hat{\theta }_f<1=\frac{e^{-(\hat{\theta }_f-1)T_s/\hat{\tau }}z^{-1}}{1-e^{T_s/\hat{\tau }}z^{-1}}. \end{aligned}$$
(14)

Proof

Considering the LHS of (14) with the time-shifting property of Laplace transform, to get:

$$\begin{aligned} \mathcal {Z}\left[ \mathcal {L}^{-1}\left\{ \frac{\hat{\tau }e^{-s\hat{\theta }_fT_s}}{\hat{\tau }s-1} \right\} \right] =\mathcal {Z}\left[ e^{(t-\hat{\theta }_fT_s)/\hat{\tau }}1(t-\hat{\theta }_fT_s) \right] , \end{aligned}$$
(15)

where \({1(t - {{\hat{\theta }}_{f}}{T_s})}\) represents an unit step signal delayed by \({{\hat{\theta }}_{f}}{T_s}\).

Now, computing the sum of geometric progression with infinite terms and \(\left| z \right| >\left| {{e}^{T_s/\hat{\tau }}} \right| \), to have

$$\begin{aligned} {e^{ - {{\hat{\theta }}_{f}}{T_s}/\hat{\tau }}}\sum \limits _{n = 1}^\infty {{e^{n{T_s}/\hat{\tau }}}{z^{ - n}}} = \frac{{{e^{ - ({{\hat{\theta }}_{f}} - 1){T_s}/\hat{\tau }}}{z^{ - 1}}}}{{1 - {e^{{T_s}/\hat{\tau }}}{z^{ - 1}}}}. \end{aligned}$$
(16)

Corollary 1

For a delayed integral transfer function the modified Z-transform is given as:

$$\begin{aligned} \mathcal {Z}\left[ {{\mathcal {L}^{ - 1}}\left\{ {\frac{1}{s}{e^{ - s{{\hat{\theta }}_{f}}{T_s}}}} \right\} } \right] ;-1<\hat{\theta }_f<1 = \frac{{{z^{ - 1}}}}{{1 - {z^{ - 1}}}}. \end{aligned}$$
(17)

Proof

To proof this, do the substitution of \(1/\hat{\tau }=0\), in (14), to get

$$\begin{aligned} \mathcal {Z}\left[ \mathcal {L}^{-1}\left\{ \frac{1}{s}e^{-s\hat{\theta }_fT_s} \right\} \right] =\frac{z^{-1}}{\left( 1-z^{-1} \right) }. \end{aligned}$$
(18)

Now, applying the outcomes of Lemma 1, and Corollary 1, in (13), to get

$$\begin{aligned} {\hat{G}}({z^{ - 1}}) = (1 - {z^{ - 1}}){z^{ - {{\hat{\theta }}_I}}}{\hat{K}}\left[ {\frac{{{e^{ - ({{\hat{\theta }}_{f}} - 1){T_s}/\hat{\tau }}}{z^{ - 1}}}}{{1 - {e^{{T_s}/\hat{\tau }}}{z^{ - 1}}}} - \frac{{{z^{ - 1}}}}{{1 - {z^{ - 1}}}}} \right] \nonumber \\ \end{aligned}$$
(19)

on simplifying (19), one can have

$$\begin{aligned} \hat{G}(z^{-1})=&\hat{K}\frac{\left( e^{-(\hat{\theta }_f-1)T_s/\hat{\tau }}-1 \right) z^{-1}}{1-e^{T_s/\hat{\tau }}z^{-1}}z^{-\hat{\theta }_I}\nonumber \\ {}&+\hat{K}\frac{\left( e^{T_s/\hat{\tau }}-e^{-(\hat{\theta }_f-1)T_s/\hat{\tau }} \right) z^{-2}}{1-e^{T_s/\hat{\tau }}z^{-1}}z^{-\hat{\theta }_I} \end{aligned}$$
(20)

if in (20), each individual \(z^{-1}\) power coefficients are assigned in terms of the CLDRNN’s process model layer weights, to have

$$\begin{aligned} {\hat{G}}({z^{ - 1}}) = \frac{{w_{{{\hat{\theta }}_I} + 1}^i{z^{ - 1}} + w_{{{\hat{\theta }}_I} + 2}^i{z^{ - 2}}}}{{1 - w_1^l{z^{ - 1}}}}{z^{ - {{\hat{\theta }}_I}}}, \end{aligned}$$
(21)

where the coefficients of (21) and (20) are related by

$$\begin{aligned} w_{{{\hat{\theta }}_I} + 1}^i= & {} {\hat{K}}\left( {{e^{ - ({{\hat{\theta }}_{f}} - 1){T_s}/\hat{\tau }}} - 1} \right) , \end{aligned}$$
(22)
$$\begin{aligned} w_{{{\hat{\theta }}_I} + 2}^i= & {} {\hat{K}}\left( {{e^{{T_s}/\hat{\tau }}} - {e^{ - ({{\hat{\theta }}_{f}} - 1){T_s}/\hat{\tau }}}} \right) , \end{aligned}$$
(23)

and

$$\begin{aligned} w_1^l = {e^{{T_s}/\hat{\tau }}}. \end{aligned}$$
(24)

The model parameters of UFOD system in (8) can be computed from (22), (23) and (24) as:

$$\begin{aligned} {\hat{K}}&= \left( {w_{{{\hat{\theta }} _I} + 1}^i + w_{{{\hat{\theta }} _I} + 2}^i} \right) /(w_1^l-1), \end{aligned}$$
(25)
$$\begin{aligned} \hat{\tau }&= {T_s}/{\log }\left( {w_1^l} \right) , \end{aligned}$$
(26)
$$\begin{aligned} {{\hat{\theta }}_{f}}&= 1 - {\log }\left( {\frac{{w_{{{\hat{\theta }}_I} + 2}^i + w_{{{\hat{\theta }}_I} + 1}^iw_1^l}}{{w_{{{\hat{\theta }}_I} + 1}^i + w_{{{\hat{\theta }}_I} + 2}^i}}} \right) /{\log }(w_1^l), \end{aligned}$$
(27)

and

$$\begin{aligned} {\hat{\theta }} = ({{\hat{\theta }} _I} + {{\hat{\theta }} _{f}}){T_s}. \end{aligned}$$
(28)

Remark 3

Note that, the parameters in the expressions of (25), (26) and (27) can easily be recovered from optimized CLDRNN weights. However, the parameter \({\hat{\theta _I}}\) is estimated by an iterative algorithm, whose details are presented in the next section.

4.3 USOD System Identification Using CLDRNN

Now, consider the case when an unknown unstable process dynamics identified as the following USOD process model given by:

$$\begin{aligned} {\hat{G}}\left( s \right) = \frac{{{\hat{K}}{e^{ - \hat{\theta }s}}}}{{\left( {{{\hat{\tau }}_1}s-1} \right) \left( {{{\hat{\tau }}_2}s+1} \right) }}, \end{aligned}$$
(29)

where the notations \({\hat{K}} \), \(\hat{\theta }\) and \({{{\hat{\tau }} _1}}\) & \({{{\hat{\tau }} _2}}\) are used to represent gain, time delay and time constants of the model. The typical CLDRNN’s output response for identifying systems as USOD model in (29) is given by

$$\begin{aligned} {\hat{y}}\left( n \right)&= w_1^l{\hat{y}}\left( {n - 1}\right) + w_2^l{\hat{y}}\left( {n - 2} \right) + w_{{{\hat{\theta }} _I} + 1}^iu\left( {n - {{\hat{\theta }} _I} - 1} \right) \nonumber \\ {}&\quad + w_{{{\hat{\theta }} _I} + 2}^iu\left( {n - {{\hat{\theta }} _I} - 2} \right) + w_{{{\hat{\theta }} _I} + 3}^iu\left( {n - {{\hat{\theta }} _I} - 3} \right) , \end{aligned}$$
(30)

rewrite the expression in (30), to its equivalent discrete time-delayed transfer function form as:

$$\begin{aligned} {\hat{G}}({z^{ - 1}}) = \frac{{w_{{{\hat{\theta }} _I} + 1}^i{z^{ - 1}} + w_{{{\hat{\theta }} _I} + 2}^i{z^{ - 2}} + w_{{{\hat{\theta }} _I} + 3}^i{z^{ - 3}}}}{{\left( {1 - {\alpha _1}{z^{ - 1}}} \right) \left( {1 - {\alpha _2}{z^{ - 1}}} \right) }}{z^{ - {{\hat{\theta }} _I}}}, \end{aligned}$$
(31)

where the terms \(\alpha _1\) and \(\alpha _2\) in (31) are defined as:

$$\begin{aligned} {\alpha _1}= & {} 0.5(w_1^l + {({(w_1^l)^2} + 4w_2^l)^{0.5}}), \end{aligned}$$
(32)
$$\begin{aligned} {\alpha _2}= & {} 0.5(w_1^l - {({(w_1^l)^2} + 4w_2^l)^{0.5}}). \end{aligned}$$
(33)

The identification formulation of USOD model of (29), in terms of the CLDRNN process layer weights is presented as following:

Theorem 2

Consider the modified \({\mathcal {Z}}\)-transform of USOD system as:

$$\begin{aligned}&\mathcal {Z}\left[ {{\mathcal {L}^{ - 1}}\left\{ {\frac{{\left( {1 - {e^{ - s{T_s}}}} \right) }}{s}\frac{{{\hat{K}}}}{{\left( {{{\hat{\tau }}_1}s - 1} \right) ({{\hat{\tau }}_2}s + 1)}}{e^{ - s\left( {{{\hat{\theta } }_I} + {{\hat{\theta }}_{f}}} \right) {T_s}}}} \right\} } \right] ;\nonumber \\&-1<{\hat{\theta }}_f<1 = \frac{{w_{{{\hat{\theta } }_I} + 1}^i{z^{ - 1}} + w_{{{\hat{\theta } }_I} + 2}^i{z^{ - 2}} + w_{{{\hat{\theta }}_I} + 3}^i{z^{ - 3}}}}{{\left( {1 - {\alpha _1}{z^{ - 1}}} \right) \left( {1 - {\alpha _2}{z^{ - 1}}} \right) }}{z^{ - {{\hat{\theta } }_I}}},\nonumber \\&with\; \alpha _1\;in\; (32)\; and\; \alpha _2\;in\; 33, then\nonumber \\&\begin{array}{cc} \hat{K}=\frac{w_{\hat{\theta }_I+1}^{i}+w_{\hat{\theta }_I+2}^{i}+w_{\hat{\theta }_I+3}^{i}}{\left( \alpha _1-1 \right) \left( 1-\alpha _2 \right) },\hat{\tau }_1=\frac{T_s}{\log \left( \alpha _1 \right) },\hat{\tau }_2=-\frac{T_s}{\log \left( \alpha _2 \right) }, \end{array} \nonumber \\&\begin{array}{cc} &{}{{\hat{\theta } }_{f}} = \frac{{{{\hat{ \tau } }_1}}}{{{T_s}}}{\log }\left( {\frac{{{\hat{K}}{{\hat{\tau } }_1}{\alpha _1}\left( {{\alpha _2} - {\alpha _1}} \right) }}{{({{\hat{\tau } }_1} + {{\hat{\tau }}_2})\left[ {w_{{{\hat{\theta } }_I} + 3}^i - w_{{{\hat{\theta }}_I} + 1}^i{\alpha _1} + {\hat{K}}{\alpha _1}\left( {{\alpha _2} - 1} \right) } \right] }}} \right) , \\ &{} {\hat{\theta }} = ({{\hat{\theta }} _I} + {{\hat{\theta }} _{f}}){T_s}. \end{array} \end{aligned}$$
(34)

Proof

Let us consider the LHS term of Theorem 2, by replacing \(z^{-1}\) by \(e^{-sT_s}\), to get the expression

$$\begin{aligned}&{\hat{G}}({z^{ - 1}}) = (1 - {z^{ - 1}}){z^{ - {{\hat{\theta } }_I}}}\times \nonumber \\&\mathcal {Z}\left[ {{\mathcal {L}^{ - 1}}\left\{ {\frac{{{\hat{K}}}}{{s({{\hat{\tau } }_1}s - 1)({{\hat{\tau } }_2}s + 1)}}{e^{ - s{{\hat{ \theta } }_{f}}{T_s}}}} \right\} } \right] , \end{aligned}$$
(35)

on employing partial fraction computation in (35), to get

$$\begin{aligned}&\hat{G}(z^{-1})=\frac{(1-z^{-1})z^{-\hat{\theta }_I}\hat{K}}{\left( \hat{\tau }_1+\hat{\tau }_2 \right) }\times \nonumber \\&\mathcal {Z}\left[ \mathcal {L}^{-1}\left\{ \left( \frac{\hat{\tau }_{1}^{2}}{\left( \hat{\tau }_1s-1 \right) }+\frac{\hat{\tau }_{2}^{2}}{\left( \hat{\tau }_2s+1 \right) }-\frac{\left( \hat{\tau }_1+\hat{\tau }_2 \right) }{s} \right) e^{-s\hat{\theta }_fT_s} \right\} \right] \end{aligned}$$
(36)

by applying Lemma 1 and Corollary 1, in (36), to compute the following terms:

$$\begin{aligned}&\mathcal {Z}\left[ {{\mathcal {L}^{ - 1}}\left\{ {\frac{{{{\hat{\tau }}_1}}}{{{{\hat{\tau }}_1}s - 1}}{e^{ - s{{\hat{\theta }}_{f}}{T_s}}}} \right\} } \right] \nonumber \\&= \frac{{{e^{ - ({{\hat{\theta }}_{f}} - 1){T_s}/{{\hat{\tau }}_1}}}{z^{ - 1}}}}{{1 - {e^{{T_s}/{{\hat{\tau }}_1}}}{z^{ - 1}}}};-1<\hat{\theta }_f<1, \end{aligned}$$
(37)
$$\begin{aligned}&\mathcal {Z}\left[ {{\mathcal {L}^{ - 1}}\left\{ {\frac{{{{\hat{\tau }}_2}}}{{{{\hat{\tau }}_2}s + 1}}{e^{ - s{{\hat{\theta }}_{f}}{T_s}}}} \right\} } \right] \nonumber \\&= \frac{{{e^{({{\hat{\theta }}_{f}} - 1){T_s}/{{\hat{\tau }}_2}}}{z^{ - 1}}}}{{1 - {e^{ - {T_s}/{{\hat{\tau }}_2}}}{z^{ - 1}}}};-1<\hat{\theta }_f<1, \end{aligned}$$
(38)

and

$$\begin{aligned} \mathcal {Z}\left[ {{\mathcal {L}^{ - 1}}\left\{ {\frac{{{\hat{K}}}}{s}{e^{ - s{{\hat{\theta }}_{f}}{T_s}}}} \right\} } \right] = \frac{{{\hat{K}}{z^{ - 1}}}}{{1 - {z^{ - 1}}}};-1<\hat{\theta }_f<1, \end{aligned}$$
(39)

on substituting (37), (38) and (39) into (36), then after simplification and collecting different \(z^{-1}\) power coefficients terms, to have

$$\begin{aligned} {\hat{G}}({z^{ - 1}}) = \frac{{w_{{{\hat{\theta }}_I} + 1}^i{z^{ - 1}} + w_{{{\hat{\theta }}_I} + 2}^i{z^{ - 2}} + w_{{{\hat{\theta }}_I} + 3}^i{z^{ - 3}}}}{{\left( {1 - {\alpha _1}{z^{ - 1}}} \right) \left( {1 - {\alpha _2}{z^{ - 1}}} \right) }}{z^{ - {{\hat{\theta }}_I}}}, \end{aligned}$$
(40)

where the coefficient terms are given by

$$\begin{aligned}&w_{\hat{\theta }_I+1}^{i}=\hat{K}\left[ \frac{\hat{\tau }_1e^{-(\hat{\theta }_f-1)T_s/\hat{\tau }_1}+\hat{\tau }_2e^{(\hat{\theta }_f-1)T_s/\hat{\tau }_2}}{\hat{\tau }_1+\hat{\tau }_2}-1 \right] , \end{aligned}$$
(41)
$$\begin{aligned}&w_{{{\hat{\theta }}_I} + 2}^i = {\hat{K}}\left( {{e^{{T_s}/{{\hat{\tau }}_1}}} + {e^{ - {T_s}/{{\hat{\tau }}_2}}}} \right) \nonumber \\&\qquad \qquad - \frac{{{\hat{K}}}}{{({{\hat{\tau }}_1} + {{\hat{\tau }}_2})}}\left[ {{{\hat{\tau }}_1}{e^{ - ({{\hat{\theta }}_{f}} - 1){T_s}/{{\hat{\tau }}_1}}}\left( {1 + {e^{ - {T_s}/{{\hat{\tau }}_2}}}} \right) } \right] \nonumber \\&\qquad \qquad - \frac{{{\hat{K}}}}{{({{\hat{\tau }}_1} + {{\hat{\tau }}_2})}}\left[ {{{\hat{\tau }}_1}{e^{({{\hat{\theta }}_{f}} - 1){T_s}/{{\hat{\tau }}_2}}}\left( {1 + {e^{{T_s}/{{\hat{\tau }}_1}}}} \right) } \right] , \end{aligned}$$
(42)
$$\begin{aligned}&w_{\hat{\theta }_I+3}^{i}=\frac{\hat{K}}{(\hat{\tau }_1+\hat{\tau }_2)}\left[ \hat{\tau }_1e^{-(\hat{\theta }_f-1) T_s/\hat{\tau }_1}e^{-T_s/\hat{\tau }_2} \right] \nonumber \\&\qquad \qquad +\frac{\hat{K}}{(\hat{\tau }_1+\hat{\tau }_2)}\left[ \hat{\tau }_2e^{(\hat{\theta }_f-1) T_s/\hat{\tau }_2}e^{T_s/\hat{\tau }_1} \right] \nonumber \\&\qquad \qquad -\hat{K}e^{T_s/\hat{\tau }_1}e^{-T_s/\hat{\tau }_2}, \end{aligned}$$
(43)

and

$$\begin{aligned} {\alpha _1} = {e^{{T_s}/{{\hat{\tau }}_1}}},{\alpha _2} = {e^{ - {T_s}/{{\hat{\tau }}_2}}}. \end{aligned}$$
(44)

Now, add (41), (42) and (43) with substitution from (44), to have

$$\begin{aligned} {\hat{K}} = \frac{{w_{{{\hat{\theta }}_I} + 1}^i + w_{{{\hat{\theta }}_I} + 2}^i + w_{{{\hat{\theta }}_I} + 3}^i}}{{\left( {\alpha _1 - {1}} \right) \left( {1 - {\alpha _2}} \right) }}, \end{aligned}$$
(45)

from (44), one can have

$$\begin{aligned} {{\hat{\tau }}_1} = {T_s}/{\log }\left( {{\alpha _1}} \right) ,{{\hat{\tau }}_2} = - {T_s}/{\log }\left( {{\alpha _2}} \right) , \end{aligned}$$
(46)

on multiplying (41), with \({e^{{T_s}/{{\hat{\tau }}_1}}}\) and subtracting it from (43), with substitutions from (44), to have

$$\begin{aligned} {{\hat{\theta }}_{f}}&= \frac{{{{\hat{\tau }}_1}}}{{{T_s}}}\nonumber \\&\quad {\log }\left( {\frac{{{\hat{K}}{{\hat{\tau }}_1}{\alpha _1}\left( {{\alpha _2} - {\alpha _1}} \right) }}{{({{\hat{\tau }}_1} + {{\hat{\tau }}_2})\left[ {w_{{{\hat{\theta }}_I} + 3}^i - w_{{{\hat{\theta }}_I} + 1}^i{\alpha _1} + {\hat{K}}{\alpha _1}\left( {{\alpha _2} - 1} \right) } \right] }}} \right) , \end{aligned}$$
(47)

also, the estimated time delay parameter \(\hat{\theta }\) is computed by \({\hat{\theta }} = ({{\hat{\theta }} _I} + {{\hat{\theta }} _{f}}){T_s}\), as in (28).

Based on the formulation done in this section, a guaranteed convergence condition has been proposed and an iterative learning algorithm is developed in following section to solve the nonlinear optimization problem for identifying time-delayed systems.

5 Guaranteed Convergence Condition and Learning of CLDRNN

On the basis of the formulations done in the previous section, it can be inferred that the guaranteed convergence for obtaining optimal model parameters can only be obtained if the following condition is satisfied as:

$$\begin{aligned} -1<\hat{\theta }_f<1. \end{aligned}$$
(48)

Hence, by monitoring a single parameter value only, one can ensure the optimal model estimation and algorithms convergence at the same time. Also, for identifying the time delay \({\hat{\theta }}\), there is no direct formula for computing the integer part \({\hat{\theta _I}}\); therefore, it is recommended to extract it from the non-integer part iteratively until the convergence condition given in (48) is satisfied.

The proposed iterative process for CLDRNN training is begin with the initial choice of the parameter \(\hat{\theta }_I=0\), where an arbitrary choice of integer time delay can also be considered based on some intuitive knowledge. After each iteration, the following expression is used to update the integer part \({\hat{\theta }} _I\) from the estimated fractional part \({\hat{\theta }} _f\) as:

$$\begin{aligned}&\hat{\theta }_I(\textrm{present})=\hat{\theta }_I(\textrm{previous})+\hat{\theta }_f(\textrm{present})\nonumber \\&-\textrm{rem}\left\{ \hat{\theta }_f(\textrm{present}),1 \right\} , \end{aligned}$$
(49)

the updated value \({\hat{\theta _{I}}}(\textrm{present})\) is then used in next iteration and the same updation is repeated until the guaranteed global convergence condition \(-1< {{{\hat{\theta }}_{f}}} < 1\) is satisfied.

Remark 4

Note that, the approach discussed above plays an instrumental role in estimating unbiased parameters and in achieving global convergence even if the measurement noise severely corrupts the identification data or the modeling uncertainties are present. The reason behind this is the identification of \({\hat{\theta _{f}}}\), that enables an accurate estimate of \({\hat{\theta _I}}\), which then further improves the identification of the other model parameters as well.

Let the cost function \(F_k\) at kth (used as subscript k in all subsequent representations) training epoch is minimized to train the proposed CLDRNN as:

$$\begin{aligned} F_k = \frac{1}{2N}\sum \limits _{n = 1}^N {\varepsilon _k^2(n)}. \end{aligned}$$
(50)

where N denotes the number of training samples and \(\varepsilon _k(n)\) is the difference error at kth epoch, computed by:

$$\begin{aligned} {\varepsilon _k(n)} = {y(n)} - {{{\hat{y}}_k}(n)}. \end{aligned}$$
(51)

The terms y(n) and \({{\hat{y}}_k}(n)\) in (51) are true and identified model outputs. If all errors are accumulated in a single difference error vector \(\varXi _k\) as:

$$\begin{aligned} {\varXi _k} = {[\begin{array}{*{20}{c}} {{\varepsilon _k}(1)}&{{\varepsilon _k}(2)}&{...}&{{\varepsilon _k}(N)} \end{array}]^\textrm{T}}, \end{aligned}$$
(52)

where T denotes the transpose operation. For updating network weights of CLDRNN following rule is used

$$\begin{aligned} {W_{k + 1}} = {W_k} - {(J_k^T{J_k} + {\mu }I)^{ - 1}}{g_k}, \end{aligned}$$
(53)

where W is the weight vector, J represents Jacobian matrix, \(\mu \) denotes the scalar coefficient, which controls learning, I represents identity matrix, and the term g represents the gradient vector.

If the following terms are introduced in (53) as:

$$\begin{aligned} \Delta W_k = W_{k + 1} - W_k, \end{aligned}$$
(54)

and

$$\begin{aligned} {\eta _k} = \mathrm{{ }}{\left( {J_k^T{J_k} + {\mu }I} \right) ^{ - 1}}, \end{aligned}$$
(55)

where \(\Delta W\) is the weight deviation vector and \(\eta \) represents learning rate. Now, substituting the expressions of (54) and (55) in (53), to get

$$\begin{aligned} \Delta W_k = - \eta _kg_k. \end{aligned}$$
(56)

At kth epoch CLDRNN weight vector is defined as:

$$\begin{aligned} {W_k} = [w_k^1,w_k^2,...,w_k^M]^\textrm{T}, \end{aligned}$$
(57)

where M represents weight vector length. For each network weight, the Jacobian and gradient are computed by:

$$\begin{aligned} J_k^j = \frac{{\partial {\varXi _k}}}{{\partial w_k^j}}, \end{aligned}$$
(58)

and

$$\begin{aligned} g_k^j = \frac{1}{N}\sum \limits _{n = 1}^N {\left( {{\varepsilon _k}(n)\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k^j}}} \right) }, \end{aligned}$$
(59)

by using (55), (56) and (59), one can compute weight deviation in each weight as:

$$\begin{aligned} \Delta w_k = - \eta _k\frac{1}{N}\sum \limits _{n = 1}^N {\left( {{\varepsilon _k}(n)\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}} \right) }. \end{aligned}$$
(60)

In following discussion, a suitable choice of leaning rate \(\eta \) is computed to speedup CLDRNN training. The concept of Lyapunov theory [23, 44, 66, 67] is adapted here to derive and prove the following Theorem 3.

Theorem 3

During CLDRNN training, at kth epoch, the learning rate \(\eta _k\) should met the following condition to reduce cost function value:

$$\begin{aligned} 0< \eta _k < \frac{2}{{\frac{1}{N}{{\sum \limits _{n = 1}^N {\left( {\frac{{\partial {{{\hat{y}}}_k}(n)}}{{\partial w_k}}} \right) } }^2}}}. \end{aligned}$$
(61)

Proof

To prove this, define a Lyapunov function as

$$\begin{aligned} {V_k} = N \times {F_k} = \frac{1}{2}\sum \limits _{n = 1}^N {\varepsilon _k^2(n)}, \end{aligned}$$
(62)

let the Lyapunov function deviation is defined as:

$$\begin{aligned} \Delta {V_k} = {V_{k + 1}} - {V_k} = \frac{1}{2}\sum \limits _{n = 1}^N {\left( {\varepsilon _{k + 1}^2(n) - \varepsilon _k^2(n)} \right) }. \end{aligned}$$
(63)

If the difference error deviation is defined as:

$$\begin{aligned} \Delta {\varepsilon _k}(n) = \frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}\Delta w_k, \end{aligned}$$
(64)

where \(\partial \) is the partial derivative operator. Now by using (60), the expression in (64) can be rewritten as

$$\begin{aligned} \Delta {\varepsilon _k}(n) = - \eta _k\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}\frac{1}{N}\sum \limits _{n = 1}^N {\left( {{\varepsilon _k}(n)\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}} \right) }, \end{aligned}$$
(65)

since

$$\begin{aligned} {\varepsilon _{k + 1}}(n) = {\varepsilon _k}(n) + \Delta {\varepsilon _k}(n), \end{aligned}$$
(66)

by putting (65) and (66) into (63), to have

$$\begin{aligned} \Delta {V_k}= & {} \frac{1}{2}\sum \limits _{n = 1}^N {\left( {{\varepsilon _{k + 1}}(n) + {\varepsilon _k}(n)} \right) \left( {{\varepsilon _{k + 1}}(n) - {\varepsilon _k}(n)} \right) } \\ \Delta {V_k}= & {} \frac{1}{2}\sum \limits _{n = 1}^N {\left( {2{\varepsilon _k}(n) + \Delta {\varepsilon _k}(n)} \right) \left( {\Delta {\varepsilon _k}(n)} \right) ,} \\ \Delta {V_k}= & {} \sum \limits _{n = 1}^N {\left( {{\varepsilon _k}(n)\Delta {\varepsilon _k}(n) + \frac{1}{2}{{\left( {\Delta {\varepsilon _k}(n)} \right) }^2}} \right) } \end{aligned}$$
$$\begin{aligned} \Delta {V_k}= & {} \sum \limits _{n = 1}^N {\left( {{\varepsilon _k}(n)\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}\Delta w_k + \frac{1}{2}{{\left( {\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}\Delta w_k} \right) }^2}} \right) } \end{aligned}$$
(67)

by substituting (60) in (67), one can have

$$\begin{aligned} \Delta {V_k}= & {} - \eta _k\frac{1}{N}{\left( {\sum \limits _{n = 1}^N {{\varepsilon _k}(n)\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}} } \right) ^2} \\{} & {} + {\left( {\eta _k} \right) ^2}\frac{1}{2}\sum \limits _{n = 1}^N {{{\left( {\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}} \right) }^2}} {\left( {\frac{1}{N}\sum \limits _{n = 1}^N {{\varepsilon _k}(n)\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}} } \right) ^2} \end{aligned}$$
$$\begin{aligned} \Delta {V_k}= & {} \frac{{\eta _k}}{N}{\left( {\sum \limits _{n = 1}^N {{\varepsilon _k}(n)\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}} } \right) ^2}\left( {\frac{{\eta _k}}{{2N}}\sum \limits _{n = 1}^N {{{\left( {\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}} \right) }^2} - 1} } \right) .\nonumber \\ \end{aligned}$$
(68)

Now, observe the three terms \(\eta _k\), \(\frac{1}{N}{\sum \limits _{n = 1}^N {\left( {\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}} \right) } ^2}\) and \(\left( {\frac{{\eta _k}}{{2N}}\sum \limits _{n = 1}^N {{{\left( {\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}} \right) }^2}-1}} \right) \), in (68), where the learning rate in the first term should be \(\eta _k > 0\). The second term will remain positive \(\frac{1}{N}{\sum \limits _{n = 1}^N {\left( {\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}} \right) } ^2} \geqslant 0\).

Therefore, to satisfy the Lyapunov criterion to achieve \(\Delta V_k < 0\), which is also equivalent to get

$$\begin{aligned} V_{k+1}<V_k\,\,\text {or}\,\,F_{k+1}<F_k. \end{aligned}$$
(69)

The third term in (68), must be negative as

\(\left( {\frac{{\eta _k}}{{2N}}\sum \limits _{n = 1}^N {{{\left( {\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}}} \right) }^2} - 1} } \right) < 0\). Hence, by considering these facts, and using the relation in (51), as \(\frac{{\partial {\varepsilon _k}(n)}}{{\partial w_k}} = - \frac{{\partial {{{\hat{y}}}_k}(n)}}{{\partial w_k}}\), one can have the condition for adaptive learning rate as

$$\begin{aligned} 0< \eta _k < \frac{2}{{\frac{1}{N}{{\sum \limits _{n = 1}^N {\left( {\frac{{\partial {{{\hat{y}}}_k}(n)}}{{\partial w_k}}} \right) } }^2}}}. \end{aligned}$$
(70)

Remark 5

Note that, the condition of Theorem 3 on the adaptive learning rate \(\eta _k\) is not sufficient to achieve global convergence condition \(-1<\hat{\theta }_f<1\). This is due to the multi-model nature of the cost function optimized for the identification of time-delayed systems. However, the global convergence can be obtained by utilizing an iterative approach presented in the proposed Algorithm 1 with adaptive training of the CLDRNN until satisfying the global convergence condition \(-1<\hat{\theta }_f<1\).

The complete proposed methodology is summarized as sequential steps in Algorithm 1. Moreover, a connection architecture is presented in Fig. 4, which shows the detailed interaction between the proposed algorithm and the CLDRNN to identify and model an unknown unstable delayed dynamics models.

Algorithm 1
figure a

Proposed Identification Algorithm using CLDRNN

Full size image
Fig. 4
figure 4

Connection architecture for the closed-loop time-delayed process identification using CLDRNN

Full size image

6 Simulation Study

In this section, some examples of unstable process dynamics are used for validating the proposed identification method. The proposed Algorithm 1 is applied to the CLDRNN architecture, which is then trained with closed-loop identification data to model the unstable time-delayed systems.

The MSE (mean square of errors) criteria for closed-loop data has been adapted here for the identified models comparison as:

$$\begin{aligned} \text {MSE} = \frac{1}{2N}\sum \limits _{n = 1}^N {{{\left( {y\left( {n} \right) - {\hat{y}}\left( {n} \right) } \right) }^2}} \end{aligned}$$
(71)

where y(n) is the actual output, \({\hat{y}}(n)\) is the output of the identified model, and N is the number of training samples. To test the identification robustness of proposed method a white Gaussian noise as disturbance signal d(n) is added in the true output. The mean value of noise signal is (m) considered ‘zero’, while variance (\(\sigma ^2\)) is ’nonzero’. The resulting signal to noise ratio (SNR) is expressed in dB scale in terms of signal power (\({{P_\textrm{signal}}}\)) and noise power (\({{P_\textrm{noise}}}\)) as

$$\begin{aligned} \text {SNR} = 10{\log _{10}}\left( {\frac{{{P_\textrm{signal}}}}{{{P_\textrm{noise}}}}} \right) \textrm{dB}. \end{aligned}$$
(72)

Some random experiments as Monte-Carlo tests are performed for analyzing the ability of the identification technique to handle the uncertainties caused due to measurement noise. Therefore, for a given SNR, total 100 Monte-Carlo tests where each simulation is performed with different noise seeds to test the accuracy and convergence of the proposed approach, where to represent the identification results each estimated parameter’s mean and standard deviation values are computed. All the simulation experiments of this section are performed using the MATLAB (Version R2018b) software.

Table 1 CLDRNN’s training parameters
Full size table
Table 2 Comparison of the identified model parameters for Example 1
Full size table
Table 3 Results of 100 Monte-Carlo simulation for Example 1
Full size table

6.1 Example 1

The first-order unstable process with time delay commonly used to model bio-reactors and chemical process plants. In this example, we consider an unstable first-order process, studied in [16, 45, 50, 57], as

$$\begin{aligned} G\left( s \right) =\frac{4}{4s-1}e^{-2s}. \end{aligned}$$
(73)
Fig. 5
figure 5

Nyquist plots of the identified models for the 100 Monte-Carlo simulations of Example 1, with 20 dB SNR. Identified models (yellow line), actual process (blue line)

Full size image

A PI controller with \(K_p=0.5\) and \(K_i=0.004\) is used to ensure the closed-loop stability of the system in (73). The closed-loop system is simulated with pseudo-random binary sequence (PRBS) input having 5000 samples each at 0.12 s interval and the clock period is 20 samples. This identification data is then used in the proposed CLDRNN identification Algorithm 1, with training parameters given in Table 1. The fixed controller layer weights computed by (3) to (7) as \(w_0^c = 0.5,\) \(w_1^c = - 0.9995,\) \(w_2^c = 0.4995,\) \(w_3^c = 2,\) and \(w_4^c = - 1\). The identified model using the proposed approach compared with other literature methods in Table 2. All the identified models in Table 2 are validated using the MSE criterion in (71), for a closed-loop unit step response of 50 s duration. The identification results of Table 2 show that the model estimated by proposed approach produces minimum error compared to other methods.

Fig. 6
figure 6

Evolution of the CLDRNN’s process layer weights for the 100 Monte-Carlo simulations of Example 1, with 20 dB SNR

Full size image
Fig. 7
figure 7

Evolution and convergence of the MSE (\(F_k\)) for the 100 Monte-Carlo simulations of Example 1, with 20 dB SNR

Full size image
Fig. 8
figure 8

Evolution of estimated parameters for varying time delay in Example 1, with 20 dB SNR

Full size image

The proposed method is also validated when the identification data is corrupted by the measurement noise with three different cases of SNR’s of 20-dB, 30-dB, and 40-dB, respectively. A total of 100 Monte-Carlo simulations are performed with different noise seeds for each SNR value. The identification results presented in Table 3, where all the estimated process parameters are written in terms of their mean and standard deviation values. It is observed in Table 3, that the proposed method is robust and maintains identification consistency even in the presence of high measurement noise with accurate mean parameter and less standard deviation values.

Furthermore, in order to visualize the consistent identification accuracy of the proposed method, the case of 100 Monte-Carlo simulations with 20 dB SNR is considered. The results of all 100 simulations are plotted as the Nyquist graphs and the evolution of the CLDRNN weights with iterations in Figs. 5 and 6. The Nyquist plots in Fig. 5 show that all the identified model’s frequency responses accurately follow the true one. The evolution of the CLDRNN weights is shown in Fig. 6, where it can be observed that the weight corresponding to the unstable pole (\(w_1^l>1\)) has small deviation and fast convergence, while the weights \(w_{{{\hat{\theta }}_I} + 1}^i\) and \(w_{{{\hat{\theta }}_I} + 2}^i\) has more deviation and takes more iterations to converge.

The evolution of the MSE cost function \(F_k\) with training epochs (k) is depicted in Fig. 7, where one can observe that for all the 100 Monte-Carlo simulations, the MSE (\(F_k\)) value decrease with each training epoch by using the adaptive learning rate as described in Theorem 3 and converges to a value nearer to zero.

Table 4 Comparison of the identified UFOD and USOD models for Example 2
Full size table

To include the case of identifying time varying system a situation is considered, where it is assumed that the time delay of the system in (73) is changed from 1 s second to 2 s at time 1200 s. The identification experiment is performed for 2400 s with same settings. The proposed identification Algorithm 1 is applied on batch data and the evolution of estimated parameters are shown in Fig. 8. As one can observe in Fig. 8 that the proposed method accurately tracks the changed time delay \(\hat{\theta }\), without affecting the estimates of other model parameters.

Table 5 Identified model parameters’ mean and standard deviation values for 100 Monte-Carlo simulation of Example 2, with different SNR
Full size table
Fig. 9
figure 9

Nyquist plots of the identified models for the 100 Monte-Carlo simulations of Example 2, with 20 dB SNR. Identified models (yellow line), actual system (blue line)

Full size image
Fig. 10
figure 10

Evolution of the CLDRNN’s process layer weights for the 100 Monte-Carlo simulations of Example 2, with 20 dB SNR

Full size image
Fig. 11
figure 11

Evolution and convergence of the MSE (\(F_k\)) for the 100 Monte-Carlo simulations of Example 2, with 20 dB SNR

Full size image

6.2 Example 2

In general, the industrial food processing and biochemical units show the characteristics similar to a second-order unstable process with time delay. The following process model studied in literature by [46, 52, 55], used to test and validate the proposed technique as:

$$\begin{aligned} G\left( s \right) =\frac{1}{(2s-1)(0.5s+1)}e^{-0.5s}. \end{aligned}$$
(74)

A PI controller with \(K_p=2\) and \(K_i=0.01\) is used to keep output bounded. A PRBS input is used having 5000 samples with 0.04 s sample time and clock period of 2.0 s for data generation. The proposed CLDRNN identification Algorithm 1 is used with same training parameters as in Example 1, having fixed controller layer weights computed by (3) to (7) as: \(w_0^c = 2,\) \(w_1^c = - 0.0026,\) \(w_2^c = 0.0069,\) \(w_3^c = 2,\) and \(w_4^c = - 1\). In Table 4, the identified models are compared with other methods based on the MSE criterion described in (72). From the results of Table 4, one can say that the proposed approach is more accurate with lesser MSE values. In addition, for each noisy measurement of 20 dB, 30 dB, and 40 dB SNR, 100 random Monte-Carlo identification experiments are conducted. The simulation results are summarized in Table 5, where it is observed that the estimated parameters have accurate mean values with small deviations.

Moreover, for 20 dB SNR case, the 100 Monte-Carlo simulations are considered to visualize the consistent identification accuracy of the proposed method. The simulation results of all 100 identification experiments are depicted as the Nyquist graphs and evolution of network weights with iterations in Figs. 9 and 10, respectively. The Nyquist plots in Fig. 9 show that all the identified model’s frequency responses accurately follow the true one. From the CLDRNN’s weights evolution in Fig. 10, one can observe that the recurrent weights \(w_1^l\) and \(w_2^l\) have less deviation and fast convergence, while the weights \(w_{{{\hat{\theta }}_I} + 1}^i\), \(w_{{{\hat{\theta }}_I} + 2}^i\) and \(w_{{{\hat{\theta }}_I} + 3}^i\) have more deviation and takes more iterations to converge. The evolution of the MSE cost function \(F_k\) with training epochs (k) are depicted in Fig. 11, where one can observe that for all the 100 Monte-Carlo simulations, the MSE (\(F_k\)) value decrease with each training epoch by using the adaptive learning rate as described in Theorem 3 and converges at the proximity to zero.

6.3 Example 3

In this example, the proposed method is tested under the condition of model mismatch. A \(3^{rd}\)-order unstable delayed system studied by [58] is considered as:

$$\begin{aligned} G(s) = \frac{{1.0{e^{ - 0.5s}}}}{{(5.0s-1)(2.0s+1)(0.5s+1)}} \end{aligned}$$
(75)

A PID-type regulator having parameters \(K_p=1.5\), \(K_i=0.05\), \(K_\textrm{d}=0.6\) and \(\beta =10\), is used for the system in (75) to keep the output bounded. The closed-loop system is simulated to generate identification data using a PRBS input of 200 s duration with 0.08 s sampling interval and 4 s clock period. This identification data is then used in the proposed CLDRNN identification algorithm for system modeling with fixed controller layer weights computed using expressions (3) to (7) as \(w_0^c = 7.5,\) \(w_1^c = 0.0043,\) \(w_2^c = -0.0077,\) \(w_3^c = 1.2,\) and \(w_4^c = - 0.2\). The identified models are included for comparison and presented in Table 6. All the identified models in Table 6 are validated using MSE criterion in (72), for a closed loop unit step response of 50 s duration. The results shown in Table 6 indicate that the accuracy of proposed technique is better than other techniques.

Table 6 Comparison of identified UFOD and USOD models for Example 3
Full size table
Fig. 12
figure 12

Identified models responses in comparison to the measured response having 25 dB SNR for Example 3

Full size image
Fig. 13
figure 13

Nyquist plots of identified models in comparison to the true system of Example 3

Full size image

In addition, the proposed algorithm is tested when the identification data is noisy with 20 dB SNR. The identified UFOD and USOD models for a case of noisy measurements are presented as follows:

$$\begin{aligned} {{\hat{G}}_\textrm{UFOD}}(s) = \frac{{0.9759{e^{ - 3.1378s}}}}{{5.4719s - 1}}, \end{aligned}$$
(76)

and

$$\begin{aligned} {{\hat{G}}_\textrm{USOD}}(s) = \frac{{1.0018{e^{ - 0.9775s}}}}{{10.3214{s^2} + 2.9603s - 1}}. \end{aligned}$$
(77)

The measured output and the identified model’s responses for a single simulation run are plotted in Fig. 12, which shows that both identified UFOD and USOD models follow the measured output, with the latter one being more accurate than the former one. The Nyquist plots of the identified model are depicted in Fig. 13, for a particular case of noisy measurements. In Fig. 13, it can be observed that the USOD model closely follows the actual system for all frequencies as compared to the UFOD model, which is accurate only nearer to the critical point of \((-1\pm 0j)\) in the Nyquist plot.

7 Conclusion

For solving the problem of closed-loop identification of unstable delayed dynamical systems has been reported here. A neural architecture with delayed links is proposed which iteratively trains to ensure guaranteed convergence even with noisy measurements. The proposed CLDRNN architecture can mimic the complete closed-loop system within its architecture, including the controller information. The unknown unstable delayed system parameters can be directly extracted through CLDRNN. The benchmark unstable process model examples are incorporated for validating the algorithm, where the effects of measurement noise and model mismatch are also considered. The simulated experiments confirm that the proposed method is more general, accurate, robust and consistent as compared to the existing literature methods.

The directions for future work will be to extend the proposed concept to model time-delayed deep neural architectures to include further complex system dynamics with unknown time delays. Furthermore, the proposed idea could also be combined with the model reference adaptive control (MRAC) approach to carry out both identification and controller design simultaneously using the same neural network architecture. Also, the proposed concept will be more prominent in large-scale networked systems, where each subsystem operating in closed-loop required to be identified and controlled.