Adaptive neural network control of uncertain MIMO nonlinear systems with input saturation

Abstract

In this paper, an adaptive neural network (NN) tracking controller is developed for a class of uncertain multi-input multi-output (MIMO) nonlinear systems with input saturation. Radial basis function neural networks are utilized to approximate the unknown nonlinear functions in the MIMO system. A novel auxiliary system is developed to compensate the effects induced by input saturation (in both magnitude and rate) during tracking control. Endowed with a switching structure that integrates two existing representative auxiliary system designs, this novel auxiliary system improves control performance by preserving their advantages. It provides a comprehensive design structure in which parameters can be adjusted to meet the required control performance. The auxiliary system signal is utilized in both the control law and the neural network weight-update laws. The performance of the resultant closed-loop system is analyzed, and the bound of the transient error is established. Numerical simulations are presented to demonstrate the effectiveness of the proposed adaptive neural network control.

1 Introduction

The control of multi-input multi-output (MIMO) nonlinear systems is a practical yet challenging problem since most of engineering systems are multivariable and nonlinear. The control challenge is mainly due to the couplings of both inputs and outputs. Moreover, the uncertainties and nonlinearities in the input coupling matrix lead to further complication [1]. It is therefore important to develop effective control techniques for uncertain MIMO systems. Among the available control techniques for control of uncertain MIMO nonlinear systems (e.g., [2–4]), neural network (NN)-based adaptive controller has attracted considerable interests [5–9]. Various control strategies have been developed, with most of them focusing on integrating the neural networks to the robust adaptive control techniques under the scheme of the popular backstepping approach [1, 10–12]. In [1], the singularity problem of the control input matrix has been overcome by leveraging on the properties of the MIMO systems in block triangular form. In [10], the developed NN-based robust control design relaxes the requirement for off-line training. These results have demonstrated that NN-based controllers are effective for control of highly nonlinear systems with uncertainties.

Physical dynamical systems inevitably suffer from input constraint due to actuator limitations in magnitude and rate. This may severely degrade system performance if handled inappropriately. Various attempts have been made to address this issue for both single-input single-output (SISO) (e.g., [13–17]) systems and MIMO systems (e.g., [18–31]). In [26], a modified tracking error system was developed as a novel strategy to deal with the adaptation process for online approximation when input saturation occurs. The main advantage of the proposed control system is to protect the learning capabilities in the presence of input saturation. In [28], an adaptive backstepping control scheme using command filters to emulate actuator physical constraints on both the control law and the virtual control laws was presented. The issue of input constraints is more complicated for uncertain nonlinear MIMO systems. In [29], the auxiliary system design in [26] was extended to guarantee the $H^{\infty }$ performance for a general class of nonlinear MIMO systems with uncertainties in the presence of both disturbances and control input constraints. A model-based adaptive control was developed in [30] to handle the nonsymmetric input saturation, and a NN-based robust controller was developed in [31] to resolve a general input nonlinearity concerning both input saturation and deadzone. In both works, a new type of auxiliary system design is proposed with its signal utilized in the designed control law. The semi-global uniformly ultimate boundedness of all the signals in the closed-loop system is achieved in the presence of input saturations by virtue of the special design of the auxiliary system.

In this work, we address the tracking control problem for a class of uncertain MIMO nonlinear systems with input constraints in magnitude and rate. The developed control adopts the extensively studied neural networks with radial basis function (RBFNNs) to approximate the unknown dynamics of the MIMO system on account of its outstanding capability in modeling highly nonlinear functions. A novel auxiliary system is proposed to accommodate the effects of input constraints. The design of the auxiliary system is motivated by the works in [30] and [31], where the auxiliary system takes on a special structure based on the norm of the auxiliary signal. In both works, to achieve the control objective (of guaranteeing the desired tracking performance in the presence of input saturation), the auxiliary system is designed to indicate the level of saturation of the system input and respond to it properly to mitigate the effects of the input saturation. To achieve this, whenever the current auxiliary system is about to lose its capability of indicating the level of saturation, it will be reset with a new initial condition. If the auxiliary system loses its capability of indicating the level of saturation in a short time after it is reset with a new initial condition, this initial condition is considered as not able to properly indicate the level of saturation. Under this circumstance, the results of the auxiliary system in mitigating the effects of input saturation are limited. Thus, a more efficient auxiliary system needs to be developed to solve this issue.

This work proposes a modified auxiliary system design to further improve the control performance in the presence of input saturation. The proposed modified auxiliary system is endowed with a switching structure that integrates the auxiliary system design proposed in [30] and the direct learning control scheme proposed in [26]. The modified auxiliary system no longer requires a proper selection of the initial condition to be able to indicate the input saturation. Moreover, new design parameters of the auxiliary system are introduced to guarantee its performance. Furthermore, these design parameters can be adjusted in accordance with the control requirements. By utilizing the signals of the proposed auxiliary system in both the control law and NN weight-update laws, the advantages of the auxiliary system design in both [26] and [30] are preserved. The performance of the resultant closed-loop system with input saturations under the proposed switching control scheme is analyzed, and explicit bound of the tracking error is established. The remainder of this paper is organized as follows. Section 2 formulates the problem. Section 3 presents the proposed adaptive NN controller and the stability analysis. Section 4 reports the results of numerical simulations conducted to verify the effectiveness of the proposed approach. Section 5 summarizes the paper.

Notations :  $\Vert \cdot \Vert$ denotes Frobenius norm of matrices or the standard Euclidean norm of vectors. Given a matrix A and a vector $\xi$, the Frobenius norm and Euclidean norm are defined as $\Vert A \Vert ^{2} = \text{ tr }(A^{T}A) = \sum _{i,j}a_{ij}^{2}$ and $\Vert \xi \Vert ^{2} = \sum _{i} \xi _{i}^{2}$, respectively. $\lambda _{max} (B)$ and $\lambda _{min}(B)$ denote the largest and smallest eigenvalues of a square matrix B, respectively. $I_n$ represents the identity matrix of dimension $n\times n$.

2 Problem formulation

Consider the following MIMO nonlinear system

$$\begin{aligned} \dot{x} &= F(x) + G(x)\varPhi (u) \nonumber \\ y &= x \end{aligned}$$

(1)

where $x\in {\mathbb {R}}^{n}$ is the state vector, $F \in {\mathbb {R}}^{n}$ and $G\in {\mathbb {R}}^{n\times n}$ are unknown nonlinear functions and input coefficient matrices, respectively, $y\in {\mathbb {R}}^{n}$ is the system output vector, $u= [u_{1},\ldots ,u_{n}]^{T}$ is the designed control input and $\varPhi (u) = [\varPhi (u_{1}),\ldots ,\varPhi (u_{n}) ]^{T}$ is the actual input to system (1) with $\varPhi (\cdot )$ being a nonlinear function defining the magnitude and rate constrains of the control input.

Assumption 1

The magnitude limitations on design control input u are given by [29]

$$\begin{aligned} \varPhi (u_{i}) = \left\{ \begin{array}{lll} u_{i\ \mathrm{max}},&{}\text{ if } &{} u_{i} > u_{i\ \mathrm{max}} \\ u_{i}, &{}\text{ if } &{} u_{i\ \mathrm{min}} \le u_{i} \le u_{i\ \mathrm{max}} \\ u_{i\ \mathrm{min}},&{}\text{ if } &{} u_{i} <u_{i\ \mathrm{min}} \end{array}\right. \end{aligned}$$

(2)

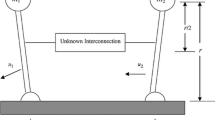
where $u_{i}$ is an element of the vector u, $u_{i\ \mathrm{max}}$ and $u_{i\ \mathrm{min}}$ are the known upper limit and lower limit of input saturation constraints, respectively. The rate limitation nonlinearity is defined similarly. The bound of $\varPhi (u)$ is denoted as $u_{m}$, i.e., $\Vert \varPhi (u) \Vert \le u_{m}$ ($u_{m}$ is known constant). A first-order model filter (as shown in Fig. 1) same as that used in [29] is employed for producing $\varPhi (u_{i})$ in implementation.

Fig. 1

Configuration of filter-emulating input constraints, where $w_{i}$ is the bandwidth parameter

The control objective is to design a control u so that the output y follows the desired trajectories $x_{d}$ (generated from smooth bounded $\dot{x}_{d}$) in the presence of input constraints imposed by $\varPhi (\cdot )$. The tracking error is defined as $e \, \triangleq \, x - x_{d}$.

3 Adaptive tracking controller design

In this section, an adaptive tracking controller is designed for the uncertain MIMO nonlinear system (1) using RBFNNs. To facilitate the control development, the following functions are introduced and approximated by RBFNNs:

$$\begin{aligned} h_{f}(Z_{f}) &= {} F(x) \end{aligned}$$

(3)

$$\begin{aligned} h_{g}(Z_{g}) &= {} G(x) \end{aligned}$$

(4)

where $Z_{f} = Z_{g} = x$.

3.1 NN approximation

RBFNN is an efficient tool for modeling nonlinear functions [1]. With the ideal weights $W_{f}^{*}\in {\mathbb {R}}^{L_{f}}$ and $W_{g}^{*}\in {\mathbb {R}}^{L_{g}\times n}$, the basis function vector $S_{f}(Z_{f})\in {\mathbb {R}}^{L_{f}}$, and the basis function matrix $S_{g}(Z_{g})\in {\mathbb {R}}^{L_{g}\times n}$, $h_{f}(Z_{f})$ and $h_{g}(Z_{g})$ can be represented by RBFNNs as

$$\begin{aligned} h_{f}(Z_{f}) &= {} W_{f}^{*T} S_f(Z_{f}) + \epsilon _{f} \end{aligned}$$

(5)

$$\begin{aligned} h_{g}(Z_{g}) &= {} W_{g}^{*T} S_g(Z_{g}) + \epsilon _{g} \end{aligned}$$

(6)

where $\epsilon _{f}$ and $\epsilon _{g}$ are the approximation errors corresponding to the ideal weights.

The approximation of $h_{f}(Z_{f})$ and $h_{g}(Z_{g})$ are given as

$$\begin{aligned} \hat{h}_{f}(Z_{f}) &= {} \hat{W}_{f}^{T} S_{f}(Z_{f}) \end{aligned}$$

(7)

$$\begin{aligned} \hat{h}_{g}(Z_{g}) &= {} \hat{W}_{g}^{T} S_{g}(Z_{g}) \end{aligned}$$

(8)

where $\hat{W}_{f}\in {\mathbb {R}}^{L_{f}}$ and $\hat{W}_{g}\in {\mathbb {R}}^{L_{g}\times n}$ are the estimates of the NN weight matrices.

The RBFNNs estimation employed here has the following properties to facilitate subsequent control development.

Property 1

[1: The ideal weights $W^{*}$ are defined as the weights that minimize the norm of approximation error for all $Z \in \varOmega _{Z} \subset R^{L}$ .

$$\begin{aligned} W^{*} \, \triangleq \, \text{ arg } \min \limits _{\hat{W} \in \varOmega _{W}} \left\{ \sup \limits _{Z\in \varOmega _{Z}} | h(Z) - \hat{W}^{T}S(Z)| \right\} \end{aligned}$$

(9)

where $\varOmega _{W}$ is some suitable prefixed large compact set.

Property 2

[1]: The Gaussian RBFNN adopted in this work uses the Gaussian functions of the form

$$\begin{aligned} s_{i}(Z) = \text{ exp } \left[ \frac{-( Z- a_{i})^{T}(Z - a_{i})}{b_{i}^{2}} \right] , \quad i = 1,2,\ldots ,L \end{aligned}$$

(10)

where $a_{i}$ and $b_{i}$ are the center of the receptive field and the width of the Gaussian function, respectively.

Property 3

[31]: $\Vert S(Z) \Vert$ is bounded by known constant, i.e., $\Vert S_{f}(Z_{f}) \Vert \le \zeta _{f}$, $\Vert S_{g}(Z_{g}) \Vert \le \zeta _{g}$, with $\zeta _{f}>0$ and $\zeta _{g}>0$.

Property 4

[31]: The ideal weights are assumed to exist and bounded, i.e., $\Vert W_{f}^{*} \Vert \le \bar{W}_{f}$, $\Vert W_{g}^{*} \Vert \le \bar{W}_{g}$, with $\bar{W}_{f}>0$ and $\bar{W}_{g}>0$ .

Property 5

[1, 31]: The NN approximation errors corresponding to the ideal weights are bounded over a compact set, i.e., $\Vert \epsilon _{f} \Vert \le \bar{\epsilon }_{f}$, $\Vert \epsilon _{g} \Vert \le \bar{\epsilon }_{g}$, with $\bar{\epsilon }_f> 0$ and $\bar{\epsilon }_g> 0$.

3.2 Control law synthesis

Define $\Delta u = \varPhi (u)-u$. To compensate for effects induced by the rate and magnitude limitations as defined by $\varPhi (u)$, an auxiliary system with state $\xi \in {\mathbb {R}}^{n}$ is introduced. Let $\xi (0)$ denote the initial condition of $\xi$. With $\varepsilon _{1}$ and $\varepsilon _{2}$ denoting two positive designed constants satisfying $\varepsilon _{1} \ge \Vert \xi (0) \Vert$ and $\varepsilon _{2} \, < \, \varepsilon _{1}$, the idea of the design of the auxiliary system is described as follows. If $\xi (0) \,< \, \varepsilon _{1}$, $\xi$ is initially set to be driven by a designed function $\chi _{1}\in {\mathbb {R}}^{n}$ (i.e., $\dot{\xi } = \chi _{1}$) until $\Vert \xi (t) \Vert =\varepsilon _{1}$. After which, $\xi$ is set to be driven by function $\chi _{2}\in {\mathbb {R}}^{n}$ (i.e., $\dot{\xi } = \chi _{2}$), which is designed to force $\Vert \xi \Vert$ to decrease from $\varepsilon _{1}$ to $\varepsilon _{2}$. Subsequently, $\xi$ is set to be driven by $\chi _{1}$ again. The process repeats in such a way that every time when $\Vert \xi \Vert$ increases to $\varepsilon _{1}$, $\xi$ is set to be driven by $\chi _{2}$, and when $\Vert \xi \Vert$ reduces to $\varepsilon _{2}$, $\xi$ is set to be driven by $\chi _{1}$. If $\xi (0) = \varepsilon _{1}$, $\xi$ is driven by $\chi _{2}$ first. The algorithm of the design of $\xi$ is provided below.

To facilitate the description of the auxiliary system, two sets of time sequences $T_{1}$ and $T_{2}$ are defined depending on $\Vert \xi (t) \Vert$, $\varepsilon _{1}$ and $\varepsilon _{2}$. If $\Vert \xi \Vert < \varepsilon _{1}$ holds for all t, then $T_{1} = {\emptyset }$ and $T_{2} = \emptyset$. If $\Vert \xi \Vert = \varepsilon _{1}$ occurs for some t, then $T_{1} = \{t_{11}, t_{12}, \ldots \}$ is the set contains all the time instants when $\Vert \xi \Vert = \varepsilon _{1}$, where $t_{1i}(i = 1,2,\ldots )$ denotes the time instant when $\Vert \xi \Vert = \varepsilon _{1}$ for the $i^{\text{ t }h}$ time, and $T_{2} = \{ t_{21}, t_{22},\dots \}$, where each element $t_{2i}$ ($i = 1,2,\ldots$) uniquely corresponds to the element $t_{1i}$ in $T_{1}$ in the following way: $t_{2i}$ denotes the time instant when $\Vert \xi \Vert = \varepsilon _{2}$ occurs for the first time after $t_{1i}$. Notice that $t_{1i}$ and $t_{2i}$ exist in pair since $\Vert \xi \Vert$ only decreases when $\xi$ is driven by $\chi _{2}$ (i.e., $t_{1i}\,\le\, t \,\le\, t_{2i}$). The number of the elements of $T_{1}$ and $T_{2}$ is denoted as M, which depends on both the system and the design of the auxiliary system. It is noted that M can be 0 (i.e., $T_{1} = T_{2} = \emptyset$).

Define

$$\begin{aligned} \varOmega _{t} \, \triangleq \, \left\{ \begin{array}{lll} \emptyset , &{}\text{ if }&{} M = 0\\ \{ t\ |\ t_{1i} \le t \le t_{2i}, i = 1,\dots ,M\}, &{}\text{ if }&{}M\ge 1 \end{array} \right. \end{aligned}$$

(11)

The auxiliary system is designed as:

$$\begin{aligned} \dot{\xi }(t) = \left\{ \begin{array}{lll} \chi _{1}\left( \xi ,h_{g}^{\prime }, u, \varPhi (u)\right) , &{}\text{ if }&{} t \notin \varOmega _{t} \\ \chi _{2}\left( \xi ,e, h_{g}^{\prime }, u, \varPhi (u)\right) , &{}\text{ if }&{} t \in \varOmega _{t}. \end{array} \right. \end{aligned}$$

(12)

where

$$\begin{aligned} &\chi _{1}= {} -K_{1}\xi + h_{g}^{\prime }\left( Z_{g}\right) (\varPhi (u)-u) \\ &\chi _{2}= {} -K_{1}\xi - \chi _{20}\left( e, h_{g}^{\prime }, u, \varPhi (u)\right) + h_{g}^{\prime }\left( Z_{g}\right) (u-\varPhi (u))\\ &\chi _{20}\left( e, h_{g}^{\prime }, u, \varPhi (u)\right)= {} \chi _{21}\left( e, h_{g}^{\prime }, u, \varPhi (u)\right) \,\xi /\Vert \xi \Vert ^{2} \\ &\chi _{21}\left( e, h_{g}^{\prime }, u, \varPhi (u)\right)= {} \frac{1}{2}\Vert e^{T}K_{1}\Vert ^{2}+\vert e^{T}h_{g}^{\prime }\Delta u\vert +\vert e^{T}\vartheta \varPhi (u) \vert \\&\quad+\frac{1}{2}\Vert e \Vert ^{2}\Vert \varPhi (u) \Vert ^{2}+\frac{1}{2}\Vert h_{g}^{\prime }\Delta u \Vert ^{2} \end{aligned}$$

with $K_{1}=K_{1}^{T}>0$ and $h^{\prime }_{g}\in {\mathbb {R}}^{n\times n}$ a designed function matrix satisfying

$$\begin{aligned}&i. \quad h_{g}^{\prime }\,\, \text{ is } \text{ nonsingular } \end{aligned}$$

(13)

$$\begin{aligned}&ii.\quad \Vert \vartheta \Vert \le \nu ,\,\,\, \vartheta \, \triangleq \, \hat{W}_{g}^{T}S_{g}\left( Z_{g}\right) -h_{g}^{\prime } \end{aligned}$$

(14)

where $\nu$ is any bounded time-varying positive scalar, i.e., $0\le \nu \le \nu _{m}$. The entity $h_{g}^{\prime }$ is introduced to overcome the singularity problem of the estimated input coupling matrix $h_{g}(Z_{g})$ (i.e., G(x)). Noting that $h_{g}^{\prime }$ is not required to be continuous, it can be simply designed as

$$\begin{aligned} h_{g}^{\prime } = \left\{ \begin{array}{lll} \hat{h}_{g}, &{}\text{ if }&{} \hat{h}_{g}\, \text{ is } \text{ nonsingular } \\ \hat{h}_{g} + \Delta , &{}\text{ if }&{} \hat{h}_{g}\, \text{ is } \text{ singular } \end{array} \right. \end{aligned}$$

where $\Delta$ is any scalar matrix to render $\hat{h}_{g} + \Delta$ nonsingular. Moreover, $\Delta$ satisfying $\Vert \Delta \Vert \le \nu$ can be different for each singular $\hat{h}_{g}$. The merit of introducing $h_{g}^{\prime }$ is to introduce more freedom in designing the control, since any $h_{g}^{\prime }$ satisfying (13) and (14) can be chosen even though it is preferable to choose it close to $\hat{h}_{g}$.

Remark 1

Let $V_{\xi } = \frac{1}{2}\xi ^{T}\xi$. Provided $K_{1} - \frac{1}{2}I_{n}>0,$ it is easy to deduce from (12) that

$$\begin{aligned} \dot{V}_{\xi } \le -\left( K_{1} - \frac{1}{2}I_{n}\right) \xi ^{T}\xi \quad \text{ for }\quad t\in [t_{1i}, t_{2i}] \end{aligned}$$

(15)

Equation (15) indicates that $\Vert \xi \Vert$ decreases when $t\in [t_{1i}, t_{2i}]$. In the case of no input saturation (i.e., $\Delta u = 0$), $\xi$ will remain at zero if $\xi (0) = 0$. If $\xi (0) \ne 0$, $\xi$ will converge exponentially to zero and remain at zero afterward.

The designed control input u is given by:

$$\begin{aligned} &u = {} h^{\prime -1}_{g}(Z_{g})u_{0} \nonumber \\ &u_{0}= {} \left\{ \begin{array}{lll} - \hat{W}_{f}^{T}S_{f}(Z_{f}) - K_{1}e + \dot{x}_{d}, &{}\text{ if }&{} t \notin \varOmega _{t} \\ - \hat{W}_{f}^{T}S_{f}(Z_{f}) - K_{1}(e - \xi ) + \dot{x}_{d}, &{}\text{ if }&{} t \in \varOmega _{t} \end{array}\right. \end{aligned}$$

(16)

Note that u may not be continuous. This is acceptable since the issue of input limitation on rate has been considered.

Define $e_{1} \, \triangleq \, e - \xi$. The adaptive control laws for $\hat{W}_{f}$ and $\hat{W}_{g}$ are designed as

$$\begin{aligned} \dot{\hat{W}}_{f}= & {} \left\{ \begin{array}{lll} \varLambda _{f}\left( S_{f}(Z_{f})e_{1}^{T} - \beta _{f}\hat{W}_{f}\right) ,\ &{}\text{ if }&{} t \notin \varOmega _{t} \qquad \\ \varLambda _{f}\left( S_{f}(Z_{f})e^{T} - \beta _{f}\hat{W}_{f}\right) ,\ &{}\text{ if }&{} t \in \varOmega _{t} \end{array} \right. \end{aligned}$$

(17)

$$\begin{aligned} \dot{\hat{W}}_{g}= & {} \left\{ \begin{array}{lll} \varLambda _{g}\left( S_{g}(Z_{g})\varPhi (u) e_{1}^{T}- \beta _{g}\hat{W}_{g}\right) , &{}\text{ if }&{} t \notin \varOmega _{t} \\ \varLambda _{g}\left( S_{g}(Z_{g})\varPhi (u) e^{T}- \beta _{g}\hat{W}_{g}\right) , &{}\text{ if }&{} t\in \varOmega _{t} \end{array}\right. \end{aligned}$$

(18)

where $\varLambda _{f} = \varLambda _{f}^{T}>0$, $\varLambda _{g} = \varLambda _{g}^{T} > 0$, $\beta _{f}>0$, $\beta _{g}>0$.

3.3 Stability analysis

The control law (i.e., (16)) and the adaptive control laws (i.e., (17) and (18)) for $t\in \varOmega _{t}$ resemble the control techniques proposed in [30] and [31], while those for $t\notin \varOmega _{t}$ are motivated by the control scheme proposed in [26–29]. With the proposed switching structure, the auxiliary system for $t\in [t_{1i},\ t_{2i}]$ will have an initial condition with relatively large norm (i.e., $\varepsilon _{1}$), which is desirable in [30] and [31]. Moreover, when the norm of the auxiliary signal decreases to a small constant (i.e., $\varepsilon _{2}$) before the input saturation disappears, it is not necessary to reset the auxiliary system with a new initial condition. The integration of the direct learning control scheme proposed in [26] serves to protect the learning capability under input saturation. By properly selecting the design parameters ($\varepsilon _{1}$, $\varepsilon _{2}$ and $\xi (0)$), the proposed switching scheme is able to preserve the advantages of both control strategies. The performance of the system under the proposed control scheme is summarized in the following theorem.

Theorem

Consider the nonlinear MIMO uncertain system (1) with input constraints on magnitude and rates satisfying Assumption 1. Provided bounded initial conditions, under the control law (16) and parameter update laws (17) and (18), there exist control parameters $K_{1} = K_{1}^{T} > 0$, $\varLambda _{f} = \varLambda _{f}^{T}>0$, $\varLambda _{g} = \varLambda _{g}^{T}>0$, $\beta _{f}>0$ and $\beta _{g} > 0$ such that the following statements hold: (i) A bound of the transient tracking error can be established as indicated in (39); (ii) during each time period when $t\in \varOmega _{t}$ (i.e., $t_{1i}\le t \le t_{2i}$), tracking error e exponentially converges to a compact set as indicated in (40); (iii) during each time period when $t\notin \varOmega _{t}$, modified tracking error $e_{1}$ exponentially converges to a compact set as indicated in (48).

Proof

To establish the bound of the transient tracking error, we consider the following Lyapunov candidate

$$\begin{aligned} V_{1}^{*} = \frac{1}{2}e^{T}e + \frac{1}{2}\xi ^{T}\xi \end{aligned}$$

(19)

Define $\tilde{W}_{1} \, \triangleq \, \hat{W}_{1} - W_{1}^{*}$ and $\tilde{W}_{2} \, \triangleq \, \hat{W}_{2} - W_{2}^{*}$. By utilizing (3)–(8), the time derivative of $V_{1}^{*}$ can be expressed as

$$\begin{aligned} \dot{V}_{1}^{*} =&\, e^{T}\hat{W}_{f}^{T} S_{f}(Z_{f}) + e^{T}h_{g}^{\prime }(Z_{g})\varPhi (u) -e^{T}\tilde{W}_{f}^{T} S_{f}(Z_{f}) \nonumber \\ &- e^{T}\tilde{W}_{g}^{T} S_{g}(Z_{g})\varPhi (u) + e^{T}\epsilon _{f} +e^{T}\epsilon _{g}\varPhi (u)-e^{T}\dot{x}_{d} \nonumber \\&+ e^{T}\vartheta \varPhi (u) + \xi ^{T}\dot{\xi } \end{aligned}$$

(20)

The rest of the proof for statement (i) is presented by considering the two cases of $\dot{\xi }$ as follows.

Case 1: $\dot{\xi } = \chi _{1}$. Substituting (12) (16) into (20) yields

$$\begin{aligned} \dot{V}_{1}^{*}= & {} -e^{T}K_{1}e -\xi ^{T}K_{1}\xi + e^{T}\epsilon _{f} + e^{T}\epsilon _{g}\varPhi (u) + e^{T}\vartheta \varPhi (u) \nonumber \\&\quad e^{T}h_{g}^{\prime }\Delta u + \xi ^{T}h_{g}^{\prime }\Delta u - e^{T}\tilde{W}_{f}^{T}S_{f}(Z_{f})- e^{T}\tilde{W}_{g}^{T}S_{g}(Z_{g}) \end{aligned}$$

(21)

From Eqs. (2) and (14), it follows that

$$\begin{aligned} e^{T}\epsilon _{g}\varPhi (u)& \le {} \frac{1}{2\sigma _{0}}\Vert e \Vert ^{2} + \frac{\sigma _{0}u_{m}^{2}}{2}\Vert \epsilon _{g} \Vert ^{2} \end{aligned}$$

(22)

$$\begin{aligned} e^{T}\epsilon _{f} &\le {} \frac{1}{2 \sigma _{1}}\Vert e \Vert ^{2} + \frac{\sigma _{1}}{2} \Vert \epsilon _{f} \Vert ^{2} \end{aligned}$$

(23)

$$\begin{aligned} e^{T}\vartheta \varPhi (u)\le & {} \frac{1}{2 \sigma _{2}}\Vert e \Vert ^{2}+\frac{\sigma _{2} u_{m}^{2}\nu _{m}^{2}}{2} \end{aligned}$$

(24)

$$\begin{aligned} e^{T}h_{g}^{\prime }(\varPhi (u)-u)\le & {} \frac{1}{2 }\Vert e \Vert ^{2} + \frac{1 }{2}\Vert h_{g}^{\prime } \Delta u \Vert ^{2} \end{aligned}$$

(25)

$$\begin{aligned} \xi ^{T}h_{g}^{\prime }(\varPhi (u)-u)\le & {} \frac{1}{2 }\Vert \xi \Vert ^{2} + \frac{1 }{2}\Vert h_{g}^{\prime } \Delta u \Vert ^{2} \end{aligned}$$

(26)

where $\sigma _{0}$, $\sigma _{1}$ and $\sigma _{2}$ are designed positive constants.

With above inequalities, $\dot{V}_{1}^{*}$ can be upper-bounded as

$$\begin{aligned} \dot{V}_{1}^{*}\le & {} -e^{T}K_{11} e - \xi ^{T}K_{12}\xi + \frac{\sigma _{1}}{2} \Vert \epsilon _{f} \Vert ^{2}+ \frac{\sigma _{0}u_{m}^{2}}{2}\Vert \epsilon _{g} \Vert ^{2} \nonumber \\&+ \frac{\sigma _{2} u_{m}^{2}\nu _{m}^{2}}{2} + \Vert h_{g}^{\prime } \Delta u \Vert ^{2}- e^{T}\tilde{W}_{f}^{T}S_{f}(Z_{f}) \nonumber \\&- e^{T}\tilde{W}_{g}^{T}S_{g}(Z_{g}) \end{aligned}$$

(27)

where $K_{11} = K_{1} - (\frac{1}{2 \sigma _{0}} + \frac{1}{2 \sigma _{1}}+ \frac{1}{2 \sigma _{2}}+\frac{1}{2})I_{n}$ and $K_{12} = K_{1} - \frac{1}{2}I_{n}$.

Considering the NN weight error signals $\tilde{W}_{f}$ and $\tilde{W}_{g}$, an augmented Lyapunov function candidate is chosen as

$$\begin{aligned} V_{1} = V_{1}^{*} + \frac{1}{2}\text{ tr } \left( \tilde{W}_{f}^{T}\varLambda _{f}^{-1}\tilde{W}_{f}\right) + \frac{1}{2}\text{ tr } \left( \tilde{W}_{g}^{T}\varLambda _{g}^{-1}\tilde{W}_{g}\right) \end{aligned}$$

(28)

Substituting (17) and (18) into (28) and noting the facts

$$\begin{aligned} {-\text{tr}}\left( \tilde{W}_{f}^{T}\hat{W}_{f}\right)= & {} -\frac{\Vert \tilde{W}_{f}\Vert ^{2}}{2}-\frac{\Vert \hat{W}_{f}\Vert ^{2}}{2} + \frac{\Vert W^{*}_{f}\Vert ^{2}}{2} \end{aligned}$$

(29)

$$\begin{aligned} {-\text{ tr}}\left( \tilde{W}_{g}^{T}\hat{W}_{g}\right)= & {} -\frac{\Vert \tilde{W}_{g}\Vert ^{2}}{2}-\frac{\Vert \hat{W}_{g}\Vert ^{2}}{2} + \frac{\Vert W^{*}_{g}\Vert ^{2}}{2} \end{aligned}$$

(30)

$$\begin{aligned} -\xi ^{T}\tilde{W}_{f}^{T}S_{f}(Z_{f})&\le {} \frac{1}{2 \sigma _{3}}\Vert \xi \Vert ^{2} + \frac{\sigma _{3}\zeta _{f}}{2}\Vert \tilde{W}_{f}\Vert ^{2} \end{aligned}$$

(31)

$$\begin{aligned} -\xi ^{T}\tilde{W}_{g}^{T}S_{g}(Z_{g})&\le {} \frac{1}{2 \sigma _{4}}\Vert \xi \Vert ^{2} + \frac{\sigma _{4}\zeta _{g}}{2}\Vert \tilde{W}_{g}\Vert ^{2} \end{aligned}$$

(32)

the upper bound of $\dot{V}_{1}$ can be rewritten as

$$\begin{aligned} \dot{V}_{1}\le & {} -e^{T}K_{11} e - \xi ^{T}K_{13}\xi - k_{f}\Vert \tilde{W}_{f}\Vert ^{2}-k_{g}\Vert \tilde{W}_{g}\Vert ^{2} \nonumber \\&+ \frac{\sigma _{1}}{2} \Vert \epsilon _{f} \Vert ^{2}+ \frac{\sigma _{0}u_{m}^{2}}{2}\Vert \epsilon _{g} \Vert ^{2}+ \frac{\sigma _{2} u_{m}^{2}\nu _{m}^{2}}{2}+ \frac{\beta _{f}\Vert W^{*}_{f}\Vert ^{2}}{2} \nonumber \\&\frac{\beta _{g}\Vert W^{*}_{g}\Vert ^{2}}{2} + \Vert h_{g}^{\prime } \Delta u \Vert ^{2} \nonumber \\\le & {} -\lambda _{11} V_{1} + c_{11} + \Vert h_{g}^{\prime } \Delta u \Vert ^{2} \end{aligned}$$

(33)

where $\sigma _{3}$, $\sigma _{4}>0$, $K_{13} = K_{1} - (\frac{1}{2}+\frac{1}{2 \sigma _{3}}+\frac{1}{2 \sigma _{4}} )I_{n}$, $k_{f} = \frac{1}{2}(\beta _{f} - \sigma _{3} \zeta _{f})$, $k_{g} = \frac{1}{2}(\beta _{g} - \sigma _{4} \zeta _{g})$, $\lambda _{11} = \text{ min }\{ 2\lambda _\mathrm{min}(K_{11}), 2\lambda _\mathrm{min}(K_{13}), \frac{k_{f}}{\lambda _\mathrm{max}(\varLambda _{f}^{-1})}, \frac{k_{g}}{\lambda _\mathrm{max}(\varLambda _{g}^{-1})} \}$ and $c_{11} = \frac{1}{2}(\sigma _{1} \Vert \epsilon _{f} \Vert ^{2}+ \sigma _{0}u_{m}^{2}\Vert \epsilon _{g} \Vert ^{2}+ \sigma _{2} u_{m}^{2}\nu _{m}^{2}+\beta _{f}\Vert W^{*}_{f}\Vert ^{2} + \beta _{g}\Vert W^{*}_{g}\Vert ^{2})$.

Case 2: $\dot{\xi } = \chi _{2}$.

Substituting (12) into (20) and considering (16), (20), (23) and the following facts:

$$\begin{aligned} e^{T}K_{1}\xi\le & {} \frac{1}{2} \Vert e^{T}K_{1} \Vert ^{2} + \frac{1}{2}\Vert \xi \Vert ^{2} \end{aligned}$$

(34)

$$\begin{aligned} e^{T}\epsilon _{g}\varPhi (u)\le & {} \frac{1}{2}\Vert \epsilon _{g} \Vert ^{2} + \frac{1}{2}\Vert e \Vert ^{2}\Vert \varPhi (u) \Vert ^{2} \end{aligned}$$

(35)

it yields

$$\begin{aligned}\dot{V}_{1}^{*} \le& -e^{T}K_{14}e - \xi ^{T} K_{15}\xi - e^{T}\tilde{W}_{f}^{T} S_{f}(Z_{f}) \nonumber \\ &- e^{T}\tilde{W}_{g}^{T} S_{g}(Z_{g})\varPhi (u) + \frac{\sigma _{1}}{2}\Vert \epsilon _{f} \Vert ^{2} + \frac{1}{2}\Vert \epsilon _{g}\Vert ^{2} \end{aligned}$$

(36)

where $K_{14} = K_{1} - \frac{1}{2\sigma _{1}}I_{n}$ and $K_{15} = K_{1} - I_{n}$.

Substituting (17), (18), (29), (30) and (36) into the augmented Lyapunov function (28), $\dot{V}_{1}$ can be upper-bounded as

$$\begin{aligned} \dot{V}_{1} \le -\lambda _{12} V_{1} + c_{12} \end{aligned}$$

(37)

where $\lambda _{12} = \text{ min } \left\{ 2\lambda _\mathrm{min}(K_{14}), 2\lambda _\mathrm{min}(K_{15}), \frac{\beta _{f}}{\lambda _\mathrm{max}(\varLambda _{f}^{-1})},\right.$ $\left. \frac{\beta _{g}}{\lambda _\mathrm{max}(\varLambda _{g}^{-1})} \right\}$ and $c_{12} = \frac{1}{2}(\sigma _{1}\Vert \epsilon _{f} \Vert ^{2} + \Vert \epsilon _{g} \Vert ^{2} + \beta _{f}\Vert W^{*}_{f}\Vert ^{2} + \beta _{g}\Vert W^{*}_{g}\Vert ^{2}).$

For $t\in [0, + \infty ]$, to ensure $\lambda _{11}$, $\lambda _{12}$, $c_{11}$and $c_{12}>0$, the sufficient gain conditions are $K_{1} - (\frac{1}{2} + \frac{1}{2 \sigma _{0}}+ \frac{1}{2 \sigma _{1}}+ \frac{1}{2 \sigma _{2}} + \frac{1}{2 \sigma _{3}}+\frac{1}{2 \sigma _{4}}) > 0$, $\beta _{f} - \sigma _{3}\zeta _{f} > 0$, $\beta _{g} - \sigma _{4}\zeta _{g} > 0$. $\sigma _{0}$ is chosen such that $\frac{\sigma _{0}u_{m}^{2}}{2}\ge 1$. Thus, $\lambda _{11} \le \lambda _{12}$ and $c_{11}\ge c_{12}$. Subsequently,

$$\begin{aligned} \dot{V}_{1}\le -\lambda _{11}V_{1} + c_{11} + \Vert h_{g}^{\prime } \Delta u \Vert ^{2} \quad \text{ for } \quad t\in [0,\ +\infty ] \end{aligned}$$

(38)

According to Lemma 1.2 in [1], (38) indicates that a transient bound of e can be established as

$$\begin{aligned} \Vert e(t) \Vert \le \sqrt{2(V_{1}(0) + \frac{c_{11}}{\lambda _{11}} + \frac{1}{\lambda _{11}}\sup _{\tau \in [0,t]}[\Vert h_{g}^{\prime } \Delta u (\tau ) \Vert ^{2}}]) \end{aligned}$$

(39)

where $V_{1}(0) = (1/2)e^{T}(0)e(0) + (1/2)\xi ^{T}(0)\xi (0)+ (1/2)\tilde{W}_{f}^{T}(0) \varLambda _{f}^{-1} \tilde{W}_{f}(0)+ (1/2)\tilde{W}_{g}^{T}(0) \varLambda _{g}^{-1} \tilde{W}_{g}(0)$. This concludes the proof of statement (i).

Note that the analysis for case 2 applies for $t\in [t_{1i},\ t_{2i}]$, i.e.,

$$\begin{aligned} \dot{V}_{1} \le - \lambda _{12} V_{1} + c_{12}\quad \text{ for } \quad t \in [t_{1i},\ t_{2i}] \end{aligned}$$

(40)

(40) indicates that tracking error e exponentially converges to a compact set and the transient error bound is given by

$$\begin{aligned} \Vert e \Vert \le \sqrt{2\left( V_{1}(t_{1i}) + c_{12}/\lambda _{12}\right) } \end{aligned}$$

(41)

Noting that $\lambda _{12} \ge \lambda _{11}$ and $c_{12}\le c_{11}$, if the time period $[t_{1i},\ t_{2i}]$ is long enough, it is possible that a good tracking performance is achieved. This concludes the proof of statement (ii).

The control performance for $t\notin \varOmega _{t}$ is further discussed by considering the following Lyapunov function

$$\begin{aligned} V_{2}^{*} = \frac{1}{2}e_{1}^{T}e_{1} \end{aligned}$$

(42)

Without loss of generality, we assume that $M\ge 2$ and $\xi (0)<\varepsilon _{1}$. In this case, noting (2)–(6), (14) and following facts

$$\begin{aligned} e_{1}^{T}\epsilon _{f}\le & {} \frac{1}{2\sigma _{1}}\Vert e_{1} \Vert ^{2}+\frac{\sigma _{1}}{2}\Vert \epsilon _{f} \Vert ^{2} \end{aligned}$$

(43)

$$\begin{aligned} e_{1}^{T}\epsilon _{g}\varPhi (u)\le & {} \frac{u_{m}^{2}}{2} \Vert \epsilon _{g} \Vert ^{2} + \frac{1}{2}\Vert e_{1} \Vert ^{2} \end{aligned}$$

(44)

$$\begin{aligned} e_{1}^{T}\vartheta \varPhi (u)\le & {} \frac{\sigma _{2} u_{m}^{2}\nu _{m}^{2}}{2}+\frac{1}{2\sigma _{2}}\Vert e_{1} \Vert ^{2} \end{aligned}$$

(45)

the time derivative of $V_{2}^{*}$ for $t\in [0,\ t_{11}]$ can be expressed as

$$\begin{aligned} \dot{V}_{2}^{*}\le & {} -e_{1}^{T}K_{16}e_{1}- e_{1}^{T}\tilde{W}_{f}^{T} S_{f}(Z_{f}) - e_{1}^{T}\tilde{W}_{g}^{T} S_{g}(Z_{g})\varPhi (u) \nonumber \\&+\frac{\sigma _{2}u_{m}^{2}\nu _{m}^{2}}{2}+\frac{\sigma _{1}}{2}\Vert \epsilon _{f} \Vert ^{2}+\frac{u_{m}^{2}}{2} \Vert \epsilon _{g} \Vert ^{2} \end{aligned}$$

(46)

where $K_{16} = K_{1} - (\frac{1}{2\sigma _{1}} + \frac{1}{2\sigma _{2}} + \frac{1}{2})I_{n}>0$.

Considering the augmented Lyapunov function

$$\begin{aligned} V_{2} = V_{2}^{*} + \frac{1}{2}\text{ tr }\left( \tilde{W}_{f}^{T}\varLambda _{f}^{-1} \tilde{W}_{f}\right) + \frac{1}{2}\text{ tr }\left( \tilde{W}_{g}^{T}\varLambda _{g}^{-1} \tilde{W}_{g}\right) \end{aligned}$$

(47)

Substituting (17), (18), (29), (30) and (46) into (47) yields

$$\begin{aligned} \dot{V}_{2} \le - \lambda _{2} V_{2} + c_{2} \end{aligned}$$

(48)

where $\lambda _{2} = \text{ min } \left\{ 2\lambda _\mathrm{min}(K_{16}), \frac{\beta _{f}}{\lambda _\mathrm{max}(\varLambda _{f}^{-1})}, \frac{\beta _{g}}{\lambda _\mathrm{max}(\varLambda _{g}^{-1})} \right\}$ and $c_{2} = \frac{1}{2}(\sigma _{2}u_{m}^{2}\nu _{m}^{2}+\sigma _{1}\Vert \epsilon _{f} \Vert ^{2}+ u_{m}^{2} \Vert \epsilon _{g} \Vert ^{2}+ \beta _{f}\Vert W^{*}_{f}\Vert ^{2})$.

Provided bounded initial condition, (48) indicates

$$\begin{aligned} \Vert e_{1} \Vert \le \sqrt{2(V_{2}(0) + c_{2}/\lambda _{2})} \end{aligned}$$

(49)

Furthermore, noticing that the analysis is conducted under the condition that $\Vert \xi \Vert \,< \, \varepsilon _{1}$, we obtain

$$\begin{aligned} \Vert e \Vert \le \Vert e_{1} \Vert + \Vert \xi \Vert < \sqrt{2\left( V_{2}(0) + c_{2}/\lambda _{2}\right) } + \varepsilon _{1} \end{aligned}$$

(50)

The analysis for $t\in [t_{2i},\ t_{1(i+1)}]\cup [t_{2M},\ +\infty ] (i=1,\dots ,M-1)$ is similar as above. Moreover, if M is assumed to satisfy $M \le d < {{+}\infty}$ where d is any positive integer, an explicit bound of tracking error e during $t\in [t_{2i},\ t_{1(i+1)}]$ can be found by repeating the above analysis. This concludes the proof of statement (iii). $\square$

Remark 2

Proper selection of $\xi (0)$, $\varepsilon _{1}$ and $\varepsilon _{2}$ may further improve the control performance in the presence of input saturations. For NN-based adaptive controllers, input saturation may only occur in the initial stage of control when the NN weights have not been well tuned. As such, if choosing $\xi (0) = \varepsilon _{1}$ (i.e., $t_{11} = 0$) with suitable $\varepsilon _{1}$ and $\varepsilon _{2}$, it is possible that input saturation disappears before $t_{21}$ and does not occur afterward. In this case, as indicated in Eq. (37), the tracking error converges exponentially to a compact set. Moreover, during the entire process (i.e., $t\in [0, +\infty ]$), the tracking performance is guaranteed despite the uncertainties and input saturation. It is worth pointing out that requiring $\Vert \xi (0) \Vert \le \varepsilon _{1}$ is not necessary. In fact, $\Vert \xi (0) \Vert > \varepsilon _{1}$ can be chosen and it can be treated in the same way as $\Vert \xi (0) \Vert = \varepsilon _{1}$. Notice that in this case $t_{11}$ is defined as 0 instead of the time instant when $\Vert \xi \Vert = \varepsilon _{1}$ for the first time.

4 Numerical simulation

To verify the effectiveness of the proposed adaptive neural network controller, the following uncertain MIMO nonlinear system is considered for numerical simulations:

$$\begin{aligned} \dot{x}_{1} =& {} - \left( x_{1} + x_{2}^{2}\right) + 2 \varPhi (u_{1}) + \left( 2+\sin (x_{2})\right) \varPhi (u_{2}) \nonumber \\ \dot{x}_{2}= & {} - x_{1}^{2}x_{2} + \sin (x_{1})\cos (x_{2}) \varPhi (u_{1}) + \varPhi (u_{2}) \nonumber \\ y_{1}= &\, {} x_{1} \quad y_{2}\,\,\, =\,\,\, x_{2} \nonumber \\ x_{1}(0)= & \,{} 0.2 \quad x_{2}(0)\,\,\, =\,\,\, -0.2 \end{aligned}$$

(51)

where $u_{i} (i = 1,2)$ is the input to be designed and $\varPhi (u_{i}) (i = 1,2)$ is the known function of input saturation. The control objective is to design $u_{1}$ and $u_{2}$ for system (51) such that $y_{1}$ and $y_{2}$ follow $x_{1d} = 0.5 [\sin (t) + \sin (2t)]$ and $x_{2d} = 0.7\sin (t) + 0.3 \sin (0.5t)$, respectively. The input saturations are defined as $\vert \varPhi (u_{i}) \vert \le 1.5$, and $\vert \dot{\varPhi }(u_{i})\vert \le 15$ ($i = 1,2$). The design parameters are chosen as $K_{1} = \text{ diag }\{ 20,20\}$, $\varepsilon _1 = 0.5$, $\varepsilon _{2} = 0.05$ and $\xi (0) = 0$. The dimensions of the NNs are chosen as $L_{f} = L_{g} = 50$. The other parameters are designed as $\nu = 0.05$ and $\omega _1 = \omega _{2} = 20$.

Simulation results are presented in Figs. 2, 3 and 4. Figure 2 indicates that $x_{1}$ and $x_{2}$ follow closely the reference trajectories $x_{1d}$ and $x_{2d}$, respectively. Figure 3 shows the trajectories of input signals $\varPhi (u_{1})$ and $\varPhi (u_{2})$. The input saturation in magnitude is observed in the transient phase of the control process. Figure 4 shows the rate of the input signals $\dot{\varPhi }(u_{1})$ and $\dot{\varPhi }(u_{2})$. Similar as the control input, the rate saturation only occurs in the transient phase. The auxiliary system signal $\xi$ is shown in terms of its norm in Fig. 5. It can be concluded that $\xi$ works as desired in the presence of input saturation.

Fig. 2

Output follows reference signal a $x_{1}$ (solid blue line) tracks $x_{1d}$ (dashed red line) b $x_{2}$ (solid blue line) tracks $x_{2d}$ (dashed red line) (color figure online)

Fig. 3

Magnitude of control input signal

Fig. 4

Rate of control input signal rate

Fig. 5

Norm of auxiliary signal

5 Conclusions

We have developed a novel adaptive neural network tracking controller for a class of uncertain nonlinear MIMO systems with the objective of guaranteeing control performance in the presence of input saturation in both magnitude and rate. The development of the adaptive control is based on a designed auxiliary system endowed with a switching structure. Results from numerical simulations have demonstrated the effectiveness of the proposed control scheme. Our proposed approach extends the existing control techniques based on auxiliary system design by removing a key assumption that restricts the selection of initial conditions for the designed auxiliary system. Specifically, the introduction of $\varepsilon _{1}$ and $\varepsilon _{2}$ enables more freedom in designing a proper controller since their values (which characterize the switching conditions) can be adjusted according to the desired control performance. The future direction of this work is to incorporate the proposed adaptive neural network tracking controller with nonlinear MIMO systems of more general form. In particular, to further extend the practical applicability of the proposed control strategy, the external disturbance in the system and the application on a practical system will be investigated.