1 Introduction

During the past decades, the problem of adaptive control for nonlinear systems has been extensively investigated in the control community, and many remarkable results have been reported in the literature; see references [1–5]. By introducing the backstepping technique, the restriction of the matching condition has been removed for nonlinear systems [1]. In addition, many approximation-based adaptive control schemes have been reported to deal with uncertain nonlinear systems with unknown nonlinear functions; see [6–16] for the deterministic cases, and [17–22] and the references therein for stochastic nonlinear systems. In [16], a novel adaptive fuzzy control scheme was proposed for nonlinear strict-feedback systems, which contains only one adaptive parameter needed to be estimated online regardless of the order of systems. By combining fuzzy logical systems (FLS) with the backstepping technique, in [17], a class of strict-feedback stochastic nonlinear system was considered, where the virtual control gain function sign is unknown. In [18–20], some adaptive fuzzy output-feedback control schemes were presented when the states of the stochastic nonlinear systems are not all available. However, in the aforementioned literatures, the authors have not considered time delays.

Time delays and stochastic disturbances, which are often encountered in practical applications, are sources of instability and degradation of system performance. Recently, the stability analysis and controller design problems for nonlinear time-delay system have been payed more and more attention; see [23–35]. In general, there are two main methods for solving nonlinear systems with time delays. One is to use the Lyapunov–Krasovskii theory. Without the measurements of the states taken into consideration, authors in [29] designed adaptive neural output-feedback controller for a class of stochastic nonlinear strict-feedback time-varying delays systems. The other is the Lyapunov–Razumikhin approach, which is more brief than the Lyapunov–Krasovskii method for dealing with the problems of stability analysis and controller design. Nevertheless, a few works [32–35] have been done to investigate the adaptive neural control or fuzzy control of nonlinear time-varying delay systems by the Lyapunov–Razumikhin approach. It is worth noting that the main limitation of the aforementioned results is that time-delay functions only include the previous time-varying delay states. Thus, it is imperative to put forward an adaptive neural control scheme for stochastic nonlinear systems with all state time-varying delays by the Lyapunov–Razumikhin approach.

As another source of instability and performance degeneration of practical systems, input saturation has been attracting significant attention. There exits extensive research on the control systems with input saturation [36–43]. In [38], authors investigated the problem of robust controller design for uncertain discrete time-delay systems with control input saturation. By introducing an auxiliary design system, an adaptive tracking control scheme was proposed for a class of uncertain multi-input and multi-output nonlinear systems with non-symmetric input constraints [40]. However, to the best of our knowledge, there are no results reported on the adaptive neural or fuzzy control for stochastic nonlinear time-varying delay systems with input saturation.

Motivated by the aforementioned observation, we investigate the problem of adaptive neural control for strict-feedback stochastic nonlinear systems with multiple time-varying delays and input saturation in this paper. In order to design the controller, neural networks are employed to approximate the unknown nonlinear functions, and Razumikhin lemma is used to deal with the time-delay terms. The proposed controller guarantees that all the signals in the closed-loop system are bounded in probability. The main contributions are summarized as follows: (1) for the first time, the Lyapunov–Razumikhin approach is utilized to solve the problem of a class of strict-feedback stochastic nonlinear systems with all state time-varying delays, along with the guaranteed stability of the closed-loop system. (2) A novel adaptive neural control scheme is successfully given for strict-feedback stochastic nonlinear time-delay systems with input saturation, which is more general than the existing results [32–34]. (3) The designed control scheme contains only one adaptive parameter required to be estimated online, so the computation complexity can be significantly alleviated, which makes the algorithm easy to implement in practice.

The remainder of this paper is organized as follows. Section 2 provides some preliminary results and problem formulation. The controller design and stability analysis are given in Sect. 3. Two examples are provided to demonstrate effectiveness of the results in Sect. 4. Section 5 concludes the paper.

2 Preliminaries and problem formulation

In this section, some useful conceptions and lemmas are introduced to develop the main result of the paper, then neural networks are given to approximate the unknown nonlinear function. Finally, the problem of adaptive neural control for a class of stochastic nonlinear time-varying delay systems is formulated.

2.1 Preliminary results

Consider the following stochastic nonlinear time-delay system

$${\text{d}}x = f(t,x(t),x(t - \tau (t))){\text{d}}t + g(t,x(t)){\text{d}}w,$$
(1)

with initial condition \(\{x(s):-\tau\leq s \leq 0\}=\xi\in C_{F_{0}}^{b}\times([-\tau,0],R^{n})\), where \(\tau(t):R^{+}\rightarrow[0,\tau]\) is a Borel measurable function; \(x(t) \in R^{n}\) denotes the state variable and x(t − τ(t)) is the state vectors with time-delay; w is an r-dimensional standard Wiener process defined on the complete probability space \((\Upomega, F, \{F_{t}\}_{t\geq 0},P)\) with \(\Upomega\) being a sample space, F being a σ-field, {F t } t≥0 being a filtration, and P being a probability measure. \(f(\cdot),\,g(\cdot)\) are locally Lipschitz functions and satisfy f(t, 0, 0) = 0, g(t, 0, 0) = 0.

Definition 1

For any given \(V(t, x)\in C^{1,2}([-\tau,\infty]\times R^{n})\) related to the stochastic nonlinear time-delay system (1), define the infinitesimal generator \(\mathcal{L}\) as follows:

$${\mathcal{L}} V(t,x) = \frac{\partial V}{\partial t} + \frac{\partial V}{\partial x}f(t,x,x(t-\tau(t)))+\frac{1}{2}Tr\left\{g(t,x)^{T} \frac{\partial^{2} V}{\partial x^{2}}g(t,x)\right\},$$
(2)

where Tr(A) is the trace of a matrix A.

Definition 2

([34]) Let p ≥ 1, the solution {x(t), t ≥ 0} of the stochastic nonlinear time-delay system (1) with initial condition \(\xi \in \Upomega_{0} (\Upomega_{0}\) is some compact set including the origin) is said to be p-moment semi-globally uniformly ultimately bounded if there exists a constant \(\bar{d}\), it holds that

$$E\{\|x(t,\xi)\|^{p}\}\leq \bar{d}, \quad \forall t\geq T, \quad {\text{for}} \; {\text{some}} \quad T \geq 0.$$

Lemma 1

(Razumikhin Lemma [34]) Let p ≥ 1, consider the stochastic nonlinear time-delay system (1), if there exist function \(V(t,x)\in C^{1,2}([-\tau,\infty]\times R^{n})\) and some positive constants c 1, c 2, μ 1,  μ 2, q > 1 satisfying the following inequalities

$$c_{1}|x|^{p} \leq V(t,x)\leq c_{2}|x|^{p}, \quad t\geq -\tau, \quad x \in R^{n},$$
(3)
$$E V(t+s,x(t+s)) < q E V(t,x(t)), \quad \forall s \in [-\tau,0],$$
(4)

for all t ≥ 0, such that

$$E {\mathcal{L}} V(t,x) \leq -\mu_{1}V(t,x)+\mu_{2}.$$
(5)

Then the solution x(t, ξ) of system (1) is p-moment uniformly ultimately bounded.

Lemma 2

(Young’s inequality [2]) For \(\forall(x,y)\in R ^{2}\), the following inequality holds:

$$x y \leq \frac{\varepsilon^{p}}{p}|x|^{p}+\frac{1}{q\varepsilon^{q}}|y|^{q},$$
(6)

where \(\varepsilon > 0, p>1, q>1\), and (p − 1) (q − 1) = 1.

Lemma 3

([6]) For any \(\eta \in R\) and \(\varepsilon > 0\), the following holds:

$$0 \le |\eta | - \eta \tanh \left( {\frac{\eta }{\sigma }} \right) \le \delta \sigma ,$$
(7)

where δ is a constant that satisfies δ = e −(δ+1); i.e., δ = 0.2875.

Lemma 4

([25]) Consider dynamic system of the following form

$$\dot{\hat{\theta}}(t)=-\varrho\hat{\theta}(t)+\kappa w(t),$$
(8)

where ϱ and κ are positive constants and w(t) is a positive function. By choosing the initial condition \(\hat{\theta}(0) \geq 0\), we have \(\hat{\theta}(t) \geq 0\) for all t ≥ 0.

Remark 1

Since \(\hat{\theta}(\cdot)\) is an estimation of the unknown positive constant θ, it follows that \(\hat{\theta}(0) \geq 0\) is always reasonable. This result will be used in the backstepping design procedure.

2.2 Neural networks

In this paper, the radial basis function (RBF) neural networks are used to approximate an unknown continuous function \(f(Z): R^{q}\rightarrow R\),

$$f_{nn}(Z) = W^{T}S(Z),$$
(9)

where \(Z \in \Upomega_{Z} \subset R^{q}\) represents the input vector and q denotes the neural network input dimension. \(W=[w_{1}, w_{2}, \dots, w_{l}]^{T} \in R^{l}\) is the weight vector; l > 1 denotes the neural network node number. \(S(Z)=[s_{1}(Z), s_{2}(Z), \dots, s_{l}(Z)]^{T} \in R^{l}\) is the basis function vector with s i (Z) defined by

$$s_{i}(Z)=\exp\left[-\frac{\|Z-\mu_{i}\|^{2}}{\eta_{i}^{2}}\right], \quad i=1, 2, \ldots, l,$$
(10)

where \(\mu_{i} = [\mu_{i1}, \mu_{i2}, \ldots, \mu_{iq}]^{T}\) is the center of the receptive field and η is the width of the Gaussian function. For any unknown nonlinear function f(Z) defined over a compact set \(\Upomega_{Z}\in R^{q},\) there exit the neural network \(W^{\ast^{T}}S(Z)\) and arbitrary accuracy \(\varepsilon>0\) such that

$$f(Z)= W^{\ast^{T}}S(Z)+\delta(Z), \quad \forall Z \in \Upomega_{Z} \subset R^{q},$$
(11)

where \(W^{\ast}\) is the ideal constant weight vector and is expressed as

$$W^{\ast}:={\text{arg}} \min_{W\in R^{l}}\{\sup_{Z\in \Upomega_{Z}}|f(Z)-W^{T}S(Z)|\},$$

and δ(Z) is the approximation error, which satisfies \(|\delta(Z)| \leq \varepsilon\).

Lemma 5

([25]) Consider the Gaussian RBF networks (9) and (10). Let \(\rho := \frac{1}{2}\min _{i\neq j}\|\mu_{i}-\mu_{j}\|\). Then we can take an upper bound of \(\|S(Z)\|\) as

$$\|S(Z)\| \leq \sum_{k=0}^{\infty} 3q(k+2)^{q-1}e^{-2\rho^{2}k^{2}/\eta^{2}}:=s.$$
(12)

Remark 2

It has been pointed out that the constant s is a limited value, which is independent with the neural networks input and neural network node numbers in [25].

2.3 Problem formulation

Consider a class of strict-feedback stochastic nonlinear time-varying delays systems in the following form

$$\left\{ {\begin{array}{*{20}c} \begin{aligned} {\text{d}}x_{i} & = (g_{i} (\bar{x}_{i} )x_{{i + 1}} + f_{i} (\bar{x}_{i} ) + q_{i} (\bar{x}_{{n,\tau (t)}} )){\text{d}}t + \psi _{i}^{T} (\bar{x}_{i} ){\text{d}}w, \\ & \quad 1 \le i \le n - 1, \\ \end{aligned} \\ \begin{aligned} {\text{d}}x_{n} & = (g_{n} (\bar{x}_{n} )u + f_{n} (\bar{x}_{n} ) + q_{n} (\bar{x}_{{n,\tau (t)}} )){\text{d}}t + \psi _{n}^{T} (\bar{x}_{n} ){\text{d}}w, \\ & \quad y = x_{1} ,\bar{x}_{n} (t) = \phi (t), - \tau \le t \le 0, \\ \end{aligned} \\ \end{array} } \right.$$
(13)

where \(\bar{x}_{n}=[x_{1},\ldots, x_{n}]^{T}\in R^{n}\) and \(y \in R\) denote the state vector of the system and output of the system, respectively; \(\bar{x}_{i}=[x_{1},\ldots, x_{i}]^{T}\in R^{i}\), \((i=1, 2, \ldots, n); w\) is defined as in the system (1); \(q_{i}(\bar{x}_{n, \tau(t)})\) is unknown smooth nonlinear time-delay functions with q i (0) = 0, which is defined by \(q_{i}(\bar{x}_{n, \tau(t)})= q_{i}(x_{1}(t-\tau_{1}(t)), x_{2}(t-\tau_{2}(t)), \ldots, x_{n}(t-\tau_{n}(t))); \tau_{i}(t): R^{+}\rightarrow [0,\tau]\) is uncertain time-varying delay. For \(t \in [-\tau, 0]\), \(\bar{x}_{n}(t)=\phi(t)\), where the initial function, ϕ(t), is smooth and bounded. \(f_{i}(\cdot), g_{i}(\cdot):R^{i}\rightarrow R , \psi_{i}^{T}(\cdot):R^{i}\rightarrow R^{r}\) represent the unknown smooth nonlinear functions with f i (0) = 0, ψ T i (0) = 0, (1 ≤ i ≤ n). Moreover, \(u \in R\) denotes the input signal subject to symmetric saturation nonlinearity expressed as follows:

$$u(v(t)) = {\text{sat}}(v(t)) = \left\{ \begin{array}{lll} {\text{sign}}(v(t))u_{M}, & \hbox{ if }& |v(t)| \geq u_{M}\\ v(t), & \hbox{ if } & |v(t)|< u_{M} \end{array}\right.$$
(14)

where u M  > 0 is a known bound of u(t). Obviously, if v(t) = |u M |, then there exist two sharp corners. Thus, backstepping technique is invalid. To solve this problem, the saturation is approximated by a smooth function defined as

$$g(v) = u_{M} \times \tanh \left( {\frac{v}{{u_{M} }}} \right) = u_{M} \times \frac{{e^{{v/u_{M} }} - e^{{ - v/u_{M} }} }}{{e^{{v/u_{M} }} + e^{{ - v/u_{M} }} }}.$$

It follows that Eq. (14) becomes

$$u(v(t)) = {\text{sat}}(v(t)) = g(v) + d(v) = u_{M} \times \tanh \left( {\frac{v}{{u_{M} }}} \right) + d(v),$$
(15)

where d(v) = sat(v) − g(v) is a bounded function in time and its bound can be constrained by

$$d(v)=|{\text{sat}}(v)-g(v)| \leq u_{M}(1-\tanh(1))=D.$$
(16)

Applying the mean-value theorem and choosing v 0 = 0, it is easy to obtain that

$$g(v)=g(v_{0})+g_{v_{u}}(v-v_{0})=g_{v_{u}}v.$$
(17)

From (15)−(17), system (13) can be transformed as follows:

$$\left\{ {\begin{array}{l} {\text{d}}x_{i} = (g_{i} (\bar{x}_{i} )x_{{i + 1}} + f_{i} (\bar{x}_{i} ) + q_{i} (\bar{x}_{{n,\tau (t)}} )){\text{d}}t + \psi _{i}^{T} (\bar{x}_{i} ){\text{d}}w, \\ \quad 1 \le i \le n - 1, \\ {\text{d}}x_{n} = (g_{n} (\bar{x}_{n} )(g_{{v_{u} }} v + d(v)) + f_{n} (\bar{x}_{n} ) + q_{n} (\bar{x}_{{n,\tau (t)}} )){\text{d}}t + \psi _{n}^{T} (\bar{x}_{n} ){\text{d}}w, \\ y = x_{1} ,\bar{x}_{n} (t) = \phi (t), - \tau \le t \le 0. \\ \end{array} } \right.$$
(18)

The control objective is to design an adaptive neural controller for system (13) such that the error variables are semi-globally uniformly ultimately bounded in the sense of four-moment, while all the signals in the closed-loop system are bounded in probability.

To achieve the goal, the following assumptions are imposed on the system (18).

Assumption 1

The signs of \(g_{i}(\bar{x}_{i}), i=1, 2, \ldots, n\) are known. There exist unknown constants b m and b M such that \(g_{i}(\bar{x}_{i})\) satisfies

$$0 < b_{m} \leq |g_{i}(\bar{x}_{i})| \leq b_{M}<\infty, \quad\forall \bar{x}_{i}\in R^{i}, \quad i=1, 2, \ldots, n.$$
(19)

Remark 3

Assumption 1 exhibits that the function \(g_{i}(\bar{x}_{i})\) is either strictly positive or negative. Without loss of generality, it is further assumed that \(b_{m} \leq g_{i}(\bar{x}_{i}) \leq b_{M}.\) The constants b m and b M are not included in the design controller, so they can be unknown.

Assumption 2

([43]) For the function \(g_{{v_{u} }}\) there exists an unknown positive constant g m such that

$$0<g_{m}<g_{v_{u}}<1.$$
(20)

Remark 4

According to the Assumptions 1, 2, the following inequality holds:

$$0< b \leq g_{i}(\bar{x}_{i}), \quad i=1,2,\ldots, n-1, \quad 0< b \leq g_{n}g_{v_{u}},$$
(21)

with b = min{b m , b m g m } being an unknown constant.

Assumption 3

([35]) Suppose that \(Q_{ij}(\cdot)\) is a class-\(\mathcal{K}_{\infty}\) function, and the time-delay term \(q_{i}(\bar{x}_{n, \tau(t)})\) satisfies

$$|q_{i}(\bar{x}_{n, \tau(t)})| \leq \sum _{j=1}^{n} Q_{ij}(|x_{j}(t-\tau_{j}(t))|),\quad 1\leq i \leq n.$$
(22)

To develop the backstepping design scheme, we need make the following coordinate transformations:

$$z_{1}=x_{1}, \quad z_{i}=x_{i}-\alpha_{i-1}(Z_{i-1}), \quad i=2, 3, \ldots, n.$$
(23)

Based on the Razumikhin lemma, the intermediate control function α i (Z i ), the actual control law v and the adaptive law \(\hat{\theta}\) are obtained in the backstepping procedure. Define a constant

$$\theta = \max\left \{\frac{1}{b}\|W_{i}^{*}\|,i=1, 2, \ldots, n\right\},$$
(24)

where b is given in Remark 4. \(\|W_{i}^{*}\|\) will be specified later. Let \(\hat{\theta}\) denotes the estimation of the unknown constant θ. Moreover, \(\tilde{\theta}=\theta-\hat{\theta}\) is the parameter error.

The intermediate control function α i , the control law v and the adaption law \(\hat{\theta}\) for strict-feedback stochastic nonlinear time-delay system (13) will be constructed in the following forms:

$$\alpha_{i}(Z_{i})=-\left(k_{i}+\frac{3}{4}\right)z_{i}-\hat{\theta}\|S_{i}\|\tanh \left(\frac{z_{i}^{3}\|S_{i}\|}{\epsilon_{i}}\right), \quad i=1, 2, \ldots, n-1,$$
(25)
$$v(Z_{n})=-\left(k_{n}+\frac{3}{4\eta^{2}}\right)z_{n}-\hat{\theta}\|S_{n}\|\tanh\left(\frac{z_{n}^{3}\|S_{n}\|}{\epsilon_{n}}\right),$$
(26)
$$\dot{\hat{\theta}}=\sum_{i=1}^{n}\lambda z_{i}^{3}\|S_{i}\|\tanh\left(\frac{z_{i}^{3}\|S_{i}\|}{\epsilon_{i}}\right)-\gamma\hat{\theta},$$
(27)

where \(k_{i}, \epsilon_{i}, \lambda, \gamma, \eta\) are positive design parameters, \(Z_{1}=x_{1}\in\Upomega_{Z_{1}}\subset R^{1}\), \(Z_{i}=[\bar{x}^{T}_{i}, \hat{\theta}]\in\Upomega_{Z_{i}}\subset R^{i+1}, (i=2, 3,\ldots, n)\).

Before the backstepping design procedure, we give a useful lemma first, which will be used to deal with the time-delay term in the control design procedure.

Lemma 6

For the coordinate transformations (23), the following inequality holds:

$$|x_{i}| \leq \|\bar{x}_{i}\| \leq \phi(\|Z(t)\|)+\varrho,$$
(28)

where \(Z(t)=[z_{1}, z_{2}, \ldots, z_{n}, |\tilde{\theta}|^{1/2}]^{T}, \varrho\) is a constant; ϕ(s) = s(a 0 s + b 0) is an unknown class \(\mathcal{K}_{\infty}\) function with a 0 and b 0 being positive constants.

Proof

From Lemma 5 and the definition of α i in (25), it follows that

$$|\alpha _{j} | \le \left( {k_{j} + \frac{3}{4}} \right)|z_{j} | + s_{j} |\hat{\theta }|.$$
(29)

Substituting (29) into (23) gives

$$\begin{aligned} |x_{i}| \leq& \|\bar{x}_{i}\| \leq \|\bar{z}_{i}\|+\|\bar{\alpha}_{i-1}\| \leq \|Z(t)\|+\sum_{j=1}^{i-1}|\alpha_{j}|\\ \leq& \|Z(t)\|+\sum_{j=1}^{i-1}\left(\left(k_{j}+\frac{3}{4}\right)|z_{j}|+s_{j}|\hat{\theta}|\right)\\ \leq& \|Z(t)\|+\sum_{j=1}^{i-1}\left(\left(k_{j}+\frac{3}{4}\right)\|Z(t)\|+s_{j}(\|Z(t)\|^{2}+|\theta|)\right)\\ \leq& \|Z(t)\|+\sum_{j=1}^{n}\left(\left(k_{j}+\frac{3}{4}\right)\|Z(t)\|+s_{j}(\|Z(t)\|^{2}+|\theta|)\right)\\ \leq& \phi(\|Z(t)\|)+\varrho, \end{aligned}$$

where \(Z(t)=\left[z_{1}, z_{2}, \ldots, z_{n}, |\tilde{\theta}|^{1/2}\right]^{T}, \phi(s)=s(a_{0}s+b_{0}), a_{0}= \sum\nolimits_{j=1}^{n}s_{j}, b_{0}=\sum\nolimits_{j=1}^{n}\left(k_{j}+\frac{3}{4}\right)+1\), and \(\varrho=\sum\nolimits_{j=1}^{n}s_{j}|\theta|\).

3 Controller design and stability analysis

3.1 Controller design

The backstepping design procedure is given to construct adaptive neural controller in this section. In each step, RBF neural networks are employed to approximate the unknown continuous nonlinear functions, and an intermediate control function α i will be obtained to stabilize subsystem, while the actual control law v will be designed in the final step. For the sake of simplicity, sometimes function S i (Z i ) is denoted by S i ; f i stands for f i (x i ); g i represents g i (x i ); ψ i denotes ψ i (x i ).

Step 1: Let z 1 = x 1. Then we have

$${\text{d}}z_{1} = \left( {g_{1} x_{2} + f_{1} + q_{1} \left( {\bar{x}_{{n,\tau (t)}} } \right)} \right){\text{d}}t + \psi _{1}^{T} (x_{1} ){\text{d}}w.$$
(30)

Consider a Lyapunov function V 1 as

$$V_{1} = \frac{1}{4}z_{1}^{4}+\frac{1}{2\lambda}b\tilde{\theta}^{2}.$$

From (2), the infinitesimal generator of V 1 satisfies

$${\mathcal{L}}V_{1} = z_{1}^{3}\left(g_{1}x_{2}+f_{1}+q_{1}(\bar{x}_{n,\tau(t)})\right)+\frac{3}{2}z_{1}^{2}\psi_{1}^{T}\psi_{1}-\frac{b}{\lambda}\tilde{\theta}\dot{\hat{\theta}}.$$
(31)

By using Young’s inequality, it follows that

$$\frac{3}{2}z_{1}^{2}\psi_{1}^{T}\psi_{1}=\frac{3}{2}z_{1}^{2}\|\psi_{1}\|^{2}\leq\frac{9}{4\eta_{1}^{2}}z_{1}^{4}\|\psi_{1}\|^{4}+\frac{1}{4}\eta_{1}^{2}.$$
(32)

For the time-delay term \(q_{1}(\bar{x}_{n,\tau(t)}),\) by using Assumption 3 and Lemma 6, we can obtain the following inequality

$$\begin{aligned} z_{1}^{3}q_{1}\left(\bar{x}_{n,\tau(t)}\right)\leq& |z_{1}^{3}|\sum_{j=1}^{n}Q_{1j}\left(x_{j}(t-\tau_{j}(t))\right)\\ \leq& |z_{1}^{3}|\sum_{j=1}^{n}Q_{1j}\left(\phi\|Z(t-\tau_{j}(t))\|+\varrho\right)\\ \leq& |z_{1}^{3}|\sum_{j=1}^{n}\left(\bar{Q}_{1j}(\|Z(t-\tau_{j}(t))\|)+Q_{1j}(2\varrho)\right), \end{aligned}$$

where \(\bar{Q}_{1j}(s)=Q_{1j}(2\phi(s))\). \(\bar{Q}_{1j}(s)\) is still a class \(\mathcal{K}_{\infty}\) function, and it can be rewritten as \(\bar{Q}_{1j}(s)=s\phi_{1j}(s)\) with ϕ 1j (s) being a continuous function.

By combining \(\|Z\| \leq \|\bar{Z}_{1}\|+\sum\nolimits_{k=2}^{n}|z_{k}|\) with Lemma 3, it yields

$$\begin{aligned} z_{1}^{3}q_{1}(\bar{x}_{n,\tau(t)}) \leq& |z_{1}^{3}|\sum_{j=1}^{n}\left(\bar{Q}_{1j}(q\|Z(t)\|)+Q_{1j}(2\varrho)\right)\\ \leq& |z_{1}^{3}|\sum_{j=1}^{n}\left(\bar{Q}_{1j}(l_{1}\|\bar{Z}_{1}\|) +\sum_{k=2}^{n}\bar{Q}_{1j}(l_{1}|z_{k}|)+Q_{1j}(2\varrho)\right)\\ \leq& \sum_{j=1}^{n}\sum_{k=2}^{n}\frac{3}{4}l_{1}^{\frac{4}{3}}z_{1}^{4} +\sum_{j=1}^{n}\sum_{k=2}^{n}\frac{1}{4}z_{k}^{4}\phi_{1j}^{4}(l_{1}|z_{k}|) +z_{1}^{3}F_{1}\tanh\left(\frac{z_{1}^{3}F_{1}}{\sigma_{1}}\right)+\delta\sigma_{1}, \end{aligned}$$
(33)

where l 1 = qn, and \(F_{1}=\sum\nolimits_{j=1}^{n}(\bar{Q}_{1j}(l_{1}\|\bar{Z}_{1}\|)+Q_{1j}(2\varrho))\).

Substituting inequalities (32) and (33) into (31), we have

$${\mathcal{L}}V_{1} \leq z_{1}^{3}(g_{1}x_{2}+\bar{f}_{1})-\frac{3}{4}z_{1}^{4}+\delta\sigma_{1}+\frac{1}{4}\eta_{1}^{2}+\sum_{j=1}^{n}\sum_{k=2}^{n}\frac{1}{4}z_{k}^{4}\phi_{1j}^{4}(l_{1}|z_{k}|)-\frac{b}{\lambda}\tilde{\theta}\dot{\hat{\theta}},$$
(34)

where \(\bar{f}_{1}=f_{1}+\sum\nolimits_{j=1}^{n}\sum\nolimits_{k=2}^{n}\frac{3}{4}l_{1}^{\frac{4}{3}}z_{1}+\frac{9}{4\eta_{1}^{2}}\|\psi_{1}\|^{4}+F_{1}\tanh\left(\frac{z_{1}^{3}F_{1}}{\sigma_{1}}\right)+\frac{3}{4}z_{1}\). Obviously, \(\bar{f}_{1}\) is an unknown nonlinear function as it contains unknown functions f 1, ψ 1, which cannot be implemented in practice. Hence, there exist a neural network \(W_{1}^{*^{T}}S_{1}(Z_{1}), Z_{1}=x_{1}\in \Upomega_{Z_{1}}\subset R^{1}\) such that

$$\bar{f}_{1} = W_{1}^{*^{T}}S_{1}(Z_{1})+\delta_{1}(Z_{1}), \quad |\delta_{1}(Z_{1})|\leq \varepsilon_{1},$$
(35)

where δ1(Z 1) denotes the approximation error and \(\varepsilon_{1}\) is a positive constant.

Based on Lemma 3 and the definition of θ, we have

$$\begin{aligned} z_{1}^{3}\bar{f}_{1} = & z_{1}^{3} W_{1}^{*^{T}}S_{1}(Z_{1})+z_{1}^{3}\delta_{1}(Z_{1})\leq |z_{1}^{3}|\|W_{1}^{*}\|\|S_{1}(Z_{1})\|+\frac{3}{4}z_{1}^{4}+\frac{1}{4}\varepsilon_{1}^{4}\\ \leq& b\theta z_{1}^{3}\|S_{1}\|\tanh\left(\frac{z_{1}^{3}\|S_{1}\|}{\epsilon_{1}}\right)+b\theta \delta \epsilon_{1}+\frac{3}{4}z_{1}^{4}+\frac{1}{4}\varepsilon_{1}^{4}. \end{aligned}$$
(36)

By combining inequalities (34) with (36), it implies that the following inequality holds

$${\mathcal{L}}V_{1} \leq z_{1}^{3}g_{1}x_{2}+b\theta z_{1}^{3}\|S_{1}\|\tanh\left(\frac{z_{1}^{3}\|S_{1}\|}{\epsilon_{1}}\right)+\delta(\sigma_{1}+b\theta\epsilon_{1})+\frac{1}{4}\left(\varepsilon_{1}^{4}+\eta_{1}^{2}\right)+\sum_{j=1}^{n}\sum_{k=2}^{n}\frac{1}{4}z_{k}^{4}\phi_{1j}^{4}(l_{1}|z_{k}|)-\frac{b}{\lambda}\tilde{\theta}\dot{\hat{\theta}}.$$
(37)

Adding and subtracting α 1 in (37) and by z 2 = x 2 − α 1, we get

$$\begin{aligned} {\mathcal{L}}V_{1} \leq& z_{1}^{3}g_{1}z_{2}+z_{1}^{3}g_{1}\alpha_{1}+b\hat{\theta}z_{1}^{3}\|S_{1}\|\tanh\left(\frac{z_{1}^{3}\|S_{1}\|}{\epsilon_{1}}\right)+\delta(\sigma_{1}+b\theta\epsilon_{1})+\frac{1}{4}(\varepsilon_{1}^{4}+\eta_{1}^{2})\\ &+\sum_{j=1}^{n}\sum_{k=2}^{n}\frac{1}{4}z_{k}^{4}\phi_{1j}^{4}(l_{1}|z_{k}|)+\frac{b}{\lambda}\tilde{\theta}(\lambda z_{1}^{3}\|S_{1}\|\tanh\left(\frac{z_{1}^{3}\|S_{1}\|}{\epsilon_{1}}\right)-\dot{\hat{\theta}}). \end{aligned}$$
(38)

Letting the intermediate control function in (25) with i = 1 and applying Young’s inequality gives

$$z_{1}^{3}g_{1}\alpha_{1} \leq -k_{1}bz_{1}^{4}-\frac{3}{4}g_{1}z_{1}^{4}-b\hat{\theta}z_{1}^{3}\|S_{1}\|\tanh\left(\frac{z_{1}^{3}\|S_{1}\|}{\epsilon_{1}}\right),$$
(39)
$$z_{1}^{3}g_{1}z_{2}\leq \frac{3}{4}g_{1}z_{1}^{4}+\frac{1}{4}g_{1}z_{2}^{4}.$$
(40)

By using inequalities (39) and (40), it follows that

$$\begin{aligned} {\mathcal{L}}V_{1} \leq& -k_{1}bz_{1}^{4}+\frac{b}{\lambda}{\tilde{\theta}}\left({\lambda} z_{1}^{3}\|S_{1}\|\tanh\left(\frac{z_{1}^{3}\|S_{1}\|}{\epsilon_{1}}\right)-\dot{\hat{\theta}}\right)+\delta(\sigma_{1}+b\theta\epsilon_{1})+\frac{1}{4}(\varepsilon_{1}^{4}+\eta_{1}^{2})\\ &\quad+\sum_{j=1}^{n}\sum_{k=2}^{n}\frac{1}{4}z_{k}^{4}\phi_{1j}^{4}(l_{1}|z_{k}|)+\frac{1}{4}g_{1}z_{2}^{4}\\ \leq& -c_{1}z_{1}^{4}+\frac{b}{\lambda}{\tilde{\theta}}\left({\lambda} z_{1}^{3}\|S_{1}\|\tanh\left(\frac{z_{1}^{3}\|S_{1}\|}{\epsilon_{1}}\right)-\dot{\hat{\theta}}\right)+\sum_{j=1}^{n}\sum_{k=2}^{n}\frac{1}{4}z_{k}^{4}\phi_{1j}^{4}(l_{1}|z_{k}|)+\rho_{1}+\frac{1}{4}b_{M}z_{2}^{4}, \end{aligned}$$
(41)

where \(c_{1}=k_{1}b>0, \rho_{1}=\delta(\sigma_{1}+b\theta\epsilon_{1})+\frac{1}{4}(\varepsilon_{1}^{4}+\eta_{1}^{2})\). The last term in (41) will be dealt in the next step.

Step i (2 ≤ i ≤ n − 1): Let z i  = x i  − α i−1. The error dynamic system can be written as

$$dz_{i} = \left(g_{i}x_{i+1}+f_{i}+q_{i}(\bar{x}_{n,\tau(t)})-{\mathcal{L}}\alpha_{i-1}\right){\text{d}}t +\left(\psi_{i}-\sum_{j=1}^{i-1}\frac{\partial\alpha_{i-1}}{\partial x_{j}}\psi_{j}\right)^{T}{\text{d}}w,$$
(42)

where

$${\mathcal{L}}\alpha_{i-1} = \sum_{m=1}^{i-1}\frac{\partial\alpha_{i-1}}{\partial x_{m}}\left(g_{m}x_{m+1}+f_{m}+q_{m}(\bar{x}_{n,\tau(t)})\right)+\frac{\partial\alpha_{i-1}} {\partial\hat{\theta}}\dot{\hat{\theta}}+\frac{1}{2}\sum_{p,q=1}^{i-1} \frac{\partial^{2}\alpha_{i-1}}{\partial x_{p}\partial x_{q}}\psi_{p}^{T}\psi_{q}.$$
(43)

Choosing the following Lyapunov candidate V i as

$$V_{i} = V_{i-1}+\frac{1}{4}z_{i}^{4}.$$
(44)

According to (42)–(44) and (2), we have

$${\mathcal{L}}V_{i} = {\mathcal{L}}V_{i-1}+z_{i}^{3}\left(g_{i}x_{i+1}+f_{i}+q_{i}(\bar{x}_{n,\tau(t)}) -{\mathcal{L}}\alpha_{i-1}\right)+\frac{3}{2}z_{i}^{2}\left(\psi_{i}-\sum_{j=1}^{i-1} \frac{\partial\alpha_{i-1}}{\partial x_{j}}\psi_{j}\right)^{T}\left(\psi_{i}-\sum_{j=1}^{i-1}\frac{\partial\alpha_{i-1}}{\partial x_{j}}\psi_{j}\right).$$
(45)

Via repeatedly deduction as Step 1, it obtains that

$$\begin{aligned} {\mathcal{L}}V_{i-1}\leq& -\sum_{j=1}^{i-1}c_{j}z_{j}^{4}+\frac{b}{\lambda}\tilde{\theta}\left(\sum_{j=1}^{i-1}\lambda z_{j}^{3}\|S_{j}\|\tanh\left(\frac{z_{j}^{3}\|S_{j}\|}{\epsilon_{j}}\right)-\dot{\hat{\theta}}\right) +\sum_{j=1}^{i-1}\rho_{j}+\sum_{j=2}^{i-1}\left(z_{j}^{3}\varphi_{j}(Z_{j})-z_{j}^{3} \frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\dot{\hat{\theta}}-\delta\kappa_{j} \right)\\ &+\frac{1}{4}b_{M}z_{i}^{4}+\sum_{s=1}^{i-1}\sum_{m=1}^{s}\sum_{j=1}^{n} \sum_{k=i}^{n}\frac{1}{4}z_{k}^{4}\phi_{mj}^{4}(l_{s}|z_{k}|), \end{aligned}$$
(46)

where \(c_{j}=k_{j}b > 0,\,(j=1,2,\ldots,i-1)\), and \(\rho _{1} = \delta (\sigma _{1} + b\theta \smallint _{1} ) + \frac{1}{4}\left( {\varepsilon _{1}^{4} + \eta _{1}^{2} } \right),\rho _{j} = \delta \left( {\sigma _{j} + \kappa _{j} + b\theta \smallint _{j} } \right) + \frac{1}{4}\left( {\varepsilon _{j}^{4} + \eta _{j}^{2} } \right),j = 2,3, \ldots ,i - 1\).

From Young’s inequality, the rightmost term in (45) gets

$$\frac{3}{2}z_{i}^{2}\|\psi_{i}-\sum_{j=1}^{i-1}\frac{\partial\alpha_{i-1}}{\partial x_{j}}\psi_{j}\|^{2} \leq \frac{9}{4\eta_{i}^{2}}z_{i}^{4}\|\psi_{i}-\sum_{j=1}^{i-1}\frac{\partial\alpha_{i-1}}{\partial x_{j}}\psi_{j}\|^{4}+\frac{1}{4}\eta_{i}^{2}.$$
(47)

By using the Razumikhin Lemma, Young’s inequality and Lemma 3 to deal with the time-delay term in (45), the following inequalities hold

$$z_{i}^{3}q_{i}(\bar{x}_{n,\tau(t)}) \leq \sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{3}{4}l_{i}^{\frac{4}{3}}z_{i}^{4}+\sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{1}{4}z_{k}^{4}\phi_{ij}^{4}(l_{i}|z_{k}|)+|z_{i}^{3}|\sum_{j=1}^{n}(\bar{Q}_{ij}(l_{i}\|\bar{Z}_{i}\|)+Q_{ij}(2\varrho)),$$
(48)
$$\begin{aligned} -z_{i}^{3}\sum_{m=1}^{i-1}\frac{\partial\alpha_{i-1}}{\partial x_{m}}q_{m}(\bar{x}_{n,\tau(t)})\leq&\sum_{m=1}^{i-1}\sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{3}{4}l_{i}^{\frac{4}{3}}\left|\frac{\partial\alpha_{i-1}}{\partial x_{m}}\right|^{\frac{4}{3}}z_{i}^{4}+\sum_{m=1}^{i-1}\sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{1}{4}z_{k}^{4}\phi_{mj}^{4}(l_{i}|z_{k}|)\\ &+\sum_{m=1}^{i-1}\sum_{j=1}^{n}|z_{i}^{3}|\left|\frac{\partial\alpha_{i-1}}{\partial x_{m}}\right|(\bar{Q}_{mj}(l_{i}\|\bar{Z}_{i}\|)+Q_{mj}(2\varrho)), \end{aligned}$$
(49)

where \(\bar{Z}_{i}=[z_{1},z_{2},\ldots,z_{i},|\tilde{\theta}|^{1/2}]^{T}, l_{i} = q((n-i)+1),\) and \(\bar{Q}_{ij}(s)=s\phi_{ij}(s)\).

On the basis of (48) and (49), we have

$$\begin{aligned} z_{i}^{3}q_{i}(\bar{x}_{n,\tau(t)})-z_{i}^{3}\sum_{m=1}^{i-1}\frac{\partial\alpha_{i-1}}{\partial x_{m}}q_{m}(\bar{x}_{n,\tau(t)}) \leq & \sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{3}{4}l_{i}^{\frac{4}{3}}z_{i}^{4}+\sum_{m=1}^{i-1}\sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{3}{4}l_{i}^{\frac{4}{3}}\left|\frac{\partial\alpha_{i-1}}{\partial x_{m}}\right|^{\frac{4}{3}}z_{i}^{4}+\sum_{m=1}^{i}\sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{1}{4}z_{k}^{4}\phi_{mj}^{4}(l_{i}|z_{k}|)+|z_{i}^{3}|F_{i}\\ \leq & \sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{3}{4}l_{i}^{\frac{4}{3}}z_{i}^{4}+\sum_{m=1}^{i-1}\sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{3}{4}l_{i}^{\frac{4}{3}}\left|\frac{\partial\alpha_{i-1}}{\partial x_{m}}\right|^{\frac{4}{3}}z_{i}^{4}+\sum_{m=1}^{i}\sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{1}{4}z_{k}^{4}\phi_{mj}^{4}(l_{i}|z_{k}|)\\ &+z_{i}^{3}F_{i}\tanh\left(\frac{z_{i}^{3}F_{i}}{\sigma_{i}}\right)+\delta\sigma_{i}, \end{aligned}$$
(50)

where \(F_{i} =\sum\nolimits_{j=1}^{n}(\bar{Q}_{ij}(l_{i}\|\bar{Z}_{i}\|)+Q_{ij}(2\varrho))+\sum\limits_{m=1}^{i-1}\sum\limits_{j=1}^{n}\left|\frac{\partial\alpha_{i-1}}{\partial x_{m}}\right|(\bar{Q}_{mj}(l_{i}\|\bar{Z}_{i}\|)+Q_{mj}(2\varrho))\).

Substituting (46), (47) and (50) into (45), it follows that

$$\begin{aligned} {\mathcal{L}}V_{i} \leq&-\sum_{j=1}^{i-1}c_{j}z_{j}^{4}+\frac{b}{\lambda}\tilde{\theta}\left(\sum_{j=1}^{i-1}\lambda z_{j}^{3}\|S_{j}\|\tanh\left(\frac{z_{j}^{3}\|S_{j}\|}{\epsilon_{j}}\right)-\dot{\hat{\theta}}\right) +\sum_{j=1}^{i-1}\rho_{j}+\sum_{j=2}^{i}\left(z_{j}^{3}\varphi_{j}(Z_{j})-z_{j}^{3} \frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\dot{\hat{\theta}}-\delta\kappa_{j}\right)\\ &+\sum_{s=1}^{i}\sum_{m=1}^{s}\sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{1}{4}z_{k}^{4} \phi_{mj}^{4}(l_{s}|z_{k}|)+z_{i}^{3}\left(g_{i}x_{i+1}+\bar{f}_{i}(Z_{i})\right) +\delta(\sigma_{i}+\kappa_{i})+\frac{1}{4}\eta_{i}^{2}-\frac{3}{4}z_{i}^{4}, \end{aligned}$$
(51)

where

$$\begin{aligned} \bar{f}_{i}(Z_{i}) = & f_{i}-\sum_{m=1}^{i-1}\frac{\partial\alpha_{i-1}}{\partial x_{m}}(g_{m}x_{m+1}+f_{m})-\frac{1}{2}\sum_{p,q=1}^{i-1}\frac{\partial^{2}\alpha_{i-1}}{\partial x_{p}\partial x_{q}}\psi_{p}^{T}\psi_{q}+\sum_{s=1}^{i-1}\sum_{m=1}^{s}\sum_{j=1}^{n}\frac{1}{4}z_{i}\phi_{mj}^{4}(l_{s}|z_{i}|)+\frac{1}{4}b_{M}z_{i}\\ &+\sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{3}{4}l_{i}^{\frac{4}{3}}z_{i}+\sum_{m=1}^{i-1}\sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{3}{4}l_{i}^{\frac{4}{3}}\left|\frac{\partial\alpha_{i-1}}{\partial x_{m}}\right|^{\frac{4}{3}}z_{i}+F_{i}\tanh\left(\frac{z_{i}^{3}F_{i}}{\sigma_{i}}\right)+\frac{9}{4\eta_{i}^{2}}z_{i}\left\|\psi_{i}-\sum_{j=1}^{i-1}\frac{\partial\alpha_{i-1}}{\partial x_{j}}\psi_{j}\right\|^{4} \\ &-\varphi_{i}(Z_{i})+\frac{3}{4}z_{i}. \end{aligned}$$

The function \(\varphi_{i}(Z_{i})\) will be specified later. Thus, \(\bar{f}_{i}(Z_{i})\) can be approximated by the neural network \(W_{i}^{*^{T}}S_{i}(Z_{i}), Z_{i}=[\bar{x}_{i}, \hat{\theta}]^{T}\in \Upomega_{Z_{i}}\subset R^{i+1}\) such that

$$\bar{f}_{i} = W_{i}^{*^{T}}S_{i}(Z_{i})+\delta_{i}(Z_{i}),\quad |\delta_{i}(Z_{i})|\leq \varepsilon_{i}.$$
(52)

It is easy to verify

$$\begin{aligned} z_{i}^{3}\bar{f}_{i} =& z_{i}^{3} W_{i}^{*^{T}}S_{i}(Z_{i})+z_{i}^{3}\delta_{i}(Z_{i}) \leq |z_{i}^{3}|\|W_{i}^{*}\|\|S_{i}(Z_{i})\|+\frac{3}{4}z_{i}^{4}+\frac{1}{4}\varepsilon_{i}^{4}\\ \leq & b\theta z_{i}^{3}\|S_{i}\|\tanh\left(\frac{z_{i}^{3}\|S_{i}\|}{\epsilon_{i}}\right)+b\theta \delta \epsilon_{i}+\frac{3}{4}z_{i}^{4}+\frac{1}{4}\varepsilon_{i}^{4}. \end{aligned}$$
(53)

Similar to the aforementioned steps, we have

$$\begin{aligned} {\mathcal{L}}V_{i} \leq& -\sum_{j=1}^{i-1}c_{j}z_{j}^{4}+\frac{b}{\lambda}\tilde{\theta}\left(\sum_{j=1}^{i}\lambda z_{j}^{3}\|S_{j}\|\tanh\left(\frac{z_{j}^{3}\|S_{j}\|}{\epsilon_{j}}\right)-\dot{\hat{\theta}}\right)+\sum_{j=1}^{i-1}\rho_{j}+\sum_{j=2}^{i} \left(z_{j}^{3}\varphi_{j}(Z_{j})-z_{j}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}} \dot{\hat{\theta}}-\delta\kappa_{j}\right)\\ &+\sum_{s=1}^{i}\sum_{m=1}^{s}\sum_{j=1}^{n}\sum_{k=i+1}^{n}\frac{1}{4}z_{k}^{4}\phi_{mj}^{4} (l_{s}|z_{k}|)+z_{i}^{3}g_{i}z_{i+1}+z_{i}^{3}g_{i}\alpha_{i} +b\hat{\theta}z_{i}^{3}\|S_{i}\|\tanh\left(\frac{z_{i}^{3}\|S_{i}\|}{\epsilon_{i}}\right)\\ &+\delta\left(\sigma_{i}+\kappa_{i}+b\theta\epsilon_{i}\right)+\frac{1}{4} (\eta_{i}^{2}+\varepsilon_{i}^{4}). \end{aligned}$$
(54)

From the intermediate control function α i in (25) and Young’s inequality results in

$$z_{i}^{3}g_{i}\alpha_{i} \leq -k_{i}bz_{i}^{4}-\frac{3}{4}g_{i}z_{i}^{4}-b\hat{\theta}z_{i}^{3}\|S_{i}\|\tanh\left(\frac{z_{i}^{3}\|S_{i}\|}{\epsilon_{i}}\right),$$
(55)
$$z_{i}^{3}g_{i}z_{i+1} \leq \frac{3}{4}g_{i}z_{i}^{4}+\frac{1}{4}g_{i}z_{i+1}^{4}.$$
(56)

Based on (55), (56) and (54), it follows that

$$\begin{aligned} {\mathcal{L}}V_{i} \leq& -\sum_{j=1}^{i}c_{j}z_{j}^{4}+\frac{b}{\lambda}\tilde{\theta}\left(\sum_{j=1}^{i}\lambda z_{j}^{3}\|S_{j}\|\tanh\left(\frac{z_{j}^{3}\|S_{j}\|}{\epsilon_{j}}\right)-\dot{\hat{\theta}}\right)+\sum_{j=1}^{i}\rho_{j}+\sum_{j=2}^{i} \left(z_{j}^{3}\varphi_{j}(Z_{j})-z_{j}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}} \dot{\hat{\theta}}-\delta\kappa_{j}\right)\\ &+\frac{1}{4}b_{M}z_{i+1}^{4}+\sum_{s=1}^{i}\sum_{m=1}^{s}\sum_{j=1}^{n}\sum_{k=i}^{n}\frac{1}{4}z_{k}^{4}\phi_{mj}^{4} (l_{s}|z_{k}|), \end{aligned}$$
(57)

where \(c_{j}=k_{j}b > 0,\, j=1,2,\ldots,n-1, \rho_{1}=\delta(\sigma_{1}+b\theta\epsilon_{1})+\frac{1}{4}(\varepsilon_{1}^{4}+\eta_{1}^{2})\), and \(\rho_{j}=\delta(\sigma_{j}+\kappa_{j}+b\theta\epsilon_{j})+\frac{1}{4}(\varepsilon_{j}^{4}+\eta_{j}^{2}), j=2, 3,\ldots,n-1\).

Step n This is the final step. The actual controller v will be developed. From z n  = x n  − α n−1, we have

$$dz_{n} =(g_{n}(g_{v_{u}}v+d(v)) +f_{n}+q_{n}(\bar{x}_{n, \tau(t)})-{\mathcal{L}}\alpha_{n-1}){\text{d}}t +\left(\psi_{n}-\sum_{j=1}^{n-1}\frac{\partial\alpha_{n-1}}{\partial x_{j}}\psi_{j}\right)^{T}{\text{d}}w.$$
(58)

Consider the stochastic Lyapunov function V n as

$$V_{n} = V_{n-1}+\frac{1}{4}z_{n}^{4}.$$
(59)

From the Definition 1, it yields

$$\begin{aligned} {\mathcal{L}}V_{n} =& {\mathcal{L}}V_{n-1}+z_{n}^{3}\left(g_{n}(g_{v_{u}}v+d(v))+f_{n}+q_{n}(\bar{x}_{n,\tau(t)})-{\mathcal{L}}\alpha_{n-1}\right)\\ &+\frac{3}{2}z_{n}^{2}\left(\psi_{n}-\sum_{j=1}^{n-1}\frac{\partial\alpha_{n-1}}{\partial x_{j}}\psi_{j}\right)^{T}\left(\psi_{n}-\sum_{j=1}^{n-1}\frac{\partial\alpha_{n-1}}{\partial x_{j}}\psi_{j}\right), \end{aligned}$$
(60)

where \(\mathcal{L}\alpha_{n-1}\) is given in (43) with i = n, and \(\mathcal{L}V_{n-1}\) denotes (57) with i = n − 1.

For the last term in (60), applying Young’s inequality leads to

$$\frac{3}{2}z_{n}^{2}\left\|\psi_{n}-\sum_{j=1}^{n-1}\frac{\partial\alpha_{n-1}}{\partial x_{j}}\psi_{j}\right\|^{2}\leq\frac{9}{4\eta_{n}^{2}}z_{n}^{4}\left\|\psi_{n}-\sum_{j=1}^{n-1}\frac{\partial\alpha_{n-1}}{\partial x_{j}}\psi_{j}\right\|^{4}+\frac{1}{4}\eta_{n}^{2}.$$
(61)

Based on the similar method to deal with the time-delay terms in (60), the following inequality can be obtained

$$\begin{aligned} z_{n}^{3}q_{n}(\bar{x}_{n,\tau(t)})-z_{n}^{3}\sum_{m=1}^{n-1}\frac{\partial\alpha_{n-1}}{\partial x_{m}}q_{m}(\bar{x}_{n,\tau(t)}) \leq &z_{n}^{3}\left(\sum_{j=1}^{n}(\bar{Q}_{nj}(l_{n}\|\bar{Z}_{n}\|)+Q_{nj}(2\varrho))+\sum_{m=1}^{n-1}\sum_{j=1}^{n}|\frac{\partial\alpha_{n-1}}{\partial x_{m}}|(\bar{Q}_{mj}(l_{n}\|\bar{Z}_{n}\|)+Q_{mj}(2\varrho))\right)\\ \leq &z_{n}^{3}F_{n}\tanh\left(\frac{z_{n}^{3}F_{n}}{\sigma_{n}}\right)+\delta\sigma_{n}, \end{aligned}$$
(62)

where \(F_{n} = \sum\nolimits_{j=1}^{n}(\bar{Q}_{nj}(l_{n}\|\bar{Z}_{n}\|)+Q_{nj}(2\varrho))+\sum\nolimits_{m=1}^{n-1}\sum\nolimits_{j=1}^{n}|\frac{\partial\alpha_{n-1}}{\partial x_{m}}|(\bar{Q}_{mj}(l_{n}\|\bar{Z}_{n}\|)+Q_{mj}(2\varrho))\).

Substituting (61) and (62) into (60) gives

$$\begin{aligned} {\mathcal{L}}V_{n} \leq &-\sum_{j=1}^{n-1}c_{j}z_{j}^{4}+\frac{b}{\lambda}\tilde{\theta}\left(\sum_{j=1}^{n-1}\lambda z_{j}^{3}\|S_{j}\|\tanh\left(\frac{z_{j}^{3}\|S_{j}\|}{\epsilon_{j}}\right)-\dot{\hat{\theta}}\right)+\sum_{j=1}^{n-1}\rho_{j}+\sum_{j=2}^{n} \left(z_{j}^{3}\varphi_{j}(Z_{j})-z_{j}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\dot{\hat{\theta}}-\delta\kappa_{j}\right)\\ &+z_{n}^{3}(g_{n}(g_{v_{u}}v+d(v))+\bar{f}_{n}(Z_{n}))+\delta(\sigma_{n}+\kappa_{n})+\frac{1}{4}\eta_{n}^{2}-\frac{3}{4}z_{n}^{4}, \end{aligned}$$
(63)

where

$$\begin{aligned} \bar{f}_{n}(Z_{n})=&f_{n}-\sum_{m=1}^{n-1}\frac{\partial\alpha_{n-1}}{\partial x_{m}}(g_{m}x_{m+1}+f_{m})-\frac{1}{2}\sum_{p,q=1}^{n-1}\frac{\partial^{2}\alpha_{n-1}}{\partial x_{p}\partial x_{q}}\psi_{p}^{T}\psi_{q}+\sum_{s=1}^{n-1}\sum_{m=1}^{s}\sum_{j=1}^{n}\frac{1}{4}z_{n}\phi_{mj}^{4} (l_{s}|z_{n}|)\\ &+\frac{1}{4}b_{M}z_{n}+F_{n}\tanh\left(\frac{z_{n}^{3}F_{n}}{\sigma_{n}}\right)+\frac{9}{4\eta_{n}^{2}}z_{n}\|\psi_{n}-\sum_{j=1}^{n-1}\frac{\partial\alpha_{i-1}}{\partial x_{j}}\psi_{j}\|^{4}-\varphi_{n}(Z_{n})+\frac{3}{4}z_{n}. \end{aligned}$$

Hence, there exist a neural network \(W_{n}^{*^{T}}S_{n}(Z_{n}), Z_{n}=[\bar{x}_{n}, \hat{\theta}]^{T}\in \Upomega_{Z_{n}}\subset R^{n+1}\) such that

$$\begin{aligned} z_{n}^{3}\bar{f}_{n} \leq & |z_{n}^{3}|\|W_{n}^{*}\|\|S_{n}(Z_{n})\|+\frac{3}{4}z_{n}^{4}+\frac{1}{4}\varepsilon_{n}^{4}\\ \leq & b\theta z_{n}^{3}\|S_{n}\|\tanh\left(\frac{z_{n}^{3}\|S_{n}\|}{\epsilon_{n}}\right)+b\theta \delta \epsilon_{n}+\frac{3}{4}z_{n}^{4}+\frac{1}{4}\varepsilon_{n}^{4}. \end{aligned}$$
(64)

On the basis of (63), (64), we have

$$\begin{aligned} {\mathcal{L}}V_{n} \leq& -\sum_{j=1}^{n-1}c_{j}z_{j}^{4}+\frac{b}{\lambda}\tilde{\theta}\left(\sum_{j=1}^{n}\lambda z_{j}^{3}\|S_{j}\|\tanh\left(\frac{z_{j}^{3}\|S_{j}\|}{\epsilon_{j}}\right)-\dot{\hat{\theta}}\right)+\sum_{j=1}^{n-1}\rho_{j}+\sum_{j=2}^{n} \left(z_{j}^{3}\varphi_{j}(Z_{j})-z_{j}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\dot{\hat{\theta}}-\delta\kappa_{j}\right)\\ &+z_{n}^{3}g_{n}(g_{v_{u}}v+d(v))+b\hat{\theta}z_{n}^{3}\|S_{n}\|\tanh\left(\frac{z_{n}^{3}\|S_{n}\|}{\epsilon_{n}}\right) +\delta(\sigma_{n}+\kappa_{n}+b\theta\epsilon_{n})+\frac{1}{4}(\eta_{n}^{2}+\varepsilon_{n}^{4}). \end{aligned}$$
(65)

Based on the inequality (16) and the actual control input v in (26), the following inequalities hold

$$z_{n}^{3}g_{n}g_{v_{u}}v \leq -k_{n}bz_{n}^{4}-\frac{3}{4\eta^{2}}g_{n}g_{m}z_{n}^{4}-b\hat{\theta}z_{n}^{3}\|S_{n}\|\tanh\left(\frac{z_{n}^{3}\|S_{n}\|}{\epsilon_{n}}\right),$$
(66)
$$z_{n}^{3}g_{n}d_{v} \leq \frac{3}{4\eta^{2}}g_{n}g_{m}z_{n}^{4}+\frac{1}{4g_{m}}\eta^{2}b_{M}D^{4}.$$
(67)

In view of inequalities (66) and (67), we have

$$\begin{aligned} {\mathcal{L}}V_{n} \leq& -\sum_{j=1}^{n}c_{j}z_{j}^{4}+\frac{b}{\lambda}\tilde{\theta}\left(\sum_{j=1}^{n}\lambda z_{j}^{3}\|S_{j}\|\tanh\left(\frac{z_{j}^{3}\|S_{j}\|}{\epsilon_{j}}\right)-\dot{\hat{\theta}}\right)+\sum_{j=2}^{n} \left(z_{j}^{3}\varphi_{j}(Z_{j})-z_{j}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\dot{\hat{\theta}}-\delta\kappa_{j}\right)+\sum_{j=1}^{n-1}\rho_{j}\\ &+\delta(\sigma_{n}+\kappa_{n}+b\theta\epsilon_{n})+\frac{1}{4}(\eta_{n}^{2}+\varepsilon_{n}^{4})+\frac{1}{4g_{m}}\eta^{2}b_{M}D^{4}. \end{aligned}$$
(68)

Furthermore, choosing the adaptation law as described in (27)

$$\dot{\hat{\theta}}=\sum_{j=1}^{n}\lambda z_{j}^{3}\|S_{j}\|\tanh\left(\frac{z_{j}^{3}\|S_{j}\|}{\epsilon_{j}}\right)-\gamma\hat{\theta},$$
(69)

From Young’s inequality, the following inequality holds

$$\frac{b\gamma}{\lambda}\tilde{\theta}\hat{\theta}=\frac{b\gamma}{\lambda}\tilde{\theta}(\theta-\tilde{\theta}) \leq -\frac{b\gamma}{2\lambda}\tilde{\theta}^{2}+\frac{b\gamma}{2\lambda}\theta^{2}.$$
(70)

Then, with the help of (68) and (70), it follows that

$${\mathcal{L}}V_{n} \leq-\sum_{j=1}^{n}c_{j}z_{j}^{4}-\frac{b\gamma}{2\lambda}\tilde{\theta}^{2}+\sum_{j=1}^{n}\rho_{j}+\sum_{j=2}^{n} \left(z_{j}^{3}\varphi_{j}(Z_{j})-z_{j}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\dot{\hat{\theta}}-\delta\kappa_{j}\right),$$
(71)

where \(c_{j}=k_{j}b > 0,\,(j=1,2,\ldots,n), \rho_{1}=\delta(\sigma_{1}+b\theta\epsilon_{1})+\frac{1}{4}(\varepsilon_{1}^{4}+\eta_{1}^{2}), \rho_{j}=\delta(\sigma_{j}+\kappa_{j}+b\theta\epsilon_{j})+\frac{1}{4}(\varepsilon_{j}^{4}+\eta_{j}^{2}),\, (j=2, 3,\ldots,n-1)\), and \(\rho_{n}=\delta(\sigma_{n}+\kappa_{n}+b\theta\epsilon_{n})+\frac{1}{4}(\eta_{n}^{2}+\varepsilon_{n}^{4})+\frac{1}{4g_{m}}\eta^{2}b_{M}D^{4}+\frac{b\gamma}{2\lambda}\theta^{2}\).

3.2 Stability analysis

So far, based on Razumikhin Lemma and backstepping technique, the adaptive neural controller design has been completed. Now, the main result is summarized by the following theorem.

Theorem 1

Consider the stochastic nonlinear time-delay systems in (13) subject to input saturation (14) under Assumptions 1–3. For bounded initial conditions with \(\hat{\theta} \geq 0,\) the intermediate control function α i (25), the actual control law v (26), and the adaptive law \(\hat{\theta}\) (27) guarantee that the error variables are semi-globally uniformly ultimately bounded in the sense of four-moment while all the signals in the closed-loop system are bounded in probability.

Proof

Choosing the stochastic Lyapunov function as V = V n yields

$${\mathcal{L}}V \leq -\sum_{j=1}^{n}c_{j}z_{j}^{4}-\frac{b\gamma}{2\lambda}\tilde{\theta}^{2}+\sum_{j=1}^{n}\rho_{j}+\sum_{j=2}^{n} \left(z_{j}^{3}\varphi_{j}(Z_{j})-z_{j}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\dot{\hat{\theta}}-\delta\kappa_{j}\right).$$
(72)

From the definition of \(\hat{\theta}\), we have

$$\begin{aligned} -\sum_{j=2}^{n}z_{j}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\dot{\hat{\theta}} =&\sum_{j=2}^{n}z_{j}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\gamma\hat{\theta}-\sum_{j=2}^{n}z_{j}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\sum_{i=1}^{n}\lambda z_{i}^{3}\|S_{i}\|\tanh\left(\frac{z_{i}^{3}\|S_{i}\|}{\epsilon_{i}}\right)\\ =&\sum_{j=2}^{n}z_{j}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\gamma\hat{\theta}-\sum_{j=2}^{n}z_{j}^{3}\sum_{i=1}^{j-1}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\lambda z_{i}^{3}\|S_{i}\|\tanh\left(\frac{z_{i}^{3}\|S_{i}\|}{\epsilon_{i}}\right)\\ &-\sum_{j=2}^{n}z_{j}^{3}\sum_{i=j}^{n}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\lambda z_{i}^{3}\|S_{i}\|\tanh\left(\frac{z_{i}^{3}\|S_{i}\|}{\epsilon_{i}}\right). \end{aligned}$$
(73)

Applying Lemma 4 to the last term in (73) results in

$$\begin{aligned} -\sum_{j=2}^{n}z_{j}^{3}\sum_{i=j}^{n}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\lambda z_{i}^{3}\|S_{i}\|\tanh\left(\frac{z_{i}^{3}\|S_{i}\|}{\epsilon_{i}}\right) \leq& \sum_{j=2}^{n}|z_{j}^{3}|\sum_{i=j}^{n}|z_{i}^{3}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}|\lambda\|S_{i}\|\\ =& \sum_{j=2}^{n}\lambda|z_{j}^{3}|\|S_{j}\|\sum_{i=2}^{j}|z_{i}^{3}\frac{\partial\alpha_{i-1}}{\partial\hat{\theta}}|\\ \leq& \sum_{j=2}^{n} \left(z_{j}^{3}\Uptheta_{j}\tanh\left(\frac{z_{j}^{3}\Uptheta_{j}}{\kappa_{j}}\right)+\delta\kappa_{j}\right), \end{aligned}$$
(74)

where \(\Uptheta_{j}=\lambda s_{j}\sum\nolimits_{i=2}^{j}|z_{i}^{3}\frac{\partial\alpha_{i-1}}{\partial\hat{\theta}}|\), which means that

$$\varphi_{j}(Z_{j})=-\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\gamma\hat{\theta}+\sum_{i=1}^{j-1}\frac{\partial\alpha_{j-1}}{\partial\hat{\theta}}\lambda z_{i}^{3}\|S_{i}\|\tanh\left(\frac{z_{i}^{3}\|S_{i}\|}{\epsilon_{i}}\right)-\Uptheta_{j}\tanh\left(\frac{z_{j}^{3}\Uptheta_{j}}{\kappa_{j}}\right),\quad j=2, 3, \ldots, n.$$
(75)

Together (73), (74) with (75), it is easy to know that the rightmost term of (72) are negative. Clearly,

$$\begin{aligned} {\mathcal{L}}V \leq& -\sum_{j=1}^{n}c_{j}z_{j}^{4}-\frac{b\gamma}{2\lambda}\tilde{\theta}^{2}+\sum_{j=1}^{n}\rho_{j}\\ \leq& -\mu_{1}V+\mu_{2}, \end{aligned}$$
(76)

where \(\mu_{1}=\min\{4c_{j}, \gamma, j=1, 2, \ldots, n \}\) and \(\mu_{2}=\sum\nolimits_{j=1}^{n}\rho_{j}\).

Hence, from (76) and Razumikhin Lemma, it is easy to obtain that the error variables are semi-globally uniformly ultimately bounded in the sense of four-moment, and \(\tilde{\theta}\) is bounded in probability. Since θ is a constant, \(\hat{\theta}\) is bounded in probability. α i is a function of z i and \(\hat{\theta}\), so α i is also bounded in probability. Furthermore, all the signals in the closed-loop system are bounded in probability.

Remark 5

By appropriately choosing the design parameters \(k_{i}, \epsilon_{i}, \lambda, \gamma, \eta\), for example, first properly choosing the design parameters k i , γ, then choosing \(\epsilon_{i}, \eta\) sufficiently small and λ sufficiently large, all the signals in the closed-loop system converge to a small neighborhood of the origin.

4 Simulation examples

In this section, two simulation examples are used to illustrate the effectiveness of the proposed control approach in this paper.

Example 1

Consider the following second-order nonlinear time-delay system

$$\left\{\begin{array}{l} dx_{1} = ((1+x_{1}^{2})x_{2}+x_{1}e^{-0.5x_{1}}+2x_{1}^{2}(t-\tau_{1}(t))x_{2}(t-\tau_{2}(t))){\text{d}}t+x_{1}^{2}\cos(x_{1}){\text{d}}w,\\ dx_{2} = ((3+\sin(x_{1}x_{2}))u+x_{1}x_{2}^{2}+0.1x_{1}(t-\tau_{1}(t))x_{2}^{2}(t-\tau_{2}(t))){\text{d}}t+x_{2}^{2}\sin(x_{1}x_{2}){\text{d}}w,\\ \quad y = x_{1}, \end{array} \right.$$
(77)

where u M is chosen as u M  = 6. The nonlinear time-delay terms are defined as \(\tau_{1}(t)=1+5\sin(t)\), \(\tau_{2}(t)=1+3\cos(t)\). According to Theorem 1, the intermediate control function α 1 and the control law v are chosen, respectively, as

$$\alpha _{1} (Z_{1} ) = - \left( {k_{1} + \frac{3}{4}} \right)z_{1} - \hat{\theta }\left\| {S_{1} (Z_{1} )} \right\|\tanh \left( {\frac{{z_{1}^{3} {\text{ }}\left\| {S_{1} (Z_{1} )} \right\|}}{{ \epsilon _{1} }}} \right),$$
(78)
$$v (Z_{2}) = -(k_{2}+\frac{3}{4\eta^{2}})z_{2}-\hat{\theta}\|S_{2}(Z_{2})\|\tanh\left(\frac{z_{2}^{3}\|S_{2}(Z_{2})\|}{\epsilon_{2}}\right),$$
(79)

where \(z_{1}=x_{1}, z_{2}=x_{2}-\alpha_{1}, Z_{1}=z_{1} \in R^{1}, Z_{2}=[z_{1}, z_{2}, \hat{\theta}]\in R^{3}\). The adaptive law is given as

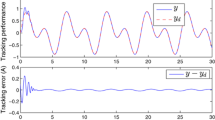
$$\dot{\hat{\theta}} = \sum_{i=1}^{2}\lambda z_{i}^{3}\|S_{i}(Z_{i})\|\tanh\left(\frac{z_{i}^{3}\|S_{i}(Z_{i})\|}{\epsilon_{i}}\right)-\gamma\hat{\theta}.$$
(80)

In the simulation, neural network \(W_{1}^{\ast^{T}}S_{1}(Z_{1})\) contains 7 nodes with centers spaced evenly in [−3, 3], neural network \(W_{2}^{\ast^{T}}S_{2}(Z_{2})\) includes 343 nodes with centers spaced evenly in [ −3, 3] × [ −3, 3] × [0, 3], and widths are equal to 1. The design parameters are chosen as \(k_{1}=15, k_{2}=5, \epsilon_{1}=\epsilon_{2}=2, \lambda=0.5, \gamma=1\) and η = 1. The simulation results are shown in Figs. 1, 2, 3 and 4 with the initial condition \(\phi(t)=[0.1,-0.2]^{T}, t\in[-\tau, 0], \hat{\theta}(0)=0\). Figure 1 gives the response of the state variable x 1 and x 2. Figure 2 illustrates the trajectory of adaptive law \(\hat{\theta}\). Figure 3 depicts the trajectory of saturation function output signal u. Figure 4 shows the control input signal v.

Fig. 1
figure 1

States of closed-loop system x i (t) (i = 1, 2)

Full size image
Fig. 2
figure 2

Adaptive law \(\hat{\theta}\)

Full size image
Fig. 3
figure 3

Saturation function output signal u

Full size image
Fig. 4
figure 4

Control input signal v

Full size image

Example 2

Consider three-order stochastic nonlinear time-delay system in the following form to further show the control capability of the proposed approach.

$$\left\{\begin{array}{l} dx_{1} = ((0.2+x_{1}^{2})x_{2}+x_{1}\sin(x_{1})+0.1x_{1}^{2}(t-\tau_{1}(t))\sin(x_{2}(t-\tau_{2}(t))x_{3}(t-\tau_{3}(t)))){\text{d}}t+x_{1}^{2}\cos(x_{1}){\text{d}}w,\\ dx_{2} = ((1+x_{1}^{2})x_{3}+x_{2}e^{-0.5x_{1}}+0.8x_{1}(t-\tau_{1}(t))x_{2}^{2}(t-\tau_{2}(t))x_{3}(t-\tau_{3}(t))){\text{d}}t+x_{1}x_{2}\cos(x_{2}){\text{d}}w,\\ dx_{3} =((2+\cos(x_{1}x_{2}))u+x_{1}x_{2}x_{3}+0.3x_{1}(t-\tau_{1}(t))x_{2}(t-\tau_{2}(t))x_{3}^{2}(t-\tau_{3}(t))){\text{d}}t+0.5x_{2}^{2}\sin(x_{3}){\text{d}}w,\\ \quad y = x_{1}, \end{array} \right.$$
(81)

where u M  = 6 is the upper bound of input saturation, \(\tau_{1}(t)=1+2\sin(t), \tau_{2}(t)=2+4\cos(t), \tau_{3}(t)=5+3\sin(t)\) are the nonlinear time-delay terms. The intermediate control function α i , the control law v, and the adaptive law \(\hat{\theta}\) are chosen as

$$\alpha_{i}(Z_{i})=-\left(k_{i}+\frac{3}{4}\right)z_{i}-\hat{\theta}\|S_{i}(Z_{i})\|\tanh\left(\frac{z_{i}^{3}\|S_{i}(Z_{i})\|}{\epsilon_{i}}\right),\quad i=1,2,$$
(82)
$$v(Z_{3})=-\left(k_{3}+\frac{3}{4\eta^{2}}\right)z_{3}-\hat{\theta}\|S_{3}(Z_{3})\|\tanh\left(\frac{z_{3}^{3}\|S_{3}(Z_{3})\|}{\epsilon_{3}}\right),$$
(83)
$$\dot{\hat{\theta}}=\sum_{i=1}^{3}\lambda z_{i}^{3}\|S_{i}(Z_{i})\|\tanh\left(\frac{z_{i}^{3}\|S_{i}(Z_{i})\|}{\epsilon_{i}}\right)-\gamma\hat{\theta},$$
(84)

where \(z_{1}=x_{1}, z_{2}=x_{2}-\alpha_{1}, z_{3}=x_{3}-\alpha_{2}, Z_{1}=z_{1}\in R^{1}, Z_{2}=[z_{1}, z_{2}, \hat{\theta}]\in R^{3}, Z_{3}=[z_{1}, z_{2}, z_{3}, \hat{\theta}]\in R^{4}\).

The design parameters are chosen as \(k_{1}=5, k_{2}=8, k_{3}=10, \epsilon_{1}=\epsilon_{2}=4, \epsilon_{3}=5, \lambda=2, \gamma=0.4\) and η = 2 in the simulation. The initial condition are chosen as \(\phi(t)=[0.1,-0.2,0.3]^{T}, t\in[-\tau, 0], \hat{\theta}(0)=0.4\), and neural networks are chosen as follows. Neural networks \(W_{1}^{\ast^{T}}S_{1}(Z_{1})\) and \(W_{2}^{\ast^{T}}S_{2}(Z_{2})\) are given as in Example 1, and \(W_{3}^{\ast^{T}}S_{3}(Z_{3})\) is chosen to contain 2401 nodes with centers spaced evenly in [ − 3, 3] × [ − 3, 3] × [ − 3, 3] × [0, 3], and widths are equal to 1. The simulation results are shown by Figures 5, 6, 7 and 8. Figure 5 exhibits the response of the state variable x 1, x 2 and x 3. The trajectory of adaptive law \(\hat{\theta}\) is given in Figure 6. Figure 7 depicts the trajectory of saturation function output signal u. The control input signal v is shown in Fig. 8.

Fig. 5
figure 5

States of closed-loop system x i (t) (i = 1, 2, 3)

Full size image
Fig. 6
figure 6

Adaptive law \(\hat{\theta}\)

Full size image
Fig. 7
figure 7

Saturation function output signal u

Full size image
Fig. 8
figure 8

Control input signal v

Full size image

5 Conclusions

In this paper, an adaptive neural control design scheme has been successfully proposed for a class of stochastic nonlinear systems with multiple time-varying delays and input saturation. In addition, the number of the online adaptive learning parameters is reduced to one, so the computation complexity can be significantly alleviated, which makes the developed results in this paper more applicable. It has been proved that the error variables are semi-globally uniformly ultimately bounded in the sense of four-moment, while all the signals in the closed-loop system are bounded in probability.