1 Introduction

Lassa fever is a deadly viral zoonotic illness instigated by Lassa virus. It is transmitted through direct contact especially between infected animals or humans and susceptible humans [14]. The disease is rampant during dry seasons due to excessive dust from dead hosts [7]. At present, there are no approved vaccines for Lassa fever [10]. However, several attempts have been made to develop reliable vaccines for Lassa virus [9, 17, 18, 29].

Lassa fever is endemic in West Africa and there have been frequent emergence and re-emergence of the disease in Mali, Sierra-Leone, Ghana, Liberia, Benin, Guinea and Nigeria [12]. Reliable data attributed about 5000 mortalities and 300,000 new infections to Lassa fever across West African countries each year [27]. The first case of Lassa fever was confirmed in the Nigerian town called Lassa in 1969 and the disease has been occurring from time to time in the country since then [6]. Within the first two months in 2020, the case fatality ratio of Lassa fever in Nigeria is about 41.9% with 72 mortalities from 172 confirmed cases [10].

The primary hosts of Lassa virus are rodents that belong to the genus Mastomys usually regarded as “multimammate rats” [8]. Mastomys rodents infected with the Lassa virus never become sick, but can spread the virus to other primates and man through their excreta [28].

Many scholars have contributed and dedicated much time to the study of Lassa fever and several models have been developed to study the transmission dynamics of Lassa fever theoretically [1, 5, 11, 13, 22,23,24,25]. Lassa fever can be attributed to many factors but existing studies have been motivated by factors like isolation, re-infection and latency [3, 15, 21, 28]. The spread of Lassa fever and effect of available intervention strategies have also been a subject of intense theoretical study [2, 4, 16, 19, 20, 26, 30].

When an infection is fully incubated, treatment becomes imperative. However, the rate of compliance to treatment guidelines might not be 100% due to many factors like ignorance and poverty especially in poor resource setting communities. Attentions have not been paid to these factors in the literature but can seriously affect the dynamics of Lassa fever. On this ground, a stage of infection when the disease has been fully incubated is considered and a new mathematical model is designed to examine the effect of treatment compliance on the dynamics and control of Lassa fever.

2 Model formulation

The compartments of the model are classified into seven namely susceptible humans \((S_h)\), infected humans \((I_h)\), non-treatment compliant humans \((NT_h)\), treatment compliant humans \((T_h)\), recovered humans \((R_h)\), susceptible rodents \((S_r)\) and infected rodents \((I_r)\). The model is formulated based on the following assumptions:

  1. 1.

    A poor resource setting community is considered and susceptible humans are not protected against infections.

  2. 2.

    When an infection is fully developed, treatment becomes inevitable therefore asymptomatic stage is neglected.

  3. 3.

    Individuals who are treatment compliant do follow treatment guidelines strictly. They do not interact with susceptible humans or rodents and do not spread the disease.

  4. 4.

    Non-treatment compliant individuals are negligent and do mix with the susceptible humans and rodents and do spread the disease.

  5. 5.

    Recovery is not permanent and there is tendency for reinfection.

  6. 6.

    Lassa fever deaths only occur for infectious humans \((I_h)\) while individuals under treatment \((T_h)\) and \((NT_h)\) do not die of Lassa fever infections.

  7. 7.

    Infectious humans \((I_h)\) and non-treatment compliant humans \((NT_h)\) do not spread infection to susceptible rodents.

Following these assumptions, the flow between the compartments is displayed in Fig. 1.

Fig. 1
figure 1

Transmission diagram of the model

Full size image

The definitions for the model parameters are presented in Table 1.

Table 1 Definitions for model parameters
Full size table

The transfer diagram in Fig. 1 is translated into the following system of nonlinear first-order ordinary differential equations

$$\begin{aligned} \dfrac{dS_h}{dt}&=\beta _h+\phi R_h -(\alpha _1I_h+\alpha _2I_r+\alpha _3NT_h)S_h-d_1S_h, \end{aligned}$$
(1)
$$\begin{aligned} \dfrac{dI_h}{dt}&=(\alpha _1I_h+\alpha _2I_r+\alpha _3NT_h)S_h-(1-\eta )\tau I_h-\eta \tau I_h-(d_1+\vartheta )I_h,\end{aligned}$$
(2)
$$\begin{aligned} \dfrac{dNT_h}{dt}&=(1-\eta )\tau I_h-\gamma _1 NT_h-d_1NT_h, \end{aligned}$$
(3)
$$\begin{aligned} \dfrac{dT_h}{dt}&=\eta \tau I_h-\gamma _2 T_h-d_1T_h, \end{aligned}$$
(4)
$$\begin{aligned} \dfrac{dR_h}{dt}&=\gamma _1 NT_h+\gamma _2 T_h-\phi R_h-d_1R_h, \end{aligned}$$
(5)
$$\begin{aligned} \dfrac{dS_r}{dt}&=\varphi _r-\epsilon S_rI_r-d_2S_r, \end{aligned}$$
(6)
$$\begin{aligned} \dfrac{dI_r}{dt}&=\epsilon S_rI_r-d_2I_r. \end{aligned}$$
(7)

The population of man and mastomys at time t is split to Eqs. (8) and (9) respectively

$$\begin{aligned} N_H&=S_h(t)+I_h(t)+NT_h(t)+R_h(t), \end{aligned}$$
(8)
$$\begin{aligned} N_R(t)&=S_r(t)+I_r(t), \end{aligned}$$
(9)

subject to initial conditions,

$$\begin{aligned} S_{0h}>0, I_{0h}\ge 0, NT_{0h}\ge 0, T_{0h}\ge 0, R_{0h}\ge 0, S_{0r}>q0, I_{0r}\ge 0. \end{aligned}$$
(10)

The growth for man and mastomys populations is described by

$$\begin{aligned} \dfrac{dN_H}{dt}t&=\beta _h-d_1N_H(t)-\vartheta I_h,\end{aligned}$$
(11)
$$\begin{aligned} \dfrac{dN_R}{dt}t&=\varphi _r-d_2N_R(t). \end{aligned}$$
(12)

The model must satisfy positivity and boundedness properties before it can be valid. Besides, it must be mathematically and biologically well-posed. Each of the properties shall be verified one after the other to establish the validity of the model.

2.1 Positivity of solutions

The solutions of the model must be positive since the model monitors human and animal populations. We shall show that the solutions of the system are positive for all \(t>0.\)

Theorem 1

Given the positive initial variables \(S_{0\,h}>0, I_{0\,h}>0, NT_{0\,h}>0, T_{0\,h}>0, R_{0\,h}>0, S_{0r}>0, I_{0r}>0,\) the solutions \((S_h,I_h,NT_h,T_h,R_h,S_r,I_r)\) of the system are positive for all \(t>0.\)

From Eqs. (11) and (12),

$$\begin{aligned}&\lim _{t\rightarrow \infty } Sup N_H(t)\le \dfrac{\beta _h}{d_1},\end{aligned}$$
(13)
$$\begin{aligned}&\lim _{t\rightarrow \infty } Sup N_R(t)\le \dfrac{\varphi _r}{d_2}. \end{aligned}$$
(14)

Proof

Assuming \(\nabla _L=Sup~~t>0:S_h(t)>0, I_h(t)>0, NT_h(t)>0, T_h(t)>0, R_h(t)>0, S_r(t)>0, I_r(t)>0\) then \(\nabla _L>0.\) Supposing also that \(\nabla _L>\infty \) then \(S_h,I_h,NT_h,T_h,R_h,S_r,I_r\) becomes zero at \(\nabla _L.\) Therefore, from Eq. (1), it follows that

$$\begin{aligned} \begin{aligned} \dfrac{d}{dt}S_h(t) exp[(\alpha _1I_h+\alpha _2I_r+\alpha _3NT_h+d_1)t]&= \int _0^{\nabla _L}(\beta _h+\phi R_h)exp[(\alpha _1I_h\\ {}&\quad +\alpha _2I_r+\alpha _3NT_h+d_1)p]dp. \end{aligned} \end{aligned}$$
(15)
$$\begin{aligned} \begin{aligned} \Longrightarrow ~~ S_h(\nabla _L)=&S_h(0) exp[-(\alpha _1I_h+\alpha _2I_r+\alpha _3NT_h+d_1)\nabla _L]\\&+exp[-(\alpha _1I_h+\alpha _2I_r+\alpha _3NT_h+d_1)\nabla _L]\\&\times \int _0^{\nabla _L}(\beta _h+\phi R_h)exp[(\alpha _1I_h+\alpha _2I_r+\alpha _3NT_h+d_1)p]dp>0. \end{aligned} \end{aligned}$$
(16)

By the same procedure, it can be shown that \(I_h>0,\) \(NT_h>0,\) \(T_h>0,\) \(R_h>0,\) \(S_r>0,\) \(I_r>0,\) \(\forall ~~t>0\). \(\square \)

2.2 Boundedness of solutions

Theorem 2

The solutions \((S_h,I_h,NT_h,T_h,R_h,S_r,I_r)\) of the model are bounded.

Proof

From Eq. (11)

$$\begin{aligned} \dfrac{d}{dt}N_H(t)=\beta _h-d_1N_H(t)-\vartheta I_h. \end{aligned}$$

With no infection,

$$\begin{aligned} \begin{aligned}&\dfrac{d}{dt}N_H(t)\le \beta _h-d_1N_H(t),\\&\dfrac{d}{dt}N_H(t)+d_1N_H(t)\le \beta _h \end{aligned} \end{aligned}$$
(17)

Integrating inequality (17),

$$\begin{aligned} \begin{aligned}&e^{d_1t}N_H(t)\le \int \beta _h e^{d_1t}dt+c_1,\\ \Longrightarrow ~~&e^{d_1t}N_H(t)\le \dfrac{\beta _h}{d_1}e^{d_1t}+c_1,\\&N_H(t)\le \dfrac{\beta _h}{d_1}+c_1e^{-d_1t}. \end{aligned} \end{aligned}$$

When \(t=0,\)

$$\begin{aligned} \begin{aligned}&c_1\ge N_H(0)-\dfrac{\beta _h}{d_1},\\ \therefore ~~&N_H(t)\le \dfrac{\beta _h}{d_1}+\left( N_H(0)-\dfrac{\beta _h}{d_1}\right) e^{-d_1t}. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} N_H(t)\le N_H(0)e^{-d_1t}+\dfrac{\beta _h}{d_1}(1-e^{-d_1t}). \end{aligned}$$
(18)

Also, from Eq. (12),

$$\begin{aligned} \dfrac{d}{dt}N_R(t)=\varphi _r-d_2N_R(t). \end{aligned}$$

With no infection,

$$\begin{aligned} \begin{aligned}&\dfrac{d}{dt}N_R(t)\le \varphi _r-d_2N_R(t),\\&\dfrac{d}{dt}N_R(t)+d_2N_R(t)\le \varphi _r \end{aligned} \end{aligned}$$
(19)

Integrating inequality (19),

$$\begin{aligned} \begin{aligned}&e^{d_2t}N_R(t)\le \int \varphi _r e^{d_2t}dt+c_2,\\ \Longrightarrow ~~&e^{d_2t}N_R(t)\le \dfrac{\varphi _r}{d_2}e^{d_2t}+c_2,\\&N_R(t)\le \dfrac{\varphi _r}{d_2}+c_2e^{-d_2t}. \end{aligned} \end{aligned}$$

When \(t=0,\)

$$\begin{aligned} \begin{aligned}&c_2\ge N_R(0)-\dfrac{\varphi _r}{d_2},\\ \therefore ~~&N_R(t)\le \dfrac{\varphi _r}{d_2}+\left( N_R(0)-\dfrac{\varphi _r}{d_2}\right) e^{-d_2t}. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} N_R(t)\le N_R(0)e^{-d_2t}+\dfrac{\varphi _r}{d_2}(1-e^{-d_2t}). \end{aligned}$$
(20)

Following Birkhoff and Rota’s theorem [31, 45, 46], Eqs. (18) and (20) becomes

$$\begin{aligned} 0\le N_H(t)\le \dfrac{\beta _h}{d_1}~~\text{ and }~~0\le N_R(t)\le \dfrac{\varphi _r}{d_2}~~\text{ as }~~t\rightarrow \infty . \end{aligned}$$

Paticularly, \(N_H(t)\le \dfrac{\beta _h}{d_1}\) and \(N_R(t)\le \dfrac{\varphi _r}{d_2}\) if \(N_H(0)\le \dfrac{\beta _h}{d_1}\) and \(N_R(0)\le \dfrac{\varphi _r}{d_2}\) respectively. Therefore, all the solutions of the model enter

$$\begin{aligned} \Omega =\left\{ \Omega _H\cup \Omega _R\in I\!\!\!\!R_+^5\times I\!\!\!\!R_+^2\right\} , \end{aligned}$$

where

$$\begin{aligned} \Omega =\left\{ (S_h,I_h,NT_h,T_h,R_h)\in I\!\!\!\!R_+^5; N_H(t)\le \dfrac{\beta _h}{d_1}, (S_r,I_r)\in I\!\!\!\!R_+^2;N_R(t)\le \dfrac{\varphi _r}{d_2}\right\} . \end{aligned}$$
(21)

Hence, all the solutions of the system with nonnegative initial conditions in \(\Omega \) remain in \(\Omega \) for all \(t>0.\) It therefore follows that \(\Omega \) is positively invariant. Hence, the disease dynamics governed by the system (1)–(7) can be considered in \(\Omega \) where the system is mathematically and epidemiologically well posed. \(\square \)

3 Qualitative analysis

3.1 Equilibria

The model equilibrium points are obtained to analyze the long-term dynamics of the disease. The system of Eqs. (1)–(7) is set to zero to obtain two equilibria. i.e.

$$\begin{aligned} \dfrac{dS_h}{dt}=\dfrac{dI_h}{dt}=\dfrac{dNT_h}{dt}=\dfrac{dT_h}{dt}=\dfrac{dR_h}{dt}=\dfrac{dS_r}{dt}=\dfrac{dI_r}{dt}=0 \end{aligned}$$
(22)

The solutions \(S_h^{\circ }, I_h^{\circ }, NT_h^{\circ }, T_h^{\circ }, R_h^{\circ }, S_r^{\circ }\) and \(I_r^{\circ }\) satisfy Eq. (22) and clearly indicate that the equilibrium is not trivial and the populations do not go into extinction as long as human recruitment rate \(\beta _h\) and the mastomys recruitment rate \(\varphi _r\) are not zero. Hence, \(I_h=NT_h=T_h=R_h=0\) when Lassa virus is totally absent from the community and the system admits a steady state, \(H_{\circ },\) that represents the infection-free equilibrium (DFE). Therefore, the system has the DFE denoted by

$$\begin{aligned} H_{\circ }=(S_h^{\circ }, I_h^{\circ }, NT_h^{\circ }, T_h^{\circ }, R_h^{\circ }, S_r^{\circ }, I_r^{\circ })= \left( \dfrac{\beta _h}{d_1},0,0,0,0,\dfrac{\varphi _r}{d_2},0\right) . \end{aligned}$$

However, if the community is invaded with Lassa virus, each of the variables become nonzero and the condition \(I_h=NT_h=T_h=R_h=0\) fails to hold. Assuming \(H^{*}\) defines the system’s steady state when the community is invaded with the virus with points \(S_h^{*}, I_h^{*}, NT_h^{*}, T_h^{*}, R_h^{*}, S_r^{*}, I_r^{*}\). Then, solving the system at the endemic equilibrium, the points are obtained as

$$\begin{aligned} \begin{aligned} S_h^{*}&=\dfrac{1}{\left( \dfrac{\left\{ \alpha _1(\gamma _1+d_1)+\alpha _3(1-\eta )\tau \right\} I_h^{*}}{(\gamma _1+d_1)}+\alpha _2\left( \dfrac{\varphi _r}{d_2}-\dfrac{d_2}{\epsilon }\right) +d_1\right) }\\&\quad \times \left[ \beta _h+\dfrac{\phi }{\phi +d_1}\left( \dfrac{\left\{ \gamma _1(1-\eta )\tau +\gamma _2\eta \tau \right\} I_h^{*}}{(\gamma _1+d_1)} \right) \right] , \end{aligned} \end{aligned}$$
(23)
$$\begin{aligned} \begin{aligned} I_h^{*}&=\dfrac{1}{\tau +d_1+\vartheta -\left( \dfrac{\left\{ \alpha _1(\gamma _1+d_1)+\alpha _3(1-\eta )\tau \right\} }{(\gamma _1+d_1)}\right) S_h^{*}}\\&\quad \times \left[ \alpha _2\left( \dfrac{\varphi _r}{d_2}-\dfrac{d_2}{\epsilon }\right) \right] , \end{aligned} \end{aligned}$$
(24)
$$\begin{aligned} NT_h^{*}&=\dfrac{(1-\eta )\tau I_h^{*}}{(\gamma _1+d_1)}, \end{aligned}$$
(25)
$$\begin{aligned} T_h^{*}&=\dfrac{\eta \tau I_h^{*}}{(\gamma _2+d_1)}, \end{aligned}$$
(26)
$$\begin{aligned} R_h^{*}&=\dfrac{1}{(\phi +d_1)}\left[ \dfrac{\gamma _1(1-\eta )\tau I_h^{*}}{(\gamma _1+d_1)}+\gamma _2\dfrac{\eta \tau I_h^{*}}{(\gamma _1+d_1)}\right] , \end{aligned}$$
(27)
$$\begin{aligned} S_r^{*}&=\dfrac{d_2}{\epsilon }, \end{aligned}$$
(28)
$$\begin{aligned} I_r^{*}&=\dfrac{\varphi _r}{d_2}-\dfrac{d_2}{\epsilon }. \end{aligned}$$
(29)

3.2 Reproduction number

To predict the transmission potential of the virus when an infectious agent emerges in a population where every individual and mastomys are completely susceptible, we compute the reproduction number, \(R_{\circ }\), which is defined by Diekmann et al. [32] as the average number of secondary cases instigated by an infectious agent in a naive population throughout the period of his infectiousness. For our model, \(R_{\circ }\) is computed following the procedure in Driesche and Watmough [33] which quantifies Lassa fever spread in terms of infections from humans and rodents. Infections from humans include infections from both infected \(I_h\) and the non-treatment compliance \(NT_h\). Therefore, at the DFE, the rate of appearance of new infections and the transfer of humans and mastomys are partitioned into two Jacobian matrices F and V such that

$$\begin{aligned} F= \begin{pmatrix} \dfrac{\alpha _1\beta _h}{d_1}&{}\quad \dfrac{\alpha _3\beta _h}{d_1}&{}\quad \dfrac{\alpha _2\beta _h}{d_1}\\ 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \dfrac{\epsilon \varphi _r}{d_2} \end{pmatrix},\quad V= \begin{pmatrix} \tau +d_1+\vartheta &{}\quad 0&{}\quad 0\\ -(1-\eta )\tau &{}\quad (\gamma _1+d_1)&{}\quad 0\\ 0&{}\quad 0&{}\quad d_2 \end{pmatrix}. \end{aligned}$$
(30)
$$\begin{aligned} V^{-1}= \begin{pmatrix} \dfrac{1}{(\tau +d_1+\vartheta )}&{}\quad 0&{}\quad 0\\ \dfrac{(1-\eta )\tau }{(\gamma _1+d_1)(\tau +d_1+\vartheta )}&{}\quad \dfrac{1}{(\gamma _1+d_1)}&{}\quad 0\\ 0&{}\quad 0&{}\quad \dfrac{1}{d_2} \end{pmatrix}. \end{aligned}$$
(31)

The spectral radius of matrix \(FV^{-1}\) defines the \(R_{\circ }\) for the model. \(R_{\circ }\) for the model is made up of \(R_H\) and \(R_r\), the infection spread from humans and mastomys respectively. Therefore, \(R_{\circ }=\) max\((R_H,R_r)\) such that

$$\begin{aligned} R_H=\dfrac{\alpha _1\beta _h}{d_1(\tau +d_1+\vartheta )}+\dfrac{\alpha _3\beta _h(1-\eta )\tau }{d_1(\gamma _1+d_1)(\tau +d_1+\vartheta )}, R_r=\dfrac{\epsilon \varphi _r}{d_2^2}. \end{aligned}$$
(32)

While \(R_H\) governs the number of new cases of Lassa fever due to infections from infectious individuals who are yet to access treatment \((I_h)\) and those who are under treatment but who do not comply with treatment guidelines \((NT_h)\), \(R_r\) governs the average number of new cases of Lassa fever due to infections from infectious rodents \((I_r)\). The transmissibility of Lassa virus depends on the numerical values of \(R_H\) and \(R_r\). If \(R_H\) and \(R_r\) are less than one, the virus will not spread but if one or both \(R_H\) and \(R_r\) are greater than one, the virus will spread in the population.

3.3 Local stability of the equilibria, \(H_{\circ }\) and \(H^{*}\)

The DFE \(H_{\circ }\), the endemic equilibrium \(H^{*}\) and the \(R_{\circ }\) of the model have been derived. The stability of the equilibria \(H_{\circ }\) and \(H^{*}\) have to be investigated to examine the possibility of Lassa fever extinction or persistence in the population.

Theorem 3

The DFE \(H_{\circ }\) is locally asymptotically stable if \(R_H<1\) and \(R_r<1\) but unstable if one or both \(R_H\) and \(R_r\) are greater than one

Proof

The Jacobian of the model evaluated at DFE \(H_{\circ }\) is obtained as

$$\begin{aligned} J(H_{\circ })= \begin{pmatrix} -d_1&{}\quad -\dfrac{\alpha _1\beta _h}{d_1}&{}\quad -\dfrac{\alpha _3\beta _h}{d_1}&{}\quad 0&{}\quad \phi &{}\quad 0&{}\quad -\dfrac{\alpha _2\beta _h}{d_1}\\ 0&{}\quad \dfrac{\alpha _1\beta _h}{d_1}-(\tau +d_1+\vartheta )&{}\quad \dfrac{\alpha _3\beta _h}{d_1}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \dfrac{\alpha _2\beta _h}{d_1}\\ 0&{}\quad (1-\eta )\tau &{}\quad -(\gamma _1+d_1)&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad \eta \tau &{}\quad 0&{}\quad -(\gamma _2+d_1)&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \gamma _1&{}\quad \gamma _2&{}\quad -(\phi +d_1)&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -d_2&{}\quad -\dfrac{\epsilon \varphi _r}{d_2}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \dfrac{\epsilon \varphi _r}{d_2}-d_2 \end{pmatrix} \nonumber \\ \end{aligned}$$
(33)

Solving \(|J(H_{\circ })-\lambda I|=0\) yields

$$\begin{aligned} (d_1+\lambda )\left( d_2-\dfrac{\epsilon \varphi _r}{d_2}+\lambda \right) (d_2+\lambda )(\phi +d_1+\lambda )(\gamma _2+d_1+\lambda )\left| \begin{array}{cc} \dfrac{\alpha _1\beta _h}{d_1}-(\tau +d_1+\vartheta )&{}\quad \dfrac{\alpha _3\beta _h}{d_1}\\ (1-\eta )\tau &{}\quad -(\gamma _1+d_1)\end{array}\right|&=0. \end{aligned}$$
(34)
$$\begin{aligned} \Longrightarrow ~~(d_1+\lambda )\left( d_2-\dfrac{\epsilon \varphi _r}{d_2}+\lambda \right) (d_2+\lambda )(\phi +d_1+\lambda )(\gamma _2+d_1+\lambda )&=0 \end{aligned}$$
(35)

or

$$\begin{aligned} \left| \begin{array}{cc} \dfrac{\alpha _1\beta _h}{d_1}-(\tau +d_1+\vartheta )&{}\quad \dfrac{\alpha _3\beta _h}{d_1}\\ (1-\eta )\tau &{}\quad -(\gamma _1+d_1)\end{array}\right| =0. \end{aligned}$$
(36)

From Eq. (35),

$$\begin{aligned} \lambda _1=-d_1, \lambda _2=-d_2, \lambda _3=-(\phi +d_1), \lambda _4=-(d_1+\gamma _1), \lambda _5=\dfrac{\epsilon \varphi _r}{d_2}-d_2. \end{aligned}$$

\(\lambda _5\) can be further expressed as

$$\begin{aligned}&\lambda _5=d_2\left( \dfrac{\epsilon \varphi _r}{d_2^2}-1\right) ,\\ \therefore ~~&\lambda _5=d_2(R_r-1). \end{aligned}$$

Hence, \(\lambda _5<0\) if \(R_r<1\). Suppose the matrix in Eq. (36) is considered and suppose it is M. The trace and determinant of M are respectively

$$\begin{aligned} Tr(M)=\dfrac{\alpha _1\beta _h}{d_1}-[(\tau +d_1+\vartheta )+(d_1+\gamma _1)] \end{aligned}$$
(37)
$$\begin{aligned} Det(M){} & {} =-(d_1+\gamma _1)\left[ \dfrac{\alpha _1\beta _h}{d_1}-(\tau +d_1+\vartheta )\right] -\dfrac{\alpha _3\beta _h}{d_1}(1-\eta )\tau \nonumber \\{} & {} =(d_1+\gamma _1)(\tau +d_1+\vartheta )\left[ 1-\left\{ \dfrac{\alpha _1\beta _h}{d_1(\tau +d_1+\vartheta )}+\dfrac{\alpha _3\beta _h(1-\eta )\tau }{d_1(d_1+\gamma _1)(\tau +d_1+\vartheta )} \right\} \right] \nonumber \\{} & {} \Longrightarrow ~~Det(M)=(d_1+\gamma _1)(\tau +d_1+\vartheta )[1-R_H]. \end{aligned}$$
(38)

Therefore, \(Det(M)>0\) if \(R_H<1\). Also in Eq. (37), following the definition of \(R_H\), if \(R_H<1\) then \(\alpha _1\rightarrow 0\) and \(Tr(M)<0\). Hence, all the roots of \(|J(H_{\circ })-\lambda I|=0\) are negative and the DFE \(H_{\circ }\) is locally asymptotically stable if \(R_H<1\) and \(R_r<1\). \(\square \)

The investigation of the local stability of the endemic equilibrium \(H^{*}\) shall follow after the necessary and sufficient conditions for local asymptotic stability of the DFE \(H_{\circ }\) have been derived.

Theorem 4

The endemic equilibrium \(H^{*}\) exists and is locally asymptotically stable if \(R_{\circ }>1\) otherwise \(H^{*}\) is locally asymptotically unstable (i.e. if \(R_{\circ }<1\))

Proof

Linearization approach will prove difficult to establish the local stability of \(H^{*}\) due to the dimension of the system. Therefore, Theorem 4.1 (iv) in Castillo-Chavez and Song [34] shall be employed to examine the local stability of \(H^{*}\) of the model. The Jacobian of the system evaluated at DFE \(H_{\circ }\) with \(\alpha _3=\alpha _3^{*}\) chosen as the bifurcation parameter is derived as

$$\begin{aligned} J^{*}=J(H_{\circ })|_{\alpha _3=\alpha _3^{*}} \begin{pmatrix} -d_1&{}\quad -\dfrac{\alpha _1\beta _h}{d_1}&{}\quad -\dfrac{\alpha _3^{*}\beta _h}{d_1}&{}\quad 0&{}\quad \phi &{}\quad 0&{}\quad -\dfrac{\alpha _2\beta _h}{d_1}\\ 0&{}\quad \dfrac{\alpha _1\beta _h}{d_1}-k_1&{}\quad \dfrac{\alpha _3^{*}\beta _h}{d_1}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \dfrac{\alpha _2\beta _h}{d_1}\\ 0&{}\quad (1-\eta )\tau &{}\quad -k_2&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad \eta \tau &{}\quad 0&{}\quad -k_3&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \gamma _1&{}\quad \gamma _2&{}\quad -k_4&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -d_2&{}\quad -\dfrac{\epsilon \varphi _r}{d_2}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad k_5 \end{pmatrix}, \nonumber \\ \end{aligned}$$
(39)

where

$$\begin{aligned}k_1=(\tau +d_1+\vartheta ), k_2=(\gamma _1+d_1), k_3=(\gamma _2+d_1), k_4=(\phi +d_1), k_5=\dfrac{\epsilon \varphi _r}{d_2}-d_2.\end{aligned}$$

\(\alpha _3=\alpha _3^{*}\) is chosen as the bifurcation parameter to examine whether or not poor compliance with treatment guidelines can trigger Lassa fever outbreak. The right-eigen vectors of \(J^{*}=J(H_{\circ })|_{\alpha _3=\alpha _3^{*}}\) in terms of \(w_2\) where \(w_2=w_2>0\) consists of

$$\begin{aligned}&w_1=\dfrac{1}{d_1}\left\{ \dfrac{\phi }{k_4}\left( \dfrac{\gamma _1(1-\eta )\tau }{k_2}+\dfrac{\gamma _2\eta \tau }{k_3} \right) -k_1\right\} w_2, \end{aligned}$$
(40)
$$\begin{aligned}&w_2=w_2>0, \end{aligned}$$
(41)
$$\begin{aligned}&w_3=\dfrac{(1-\eta )\tau }{k_2}w_2, \end{aligned}$$
(42)
$$\begin{aligned}&w_4=\dfrac{\eta \tau }{k_3}w_2, \end{aligned}$$
(43)
$$\begin{aligned}&w_5=\dfrac{1}{k_4}\left( \dfrac{\gamma _1(1-\eta )\tau }{k_2}+\dfrac{\gamma _2\eta \tau }{k_3} \right) w_2, \end{aligned}$$
(44)
$$\begin{aligned}&w_6=\dfrac{\varphi _rd_1}{d_2^2\alpha _2\beta _h}\left[ \dfrac{\alpha _1\beta _h}{d_1}+\dfrac{\alpha _3^{*}\beta _h(1-\eta )\tau }{d_1k_2}-k_1 \right] w_2, \end{aligned}$$
(45)
$$\begin{aligned}&w_7=\dfrac{d_1}{\alpha _2\beta _h}\left[ k_1-\left\{ \dfrac{\alpha _1\beta _h}{d_1}+\dfrac{\alpha _3^{*}\beta _h(1-\eta )\tau }{d_1k_2}\right\} \right] w_2. \end{aligned}$$
(46)

Also, \(J^{*}=J(H_{\circ })|_{\alpha _3=\alpha _3^{*}}\) has the left eigen-vectors satisfying the condition \(\mathbf {v.w}=1\) such that \(v_1=v_3=v_4=v_5=v_6=v_7=0\) but \(v_2=v_2>0\). The stability of \(H^{*}\) is governed by the signs of the coefficients of \('a'\) and \('b'\) whose formulae are respectively defined in Theorem 4.1 (iv) in [34] as

$$\begin{aligned}&a=\sum \limits _{k,i,j=1}^{7}v_kw_iw_j\dfrac{\partial ^2f_k}{\partial x_i\partial x_j}(0,0), \end{aligned}$$
(47)
$$\begin{aligned}&b= \sum \limits _{k,i=1}^{7}v_kw_i\dfrac{\partial ^2f_k}{\partial x_i\partial \alpha _3^{*}}(0,0). \end{aligned}$$
(48)

Therefore, the values of a and b are determined after a few algebraic manipulations as

$$\begin{aligned}&a=\dfrac{2v_2}{d_1}\left\{ \dfrac{\phi }{k_4}\left( \dfrac{\gamma _1(1-\eta )\tau }{k_2}+\dfrac{\gamma _2\eta \tau }{k_3} \right) -k_1\right\} \left[ \alpha _1+\dfrac{(1-\eta )\tau }{k_2}\alpha _2+\dfrac{\eta \tau }{k_3}\alpha _3^{*} \right] w_2^2, \end{aligned}$$
(49)
$$\begin{aligned}&b= \dfrac{\beta _h}{d_1}v_2w_2>0. \end{aligned}$$
(50)

Since \(b>0\) and following the same Theorem 4.1 (iv) in [34], there exists an endemic equilibrium \(H^{*}\) that is locally asymptotically stable if \(a<0\). \(\square \)

Having derived the necessary and sufficient conditions for the existence of local stability of each equilibrium of the model, the investigation of the global stability the model equilibria shall follow.

3.4 Global stability of the equilibria, \(H_{\circ }\) and \(H^{*}\)

Theorem 5

The DFE \(H_{\circ }\) is globally asymptotically stable (GAS) if \(R_{\circ }<1\) but unstable if \(R_{\circ }>1\).

Proof

The comparison theorem in [35] which has been used in some existing Lassa fever model [7] shall be used to investigate the existence of global stability for the DFE \(H_{\circ }\) of our proposed Lassa fever model. By definition, the DFE \(H_{\circ }\) is GAS if all the eigenvalues of \(|(F-V)-\lambda I|=0\) are negative. From Eq. (30),

$$\begin{aligned} |(F-V)-\lambda I|= \left| \begin{array}{ccc} \dfrac{\alpha _1\beta _h}{d_1}-k_1-\lambda &{}\quad \dfrac{\alpha _3\beta _h}{d_1}&{}\quad \dfrac{\alpha _2\beta _h}{d_1}\\ (1-\eta )\tau &{}\quad -k_2-\lambda &{}\quad 0\\ 0&{}\quad 0&{}\quad k_5-\lambda \end{array}\right| =0. \end{aligned}$$
(51)
$$\begin{aligned} \Longrightarrow ~(k_5-\lambda )\left[ \left( -\dfrac{\alpha _1\beta _h}{d_1}+k_1+\lambda \right) (k_2+\lambda )-\dfrac{(1-\eta )\tau \alpha _3\beta _h}{d_1}\right] =0. \end{aligned}$$
$$\begin{aligned} \begin{aligned} \Longrightarrow ~~&(k_5-\lambda )\times \\&\left[ \lambda ^2+\left\{ -\dfrac{\alpha _1\beta _h}{d_1}+k_1+k_2 \right\} \lambda +\left\{ k_2\left( -\dfrac{\alpha _1\beta _h}{d_1}+k_1\right) -\dfrac{(1-\eta )\tau \alpha _3\beta _h}{d_1}\right\} \right] =0, \end{aligned} \nonumber \\ \end{aligned}$$
(52)

where

$$\begin{aligned} k_1=(\tau +d_1+\vartheta ), k_2=(\gamma _1+d_1), k_5=\dfrac{\epsilon \varphi _r}{d_2}-d_2. \end{aligned}$$

Equation (52) can be solved by using the principle \(a=0\) or \(b=0\) if \(a \times b=0\). Now, from Eq. (52),

$$\begin{aligned} k_5-\lambda =0 \end{aligned}$$
$$\begin{aligned} \Longrightarrow ~~ \lambda _1&=\dfrac{\epsilon \varphi _r}{d_2}-d_2\\&=d_2\left[ \dfrac{\epsilon \varphi _r}{d_2^2}-1\right] \\ \Longrightarrow ~~\lambda _1&=d_2(R_r-1).\\ \therefore ~~\lambda _1&<0 \end{aligned}$$

provided that \(R_r<1\). Or,

$$\begin{aligned} \left[ \lambda ^2+\left\{ -\dfrac{\alpha _1\beta _h}{d_1}+k_1+k_2 \right\} \lambda +\left\{ k_2\left( -\dfrac{\alpha _1\beta _h}{d_1}+k_1\right) -\dfrac{(1-\eta )\tau \alpha _3\beta _h}{d_1}\right\} \right] =0.\nonumber \\ \end{aligned}$$
(53)

On substituting for \(k_1\) and \(k_2\) and following Rourth Hurtwitz stability criteria [36, 47], the two roots in Eq. (53) are negative if

$$\begin{aligned} -\dfrac{\alpha _1\beta _h}{d_1}+(\tau +d_1+\vartheta )+(\gamma _1+d_1)>0 \end{aligned}$$
(54)

and,

$$\begin{aligned} (\gamma _1+d_1)\left( -\dfrac{\alpha _1\beta _h}{d_1}+(\tau +d_1+\vartheta )\right) -\dfrac{(1-\eta )\tau \alpha _3\beta _h}{d_1}>0. \end{aligned}$$
(55)

From inequality (55),

$$\begin{aligned}&-(\gamma _1+d_1)\left( \dfrac{\alpha _1\beta _h}{d_1}-(\tau +d_1+\vartheta )+\dfrac{(1-\eta )\tau \alpha _3\beta _h}{d_1(\gamma _1+d_1)}\right)>0,\\&(\gamma _1+d_1)(\tau +d_1+\vartheta )\left[ 1-\left( \dfrac{\alpha _1\beta _h}{d_1(\tau +d_1+\vartheta )}+\dfrac{(1-\eta )\tau \alpha _3\beta _h}{d_1(\gamma _1+d_1)(\tau +d_1+\vartheta )} \right) \right] >0, \end{aligned}$$
$$\begin{aligned} \Longrightarrow ~~(\gamma _1+d_1)(\tau +d_1+\vartheta )(1-R_H)>0. \end{aligned}$$
(56)

Inequalities (54) and (56) are true provided that \(R_H<1\). The validity of inequality (56) is clear whenever \(R_H<1\). Inequality (54) would also be true because the transmission parameter \(\alpha _1\rightarrow 0\) when \(R_H<1\). Hence, all the eigenvalues of Eq. (51) are negative if \(R_H<1\) and \(R_r<1.\) Therefore, it is sufficient to conclude that the global stability of the DFE \(H_{\circ }\) of the proposed model is a function of the numerical values of \(R_H<1\) and \(R_r<1.\) \(\square \)

Having examined the global stability the DFE \(H_{\circ }\) of the model, we proceeded to investigate the global stability of the endemic equilibrium \(H^{*}\).

Theorem 6

The endemic equilibrium \(H^{*}\) of the model is globally asymptotically stable if \(R_{\circ }>1.\)

Proof

Suppose L is a nonlinear Lyapunov function. The endemic equilibrium \(H^{*}\) is globally asymptotically stable if \(\dfrac{dL}{dt}\le 0\) [37, 38]. Define L as

$$\begin{aligned} L{} & {} = \left( S_h-S_h^{*}-S_h^{*}\log \frac{S_h}{S_h^{*}}\right) +\left( I_h-I_h^{*}-I_h^{*}\log \frac{I_h}{I_h^{*}}\right) \nonumber \\{} & {} \quad +\left( NT_h-NT_h^{*}-NT_h^{*}\log \frac{NT_h}{NT_h^{*}}\right) +\left( T_h-T_h^{*}-T_h^{*}\log \frac{T_h}{T_h{*}}\right) \nonumber \\{} & {} \quad +\left( R_h-R_h^{*}-R_h^{*}\log \frac{R_h}{R_h^{*}}\right) +\left( S_r-S_r^{*}-S_r^{*}\log \frac{S_r}{S_r^{*}}\right) \nonumber \\{} & {} \quad +\left( I_r-I_r^{*}-I_r^{*}\log \frac{I_r}{I_r^{*}}\right) , \end{aligned}$$
(57)
$$\begin{aligned} \frac{dL}{dt}{} & {} =\left( 1-\frac{S_h^{*}}{S_h}\right) \frac{dS_h}{dt}+\left( 1-\frac{I_h^{*}}{I_h}\right) \frac{dI_h}{dt}\nonumber \\{} & {} \quad +\left( 1-\frac{NT_h^{*}}{NT_h}\right) \frac{dNT_h}{dt}+\left( 1-\frac{T_h^{*}}{T_h}\right) \frac{dT_h}{dt}\nonumber \\{} & {} \quad +\left( 1-\frac{R_h^{*}}{R_h}\right) \frac{dR_h}{dt}+\left( 1-\frac{S_r^{*}}{S_r}\right) \dfrac{dS_r}{dt}+\left( 1-\frac{I_r^{*}}{I_r}\right) \frac{dI_r}{dt}, \end{aligned}$$
(58)
$$\begin{aligned} \Longrightarrow ~~\frac{dL}{dt}{} & {} =\left( 1-\frac{S_h^{*}}{S_h}\right) [\beta _h+\phi R_h -(\alpha _1I_h+\alpha _2I_r+\alpha _3NT_h)S_h-d_1S_h]\nonumber \\{} & {} \quad {+}\left( 1-\frac{I_h^{*}}{I_h}\right) [(\alpha _1I_h{+}\alpha _2I_r{+}\alpha _3NT_h)S_h-(1-\eta )\tau I_h{-}\eta \tau I_h-(d_1+\vartheta )I_h]\nonumber \\{} & {} \quad +\left( 1-\frac{NT_h^{*}}{NT_h}\right) [(1-\eta )\tau I_h-\gamma _1 NT_h-d_1NT_h],\nonumber \\{} & {} \quad +\left( 1-\frac{T_h^{*}}{T_h}\right) [\eta \tau I_h-\gamma _2 T_h-d_1T_h],\nonumber \\{} & {} \quad +\left( 1-\frac{R_h^{*}}{R_h}\right) [\gamma _1 NT_h+\gamma _2 T_h-\phi R_h-d_1R_h],\nonumber \\{} & {} \quad +\left( 1-\frac{S_r^{*}}{S_r}\right) [\varphi _r-\epsilon S_rI_r-d_2S_r],\nonumber \\{} & {} \quad +\left( 1-\frac{I_r^{*}}{I_r}\right) [\epsilon S_rI_r-d_2I_r]. \end{aligned}$$
(59)

Simplifying Eq. (59) in terms of \( S_h^{*} \& S_h, I_h^{*} \& I_h, NT_h^{*} \& NT_h, T_h^{*} \& T_h, R_h^{*} \& R_h, S_r^{*} \& S_r\) and \( I_r^{*} \& I_r\) then

$$\begin{aligned} \frac{dL}{dt}&=\left( 1-\frac{S_h^{*}}{S_h}\right) [(\alpha _1I_h+\alpha _2I_r+\alpha _3NT_h+d_1)S_h^{*}-(\alpha _1I_h+\alpha _2I_r+\alpha _3NT_h+d_1)S_h]\\&\quad +\left( 1-\frac{I_h^{*}}{I_h}\right) [(\tau +d_1+\vartheta )I_h^{*}-(\tau +d_1+\vartheta )I_h]\\&\quad +\left( 1-\frac{NT_h^{*}}{NT_h}\right) [(d_1+\gamma _1)NT_h^{*} -(d_1+\gamma _1)NT_h],\\&\quad +\left( 1-\frac{T_h^{*}}{T_h}\right) [(d_1+\gamma _2)T_h^{*}-(d_1+\gamma _2)T_h],\\&\quad +\left( 1-\frac{R_h^{*}}{R_h}\right) [(d_1+\phi )R_h^{*}-(d_1+\phi )R_h],\\&\quad +\left( 1-\frac{S_r^{*}}{S_r}\right) [(\epsilon I_r+d_2)S_r^{*}-(\epsilon I_r+d_2)S_r],\\&\quad +d_2 \left( 1-\frac{I_r^{*}}{I_r}\right) [I_r^{*}-I_r]. \end{aligned}$$
$$\begin{aligned} \begin{aligned} \Longrightarrow ~~\frac{dL}{dt}&=-\left( 1-\frac{S_h^{*}}{S_h}\right) (\alpha _1I_h+\alpha _2I_r+\alpha _3NT_h+d_1)(S_h-S_h^{*})\\&\quad -\left( 1-\frac{I_h^{*}}{I_h}\right) (\tau +d_1+\vartheta )(I_h-I_h^{*})\\&\quad -\left( 1-\frac{NT_h^{*}}{NT_h}\right) (d_1+\gamma _1) (NT_h-NT_h^{*}),\\&\quad -\left( 1-\frac{T_h^{*}}{T_h}\right) (d_1+\gamma _2)(T_h-T_h^{*}),\\&\quad -\left( 1-\frac{R_h^{*}}{R_h}\right) (d_1+\phi )(R_h-R_h^{*}),\\&\quad -\left( 1-\frac{S_r^{*}}{S_r}\right) (\epsilon I_r+d_2)(S_r-S_r^{*}),\\&\quad -d_2 \left( 1-\frac{I_r^{*}}{I_r}\right) (I_r-I_r^{*}). \end{aligned} \end{aligned}$$
(60)

Thus, \(\dfrac{dL}{dt}\le 0\). Also, \(\dfrac{dL}{dt}=0\) provided that \(S_h=S_h^{*}, I_h=I_h^{*}, NT_h=NT_h^{*}, T_h=T_h^{*}, R_h=R_h^{*}, S_r=S_r^{*}, I_r=I_r^{*}\). The only largest invariant set in \(\left\{ (S_h, I_h, NT_h, T_h, R_h, S_r, I_r)\in \Omega :\dfrac{dL}{dt}=0 \right\} \) is \(H^{*}\). Therefore, \(H^{*}\) is GAS in the interior \(\Omega \) by LaSalle’s invariance principle [39, 40]. \(\square \)

3.5 Sensitivity analysis

The contribution of the model parameters to increase or decrease in the reproduction numbers \(R_H\) and \( R_r\) can be investigated by the sensitivity index formula which has been widely employed in the literature [7, 15, 41].This will enable the policy makers to identify the parameters to be targeted for intervention to control the spread of Lassa fever. The indices for \(\beta _h, \alpha _1, \alpha _3, \eta , \gamma _1, d_1, \tau \) and \(\vartheta \) in terms of \(R_H\) are determined one after the other as follows:

$$\begin{aligned} \beta _h&: \dfrac{\partial R_H}{\partial \beta _h}\times \dfrac{\beta _h}{R_H}= \left( \dfrac{\alpha _1}{d_1(\tau +d_1+\vartheta )}+\dfrac{\alpha _3(1-\eta )\tau }{d_1(\gamma _1+d_1)(\tau +d_1+\vartheta )}\right) \times \dfrac{\beta _h}{R_H}, \end{aligned}$$
(61)
$$\begin{aligned} \alpha _1&: \dfrac{\partial R_H}{\partial \alpha _1}\times \dfrac{\alpha _1}{R_H}=\dfrac{1}{R_H}\left( \dfrac{\alpha _1\beta _h}{d_1(\tau +d_1+\vartheta )}\right) ,\end{aligned}$$
(62)
$$\begin{aligned} \alpha _3&: \dfrac{\partial R_H}{\partial \alpha _3}\times \dfrac{\alpha _3}{R_H}=\dfrac{1}{R_H}\left( \dfrac{\alpha _3\beta _h(1-\eta )\tau }{d_1(\gamma _1+d_1)(\tau +d_1+\vartheta )}\right) ,\end{aligned}$$
(63)
$$\begin{aligned} \eta&: \dfrac{\partial R_H}{\partial \eta }\times \dfrac{\eta }{R_H}=-\dfrac{1}{R_H}\left( \dfrac{\alpha _3\beta _h\eta \tau }{d_1(\gamma _1+d_1)(\tau +d_1+\vartheta )}\right) ,\end{aligned}$$
(64)
$$\begin{aligned} \gamma _1&: \dfrac{\partial R_H}{\partial \gamma _1}\times \dfrac{\gamma _1}{R_H}=-\dfrac{1}{R_H}\left( \dfrac{\alpha _3\beta _h(1-\eta )\tau \gamma _1}{d_1(\gamma _1+d_1)^2(\tau +d_1+\vartheta )}\right) ,\end{aligned}$$
(65)
$$\begin{aligned} d_1&: \dfrac{\partial R_H}{\partial d_1}\times \dfrac{d_1}{R_H}=-\dfrac{\alpha _1\beta _h(\tau +2d_1+\vartheta )}{(d_1(\tau +d_1+\vartheta ))^2}-\dfrac{\alpha _3\beta _h(1-\eta )\tau m_1}{m_2}\times \dfrac{d_1}{R_H},\end{aligned}$$
(66)
$$\begin{aligned} \tau&: \dfrac{\partial R_H}{\partial \tau }\times \dfrac{\tau }{R_H}=-\dfrac{\alpha _1\beta _h}{d_1m_4^2}+\dfrac{d_1m_3m_4\alpha _3\beta _h(1-\eta )-m_3\alpha _3\beta _hd_1(1-\eta )\tau }{(d_1m_3m_4)^2}\times \dfrac{\tau }{R_H}, \nonumber \\ \end{aligned}$$
(67)
$$\begin{aligned} \vartheta&: \dfrac{\partial R_H}{\partial \vartheta }\times \dfrac{\vartheta }{R_H}=-\dfrac{\alpha _1\beta _h}{d_1m_4^2}-\dfrac{\alpha _3\beta _h(1-\eta )\tau }{d_1m_3m_4^2}\times \dfrac{\vartheta }{R_H}. \end{aligned}$$
(68)

Also, the indices for \(\varphi _r, \epsilon \) and \(d_2\) in terms of \(R_r\) are determined as

$$\begin{aligned} \varphi _r&: \dfrac{\partial R_r}{\partial \varphi _r}\times \dfrac{\varphi _r}{R_r}=\dfrac{\epsilon }{d_2^2}\times \dfrac{\varphi _r}{R_r},\end{aligned}$$
(69)
$$\begin{aligned} \epsilon&: \dfrac{\partial R_r}{\partial \epsilon }\times \dfrac{\epsilon }{R_r}=\dfrac{\varphi _r}{d_2^2}\times \dfrac{\epsilon }{R_r},\end{aligned}$$
(70)
$$\begin{aligned} d_2&: \dfrac{\partial R_r}{\partial d_2}\times \dfrac{d_2}{R_r}=-\dfrac{\epsilon \varphi _r}{d_2^3}\times \dfrac{d_2}{R_r}, \end{aligned}$$
(71)

where   \(m_1=\tau \gamma _1+2d_1\gamma _1+\vartheta \gamma _1+2d_1\tau +3d_1^2+2d_1\vartheta ,~~ m_2=(d_1(\tau \gamma _1+d_1\gamma _1+\vartheta \gamma _1+d_1\tau +d_1^2+d_1\vartheta ))^2, ~~m_3=\gamma _1+d_1,~~ m_4=\tau +d_1+\vartheta .\)

4 Numerical simulation and discussion

To support the claims and illustrate what was obtained analytically in Sect. 3, some numerical simulations are performed to visualize the effect of parameter perturbations on the structure of the model. The parameter for human mortality rate, \(d_1\), is the only parameter whose value is estimated. The values for other parameters are searched from the literature and where they are not available, a logical set of values are used. The life expectancy in Nigeria in 2021 was about 60.87 years [42]. The natural death rate is generally the inverse of the life expectancy. Therefore, the natural death rate for human \(d_1=\dfrac{1}{60.87}\) year\(^{-1}\) \(=\dfrac{52}{60.87}\) week\(^{-1}\). The model parameters have been defined in Table 1 but the initial values assigned to each parameter to conduct the simulation is stated in Table 2 with the unit of measurement in a year.

Table 2 parameters’ values and sources
Full size table

Following the parameter values in Table 2, the sensitivity indices of the model parameters derived in Eqs. (61)–(71) in relation to the transmission parameters \(R_H\) are \(R_r\) are computed and the results are presented in Table 3.

Table 3 Sensitivity indices of major parameters
Full size table

In Table 3, natural death rates parameters \(d_1\) and \(d_2\), effective contact rate parameter \(\epsilon \) between infectious and susceptible rodents, mortality rate due to infection parameter \(\vartheta \) and progression rate parameter \(\tau \) into treatment compartment are less significant to the disease dynamics and are excluded in the the discussion of result for Table 3. Other key parameters, \(\beta _h, \alpha _1, \alpha _3, \eta , \gamma _1\) and \(\varphi _r\), that have major influence on the dynamics of the disease are discussed. Parameters with positive indices contribute to the spread of Lassa fever while those with negative indices inhibit Lassa fever transmission.

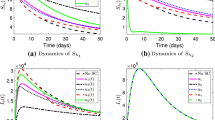
Based on the sensitivity analysis results in Table 3, \(\beta _h, \alpha _3, \eta , \varphi _r\) and \(\gamma _1\) are more crucial to Lassa fever dynamics considering the magnitude of their values. It is revealed that \((\beta _h)\), the human recruitment rate and \((\varphi _r)\), the recruitment rate for rodents have the highest sensitivity indices of 1.000. The interpretation of the value is that Lassa fever transmission (i.e., \(\mathcal {R}_0\)) approximately reduces by 10% if any of \((\beta _h)\) or \((\varphi _r)\) is reduced by 10%. This shows that any intervention that can limit the influx of Lassa fever carriers into the human population and at the same time reduce the rodent population is crucial to the eradication of Lassa fever spread. Also, the sensitivity indices for \(\alpha _3\), the effective contact rate between susceptible and infectious individuals and \(\eta \), the proportion of infected individuals who comply with treatment guidelines revealed an important information about Lassa fever transmission and management. The indices indicate that a 100% compliance with Lassa fever treatment guidelines \((\eta )\) could avert the spread of the disease in the population by 87%, whereas disregard for treatment procedures could instigate a 87% spread of the disease in the susceptible individuals’ population \((\alpha _3)\). Again, the effect of compliance with treatment guidelines is also revealed by the sensitivity index of \(\gamma _1\) which indicates that Lassa fever spread could be reduced by about 70% if \(\gamma _1\) is increased by 100%. That is, Lassa fever could be minimized if infectious individuals who are not compliant with treatment guidelines turn over a new leaf. Therefore, any strategy that aims to eliminate Lassa fever in the endemic areas has to take compliance with treatment procedure with all seriousness. The effect of treatment compliance on the transmission dynamics of Lassa fever is later examined quantitatively by varying the value of the treatment compliant parameter \((\eta )\) as well as the value of the parameter for spreading rate of Lassa virus from non-treatment compliant humans to the susceptible individuals \((\alpha _3)\). The results of the analysis are displayed in Fig. 2 using the initial values \(S_h=0.97, I_h=0.016, NT_h=0.0005, T_h=0.01, R_h=0.002, S_r=0.00097, I_r=0.0001\).

Fig. 2
figure 2

A simulation showing the effect of compliance and non-compliance with treatment guidelines on the dynamics of Lassa fever

Full size image

The impact of compliance and non-compliance with treatment guidelines on the spread of Lassa fever can be visualized in Fig. 2 especially in terms of the population of infectious individuals who are yet to be receiving treatment \(I_h(t)\). Emphasis is placed on these individuals because infectious humans who are yet to be receiving treatment have major contributions to Lassa fever escalation and their populations could be influenced by the level of compliance with treatment procedures of the infectious individuals who are under treatment. In Fig. 2a, with high rate of compliance with treatment guidelines, the population of the infectious individuals falls continuously and tends to zero after fifth year. It is shown in Fig. 2a that high rate of compliance with treatment guidelines lapses the period for new cases to attain the peak (delay instant transmission of the virus) and also elongates time to reach stability. The reproduction numbers from human-to-human \(R_H\) and rodent-to-human \(R_r\) are both less than unity, 0.852 and 0.544 respectively when there is high rate of compliance with the treatment guidelines which makes the DFE to be stable both locally and globally. Therefore, Lassa fever outbreak can be brought under control with strong adherence to Lassa fever treatment procedures.

On the other hand, the effect of disregard for compliance with the treatment procedures on the transmission of Lassa fever is illustrated in Fig. 2b in terms of the population of infectious individuals who are yet to be receiving treatment \(I_h(t)\). In Fig. 2b, with low rate of compliance with treatment guidelines signifying by the value of \(\eta \) (i.e., 0.1) which instigated \(\alpha _3=0.3, \tau =0.3, \gamma _2=0.005\), the population of the infectious individuals rises continuously. The rising nature of the curve in Fig. 2b pushes the disease to the stable endemic state as the reproduction numbers \(R_H\) and \(R_r\) equal 7.883 and 0.544 respectively. In this scenario, disregard for compliance with the Lassa fever treatment procedures alone accounts for the endemicity of the disease (i.e., \(R_H=7.883\)). It is therefore evident that total compliance with Lassa fever treatment guidelines is key to the eradication of the disease in the endemic areas.

5 Conclusion

In this work, a deterministic model was formulated via a system of first-order differential equations to examine the effect of treatment compliance on the dynamics and control of Lassa fever. The human and rodent populations were considered and model validity was established. The threshold quantities \(R_H\) and \(R_r\), that governed disease spread or elimination, were also derived. The necessary and sufficient conditions for the existence of both local and global stability of the DFE and the endemic equilibrium in relation to the threshold quantities \(R_H\) and \(R_r\) were also derived. Sensitivity analysis was further carried out for the threshold quantities \(R_H\) and \(R_r\) to quantify the effect of each model parameter on the spread and management of Lassa fever. The result revealed that the most sensitive parameters on the threshold quantities \(R_H\) and \(R_r\) were the human recruitment rate \((\beta _h)\), the recruitment rate for rodents \((\varphi _r)\), the effective contact rate between susceptible and infectious humans \((\alpha _3)\) and the proportion of infected individuals who comply with treatment guidelines \((\eta )\). Based on this result, simulations were conducted to investigate the impact of the sensitive parameters on the dynamical spread of the disease in terms of the population of the infectious individuals. In general, the outcomes of this work indicate that any interventions that ensure strict compliance with Lassa fever treatment guidelines and at the same time, reduce the population of rodents, will revolutionize the eradication of Lassa virus approaches in the endemic regions. A good instance of such interventions is to make disregard for Lassa fever treatment guidelines an offense punishable under the law. Also, rodent population may be reduced by a means of sanitation as well as application of any of the available rodent killer such as traps and rodenticides.