1 Introduction

In recent years, fractional calculus have been employed in many areas such as electrical networks, control theory of dynamical systems, probability and statistics, electrochemistry of corrosion, chemical physics, optics, engineering, acoustics, viscoelasticity, material science, and signal processing can be successfully modeled by linear or nonlinear fractional order differential equations [1–9]. But these nonlinear fractional differential equations are difficult to get their exact solutions [10].

Late eighteenth-century biologists began to develop techniques in population modeling in order to understand the dynamics of growing and shrinking populations of living organisms. Thomas Malthus was one of the first to note that populations grew with a geometric pattern while contemplating the fate of humankind [11]. One of the most basic and milestone models of population growth was the logistic model of population growth formulated by Pierre Francois Verhulst in 1838. The logistic model takes the shape of a sigmoid curve and describes the growth of a population as exponential, followed by a decrease in growth, and bound by a carrying capacity due to environmental pressures [12]. Population modeling became of particular interest to biologists in the twentieth century as pressure on limited means of sustenance due to increasing human populations in parts of Europe was noticed by biologist such as Raymond Pearl. In 1921, Pearl invited physicist Alfred J. Lotka to assist him in his laboratory. Lotka developed paired differential equations that showed the effect of a parasite on its prey. Mathematician Vivo Volterra equated the relationship between two species independent from Lotka. Together, Lotka and Volterra formed the Lotka–Volterra model for competition that applies the logistic equation to two species illustrating competition, predation, and parasitism interactions between species [3]. In 1939, contributions to population modeling were given by Patrick Leslie as he began work in biomathematics.

In this paper, we extend the make use of a modified iteration method to the time-fractional biological population model [13], and a representative biological population diffusion equation is u t (x, y, t) = u 2 x,x  + u 2 y,y  + σ(u) where u(x, y, t) denotes the population density and σ(u) represents the population supply due to births and deaths. In this paper, a generalized time-fractional nonlinear biological population diffusion equation of the following form is considered:

$$ \frac{{\partial^{\alpha } u(x,y,t)}}{{\partial t^{\alpha } }} = \frac{{\partial^{2} u^{2} (x,y,t)}}{{\partial x^{2} }} + \frac{{\partial^{2} u^{2} (x,y,t)}}{{\partial y^{2} }} + hu^{a} (x,y,t)\left( {1 - ru^{b} (x,y,t)} \right) $$
(1)

Subject to the initial condition

$$ u\left( {x,y,0} \right) = g(x,y) $$
(2)

where a, b, r, and h are real numbers, and according to Malthusian law and Verhulst law, we consider a more general form of σ(u) as

$$ \sigma \left( u \right) = hu^{a} \left( {x,y,t} \right)\left( {1 - ru^{b} (x,y,t)} \right) $$
(3)

The derivative in Eq. (1) is the Caputo derivative. Linear and nonlinear population systems were solved in [13] and [14] by using variational iteration method (VIM) and Adomian decomposition method (ADM). However, one of the disadvantages of ADM is the inherent difficulty in calculating the Adomian polynomials, VIM, the Lagrange multiplier, and the so-called correctional function. In this letter, we are interested in extending the applicability of HDM to population systems of fractional differential Eq. (1). The homotopy decomposition method (HDM) was recently proposed by Atangana [15–17] to solve fractional derivatives equation. To demonstrate the effectiveness of the HDM algorithm, several numerical examples of fractional biological population systems shall be presented.

2 Fundamental characters of the homotopy decomposition method

To exemplify the fundamental suggestion of this method, we think about a universal nonlinear nonhomogeneous fractional partial differential equation with initial conditions of the following form [15, 16]

$$ \frac{{\partial^{\alpha } U(x, t)}}{{\partial t^{\alpha } }} = L\left( {U\left( {x,t} \right)} \right) + N\left( {U\left( {x,t} \right)} \right) + f\left( {x,t} \right), \alpha > 0 $$
(4)

Subject to the initial condition

$$ \begin{gathered} D_{0}^{\alpha - k} U\left( {x,0} \right) = f_{k} \left( x \right), \left( {k = 0, \ldots ,n - 1} \right), D_{0}^{\alpha - n} U\left( {x,0} \right) = 0 {\text{\,and }}n = \left[ \alpha \right] \hfill \\ D_{0}^{k} U\left( {x,0} \right) = g_{k} \left( x \right), \left( {k = 0, \ldots ,n - 1} \right), D_{0}^{n} U\left( {x,0} \right) = 0 {\text{\,and }} n = \left[ \alpha \right] \hfill \\ \end{gathered} $$

Where \( \frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }} \) denotes the Caputo or Riemann–Liouville fractional derivative operator, f is a known function, N is the general nonlinear fractional differential operator, and L represents a linear fractional differential operator. The technique first movement here is to change the fractional partial differential equation to the fractional partial integral equation by applying the inverse operator \( \frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }} \) of on both sides of Eq. (4) to obtain: In the case of Riemann–Liouville fractional derivative

$$ U\left( {x,t} \right) = \mathop \sum \limits_{j = 1}^{n - 1} \frac{{f_{j} \left( x \right)}}{\varGamma (\alpha - j + 1)}t^{\alpha - j} + \frac{1}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \left( {t - \tau } \right)^{\alpha - 1} \left[ {L(U(x,\tau ) ) + N(U(x,\tau ) ) + f(x,\tau )} \right]d\tau $$
(5)

In the case of Caputo fractional derivative

$$ U\left( {x,t} \right) = \mathop \sum \limits_{j = 1}^{n - 1} \frac{{g_{j} \left( x \right)}}{\varGamma (\alpha - j + 1)}t^{\alpha - j} + \frac{1}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \left( {t - \tau } \right)^{\alpha - 1} \left[ {L(U(x,\tau ) ) + N(U(x,\tau ) ) + f(x,\tau )} \right]d\tau $$

or in general by putting

$$ \mathop \sum \limits_{j = 1}^{n - 1} \frac{{f_{j} \left( x \right)}}{\varGamma (\alpha - j + 1)}t^{\alpha - j} = f\left( {x,t} \right) \rm\, or\,\, \it f\left( {x,t} \right) = \mathop \sum \limits_{j = 1}^{n - 1} \frac{{g_{j} \left( x \right)}}{\varGamma (\alpha - j + 1)}t^{\alpha - j} $$

We obtain the following:

$$ U\left( {x,t} \right) = T(x,t) + \frac{1}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \left( {t - \tau } \right)^{\alpha - 1} \left[ {L(U(x,\tau ) ) + N(U(x,\tau ) ) + f(x,\tau )} \right]{\text{d}}\tau $$
(6)

In the HDM, the basic assumption is that the solutions can be written as a power series in p

$$ U(x,t,p) = \mathop \sum \limits_{n = 0}^{\infty } p^{n} U_{n} \left( {x,t} \right), $$
(7)
$$ U\left( {x,t} \right) = \mathop {\lim }\limits_{p \to 1} U(x,t,p) $$
(8)

and the nonlinear term can be decomposed as

$$ N\varPhi \left( {x,t} \right) = \mathop \sum \limits_{n = 0}^{\infty } p^{n} {\mathcal{H}}_{n} (U) $$
(9)

where \( p\int (0, 1] \) is an embedding parameter. \( {\mathcal{H}}_{n} (U) \) [21, 22] is the He’s polynomials that can be generated by

$$ \left( {{\mathcal{H}}_{n} \left( {U_{0} , \ldots ,U_{n} } \right) = \frac{1}{n!}\frac{{\partial^{n} }}{{\partial p^{n} }}\left[ {N\left( {\mathop \sum \limits_{j = 0}^{\infty } p^{j} U_{j} (x,t)} \right)} \right],n = 0,1,2 \ldots } \right) $$
(10)

The HDM is obtained by means of the refined combination of homotopy technique with He’s polynomials and is given by

$$ \mathop \sum \limits_{n = 0}^{\infty } p^{n} U_{n} (x,t) - T\left( {x,t} \right) = \frac{p}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \left( {t - \tau } \right)^{\alpha - 1} \left[ {f\left( {x,\tau } \right) + L\left( {\mathop \sum \limits_{n = 0}^{\infty } p^{n} U_{n} (x,\tau )} \right) + N\left( {\mathop \sum \limits_{n = 0}^{\infty } p^{n} U_{n} (x,\tau )} \right)} \right]d\tau $$
(11)

Comparing the terms of same powers of p gives solutions of various orders with the first term:

$$ U_{0} \left( {x,t} \right) = T(x,t) .$$
(12)

3 Convergence and uniqueness analysis

In the literature, there exist a lot of papers dealing with solutions of nonlinear differential equation. However, the stability and uniqueness analysis are not presented, and this leads to thing that these classes of papers are just a high school exercise since there is no piece of mathematics in, just presentation of some examples and figures. It is perhaps important to point out that the most difficult task after presenting these examples is to prove the stability of the method. We will devote this section to the analysis of the convergence of the method used for fractional biological equation and the uniqueness of the special solution obtained by using this method. We shall start this section by presenting the following useful definition (Fig. 1).

Fig. 1
figure 1

Absolute value of approximate solution for \( \varvec{\alpha}= 0.8 \)

Full size image

Definition 1

Let \( \varOmega = [a b]\left( { - \infty \le a < b \le \infty } \right) \) be a finite or infinite interval of real axis \( {\mathbb{R}} = \left( { - \infty , \infty } \right) \). We denote by \( L_{p} \left( {a, b} \right)\left( {1 \le p \le \infty } \right) \) the set of those Lebesgue complex-valued measurable functions f on Ω for which \( \left\| f \right\|_{p} < \infty, \) where

$$ \left\| f \right\|_{p} = \left( {\mathop \int \limits_{a}^{b} \left| {f(t)} \right|^{p} dt} \right)^{\frac{1}{p}} \left( {1 \le p \le \infty } \right) $$
(13)

We shall in addition of the above definition present, the following useful theorem.

Theorem 1

If \( h(t) \in L_{1} \left( {\mathbb{R}} \right) \) and \( h_{1} (t) \in L_{p} \left( {\mathbb{R}} \right) \) , then their convolution \( \left( {h*h_{1} } \right)\left( x \right) \in L_{p} \left( {\mathbb{R}} \right)\left( {1 \le p \le \infty } \right) \) , and the following inequality holds [3]:

$$ \left\| {f\left( {h * h_{1} } \right)\left( x \right)} \right\|_{p} < \left\| h \right\|_{1} \left\| {h_{1} } \right\|_{p} $$
(14)

In particular, if \( h(t) \in L_{1} \left( {\mathbb{R}} \right) \) and \( h_{1} (t) \in L_{2} \left( {\mathbb{R}} \right) \) , then their convolution \( \left( {h*h_{1} } \right)\left( x \right) \in L_{2} \left( {\mathbb{R}} \right) \) then,

$$ \left\| {f\left( {h * h_{1} } \right)\left( x \right)} \right\|_{2} < \left\| h \right\|_{1} \left\| {h_{1} } \right\|_{2} .$$

There exists a vast literature on different definitions of fractional derivatives. The most popular ones are the Riemann–Liouville and the Caputo derivatives. For Caputo, we have

$$ {}_{0}^{C} D_{x}^{\alpha } \left( {f\left( x \right)} \right) = \frac{1}{\varGamma (n - \alpha )}\mathop \int \limits_{0}^{x} \left( {x - t} \right)^{n - \alpha - 1} \frac{{{\text{d}}^{n} f(t)}}{{{\text{dt}}^{n} }}{\text{dt}} $$
(15)

For the case of Riemann–Liouville we have the following definition

$$ D_{x}^{\alpha } \left( {f\left( x \right)} \right) = \frac{1}{\varGamma (n - \alpha )}\frac{{d^{n} }}{{dx^{n} }}\mathop \int \limits_{0}^{x} \left( {x - t} \right)^{n - \alpha - 1} f(t){\text{dt}} $$
(16)

Each one of these fractional derivative presents some compensations and weakness [2, 6]. The Riemann–Liouville derivative of a constant is not zero, while Caputo’s derivative of a constant is zero but demands higher conditions of regularity for differentiability [2, 6]: To compute the fractional derivative of a function in the Caputo sense, we must first calculate its derivative. Caputo derivatives are defined only for differentiable functions, while functions that have no first-order derivative might have fractional derivatives of all orders less than one in the Riemann–Liouville sense [18, 19]. Recently, Guy Jumarie (see [20]) proposed a simple alternative definition to the Riemann–Liouville derivative.

$$ D_{x}^{\alpha } \left( {f\left( x \right)} \right) = \frac{1}{\varGamma (n - \alpha )}\frac{{d^{n} }}{{{\text{dx}}^{n} }}\mathop \int \limits_{0}^{x} \left( {x - t} \right)^{n - \alpha - 1} \left\{ {f\left( t \right) - f(0)} \right\}{\text{dt}} $$
(17)

His modified Riemann–Liouville derivative seems to have advantages of both the standard Riemann–Liouville and Caputo fractional derivatives: It is defined for arbitrary continuous (nondifferentiable) functions, and the fractional derivative of a constant is equal to zero. However, from its definition, we do not actually give a fractional derivative of a function says f(x) but the fractional derivative of f(x) − f(0) and always leads to fractional derivative that is not defined at the origin for some function that does not exist at the origin.

Lemma 1

[3] the fractional integration operators with \( \Re (\alpha ) > 0 \) are bounded in \( L_{p} \left( {a, b} \right)\left( {1 \le p \le \infty } \right) \)

$$\left\| {I_{a}^{\alpha } f} \right\|_{p} \le K \left\| {f} \right\|_{p} , K = \frac{{\left( {b - a} \right)^{\Re (\alpha )} }}{{\Re (\alpha )\left| {\varGamma \left( \alpha \right)} \right|}} $$
(18)

To prove the convergence and the uniqueness, let us consider equation in the Hilbert space \( {\mathcal{H}} = L^{2} \left( {\left( {\eta , \lambda } \right) \times \left[ {0, T} \right]} \right) \), defined as

$$ {\mathcal{H}} = \left\{ {\left( {u,v} \right): \left( {\eta , \lambda } \right) \times \left[ {0, T} \right]{\text{\,with}}, \mathop \int \nolimits uvd\iota d\kappa < \infty } \right\} $$

Then, the operator is of the form

$$ R\left( u \right) = \frac{{\partial^{2} u^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} u^{2} }}{{\partial y^{2} }} + hu^{a} \left( {1 - ru^{b} } \right) $$
(19)

The projected investigative is convergent if the subsequent necessities are congregated.

Proposition 1

There is a possibility for us to establish a positive constant says β such that the inner product holds in \( {\mathbf{\mathcal{H}}} \)

$$ \left( {R\left( u \right) - R\left( v \right), u - v} \right) \le \beta \left\| {u - v} \right\|, \rm for\, all\, v,u \in {\mathcal{H}} $$
(20)

Proposition 2

To the extent that for all \( v,u \in H \) are circumscribed entailing, we can come across a positive constant says χ such that: \( \left\| u \right\|,\left\| v \right\| \le \chi \), then we can discover \( \varPhi \left( \chi \right) > 0 \) such that

$$ \left( {R\left( u \right) - R\left( v \right), m} \right) \le \varPhi \left( \chi \right)\left\| {u - v} \right\|\left\| m \right\|, {\text{for all\,\,}} m \in H $$

We can as a result shape the ensuing theorem for the sufficient condition for the convergence of Eq. (1)

Theorem 2

Let us think about

$$ R\left( u \right) = \frac{{\partial^{\alpha } u}}{{\partial t^{\alpha } }} = \frac{{\partial^{2} u^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} u^{2} }}{{\partial y^{2} }} + hu^{a} \left( {1 - ru^{b} } \right) $$

and consider the initial and boundary condition for Eq. (1), then the proposed method leads to a special solution of Eq. (1). We shall present the proof of this theorem by just verifying the hypothesis 1 and 2.

Proof 1

Using the defined operator, we obtain the following

$$ R\left( u \right) - R\left( v \right) = \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {u^{2} - v^{2} } \right] + \frac{{\partial^{2} }}{{\partial y^{2} }}\left[ {u^{2} - v^{2} } \right] + h\left[ {u^{a} - v^{a} } \right] + hr\left[ {v^{a + b} - u^{a + b} } \right] $$
(21)

With the above reduction in hand, it is therefore possible for us to evaluate the following inner product

$$ \begin{aligned} \left( {R\left( u \right) - R\left( v \right),u - v} \right) & = \left( {\frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {u^{2} - v^{2} } \right],u - v} \right) + \left( {\frac{{\partial^{2} }}{{\partial y^{2} }}\left[ {u^{2} - v^{2} } \right],u - v} \right) \\ & \quad + \left( {h\left[ {u^{a} - v^{a} } \right],u - v} \right) - \left( {hr\left[ {u^{a + b} - v^{a + b} } \right], u - v} \right) \\ \end{aligned} $$
(22)

We shall assume that \( u, v \) are bounded, and we can find a positive constant l such that their inner product is bounded as \( \left( {u,v} \right),\left( {v,v} \right) \rm and \left( {\it u,u} \right) < l \). By employing the so-called Schwartz inequality, we obtain first

$$ \left( {\frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {u^{2} - v^{2} } \right],u - v} \right) \le \left\| {\left( {u^{2} - v^{2} } \right)_{xx} } \right\|\left\| {u - v} \right\| $$
(23)

And in view of the fact that, we are able to find two positive constant \( \rho_{1} , \rho_{2} \) such that \( \left\| {\left( {u^{2} - v^{2} } \right)_{xx} } \right\| \le \rho_{1} \rho_{2} \left\| {u^{2} - v^{2} } \right\| \) in addition to this, since (u, u) < l, then we have the following

$$ \left\| {\left( {u^{2} - v^{2} } \right)_{xx} } \right\| \le 4l^{2} \rho_{1} \rho_{2} $$
(24)

So that

$$ \left( {\frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {u^{2} - v^{2} } \right],u - v} \right) \le 4l^{2} \rho_{1} \rho_{2} \left\| {u - v} \right\| $$
(25)

In the same manner, we obtain that

$$ \left( {\frac{{\partial^{2} }}{{\partial y^{2} }}\left[ {u^{2} - v^{2} } \right],u - v} \right) \le 4l^{2} \rho_{3} \rho_{4} \left\| {u - v} \right\| $$
(26)

Let us take care of the following expression (h[u a − v a], u - v), now using again the Schwartz inequality

$$ \left( {h\left[ {u^{a} - v^{a} } \right],u - v} \right) \le h \left\| {u^{a} - v^{a}} \right\| \left\| {u - v} \right\| $$
(27)

Note that,

$$ u^{a} - v^{a} = \left( {u - v} \right)\mathop \sum \limits_{k = 0}^{a - 1} \left( {\begin{array}{*{20}c} a \\ k \\ \end{array} } \right)u^{k} v^{a - 1 - k} ,\left( {\begin{array}{*{20}c} a \\ k \\ \end{array} } \right) = \frac{{\varGamma \left( {\alpha + 1} \right)}}{{k!\varGamma \left( {\alpha - k + 1} \right)}} , \varGamma \left( x \right) = \mathop \int \limits_{0}^{\infty } t^{x - 1} e^{ - t} dz $$
(28)

Therefore, using the fact that \( \left( {u,v} \right),\left( {v,v} \right) and \left( {u,u} \right) < l \). Then, we can obtain the following inequality

$$ \left( {h\left[ {u^{a} - v^{a} } \right],u - v} \right) \le 2hl ^{a} \left| {\mathop \sum \limits_{k = 0}^{a - 1} \frac{{\varGamma \left( {a + 1} \right)}}{{k!\varGamma \left( {a - k + 1} \right)}}} \right|\left\| {u - v} \right\| $$
(29)

In the similar manner, we can obtain

$$ \left( {hr\left[ {v^{a + b} - u^{a + b} } \right], u - v} \right) \le 2hl ^{a + b} \left| {\mathop \sum \limits_{k = 0}^{a - 1} \frac{{\varGamma \left( {a + b + 1} \right)}}{{k!\varGamma \left( {a + b - k + 1} \right)}}} \right|\left\| {u - v} \right\| $$
(30)

We can therefore conclude without fear that

$$ \left( {R\left( u \right) - R\left( v \right),u - v} \right) \le \left( { 4l^{2} \rho_{1} \rho_{2} + 4l^{2} \rho_{3} \rho_{4} + 2hl ^{a} \left| {\mathop \sum \limits_{k = 0}^{a - 1} \frac{{\varGamma \left( {a + 1} \right)}}{{k!\varGamma \left( {a - k + 1} \right)}}} \right| + 2hl ^{a + b} \left| {\mathop \sum \limits_{k = 0}^{a - 1} \frac{{\varGamma \left( {a + b + 1} \right)}}{{k!\varGamma \left( {a + b - k + 1} \right)}}} \right|} \right)\left\| {u - v} \right\| $$
(31)

Take now

$$ \beta = 4l^{2} \rho_{1} \rho_{2} + 4l^{2} \rho_{3} \rho_{4} + 2hl ^{a} \left| {\mathop \sum \limits_{k = 0}^{a - 1} \frac{{\varGamma \left( {a + 1} \right)}}{{k!\varGamma \left( {a - k + 1} \right)}}} \right| + 2hl ^{a + b} \left| {\mathop \sum \limits_{k = 0}^{a - 1} \frac{{\varGamma \left( {a + b + 1} \right)}}{{k!\varGamma \left( {a + b - k + 1} \right)}}} \right| $$
(32)

We conclude that

$$ \left( {R\left( u \right) - R\left( v \right), u - v} \right) \le \beta \left\| {u - v} \right\|, {\text{for all}}\, v,u \in {\mathcal{H}} $$

Then, proposition 1 is verified. Let us handle now proposition 2. To do this, we compute

$$ \left( {R\left( u \right) - R\left( v \right),m} \right) = \left( {\frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {u^{2} - v^{2} } \right],m} \right) + \left( {\frac{{\partial^{2} }}{{\partial y^{2} }}\left[ {u^{2} - v^{2} } \right],m} \right) + \left( {h\left[ {u^{a} - v^{a} } \right],m} \right) - \left( {hr\left[ {u^{a + b} - v^{a + b} } \right], m} \right) \le \varPhi \left( \chi \right)\left\| {u - v} \right\|\left\| m \right\| $$
(33)

With

$$ \varPhi \left( \chi \right) = 2\chi \rho_{1} \rho_{2} + 2\chi \rho_{3} \rho_{4} + 2h\chi ^{a - 1} \left| {\mathop \sum \limits_{k = 0}^{a - 1} \frac{{\varGamma \left( {a + 1} \right)}}{{k!\varGamma \left( {a - k + 1} \right)}}} \right| + 2hl ^{a + b - 1} \left| {\mathop \sum \limits_{k = 0}^{a - 1} \frac{{\varGamma \left( {a + b + 1} \right)}}{{k!\varGamma \left( {a + b - k + 1} \right)}}} \right| $$

And proposition 2 is also verified. Now, in the light of theorem 1, proposition 1, and 2 together with lemma 1, we can happily conclude that the decomposition method used here works perfectly for fractional biological population equation.

Theorem 3

Taking into account the initial conditions for Eq. ( 1 ) then the special solution of Eq. ( 1 ) u esp to which u convergence is unique.

Proof 3

Assuming that we can find another special solution say v esp, then by making use of the inner product together with hypothesis (1), we have the following

$$ \left( {R(u_{\text{esp}} ) - R\left( {v_{\text{esp}} } \right),\left( {u_{\text{esp}} - v_{\text{esp}} } \right)} \right) \le \beta \left\| {u_{\text{esp}} - v_{\text{esp}} } \right\| $$
(34)

using the fact that we can find a small natural number m 1 for which we can find a very small number ɛ such respecting the following inequality

$$ \left\| {u_{\text{esp}} - u} \right\| \le \frac{\varepsilon }{2\beta } $$
(35)

Also, we can find another natural number m 2 for which we can find a very small positive number ɛ that can respect the fact that

$$ \left\| {v_{\text{esp}} - u} \right\| \le \frac{\varepsilon }{2\beta } $$
(36)

taking therefore \( m = \hbox{max} \left( {m_{1} , m_{2} } \right) \) we have without fear that,

$$ \left( {R\left( {u_{\text{esp}} } \right) - R\left( {v_{\text{esp}} } \right),\left( {u_{\text{esp}} - v_{\text{esp}} } \right)} \right) \le \beta \left\| {u_{\text{esp}} - v_{\text{esp}} } \right\| = \beta \left\| {u_{\text{esp}} - u + u - v_{\text{esp}} } \right\| $$
(37)

Making use of the triangular inequality, we obtain the following

$$ \left( {R\left( {u_{\text{esp}} } \right) - R\left( {v_{\text{esp}} } \right),\left( {u_{\text{esp}} - v_{\text{esp}} } \right)} \right) \le \beta \left( {\left\| {u_{\text{esp}} - u} \right\| + \left\| {v_{\text{esp}} - u} \right\|} \right) \le \varepsilon . $$

It therefore turns out that

$$ \left( {R\left( {u_{\text{esp}} } \right) - R\left( {v_{\text{esp}} } \right),\left( {u_{\text{esp}} - v_{\text{esp}} } \right)} \right) = 0. $$
(38)

But according to the law of the inner product, the above equation implies that

$$ R\left( {u_{\text{esp}} } \right) - R\left( {v_{\text{esp}} } \right) = 0 {\text{or}} \left( {u_{\text{esp}} - v_{\text{esp}} } \right) = 0 $$

This concludes the uniqueness of our special solution.

4 Application of algorithm

In this section, we apply this method for solving fractional biological population equation with time- and space-fractional derivatives.

Example 1

Consider (1) with a = 1, r = 0, corresponding to Malthusian law, we have the following fractional biological population equation:

$$ \frac{{\partial^{\alpha } u}}{{\partial t^{\alpha } }} = \frac{{\partial^{2} u^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} u^{2} }}{{\partial y^{2} }} + hu $$
(39)

Subject to the initial condition

$$ u\left( {x,y,0} \right) = \root{}\of{xy} $$
(40)

According to the HDM that was presented earlier in Sect. 3, we obtain the following equation.

$$ \mathop \sum \limits_{n = 0}^{\infty } p^{n} u_{n} \left( {x,y,t} \right) = u\left( {x,y,0} \right) + \frac{p}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \partial_{xx} \left( {\mathop \sum \limits_{n = 0}^{\infty } p^{n} u_{n} \left( {x,y,t} \right)} \right)^{2} + \partial_{yy} \left( {\mathop \sum \limits_{n = 0}^{\infty } p^{n} u_{n} \left( {x,y,t} \right)} \right)^{2} + h\mathop \sum \limits_{n = 0}^{\infty } p^{n} u_{n} \left( {x,y,t} \right) $$
(41)

Comparing the terms of the same power of p yields:

$$ \begin{gathered} p^{0} : u_{0} \left( {x,y,t} \right) = u\left( {x,y,0} \right) = \root{}\of{xy} \hfill \\ p^{1} : u_{1} \left( {x,y,t} \right) = \frac{1}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \partial_{x,x} u_{0}^{2} \left( {x,y,\tau } \right) + \partial_{y,y} u_{0}^{2} \left( {x,y,\tau } \right) + hu_{0} \left( {x,y,\tau } \right)d\tau ,u_{1} \left( {x,y,0} \right) = 0 \hfill \\ p^{n} : u_{n} \left( {x,y,t} \right) = \frac{1}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \mathop \sum \limits_{j = 0}^{n - 1} \left( {u_{j} } \right)_{xx} \left( {u_{n - j - 1} } \right)_{xx} + \mathop \sum \limits_{j = 0}^{n - 1} \left( {u_{j} } \right)_{yy} \left( {u_{n - j - 1} } \right)_{yy} + hu_{n - 1} \left( {x,y,\tau } \right)d\tau ,u_{n} \left( {x,y,0} \right) = 0, n \ge 2 \hfill \\ \end{gathered} $$
(42)

The following solutions are obtained

$$ \begin{aligned} &u_{0} \left( {x,y,t} \right) = u\left( {x,y,0} \right) = \root{}\of{xy} \\ &u_{1} \left( {x,y,t} \right) = \frac{{ht^{\alpha } }}{\varGamma (1 + \alpha )}\root{}\of{xy} \\ &u_{2} \left( {x,y,t} \right) = \frac{{h^{2} t^{2\alpha } }}{\varGamma (1 + 2\alpha )}\root{}\of{xy} \\ &u_{3} \left( {x,y,t} \right) = \frac{{h^{3} t^{3\alpha } }}{\varGamma (1 + 3\alpha )}\root{}\of{xy} \\ &u_{4} \left( {x,y,t} \right) = \frac{{h^{4} t^{4\alpha } }}{\varGamma (1 + 4\alpha )}\root{}\of{xy} \\ &\vdots \\ &u_{n} \left( {x,y,t} \right) = \frac{{h^{n} t^{n\alpha } }}{\varGamma (1 + n\alpha )}\root{}\of{xy} . \\ \end{aligned} $$
(43)

It follows that for N = n the approximated solution from HDM is

$$ u_{N = n} \left( {x,y,t} \right) = \mathop \sum \limits_{n = 0}^{N} \frac{{h^{n} t^{n\alpha } }}{\varGamma (1 + n\alpha )}\root{}\of{xy} , $$
(44)

therefore

$$ u\left( {x,y,t} \right) = \sum\limits_{n = 0}^{\infty } {\frac{{h^{n} t^{n\alpha } }}{\varGamma (1 + n\alpha )}\root{}\of{xy} = \root{}\of{xy} E_{\alpha } (ht^{\alpha } )} $$
(45)

Here, E α (ht α) is the Mittag–Leffler function, defined as

$$ \mathop \sum \limits_{n = 0}^{\infty } \frac{{x^{n\alpha } }}{\varGamma (1 + n\alpha )} = E_{\alpha } (x^{\alpha } ) $$
(46)

Now, notice that if α = 1, Eq. (46) is reduced to the following:

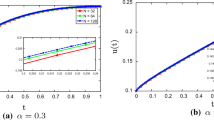
$$ u\left( {x,y,t} \right) = \mathop \sum \limits_{n = 0}^{\infty } \frac{{h^{n} t^{n} }}{\varGamma (1 + n)}\root{}\of{xy} = \root{}\of{xy} {\text{Exp}}(ht) $$
(47)

This is the exact solution for example 1 when α = 1. The following figures show the graphical representation of the approximated solution (45) and the exact solution for different values of α. It is easy to conclude that the approximate solution of fractional biological population model is continuous increasing function of alpha, as the parameter alpha is decreasing (Fig. 2).

Fig. 2
figure 2

Absolute value of approximated solution or exact solution \( \varvec{ \alpha } = 1 \)

Full size image

Example 2

Let us consider the following fractional biological population model

$$ \partial_{t}^{\alpha } u\left( {x,y,t} \right) = \partial_{xx} u^{2} (x,y,t) + \partial_{yy} u^{2} (x,y,t) - u(x,y,t)\left( {1 + \frac{8}{9}u(x,y,t)} \right) $$
(48)

Subject to the initial condition

$$ u\left( {x,y,0} \right) = \exp \left( {\frac{1}{3}x + y} \right) $$
(49)

Following the discussion presented earlier in Sect. 3, we arrive to the following:

$$ \begin{gathered} p^{0} : u_{0} \left( {x,y,t} \right) = u\left( {x,y,0} \right) = \exp \left( {\frac{1}{3}x + y} \right) \hfill \\ p^{1} : u_{1} \left( {x,y,t} \right) = \frac{1}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \partial_{x,x} u_{0}^{2} + \partial_{y,y} u_{0}^{2} - u_{0} \left( {1 + \frac{8}{9}u_{0} } \right)d\tau ,u_{1} \left( {x,y,0} \right) = 0 \hfill \\ \end{gathered} $$
$$ p^{n} : u_{n} \left( {x,y,t} \right) = \frac{1}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \mathop \sum \limits_{j = 0}^{n - 1} \left( {u_{j} } \right)_{xx} \left( {u_{n - j - 1} } \right)_{xx} + \mathop \sum \limits_{j = 0}^{n - 1} \left( {u_{j} } \right)_{yy} \left( {u_{n - j - 1} } \right)_{yy} - u_{n - 1} - \frac{8}{9}\mathop \sum \limits_{j = 0}^{n - 1} u_{j} u_{n - j - 1} d\tau ,u_{n} \left( {x,y,0} \right) = 0,n \ge 2. $$
(50)

The following solutions are obtained

$$ \begin{gathered} u\left( {x,y,0} \right) = \exp \left( {\frac{1}{3}x + y} \right) \hfill \\ u_{1} \left( {x,y,t} \right) = \frac{{ - t^{\alpha } }}{\varGamma (1 + \alpha )}\exp \left( {\frac{1}{3}x + y} \right) \hfill \\ u_{2} \left( {x,y,t} \right) = \frac{{t^{2\alpha } }}{\varGamma (1 + 2\alpha )}\exp \left( {\frac{1}{3}x + y} \right) \hfill \\ u_{3} \left( {x,y,t} \right) = \frac{{ - t^{3\alpha } }}{\varGamma (1 + 3\alpha )}\exp \left( {\frac{1}{3}x + y} \right) \hfill \\ u_{4} \left( {x,y,t} \right) = \frac{{t^{4\alpha } }}{\varGamma (1 + 4\alpha )}\exp \left( {\frac{1}{3}x + y} \right) \hfill \vdots\\ \hfill \\ u_{n} \left( {x,y,t} \right) = \frac{{( - 1)^{n} t^{n\alpha } }}{\varGamma (1 + n\alpha )}\exp \left( {\frac{1}{3}x + y} \right) \hfill \\ \end{gathered} $$
(51)

It follows that for N = n the approximated solution from HDM is

$$ u_{N = n} \left( {x,y,t} \right) = \mathop \sum \limits_{n = 0}^{N} \frac{{( - 1)^{n} t^{n\alpha } }}{\varGamma (1 + n\alpha )}\exp \left( {\frac{1}{3}x + y} \right) $$
(52)

Therefore,

$$ u\left( {x,y,t} \right) = \mathop \sum \limits_{n = 0}^{\infty } \frac{{( - 1)^{n} t^{n\alpha } }}{\varGamma (1 + n\alpha )}\exp \left( {\frac{1}{3}x + y} \right) = \exp \left( {\frac{1}{3}x + y} \right)E_{\alpha } ( - t^{\alpha } ) $$
(53)

Now, notice that if α = 1, Eq. (4) is reduced to the following:

$$ u\left( {x,y,t} \right) = \exp \left( {\frac{1}{3}x + y - t} \right) $$
(54)

This is the exact solution for example 2 when α = 1.

Example 3

Consider (1.1) with \( a = 1, r = 0\rm\, and \,\it h = 1 \), corresponding to Malthusian law, we have the following fractional biological population equation:

$$ \frac{{\partial^{\alpha } u}}{{\partial t^{\alpha } }} = \frac{{\partial^{2} u^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} u^{2} }}{{\partial y^{2} }} + u $$
(55)

Subject to the initial condition

$$ u\left( {x,y,0} \right) = \root{}\of{\sin \left( x \right)\sin (y)} $$
(56)

According to the HDM that was presented earlier in Sect. 3, we obtain the following equation.

$$ \mathop \sum \limits_{n = 0}^{\infty } p^{n} u_{n} \left( {x,y,t} \right) = u\left( {x,y,0} \right) + \frac{p}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \partial_{xx} \left( {\mathop \sum \limits_{n = 0}^{\infty } p^{n} u_{n} \left( {x,y,t} \right)} \right)^{2} + \partial_{yy} \left( {\mathop \sum \limits_{n = 0}^{\infty } p^{n} u_{n} \left( {x,y,t} \right)} \right)^{2} + \mathop \sum \limits_{n = 0}^{\infty } p^{n} u_{n} \left( {x,y,t} \right) $$
(57)

Comparing the terms of the same power of p yields:

$$ \begin{gathered} p^{0} : u_{0} \left( {x,y,t} \right) = u\left( {x,y,0} \right) = \root{}\of{\sin \left( x \right)\sin (y} ) \hfill \\ p^{1} : u_{1} \left( {x,y,t} \right) = \frac{1}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \partial_{x,x} u_{0}^{2} \left( {x,y,\tau } \right) + \partial_{y,y} u_{0}^{2} \left( {x,y,\tau } \right) + u_{0} \left( {x,y,\tau } \right)d\tau , u_{1} \left( {x,y,0} \right) = 0 \hfill \\ \vdots \hfill \\ p^{n} : u_{n} \left( {x,y,t} \right) = \frac{1}{\varGamma (\alpha )}\mathop \int \limits_{0}^{t} \mathop \sum \limits_{j = 0}^{n - 1} \left( {u_{j} } \right)_{xx} \left( {u_{n - j - 1} } \right)_{xx} + \mathop \sum \limits_{j = 0}^{n - 1} \left( {u_{j} } \right)_{xx} \left( {u_{n - j - 1} } \right)_{xx} + u_{n - 1} \left( {x,y,\tau } \right)d\tau ,u_{n} \left( {x,y,0} \right) = 0, n \ge 2 \hfill \\ \end{gathered} $$
(58)

The following solutions are obtained

$$ \begin{gathered} u_{0} \left( {x,y,t} \right) = u\left( {x,y,0} \right) = \root{}\of{\sin \left( x \right)\sin (y)} \hfill \\ u_{1} \left( {x,y,t} \right) = \frac{{t^{\alpha } }}{\varGamma (1 + \alpha )}\root{}\of{\sin \left( x \right)\sin (y)} \hfill \\ u_{2} \left( {x,y,t} \right) = \frac{{t^{2\alpha } }}{\varGamma (1 + 2\alpha )}\root{}\of{\sin \left( x \right)\sin (y)} \hfill \\ u_{3} \left( {x,y,t} \right) = \frac{{t^{3\alpha } }}{\varGamma (1 + 3\alpha )}\root{}\of{\sin \left( x \right)\sin (y} \hfill \\ \vdots \hfill \\ u_{n} \left( {x,y,t} \right) = \frac{{t^{n\alpha } }}{\varGamma (1 + n\alpha )}\root{}\of{\sin \left( x \right)\sin (y)} \hfill \\ \end{gathered} $$
(59)

It follows that for N = n the approximated solution from HDM is

$$ u_{N = n} \left( {x,y,t} \right) = \mathop \sum \limits_{n = 0}^{N} \frac{{t^{n\alpha } }}{\varGamma (1 + n\alpha )}\root{}\of{\sin \left( x \right)\sin (y)} $$
(60)

Therefore

$$ u\left( {x,y,t} \right) = \mathop \sum \limits_{n = 0}^{\infty } \frac{{t^{n\alpha } }}{\varGamma (1 + n\alpha )}\root{}\of{xy} = \root{}\of{\sin \left( x \right)\sin (y)} E_{\alpha } (t^{\alpha } ) $$
(61)

Now notice that if α = 1, Eq. (1) is reduced to the following:

$$ u\left( {x,y,t} \right) = \mathop \sum \limits_{n = 0}^{\infty } \frac{{t^{n} }}{\varGamma (1 + n)}\root{}\of{\sin \left( x \right)\sin (y)} = \root{}\of{\sin \left( x \right)\sin (y)} Exp(t) $$
(62)

This is the exact solution for example 3 when α = 1. The following mure show the graphical representation of the approximated solution (62) when α = 1 (Fig. 3)

Fig. 3
figure 3

Absolute value of approximated solution or exact solution \( \varvec{ \alpha } = 1 \)

Full size image

Example 4

Consider (1.1) with a = 1, b = 1, corresponding to Malthusian law, we have the following fractional biological population equation:

$$ \frac{{\partial^{\alpha } u}}{{\partial t^{\alpha } }} = \frac{{\partial^{2} u^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} u^{2} }}{{\partial y^{2} }} + hu\left( {1 - ru} \right) $$
(63)

Subject to the initial condition

$$ u\left( {x,y,0} \right) = exp\left( {\root{}\of{\frac{hr}{8}} \left( {x + y} \right)} \right) $$
(64)

Following the discussion presented earlier in Sect. 3, we arrive to the following:

$$ \begin{gathered} u_{0} \left( {x,y,t} \right) = u\left( {x,y,0} \right) = \exp \left( {\sqrt{\frac{hr}{8}} \left( {x + y} \right)} \right) \hfill \\ u_{1} \left( {x,y,t} \right) = \frac{{h^{\alpha } t^{\alpha } }}{\varGamma (1 + \alpha )}\exp \left( {\sqrt{\frac{hr}{8}} \left( {x + y} \right)} \right) \hfill \\ u_{2} \left( {x,y,t} \right) = \frac{{h^{2\alpha } t^{2\alpha } }}{\varGamma (1 + 2\alpha )}\exp \left({\sqrt{\frac{hr}{8}} \left( {x + y} \right)} \right) \hfill \\ u_{3} \left( {x,y,t} \right) = \frac{{h^{3\alpha } t^{3\alpha } }}{\varGamma (1 + 3\alpha )}\exp \left( {\sqrt{\frac{hr}{8}} \left( {x + y} \right)} \right) \hfill \\ \vdots \hfill \\ u_{n} \left( {x,y,t} \right) = \frac{{h^{n\alpha } t^{n\alpha } }}{\varGamma (1 + n\alpha )}\exp \left( {\sqrt{\frac{hr}{8}} \left( {x + y} \right)} \right) \hfill \\ \end{gathered} $$
(65)

It follows that for N = n the approximated solution from HDM is

$$ u_{N = n} \left( {x,y,t} \right) = \mathop \sum \limits_{n = 0}^{N} \frac{{h^{n\alpha } t^{n\alpha } }}{\varGamma (1 + n\alpha )}\exp \left( {\root{}\of{\frac{hr}{8}} \left( {x + y} \right)} \right) $$

Therefore,

$$ u\left( {x,y,t} \right) = \mathop \sum \limits_{n = 0}^{\infty } \frac{{h^{n\alpha } t^{n\alpha } }}{\varGamma (1 + n\alpha )}\exp \left( {\root{}\of{\frac{hr}{8}} \left( {x + y} \right)} \right) = \root{}\of{\exp \left( {\root{}\of{\frac{hr}{8}} \left( {x + y} \right)} \right)} E_{\alpha } (h^{\alpha } t^{\alpha } ) $$
(66)

Now, notice that if α = 1, Eq. (4) is reduced to the following:

$$ u\left( {x,y,t} \right) = \mathop \sum \limits_{n = 0}^{\infty } \frac{{h^{n} t^{n} }}{\varGamma (1 + n)}\exp \left( {\root{}\of{\frac{hr}{8}} \left( {x + y} \right)} \right) = \exp \left( {\root{}\of{\frac{hr}{8}} \left( {x + y} \right)} \right){\rm exp}(ht) $$
(67)

This is the exact solution for example 4 when α = 1.

5 Conclusion

Although many analytical techniques have been proposed in the recent decade to deal with nonlinear equations, most of them have their weakness and limitations. In this paper, we put into operation new analytical techniques, the HDM, for solving nonlinear fractional partial differential equations arising in biological population dynamics system. Population biology is a study of populations of organisms, exceptionally the adaptation of population size; life history traits for instance clutch size; and extinction. The expression population biology is frequently used interchangeably with population ecology, even though population biology is supplementary generally used when studying diseases, viruses, and microbes, and population ecology is used more frequently when studying plants and animals.

The most challenging part while using iteration method is to provide the stability of the method on one hand, and the other to show in detail the convergence and the uniqueness analysis. We have in this paper with care presented the stability, the convergence, and the uniqueness analysis. We have shown some example analytical solutions, and some properties of these solutions show signs of biologically matter-of-fact reliance on the parameter values. The uniformity of this procedure and the lessening in computations award a wider applicability. In all examples, in the limit of infinitely many terms of the series solution yields the exact solution.