Abstract
In this paper, based on the dynamical system method, a new approach for investigating solutions of nonlinear time-fractional partial differential equations (PDEs) is introduced. By proposing a novel technique with separation variables, the phase portraits of system derived from the nonlinear time-fractional PDEs are analyzed, and the issue of existence for the solution of the time-fractional PDEs is considered. Moreover, the dynamical properties of the solution of the time-fractional PDEs are studied in detail. As examples, three nonlinear time-fractional models such as the reaction–diffusion model, the biology population model and the fluid model are studied by using this new approach. In some special parametric conditions, exact solutions of these models are obtained. The dynamical properties of some exact solutions are illustrated by graphs. Compared with the results in current studies, the results obtained in this paper are new.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Since the concept of fractional-order calculus was born in 1695, there have been many definitions of fractional-order derivative, so far, there are more than a dozen kinds of definitions. However, the more frequently used, classical and very widely influential definitions are still Riemann–Liouville definition, Caputo definition and Grünwald–Letnikov definition. We all know that the concept of fractional-order calculus appeared only one or two decades later than the concept of integer-order calculus, both of them arose Leibniz’s times. But the theory of fractional-order calculus develops very slowly and difficultly than the theory of integer-order calculus. As far as we know, there should be three reasons. The first reason which restricts the development of theory of fractional-order calculus is that the definitions of fractional-order derivative are too many to be unified, so they are very inconvenient to use in scientific and engineering fields. The second reason is that fractional-order calculus has been lack of application background for a long time in the past. The third reason is that fractional-order calculus has been lack of effective methods of solving and analytical tools on investigating solutions of fractional-order differential equations (FDEs). Phylogeny of fractional-order calculus and cruel reality tells us that the first problem is almost impossible to solve. However, on the other two issues, very good improvements have been made since the 1960s. On the application background of fractional-order differential models, it is found that more and more complex problems can be modeled by FDEs since the 1960s. Now, models that are established by the FDEs play very important roles in a range of scientific fields such as physics, chemistry, biology, mechanics, engineering, control theory and many other fields. Many experts and scholars in the fractional-order fields know that there are so many references in above fields. Unfortunately, the references are too much to all quote them at here. Although more and more FDEs are proposed, compared with the PDEs in the field of integer-order calculus, the FDEs are still less actually. In order to meet the shortcomings of the research for solving methods of FDEs, some classical PDEs in integer-order field are often directly transformed into FDEs. On the method of solving FDEs, in recent years, many effective methods have been used to solve FDEs; these methods contain the Adomian decomposition method [1, 2], homotopy analysis method [3, 4], first integral method [5], invariant analysis method [6, 7], fractional variational iteration method [8,9,10], invariant subspace method [11,12,13,14], method of fractional complex transformation [15,16,17,18], method of separating variables [19,20,21], and so forth. Although these methods can be successfully used to solve many FDEs, this is far from enough on discussing existence and dynamical properties of solutions of a more complex nonlinear FDE. In addition, the development of new analytical methods and techniques in the research fields of nonlinear FDEs is also primary task in the future.
Among the above-mentioned methods, we especially notice the method of fractional complex transformation. In references [15,16,17,18], some authors employed a fractional complex transformation such as \(u(x,t)=U(\xi ),\ \xi =\frac{p x^{\beta }}{\Gamma (1+\beta )}+\frac{q x^{\alpha }}{\Gamma (1+\alpha )}\) and the Jumarie’s fractional chain rule [22,23,24] such as \(D_x^{\alpha } f[u(x)]=f^{\prime }(u)D_x^{\alpha } u(x)=D_u^{\alpha } f(u)(u^{\prime }(x))^{\alpha },\) and then, they solved some fractional-order partial differential equations (PDEs) formed as
Finally, many exact traveling wave solutions of some nonlinear fractional-order PDEs formed as (1.1) have been obtained. At first glance, the effect of this method seems to be very good. However, the Jumarie’s fractional-order chain rule does not hold, which has been successively verified in Refs. [25,26,27]. So, we cannot use the Jumarie’s fractional chain rule to obtain exact traveling wave solutions of those nonlinear fractional-order PDEs defined by Riemann–Liouville derivative and Caputo derivative. Indeed, under the above two derivative definitions, people cannot truly obtain exact traveling wave solutions of nonlinear fractional-order PDEs such as those results in [15,16,17,18]. In order to remedy this shortcoming, we introduce a method for discussing existence and dynamical property of solutions of nonlinear fractional-order PDEs based on our previous works [27,28,29,30] and combined with bifurcation theory of differential dynamics [31,32,33,34]. We call this method the dynamic system method. As example, by using the introduced dynamic system method, we will discuss the existence and dynamic property of solutions of a kind of nonlinear time-fractional PDE named biology population model. Next, we will introduce the application background of this model.
In early research, biologists agree that the phenomenon of diffusion (or emigration) is a major factor in the change of the response biological population, which plays an important role in the regulation of population of biological species. Recently, biologists have also found that the phenomena of memory and anomalous diffusion are also two important factors in the change of the response biological population. If only the diffusion phenomenon is considered in the differential model of biological population, then the established model must be an nonlinear partial differential equation (PDE) of integer order. But if the phenomena of memory and anomalous diffusion are taken into account in modeling, the model can only be an nonlinear fractional partial differential equation (FPDE). When the phenomena of memory and diffusion are considered, according to the law of population balance, the total rate of change of biological population is satisfied by the following equation
where the function \(u=u(\vec {X},t)\) denotes population density which provides the number of individual persons per unit volume, the vector \(\vec {X}=(x,y)\) denotes the position in a local region D, the vector function \(\vec {\mu }=\vec {\mu }(\vec {X},t)\) denotes the diffusion velocity, the function \(f=f(\vec {X},t)\) denotes the rate of change of individual supplies per unit volume at position \(\vec {X},\) the A denotes the area of the region formed by the boundary of D, the V denotes the spatial volume, the \({\hat{n}}\) is the normal unit vector outward side of boundary of the region D, the \(\frac{d^{\alpha }}{\mathrm{d}t^{\alpha }}\) denotes the fractional-order derivative defined by Riemann–Liouville type or Caputo type and
where \(u>0,\ \eta (u)>0\) and \(\nabla \) is the Laplace operator. According to relations of (1.2) and (1.3), the following two-dimensional nonlinear degenerate parabolic PDE (of time-fractional order) for the population density can be obtained as
As an example for the modeling of the population of animals, Gurney and Nisbet [35] employed a special case of \(\phi (u).\) In particular, when \(\phi (u)=u^2,\) Eq. (1.4) becomes the following normal nonlinear time-fractional biology populations model [36]
where the sign \(\frac{\partial ^\alpha }{\partial t^\alpha }\) denotes fractional differential operator defined by the Riemann–Liouville derivative \( _0^{RL}D_t^{\alpha }\) or Caputo derivative \( _0^{C}D_t^{\alpha }\), and \(u=u(x,y,t),\)\(\alpha \in (0,1).\) As a special case, when \(f(u)=hu^a(1-ru^b),\) the numerical solutions of Eq. (1.5) are studied by Liu, Li and Zhang in [37].
When \(\alpha \rightarrow 1,\) Eq. (1.5) becomes a classical integer-order model as follows:
Some properties such as Hölder estimates of solutions of Eq. (1.6) have been studied by Lu in [38]. In particular, when \(f(u)=\delta u\) and \(\delta \) is an nonzero constant, Eq. (1.6) is a biology population model which satisfies the Malthusian growth law [39], where the variable u denotes the population density and f(u) represents the population supply due to births and deaths. When \(f(u)=\delta u-{\hat{\kappa }} u^2\) and \(\delta ,\ {\hat{\kappa }}\) are positive constants, Eq. (1.6) is a biology population model which satisfies the Verhulst growth law [39]. When \(f(u)=-{\hat{\kappa }} u^p\) and \({\hat{\kappa }}>0,\) Eq. (1.6) is a fluid model in porous media [40, 41]. Of course, we also can be regarded as that the time-fractional PDE (1.5) obtained directly by replacing the derivative term of the time part of the integer-order model (1.6). The reason of using time-fractional PDEs is that they are naturally related to models with memory and anomalous diffusion which exists many biological systems and diffusion-reaction systems. For example, biological populations (animals) can remember the change and distribution of food quantity affected by season and regional environment, and they know what season or area there will be a lot of food. Therefore, the biological population will migrate to the food-rich area, which will cause the biological population density to increase in this area for a period of time, which indicates that memory is also an important factor to determine the change and distribution of the biological population density. Therefore, in the modeling of this kind of problems, mathematicians and biologists usually use time-fractional derivatives to describe or denote memory phenomena. In addition, the results derived from the time-fractional PDE (1.5) are more general in nature than the corresponding integer-order PDE (1.6). The resulting solutions of the time-fractional PDE (1.5) spread faster than the classical solutions of the corresponding integer-order PDE (1.6) and may exhibit asymmetry. By the way, when \(0<\alpha <1,\ f(u)={\tilde{h}}(u^2-r)\) and \({\tilde{h}},\ r\) are constants, Eq. (1.5) becomes another nonlinear time-fractional biological population model as follows:
which is first appeared in [36]. By using the Adomian’s decomposition method, EI-Sayed et al. studied the exact solutions and approximate analytical solutions of model (1.7) in [36]. In [42], by using the fractional sub-equation method, the authors studied exact solutions of model (1.7). In [29], by using the method of separation variables combined with the homogeneous balance principle, Wu and Rui studied exact solutions of model (1.7).
The rest of this paper is organized as follows: In Sect. 2, based on the method of separation of variables and combined with bifurcation theory of dynamic system, we will introduce a new and effective way for discussing the existence of solution and dynamical property of solutions for nonlinear time-fractional PDE. In Sect. 3, by using the new method introduced in Sect. 2, under the case \(f(u)=\delta u+\kappa u^2,\) we will discuss the existence of solution and dynamical property of solutions for Eq. (1.5).
2 Summary of method for investigating solutions of nonlinear time-fractional PDE
Avoided Jumarie’s fractional chain rule, we will introduce a new and effective analytical approach for discussing the existence of solution and dynamical property of solutions for an nonlinear time-fractional PDE in this section. Compared with the method provided in references [27,28,29,30], the biggest difference between this new method and the previous method is that it adds the analysis function of dynamic system, that is, the method of phase portrait analysis. With the addition of this function, the new method can not only obtain some exact solutions of time-fractional nonlinear PDEs, but also discuss the existence, dynamical properties and dynamical behavior of their solutions. This is something that the previous method could not achieve. By using the method in references [27,28,29,30], we can only obtain the exact solution of time-fractional PDEs under some special conditions or in some specific range of parameters and adopt the new method to be introduced in this paper; we can discuss the existence and dynamic properties of solutions of time-fractional PDEs under general conditions or in the general range of parameters.
As a general example, we assume that an nonlinear time-fractional PDE has the following form:
where the function \(u=u(x,y,t)\) and the sign \(\frac{\partial ^\alpha }{\partial t^\alpha }\) denotes the fractional differential operator of Riemann–Liouville type or Caputo type, \(\alpha \in (0,1), t>0,\ x,y\in {\mathbb {R}}.\) Obviously, Eq. (2.1) is a time-fractional PDE of \(2+1\)-dimension, which contains model (1.5) and other time-fractional models. In particular, when u becomes binary function \(u=u(x,t),\) Eq. (2.1) can be reduced by time-fractional PDE of \(1+1\)-dimension, which contains many time-fractional models such as time-fractional diffusion-wave (dispersive) models [30], time-fractional reaction–diffusion models [10, 12, 27], time-fractional heat transfer models [41] and so on.
Based on our previous works [27,28,29,30], under definitions of Riemann–Liouville derivative and Caputo derivative, we, respectively, suppose that Eq. (2.1) has two forms of exact solutions of separation variable type as follows:
or
where the function \(v=v(x,y)\) is the undetermined function, the \(a_0,\ a_1,\ \lambda \) are three undetermined coefficients, the \(\gamma \) is an undetermined constant, all of them can be determined later, and the \(E_{\alpha ,1}(\lambda t^{\alpha })=E_{\alpha }(\lambda t^{\alpha })\) is the Mittag–Leffler function. In many cases, (2.2) and (2.3) are still general forms for the solutions of Eq. (2.1) when \(a_0=0.\) But under the case of \(a_0\not =0,\) the calculation often becomes complex or difficult when we search exact solutions of Eq. (2.1). In this case, we always let \(a_0=0\) in (2.2) and (2.3) directly. The above structures are different from those of the classical method of separation variables; in the classical method of separation variables, the solution of Eq. (2.1) always is supposed that the following product form
where G(x, y) is a binary function of x and y, T(t) is a function of t alone, all of them are undetermined. But, in Eqs. (2.2) and (2.3), the part of T(t) has been fixed as power function \(t^{\gamma }\) or Mittag–Leffler function \(E_{\alpha ,1}(\lambda t^{\alpha }).\) Thus, under the hypothetical structures (2.2) and (2.3) of the solutions, the dynamic properties of the fractional derivative part of Eq. (2.1) can only be reflected by the properties of the power function \(t^{\gamma }\) and Mittag–Leffler function \(E_{\alpha ,1}(\lambda t^{\alpha }).\) It is easy to know that the power function \(t^{\gamma }\) has a strong attenuating property when \(-1<\gamma <0\) and the Mittag-Leffler function \(E_{\alpha ,1}(\lambda t^{\alpha })\) has a super attenuating property when \(\lambda <0.\) The greater the absolute value of \(\gamma \) or \(\lambda ,\) the faster the attenuation of the corresponding mechanical process. On the contrary, as in references [11,12,13,14], the function G(x, y) can be fixed as some specific functions in invariant subspace such as power function \((x+\omega y)^{\gamma }\), trigonometric function \(\sin [\lambda (x+\omega y)],\) exponential function \(e^{\eta (x+\omega y)}\) and so forth, and then, let the function T(t) to be determined; this is the idea of invariant subspace method. By using the invariant subspace method, we can only obtain the exact solution of FDE (2.1); it is difficult to discuss the dynamic properties of fractional dynamic system which was reduced by FDE (2.1).
According to the definition of fractional derivative of Riemann–Liouville type, we know that the fractional derivative of power function is given by the following formula
According to the definition of fractional derivative of Caputo type, we obtain the following formula of fractional derivative of Mittag–Leffler function
As an example, substituting (2.2) into (2.1) and regarding t as the coefficient of equation, we can obtain a reduced nonlinear PDE defined by v(x, y) with variable coefficients about t. As in [27,28,29,30], by using homogeneous balance principle, we let the power exponents of t of all terms to be equal in this reduced nonlinear PDE; therefore, we can determine the value of \(\gamma \) in the range of \(\gamma >-1\). And then, substituting the value of \(\gamma \) into this reduced nonlinear PDE again, the variable t can be divided out because the power exponents of t of all terms are same; thus, we can obtain a nonlinear PDE with constant coefficients as follows:
We make the following transformation
where \(\xi \) is a compound variable of x and y. By substituting the above transformation into (2.7), it can be reduced to the following nonlinear ODE
In particular, when the highest order of derivatives is two in the nonlinear ODE (2.9), it can be reduced to a planar system as follows:
Of course, when the highest order of derivatives is three in the nonlinear ODE (2.9), it can be reduced to a three-dimensional system, and so on. Although \(\xi \) does not represent time, we can use the bifurcation theory of dynamical system [31,32,33,34] to study the dynamical properties of system (2.10), so as to investigate the existence and various properties of the solution \(v(\xi )\) of ODE (2.9). And then using structure of solution (2.2) and transformation (2.8), we can finish investigations for the existence and various properties of the solutions of the nonlinear time-fractional PDE (2.1).
Similarly, by using (2.3), as in the above processions, we can also discuss the existence and various properties of the solutions of the nonlinear time-fractional PDE (2.1). Here, we omit these introductions because these processions are very similar. By the way, (2.2) is very suitable for solving time-fractional PDEs, which are defined by the Riemann–Liouville derivative, and contains many nonlinear terms, but (2.3) is very suitable for solving time-fractional PDEs, which are defined by Caputo derivative and contains many linear terms. As a reader, you may ask whether the above two special solutions’ dynamical property is general for all solutions of the considered nonlinear time-fractional PDEs. In fact, we are not entirely sure of this, but from the results in references [11,12,13,14] and [27,28,29,30], we know that the dynamical properties of these two special solutions are very suitable for most nonlinear time-fractional PDEs with the phenomenon of memory or diffusion. We believe that the structures of the two special solutions are also great help in the study of other types of time-fractional PDEs.
3 Existence of solution and dynamical properties of solutions for the time-fractional model (1.5)
In the section, by using the method introduced in Sect. 2, we will discuss the existence of solution and dynamical properties of solutions for model (1.5) in a classical case.
When \(f(u)=\delta u+\kappa u^2,\) Eq. (1.5) becomes the following nonlinear time-fractional PDE
where the sign \(\frac{\partial ^\alpha }{\partial t^\alpha }\) denotes the fractional differential operator of Riemann–Liouville type or Caputo type, the function \(u=u(x,y,t),\)\(0<\alpha <1,\ t>0,\ x,y\in {\mathbb {R}}\) and the \(\delta ,\ \kappa \) are two constants. Equation (3.1) contains three kinds of models such as time-fractional biology model, time-fractional reaction–diffusion model and time-fractional fluid model in porous media. When \(\alpha \rightarrow 1,\ \delta >0,\ \kappa <0,\) Eq. (3.1) is a biology population model which satisfies the Verhulst growth law [39]. When \(\delta =0,\) Eq. (3.1) is reduced to the following nonlinear time-fractional reaction–diffusion model or time-fractional fluid model in porous media [39, 43]
When \(\kappa <0,\) Eq. (3.2) defines a time-fractional fluid model. When \(\kappa \) is an arbitrary nonzero constant, Eq. (3.2) defines a time-fractional reaction–diffusion model. In addition, when \(\delta \) and \(\kappa \) are arbitrary nonzero constants, Eq. (3.1) can be regard as a time-fractional reaction–diffusion model of \(2+1\)-dimension. A sample nonlinear time-fractional reaction–diffusion model of \(1+1\)-dimension can be written as
where \(G(u),\ f(u)\) are two smooth functions of u. Clearly, \([G(u)u_x]_x=(u^2)_{xx}\) if \(G(u)=2u\) in Eq. (3.3). What’s more, Eq. (3.3) becomes a classical integer-order reaction–diffusion model [44, 45] when \(\alpha \rightarrow 1\) and \(G(u)=m u^{m-1},\ f(u)=\kappa u^n(1-u)\).
We will study Eqs. (3.1) and (3.2) in the order of simplicity to complexity. First, we investigate the existence and dynamical properties of solutions of the nonlinear time-fractional fluid model (3.2) in the following subsection.
3.1 Existence of solution and dynamical properties of solutions for model (3.2)
If the time-fractional differential operator of Eq. (3.2) is Riemann–Liouville type, then we suppose that it has solutions that formed as follows:
where \(v=v(x,y)\) is an undetermined function of space variables x and y, the \(a_0,\ a_1\) are two undetermined coefficients and \(\gamma \) is an undetermined constant. Substituting (3.4) into (3.2), it yields
where \(\Omega _0=\frac{\Gamma (1+\gamma )}{\Gamma (1+\gamma -\alpha )}.\) In Eq. (3.5), we let all power exponents of time variable t equal, and it yields
Solving (3.6), we get
Obviously, \(\gamma =-\alpha >-1\) because \(0<\alpha <1\) and \(\Omega _0=\frac{\Gamma (1-\alpha )}{\Gamma (1-2\alpha )}.\) Plugging (3.7) into (3.5) and then dividing out the variable \(t^{-2\alpha }\) of all terms, we have
We make a transformation as follows:
where \(\omega \) is nonzero constant. Under transformation (3.9), Eq. (3.8) can be reduced to the following nonlinear ODE
Letting \(\frac{\mathrm{d}v}{\mathrm{d}\xi }=z,\) Eq. (3.10) can be rewritten as the following planar system
The structure of (3.11) is very much like a dynamical system except that \(\xi \) is independent with time. Therefore, we can use the method of dynamical system to study the nonlinear system (3.11). It is easy to know that system (3.11) is not completely equivalent to Eq. (3.10) because the \(\frac{\mathrm{d}z}{\mathrm{d}\xi }\) is not defined if \(v=-\frac{a_0}{a_1}.\) However, the \(v=-\frac{a_0}{a_1}\) is a travel solution of Eq. (3.10). So we usually call the \(v=-\frac{a_0}{a_1}\) a singular line. In order to obtain a completely equivalent system for Eq. (3.10) in the condition \(v=-\frac{a_0}{a_1},\) we make the following scalar transformation
Under transformation (3.12), the singular system (3.11) can be reduced to the following regular system
Indeed, systems (3.11) and (3.13) have the same first integral as follows:
where h is an integral constant. Obviously, system (3.13) is an integrable system with the first integral. In order to facilitate the discussion of the related issues for (3.13) and (3.14) in the below investigation, let us write
Next, we will discuss equilibrium points of system (3.13) and their dynamical characteristics. For the convenience of discussion, we write Jacobian matrix and its determinant of system (3.13) as follows:
Obviously, system (3.13) has two equilibrium points \(A(v_1,\ 0)\) and \(B(v_2,\ 0)\) at the \(v-\)axis, where \(v_1=-\frac{a_0}{a_1}\) and \(v_2=-\frac{a_0}{a_1}+\frac{\Omega _0}{a_1 \kappa }\). Substituting the above two equilibrium points into (3.15) and (3.17), it yields
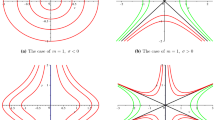
Phase portraits of system (3.11) in the conditions of \(\kappa>0,\ a_1>0\)
Phase portraits of system (3.11) in the conditions of \(\kappa >0,\ a_1<0\)
where \(\Omega _0=\frac{\Gamma (1-\alpha )}{\Gamma (1-2\alpha )}\) has been given above. According to bifurcation theory of planar dynamical system [31,32,33,34], we have two lemmas as follows:
Lemma 1
For an equilibrium point of an integrable system such as (3.13), it has three conclusions as follows:
- (i)
The equilibrium point is a saddle point if the value of determinant of equilibrium point \((v_i,0)\) satisfies \(J(v_i,0)<0\);
- (ii)
The equilibrium point is a center point if the value of determinant of equilibrium point \((v_i,0)\) satisfies \(J(v_i,0)>0\) and \(Trace\ M(v_i,0)=0\);
- (iii)
The equilibrium point is a node if the value of determinant of equilibrium point \((v_i,0)\) satisfies \(J(v_i,0)>0\) and \([Trace\ M(v_i,0)]^2-4J(v_i,0)>0\);
- (iv)
The equilibrium point is a cusp point if the value of determinant of equilibrium point \((v_i,0)\) satisfies the case of \(J(v_i,0)=0\) and the Poincaré index of this equilibrium point is zero.
Lemma 2
Supposing \(v(x,y)=v(\xi )\) is a continuous solution of an nonlinear ODE such as Eq. (3.10) on the interval \(\xi \in (-\infty ,\infty )\) and satisfies conditions \(\lim _{\xi \rightarrow -\infty }=a\), \(\lim _{\xi \rightarrow \infty }=b,\) it has two conclusions as follows:
- (i)
The solution \(v(\xi )\) is a homoclinic solution formed as solitary wave if \(a=b\);
- (ii)
The solution \(v(\xi )\) is a heteroclinic solution formed as kink or anti-kink wave if \(a\not =b\). From expressions (3.16) and (3.19), we know that \(Trace M(v_{1,2},0)\equiv 0\) and \(J_A=0.\) Also, we know that \(J_B<0\) if \(\kappa <0\) and \(J_B>0\) if \(\kappa >0.\) By using Lemma 1, it is easy to know that the equilibrium point \(A(v_1,0)\) is always a cusp point. We also know that the equilibrium point \(B(v_2,0)\) is a saddle point if \(\kappa <0;\) the equilibrium point \(B(v_2,0)\) is a center point if \(\kappa >0.\)
By using Lemma 2, we know that a homoclinic solution of Eq. (3.10) corresponds to a homoclinic orbit of system (3.11), a heteroclinic solution of Eq. (3.10) corresponds to a heteroclinic orbit of system (3.11), a periodic solution of Eq. (3.10) corresponds to a closed orbit of system (3.11). In fact, the phase portraits of system (3.11) and system (3.13) are almost the same except for topological structure near the singular line \(v=-\frac{a_0}{a_1}\). Therefore, the phase portraits of the singular system (3.11) are constructed by the topological structure around the singular line \(v=-\frac{a_0}{a_1}\) and the phase portraits of the regular system (3.13).
According to the above information, under different parametric conditions, we draw the phase portraits (phase diagram) of system (3.11), which are shown in the figures (Figs. 1, 2, 3, 4) of the below. By the way, the orbital curves in all graphs do not intersect outside the equilibrium point. And one orbit corresponds to one solution of (3.10).
Phase portraits of system (3.11) in the conditions of \(\kappa <0,\ a_1>0\)
Phase portraits of system (3.11) in the conditions of \(\kappa<0,\ a_1<0\)
According to information and four bifurcation figures of the phase portraits given above, we have two theorems as follows:
Theorem 3.1
Suppose that the parameter \(\kappa >0\) in equations (3.2) and (3.10), the following conclusions hold.
- (i)
If \(h=h_A\) in (3.14), then Eq. (3.10) has a smooth periodic solution \(v=v(\xi ).\) Accordingly, Eq. (3.2) has a stable solution with periodic property and attenuating property, which satisfies \(u\rightarrow 0\) when time \(t\rightarrow +\infty \).
- (ii)
If \(h_B<h<h_A\) in (3.14), then Eq. (3.10) has a family of smooth periodic solutions \(v=v(\xi ),\) Accordingly, Eq. (3.2) has a family of stable solutions with periodic property and attenuating property, which satisfy \(u\rightarrow 0\) when time \(t\rightarrow +\infty \).
- (iii)
If \(h>h_A\) in (3.14), then Eq. (3.10) has a family of compacton \(v=v(\xi ).\) Accordingly, Eq. (3.2) has a family of stable solutions with compacton shape and attenuating property, which satisfy \(u\rightarrow 0\) when time \(t\rightarrow +\infty \).
Note A family of solutions is equivalent to a general solution, when the values of h vary in the range of \(h_B<h<h_A\) or \(h>h_A,\) and they contain infinitely many solutions. Once the value of h is fixed by the initial condition, the general solution becomes an unique particular solution.
Theorem 3.2
Suppose that the parameter \(\kappa <0\) in Eqs. (3.2) and (3.10), the following conclusions hold.
- (1)
If \(h=h_B\) in (3.14), then Eq. (3.10) has two heteroclinic solutions. Thereby, Eq. (3.2) has two stable solutions with attenuating property, and the two solutions satisfy \(u\rightarrow 0\) when time \(t\rightarrow +\infty \).
- (2)
If \(h_A<h<h_B\) in (3.14), then Eq. (3.10) has a family of compacton solutions. Thus, Eq. (3.2) has a family of stable solutions with compacton property and attenuating property, all of them satisfy \(u\rightarrow 0\) when time \(t\rightarrow +\infty \).
- (3)
If \(h=h_A\) in (3.14), then Eq. (3.10) has an unbounded solution. Correspondingly, Eq. (3.2) has a solution with unbounded property and attenuating property, and it satisfies \(u\rightarrow 0\) when time \(t\rightarrow +\infty \).
Dynamical profiles of solution (3.23) in space (x, t, u) and space (y, t, u)
Proof of Theorem 3.1
(i) When \(\kappa >0\) and \(h=h_A,\) system (3.11) always has a smooth closed orbit (marked by black) passing through the two points \((v_1,0)\) and \((v_m,0)\) no matter how the position of the point \((v_2,0)\) changes, where \((v_m,0)\) is the point of the closed orbit at the v-axis. When \(a_1>0,\) the closed orbit is on the right side of the singular line \(v=v_1\) and \(v\in [v_1,v_m]\) which is shown in Fig.1a, b or c. When \(a_1<0,\) the closed orbit is on the left side of the singular line \(v=v_1\) and \(v\in [v_m,v_1]\), which is shown in Fig.2a, b or c. Substituting \(h=h_A=\frac{a_0^3(4\Omega _0-3a_0\kappa )}{12a_1^2(1+\omega ^2)}\) into Eq. (3.14), it yields
where \(v_1=-\frac{a_0}{a_1},\ v_m=\frac{4\Omega _0-3a_0\kappa }{3a_1\kappa }.\) Obviously, the first-order derivative \(z=\frac{\mathrm{d}v}{\mathrm{d}\xi }\) exists when \(v=v_1=-\frac{a_0}{a_1}\); this implies that solution of Eq. (3.10) is smooth under the above conditions. According to Lemma 2, Eq. (3.10) has a smooth periodic solution and is bounded and stable. In fact, we can obtain this periodic solution of Eq. (3.10) in the next process. Substituting (3.20) into the first equation \(\frac{\mathrm{d}v}{\mathrm{d}\xi }=z\) of system (3.11) and integrating it along the closed orbit of passing point \((v_m,0)\), it yields
Solving (3.21), we obtain a smooth periodic solution of (3.10) as follows:
Plugging (3.22) and \(\gamma =-\alpha ,\)\(\xi =x+\omega y,\)\(v_1=-\frac{a_0}{a_1},\ v_m=\frac{4\Omega _0-3a_0\kappa }{3a_1\kappa }\) into (3.4), we obtain an exact solution of Eq. (3.2) as follows:
(3.23) is a stable solution with periodic property and attenuating property, which satisfies \(u\rightarrow 0\) as time \(t\rightarrow +\infty \) because of \(t^{-\alpha }\rightarrow 0\) as time \(t\rightarrow +\infty .\) In order to show dynamical property of solution (3.23) intuitively, taking \(\kappa =2,\ \omega =0.5,\ \alpha =0.45\)\(t\in [1,7],\ x\in [-15,15]\) or \(y\in [-30,30],\) we plot dynamical profiles of solution (3.23) in space (x, t, u) and space (y, t, u), respectively, which are shown in Fig.5a, b. \(\square \)
As can be seen from Fig. 5, in the above parametric conditions, the density of the biological population is periodically changed in the local region, but with the increase in time, because the consumption of the food is exhausted, the biological population will migrate to other regions, so that the number of the population in the region is gradually reduced, the migration is complete until the quantity of the population is decremented to zero.
(ii) When \(\kappa >0\) and \(h_B<h<h_A,\) system (3.11) has a family of closed orbits around the center point \(B(v_2,0),\) two representative orbits of them are marked by brown, which are shown in Figs. 1 and 2. When \(a_1>0,\) all these closed orbits are on the right side of the singular line \(v=v_1\) and \(v\in (v_1,v_m)\), which are shown in Fig. 1a, b or c. When \(a_1<0,\) all these closed orbits are on the left side of the singular line \(v=v_1\) and \(v\in (v_m,v_1)\), which are shown in Fig. 2a, b or c. From (3.14), we know that the expression of all these closed orbits is very complex. To facilitate the discussion, we will give a simple example in the range of the above conditions. In the range of \(h_B<h<h_A,\) letting \(a_0=0\) directly, (3.14) can be reduced to the following simple expression
From Figs. 1 and 2, we can see that every one closed orbit has two points on the v-axis. We suppose coordinates of the two points are \((\phi _M,0)\) and \((\phi _m,0)\) and \(\phi _M>\phi _m\). Under the above assumption, Eq. (3.24) is reduced to the following form
where \(\phi _M,\ \phi _m\) are two real roots of equation \(\frac{4h(1+\omega ^2)}{a_1^2\kappa }+\frac{4\Omega _0}{3a_1\kappa }v^3-v^4=0,\) and \(s,\ {\bar{s}}\) are two conjugate complex roots of this equation, all of them can be solved by computer for the specific values of parameters. According to Lemma 2, Eq. (3.10) has a family of smooth periodic solutions. As in the above computational processes, we also obtain these periodic solutions of Eq. (3.10) in the next. Under the case \(a_0=0,\) substituting (3.25) into the first equation \(\frac{\mathrm{d}v}{\mathrm{d}\tau }=2a_1(1+\omega ^2)(a_0+a_1v)z\) of system (3.13) and integrating it along the orbit passing point \((\phi _m,0)\), we get
Solving (3.26), we obtain a common expression of these periodic solutions as follows:
where \(\text {cn}(\sigma \tau ,k)\) is the Jacobian elliptic function, it is an even function, \(\tau \) is a parameter and \(a=\sqrt{\left( \phi _M-\frac{s+{\bar{s}}}{2}\right) ^2 -\frac{(s-{\bar{s}})^2}{4}},\)\(b=\sqrt{\left( \phi _m-\frac{s+{\bar{s}}}{2}\right) ^2 -\frac{(s-{\bar{s}})^2}{4}},\)\(\sigma =a_1^2\sqrt{ab\kappa (1+\omega ^2)},\)\(k=\sqrt{\frac{(\phi _M-\phi _m)^2-(a-b)^2}{4ab}},\)\(\beta =\frac{a-b}{a+b},\)\(\beta _1=\frac{a\phi _m-b\phi _M}{a\phi _m+b\phi _M}.\) Substituting \(a_0=0\) and (3.27) into (3.12) and then integrating it, we obtain
where the \(\Pi \left( \text {am}(\sigma \tau ),\frac{\beta ^2}{\beta ^2-1},k \right) \) is a normal elliptic integral function of the third kind and \(k_1=\sqrt{1-k^2},\)\(f_1=\sqrt{\frac{1-\beta ^2}{k^2+k_1^2\beta ^2}}\arctan \left[ \sqrt{\frac{k^2+k_1^2\beta ^2}{1-\beta ^2}}\ \text {sd}(\sigma \tau ,k)\right] .\) After substituting (3.27) and \(\gamma =-\alpha ,\)\(\xi =x+\omega y,\ a_0=0\) into (3.4), combining with (3.28), we obtain the exact solution of Eq. (3.2) as follows:
where \(\tau \) is parameter, the \(\text {am}(\sigma \tau ,k)\) is a Jacobian elliptic function, \(a_1\) is an arbitrary nonzero constant and the other parameters have been given above. Also, (3.29) defines a family of stable solutions with periodic property and attenuating property, which satisfy \(u\rightarrow 0\) as time \(t\rightarrow +\infty .\) The dynamical property and profile are very similar to those of the solution (3.23).
(iii) When \(\kappa >0\) and \(h>h_A,\) system (3.11) has a family of open orbits shaped as bow, four representative orbits of them are marked by blue, which are shown in Figs. 1 and 2. These open orbits always appear in pairs, where one to the right and another to the left. The symmetry axis of all open orbits is the v-axis. Each pair of open orbits has two points on the v-axis. According to Lemma 2, Eq. (3.10) has a family of compacton solutions, which are defined by even functions. The expressions of these open orbits are too complex to obtain exact solutions of Eq. (3.10) by them. But we can obtain two solutions of them in the special case. It is easy to know that \(h_A<0\) when \(\kappa >0\) and \(0<\frac{4\Omega _0}{3\kappa }<a_0.\) Without loss of generality, in the range of \(h>h_A,\ \kappa >0\) and \(0<\frac{4\Omega _0}{3\kappa }<a_0,\) we take \(h=0\) and \(a_0=\frac{2\Omega _0}{\kappa },\) and thus, two representative open orbits can be reduced to the following simple expression by (3.14),
and
where
Substituting \(a_0=\frac{2\Omega _0}{\kappa }\) and (3.30) into the first equation \(\frac{\mathrm{d}v}{\mathrm{d}\xi }=2a_1(1+\omega ^2)(a_0+a_1v)z\) of system (3.13) to integrate it along the orbit of passing point (0, 0), it results
Completing the above two integrals, we obtain a solution of Eq. (3.10) as follows:
where \(A=\sqrt{\left( \eta -\frac{r+{\bar{r}}}{2}\right) ^2-\frac{(r-{\bar{r}})^2}{2}},\)\(B=\sqrt{r{\bar{r}}},\)\(\sigma =a_1^2\sqrt{\kappa AB(1+\omega ^2)},\)\(k=\sqrt{\frac{\eta ^2-(A-B)^2}{4AB}},\)\(\beta =\frac{A-B}{A+B}.\) Substituting \(a_0=\frac{2\Omega _0}{\kappa }\) and (3.33) into (3.12) and then integrating it, we obtain
where \(f_1=\sqrt{\frac{1-\beta ^2}{k^2+k_1^2\beta ^2}}\arctan \left[ \sqrt{\frac{k^2+k_1^2\beta ^2}{1-\beta ^2}}\ \text {sd}(\sigma \tau ,k)\right] ,\)\(k_1=\sqrt{1-k^2}.\) Plugging \(\gamma =-\alpha ,\ a_0=\frac{2\Omega _0}{\kappa }\) and (3.33) into (3.4) and combining with (3.34), we obtain an exact solution of parametric type of Eq. (3.2) as follows:
where \(\tau \) is parameter, \(a_1\) is an arbitrary nonzero constant and the other parameters such as \( f_1,\ \beta ,\ k\) have been given above. Also, (3.35) is a stable solution with compacton property and it satisfies \(u\rightarrow 0\) as time \(t\rightarrow +\infty .\)
Dynamical profiles of solution (3.35) in space (x, t, u) and space (y, t, u)
Taking \(a_1=0.2,\ \omega =0.5,\ \kappa =4,\ \alpha =0.25,\)\(t\in [0.1,8],\ \tau \in [-4,4],\) we plot dynamical profiles of solution (3.35) in space (x, t, u) and space (y, t, u), respectively, which are shown in Fig. 6a, b. It can be seen from Fig. 6 that the density of biological population reaches the maximum at the center of the region and decreases gradually at the boundary of the region under the above parameters. Generally speaking, with the increase in time, also due to the consumption of food, biological populations will migrate to other areas, resulting in a gradual decline in the number of populations in the region to zero.
Similarly, plugging (3.31) into the first equation of system (3.13) to integrate it along the orbit of passing point \((\eta ,0)\) and using (3.4), we obtain an attenuation solution of Eq. (3.2) as follows:
where \(A=\sqrt{r{\bar{r}}},\)\(B=\sqrt{\left( \eta -\frac{r+{\bar{r}}}{2}\right) ^2 -\frac{(r-{\bar{r}})^2}{2}}\) and the other parameters \(\sigma ,\ \beta ,\ f_1,\ \beta ,\ k\) are same as in (3.35). Also, the dynamical property and profile of solution (3.36) are very similar to those of solution (3.35).
Proof of Theorem 3.2
(1) When \(\kappa <0\) and \(h=h_B,\) there are two heteroclinic orbits passing through the saddle point \(B(v_2,0)\), and we mark them red in the phase portraits of Figs. 3 and 4. When \(a_1>0,\) the two heteroclinic orbits are on the left side of the singular line \(v=v_1\) and \(v\in (v_2,v_1)\), which is shown in Fig. 3a, b or c. When \(a_1<0,\) the two heteroclinic orbits are on the right side of the singular line \(v=v_1\) and \(v\in (v_1,v_2)\) which is shown in Fig. 4a, b or c. According to Lemma 2, Eq. (3.10) has two heteroclinic solutions and we can obtain them in the next. Substituting \(h=h_B=-\frac{(\Omega _0-a_0\kappa )^2[(\Omega _0+a_0\kappa )^2 +2a_0^2\kappa ^2]}{12a_1^2\kappa ^3(1+\omega ^2)}\) into Eq. (3.14), it is reduced to
Dynamical profiles of solution (3.41) under “\(+\)” and “−” in space (y, t, u)
Also, the expression of (3.37) is more complex. In order to obtain the two exact solutions easily, we might as well let \(a_0=\frac{\Omega _0}{\kappa }.\) Under this parametric condition, (3.37) can be reduced to
By substituting (3.38) into the first equation \(\frac{\mathrm{d}v}{\mathrm{d}\xi }=z\) of system (3.11), it results
Completing the two integrals of (3.39) and setting integral constant as zero, we obtain two implicit solutions of (3.10) as follows:
where \(V=v^2+\frac{8\Omega _0}{3a_1\kappa }v+\frac{2\Omega _0^2}{3a_1^2\kappa ^2}.\) Substituting \(\gamma =-\alpha ,\ a_0=\frac{\Omega _0}{\kappa }\) into (3.4) and combining with (3.40), we obtain two exact solutions of (3.2) as follows:
where v is a parameter and \(V=v^2+\frac{8\Omega _0}{3a_1\kappa }v+\frac{2\Omega _0^2}{3a_1^2\kappa ^2}\). (3.41) defines two attenuation solutions which satisfied \(u\rightarrow 0\) as \(t\rightarrow +\infty .\) Under the parameters \(a_1=2,\ \kappa =-1,\ \omega =0.5,\ \alpha =0.25,\ x=1,\)\(t\in [0.1,10],\ v\in [0,1],\) we plot dynamical profiles of solution (3.41) in space (y, t, u), which are shown in Fig. 7a, b. \(\square \)
(2) When \(\kappa <0\) and \(h_A<h<h_B,\) system (3.11) has a family of open orbits on both sides of the saddle point \(B(v_2,0)\), one parts of them are unbounded, another parts of them are bounded and between the equilibrium points \(A(v_1,0)\) and \(B(v_2,0).\) The two representative orbits of them are marked by brown which are shown in Figs. 3 and 4. Here, we only discuss those bound orbits shaped as bow. According to Lemma 2, corresponding to those bounded orbits shaped as bow, Eq. (3.10) has an infinite number of compacton solutions, which are defined by even functions. Letting \(a_0=0\) directly, (3.14) can be reduced to the following simple expression
Suppose that equation \(-\frac{4h(1+\omega ^2)}{a_1^2\kappa }-\frac{4\Omega _0}{3a_1\kappa }v^3+v^4=0\) has two real roots \(\phi _1,\ \phi _2\) and two conjugate complex roots \(c,\ {\bar{c}},\) all of them can be solved by computer. Under this assumption, Eq. (3.42) can be reduced to the following simple equation
Substituting \(a_0=0\) and (3.43) into the first equation of system (3.13) to integrate it along the orbit of passing point \((\phi _2,0)\), we get
where \(\tau \) is a parameter and \(\,a=\sqrt{\left( \phi _1-\frac{c+{\bar{c}}}{2}\right) ^2 -\frac{(c-{\bar{c}})^2}{4}},\)\(b=\sqrt{\left( \phi _2-\frac{c+{\bar{c}}}{2}\right) ^2 -\frac{(c-{\bar{s}})^2}{4}},\)\(\sigma =a_1^2\sqrt{-ab\kappa (1+\omega ^2)},\)\(k=\sqrt{\frac{(a+b)^2-(\phi _1-\phi _2)^2}{4ab}},\)\(\beta =\frac{a+b}{b-a},\)\(\beta _1=\frac{b\phi _1+a\phi _2}{b\phi _1-a\phi _2}.\) Substituting \(a_0=0\) and (3.44) into (3.12) and then integrating it, we obtain
where \(k_1=\sqrt{1-k^2},\)\(f_2=\frac{1}{2}\sqrt{\frac{\beta ^2-1}{k^2+k_1^2\beta ^2}}\ln \left[ \frac{\sqrt{k^2+k_1^2\beta ^2}\ \text {dn}(\sigma \tau ,k)+\sqrt{\beta ^2-1}\ \text {sn}(\sigma \tau ,k)}{\sqrt{k^2+k_1^2\beta ^2}\ \text {dn}(\sigma \tau ,k)-\sqrt{\beta ^2-1}\ \text {sn}(\sigma \tau ,k)}\right] .\) Plugging (3.44) and \(\gamma =-\alpha ,\)\(\xi =x+\omega y,\ a_0=0\) into (3.4) and then combining with (3.45), we obtain the exact solution of Eq. (3.2) as follows:
where \(\tau \) is parameter, \(a_1\) is an arbitrary nonzero constant and the other parameters have been given above. Also, (3.46) defines a family of stable solutions with compacton property, which satisfy \(u\rightarrow 0\) as time \(t\rightarrow +\infty .\)
(3) When \(\kappa <0\) and \(h=h_A,\) system (3.11) has a open orbit (marked by black) passing through the point \((v_1,0)\). When \(a_1>0,\) the open orbit is on the right side of the singular line \(v=v_1\), which is shown in Fig. 3a, b or c. When \(a_1<0,\) the open orbit is on the left side of the singular line \(v=v_1,\) which is shown in Fig. 4a, b or c. Substituting \(h=h_A=\frac{a_0^3(4\Omega _0-3a_0\kappa )}{12a_1^2(1+\omega ^2)}\) into Eq. (3.14), it yields
where \(v_1=-\frac{a_0}{a_1},\ v_m=\frac{4\Omega _0-3a_0\kappa }{3a_1\kappa }.\) According to Lemma 2, Eq. (3.10) has an unbounded solution and we can obtain its expression in the next process. After plugging (3.47) into the first equation of system (3.11), integrating it along the orbit of passing point \((v_1,0)\), we obtain an unbounded solution of (3.10) as follows:
Plugging (3.48) and \(\gamma =-\alpha ,\)\(\xi =x+\omega y,\)\(v_1=-\frac{a_0}{a_1},\ v_m=\frac{4\Omega _0-3a_0\kappa }{3a_1\kappa }\) into (3.4), we obtain an exact solution of Eq. (3.2) as follows:
Also, (3.49) defines a stable solution with attenuating property and it satisfies \(u\rightarrow 0\) as time \(t\rightarrow +\infty .\)
Next, we investigate the existence and dynamical properties of solutions of the time-fractional biology model or reaction–diffusion model in the following subsection.
3.2 Existence of solution and dynamical properties of solutions for model (3.1)
If the time-fractional derivative of Eq. (3.1) is Caputo type, then we suppose that it has solutions formed as follows:
where \(v=v(x,y)\) is an undetermined binary function defined by space variables x and y, the \(a_0,\ a_1\) are two undetermined coefficients and \(\lambda \) is an undetermined constant. All of them can be determined in the next discussion. By substituting (3.50) into (3.1), it results
In the left side of Eq. (3.51), letting \(\lambda -\delta =0,\) we get
In the condition of (3.52), Eq. (3.51) can be reduced to
Phase portraits of system (3.57) in the conditions of \(\kappa <0\)
By eliminating the \(E_{\alpha }^2(\lambda t^{\alpha })\) in Eq. (3.53), we obtain the following nonlinear PDE
As in Sect. 3.1, under the transformation
the nonlinear PDE (3.54) can be reduced to the following nonlinear ODE,
Letting \(\frac{\mathrm{d}v}{\mathrm{d}\xi }=z,\) Eq. (3.56) can be rewritten as:
Also, we make the following scalar transformation
Under transformation (3.58), the singular system (3.57) can be transformed into the following regular system,
Systems (3.57) and (3.59) have the same first integral as follows:
where h is an integral constant. Equation (3.60) can be rewritten as:
Obviously, system (3.59) has only one equilibrium point \(N\left( -\frac{a_0}{a_1},0\right) \) at the singular line \(v=-\frac{a_0}{a_1}.\) Substituting \(N(-\frac{a_0}{a_1},0)\) into (3.61), it yields
As analysis in Sect. 3.1, we know that the point \(N\left( -\frac{a_0}{a_1},0\right) \) is high-order equilibrium point, it has character of saddle point when \(\kappa <0\) and it has character of center point when \(\kappa >0.\) Under different parametric conditions, we plot the phase portraits of system (3.57), which are shown in Figs. 8 and 9, where the singular line is marked by blue.
Phase portraits of system (3.57) in the conditions of \(\kappa >0\)
Dynamical profiles of solution (3.66) in space (x, t, u) and space (y, t, u)
According to the above information, under some special conditions, we can obtain exact solutions of Eq. (3.1). For examples, when \(\kappa <0,\) by substituting \(h=h_N=0\) into (3.60), we obtain expressions of two orbits of straight line (marked by black in Fig. 8a–c) as follows:
Plugging (3.63) into the first equation \(\frac{\mathrm{d}v}{\mathrm{d}\xi }=z\) of (3.57) to integrate, we get two exact solutions of Eq. (3.56) as follows:
and
where C is an arbitrary nonzero constant. Substituting \(\xi =x+\omega y,\ \lambda =\delta ,\) (3.64) and (3.65) into (3.50), respectively, we obtain two exact solutions of Eq. (3.1) as follows:
and
When \(\delta <0,\)\( E_{\alpha }\left( \delta t^{\alpha }\right) \) is a decreasing function, it has property of super attenuation. Thus, when \(\delta <0,\) the amplitude of solutions (3.66) and (3.67) decreases with the increase in time. Under \(C=0.2,\ \omega =0.1,\ \delta =-2,\ \alpha =0.5,\ \kappa =-1,\)\(t\in [0.1,12],\ x\in [-4,4]\) and \(y\in [-8,8],\) we plot 3D graphs of solution (3.66) in the space (x, t, u) and space (y, t, u), respectively, which are shown in Fig. 10a, b.
Dynamical profiles of the solution (3.71) in space (x, t, u) and space (y, t, u)
When \(\kappa>0,\ h>0,\) substituting \(a_0=0\) into (3.60), we obtain expressions of each pair of bow-shaped orbits (marked by green, brown or red in Fig. 9b) as follows:
By substituting \(a_0=0\) and (3.68) into the first equation \(\frac{\mathrm{d}v}{\mathrm{d}\tau }=2a_1(1+\omega ^2)(a_0+a_1v)z\) of (3.59) and integrating it along the orbit of passing point \(\left( \root 4 \of {\frac{4h(1+\omega ^2)}{a_1^2\kappa }},\ 0\right) \), we obtain
where \(b=\root 4 \of {\frac{4h(1+\omega ^2)}{a_1^2\kappa }},\)\(\sigma =a_1^2b\sqrt{2\kappa (1+\omega ^2)},\)\(k=\frac{\sqrt{2}}{2}.\) Plugging (3.69) into (3.58) and then completing integrals, we get
Plugging \(a_0=0,\ \xi =x+\omega y,\) (3.52) and (3.69) into (3.50) and then combining with (3.70), we obtain an exact solution of Eq. (3.1) as follows:
where the parameters \(b,\ \sigma ,\ k\) have been given above. Solution (3.71) has property of super attenuation when \(\delta <0\); its amplitude decreases with the increase in time. Under \(a_1=1,\ \omega =0.1,\ \delta =-2,\ \alpha =0.5,\ \kappa =3,\)\(t\in [1,7],\ \tau \in [0.04,1.2],\) we plot 3D graphs of solution (3.71) in the space (x, t, u) and space (y, t, u), respectively, which are shown in Fig. 11a, b. In addition, when \(\kappa >0\) and \(h<0,\) Eq. (3.60) does not hold, so Eq. (3.1) has not any real solutions in this case.
As can be seen from Fig. 11, in the above case, the density of the biological population gradually decreases from the region center to the boundary direction. And as time increases, the population will migrate to other regions because of the consumption of food, and the number of populations in the boundary region will decline rapidly to zero.
4 Conclusions
In this work, by avoiding an invalid fractional chain rule, we introduced a new analytical approach for investigating the existence and dynamical property of solutions of an nonlinear time-fractional PDE. By using this approach, three time-fractional models are studied. Under the fractional derivative definition of Riemann–Liouville type, employing (2.2), the existence and dynamical properties of solutions of model (3.2) are discussed. Under the fractional derivative definition of Caputo type, using (2.3), the existence and dynamical properties of solutions of model (3.1) are investigated. In some special parametric conditions, different kinds of exact solutions are obtained, some of them (such as solutions (3.23) and (3.29)) have periodic property, some of them (such as solutions (3.35), (3.46) and (3.71)) have compacton property, some of them [such as solutions (3.49) and (3.66)] have unbounded characteristic. Most of them have an attenuating property (decay characteristic) according to increase in time, which satisfy \(u\rightarrow 0\) as time \(t\rightarrow +\infty .\)
According to the symmetrical characteristic, this new approach can also be used to investigate the existence and dynamical property of solutions of an nonlinear space-fractional PDE. Of course, Eq. (2.3) in this new approach is very suitable for solving linear time-fractional PDEs formed as
where \(\frac{\partial ^{\alpha }u}{\partial t^{\alpha }}\) is time-fractional derivative of Caputo type. Substituting (2.3) into (4.1) and then dividing out the Mittag–Leffler function \(E_{\alpha }(\lambda t^{\alpha })\) of time variable, it yields
where \(v=v(x,y),\ b=b(x,y),\ c=c(x,y),\ d=d(x,y).\) Obviously, Eq. (4.2) is a linear PDE; there are many ways to investigate solutions and dynamical properties of this equation. In particular, when all coefficients \(b,\ c\) and d become constants, exact solutions of PDE (4.2) can be easily obtained by a simple transformation \(v=v(\xi )\) with \(\xi =x+\omega y.\)
In addition, we naturally ask that there will be any other types of solutions for the kind of nonlinear fractional PDEs such as (1.5) besides the above two special types of solutions? Our answer is that there may be other types of solutions, but because there are too few formulas for fractional derivatives in fractional calculus, it is difficult to deduce this kind of equations in the process of solving them. There are still few methods for solving nonlinear fractional PDEs at present, so it is very difficult to obtain other types of solutions. We hope that readers and researchers will pay attention to this research in the future.
References
Daftardar-Gejji, V., Jafari, H.: Adomian decomposition: a tool for solving a system of fractional differential equations. J. Math. Anal. Appl. 301(2), 508–518 (2005)
Bakkyaraj, T., Sahadevan, R.: An approximate solution to some classes of fractional nonlinear partial differential difference equation using a domian decomposition method. J. Fract. Calc. Appl. 5(1), 37–52 (2014)
Bakkyaraj, T., Sahadevan, R.: Approximate analytical solution of two coupled time fractional nonlinear Schrodinger equations. Int. J. Appl. Comput. Math. 2(1), 113–135 (2016)
Bakkyaraj, T., Sahadevan, R.: On solutions of two coupled fractional time derivative Hirota equations. Nonlinear Dyn. 77(4), 1309–1322 (2014)
Eslami, M., Vajargah, B.F., Mirzazadeh, M., Biswas, A.: Applications of first integral method to fractional partial differential equations. Indian J. Phys. 88(2), 177–184 (2014)
Sahadevan, R., Bakkyaraj, T.: Invariant analysis of time fractional generalized Burgers and Korteweg-de Vries equations. J. Math. Anal. Appl. 393(2), 341–347 (2012)
Bakkyaraj, T., Sahadevan, R.: Invariant analysis of nonlinear fractional ordinary differential equations with Riemann-Liouville derivative. Nonlinear Dyn. 80(1), 447–455 (2015)
Odibat, Z.M., Shaher, M.: The variational iteration method: an efficient scheme for handling fractional partial differential equations in fluid mechanics. Comput. Math. Appl. 58, 2199–2208 (2009)
Wu, G., Lee, E.W.M.: Fractional variational iteration method and its application. Phys. Lett. A 374(25), 2506–2509 (2010)
Momani, S., Zaid, O.: Comparison between the homotopy perturbation method and the variational iteration method for linear fractional partial differential equations. Comput. Math. Appl. 54(7), 910–919 (2007)
Sahadevan, R., Bakkyaraj, T.: Invariant subspace method and exact solutions of certain nonlinear time fractional partial differential equations. Fract. Calc. Appl. Anal. 18(1), 146–162 (2015)
Harris, P.A., Garra, R.: Analytic solution of nonlinear fractional Burgers-type equation by invariant subspace method. Nonlinear Stud. 20(4), 471–481 (2013)
Sahadevan, R., Prakash, P.: Exact solution of certain time fractional nonlinear partial differential equations. Nonlinear Dyn. 85(1), 659–673 (2016)
Artale Harris, P., Garra, R.: Nonlinear time-fractional dispersive equations. Commun. Appl. Ind. Math. 6(1), e-487 (2014)
Elsayed, M.E.Z., Yasser, A.A., Reham, M.A.S.: The fractional complex transformation for nonlinear fractional partial differential equations in the mathematical physics. J. Assoc. Arab Univ. Basic Appl. Sci. 19, 59–69 (2016)
Li, Z.B., Zhu, W.H., He, J.H.: Exact solutions of time-fractional heat conduction equation by the fractional complex transform. Thermal Sci. 16(2), 335–338 (2012)
Li, Z.B., He, J.H.: Fractional complex transform for fractional differential equations. Math. Comput. Appl. 15(5), 970–973 (2010)
Kaplan, M., Bekir, A.: A novel analytical method for time-fractional differential equations. Optik 127, 8209–8214 (2016)
Chen, J., Liu, F., Anh, V.: Analytical solution for the time-fractional telegraph equation by the method of separating variables. J. Math. Anal. Appl. 338, 1364–1377 (2008)
Jiang, H., Liu, F., Turner, I., Burrage, K.: Analytical solutions for the multi-term time-fractional diffusion-wave/diffusion equations in a finite domain. Comput. Math. Appl. 64, 3377–3388 (2012)
Luchko, Y.: Some uniqueness and existence results for the initial-boundary-value problems for the generalized time-fractional diffusion equation. Comput. Math. Appl. 59, 1766–1772 (2010)
Jumarie, G.: Fractional partial differential equations and modified Riemann-Liouville derivative new methods for solution. J. Appl. Math. Comput. 24(1–2), 31–48 (2007)
Jumarie, G.: Modified Riemann-Liouville derivative and fractional Taylor series of non-differentiable functions further results. Comput. Math. Appl. 51(9–10), 1367–1376 (2006)
Jumarie, G.: Cauchy’s integral formula via the modified Riemann-Liouville derivative for analytic functions of fractional order. Appl. Math. Lett. 23(12), 1444–1450 (2010)
He, J.H.: Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys. Lett. A 376, 257–259 (2012)
Tarasov, V.E.: On chain rule for fractional derivatives. Commun. Nonlinear Sci. Numer. Simul. 30(1), 1–4 (2016)
Rui, W.: Applications of homogenous balanced principle on investigating exact solutions to a series of time fractional nonlinear PDEs. Commun. Nonlinear Sci. Numer. Simul. 47, 253–266 (2017)
Rui, W.: Applications of integral bifurcation method together with homogeneous balanced principle on investigating exact solutions of time fractional nonlinear PDEs. Nonlinear Dyn. 91, 679–712 (2018)
Wu, C., Rui, W.: Method of separation variables combined with homogenous balanced principle for searching exact solutions of nonlinear time-fractional biological population model. Commun. Nonlinear Sci. Numer. Simul. 63, 88–100 (2018)
Rui, W.: Ideal of invariant subspace combined with elementary integral method for investigating exact solutions of time-fractional NPDEs. Appl. Math. Comput. 339, 158–171 (2018)
Li, J., Liu, Z.: Smooth and non-smooth traveling waves in a nonlinearly dispersive equation. Appl. Math. Model. 25(1), 41–56 (2000)
Li, J., Zhang, L.: Bifurcations of travelling wave solutions in generalized Pochhammer–Chree equation. Chaos Solitons Fractals 14(4), 581–593 (2002)
Li, J., Li, H., Li, S.: Bifurcations of travelling wave solutions for the generalized Kadomtsev–Petviashili equation. Chaos Solitons Fractals 20, 725–734 (2004)
Li, J., Chen, G.: Bifurcations of traveling wave solutions for four classes of nonlinear wave equations. Int. J. Bifurc. Chaos 15(2), 3973–3998 (2005)
Gumey, W.S.C., Nisbet, R.M.: The regulation of inhomogenous populations. J. Theor. Biol. 52, 441–457 (1975)
El-Sayed, A.M.A., Rida, S.Z., Arafa, A.A.M.: Exact solutions of fractional-order biological population model. Commun. Theor. Phys. 52(6), 992–996 (2009)
Li, Y., Li, Z., Zhang, Y.: Homotopy perturbation method to fractional biological population equation. Fract. Differ. Calc. 1, 117–124 (2011)
Lu, Y.G.: Hölder estimates of solutions of biological population equations. Appl. Math. Lett. 13(6), 123–126 (2000)
Gurtin, M.E., Maccamy, R.C.: On the diffusion of biological populations. Math. Biosci. 33(1–2), 35–49 (1977)
Bear, J.: Dynamics of Fluids in Porou Media. American Elsevier, New York (1972)
Okubo, A.: Diffusion and Ecological Problem. Mathematical Models, Biomathematics 10. Springer, berlin (1980)
Zhang, S., Zhang, H.Q.: Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 375(7), 1069–1073 (2011)
Blasiak, S.: Time-fractional heat transfer equations in modeling of the non-contacting face seals. Int. J. Heat Mass Transf. 100, 79–88 (2016)
Malaguti, L., Marcelli, C.: Sharp profiles in degenerate and doubly degenerate Fisher-KPP equations. J. Differ. Equ. 195(2), 471–496 (2003)
de Pablo, A., Vázquez, J.L.: Travelling waves and finite propagation in a reaction-diffusion equation. J. Differ. Equ. 93(1), 19–61 (1991)
Acknowledgements
This study was funded by the National Natural Science Foundation of China (Grant No. 11361023), the Natural Science Foundation in Chongqing City of China (Grant No. cstc2018jcyjAX0766) and the Special Support Program for High-level Talents in Chongqing City of China (Grant No. cstc2018kjcxljrc0049).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Rui, W. Dynamical system method for investigating existence and dynamical property of solution of nonlinear time-fractional PDEs. Nonlinear Dyn 99, 2421–2440 (2020). https://doi.org/10.1007/s11071-019-05410-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-019-05410-x