1 Introduction

In the past few decades, complex networks have attracted great attention from researchers in various fields. The main reason is that many real systems, such as electrical power grids, food webs, World Wide Web and social networks, can be described as complex dynamical networks [1–4]. Recently, there has been a growing number of studies in the synchronization of the complex networks [5–25].

The coupled neural networks, as a special case of complex networks, have been found to exhibit complex behavior, and their synchronization has been investigated [16–24]. Due to the historical observation of Huygens on pendulum clocks, it has been reported that there are synchronization phenomena in many real systems, such as in language emergence and development as well as in an array composing of identical delayed neural networks [20]. The synchronization problems for fractional order systems have been investigated by different methods in [26, 27]. There are many benefits of having synchronization in coupled networks and systems in engineering applications such as secure communication, harmonic oscillation generation and signal generators design, which has taken a very special position in science and technology [2, 5, 16, 20]. On the other hand, it has been well known that the network traffic congestions and the finite speed of signal transmission over the links may lead to the oscillation phenomenon or instability of the networks [28, 29], and therefore, synchronization problem for complex networks with time delays has gained increasing research attention [16–24]. For example, the global exponential synchronization in arrays of coupled identical delayed neural networks with constant and delayed coupling was investigated [16, 18]. The globally exponential synchronization for linearly coupled neural networks with time-varying delay and impulsive disturbances was studied [19]. In [25], the problem of non-fragile synchronization control for complex networks with time-varying coupling delay and missing data was investigated. As a particular kind of time delay, the distributed time delay has also received much attention since a network usually has a spatial nature due to the presence of an amount of parallel pathways of a variety of axon sizes and lengths [8, 20]. Note that there are very few results for synchronization of the neural networks with distributed time-varying delay nonlinear coupling.

From the practical point of view, the network coupling and network parameters may be the uncertainties or inaccuracies, which could break the dynamic behaviors of the system. In order to deal with this case, robust synchronization of coupled neural networks with uncertainties becomes very important [22–24]. In [22], the robust synchronization in arrays of coupled networks with delay and mixed coupling was studied. In [23], the robust synchronization problem for an array of coupled stochastic discrete-time neural networks with time-varying delay was investigated. In [24], the synchronization problem for an array of neural networks with hybrid coupling and interval time-varying delay was concerned. In [30, 31], the fuzzy neural control problems for uncertain chaotic systems and interconnected unknown chaotic systems were studied, respectively.

According to whether the neuron states (the external states of neurons) or local field states (the internal states of neurons) of the neurons are chosen as basic variables to describe the evolution rule of an neural networks, neural networks can be classified as static neural networks or local field neural networks [32]. There are many results for local field neural networks. In [29], the stability problem of a class of recurrent neural networks with time-varying delay was studied by a weighting-delay-based method. In [33], a non-fragile procedure was introduced to study the problem of synchronization of neural networks with time-varying delay. In [34], the synchronization problem for neural networks with time-varying delay under sampled-data control was investigated. As a tool for scientific computing and engineering application, an obvious characteristic of static neural networks is its capability for implementing a nonlinear mapping from many neural inputs to many neural outputs [35]. The static neural network model plays an important role in many types of problems, for example, the linear variational inequality problem that contains linear and convex quadratic programming problems and linear complementary problems [36]. When static neural networks are used to deal with parallel computing, many calculations are carried out simultaneously and large problems can often be divided into smaller ones and then solved concurrently, which causes coupling. By using parallel algorithm, one not only needs to consider the problem itself, but also the parallel model and network connection, which is more effective to solve practical problem. Most coupled neural network synchronization problems are about local field neural networks, and there are few synchronization problems for static neural networks. When it comes to parallel computing, the static neural networks are useful tools, which motivates us to write this paper.

In [36], a static neural network was shown by

$$\left\{ \begin{array}{l} \dot{x}(t)=-Ax(t)+g(Wx(t-d(t))), \\ x(t)= \varphi(t),t\in[-{\rm max}\{d(t)\},0], \\ \end{array} \right.$$

where x(t) is the state vector associated with the n neurons, \(A=diag\{a_1,a_2,\ldots,a_n\}>0, W=[\hat{W}_{1}^{T},\hat{W}_{2}^{T},\ldots,\hat{W}_{n}^{T}]^{T}\) is the delayed connection weight matrix, \(g(Wx(t))=[g_1(\hat{W}_{1}x(t)),g_2(\hat{W}_{2}x(t)),\ldots,g_n(\hat{W}_{n}x(t))]^{T}\) is the activation function of neurons, \(\varphi(t)\) is the initial condition, and d(t) is the time-varying delay.

Motivated by the aforementioned discussions, in this paper, the robust synchronization problem is studied for an array of static delayed neural networks with nonlinear hybrid coupling. We propose a nonlinear hybrid coupled static delayed neural network model with uncertainties in the coupling configuration matrices terms, firstly. Secondly, the new augmented Lyapunov–Krasovskii and free-weighting matrices are used, which reduce the conservativeness. Thirdly, the novel delay-dependent robust synchronization criterion is deduced, which is less conservative, especially when the time delay is comparatively small.

The rest of this paper is organized as follows. In Sect. 2, nonlinear hybrid coupled static delayed neural networks with uncertainties and some preliminaries are introduced. The robust synchronization criteria for coupled static neural network are derived in Sect. 3. In Sect. 4, numerical simulation is given to demonstrate the effectiveness of the proposed results. Finally, the conclusions are drawn in Sect. 5.

Notation

The notations used throughout this paper are fairly standard. R n denotes the n-dimensional Euclidean space. R m × n is the set of all m × n real matrices. The symbol ⊗ is Kronecker product. X T denotes the transpose of matrix X. X ≥ 0 (X < 0), where \(X\in R^{n \times n}\), means that X is real positive semidefinite matrix (negative definite matrix). I n represents the n-dimensional identity matrix. For a matrix \(A\in R^{n\times n}, \lambda_{\rm max}(A)\) and λmin(A) denote the maximum and minimum eigenvalues of A, respectively. \(\left(\begin{array}{cc} X & Y \\ {*} & Z \\ \end{array}\right)\) stands for \(\left( \begin{array}{cc} X & Y \\ Y^{T} & Z \\ \end{array}\right)\). \(diag\{\cdots\}\) stands for a block-diagonal matrix. Matrix dimensions, if not explicitly stated, are assumed to be compatible for algebraic operations.

2 Problem statement and preliminaries

In this paper, we consider time-varying delayed static neural networks with uncertainties and nonlinear hybrid coupling

$$\begin{aligned} \dot{x_{i}}(t)=&-Ax_{i}(t)+g(Wx_{i}(t-\tau(t)))+\sum_{j=1}^{N}\upsilon^{(1)}_{ij}(\Upgamma_{1}+\Updelta \Upgamma_{1}(t))f(x_{j}(t))\\ &+\sum_{j=1}^{N}\upsilon^{(2)}_{ij}(\Upgamma_{2}+\Updelta \Upgamma_{2}(t))f(x_{j}(t-\tau(t)))\\ &+\sum_{j=1}^{N}\upsilon^{(3)}_{ij}(\Upgamma_{3}+\Updelta \Upgamma_{3}(t))\int\limits_{t-\tau(t)}^{t}f(x_{j}(s)){\rm d}s,\quad i=1,2,\ldots,N. \end{aligned}$$
(1)

Here, \(x_{i}(t)=[x_{i1}(t),x_{i2}(t),\ldots,x_{in}(t)]^{T}\in R^{n}\) is the state vector associated with the n neurons, \(A=diag\{a_{1},a_{2}, \ldots,a_{n}\}\) is diagonal matrix with positive diagonal entries. W = (w ij ) n × n is the delayed connection weight matrix, \(g(Wx_{i}(t-\tau(t)))=[g_{1}(\hat{W}_{1}x_{i}(t-\tau(t))), \quad g_{2}(\hat{W}_{2}x_{i}(t-\tau(t))),\ldots, \quad g_{n}(\hat{W}_{n}x_{i}(t-\tau(t)))]^{T}\) is the activation function of neurons. \(f(x_{i}(t))=[f_{1}(x_{i1}(t)), \quad f_{2}(x_{i2}(t)), \ldots, \quad f_{n}(x_{in}(t))]^{T}\in R^{n}\) denotes the coupling function which is nonlinear functions. τ(t) is the time-varying delay, which satisfies 0 ≤ τ(t) ≤ τ and \(\dot\tau(t)\leq d,\) where τ and d are positive real constants. υ (r) = (υ (r) ij ) N × N ,  (r = 1, 2, 3) are the coupling configuration matrices representing coupling strength and the topological structures of the network and satisfy the following conditions:

$$\upsilon^{(r)}_{ij}=\upsilon^{(r)}_{ji}\geq 0\ i\neq j,\,\upsilon^{(r)}_{ii}=-\sum\limits_{i=1,j\neq i}^{N}\upsilon^{(r)}_{ij}.$$
(2)

\(\Upgamma_{1},\,\Upgamma_{2}\), and \(\Upgamma_{3}\in R^{n\times n}\) represent the inner coupling matrices. \(\Updelta \Upgamma_{1}(t),\, \Updelta \Upgamma_{2}(t)\), and \(\Updelta \Upgamma_{3}(t)\) denote the parameter uncertainties of the system, which are assumed to have the following form

$$[\Updelta \Upgamma_{1}(t),\Updelta \Upgamma_{2}(t),\Updelta \Upgamma_{3}(t)]=M \nabla(t)[E_{\Upgamma_{1}},E_{\Upgamma_{2}},E_{\Upgamma_{3}}],$$
(3)

where \(M,E_{\Upgamma_{1}},E_{\Upgamma_{2}}, E_{\Upgamma_{3}}\) are known constant matrices and ∇(t) is an unknown matrix function satisfying ∇T(t)∇(t) ≤ I n .

Denote \(x_{i}(s)=\varphi_{i}(t)\in\mathcal{C}([-\tau,0],R^{n})\ (i=1,2,\ldots,N)\) as the initial conditions with system (1), where \(\tau=\sup_{t\in R}{\tau(t)}\) and \(\mathcal{C}([-\tau,0],R^{n})\) is the set of continuous functions from [−τ, 0] to R n.

Throughout this paper, the following assumptions are made.

Assumption 1

[21] For any \(x_1, x_2 \in R\), there exist constants e − r ,  e + r , h − r and h + r such that

$$e_r^ - \le \frac{{{g_r}({x_1}) - {g_r}({x_2})}}{{{x_1} - {x_2}}} \le e_r^+,\,h_r^ - \le \frac{{{f_r}({x_1}) - {f_r}({x_2})}}{{{x_1} - {x_2}}} \le h_r^+,\,r = 1,2, \ldots, n.$$

We denote

$$\begin{aligned} {E_1} &= diag(e_1^ + e_1^ -, \ldots, e_n^ + e_n^ - ),\, {E _2} = diag(\frac{{e _1^ + + e _1^ - }}{2}, \ldots, \frac{{e_n^ + + e_n^ - }}{2}),\\ {H_1} &= diag(h_1^ + h_1^ -, \ldots, h_n^ + h_n^ - ),\, {H _2} = diag(\frac{{h _1^ + + h _1^ - }}{2}, \ldots, \frac{{h_n^ + + h_n^ - }}{2}). \end{aligned}$$

Remark 1

In the system (1), the coupled static neural networks contain the nonlinear coupling, the discrete-time-varying delay nonlinear coupling and distributed time-varying delay nonlinear coupling. Note that in almost all literature regarding synchronization of neural networks, the nonlinear coupling phenomenon has been seldom considered.

Remark 2

The coupled static neural networks can be used in parallel computing, which can deal with the wireless network optimization system, image processing and so on.

Remark 3

In the Assumption 1, the e − r ,  e + r , h − r and h + r are allowed to be positive, negative or zero, which makes the activation functions more general than nonnegative sigmoidal functions.

Definition 1

The coupled static neural networks system is globally synchronized, for any initial conditions \(\varphi_{i}(t)\in\mathcal{C}([-\tau,0],R^{n})\ (i=1,2,\ldots,N)\), if the following holds \(\lim\nolimits_{t \rightarrow \infty }\|x_{i}(t)-x_{j}(t)\|=0\).

Lemma 1

[8] Let \(U=(u_{ij})_{N\times N}, P\in R^{n\times n}, x=[x_{1}^{T}, x_{2}^{T}, \ldots, x_{N}^{T}]^{T}\), and \(y=[y_{1}^{T}, y_{2}^{T}, \ldots, y_{N}^{T}]^{T}\), with \(x_{k},\,y_{k}\in R^{n},\,(k=1, 2, \ldots, N)\). If U = U T and and each row sum of U is zero, then

$$x^T(U\otimes P)y=-\sum\limits_{i=1}^{N-1}\sum\limits_{j=i+1}^{N}u_{ij}(x_i-x_j)^{T}P(y_i-y_j).$$

Lemma 2

[37] Assume that the vector function \(\omega \,:\,[0,r]\rightarrow R^{m}\) is well defined for the following integrations. For any symmetric matrix \(W\in R^{m\times m}\) and scalar r > 0, one has

$$r \int\limits_{0}^{r}{\omega ^{T} (s)}W \omega (s){\rm d}s\geq {\left(\int\limits_{0}^{r}\omega (s){\rm d}s\right)}^{T}W\left(\int\limits_{0}^{r}\omega (s){\rm d}s\right).$$

Lemma 3

[38] The Kronecker product has the following properties:

  1. 1.

    (α A) ⊗ B = A ⊗ (α B),

  2. 2.

    (A + B) ⊗ C = A ⊗ C + B ⊗ C,

  3. 3.

    (A ⊗ B)(C ⊗ D) = (AC) ⊗ (BD).

Lemma 4

[39] If U, V, W are real matrices of appropriate dimension with M satisfying M = M T, then M + UVW + W T V T U T < 0, for all V T V ≤ I, and only if there exists a positive constant \(\varepsilon\) such that \(M+\varepsilon^{-1}UU^T+\varepsilon W^TW<0.\)

3 Main results

In this section, we investigate the robust synchronization for the hybrid nonlinear coupled time-varying delay static neural networks. To facilitate further development, let \(x(t)=[x_{1}^{T}(t),x_{2}^{T}(t),\ldots,\quad x_{N}^{T}(t)]^{T},\quad G((I_N\otimes W)x(t-\tau(t)))=[g^T(Wx_{1}(t-\tau(t))),\quad g^T(Wx_{2}(t-\tau(t))),\cdots,\; g^T(Wx_{N}(t-\tau(t)))]^T,\quad F(x(t))=[f^T(x_{1}(t)), f^T(x_{2}(t)),\cdots,\quad f^T(x_{N}(t))]^T,\quad \hat{\Upgamma}_{1}=\Upgamma_{1}+\Updelta \Upgamma_{1}(t),\quad \hat{\Upgamma}_{2}=\Upgamma_{2}+\Updelta \Upgamma_{2}(t),\quad \hat{\Upgamma}_{3}=\Upgamma_{3}+\Updelta \Upgamma_{3}(t)\).

Then model (1) can be written as

$$\begin{aligned} \dot{x}(t)=&-(I_N\otimes A)x(t)+G((I_N\otimes W)x(t-\tau(t)))+(\upsilon ^{(1)}\otimes \hat{\Upgamma}_{1})F(x(t))\\ &+(\upsilon ^{(2)} \otimes\hat{\Upgamma}_{2})F(x(t-\tau(t)))+(\upsilon ^{(3)}\otimes\hat{\Upgamma}_{3})\int\limits_{t-\tau(t)}^{t}F(x(s)){\rm d}s. \\ \end{aligned}$$
(4)

Theorem 1

Under Assumptions 1, the nonlinear hybrid coupled static delayed neural networks (4) are globally robustly synchronized, if there exist positive definite matrices R i   (i = 1, 2, 3), positive definite matrices \(P=\left( \begin{array}{cc} P_{11} & P_{12} \\ * & P_{22} \\ \end{array} \right)\), \(Q=\left( \begin{array}{cc} Q_{11} & Q_{12} \\ * & Q_{22} \\ \end{array} \right)\), positive diagonal matrices S i (i = 1, 2, 3, 4), real matrices M 1, M 2, and positive constant \(\varepsilon\), such that the following linear matrix inequalities hold for all 1 ≤ i < j ≤ N,

$$\begin{aligned} \Upphi_{ij}= \left( \begin{array}{lllllllllll} \Upphi_{ij11} & 0 & \Upphi_{ij13} & \Upphi_{ij14} & R_1 & \Upphi_{ij16} & \Upphi_{ij17} & \Upphi_{ij18} & 0 & 0 & R_1M \\ * & \Upphi_{ij22} & M^T_1 & 0 & \Upphi_{ij25} & 0 & H_2S_4 & 0 & 0 & 0 & 0 \\ * & * & \Upphi_{ij33} & 0 & M_2 & \Upphi_{ij36} & \Upphi_{ij37} & \Upphi_{ij38} & 0 & M_1 & M_2M \\ * & * & * & \Upphi_{ij44} & 0 & \Upphi_{ij46} & 0 & 0 & 0 & 0 & 0 \\ * & * & * & * & \Upphi_{ij55} & 0 & \Upphi_{ij57} & 0 & 0 & 0 & 0 \\ * & * & * & * & * & \Upphi_{ij66} & \Upphi_{ij67} & \Upphi_{ij68} & 0 & 0 & 0 \\ * & * & * & * & * & * & \Upphi_{ij77} & \Upphi_{ij78} & 0 & 0 & 0 \\ * & * & * & * & * & * & * & \Upphi_{ij88} & \frac{-1}{\tau}Q^{T}_{12} & 0 & 0 \\ * & * & * & * & * & * & * & * & \frac{-1}{\tau}Q_{11} & 0 & 0 \\ * & * & * & * & * & * & * & * & * & \frac{-1}{\tau}R_{3} & 0 \\ * & * & * & * & * & * & * & * & * & * & -\varepsilon I_n \\ \end{array} \right)\\ &<0, \end{aligned}$$
(5)

\( \Upphi_{ij11}=-R_1A-A^{T}R_1-W^TE_1S_1W-H_1S_2+R_2, \Upphi_{ij13}=-M^T_1-A^TM^T_2, \quad \Upphi_{ij14}=W^TE_2S_1, \quad \Upphi_{ij16}=-Nv^{(1)}_{ij}R_1\Upgamma_1+H_2S_2,\; \Upphi_{ij17}=-Nv^{(2)}_{ij}R_1\Upgamma_2, \quad \Upphi_{ij18}=-Nv^{(3)}_{ij}R_1\Upgamma_3, \quad \Upphi_{ij22}=-(1-d)R_{2}-W^TE_1S_3W-H_1S_4, \quad \Upphi_{ij25}=W^T{E_2}{S_3}, \quad \Upphi_{ij33}=\tau R_3-M_2-M^{T}_2, \Upphi_{ij36}=-Nv^{(1)}_{ij}M_2\Upgamma_1, \quad \Upphi_{ij37}=-Nv^{(2)}_{ij}M_2\Upgamma_2, \quad \Upphi_{ij38}=-Nv^{(3)}_{ij}M_2\Upgamma_3, \quad \Upphi_{ij44}=P_{11}+\tau Q_{11}-S_1, \quad \Upphi_{ij46}=P_{12}+\tau Q_{12}, \Upphi_{ij55}=-(1-d)P_{11}-S_3, \quad \Upphi_{ij57}=-(1-d)P_{12}, \quad \Upphi_{ij66}=P_{22}+\tau Q_{22}-S_2+\varepsilon (Nv^{(1)}_{ij})^{2}E^T_{\Upgamma_1}E_{\Upgamma_1}, \quad \Upphi_{ij67}=\varepsilon N^{2}v^{(1)}_{ij}v^{(2)}_{ij}E^T_{\Upgamma_1}E_{\Upgamma_2}, \Upphi_{ij68}=\varepsilon N^{2}v^{(1)}_{ij}v^{(3)}_{ij}E^T_{\Upgamma_1}E_{\Upgamma_3}, \quad \Upphi_{ij77}=-(1-d)P_{22}- S_4+\varepsilon (Nv^{(2)}_{ij})^{2}E^T_{\Upgamma_2}E_{\Upgamma_2}, \quad \Upphi_{ij78}=\varepsilon N^{2}v^{(2)}_{ij}v^{(3)}_{ij}E^T_{\Upgamma_2}E_{\Upgamma_3}, \quad \Upphi_{ij88}=\frac{-1}{\tau}Q_{22}+\varepsilon (Nv^{(3)}_{ij})^{2}E^T_{\Upgamma_3}E_{\Upgamma_3}. \)

Proof

From Assumption 1, we can get that

$$\begin{aligned} &{\left[ \begin{array}{ll} W{x_i}(t) - W{x_j}(t) \\ g(W{x_i}(t)) -g(W{x_j}(t)) \\ \end{array} \right]^T \left[ {\begin{array}{ll} {-E_{1}S_{1}} & {E_{2}S_{1}} \\ * & { - S_{1}} \\ \end{array}} \right] \left[ \begin{array}{ll} W{x_i}(t) - W{x_j}(t)\\ g(W{x_i}(t)) - g(W{x_j}(t)) \\ \end{array} \right] \geq 0,}\\ &{\left[ \begin{array}{l} {x_i}(t) - {x_j}(t) \\ f({x_i}(t)) -f({x_j}(t)) \\ \end{array} \right]^T \left[ {\begin{array}{ll} { -H_{1}S_{2}} & {H_{2}S_{2}} \\ * & { - S_{2}} \\ \end{array}} \right] \left[ \begin{array}{l} {x_i}(t) - {x_j}(t) \\ f({x_i}(t)) - f({x_j}(t)) \\ \end{array} \right] \geq 0,}\\ &{\left[ \begin{array}{l} W{x_i}(t-\tau(t)) - W{x_j}(t-\tau(t)) \\ g(W{x_i}(t-\tau(t))) - g(W{x_j}(t-\tau(t))) \\ \end{array}\right]^T \left[ {\begin{array}{ll} { -E_{1}S_{3}} & {E_{2}S_{3}} \\ * & { - S_{3}} \\ \end{array}} \right]}\\ &{\times\left[ \begin{array}{l} W{x_i}(t-\tau(t)) -W{x_j}(t-\tau(t)) \\ g(W{x_i}(t-\tau(t))) - g(W{x_j}(t-\tau(t))) \\ \end{array} \right] \geq 0,}\\ &{\left[ \begin{array}{l} {x_i}(t-\tau(t)) - {x_j}(t-\tau(t)) \\ f({x_i}(t-\tau(t))) - f({x_j}(t-\tau(t))) \\ \end{array} \right]^T \left[{\begin{array}{ll} { -H_{1}S_{4}} & {H_{2}S_{4}} \\ * & {- S_{4}} \\ \end{array}} \right] \left[ \begin{array}{l} {x_i}(t-\tau(t)) - {x_j}(t-\tau(t)) \\ f({x_i}(t-\tau(t))) -f({x_j}(t-\tau(t))) \\ \end{array} \right] \geq 0,}\\ \end{aligned}$$

which is equivalent to

$$\begin{aligned} &-({x_i}(t) - {x_j}(t))^{T}W^{T}E_{1}S_{1}W({x_i}(t) - {x_j}(t))+2({x_i}(t) - {x_j}(t))^{T}W^{T}E_{2}S_{1}\\ &(g(W{x_i}(t)) - g(W{x_j}(t)))-(g(W{x_i}(t)) - g(W{x_j}(t)))^{T}S_{1}(g(W{x_i}(t)) - g(W{x_j}(t)))\geq0,\\ \end{aligned}$$
(6)
$$\begin{aligned} &-({x_i}(t) - {x_j}(t))^{T}H_{1}S_{2}({x_i}(t) - {x_j}(t))+2({x_i}(t) - {x_j}(t))^{T}H_{2}S_{2}\\ &(f({x_i}(t)) - f({x_j}(t)))-(f({x_i}(t)) - f({x_j}(t)))^{T}S_{2}(f({x_i}(t)) - f({x_j}(t)))\geq0,\\ \end{aligned}$$
(7)
$$\begin{aligned} &-({x_i}(t-\tau(t)) -{x_j}(t-\tau(t)))^{T}W^{T}E_{1}S_{3}W({x_i}(t-\tau(t))- {x_j}(t-\tau(t)))\\ &+2({x_i}(t-\tau(t)) -{x_j}(t-\tau(t)))^{T}W^{T}E_{2}S_{3} (g(W{x_i}(t-\tau(t))) - g(W{x_j}(t-\tau(t))))\\ &-(g(W{x_i}(t-\tau(t)))-g(W{x_j}(t-\tau(t))))^{T}S_{3}(g(W{x_i}(t-\tau(t))) - g(W{x_j}(t-\tau(t))))\geq0,\\ \end{aligned}$$
(8)
$$\begin{aligned} &-({x_i}(t-\tau(t)) -{x_j}(t-\tau(t)))^{T}H_{1}S_{4}({x_i}(t-\tau(t)) - {x_j}(t-\tau(t)))\\ &+2({x_i}(t-\tau(t)) -{x_j}(t-\tau(t)))^{T}H_{2}S_{4}(f({x_i}(t-\tau(t))) - f({x_j}(t-\tau(t))))\\ &-(f({x_i}(t-\tau(t))) -f({x_j}(t-\tau(t))))^{T}S_{4}(f({x_i}(t-\tau(t))) - f({x_j}(t-\tau(t))))\geq0. \\ \end{aligned}$$
(9)

Let \(j=(1,1,\ldots,1)^{T}, J_N=jj^T\) be the N by N matrix, and U = NI N  − J. Construct the following Lyapunov–Krasovskii functional as

$$V(x(t))=[V_{1}(x(t))+V_{2}(x(t))+V_{3}(x(t))+V_{4}(x(t))+V_{5}(x(t))]$$
(10)

where

$$V_{1}(x(t))=x^T(t)(U \otimes R_1)x(t),\\$$
(11)
$$V_{2}(x(t))=\int\limits_{t-\tau (t)}^{t}{x}^{T}(s)(U\otimes R_2){x}(s){\rm d}s,$$
(12)
$$V_{3}(x(t))=\int\limits_{t-\tau(t)}^{t}\left[ \begin{array}{l} G((I_N\otimes W)x(s)) \\ F(x(s)) \\ \end{array} \right]^{T} \left(\begin{array}{ll}U \otimes P_{11} & U \otimes P_{12} \\ * & U \otimes P_{22} \\ \end{array} \right) \left[\begin{array}{l} G((I_N\otimes W)x(s)) \\ F(x(s)) \\ \end{array} \right]{\rm d}s,$$
(13)
$$V_{4}(x(t))=\int\limits_{t-\tau }^{t}\int\limits_{\theta }^{t} \left[\begin{array}{l} G((I_N\otimes W)x(s)) \\ F(x(s)) \\ \end{array} \right]^{T} \left(\begin{array}{ll}U \otimes Q_{11} & U \otimes Q_{12} \\ * & U \otimes Q_{22} \\ \end{array} \right) \left[ \begin{array}{l} G((I_N\otimes W)x(s)) \\ F(x(s)) \\ \end{array} \right] {\rm d}s{\rm d}\theta,$$
(14)
$$V_{5}(x(t))=\int\limits_{t-\tau }^{t}\int\limits_{\theta }^{t}\dot{x}^{T}(s)(U\otimes R_3)\dot{x}(s){\rm d}s{\rm d}\theta. \\$$
(15)

Calculating the time derivative of V i (x(t)), (i = 1, 2, 3, 4, 5) along the complex network (4), we get

$$\begin{aligned} \dot{{V}}_1(x(t)) &=2{x^T}(t)(U \otimes {R_1})\dot{x}(t) \\ &= 2{x^T}(t)(U \otimes {R_1})\left[ -(I_N\otimes A)x(t)+G((I_N\otimes W)x(t-\tau(t)))\right.\\ &\quad\left.+(\upsilon ^{(1)}\otimes \hat{\Upgamma}_{1})f(x(t)) +(\upsilon ^{(2)} \otimes \hat{\Upgamma}_{2})f(x(t-\tau(t)))+(\upsilon ^{(3)} \otimes \hat{\Upgamma}_{3})\int\limits_{t-\tau(t)}^{t}f(x(s)){\rm d}s\right] \\ &=2\sum\limits_{i = 1}^{N - 1} \sum\limits_{j = i + 1}^N \left[ (x_i(t)-x_j(t))^T(-R_1A)(x_i(t)-x_j(t))+(x_i(t)-x_j(t))^T R_{1}\right.\\ &\left.(g(Wx_i(t-\tau(t))) -g(Wx_j(t-\tau(t))))-N \upsilon ^{(1)}_{ij}(x_i(t)-x_j(t))^TR_{1}\hat{\Upgamma}_{1}\right.\\ &\left.(f(x_i(t))-f(x_j(t)))-N \upsilon ^{(2)}_{ij}(x_i(t)-x_j(t))^TR_{1}\hat{\Upgamma}_{2}(f(x_i(t-\tau(t)))-f(x_j(t-\tau(t))))\right.\\ &\left.\quad-N \upsilon ^{(3)}_{ij}(x_i(t)-x_j(t))^TR_{1}\hat{\Upgamma}_{3}\left(\int\limits_{t-\tau (t)}^{t}f(x_i(s)){\rm d}s-\int\limits_{t-\tau (t)}^{t}f(x_j(s)){\rm d}s\right)\right] \\ \end{aligned}$$
(16)
$$\begin{aligned} \dot{{V}}_2(x(t))&=x^{T}(t)(U \otimes {R_2})x(t)-(1-\dot{\tau}(t))x^{T}(t-\tau(t))(U \otimes {R_2})x(t-\tau(t))\\ &\quad\leq \sum\limits_{i = 1}^{N - 1}\sum\limits_{j = i + 1}^N[(x_i(t)-x_j(t))^TR_2(x_i(t)-x_j(t))-(1-d)(x_i(t-\tau(t)) \\ &\quad-x_j(t-\tau(t)))^T R_2(x_i(t-\tau(t))-x_j(t-\tau(t)))] \\ \end{aligned}$$
(17)
$$\begin{aligned} \dot{{V}}_3(x(t))&= \left[\begin{array}{l} G((I_N\otimes W)x(t)) \\ F(x(t)) \\ \end{array} \right]^{T} \left( \begin{array}{ll} U \otimes P_{11} & U \otimes P_{12} \\ * & U \otimes P_{22} \\ \end{array} \right) \left[\begin{array}{l} G((I_N\otimes W)x(t)) \\ F(x(t)) \\ \end{array} \right]\\ &\quad -(1-\dot{\tau}(t)) \left[ \begin{array}{l} G((I_N\otimes W)x(t-\tau(t))) \\ F(x(t-\tau(t))) \\ \end{array} \right]^{T} \left( \begin{array}{ll} U \otimes P_{11} & U \otimes P_{12} \\ * & U \otimes P_{22} \\ \end{array} \right)\\ & \quad \times \left[ \begin{array}{l} G((I_N\otimes W)x(t-\tau(t))) \\ F(x(t-\tau(t))) \\ \end{array} \right]\\ &\leq \sum\limits_{i = 1}^{N - 1} \sum\limits_{j = i + 1}^N \left\{ \left[ \begin{array}{l} g(Wx_i(t))-g(Wx_j(t)) \\ f(x_i(t))-f(x_j(t)) \\ \end{array} \right]^{T} \left( \begin{array}{ll} P_{11} & P_{12} \\ * & P_{22} \\ \end{array} \right) \left[ \begin{array}{l} g(Wx_i(t))-g(Wx_j(t)) \\ f(x_i(t))-f(x_j(t)) \\ \end{array} \right]\right.\\ &\quad \left.-(1-d) \left[\begin{array}{l} g(Wx_i(t-\tau(t)))-g(Wx_j(t-\tau(t))) \\ f(x_i(t-\tau(t)))-f(x_j(t-\tau(t))) \\ \end{array} \right]^{T} \left( \begin{array}{ll}P_{11} & P_{12} \\ * & P_{22} \\ \end{array} \right) \right.\\ & \quad \left.\times \left[ \begin{array}{l} g(Wx_i(t-\tau(t)))-g(Wx_j(t-\tau(t))) \\ f(x_i(t-\tau(t)))-f(x_j(t-\tau(t))) \\ \end{array} \right] \right\}. \\ \end{aligned}$$
(18)
$$\begin{aligned} \dot{{V}}_4(x(t))&=-\int\limits_{t-\tau }^{t} \left[ \begin{array}{l} G((I_N\otimes W)x(s)) \\ F(x(s)) \\ \end{array} \right]^{T} \left(\begin{array}{ll} U \otimes Q_{11} & U \otimes Q_{12} \\ * & U \otimes Q_{22} \\ \end{array} \right) \left[\begin{array}{l} G((I_N\otimes W)x(s)) \\ F(x(s)) \\ \end{array} \right]{\rm d}s\\ &\quad +\tau \left[ \begin{array}{l} G((I_N\otimes W)x(t)) \\ F(x(t)) \\ \end{array} \right]^{T} \left(\begin{array}{ll} U \otimes Q_{11} & U \otimes Q_{12} \\ * & U \otimes Q_{22} \\ \end{array}\right) \left[\begin{array}{l} G((I_N\otimes W)x(t)) \\ F(x(t)) \\ \end{array} \right] \\ &\leq \tau \left[ \begin{array}{l} G((I_N\otimes W)x(t)) \\ F(x(t)) \\ \end{array} \right]^{T} \left( \begin{array}{ll} U \otimes Q_{11} & U \otimes Q_{12} \\ * & U \otimes Q_{22} \\ \end{array} \right) \left[ \begin{array}{l} G((I_N\otimes W)x(t)) \\ F(x(t)) \\ \end{array}\right]\\ &\quad -\frac{1}{\tau} \left(\int\limits_{t-\tau (t)}^{t}\left[ \begin{array}{l} G((I_N\otimes W)x(s)) \\ F(x(s)) \\ \end{array}\right]{\rm d}s\right)^{T} \left(\begin{array}{ll} U \otimes Q_{11} & U \otimes Q_{12} \\ * & U \otimes Q_{22} \\ \end{array} \right)\\ & \quad \times\int\limits_{t-\tau (t)}^{t} \left[ \begin{array}{l} G((I_N\otimes W)x(s)) \\ F(x(s)) \\ \end{array} \right]{\rm d}s \\ &= \tau \sum\limits_{i = 1}^{N - 1} \sum\limits_{j = i + 1}^N \left\{ \left[ \begin{array}{l} g(Wx_i(t))-g(W x_j(t)) \\ f(x_i(t))-f(x_j(t)) \\ \end{array} \right]^{T} \left( \begin{array}{ll} Q_{11} & Q_{12} \\ * & Q_{22} \\ \end{array} \right) \left[ \begin{array}{l} g(Wx_i(t))-g(W x_j(t)) \\ f(x_i(t))-f(x_j(t)) \\ \end{array}\right] \right\} \\ &\quad -\frac{1}{\tau} \sum\limits_{i = 1}^{N - 1} \sum\limits_{j = i + 1}^N \left\{ \left(\int\limits_{t-\tau (t)}^{t}\left[ \begin{array}{l} g(Wx_i(t))-g(W x_j(t)) \\ f(x_i(t))-f(x_j(t)) \\ \end{array} \right]{\rm d}s\right)^{T} \left( \begin{array}{ll} Q_{11} & Q_{12} \\ * & Q_{22} \\ \end{array} \right)\right.\\ &\quad \left. \times \int\limits_{t-\tau (t)}^{t} \left[ \begin{array}{l} g(Wx_i(t))-g(W x_j(t)) \\ f(x_i(t))-f(x_j(t)) \\ \end{array} \right]{\rm d}s \right\} \\ \end{aligned}$$
(19)
$$\begin{aligned} \dot{V}_{5}(x(t))&= -\int\limits_{t-\tau }^{t}\dot{x}^{T}(s)(U\otimes R_3)\dot{x}(s){\rm d}s+\int\limits_{t-\tau }^{t}\dot{x}^{T}(t)(U\otimes R_3)\dot{x}(t){\rm d}\theta\\ & \leq \sum\limits_{i = 1}^{N - 1} \sum\limits_{j = i + 1}^N \left[ \tau ({\dot{x}_i}(t) - {\dot{x}_j}(t))^{T}R_{3}({\dot{x}_i}(t) - {\dot{x}_j}(t))\right.\\ &\quad \left.-\frac{1}{\tau}\left(\int\limits_{t-\tau (t)}^{t}(\dot{x}_i(s)-\dot{x}_j(s)){\rm d}s\right)^{T}R_3\left(\int\limits_{t-\tau (t)}^{t}(\dot{x}_i(s)-\dot{x}_j(s)){\rm d}s\right)\right]. \cr \end{aligned}$$
(20)

From the Leibniz–Newton formula and coupled static neural network system (4), for any matrices M 1 and M 2, we get

$$2[\dot{x}^{T}(t)(U\otimes M_1)]\left[-x(t)+x(t-\tau(t))+\int\limits_{t-\tau(t)}^{t}\dot{x}(s){\rm d}s\right]=0,\\$$
(21)
$$\begin{aligned} &2[\dot{x}^{T}(t)(U\otimes M_2)]\left[-(I_N\otimes A)x(t)+G((I_N\otimes W)x(t-\tau(t)))+(\upsilon ^{(1)}\otimes \hat{\Upgamma}_{1})F(x(t))\right.\\ &\left.+(\upsilon ^{(2)} \otimes \hat{\Upgamma}_{2})F(x(t-\tau(t)))+(\upsilon ^{(3)}\otimes\hat{\Upgamma}_{3})\int_{t-\tau(t)}^{t}F(x(s)){\rm d}s-\dot{x}(t)\right]=0.\\ \end{aligned}$$
(22)

Let \({\eta_{ij}(t)} = (({x_i}(t) - {x_j}(t)) ^T,({x_i}(t- \tau(t)) - {x_j}(t- \tau(t))) ^T,({\dot{x}_i}(t) - {\dot{x}_j}(t)) ^T,(g(W{x_i}(t)) - g(W{x_j}(t))) ^T, (g(W{x_i}(t- \tau(t))) - g(W{x_j}(t- \tau(t)))) ^T, (f({x_i}(t)) - f({x_j}(t)))^T\), \((f({x_i}(t- \tau(t))) - f({x_j}(t- \tau(t)))) ^T, \left(\int_{t-\tau (t)}^{t}(f(x_i(s))-f(x_j(s))){\rm d}s\right)^{T}, \left(\int_{t-\tau (t)}^{t}(g(Wx_i(s))-g(Wx_j(s))){\rm d}s\right)^{T}, \left(\int_{t-\tau(t)}^{t}(\dot{x}_i(s)-\dot{x}_j(s)){\rm d}s\right)^{T}) ^T\), combining (6–22), we get

$$\dot{V}(x(t)) \leq \sum\limits_{i = 1}^{N - 1} \sum\limits_{j = i + 1}^N [({\eta_{ij}(t)})^{T} \Upphi^{(1)}_{ij} ({\eta_{ij}(t)})],$$

where

$$\Upphi^{(1)}_{ij}= \left(\begin{array}{lllllllllll} \Upphi_{ij11}& 0 & \Upphi_{ij13} & \Upphi_{ij14} & R_1 & \Upphi^{(1)}_{ij16} & \Upphi^{(1)}_{ij17} & \Upphi^{(1)}_{ij18} & 0 & 0 \\ * & \Upphi_{ij22} & M^T_1 & 0 & \Upphi_{ij25} & 0 & H_2S_4 & 0 & 0 & 0\\ * & * & \Upphi_{ij33} & 0 & M_2 & \Upphi^{(1)}_{ij36} & \Upphi^{(1)}_{ij37} & \Upphi^{(1)}_{ij38} & 0 & M_1\\ * & * & * & \Upphi_{ij44} & 0 & \Upphi_{ij46} & 0 &0 & 0 & 0 \\ * & * & * & * & \Upphi_{ij55} & 0 &\Upphi_{ij57} & 0 & 0 & 0\\ * & * & * & * & * &\Upphi^{(1)}_{ij66} & 0 & 0 & 0 & 0 \\ * & * & * & *& * & * & \Upphi^{(1)}_{ij77} & 0 & 0 & 0 \\ * & * &* & * & * & * & * & \Upphi^{(1)}_{ij88} & \frac{-1}{\tau}Q^{T}_{12} &0 \\ * & * & * & * & * & * & * & * &\frac{-1}{\tau}Q_{11} & 0 \\ * & * & * & * & * & *& * & * & * & \frac{-1}{\tau}R_{3} \\ \end{array}\right),$$
(23)

\(\Upphi^{(1)}_{ij16}=-N\upsilon^{(1)}_{ij}R_1\hat{\Upgamma}_1+H_2S_2, \,\,\,\Upphi^{(1)}_{ij17}=-N\upsilon^{(2)}_{ij}R_1\hat{\Upgamma}_2, \,\,\,\Upphi^{(1)}_{ij18}=-N\upsilon^{(3)}_{ij}R_1\hat{\Upgamma}_3, \,\,\, \Upphi^{(1)}_{ij36}=-N\upsilon^{(1)}_{ij}M_2\hat{\Upgamma}_1, \,\,\, \Upphi^{(1)}_{ij37}=-N\upsilon^{(2)}_{ij}M_2\hat{\Upgamma}_2, \,\,\,\; \Upphi^{(1)}_{ij38}=-N\upsilon^{(3)}_{ij}M_2\hat{\Upgamma}_3, \,\,\,\Upphi^{(1)}_{ij66}=P_{22}+\tau Q_{22}-S_2, \,\,\, \Upphi^{(1)}_{ij77}=-(1-d)P_{22}-S_4, \,\,\, \Upphi^{(1)}_{ij88}=\frac{-1}{\tau}Q_{22}\).

If \(\Upphi^{(1)}_{ij}<0\), one has

$$\dot{V}(x(t)) \leq \sum\limits_{i = 1}^{N - 1} \sum\limits_{j = i + 1}^N \left[({\eta_{ij}(t)})^{T} \Upphi^{(1)}_{ij} ({\eta_{ij}(t)})\right]<0.$$
(24)

According to (3), \(\Upphi^{(1)}_{ij}<0\) is equivalent to

$$\begin{aligned} &{\Upphi^{(2)}_{ij}+\left(\begin{array}{l} R_1M \\ 0 \\ M_{2}M \\ 0_{7n \times n} \\ \end{array} \right)\nabla(t)\left(\begin{array}{lllll} 0_{n\times5n} & -N \upsilon^{(1)}_{ij}E_{\Upgamma_1} & -N\upsilon^{(2)}_{ij}E_{\Upgamma_2} & -N\upsilon^{(3)}_{ij}E_{\Upgamma_3} & 0_{n\times 2n} \\ \end{array} \right)}\\ &+{\left(\begin{array}{lllll}0_{n\times 5n} & -N\upsilon ^{(1)}_{ij}E_{\Upgamma_1} & -N \upsilon ^{(2)}_{ij}E_{\Upgamma_2} & -N\upsilon^{(3)}_{ij}E_{\Upgamma_3} & 0_{n\times 2n} \\ \end{array}\right)^{T}\nabla^{T}(t)\left(\begin{array}{l} R_1M \\ 0 \\ M_{2}M \\ 0_{7n\times n} \\ \end{array} \right)^{T}<0,} \\ \end{aligned}$$
(25)

where

$$\Upphi^{(2)}_{ij}= \left(\begin{array}{llllllllll}\Upphi_{ij11} & 0 & \Upphi_{ij13} & \Upphi_{ij14} & R_1 & \Upphi^{(2)}_{ij16} & \Upphi^{(2)}_{ij17} & \Upphi^{(2)}_{ij18} & 0 & 0 \\ * & \Upphi_{ij22} & M^T_1 & 0 & \Upphi_{ij25} & 0 & H_2S_4 & 0 & 0 & 0 \\ * & * & \Upphi_{ij33} & 0 & M_2 & \Upphi^{(2)}_{ij36} & \Upphi^{(2)}_{ij37} & \Upphi^{(2)}_{ij38} & 0 & M_1 \\ * & * & * & \Upphi_{ij44} & 0 & \Upphi_{ij46} & 0 & 0 & 0 & 0 \\ * & * & * & * & \Upphi_{ij55} & 0 & \Upphi_{ij57} & 0 & 0 & 0\\ * & * & * & * & * & \Upphi^{(1)}_{ij66} & 0 & 0 & 0 & 0 \\ * & * & * & * & * & * & \Upphi^{(1)}_{ij77} & 0 & 0 & 0 \\ * & * & * & * & * & * & * & \Upphi^{(1)}_{ij88} & \frac{-1}{\tau}Q^{T}_{12} & 0 \\ * & * & * & * & * & * & * & * & \frac{-1}{\tau}Q_{11} & 0 \\ * & * & * & * & * & * & * & * & * & \frac{-1}{\tau}R_{3} \\ \end{array}\right)$$

\(\Upphi^{(2)}_{ij16}=-N\upsilon^{(1)}_{ij}R_1{\Upgamma_1}+H_2S_2, \,\,\, \Upphi^{(2)}_{ij17}=-N\upsilon^{(2)}_{ij}R_1{\Upgamma_2}, \,\,\, \Upphi^{(2)}_{ij18}=-N\upsilon^{(3)}_{ij}R_1{\Upgamma_3}, \,\,\, \Upphi^{(2)}_{ij36}=-N\upsilon^{(1)}_{ij}M_2{\Upgamma_1}, \,\,\,\Upphi^{(2)}_{ij37}=-N\upsilon^{(2)}_{ij}M_2{\Upgamma_2}, \,\,\, \Upphi^{(2)}_{ij38}=-N\upsilon^{(3)}_{ij}M_2{\Upgamma_3}\).

According to Lemma 4, (25) holds for ∇T(t)∇(t) < I if and only if there exists \(\varepsilon >0\) such that

$$\begin{aligned} &{\Upphi^{(2)}_{ij}+\varepsilon^{-1} \left(\begin{array}{l} R_1M \\ 0\\ M_{2}M \\ 0_{7n \times n} \\ \end{array}\right) \left(\begin{array}{l} R_1M \\ 0\\ M_{2}M \\ 0_{7n\times n} \\ \end{array}\right)^{T}}\\ &{+ \varepsilon \left( \begin{array}{lllll} 0_{n\times 5n} & -N\upsilon^{(1)}_{ij}E_{\Upgamma_1} & -N\upsilon^{(2)}_{ij}E_{\Upgamma_2} & -N\upsilon^{(3)}_{ij}E_{\Upgamma_3} & 0_{n\times 2n} \\ \end{array} \right)^{T}}\\ &{\left(\begin{array}{lllll} 0_{n\times 5n} & -N\upsilon^{(1)}_{ij}E_{\Upgamma_1} & -N\upsilon^{(2)}_{ij}E_{\Upgamma_2} & -N\upsilon^{(3)}_{ij}E_{\Upgamma_3} & 0_{n\times 2n} \\ \end{array} \right)<0.} \end{aligned}$$
(26)

By Schur complement in [40], one obtains that (26) is equivalent to (5).

According to \(\dot{V}(x(t))<0\), we know that x T(t)(U ⊗ R 1)x(t) is bounded function and

$$\lim\limits_{t \rightarrow\infty }\|x_{i}(t)-x_{j}(t)\|=0.$$

We can obtain that the coupled static neural networks (4) are globally robustly synchronized. This proof is completed.

Remark 4

There are many synchronization studies for coupled local field neural networks, such as [7, 10, 11, 13, 14, 16–24, 33, 34]. However, there are few results for coupled static neural networks. In the proof, Lipschiz conditions are used to handle the nonlinear terms in the system (1). In addition, the augmented Lyapunov–Krasovskii functional is used, which alleviates the requirements of the positive definiteness of some conditional matrices. At the same time, the less conservative robust synchronization conditions for the coupled static neural networks can be obtained.

Remark 5

In Theorem 1, the robust synchronization criteria for static neural networks with uncertain coupling configuration matrices are obtained. Up to now, there are still no robust synchronization criteria for nonlinear hybrid coupled static delayed neural networks.

4 Simulation

In this section, we show one simulation example to illustrate the application of the theoretical results obtained in this paper.

Consider the robust synchronization problem for the following nonlinear hybrid coupled static neural networks with uncertainties,

$$\begin{aligned} \dot{x_{i}}(t)=&-Ax_{i}(t)+g(Wx_{i}(t-\tau(t)))+\sum_{j=1}^{3}\upsilon^{(1)}_{ij}(\Upgamma_{1}+\Updelta \Upgamma_{1}(t))f(x_{j}(t))\\ &+\sum_{j=1}^{3}\upsilon^{(2)}_{ij}(\Upgamma_{2}+\Updelta \Upgamma_{2}(t))f(x_{j}(t-\tau(t)))\\ &+\sum_{j=1}^{3}\upsilon^{(3)}_{ij}(\Upgamma_{3}+\Updelta \Upgamma_{3}(t))\int_{t-\tau(t)}^{t}f(x_{j}(s)){\rm d}s, \quad i=1,2,3. \cr \end{aligned}$$
(27)

where \(x_{i}(t)=[x_{i1}(t),x_{i2}(t)]^T, A=\left(\begin{array}{cc} 3 & 0 \\ 0 & 2\\ \end{array} \right)^{T},\quad W=\left(\begin{array}{cc} -0.4 & -0.7 \\ -0.8 & 0.5 \\ \end{array} \right), \quad \upsilon^{(1)}= \upsilon^{(2)}=\upsilon^{(3)}=\left( \begin{array}{ccc} -1 & 0.8 & 0.2 \\ 0.8 & -1 & 0.2 \\ 0.2 & 0.2 & -0.4 \\ \end{array} \right),\quad\Upgamma_1=\left( \begin{array}{cc} 0.5 & 0 \\ 0 & 0.3 \\ \end{array}\right) ,\; \,\Upgamma_2=\left(\begin{array}{cc} 0.4 & 0 \\ 0 & 0.3 \\ \end{array}\right) , \quad \Upgamma_3=\left(\begin{array}{cc} 0.3 & 0 \\ 0 & 0.4 \\ \end{array}\right) , \quad \Updelta\Upgamma_1=\Updelta\Upgamma_2=\Updelta\Upgamma_3= \left( \begin{array}{cc} 0.13cos(t) & 0.16cos(t) \\ 0.12sin(t) & 0.14sin(t) \\ \end{array} \right) , \quad g(x(t))=tanh(x(t)), f(x(t))=tanh(x(t)),\;\tau(t)=0.3+0.3sin(t)\). The initial values are \(x_1(s)=\left( \begin{array}{l} 1.7 \\ 0.6 \\ \end{array} \right), x_2(s)=\left( \begin{array}{l} -1.8 \\ 1.5 \\ \end{array} \right) , x_3(s)=\left( \begin{array}{l} 0.3 \\ 0.7 \\ \end{array} \right)\). By referring to the MATLAB linear matrix inequality (LMI) Toolbox, we solve the LMIs in (5). The following feasible solutions are obtained: \(R_1=\left( \begin{array}{ll} 1.3921 & -0.0925 \\ -0.0925 & 1.4026 \\ \end{array} \right),\quad R_2=\left( \begin{array}{ll} 1.2961 & -0.1970 \\ -0.1970 & 0.8012 \\ \end{array} \right), \quad R_3=\left( \begin{array}{ll} 0.2292 & -0.1580 \\ -0.1580 & 0.2508 \\ \end{array} \right),\quad P_{11}=\left( \begin{array}{ll} 0.4559 & -0.0116 \\ -0.0116 & 1.8369 \\ \end{array} \right),\; P_{12}=\left( \begin{array}{ll} -0.2199 & 0.1018 \\ 0.5114 & -0.7277 \\ \end{array} \right),\quad P_{22}=\left( \begin{array}{ll} 2.1150 & 0.1872 \\ 0.1872 & 1.4462 \\ \end{array} \right),Q_{11}=\left( \begin{array}{ll} 0.2159 & 0.0196 \\ 0.0196 & 0.3744 \\ \end{array} \right),\quad Q_{12}=\left( \begin{array}{ll} 0.1050 & 0.1060 \\ 0.2201 & -0.0619 \\ \end{array} \right),\quad Q_{22}=\left( \begin{array}{ll} 1.8561 & 0.2407 \\ 0.2407 & 1.8653 \\ \end{array} \right),\; S_1=\left( \begin{array}{ll} 1.1584 & 0 \\ 0 & 3.6285 \\ \end{array} \right), \quad S_2=\left( \begin{array}{ll} 6.5064 & 0 \\ 0 & 5.0903 \\ \end{array} \right), \quad S_3=\left( \begin{array}{ll} 1.0541 & 0 \\ 0 & 1.8945 \\ \end{array} \right),\quad S_4=\left( \begin{array}{ll} 0.4015 & 0 \\ 0 & 0.5701 \\ \end{array} \right),\varepsilon=1.4439\).

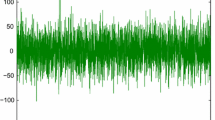
According to Theorem 1, the (27) can achieve robust synchronization. The synchronization errors of (27) are shown in Figs. 1, 2 and 3, which are calculated by \(e_1(t)=\sqrt{\sum\nolimits_{j=2}^3(x_{11}-x_{j1})^{2}}, e_2(t)=\sqrt{\sum\nolimits_{j=2}^3(x_{12}-x_{j2})^{2}}, e(t)=\sum\nolimits_{i=1}^{2}\sqrt{\sum\nolimits_{j=2}^{3}(x_{1i}-x_{ji})^{2}}\).

Fig. 1
figure 1

Robust synchronization error e 1(t) of the coupled static neural networks (27)

Full size image
Fig. 2
figure 2

Robust synchronization error e 2(t) of the coupled static neural networks (27)

Full size image
Fig. 3
figure 3

Robust total synchronization error e(t) of the coupled static neural networks (27)

Full size image

We know that, given a neural network system, the static neural networks and local field neural networks modeling approaches may both be applied to describe the system either from an external state point of view or from an internal state point of view. However, the static neural networks play a key role in linear and convex quadratic programming problems and parallel computing problems. At the same time, for a large scale of coupled static neural networks, the coupling relation among the nodes is also with the character of time delay or uncertain coupling. All these factors will impact the accuracy of synchronization of such coupled system model. Thus, it is more reasonable to consider the uncertain hybrid coupling static neural networks with time-varying delay, which is of practical significance and potential value.

5 Conclusion

In this paper, the robust synchronization of the static neural networks with constant, discrete delay and distributed delay nonlinear coupling and with uncertainties in coupling matrix terms have been investigated. The novel delay-dependent robust synchronization criteria have been derived for system (4) based on the augmented Lyapunov–Krasovskii functional, Kronecker product technique of matrices, and free-weighting matrices. The delay-dependent robust synchronization criteria are less conservative than the delay-independent ones, in particular when the delay is small. Thus, the synchronization problems in this paper are novel and have extended the earlier results. On the other hand, how to extend the results to coupled static neural networks with noise and impulse is an interesting issue.