Synchronization in complex dynamical networks based on the feedback of scalar signals

Abstract

This paper proposes a new approach of synchronization in complex dynamical networks. In this method, the scalar signals are used to instead the output variables of every node as the feedback variables and transmitted signals between every two coupling nodes. As a result, it not only simplifies the topological structure but also saves channel resources at the same time. Especially, some of the criteria are expressed in normal algebraic inequalities instead of matrix inequalities, which means that the original computational effort required is greatly decreased. Finally, several simulation examples are provided to show the effectiveness of the proposed results.

1 Introduction

A complex network is consisted of a lot of interconnected nodes with typical dynamical character. There are so many systems in nature which can be modeled as complex networks, such as the World Wide Web, food web, metabolic networks, scientific-collaboration networks, and so on [1–6]. Initially, the cognition on complex networks was only limited to the regular network. In 1960, Paul Erdös and Alfréed Rényi first proposed the theory of random graphs [1], which described a network with complex topology. However, the random graph theory still cannot describe most of the complex networks’ structure properties accurately, though it was ever considered as a breakthrough in the classical mathematical graph theory. Then after nearly 40 years, Watts and Strogatz introduced the small-world network [2] that denoted a transition from regular network to random network in 1999 [3]. At the same time, another significant discovery introduced by Barabási and Albert [4, 5] showed that a number of complex networks were with the character of scale-free in 1999. The scale-free networks are in homogeneous in nature, and it means that most nodes have very few connections, but a small number of particular nodes have many connections. After having understood most of topology properties of the complex networks [7, 8], the researchers transferred their attentions to the dynamical behavior of the network gradually [9–12]. In the complex networks, synchronization is a kind of typical collective behavior and basic motion. So analysis and control of the synchronization in dynamical networks have become a topic of great interest [13–15]. Wang and Chen [11] studied the robustness and fragility of the synchronization in a scale-free dynamical networks. Chen presented some criteria for synchronization based on the concept of matrix measure in Ref. [16]. In Ref. [12], the concept of pinning control was proposed by Wang and Chen, then Zhou presented a method of determining the number of pinning nodes by adaptive control in Refs. [17–19]. Based on the method of state-observer design, Jiang proposed the synchronization criteria by linear matrix inequality [20], while Wu presented a step-by-step approach to design a state observer for synchronization [21]. Due to the complicity of the real world, we often know little about the network, so some effective approaches for synchronization have been proposed based on unknown dynamics of every node or uncertain topology [22, 23]. Moreover, some synchronization criterions for networks with time-delay were also reported in Refs. [24, 25].

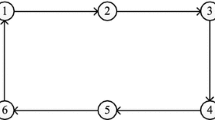
This paper further investigates the synchronization of complex networks with asymmetrical coupling matrix by using a scalar controller. In the traditional method, the coupling configuration between every two nodes is usually achieved by n state variables. Thus, the structure of the whole complex networks becomes more complicated and adds much more difficulty in researching the character of the complex networks. Here we reduce the number of coupling and feedback variables between every two connected nodes to 1. This method not only simplifies the topological structure of the network but also saves the channel resources (see Figs. 1, 2) and can be considered as an economic way, especially in the practical application. The synchronization criteria obtained in this paper do not need the coupling matrix to be symmetric or diagonalizable. At the same time, some criterions for the scalar controller design are expressed by normal algebraic inequalities instead of the matrix inequalities, which means that the original computational effort required is greatly decreased.

Fig. 1

The coupling structure between nodes with n state variables in the complex network with 4 nodes

Fig. 2

The coupling structure between nodes with 1 state variable in the complex network with 4 nodes

This paper is organized as follows: some mathematical definitions and lemmas are given in Sect. 2. The main results of this paper are given in Sect. 3. Numerical simulations are given to illustrate the results in Sect. 4. Then we obtain the conclusions in Sect. 5.

2 Network model and preliminaries

Consider a complex dynamical network consisting of N identical linearly and diffusively coupled nodes, and each of which is a n-dimensional dynamical system. Based on the approach of transforming the node’s all output variables into a scalar signal, the proposed model is described as:

$$ \dot{x}_{i}(t)=f(x_i(t))+\sum\limits_{j = 1}^N{g}_{ij}{L} {y_j}(t), \quad i=1,2,\ldots,N $$

(1)

where,

$$ {y_j}(t)=H{x_j}(t), \quad H\in{R}^{1\times{n}} $$

(2)

substituting (2) into (1), we have

$$ \dot{x}_{i}(t)=f(x_i(t))+\sum\limits_{j = 1}^N{g}_{ij}{L}{H}{x_j}(t), \quad i=1,2,\ldots,N $$

(3)

where, ${x_i(t)}=({{x}_{i1}(t)},{{x}_{i2}(t)},\ldots,{{x}_{in}(t)})^T$ is the state variable of the ith node, ${y_j}(t)\in R$ is the output variable (scalar) of the jth node and f(x _i (t)) is a nonlinear vector-valued function describing the dynamics of the isolated nodes. $A\in R^{n\times n}$ denotes the inner coupling matrix between the nodes, and $G=(g_{ij})\in R^{N \times N}$ is the coupling matrix, in which $g_{ij}\in R$ is defined as follows: if there is a coupling from node i to node j (i ≠ j), then the coupling strength g _ij  > 0; otherwise, g _ij  = 0, meanwhile, the diagonal elements of G are defined as:

$$ g_{ii}=-\sum\limits_{j = 1\,j\neq i}^N{g}_{ij} , \quad i=1,2,\ldots N $$

(4)

here, we do not need to assume that the coupling matrix G is symmetric or irreducible. Generally, the matrix G may have complex eigenvalues. Since the row sum of G are all zero, zero is an eigenvalue associated with eigenvector ${(1,1,\ldots, 1)}^T$. $L\in R^{n\times 1}$ is the observer gain matrix. $H\in R^{1\times n}$ is the state-observer matrix. Here, we assume that the matrix LH is nonnegative and the trace of (LH) is unequal to zero.

Definition 1

[26] Let D ⁰ denote a bounded open set in the state apace. If from any initial point $X(t_0)=(x_1(t_0),x_2(t_0),\ldots,x_N(t_0))^T\in D^0,$ there is $\|x_i(t)-s(t)\| \rightarrow 0$ as $t \rightarrow \infty, i=1,2,\ldots, N,$ network (1) is said to realize synchronization locally in D ⁰, and $S(t)=(s(t),s(t),\ldots,s(t))^T$ is called the synchronous state. If D ⁰ is the entire state space $\Upomega$ of network (1), then it is said to realize synchronization globally.

From the Definition 1, we know that if the nodes of network (1) get in synchronization, then

$$ y_1(t)=y_2(t)=\cdots=y_N(t)=Hs(t) $$

(5)

and the following equations could be obtained from (4) and (1),

$$ \sum\limits_{j = 1}^N{g}_{ij}Ly_j(t) = 0 $$

(6)

$$ \dot{s}(t)=f(s(t)) $$

(7)

which means that s(t) is a solution of system $\dot{x}(t)=f(x(t))$. That is to say, the synchronization state of the diffusively coupled network (1) is determined by f(x(t)). The state s(t) may be an equilibrium point, a limit cycle, an aperiodic orbit, or a chaotic orbit, such as the chaotic Lorenz, Chen, or Lü attractors [30].

Lemma 1

[21, 27] Let $G\in C^{N\times N}$ be a given complex matrix. There is a nonsingular matrix $\Upphi\in C^{N\times N},$ such that

$$ G=\Upphi{\left[\begin{array}{cccc} J_{n_1}(\lambda_1)&&&0\\ &J_{n_2}(\lambda_2)&&\\ &&\ddots&\\ 0&&&J_{n_l}(\lambda_l) \end{array}\right]}{\Upphi^{-1}}=\Upphi{J}\Upphi^{-1} $$

(8)

here, $n_1+n_2+\cdots+n_l=N$. The Jordan matrix J of G is unique up to permutation of the diagonal Jordan blocks. The eigenvalues $\lambda_i(i=1,\ldots, l)$ are not necessarily distinct. If G is a real matrix with only real eigenvalues, the similarity matrix $\Upphi$ can be taken to be real. $J_{n_i}(\lambda_i)$ is the Jordan block as follows:

$$ J_{n_i}(\lambda_i) = {\left[\begin{array}{cccc} \lambda_i &1&&0\\ &\lambda_i&\ddots &\\ &&\ddots&1\\ 0&&&\lambda_i \end{array}\right]}, \quad i=1,\ldots,l. $$

(9)

Lemma 2

[24] Given $P={(p_{ij})}\in R^{n\times n}$ is symmetric and p _ii  < 0 for all $i=1,\ldots, n$. If

$$ p_{ii}+\sum\limits_{j = 1\,j\neq i}^N{|{p}_{ij}|}< -\varepsilon, \quad i=1,2,\ldots, n $$

(10)

where $\varepsilon$ is a positive number, then $P\prec-{\varepsilon}I_n$. Here, “$\prec$” denotes that $P-{\varepsilon}I_n$ are negative definite matrix.

Lemma 3

[28] If the matrix $A\in R^{n\times n}$ is nonnegative, then,

• 1. Matrix A has a nonnegative eigenvalue r;

• 2. The moduli for all the eigenvalues of matrix A are less than or equal to r;

• 3. There is a nonnegative eigenvector associated with the eigenvalue r.

Lemma 4

[28] [Perron theory] If the matrix $A\in R^{n\times n}$ is positive and ρ(A) is the spectral radius of A;

• 1. The matrix A has a positive eigenvalue r which equal to the spectral radius of A;

• 2. There is a positive (right) eigenvector associated with the eigenvalue r;

• 3. The eigenvalue r has algebraic multiplicity 1.

3 Controllers design

In order to achieve the synchronization, we will design the linear feedback controllers on every node of the network (1). Here, the introduced feedback signals are the scalar signals instead of the output variables of all the nodes in network. Then the controlled network is described by:

$$ \dot{x}_{i}(t)=f(x_i(t))+\sum\limits_{j = 1}^N{g}_{ij}{L} {y_j}(t)+u_i, \quad k > 0, i=1,2,\ldots,N $$

(11)

where u _i  =  −kL(y _i (t) − Hs(t)). From (2) the (11) can be rewritten as:

$$ \begin{aligned} \dot{x}_{i}(t)&=f(x_i(t))+\sum\limits_{j = 1}^N{g}_{ij}{L} {y_j}(t)-kLH(x_i(t)-s(t)),\\ & \quad\quad k > 0, \quad i=1,2,\ldots,N \end{aligned} $$

(12)

Assumption 1

For any $s(t),y(t)\in \Upomega,$ there is at least a point $\bar{x}(t)\in \Upomega,$ such that

$$ f(x(t))-f(y(t))=Df(\bar{x}(t))(x(t)-y(t)) $$

(13)

where $Df(\bar{x})$ can be the Jacobian matrix of f(x(t)) at $\bar{x}$ or some other matrices relevant to f(x(t)) at $\bar{x}$.

Remark 1

The $Df(\bar{x}(t))$ in Assumption 1 is not necessarily to be the Jacobian matrix of f(x(t)) at $\bar{x(t)}$. It can be other matrices relevant to f(x(t)) at $\bar{x}(t)$ which can be more simpler or suitable to fit the expression of (13). This conclusion has been proved by Wu and Jiao [27], who extend Pecora and Carroll’ analysis [9] on local synchronization of network (11) to global synchronization and have also used the Assumption 1 to obtain global synchronization criteria for networks with nonsymmetric time-delay coupling based on linear state feedback controllers [24].

Theorem 1

Suppose the coupling matrix G has l different eigenvalues. If the controllers are designed to ensure that the zero solution of the following l–1 systems with dimensions of n _i are exponentially stable for any $\bar{x}\in\Upomega,$

$$ \dot{W}(t)=(I_{n_i}\otimes Df(\bar{x}(t))+(J_{n_i}-K_{n_i})\otimes{LH})W(t), \quad i=2,\ldots,l $$

(14)

where $2\leq l \leq N, n_2+ n_3 +\cdots+ n_l=N-1, W = (w_1,\ldots, w_j,\ldots,w_{n_i})^T \in C^{nn_i}, w_j \in C^n, J_{n_i}(\lambda_i)$ are the Jordan blocks of the coupling matrix G, $K_{n_i}=kI_{n_i},$ then, the synchronous state s(t) of network (11) is globally exponentially stable.

Proof

Let

$$ {e_i(t)}=x_i(t)-s(t),\quad i = 1,2,\ldots, N. $$

(15)

${e_i(t)}\in {R^n}$ denote the error variables between x _i (t) and s(t).

$$ \begin{aligned} \dot{e}_i(t)&=\dot{x}_i(t)-\dot{s}(t)\\ &=f(x_i(t))+\sum\limits_{j =1}^N{g}_{ij}LHx_j(t)-f(s(t))-kLHe_i(t) \end{aligned} $$

(16)

From Assumption (1), we choose a suitable matrix $\bar{x}(t)$ that fits the expression (13).

$$ f(x_i(t))-f(s(t))=Df(\bar{x}(t))e_i(t) $$

(17)

substituting (17) into (16)

$$ \dot{e}_i(t)=Df(\bar{x}(t))e_i(t)-kLHe_i(t)+\sum\limits_{j = 1}^N{g}_{ij}LHe_j(t) $$

(18)

Using the Kronecker product, (18) can be rewritten as

$$ \dot{E}(t)=({I_N}\otimes{Df(\bar{x}(t))}-K\otimes{LH}+G\otimes LH)E(t) $$

(19)

where K = kI _N , and $E(t)=(e_1^T(t),\ldots,e_N^T(t))^T\in R^{nN}$ is the error variable between X(t) and $S(t), X(t)=(x_1^T(t), x_2^T(t),\ldots, x_N^T(t))^T, S(t)=(s^T(t), s^T(t),\ldots, s^T(t))^T$. Equation (18) denotes the error componentwise of the single node in the network. In Lemma 1, there is a nonsingular matrix $\Upphi\in C^{N \times N},$ such that

$$ G=\Upphi J\Upphi^{-1} $$

(20)

We choose

$$ E(t)=(\Upphi\otimes I_n)\eta(t) $$

(21)

Take (21), (20) into (19), using some algebras, we can rewrite (19) as follows:

$$ \dot{\bar{\eta}}(t)=({I_N}\otimes {Df(\bar{x}(t))}-K\otimes LH+J\otimes LH)\bar{\eta}(t) $$

(22)

here $\bar{\eta}(t)=(\eta_1^T(t),\eta_2^T(t), \ldots,\eta_N^T(t),)^T\in C^{nN}, \eta_i(t) \in C^n.$ Thus, we can see that if the origin $\bar{\eta}(t)=0$ of (22) is exponentially stable for any $\bar{x}(t)\in \Upomega,$ the synchronous state s(t) of network (11) will be globally exponentially stable. Considering the special form of J given in (8) and (9), we can obtain (14) from (22). Thus, the proof is completed. $\square$

Theorem 2

Supposing the coupling matrix G has l different eigenvalues, then, if the controllers are designed to ensure that the zero solution of the following l–1 systems that correspond to the last node in every Jordan block are exponentially stable for any $\bar{x}\in\Upomega,$ then, the synchronous state s(t) of network (1) is globally exponentially stable.

$$ \dot{w}(t) =[Df(\bar{x}(t))+(\lambda_i-k){LH}]w(t),\quad i= 2,\ldots,l $$

(23)

where $2 \leq l \leq N, w(t)\in C^n$.

Proof

Supposing n _i  = 2, then it means that there are two nodes corresponding to the eigenvalue of $\lambda_{n_i},$ and describe the state equations as:

$$ \dot{w_1}(t) = (Df(\bar{x}(t))+(\lambda_i-k)LH)w_1(t)+ LHw_2(t) $$

(24)

$$ \dot{w_2}(t) = (Df(\bar{x}(t))+(\lambda_i-k)LH)w_2(t) $$

(25)

From the Theorem 1, the number of nodes contained in system (14) is n _i corresponding to every Jordan block $J_{n_i}(\lambda_i)$. Because of the special form of $J_{n_i}(\lambda_i)$ in Lemma 1, we know that (25) is the corresponding state expression of the last nodes contained in the designate $J_{n_i}(\lambda_i)$. If controllers in (25) are designed to ensure that the w ₂(t) approaches to zero, the (24) will become the same form as (25), which follows that the zero solution of (25) is exponentially stable. That is, if the controllers are designed to ensure the zero solution of the last node’s state equation in every corresponding Jordan block is globally exponentially stable, then, the controllers can also ensure that the synchronous state of the other node involved in the same Jordan block is globally exponentially stable. Then from the Theory 1, the synchronous state s(t) of network (11) is globally exponentially stable. The case of n _i  > 2 can be proved by the same way. Then, the proof is completed. $\square$

Theorem 3

If the controllers are designed

$$ (Df(\bar{x}(t))+(\lambda_i-k)LH)^TP+P(Df(\bar{x}(t)) +(\lambda_i-k))\preceq-\varepsilon I_n $$

(26)

where $\varepsilon > 0, P$ is an positive matrix, then the one-node systems (23) are exponentially stable for any $\bar{x}(t)\in \Upomega$.

Proof

Choose a Lyapunov function as

$$ V = w^T(t) P w(t) $$

(27)

then, the derivative of V(t) along the trajectory of (18) is

$$ \begin{aligned} \dot{V}(t) & = \dot{w}(t)^{T} Pw(t) + w^{T} (t)P\dot{w}(t) \\ & = w^{T} [(Df(\bar{x}(t)) + (\lambda _{i} - k)LH)^{T} P + P(Df(\bar{x}(t)) + (\lambda _{i} - k)LH)]w(t) \\ & \le - \varepsilon w^{T} (t)w(t) \\ & \le \frac{{ - \varepsilon }}{{\lambda _{{P_{{{\text{max}}}} }} }}V(t) \\ \end{aligned} $$

Here $\lambda_{P_{max}}$ is the largest eigenvalue of P. So the one-node systems (23) are globally exponentially stable [29], thus the proof is completed. $\square$

Let P = I _n in Theorem 2, and one can obtain the following corollary. For simplicity, we denote $\sigma(\bar{x}(t)=Df(\bar{x}(t))^T+Df(\bar{x}(t))\in R^{n\times{n}}$ in the following of this paper.

Corollary 1

The synchronous state s(t) of network (11) is globally exponentially stable, if

$$ \sigma+(\lambda_i-k)((LH)^T+LH)\preceq -\varepsilon I_n $$

(28)

Proof

Here, we choose vectors L and H. As the character of L and H, the rank of matrix (LH) is 1. Then, from lemma 3, the matrix must have n − 1 zero eigenvalues and a positive eigenvalue λ. Hence, the spectral radius ρ of matrix LH is equal to λ, and we can obtain that the nonnegative matrices LH, (LH)^T and (LH + (LH))^T are all primitive matrices. So the perron theorem is tenable, which means that $\rho_{((LH)^T+{LH})}$ is a positive, simple eigenvalue of matrix (LH)^T + LH, and it’s corresponding eigenvector is positive vector while the other eigenvalues’ modulus are less than $\rho_{((LH)^T+LH)}$ [24]. In sum, we can see that the matrix (LH)^T + LH must have a positive eigenvalue $\bar{\rho}$.

Since (LH)^T + LH is a real symmetric matrix, there must exist a unitary matrix U satisfying

$$ \begin{aligned} {((LH)^T+LH)}&\leq U^T{(\bar{\rho}{I_n})U}\\ \sigma+(\lambda_i-k)((LH)^T+LH)&\leq \sigma+(\lambda_i-k)\bar{\rho}{I_n} \end{aligned} $$

where $\lambda_i, i=2,3,\ldots l$ denotes the (l − 1) different eigenvalues of matrix G, and, $0=\lambda_1> \lambda_2 >\ldots \lambda_l,$ thus the proof is completed and we can obtain the corollary 1. $\square$

Corollary 2

If the controllers are designed

$$ \sigma+(\lambda_2-k)\bar{\rho}I_n<-\varepsilon I_n $$

(29)

where $\varepsilon> 0,$ then the synchronous state s(t) of network (11) is globally exponentially stable. From Corollary 1 and Lemma 2, one can obtain Corollary 2.

Corollary 3

If the controllers are designed

$$ \min{\left(\sigma_{ii}+\sum\limits_{j = 1\,j\neq i}^n|\sigma_{ij}|\right)}+ (\lambda_2-k)\bar{\rho}\leq -\varepsilon , \quad i=1,2,\ldots,n $$

(30)

where $\varepsilon> 0,$ then the synchronous state s(t) of network (11) is globally exponentially stable.

4 Example and simulations

In this section, a useful numerical example is given to verify the effectiveness of aforementioned synchronization criteria.

We consider a feedback loop consisting of 4 Lorenz systems. The lorenz system is described by (31) in Ref. [30], which has a chaotic attractor shown in Fig. 3 with a = 10, b = 8/3, c = 28.

$$ \left\{ {\begin{array}{*{20}c} {\mathop {x_{1} }\limits^{ \cdot } = a(x_{2} - x_{1} )} \hfill \\ {\mathop {x_{2} }\limits^{ \cdot } = cx_{1} - x_{1} x_{3} - x_{2} } \hfill \\ {\mathop {x_{3} }\limits^{ \cdot } = x_{1} x_{2} - bx_{3} } \hfill \\ \end{array} } \right. $$

(31)

Fig. 3

State trajectories of the nodes in the complex networks

In order to achieve the global synchronization, we choose the following matrix as $Df(\bar{x}(t)):$

$$ Df(\bar{x}(t))=\left(\begin{array}{ccc} -a & a&0\\ c& -1&-\bar{x}_1\\ \bar{x}_2&0&-b \end{array}\right) $$

(32)

For any $x(t), y(t)\in R^3,$ let $\bar{x}_1=(x_1 x_3 - y_1 y_3) / (x_3-y_3), \bar{x}_2=(x_1 x_2-y_1 y_2)/(x_1 - y_1),$ and $\bar{x}_3=0,$ then the matrix $Df(\bar{x}(t))$ satisfies the Assumption 1 at $\bar{x}(t)=(\bar{x}_1, \bar{x}_2, \bar{x}_3)^T$. The matrix of σ is

$$ \sigma(t)=\left(\begin{array}{ccc} -20 &38&\bar{x}_2\\ 38&-2&-\bar{x}_1\\ \bar{x}_2&-\bar{x}_1&-16/3\end{array}\right) $$

(33)

In the following, we choose the vectors $L=\left[\begin{array}{ccc} 1&2& 0\end{array}\right]^T$, and $H=\left[\begin{array}{ccc} 3&0& 1\end{array}\right]$. Consider a network consisting of 4 unified systems with global unidirectional coupling.

We choose a asymmetric coupling configuration matrix as:

$$ G=\left[\begin{array}{cccc} -3 & 1 & 1 & 1\\ 0 & -2 & 1 & 1\\ 0 & 0 & -1 & 1\\ 0 & 0 & 0 & 0\end{array}\right] $$

(34)

Simulation results show that the chaotic attractor generated by the unified system is bounded (Fig. 3): $|\bar{x}_1| < 20, |\bar{x}_2| < 25$.

Thus from the Corollary 3, the control matrix can be designed as K = 5I ₄. Simulations show that the networks all realized synchronization quickly under the controllers designed in Figs. 4, 5, 6 and 7, respectively.

Fig. 4

State trajectories of the nodes in the complex networks with 4 nodes

Fig. 5

Synchronization errors of the first state between the second node and the first node

Fig. 6

Synchronization errors of the first state between the third node and the first node

Fig. 7

Synchronization errors of the first state between the fourth node and the first node

5 Conclusion

A strategy of controlling the complex dynamical networks to achieve synchronization by the feedback of scalar signals has been presented. This method not only has simplified the topological structure but also has saved the channel resources of the network at the same time. Especially, the synchronous criteria have been designed through some simple algebraic inequalities instead of matrix inequalities, which have greatly decreased the original computational effort. At last, the numerical simulations have shown that the conclusions are feasible.