Superior robustness of power-sum activation functions in Zhang neural networks for time-varying quadratic programs perturbed with large implementation errors

Abstract

A special class of recurrent neural network termed Zhang neural network (ZNN) depicted in the implicit dynamics has recently been introduced for online solution of time-varying convex quadratic programming (QP) problems. Global exponential convergence of such a ZNN model is achieved theoretically in an error-free situation. This paper investigates the performance analysis of the perturbed ZNN model using a special type of activation functions (namely, power-sum activation functions) when solving the time-varying QP problems. Robustness analysis and simulation results demonstrate the superior characteristics of using power-sum activation functions in the context of large ZNN-implementation errors, compared with the case of using linear activation functions. Furthermore, the application to inverse kinematic control of a redundant robot arm also verifies the feasibility and effectiveness of the ZNN model for time-varying QP problems solving.

1 Introduction

The problem of quadratic programming (QP) is considered to be one of the fundamental mathematical optimization problems [1, 2], which is widely encountered in various science and engineering areas; e.g., optimal controller design [3, 4], power transmission scheduling [5], robot-arm motion planning [6–8], and digital signal processing [9]. In many engineering applications, the online (or real-time) solution of QP problems is usually desired. Owing to its fundamental roles, many algorithms/methods have been proposed and developed to solve QP problems [1, 10]. Generally speaking, numerical methods performed on digital computers are often considered to be well-accepted approaches to linear-equality constrained QP problems. As one of the most successful numerical methods, sequential quadratic programming (SQP) is developed and used to solve nonlinear programming (NLP) problems [11–13]. The basic idea of SQP is to transform the NLP problem into a QP subproblem that can be solved by using QP algorithms. Then, the solution to this subproblem can be employed to construct a sequence of approximations which converge to a theoretical solution of the NLP problem [11].

Being another general type of solution, neural networks have played important roles for online computation, which are regarded as one of the potential promising alternatives [14, 15]. Due to their parallel-distributed nature and hardware-realization convenience, neural networks can perform excellently in many application fields [16, 17]. Chua and Lin [14] developed and investigated a canonical nonlinear programming circuit for simulating general nonlinear programs. Kennedy and Chua [15] explored the stability properties of a dynamic extension of such a canonical nonlinear programming circuit model.

Recently, a special class of recurrent neural network (RNN), i.e., Zhang neural network (ZNN), has been proposed as a systematic approach to solving time-varying problems [18–22]. The design of ZNN is based on the elimination of every entry of a matrix- or vector-valued error function. This kind of error function can make the resultant ZNN model monitor and force every entry of the error to zero. In addition, ZNN is depicted generally in an implicit dynamics, which is more consistent with analog electronic circuits and systems due to Kirchhoff’s rules. The implicit dynamic equation can preserve physical parameters in the coefficient matrices, and it describes the usual and unusual parts of a dynamic system in the same form. Furthermore, ZNN exploits the time-derivative information of coefficient matrices and vectors of a given problem during its real-time solving process. This is one of the reasons why ZNN can globally exponentially converge to the exact solution of time-varying problems.

To the best of the authors’ knowledge, to date, most reported computational schemes were theoretically/intrinsically designed for time-invariant (or termed, static, constant) problems solving and/or related to gradient methods. Few studies have been published on RNN for solving such time-varying QP problems in the literature at present stage. Myung and Kim [23] proposed a time-varying two-phase (TVTP) algorithm, which, with a finite penalty parameter, can offer exact feasible solutions to constrained time-varying nonlinear optimization problems. As presented in [22], a conventional gradient-based neural network (GNN) is employed to solve the time-varying QP problems. Theoretical and simulative results in [22] have demonstrated that GNN is less effective on time-varying QP problems solving, compared with the presented ZNN.

In practice, uncertain realization errors always exist in the hardware-implementation of RNN; for example, the incapacity of electronic components would limit the performance of RNN and generate various errors (such as differentiation error and model-implementation error [24]). Owing to these realization errors, the solution of the circuit implementation for RNN may not be accurate. In this case, robustness analysis of neural networks is important and necessary. This paper presents the general framework of the ZNN model for solving time-varying QP problems, and, by using a special type of monotonically increasing odd activation functions (namely power-sum activation functions), the ZNN model with superior robustness in the context of large implementation errors is analyzed and investigated, which is compared with the ZNN model activated by linear functions.

The rest of this paper is organized as follows. Section 2 introduces the problem formulation of time-varying linear-equality constrained QP, and the general framework of the ZNN model as a real-time QP solver. By using power-sum activation functions, Sect. 3 presents the robustness analysis of the ZNN model in the context of large implementation errors, which is one of the main contributions of this paper. In Sect. 4, illustrative computer-simulation examples are shown to verify the superior robustness of the ZNN model using power-sum activation functions for time-varying QP problems solving. In Sect. 5, the ZNN model is applied to inverse kinematic control of a redundant robot arm via online solution of time-varying QP problems. Final conclusion remarks are drawn in Sect. 6.

2 Problem formulation and neural-network solver

Consider the following time-varying convex quadratic program subject to a time-varying linear equality:

$$ \hbox{minimize}\quad x^T(t)P(t)x(t)/2+q^T(t)x(t), $$

(1)

$$ \hbox{subject to} \quad A(t)x(t)=b(t), $$

(2)

where Hessian matrix $P(t)\in R^{n\times n}$ is smoothly time-varying, positive-definite and symmetric for any time instant $t\in[0,+\infty)\subset R,$ and coefficient vector $q(t)\in R^n$ is assumed smoothly time-varying as well. In (1) and (2), the time-varying decision vector $x(t)\in R^{n}$ is unknown and to be solved at any time instant $t\in[0,+\infty).$ In equality constraint (2), the coefficient matrix $A(t)\in R^{m\times n}$ being of full row rank and vector $b(t)\in R^{m}$ are both assumed smoothly time-varying. As pointed out by the authors’ previous work [22], the time-varying QP problem (1)–(2) can be solved as follows:

$$ W(t)y(t)=u(t), $$

(3)

where

$$ \begin{aligned} W(t)&:= \left[\begin{array}{cc} P(t) & A^T(t)\\ A(t) & {\bf 0}\\ \end{array}\right] \in R^{(n+m)\times(n+m)},\\ y(t)&:= \left[ \begin{array}{c} x(t)\\ \lambda(t)\\ \end{array} \right] \in R^{n+m}, \qquad u(t):= \left[ \begin{array}{c} -q(t) \\ b(t)\\ \end{array}\right] \in R^{n+m}, \end{aligned}$$

with $\lambda(t)\in R^m$ denoting the Lagrange-multiplier vector. By following ZNN-design method [18–22], we define the vector-valued error function e(t) := W(t)y(t) − u(t), and then the time-derivative $\dot{e}(t)$ of e(t) is constructed according to the general ZNN-design formula:

$$ \dot{e}(t)=-\gamma\Upphi \left(e(t)\right). $$

(4)

By expanding the above ZNN-design formula (4), we obtain the following ZNN model for solving online the time-varying QP problem (1)–(2):

$$ W(t)\dot{y}(t)=-\dot{W}(t)y(t)-\gamma\Upphi\left(W(t)y(t)-u(t)\right)+\dot{u}(t), $$

(5)

where, being the reciprocal of a capacitance parameter, the design parameter $\gamma>0\in R$ should be implemented as large as possible or selected appropriately for simulative purposes. Besides, the ith-neuron dynamic equation of ZNN (5) is given below:

$$\begin{aligned} \dot{y}_{i} & = - \sum\limits_{{k = 1}}^{{n + m}} {\dot{w}_{{ik}} y_{k} } + \sum\limits_{{k = 1}}^{{n + m}} {(\delta _{{ik}} - w_{{ik}} )\dot{y}_{k} } \\ & \quad - \gamma \phi \left( {\sum\limits_{{k = 1}}^{{n + m}} {w_{{ik}} y_{k} - u_{i} } } \right) + \dot{u}_{i} , \\ \end{aligned} $$

(6)

where

• y _i and $\dot{y}_i$, corresponding to the ith neuron of ZNN (5), denotes the ith element of state vector y(t) and its derivative $\dot{y}(t)$, respectively, $i=1,2,\ldots,n+m$;

• w _ik and $\dot{w}_{ik}$ are defined, respectively, as the ikth entries of matrix W(t) and its derivative matrix $\dot{W}(t)$;

• u _i and $\dot{u}_i$ denote the ith elements of vector u(t) and its derivative vector $\dot{u}(t)$, respectively;

• δ _ik is defined as the ikth entry of identity matrix I.

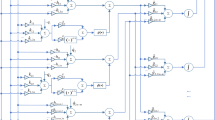
The neurons’ connection architecture of ZNN model (5) is depicted in Fig. 1, and Fig. 2 shows the corresponding (analog) circuit schematic of such a neural network model. In addition, $\Upphi(\cdot):R^{n+m}\rightarrow R^{n+m}$ denotes an activation-function (vector) array, and the array $\Upphi\left(\cdot\right)$ is made of (n + m) monotonically increasing odd activation-functions $\phi(\cdot)$. The authors’ previous work [18–22] has introduced and investigated six types of activation functions (i.e., linear activation functions, power activation functions, power-sum activation functions, sigmoid activation functions, power-sigmoid activation functions and hyperbolic sine activation functions) for the proposed ZNN models. In this paper, for comparison and for testing, the following two types of activation functions are used:

• 1. Linear activation function ϕ(e _i ) = e _i ;

• 2. Power-sum activation function ϕ(e _i ) = ∑ ^N _k=1 e ^2k−1 _i with integer parameter N > 1.

Fig. 1

Neurons’ connection-architecture of ZNN model (5)

Fig. 2

Circuit schematic which realizes ZNN model (5)

They are depicted in Fig. 3. For better understanding and utility, the convergence properties of ZNN (5) are summarized in the following lemmas [21, 22].

Fig. 3

Activation function $\phi(\cdot)$ being the ith element of array $\Upphi(\cdot)$ with N = 3 for the power-sum function

Lemma 1

Consider strictly-convex QP problem (1)–(2). If a monotonically-increasing odd activation-function array $\Upphi(\cdot)$ is used, then state vector y(t) of ZNN (5), starting from any initial state $y(0)\in R^{n+m},$ globally converges to the unique theoretical solution y ^*(t) of linear system (3), with the first n elements constituting the optimal solution to QP (1)–(2).

Lemma 2

In addition to Lemma 1, if the linear activation function is used, then the state vector y(t) of ZNN (5) globally exponentially converges to the unique theoretical solution y ^*(t) of linear system (3) with convergence rate γ; and, if the power-sum activation function is used, superior convergence is achieved for ZNN (5), as compared to the linear activation function situation. The first n elements of y ^*(t) constitute the optimal solution to QP (1)–(2).

Remark 1

The construction of ZNN model (5) allows us to have many more choices of different activation functions. In many engineering applications, it may be necessary to investigate the impact of different activation functions in the neural network, in view of the fact that nonlinear phenomenon may appear, even in the hardware implementation of a linear activation function, e.g., in the form of truncation and round-off errors in digital realization [24]. The investigation of different activation functions may give us more insights into the imprecise-implementation problem of neural networks.

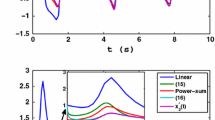
For clear visual effect and illustration, Fig. 4 shows that the solutions (denoted by solid curves) of ZNN model (5) converge rapidly to the theoretical solution (denoted by dotted curves) of a time-varying QP problem (i.e., of the first example in Sect. 4). In addition, as seen from Fig. 5, the residual errors ($\|e(t):=W(t)y(t)-u(t)\|_2$) of ZNN (5) vanish rapidly to zero. From these figures and other references [21, 22], we can confirm well the conclusions in Lemmas 1 and 2. Evidently, as shown in Table 1, the convergence rate of ZNN model (5) using power-sum activation functions is faster than that using linear activation functions. Besides, such a convergence can be expedited by increasing γ. For example, by using the linear activation functions, if γ increases from 1 to 10 (or 100), the convergence time [with the prescribed convergence accuracy $\|e(t)\|_2<10^{-2}$ achieved] can be decreased from 7.3753 to 0.7366 (or 0.0763) s; and, if γ increases to 10,000, the convergence time [with the prescribed convergence accuracy $\|e(t)\|_2<10^{-4}$ achieved] is only 0.0012 s, which may be applicable in real-time situation. Furthermore, as depicted in this table, by using the power-sum activation functions, the convergence time could be decreased further when N is increased. In summary, the above lemmas guarantee the convergence of ZNN model (5) under the ideal conditions, i.e., with no implementation errors involved. However, in practice, realization errors always exist in the hardware implementation. Thus, in the ensuing sections, the robustness properties of ZNN model (5) are investigated with large model-implementation errors considered.

Fig. 4

Online solution of a time-varying QP problem by ZNN model (5) with γ = 1. a Using linear activation functions, b using power-sum functions with N = 3

Fig. 5

Residual errors of ZNN (5) with γ = 1 for a time-varying QP problem solving. a Using linear activation functions, b using power-sum functions with N = 3

Table 1 Convergence time (s) of ZNN (5) for a time-varying QP problem solving

3 Robustness analysis

In this section, we investigate the ZNN robustness by considering the following vector-valued ZNN-design formula perturbed with a large model-implementation error $\Updelta\omega\in R^{n+m}:$

$$ \dot{e}(t)=-\gamma\Upphi \left(e(t)\right)+\Updelta\omega, $$

(7)

or to say,

$$ W(t)\dot{y}(t)=-\dot{W}(t)y(t)-\gamma\Upphi\left(W(t)y(t)-u(t)\right)+\dot{u}(t)+\Updelta\omega. $$

(8)

Evidently, we have the following theorem about the robustness of perturbed ZNN-design formula (7).

Theorem

Consider the above perturbed ZNN-design formula with a large model-implementation error $\Updelta\omega\in R^{n+m}$ as depicted finally in (7), where $\|\Updelta\omega\|_2\le\varepsilon<+\infty$ for any $t\in[0,+\infty)$, with $\varepsilon\gg\gamma$ (or at least $\varepsilon\ge\gamma$ ). For (7), if linear activation functions are exploited, then the steady-state error $\lim_{t\rightarrow\infty}\|e(t)\|_2\approx\alpha\varepsilon/\gamma$ with $\alpha:=\sqrt{n+m},$ whereas, if power-sum activation functions are exploited, then superior robustness property exists for error range $\lim_{t\rightarrow\infty}|e_i|\ge1,$ and the steady-state error $\lim_{t\rightarrow\infty}\|e(t)\|_2\le(\alpha\varepsilon/\gamma)/N$ with integer parameter N > 1, being smaller than that using linear activation functions.

Proof

Let us define a Lyapunov function candidate $v=\|e(t)\|^2_2/2=e^T(t)e(t)/2\ge0$ for the perturbed ZNN-design formula (7). Then,

$$ \begin{aligned} \dot{v}(t) & = \frac{{{\hbox{d}}v(t)}}{{{\hbox{d}}t}} = e^{T} (t)\frac{{{\hbox{d}}e(t)}}{{{\text{d}}t}} = - \gamma e^{T} \Upphi (e) + e^{T} \Updelta \omega \\ & = - \gamma \sum\limits_{{i = 1}}^{{n + m}} {e_{i} \phi (e_{i} )} + \sum\limits_{{i = 1}}^{{n + m}} {e_{i} \Updelta \omega _{i} }. \\ \end{aligned} $$

In view of $\|\Updelta \omega\|_2\le \varepsilon,$ we have $e^{T}\Updelta\omega\le \varepsilon\sum^{n+m}_{i=1}|e_i|.$ Summarizing the above facts and the property of odd-function $\phi(\cdot),$ we have the following derivation:

$$ \begin{aligned} \frac{{{\text{d}}v}}{{{\text{d}}t}} & \le - \gamma \sum\limits_{{i = 1}}^{{n + m}} | e_{i} |\phi \left( {|e_{i} |} \right) + \varepsilon \sum\limits_{{i = 1}}^{{n + m}} | e_{i} | \\ & = - \sum\limits_{{i = 1}}^{{n + m}} | e_{i} |(\gamma \phi (|e_{i} |) - \varepsilon ). \\ \end{aligned} $$

(9)

It follows that the time evolution e _i (t) may fall into the following three situations: (i) $\gamma \phi(|e_i|)-\varepsilon>0,$ (ii) $\gamma \phi(|e_i|)-\varepsilon=0,$ and (iii) $\gamma \phi(|e_i|)-\varepsilon<0,$ which are detailed below.

• If the trajectory of the system (7) with t in the time interval [t ₀, t ₁) is in the first situation, $\dot{v}<0$ and (9) implies that e(t) converges toward zero as time t evolves.

• If at any time t the trajectory of the system (7) is in the second situation, then $\dot{v}\le0$ which implies that e _i converges toward zero or remains with $\phi(|e_i|)=\varepsilon/\gamma,$ in view of $\dot{v}\le0$ containing two cases $\dot{v}<0$ and $\dot{v}=0$ in this situation.

• For any time t at which the system trajectory falls into the third situation, it follows from (9) that $\dot{v}$ is less than a positive scalar (containing two cases $\dot{v}\le0$ and $\dot{v}>0$), and thus |e _i | may not converge toward zero. Now let us analyze the worst case, i.e., $0<\dot{v}\leq -\sum^{n+m}_{i=1}|e_i|(\gamma \phi(|e_i|)-\varepsilon)$ :it is readily known that v and |e _i | would increase, which increases correspondingly $\gamma \phi(|e_i|)-\varepsilon$ from a negative value to a value with $\dot{v}=0$ [due to the odd-function property of ϕ(|e _i |)], as time t evolves. So, on average, there exists a certain time instant t ₂ such that $\gamma \phi(|e_i(t_2)|)-\varepsilon=0$ (and then > 0), which returns to the second (or the first) situation, i.e, $\dot{v}\le0,$ and the situation has $\phi(|e_i|)\rightarrow\varepsilon/\gamma.$

Summarizing the above analysis, we conclude that in general the steady-state error satisfies $\lim_{t\rightarrow\infty}\phi(|e_i|)\approx\varepsilon/\gamma.$ For the large model-implementation error $\varepsilon\gg\gamma$ (or at least $\varepsilon\ge\gamma$), we have $\lim_{t\rightarrow\infty}\phi(|e_i|)\approx\varepsilon/\gamma\gg1$ (or at least $\ge1$) and then the following results are obtained readily for (7).

• If the linear activation function is used in (7), the steady-state error $\lim_{t\rightarrow\infty}\|e(t)\|_2=\lim_{t\rightarrow\infty}\sqrt{\sum^{n+m}_{i=1}|e_i|^2}\approx\alpha\varepsilon/\gamma\gg\alpha$ (or at least $\ge\alpha$) with $\alpha:=\sqrt{n+m}.$

• If the power-sum function is used in (7), in view of $\lim_{t\rightarrow\infty}\phi(|e_i|)=\sum_{k=1}^{N}|e_i|^{2k-1}\approx\varepsilon/\gamma\gg1$ (or at least $\ge1$) with integer parameter N > 1 and for error range $\lim_{t\rightarrow\infty}|e_i|\ge1,$ we have

  $$ \begin{aligned} N\lim_{t\rightarrow\infty}\|e(t)\|_2&=\lim_{t\rightarrow\infty}\sqrt{\sum^{n+m}_{i=1}(N|e_i|)^2} \le\lim_{t\rightarrow\infty}\sqrt{\sum^{n+m}_{i=1}\sum_{k=1}^{N}(|e_i|^{2k-1})^2}\\ &=\lim_{t\rightarrow\infty}\sqrt{\sum^{n+m}_{i=1}\phi^2(|e_i|)} \approx\alpha\varepsilon/\gamma. \end{aligned} $$

  Thus, we obtain $\lim_{t\rightarrow\infty}\|e(t)\|_2\le(\alpha\varepsilon/\gamma)/N,$ which is at worst N times smaller than that in the linear-activation-function case for general N > 1. Therefore, the steady-state error $\lim_{t\rightarrow\infty}\|e(t)\|_2\le(\alpha\varepsilon/\gamma)/N\ll\alpha\varepsilon/\gamma$ (or at least $\le\alpha\varepsilon/\gamma$) with a very large integer parameter N. This shows the superior robustness of ZNN-design formula (7) using power-sum activation functions with N > 1, compared with that using linear activation functions. Moreover, the linear activation functions can be considered to be a special case of the power-sum functions when N = 1.

  The proof is thus completed.□

Remark 2

In the simulation, modeling and realization of neural networks, there may be some errors involved, resulting from truncating/roundoff errors in digital realization and high-order residual errors of circuit components in analog realization [19, 20, 24]. The theoretical analysis of this theorem has guaranteed that superior robustness can be achieved readily for ZNN formula (7) and model (8) by using power-sum activation functions, in comparison with using linear activation functions. Thus, even though the model-implementation errors are large, the ZNN model (8) using power-sum activation functions can still solve the problem quite feasibly and robustly. As a result, the power-sum activation functions might be used more widely in the real-time applications than the linear functions.

4 Simulation verification

The previous sections have presented the robustness analysis of ZNN model (5) [largely perturbed as (8)] for online solution of time-varying convex QP problem (1)–(2) subject to a time-varying linear-equality constraint. In this section, computer-simulation results and observations are provided to verify the superior characteristics of using power-sum activation functions in the context of large ZNN-implementation errors, compared with the characteristics of using linear activation functions. All simulations are carried out in MATLAB environment and on a personal digital computer with a Duo E4500 2.19GHz CPU, 2GB memory and a Windows XP Professional operating system.

Example 1

For illustration and comparison, let us consider the following time-varying convex QP problem (1)–(2) subject to a time-varying linear-equality constraint:

$$ \begin{aligned} P(t) & = \left[ {\begin{array}{*{20}c} {8 + \sin t} \hfill & {0.9\cos t} \hfill \\ {0.9\cos t} \hfill & {10 - 0.5\cos t} \hfill \\ \end{array} } \right],\qquad q(t) = \left[ {\begin{array}{*{20}c} { - 2\cos 2t} \\ { - 2\sin 2t} \\ \end{array} } \right], \\ A(t) & = \left[ {\begin{array}{*{20}c} {2\cos 3t} & {\sin 3t} \\ \end{array} } \right],\qquad b(t) = \sin t. \\ \end{aligned} $$

It follows from (3) that we have

$$ \begin{aligned} W(t) & = \left[ {\begin{array}{*{20}c} {8 + \sin t} \hfill & {0.9\cos t} \hfill & {2\cos 3t} \hfill \\ {0.9\cos t} \hfill & {10 - 0.5\cos t} \hfill & {\sin 3t} \hfill \\ {2\cos 3t} \hfill & {\sin 3t} \hfill & 0 \hfill \\ \end{array} } \right], \\ u(t) & = \left[ {\begin{array}{*{20}c} {2\cos 2t,} & {2\sin 2t,} & {\sin t} \\ \end{array} } \right]^{T} . \\ \end{aligned} $$

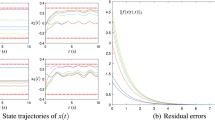
To show the robustness characteristics of the perturbed ZNN model (8), the large model-implementation error $\Updelta\omega=[10^2,10^2,10^2]^T$ is specially added in (7). Based on the theoretical results presented above, we know that, when a large model-implementation error (e.g., $\|\Updelta\omega\|_2\approx173.20$) is added to the ZNN model, using the linear activation functions will result in large residual errors. This is shown evidently in Fig. 6a. In contrast, when the power-sum activation functions are used, the steady-state residual errors of (7) decrease substantially, around 40 times smaller than that using linear activation functions. This is shown comparatively in Fig. 6a and b. Moreover, Fig. 6b is about using power-sum activation functions with design parameter N = 3, while Fig. 7a and b are about N = 5 and N = 7, respectively. It is observed that, by increasing N, the steady-state residual error $\lim_{t\rightarrow\infty}\|e(t)\|_2$ of (7) is decreased very effectively (e.g., for N = 7, which is around 75 times smaller than that using linear activation functions). In addition, if the very large model-implementation error (e.g., $\Updelta\omega=[10^3,10^3,10^3]^T$) is added to the ZNN model, the robustness results are shown in Fig. 8, from which the same conclusion can be redrawn; i.e., using power-sum activation functions has a much smaller steady-state residual error than that using linear activation functions (e.g., around 610 times smaller, as seen comparatively from Fig. 8a, b).

Fig. 6

Residual errors of largely perturbed ZNN model (8) when solving the time-varying QP problem in Example 1 (with γ = 1 and $\Updelta\omega=[10^2,10^2,10^2]^T$). a Using linear activation functions, b using power-sum functions with N = 3

Fig. 7

Residual errors of largely perturbed ZNN model (8) when solving the time-varying QP problem in Example 1 (with γ = 1 and $\Updelta\omega=[10^2,10^2,10^2]^T$). a Using power-sum functions with N = 5, b using power-sum functions with N = 7

Fig. 8

Residual errors of largely perturbed ZNN model (8) when solving the time-varying QP problem in Example 1 (with γ = 1 and $\Updelta\omega=[10^3,10^3,10^3]^T$). a Using linear activation functions, b using power-sum functions with N = 5

Example 2

Let us consider the following time-varying Toeplitz matrix P(t) with n = 4:

$$ P(t)= \left[\begin{array}{ccccc} p_1(t)& p_2(t) &p_3(t) &\cdots &p_n(t)\\ p_2(t) &p_1(t) &p_2(t) &\cdots &p_{n-1}(t)\\ p_3(t) &p_2(t) &p_1(t) &\ddots &\vdots\\ \vdots &\vdots &\ddots &\ddots &p_{2}(t)\\ p_n(t) &p_{n-1}(t) &\cdots &p_{2}(t) &p_1(t) \end{array}\right] \in R^{n\times n}, $$

where $p(t)=[p_1(t), p_2(t), p_3(t), \ldots, p_n(t)]^T$ denotes the first column vector of the matrix P(t). Let $p_1(t)=8+\cos(t)$ and $p_k(t)=\sin(t)/(k-1)(k=2,3,\ldots,n)$. The other time-varying coefficients of QP (1)–(2) are defined as follows:

$$ \begin{aligned} q(t)&=\left[-2\cos (2t), 2\cos (2t+\pi/2), 2\cos (2t+\pi), \ldots, 2\cos (2t+(n-1)\pi/2) \right]^T\in R^{n\times 1},\\ A(t)&=\left[\sin (t), \sin (t-\pi/3), \sin (t-2\pi/3), \ldots, \sin (t-(n-1)\pi/3)\right]\in R^{1\times n},\\ b(t)&=2\cos (2t+n\pi/2)\in R. \end{aligned} $$

Besides, the quite large model-implementation error $\Updelta\omega=[500,500,\ldots,500]^T\in R^{(n+1)\times 1}$ is added to the resultant ZNN model. When the design parameter γ = 1 and two types of activation functions are used, the robustness performance of the largely perturbed ZNN model can be seen from Fig. 9. From this figure, we observe that, even with quite large model-implementation errors, the computational error $\|e(t)\|_2$ synthesized by the perturbed ZNN model (8) using power-sum activation functions is still bounded and relatively small. In contrast, using linear activation functions in the context of quite large model-implementation error will still result in large computational error (e.g., more than 1,000 as depicted in Fig. 9a). Evidently, compared with the situation of using linear activation functions, superior robustness performance is achieved by using power-sum activation functions under the same simulation conditions. In summary, these computer-simulation results substantiate well the theoretical analysis presented in the previous sections.

Fig. 9

Residual errors of largely perturbed ZNN model (8) when solving the time-varying QP problem in Example 2 (with γ = 1, n = 4 and $\Updelta\omega=[500,500,500,500,500]^T$). a Using linear activation functions, b using power-sum functions with N = 3

5 Application to robot tracking

As we know and experience [6–8], recurrent neural networks have been widely exploited in motion planning and kinematic control of redundant robots with end-effectors tracking desired trajectories. In this section, the proposed ZNN model is applied to kinematic control of a redundant manipulator via online time-varying QP problem solving.

Let us consider a redundant robot manipulator of which the end-effector position vector $r(t)\in R^m$ in Cartesian space is related to the joint-space vector $\theta(t)\in R^n$ through the following forward kinematic equation

$$ r(t)=f(\theta(t)), $$

(10)

where $f(\cdot)$ is a continuous nonlinear mapping function with known structure and parameters for a given manipulator. The inverse kinematic problem is to find the joint variable θ(t) for any given r(t). By differentiating (10) with respect to time t, we have a linear relation between the Cartesian velocity $\dot {r}(t)$ and joint velocity $\dot{\theta}(t)$ as follows:

$$ J (\theta(t))\dot{\theta}(t)=\dot{r}(t), $$

(11)

where $J(\theta(t))\in R^{m\times n}$ is the so-called Jacobian matrix defined as J(θ(t)) = ∂f(θ)/∂θ. In the redundancy-resolution problem (i.e., m < n), (11) is under-determined, admitting an infinite number of feasible solutions.

As pointed out by the authors’ previous work [7], the inverse kinematic problem (or called the motion-planning problem) of robot manipulators can be formulated as the following time-varying quadratic program subject to a time-varying linear equality:

$$ \hbox{minimize}\quad x^T(t)Px(t)/2+q^T(t)x(t), $$

(12)

$$ \hbox{subject to}\quad A(t)x(t)=b(t), $$

(13)

with P := I, q(t) := μ(θ(t) − θ(0)), A(t) := J(t), and b(t) := $\dot{r}(t)$, where $\theta(t)\in R^{n}$ denotes the joint variable vector, μ > 0 is a design parameter used to scale the magnitude of the manipulator response to joint displacements, x(t) corresponds to $\dot{\theta}(t)\in R^{n}$ which is to be solved online, and $\dot{r}(t)\in R^{m}$ denotes the desired end-effector velocity vector.

In this section, as synthesized by ZNN model (5) using power-sum activation functions, a five-link planar redundant robot manipulator is simulated for further verification purposes. The five-link robot arm has three redundant degrees (because n = 5 and m = 2), and the desired path of its end-effector is an ellipse with the major radius being 0.6 m and the minor radius being 0.3 m. The motion duration is 10 s, and initial state θ(0) = [3π/4,  −π/2,  −π/4, π/6, π/3]^T rad. Design parameters μ and γ are set to be 4 and 10, respectively. The simulation results are depicted in Figs. 10, 11, and 12. Figure 10 illustrates the motion trajectories of the five-link planar robot manipulator operating in the two-dimensional space. The arrow appearing in Fig. 10 shows the motion direction. As shown in the right subplot of Fig. 10, the actual trajectory of the robot’s end-effector (denoted by blue asterisk-marked curve) is sufficiently close to the desired elliptical path (denoted by red dashed curve). The transient behaviors of joint variables and joint velocity variables of the five-link planar robot manipulator are depicted in Fig. 11. Figure 12a shows the Cartesian position error of the end-effector. From this subplot, we see that the maximum position error synthesized by ZNN model (5) is less than 2.13 × 10⁻⁶ m. In addition, the maximum velocity error is less than 4.84 × 10⁻⁷ m/s, which is shown in Fig. 12b. It means that the end-effector path-tracking task synthesized by ZNN model (5) is accomplished well. These simulation results verify further the feasibility and effectiveness of the ZNN model (5) for time-varying QP problem (12)–(13) solving.

Fig. 10

Motion trajectories and end-effector trajectory of a five-link planar manipulator synthesized by ZNN model (5) using power-sum activation functions with N = 3 when its end-effector tracks an elliptical path

Fig. 11

Joint variable and joint velocity profiles of a five-link planar robot manipulator synthesized by ZNN model (5) using power-sum activation functions with N = 3 when tracking an elliptical path. a Joint variable θ(t) (rad), b joint velocity variable θ(t) (rad/s)

Fig. 12

End-effector position and velocity errors of a five-link planar robot manipulator synthesized by ZNN model (5) using power-sum activation functions with N = 3 when tracking an elliptical path. a Position errors (m), b velocity errors (m/s)

Furthermore, we consider the situation of the five-link planar robot manipulator’s end-effector path-tracking task synthesized by ZNN model (8) in the context of large model-implementation errors $\Updelta\omega=[100,100,100,100,100,100,100]^T$. The motion duration, the initial state and the design parameter μ are the same as before. As shown in Fig. 13, the actual trajectory (denoted by blue asterisk-marked curve) of the robot’s end-effector cannot coincide well with the desired elliptical path (denoted by red dashed curve) when the design parameter γ is set to be 10⁵. In addition, the maximum position error synthesized by ZNN model (8) in this situation is roughly 0.01 m. According to the presented theoretical results (i.e., the theorem in Sect. 3), γ can be used to improve the performance and robustness of the ZNN model. So, in comparison, as depicted in Fig. 14, when γ increases to 10⁶, the end-effector path-tracking task can be accomplished well. Moreover, the maximum position error can be decreased by 10 times, which may satisfy the requirement of engineering applications, and confirm again the theoretical results shown in Sect. 3.

Fig. 13

End-effector trajectory and position errors of a five-link planar robot manipulator synthesized by largely perturbed ZNN model (8) using power-sum activation functions (with N = 3, γ = 10⁵ and $\Updelta\omega=[100,100,100,100,100,100,100]^T$) when tracking an elliptical path. a End-effector trajectory, b position errors (m)

Fig. 14

End-effector trajectory and position errors of a five-link planar robot manipulator synthesized by largely perturbed ZNN model (8) using power-sum activation functions (with N = 3, γ = 10⁶ and $\Updelta\omega=[100,100,100,100,100,100,100]^T$) when tracking an elliptical path. a End-effector trajectory, b position errors (m)

6 Conclusions

In this paper, the convergence and robustness properties of Zhang neural network using two types of activation functions have been investigated and analyzed for the online solution of time-varying convex QP problems. The theoretical analysis has guaranteed that superior robustness is achieved readily for ZNN formulas and models in the context of (very) large model-implementation errors by using power-sum activation functions, when compared to that using linear activation functions. Computer-simulation results, including those based on a five-link robot manipulator, have further substantiated the feasibility, effectiveness and robustness of Zhang neural network.

Before ending the paper, it is worth pointing out further that this paper focuses on the robustness analysis of the ZNN model for solving time-varying QP problems subject to time-varying linear-equality constraints. In the future, we will consider handling other types of constraints (e.g., inequality constraints) via the presented ZNN method and model, which is evidently a future research direction of this work.