A Finite-Time Convergent Neural Network for Solving Time-Varying Linear Equations with Inequality Constraints Applied to Redundant Manipulator

Abstract

Zhang neural network (ZNN), a special recurrent neural network, has recently been established as an effective alternative for time-varying linear equations with inequality constraints (TLEIC) solving. Still, the convergent time produced by the ZNN model always tends to infinity. In contrast to ZNN, a finite-time convergent neural network (FCNN) is proposed for the TLEIC problem. By introducing a non-negative slack variable, the initial form of the TLEIC has been transformed into a system of time-varying linear equation. Afterwards, the stability and finite-time performance of the FCNN model is substantiated by the theoretical analysis. Then, simulation results further verify the effectiveness and superiority of the proposed FCNN model as compared with the ZNN model for solving TLEIC problem. Finally, the proposed FCNN model is successfully applied to the trajectory planning of redundant manipulators with joint limitations, thereby illustrating the applicability of the new neural network model.

1 Introduction

Finding solutions for systems of linear equations with inequality constraints is the basis of many mathematical or engineering topics [1,2,3,4,5], such as robot kinematics [2], data processing [3] and control optimization [4]. Many achievements have been studied the solutions of linear equations with inequality constraints [6,7,8,9,10,11]. For example, Pang $et al.$ [6] proposed an ABS-MPVT algorithm to solve linear equations and inequality systems. Murav’eva [7] studied the consistency and inconsistent radius of linear equations and inequality solutions. Moreover, other iterative algorithms were proposed to obtain the solutions of linear equalities with bound constraints, including the abstract algorithm [10] and $\Gamma$-algorithm [11].

Due to the parallel processing characteristics of recurrent neural network (RNN), many researchers are committed to solve mathematical problems with RNN [12,13,14,15]. A special RNN, the classical Hopfield neural network (HNN), was presented in literature [12]. Following the aspiring work, Xia $et al.$ [13] investigated two RNN models based on continuous time and discrete time for time-invariant mathematical problems. Liang $et al.$ [14] proposed an improved discrete time RNN model. In [15], various RNN dynamics were developed for the solution of linear underdetermined systems with inequality constraints. Significantly, all the methods mentioned above are used to solve time-invariant systems of linear equations and inequalities. In practical applications, most systems are not static but changing over time [2]. However, there are large errors and relatively delay in solving time-varying mathematical problems with the mentioned methods.

Different from the aforementioned neural networks, Zhang neural network (ZNN), also a special RNN, was presented by Zhang $et al.$ aiming zero convergence with infinity time for solving time-varying mathematical problems [16,17,18,19,20,21]. For instance, Zhang $et al.$ proposed two newly-designed ZNN models, which aims at time-varying underdetermined linear systems in [21]. Simulation results of trajectory planning of redundant manipulators verified the validity of the two newly-designed ZNN models. However, in many real applications, the limitation of solutions should be considered when time-varying linear equations solving. For example, each joint is physically constrained within a fixed moving range in inverse-kinematics of redundant manipulators. The unexpected joint-angle position will lead to wrong trajectory of the manipulator, and even even cause damage to itself. Thus, keeping the joint variables within its physical limits is greatly important. For this purpose, two new constructed ZNN models incorporating bound constraints with time-varying linear equations were proved to have perfect convergence as long as time is infinity [22]. However, the long convergent time of time-varying linear equations with inequality constraints (TLEIC) will affect the executive effectiveness, which tends to add heavy burden for time-varying systems and is incapable to complete the given task.

To accelerate convergent speed and shorten convergent time, many studies have been done about finite-time convergence [23,24,25,26,27,28,29,30,31,32,33]. For instance, Li et al. [23] first presented a particular activation function, which can make ZNN model converge to zero within finite time. In [24], this activation function was utilized for establishing a ZNN model with finite-time characteristics to solve time-varying inequality problems. Aiming at the solution of time-varying nonlinear equation, Lin et al. also proposed two novel nonlinear activation functions in [25] for enhancing the convergence performance of the ZNN model. Jin et al. [26] used a power-versatile activation function in ZNN model to solve dynamic matrix inversion (DMI), and proved the excellent convergence performance and great robustness of the proposed model for solving DMI problem under various interference environments. Different from [23,24,25,26] (i.e., improving activation functions), some new design formulas were designed in [28,29,30,31,32] to accelerate ZNN model. For example, Jin et al. [28] replaced the error function ${\varvec{e}}(t)$ in the original ZNN design formula with a Bernoulli equation, thereby obtaining a new design formula and constructing a improved ZNN (IZNN) model to solve time-invariant and time-varying nonlinear equation. In [30,31,32], a new design formula with linear activation function was investigated by Lin et al., and established three different finite-time RNN (FTRNN) models for the online solutions of time-varying matrix inversion, time-varying matrix square root and time-varying Sylvester matrix equation. Comparative results were visualized to determine the superiority of FTRNN models. In [33], a class of new evolution formula was exploited for quadratic programming problems, and its finite-time convergence and robustness were also substantiated by the application of k-winner-take-all (k-WTA). However, at present, no research has focused on solving TLEIC directly in finite time.

Aspired by the above RNN designing rules for time-varying problems, a new finite-time convergent neural network (FCNN) is proposed in this paper to solve TLEIC. Theoretical analysis proves the stability and finite-time convergence of the proposed FCNN model in detail. The superiority of the FCNN model is substantiated in the simulation experiment. This work is attempted to show the proposed FCNN can directly handle the time-varying linear equations considering the corresponding inequality constraints. Furthermore, we apply the proposed FCNN model to trajectory planning of redundant manipulators and solve its TLEIC problem by referring to each joint variable limitations. Simulations on six-degrees-of-freedom (six-DOF) planar manipulator and PUMA560 redundant manipulator show the application of the proposed FCNN model. With its motion planning of redundant manipulators, this work serves as an improvement in the finite-time research of redundant manipulators with joint physical constraints.

The rest of this paper consists of six sections. Sect. 2 describes the specific form of TLEIC and gives out the key steps of transforming TLEIC into time-varying linear equations. In Sect. 3, the new design formula of FCNN is presented, and the corresponding FCNN model is established for TLEIC. Sect. 4 proves the stability and finite-time convergence of the proposed FCNN model. The FCNN model is further simulated and compared with the ZNN model for the TLEIC problem solving in Sect. 5. Section 6 demonstrates the application of the proposed FCNN model to trajectory planning of redundant manipulators. Finally, Sect. 7 gives a summary of this paper. It should be pointed out that the main contributions of this paper are as follows.

• 1) This paper mainly proposes a FCNN model via a novel design formula for directly solving TLEIC within finite time.

• 2) The stability and finite-time convergence of the FCNN model for TLEIC is proved in detail. Besides, the finite convergent time of the FCNN model is derived theoretically, which further proves the effectiveness in finite time.

• 3) Numerical simulation verifies the validity and finite-time convergence of the proposed FCNN model. Furthermore, the superiority of the FCNN model for solving TLEIC problem is verified, as compared with the ZNN model under various activation functions.

• 4) The feasibility and practicability of FCNN model in the application of trajectory planning for redundant manipulators with joint constraints (namely 6-DOF planar manipulator and PUMA560 redundant manipulator) are further demonstrated.

2 Problem Description and Transformation

This section mainly describes the mathematical expression of TLEIC and the transformation steps required in the solving procedure.

2.1 Problem Description

In this subsection, mathematical form of the TLEIC problem can be described as

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{{\mathcal {W}}}}(t) {\varvec{x}}(t) = {\varvec{l}}(t) \\ {\varvec{x}}_1 \le {\varvec{x}}(t) \le {\varvec{x}}_2 \end{array} \right. \end{aligned}$$

(1)

where ${\varvec{{\mathcal {W}}}}(t) \in R^{m \times n}$ is a given non-zero time-varying coefficient matrix with $m < n$, and ${\varvec{l}}(t) \in R^{m}$ is a given non-zero time-varying vector. ${\varvec{x}}(t) \in R^{n}$ is an unknown vector to be solved in TLEIC problem (1). ${\varvec{x}}_1 \in R^{n}$ and ${\varvec{x}}_2 \in R^{n}$ denote the lower and upper bounds of ${\varvec{x}}(t)$, both of which are constant vectors. Besides, to ensure the existence of ${\varvec{x}}(t)$, we assume ${\varvec{{\mathcal {W}}}}(t)$ is nonsingular in (1) at all $t \in [0, +\infty )$ in this paper.

Subsequently, the inequality constraints on ${\varvec{x}}(t)$ in TLEIC problem (1) can be transformed into a system of linear inequalities, i.e.,

$$\begin{aligned} {\varvec{U}} {\varvec{x}}(t) \le {\varvec{c}} \end{aligned}$$

where ${\varvec{U}} = \left[ -{\varvec{I}}, {\varvec{I}} \right] ^ \mathrm{{T}} \in R^{2n \times n}$, with ${\varvec{I}} \in R^{n \times n}$ denotes an identity matrix. ${\varvec{c}}\in R^{2n}$ as a vector composed of the ${\varvec{x}}_{1}$ and ${\varvec{x}}_{2}$, and the specific form is ${\varvec{c}} = \left[ -{\varvec{x}}_{1} ^ \mathrm{{T}}, {\varvec{x}}_{2} ^ \mathrm{{T}} \right] ^ \mathrm{{T}}$. Note that superscript $^{\mathrm{{T}}}$ as the transpose operation. Then, the following equations can be obtained

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{{\mathcal {W}}}}(t) {\varvec{x}}(t) = {\varvec{l}}(t) \\ {\varvec{U}} {\varvec{x}}(t) \le {\varvec{c}} \end{array}. \right. \end{aligned}$$

(2)

which is equivalent to TLEIC problem (1).

2.2 Problem Transformation

Previously, we have introduced the specific form of the TLEIC. Then, by introducing an unknown slack variable ${\varvec{s}} ^ {.2}$, which is greater than or equal to ${\varvec{0}}$ [16], the inequality constraints in (2) can be rewritten as the following time-varying nonlinear equations:

$$\begin{aligned} {\varvec{U}} {\varvec{x}}(t) + {\varvec{s}} ^ {.2}(t) - {\varvec{c}} = {\varvec{0}} \end{aligned}$$

(3)

where the superscript $^{.2}$ in ${\varvec{s}} ^ {.2}(t)$ means the square operation of each element in ${\varvec{s}}(t)$. For ease of understanding, the relationship between ${\varvec{s}}(t)$ and ${\varvec{s}} ^ {.2}(t)$ are given here:

$$\begin{aligned} {\varvec{s}}(t) = \left[ \begin{array}{cccc} s_{1}(t) \\ s_{2}(t) \\ s_{3}(t) \\ {\vdots } \\ s_{2n}(t) \end{array}\right] \in R^{2n},~ {\varvec{s}} ^ {.2}(t) = \left[ \begin{array}{cccc} s_{1} ^ {2}(t) \\[2mm] s_{2} ^ {2}(t) \\[2mm] s_{3} ^ {2}(t) \\[2mm] {\vdots } \\ s_{2n} ^ {2}(t) \end{array}\right] \in R^{2n}. \end{aligned}$$

The following system including time-varying linear and nonlinear equations can be derived from (2) through analysis above:

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{{\mathcal {W}}}}(t) {\varvec{x}}(t) = {\varvec{l}}(t) \\ {\varvec{U}} {\varvec{x}}(t) + {\varvec{s}} ^ {.2}(t) = {\varvec{c}} \end{array} \right. . \end{aligned}$$

(4)

In addition, vector ${\varvec{s}}(t)$ is determined in parallel with the solution of (1). For further discussion, we first convert ${\varvec{s}} ^ {.2}(t)$ into the following form:

$$\begin{aligned} {\varvec{s}} ^ {.2}(t) = {\varvec{V}}(t) {\varvec{s}}(t) \end{aligned}$$

(5)

where ${\varvec{V}}(t) \in R^{2n \times {2n}}$ is a time-varying diagonal matrix with all the elements in ${\varvec{s}}(t)$ as the main diagonal element, i.e.,

$$\begin{aligned} {\varvec{V}}(t)={\text {diag}}\left( s_1(t), s_2(t), s_3(t), {\cdots }, s_{2n}(t) \right) . \end{aligned}$$

Then, according to Eq. (5), we reconstruct the the time-varying linear and nonlinear equations (4) as

$$\begin{aligned} {\varvec{{\mathcal {K}}}}(t) {\varvec{z}}(t) = {\varvec{q}}(t) \end{aligned}$$

(6)

where ${\varvec{{\mathcal {K}}}}(t) \in R^{(2n+m) \times {3n}}$, ${\varvec{q}}(t) \in R^{2n+m}$ and ${\varvec{z}}(t) \in R^{3n}$ are respectively expressed as

$$\begin{aligned} {\varvec{{\mathcal {K}}}}(t) = \left[ \begin{array}{cc} {\varvec{{\mathcal {W}}}}(t) &{} {\varvec{0}} \\ {\varvec{U}} &{} {\varvec{V}}(t) \end{array} \right] , ~~{\varvec{q}}(t) = \left[ \begin{array}{cc} {\varvec{l}}(t) \\ {\varvec{c}} \end{array} \right] , ~~{\varvec{z}}(t) = \left[ \begin{array}{cc} {\varvec{x}}(t) \\ {\varvec{s}}(t) \end{array} \right] . \end{aligned}$$

Remark 1

To guarantee the transformed Eq. (6) is solvable, we assume that Eq. (6) satisfies the following condition in this paper:

$$\begin{aligned} {\text {rank}}\left( {\varvec{{\mathcal {K}}}}(t)\right) = {\text {rank}}\left( \left[ \begin{array}{cc} {\varvec{{\mathcal {K}}}}(t)&{\varvec{q}}(t) \end{array} \right] \right) = 3n \end{aligned}$$

where operator ${\text {rank}}(\cdot )$ denotes the rank of a matrix.

Based on the above transformation, solving TLEIC problem (1) is equivalent to the solution of Eq.  (4) or Eq. (6) at any $t \in [0, +\infty )$.

3 FCNN Description and Model Establishment

In this section, a finite-time convergent neural network (FCNN) model with finite-time characteristics is presented to solving the TLEIC problem (1).

Based on Eq. (6), we first define a indefinite vector-valued time-varying error function ${\varvec{e}}(t)$ as

$$\begin{aligned} {\varvec{e}}(t) = {\varvec{{\mathcal {K}}}}(t) {\varvec{z}}(t) - {\varvec{q}}(t) \end{aligned}$$

(7)

By the above definition, the time-derivative of ${\varvec{e}}(t)$, i.e., $\dot{{\varvec{e}}}(t)$, is given as

$$\begin{aligned} \dot{{\varvec{e}}}(t) = {\varvec{{\mathcal {K}}}}(t) \dot{{\varvec{z}}}(t) + \dot{{\varvec{{\mathcal {K}}}}}(t) {\varvec{z}}(t) - \dot{{\varvec{q}}}(t) \end{aligned}$$

(8)

where $\dot{{\varvec{{\mathcal {K}}}}}(t)$, $\dot{{\varvec{q}}}(t)$ and $\dot{{\varvec{z}}}(t)$ are the time-derivative of ${\varvec{{\mathcal {K}}}}(t)$, ${\varvec{q}}(t)$ and ${\varvec{z}}(t)$, respectively. Then, in order to zeroing ${\varvec{e}}(t)$, a novel design formula of FCNN is given as

$$\begin{aligned} \dot{{\varvec{e}}}(t) = {\varvec{\varPhi }} \left( -\xi _{1}{\varvec{e}}^{. d / b} (t) -\xi _{2}{\varvec{e}}(t) \right) \end{aligned}$$

(9)

where $\xi _{1}>0\in R$ and $\xi _{2} >0\in R$ are design parameters. The superscript $^{. d / b}$ in ${\varvec{e}}^{. d / b} (t)$ indicates that the exponential term d/b is added to each element in ${\varvec{e}}(t)$, and the specific expression is

$$\begin{aligned} {\varvec{e}}^{. d / b} (t) = \left[ \begin{array}{cccc} e_{1} ^ {d / b}(t) \\ e_{2}^ {d / b}(t) \\ e_{3}^ {d / b}(t) \\ {\vdots } \\ \end{array}\right] . \end{aligned}$$

Moreover, d and b as positive odd numbers in Eq. (9), and satisfy $d < b$. ${\varvec{\varPhi }} (\cdot ){\varvec{:}} R^{2n+m} \rightarrow R^{2n+m}$ denotes an activation function, which can only be a monotone increasing odd function, i.e., ${\varvec{\varPhi }}(\cdot ) = -{\varvec{\varPhi }}(-\cdot )$, such as linear function, sigmoid function, hyperbolic-sine function, etc. Note that this paper focus on the study of a design formula (i.e., Eq. (9)) to establish FCNN model for solving TLEIC problem (1). Therefore, in the experimental simulation, only linear activation function is used in the FCNN model (11).

On the basis of Eq. (5), the time-derivative of ${\varvec{s}} ^ {.2}(t)$, i.e., $\dot{{\varvec{s}}} ^ {.2}(t)$, can be obtained as

$$\begin{aligned} \dot{{\varvec{s}}} ^ {.2}(t) = 2{\varvec{V}}(t) \dot{{\varvec{s}}}(t). \end{aligned}$$

(10)

According to the Eqs. (7), (8) and (10), (9) can be expanded into the following equation:

$$\begin{aligned} \begin{aligned}&\left[ \begin{array}{cc} {\varvec{{\mathcal {W}}}}(t) &{} {\varvec{0}} \\ {\varvec{U}} &{} 2{\varvec{V}}(t) \end{array}\right] \left[ \begin{array}{c} \dot{{\varvec{x}}}(t) \\ \dot{{\varvec{s}}}(t) \end{array}\right] +\left[ \begin{array}{cc} \dot{{\varvec{{\mathcal {W}}}}}(t) &{} {\varvec{0}} \\ {\varvec{0}} &{} {\varvec{0}} \end{array}\right] \left[ \begin{array}{l} {\varvec{x}}(t) \\ {\varvec{s}}(t) \end{array}\right] -\left[ \begin{array}{c} \dot{{\varvec{l}}}(t) \\ {\varvec{0}} \end{array}\right] \\&\quad = {\varvec{\varPhi }} \left( -\xi _{1}\left( \left[ \begin{array}{cc} {\varvec{{\mathcal {W}}}}(t) &{} {\varvec{0}} \\ {\varvec{U}} &{} {\varvec{V}}(t) \end{array} \right] \left[ \begin{array}{cc} {\varvec{x}}(t) \\ {\varvec{s}}(t) \end{array} \right] - \left[ \begin{array}{cc} {\varvec{l}}(t) \\ {\varvec{c}} \end{array} \right] \right) ^{. d / b} - \xi _{2}\left( \left[ \begin{array}{cc} {\varvec{{\mathcal {W}}}}(t) &{} {\varvec{0}} \\ {\varvec{U}} &{} {\varvec{V}}(t) \end{array} \right] \left[ \begin{array}{cc} {\varvec{x}}(t) \\ {\varvec{s}}(t) \end{array} \right] - \left[ \begin{array}{cc} {\varvec{l}}(t) \\ {\varvec{c}} \end{array} \right] \right) \right) . \end{aligned} \end{aligned}$$

where $\dot{{\varvec{{\mathcal {W}}}}}(t)$, $\dot{{\varvec{x}}}(t)$, $\dot{{\varvec{s}}}(t)$ and $\dot{{\varvec{l}}}(t)$ are the time-derivative of ${\varvec{{\mathcal {W}}}}(t)$, ${\varvec{x}}(t)$, ${\varvec{s}}(t)$ and ${\varvec{l}}(t)$, respectively. Defining the time-varying matrices ${\varvec{G}}(t)$ and ${\varvec{H}}(t)$ as

$$\begin{aligned} \begin{aligned} {\varvec{G}}(t) = \left[ \begin{array}{cc} {\varvec{{\mathcal {W}}}}(t) &{} {\varvec{0}} \\ {\varvec{U}} &{} 2{\varvec{V}}(t) \end{array} \right] \in R^{(2n+m) \times {3n}}, ~~~{\varvec{H}}(t) = \left[ \begin{array}{cc} \dot{{\varvec{{\mathcal {W}}}}}(t) &{} ~~~{\varvec{0}} \\ {\varvec{0}} &{} ~~~{\varvec{0}} \end{array} ~~~\right] \in R^{(2n+m) \times {3n}} \end{aligned} \end{aligned}$$

following implicit dynamic equation can be obtained:

$$\begin{aligned} {\varvec{G}}(t) \dot{{\varvec{z}}}(t) +{\varvec{H}}(t) {\varvec{z}}(t) -\dot{{\varvec{q}}}(t) = {\varvec{\varPhi }} (-\xi _{1}({\varvec{{\mathcal {K}}}}(t) {\varvec{z}}(t) - {\varvec{q}}(t))^{. d / b} - \xi _{2}({\varvec{{\mathcal {K}}}}(t) {\varvec{z}}(t) - {\varvec{q}}(t)) ). \end{aligned}$$

Furthermore, FCNN model can be expressed as follows:

$$\begin{aligned} \dot{{\varvec{z}}}(t)= & {} {\varvec{G}} ^ {\dagger }(t) ( -{\varvec{H}}(t) {\varvec{z}}(t) +\dot{{\varvec{q}}}(t) +{\varvec{\varPhi }} (-\xi _{1}({\varvec{{\mathcal {K}}}}(t) {\varvec{z}}(t) - {\varvec{q}}(t))^{. d / b} \nonumber \\&- \xi _{2}({\varvec{{\mathcal {K}}}}(t) {\varvec{z}}(t) - {\varvec{q}}(t))) \end{aligned}$$

(11)

where ${\varvec{G}} ^ {\dagger }(t)$ is the right pseudo-inverse of ${\varvec{G}}(t)$, and its concrete expression is ${\varvec{G}} ^{\dagger }(t) = {\varvec{G}}(t)^{\mathrm{{T}}}({\varvec{G}}(t){\varvec{G}}^{\mathrm{{T}}}(t))^{-1}$.

Fig. 1

Neuron structure of FCNN model (11) for TLEIC problem (1) solving

To facilitate understanding, Fig. 1 presents the nteuron structure of FCNN model (11).

Remark 2

The i-th neuron of FCNN model (11) is expressed as

$$\begin{aligned} \begin{aligned} z_{i}=\int \sum _{j=1}^{2n+m} {\tilde{g}}_{ij}\left( -\sum _{p=1}^{3n} h_{jp} z_{p}+{\dot{q}}_{j} \phi \left( -\xi _{1}\left( \sum _{p=1}^{3n} k_{jp} z_{p}-q_{j}\right) ^{d/b} - \xi _{2}\left( \sum _{p=1}^{3n} k_{jp} z_{p}-q_{j}\right) \right) \right) \mathrm {d} t \end{aligned} \end{aligned}$$

where ${\tilde{g}}_{ij}$, $h_{jp}$, $k_{jp}$, $q_{j}$, ${\dot{q}}_{j}$ and $z_{i}$ are the ij-th element of ${\varvec{G}} ^{\dagger }(t)$, the jp-th element of ${\varvec{H}}(t)$, the jp-th element of ${\varvec{{\mathcal {K}}}}(t)$, the j-th element of ${\varvec{q}}(t)$, the j-th element of $\dot{{\varvec{q}}}(t)$ and the i-th element of ${\varvec{z}}(t)$, respectively. $\phi (\cdot )$ is an element of ${\varvec{\varPhi }}(\cdot )$.

4 Theoretical Analysis

In this section, stability and finite-time convergence of the FCNN model (11) are analyzed, which verifies the feasibility of the FCNN model for the solution of TLEIC problem (1).

4.1 Stability Analysis

Theorem 1

Given time-varying coefficient matrix ${\varvec{{\mathcal {W}}}}(t)$, time-varying vector ${\varvec{l}}(t)$ and the bounded vector constraints ${\varvec{c}}$, if ${\varvec{\varPhi }} (\cdot )$ is a monotone increasing odd function, the vector-valued ${\varvec{x}}(t)$ of FCNN model (11) can globally converges to the theoretical solution ${\varvec{x}} ^ {*}(t)$ of TLEIC problem (1).

Proof

Let’s suppose ${\varvec{x}} ^ {*}(t)$ be the theoretical solution of TLEIC problem (1), and the slack variable ${\varvec{s}}^{*.2}(t)$ will be exists that satisfies the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{{\mathcal {W}}}}(t) {\varvec{x}}^{*}(t) = {\varvec{l}}(t) \\ {\varvec{U}} {\varvec{x}}^{*}(t) + {\varvec{s}} ^ {*.2}(t) = {\varvec{c}} \end{array}\,. \right. \end{aligned}$$

(12)

Furthermore, the time-derivative of Eq. (12) can be obtained as

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{{\mathcal {W}}}}(t) \dot{{\varvec{x}}}^{*}(t) + \dot{{\varvec{{\mathcal {W}}}}}(t) {\varvec{x}}^{*}(t) = \dot{{\varvec{l}}}(t) \\ {\varvec{U}} \dot{{\varvec{x}}}^{*}(t) + \dot{{\varvec{s}}} ^ {*.2}(t) = {\varvec{0}} \end{array}\,. \right. \end{aligned}$$

(13)

Then, expanding FCNN model (11) and converting into

$$\begin{aligned} \left\{ \begin{array}{ll} {\varvec{{\mathcal {W}}}}(t) \dot{{\varvec{x}}}(t) + \dot{{\varvec{{\mathcal {W}}}}}(t) {\varvec{x}}(t) - \dot{{\varvec{l}}}(t) \\ = {\varvec{\varPhi }} (-\xi _{1} ({\varvec{{\mathcal {W}}}}(t) {\varvec{x}}(t) - {\varvec{l}}(t) ) ^ {.d/b} -\xi _{2}({\varvec{{\mathcal {W}}}}(t) {\varvec{x}}(t) - {\varvec{l}}(t))) \\ {\varvec{U}} \dot{{\varvec{x}}}(t) + \dot{{\varvec{s}}} ^ {.2}(t) \\ ={\varvec{\varPhi }}(-\xi _{1}({\varvec{U}} {\varvec{x}}(t) + {\varvec{s}}^{.2}(t) - {\varvec{c}} ) ^{.d/b} -\xi _{2}({\varvec{U}} {\varvec{x}}(t) + {\varvec{s}}^{.2}(t) - {\varvec{c}} ) ). \end{array} \right. \end{aligned}$$

Substituting Eq. (12) and Eq. (13) into the above equations, it can be obtained that

$$\begin{aligned} \left\{ \begin{array}{ll} {\varvec{{\mathcal {W}}}}(t) (\dot{{\varvec{x}}}(t) - \dot{{\varvec{x}}}^{*}(t)) + \dot{{\varvec{{\mathcal {W}}}}}(t) ({\varvec{x}}(t) - {\varvec{x}}^{*}(t)) \\ = {\varvec{\varPhi }} (-\xi _{1}({\varvec{{\mathcal {W}}}}(t) ({\varvec{x}}(t) - {\varvec{x}}^{*}(t))) ^ {.d/b} -\xi _{2} ({\varvec{{\mathcal {W}}}}(t) ({\varvec{x}}(t) - {\varvec{x}}^{*}(t)))) \\ {\varvec{U}} (\dot{{\varvec{x}}}(t) - \dot{{\varvec{x}}}^{*}(t) ) +\dot{{\varvec{s}}} ^ {.2}(t) - \dot{{\varvec{s}}} ^ {*.2}(t) \\ ={\varvec{\varPhi }}(-\xi _{1}({\varvec{U}} ({\varvec{x}}(t) - {\varvec{x}}^{*}(t) ) + {\varvec{s}}^{.2}(t) - {\varvec{s}}^{*.2}(t)) ^{.d/b} \\ ~~- \xi _{2}({\varvec{U}} \left( {\varvec{x}}(t) - {\varvec{x}}^{*}(t) \right) + {\varvec{s}}^{.2}(t) - {\varvec{s}}^{*.2}(t))) \end{array} \right. \end{aligned}$$

(14)

which can be further converted into

$$\begin{aligned} \begin{aligned}&\left[ \begin{array}{cc} {\varvec{{\mathcal {W}}}}(t) &{} {\varvec{0}} \\ {\varvec{U}} &{} {\varvec{I}} \end{array}\right] \left[ \begin{array}{cc} \dot{{\varvec{x}}}(t) - \dot{{\varvec{x}}}^{*}(t) \\ \dot{{\varvec{s}}}^{.2}(t) - \dot{{\varvec{s}}}^{*.2}(t) \end{array}\right] + \left[ \begin{array}{cc} \dot{{\varvec{{\mathcal {W}}}}}(t) &{} {\varvec{0}} \\ {\varvec{0}} &{} {\varvec{0}} \end{array}\right] \left[ \begin{array}{cc} {\varvec{x}}(t) - {\varvec{x}}^{*}(t) \\ {\varvec{s}}^{.2}(t) - {\varvec{s}}^{*.2}(t) \end{array}\right] \\&= {\varvec{\varPhi }} \left( -\xi _{1}\left( \left[ \begin{array}{cc} {\varvec{{\mathcal {W}}}}(t) &{} {\varvec{0}} \\ {\varvec{U}} &{} {\varvec{I}} \end{array}\right] \left[ \begin{array}{cc} {\varvec{x}}(t) - {\varvec{x}}^{*}(t) \\ {\varvec{s}}^{.2}(t) - {\varvec{s}}^{*.2}(t) \end{array}\right] \right) ^{.d/b} \right. \\&~~~\left. - \xi _{2} \left( \left[ \begin{array}{cc} {\varvec{{\mathcal {W}}}}(t) &{} {\varvec{0}} \\ {\varvec{U}} &{} {\varvec{I}} \end{array}\right] \left[ \begin{array}{cc} {\varvec{x}}(t) - {\varvec{x}}^{*}(t) \\ {\varvec{s}}^{.2}(t) - {\varvec{s}}^{*.2}(t) \end{array}\right] \right) \right) \end{aligned} \end{aligned}$$

(15)

where $\dot{{\varvec{s}}}^{*.2}(t)$ and $\dot{{\varvec{x}}}^{*}(t)$ are the time-derivative of ${\varvec{s}}^{*.2}(t)$ and ${\varvec{x}}^{*}(t)$, respectively. ${\varvec{I}} \in R^{2n \times {2n}}$ is a identity matrix.

Defining

$$\begin{aligned} \hat{{\varvec{e}}}(t) = \left[ \begin{array}{cc} {\varvec{{\mathcal {W}}}}(t) &{} {\varvec{0}} \\ {\varvec{U}} &{} {\varvec{I}} \end{array}\right] \left[ \begin{array}{cc} {\varvec{x}}(t) - {\varvec{x}}^{*}(t) \\ {\varvec{s}}^{.2}(t) - {\varvec{s}}^{*.2}(t) \end{array}\right] \in R^{2n+m} \end{aligned}$$

(16)

Eq. (15) can be reformulated as

$$\begin{aligned} \dot{\hat{{\varvec{e}}}}(t) = {\varvec{\varPhi }} \left( -\xi _{1}\hat{{\varvec{e}}}^{.d/b}(t)-\xi _{2}\hat{{\varvec{e}}}(t)\right) \end{aligned}$$

(17)

where $\dot{\hat{{\varvec{e}}}}(t)$ is the time-derivative of $\hat{{\varvec{e}}}(t)$. Then, the j-th element (with $j \in \{1, 2, \cdots , 2n+m\}$) in $\hat{{\varvec{e}}}(t)$ can be given as

$$\begin{aligned}&\begin{aligned} \dot{{\hat{e}}}_{j}(t)&= \varphi ({\hat{e}}_{j}(t)) \end{aligned} \end{aligned}$$

(18a)

$$\begin{aligned}&\varphi ({\hat{e}}_{j}(t)) = \phi \left( -\xi _{1}{\hat{e}}_{j}^{d/b}(t) - \xi _{2}{\hat{e}}_{j}(t) \right) \end{aligned}$$

(18b)

where $\phi (\cdot )$ is an element of ${\varvec{\varPhi }}(\cdot )$, which is a monotone increasing odd function.

We can be obtained that the equilibrium state of the dynamic equation (18a) is ${\hat{e}}_{j} = 0$. Then, we defined the Lyapunov function as

$$\begin{aligned} {v \left( {\hat{e}}_{j}\right) } =\frac{1}{2} {\hat{e}}_{j} ^ {2}(t) \end{aligned}$$

which is a positive-definite function. Subsequently, the time-derivative of $v \left( {\hat{e}}_{j}\right)$ is

$$\begin{aligned} { {\dot{v}} \left( {\hat{e}}_{j}\right) = \frac{{\text {d}}v\left( {\hat{e}}_{j}\right) }{{\text {d}}t} ={\hat{e}}_{j}(t) \dot{{\hat{e}}}_{j}(t). } \end{aligned}$$

Substituting Eq. (18a) into the above equation, ${\dot{v}} \left( {\hat{e}}_{j}\right)$ can be reformulated as

$$\begin{aligned} { {\dot{v}} \left( {\hat{e}}_{j}\right) = {\hat{e}}_{j}(t) \varphi ({\hat{e}}_{j}(t)). } \end{aligned}$$

(19)

If $\phi (\cdot )$ is a monotone increasing odd function, then

$$\begin{aligned} \varphi ({\hat{e}}_{j}(t)) \left\{ \begin{array}{l}> 0, \ {\hat{e}}_{j}< 0\\ = 0, \ {\hat{e}}_{j} = 0\\ < 0, \ {\hat{e}}_{j} > 0 \end{array} \right. \end{aligned}$$

Thus, we can obtained that

$$\begin{aligned} { {\dot{v}} \left( {\hat{e}}_{j}, t\right) = {\hat{e}}_{j}(t) \varphi ({\hat{e}}_{j}(t)) \left\{ \begin{array}{l} = 0, \ {\hat{e}}_{j} = 0\\ < 0, \ {\hat{e}}_{j} \ne 0 \end{array} \right. } \end{aligned}$$

which demonstrates ${\dot{v}} \left( {\hat{e}}_{j}\right)$ is a negative-definite function.

Then, according to Lyapunov stability theory [34], it can be concluded that dynamical equation (18a) is asymptotically stable in the equilibrium state ${\hat{e}}_{j} = 0$. Since ${\varvec{\hat{{\varvec{e}}}}}(t) = \{ {\hat{e}}_{j}(t) \}$, it’s further proved that $\hat{{\varvec{e}}}(t)={\varvec{0}}$ is the equilibrium state of dynamical equation (17) and is asymptotically stable.

Considering the previous definition of $\hat{{\varvec{e}}}(t)$, the equilibrium state $\hat{{\varvec{e}}}={\varvec{0}}$ can be expanded as

$$\begin{aligned} \hat{{\varvec{e}}}(t)= \left[ \begin{array}{l} {\varvec{{\mathcal {W}}}}(t)\left( {\varvec{x}}(t)-{\varvec{x}}^{*}(t)\right) \\ {\varvec{U}}\left( {\varvec{x}}(t)-{\varvec{x}}^{*}(t)\right) +{\varvec{s}}^{.2}(t)-{\varvec{s}}^{*.2}(t) \end{array}\right] = \left[ \begin{array}{c} 0 \\ 0\end{array}\right] \end{aligned}$$

which proves that the ${\varvec{x}}(t)$ asymptotes to the ${\varvec{x}}^{*}(t)$ at the equilibrium state $\hat{{\varvec{e}}}={\varvec{0}}$. That means the vector-valued ${\varvec{x}}(t)$ of FCNN model (11) can globally converge to the theoretical solution ${\varvec{x}}^{*}(t)$ of TLEIC problem (1). The proof of $Theorem \ 1$ is completed. $\square$

4.2 Convergence Analysis

In this subsection, finite-time convergence of FCNN model (11) without the specific activation function is analyzed. Meanwhile, the convergent time of FCNN model (11) under linear activation function is calculated.

Theorem 2

Given time-varying coefficient matrix ${\varvec{{\mathcal {W}}}}(t)$, time-varying vector ${\varvec{l}}(t)$ and the bounded vector constraints ${\varvec{c}}$, if ${\varvec{\varPhi }}(\cdot )$ is a monotone increasing odd function, then the vector-valued ${\varvec{x}}(t)$ of FCNN model (11) with any initial state ${\varvec{x}}(0)$ can converge to the theoretical solution ${\varvec{x}}^{*}$ of TLEIC problem (1) in finite time. Specifically, when the linear activation functions is used, the convergent time of FCNN model (11) is $t_{cv} = \frac{b}{\xi _{2}(b-d)} \ln \frac{\xi _{2} {\hat{e}}_{j}(0)^{(b-d) / b}+\xi _{1}}{\xi _{1}}.$

Proof

Finite-time convergence of the general monotone increasing activation functions ${\varvec{\varPhi }}(\cdot )$ has been proved in detail in [35], which is omitted here.

Then, we consider the activation function ${\varvec{\varPhi }}(\cdot )$ is a linear function, i.e., ${\varvec{\varPhi }}(\hat{{\varvec{e}}}(t)) = \hat{{\varvec{e}}}(t)$, Eq. (18a) can be reformulated as

$$\begin{aligned} \dot{{\hat{e}}}_{j}(t) = -\xi _{1}{\hat{e}}_{j}^{d/b}(t) - \xi _{2}{\hat{e}}_{j}(t), \ j \in \{1, 2, \cdots , 2n+m\}. \end{aligned}$$

(20)

Dividing both sides of Eq. (20) by ${\hat{e}}_{j}^{d/b}(t)$, it can be obtained that

$$\begin{aligned} {\hat{e}}_{j}^{-d / b}(t) \frac{\mathrm {d} {\hat{e}}_{j}}{\mathrm {d} t}+\xi _{2} {\hat{e}}_{j}^{1-d / b}(t)=-\xi _{1}. \end{aligned}$$

(21)

Let ${\hat{e}}_{j}^{1-d / b}(t) = f(t)$, then

$$\begin{aligned} \frac{\mathrm {d} f(t)}{\mathrm {d} t}=\frac{b-d}{b} {\hat{e}}_{j}^{-d / b}(t) \frac{\mathrm {d} {\hat{e}}_{j}(t)}{\mathrm {d} t}. \end{aligned}$$

Eq. (21) can be reformulated into

$$\begin{aligned} \frac{\mathrm {d} f(t)}{\mathrm {d} t}+\frac{b-d}{b} \xi _{2} f(t)=-\frac{b-d}{b} \xi _{1}. \end{aligned}$$

(22)

At this point, Eq. (22) is a first-order linear differential equation, then its general solution is

$$\begin{aligned} \begin{aligned} f(t)&=\mathrm {e}^{-\int _{0}^{t} \frac{b-d}{b} \xi _{2} \mathrm {~d} t}\left( \int _{0}^{t}-\frac{b-d}{b} \xi _{1} \mathrm {e}^{\int _{0}^{t} \frac{m-n}{m} \xi _{2} \mathrm {~d} t} \mathrm {~d} t + {\mathcal {A}}\right) \\&=\mathrm {e}^{-\int _{0}^{t} \frac{b-d}{b} \xi _{2} \mathrm {d} t}\left( \int _{0}^{t}-\frac{b-d}{b} \xi _{1} \mathrm {e}^{\frac{b-d}{b} \xi _{2} t} \mathrm {~d} t+{\mathcal {A}}\right) \end{aligned} \end{aligned}$$

(23)

where ${\mathcal {A}}$ is an arbitrary constant.

Since $t = 0$, ${\mathcal {A}}=f(0)$, then Eq. (23) can further expressed as

$$\begin{aligned} \begin{aligned} f(t)&=\mathrm {e}^{-\frac{b-d}{b} \xi _{2} t}\left( -\left. \frac{b-d}{b} \xi _{1} \frac{b}{(b-d) \xi _{2}} \mathrm {e}^{\frac{b-d}{b} \xi _{2} t}\right| _{0} ^{t}+f(0)\right) \\&=-\frac{\xi _{1}}{\xi _{2}}+\frac{\xi _{1}}{\xi _{2}} \mathrm {e}^{-\frac{b-d}{b} \xi _{2} t}+f(0) \mathrm {e}^{-\frac{b-d}{b} \xi _{2} t}. \end{aligned} \end{aligned}$$

(24)

When ${\hat{e}}_{j}(t) = 0$, $f(t) = {\hat{e}}_{j}^{1-d / b}(t) = 0$ and $t = t_{cv}$. Then, Eq. (24) can be converted into

$$\begin{aligned} \left( \frac{\xi _1}{\xi _2} + f(0) \right) \mathrm {e}^{-\frac{b-d}{b}\xi _2 t_{cv}} = \frac{\xi _1}{\xi _2}~. \end{aligned}$$

(25)

According to Eq. (25), the convergent time $t_{cv}$ from any initial state ${\hat{e}}_{j}(0)$ to equilibrium state ${\hat{e}}_{j}=0$ is

$$\begin{aligned} \begin{aligned} t_{cv}&= \frac{b}{\xi _{2}(b-d)} \ln \frac{\xi _{2} f(0)+\xi _{1}}{\xi _{1}} \\&= \frac{b}{\xi _{2}(b-d)} \ln \frac{\xi _{2} {\hat{e}}_{j}(0)^{(b-d) / b}+\xi _{1}}{\xi _{1}}\,. \end{aligned} \end{aligned}$$

(26)

It is worth noting that ${\hat{e}}_{j}(0)$ is the j-th element of $\hat{{\varvec{e}}}(0)$. Substituting Eq. (12) into Eq. (16), we can obtained that

$$\begin{aligned} \begin{aligned} \hat{{\varvec{e}}}(t)&= \left[ \begin{array}{c} {\varvec{{\mathcal {W}}}}(t){\varvec{x}}(t) - {\varvec{{\mathcal {W}}}}(t){\varvec{x}}^{*}(t)\\ {\varvec{U}}{\varvec{x}}(t)+ {\varvec{s}}^{.2}(t) - \left( {\varvec{U}}{\varvec{x}}^{*}(t)+{\varvec{s}}^{*.2}(t)\right) \end{array}\right] \\&= \left[ \begin{array}{c}{\varvec{{\mathcal {W}}}}(t){\varvec{x}}(t) - {\varvec{l}}(t) \\ {\varvec{U}}{\varvec{x}}(t)+ {\varvec{s}}^{.2}(t) - {\varvec{c}} \end{array}\right] \\&= \left[ \begin{array}{cc} {\varvec{{\mathcal {W}}}}(t) &{} {\varvec{0}} \\ {\varvec{U}} &{} {\varvec{V}}(t) \end{array}\right] \left[ \begin{array}{l} {\varvec{x}}(t) \\ {\varvec{s}}(t) \end{array}\right] -\left[ \begin{array}{l} {\varvec{l}}(t) \\ {\varvec{c}} \end{array}\right] \\&= {\varvec{{\mathcal {K}}}}(t){\varvec{z}}(t) - {\varvec{q}}(t). \end{aligned} \end{aligned}$$

Hence, $\hat{{\varvec{e}}}(0) = {\varvec{{\mathcal {K}}}}(0) {\varvec{z}}(0) - {\varvec{q}}(0)$. The proof of $Theorem \ 2$ is completed. $\square$

Remark 3

In the convergence analysis, finite-time convergence of the general monotone increasing odd functions $\varPhi (\cdot )$ has been discussed in [35]. Thus, in order to simplify the process, we only give the details of the finite-time convergence analysis of FCNN model (11) under linear activation function. Although the process of analysis is similar to the theoretical analysis presented in [30,31,32], this paper focuses on the solution of the TLEIC problem, and the corresponding solution model, i.e., FCNN model (11), is quite different from the solution model of time-varying matrix inversion, time-varying matrix square root and time-varying Sylvester matrix equation in [30,31,32].

Fig. 2

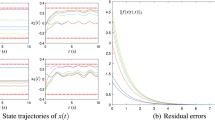
Numerical simulation results using the proposed FCNN model (11) with $\xi _{1} = 1$ and $\xi _{2} = 1$ under linear activation function for TLEIC problem (1) solving. a State trajectories of ${\varvec{x}}(t)$, b State trajectories of $\bar{{\varvec{e}}}(t)$, c Residual errors $J_{E}$ of FCNN model (11)

5 Numerical Verification of FCNN Model

In this section, the feasibility of the FCNN model (11) for TLEIC problem (1) is substantiated by numerically simulated. In addition, comparative simulation results with the ZNN model with various activation functions further verify the superiority of FCNN model (11).

5.1 Numerical Verification

In this numerical simulation, the specific forms of ${\varvec{{\mathcal {W}}}}(t)$, ${\varvec{l}}(t)$ and the constraints of ${\varvec{x}}(t)$ (i.e., ${\varvec{x}}_{1}$ and ${\varvec{x}}_{2}$) in TLEIC problem (1) are considered as

$$\begin{aligned} \begin{aligned} {\varvec{{\mathcal {W}}}}(t)&= \left[ \begin{array}{cc} 2+\sin (2t) \\ 2+\cos (t) \\ 2\cos (2t)-\sin (2t)+5 \end{array} \right] ^ \mathrm{{T}} \ \in R^{1 \times {3}} ,\\ {\varvec{l}}(t)&= ~\cos (t) + \sin (t) \ \in R~, \\ {\varvec{x}}_{1}&= \left[ \begin{array}{cc} -0.2 \\ -0.2 \\ -0.2\end{array} \right] \ \in R^{3}, \ {\varvec{x}}_{2} = \left[ \begin{array}{cc} 0.2 \\ 0.2 \\ 0.2\end{array} \right] \ \in R^{3}. \end{aligned} \end{aligned}$$

Based on the above definition, FCNN model (11) is simulated and investigated with linear activation function and different values of $\xi _{1}$. In addition, design parameters $\xi _{2} = 1$ and $d/b = 5/7$ are fixed in this simulation. The initial state ${\varvec{x}}(0) \in R^{3}$ is set as "$0.2 \times {\text {rand}}(3,1)$". The relevant simulation results are displayed in Fig. 2-4.

Fig. 3

Numerical simulation results using the proposed FCNN model (11) with $\xi _{1} = 5$ and $\xi _{2} = 1$ under linear activation function for TLEIC problem (1) solving. a State trajectories of ${\varvec{x}}(t)$, b State trajectories of $\bar{{\varvec{e}}}(t)$, c Residual errors $J_{E}$ of FCNN model (11)

Fig. 4

Numerical simulation results using the proposed FCNN model (11) with $\xi _{1} = 50$ and $\xi _{2} = 1$ under linear activation function for TLEIC problem (1) solving. a State trajectories of ${\varvec{x}}(t)$, b State trajectories of $\bar{{\varvec{e}}}(t)$, c Residual errors $J_{E}$ of FCNN model (11)

Figure 2 shows the simulation results using FCNN model (11) with linear activation function and $\xi _{1} = 1$, where the residual errors of FCNN model is defined as $J_{E} = \Vert {\varvec{{\mathcal {K}}}}(t) {\varvec{z}}(t) - {\varvec{q}}(t) \Vert _2$ and the $\Vert \cdot \Vert _2$ denotes the two-norms. The state trajectories of ${\varvec{x}}(t)$ are shown in Fig. 2awith five different initial states ${\varvec{x}}(0)$. From this figure, we can see that all the state trajectories of ${\varvec{x}}(t)$ do not exceed $[-0.2, 0.2]$. To further verify that the ${\varvec{x}}(t)$ presented in Fig. 2a satisfy the linear equations of TLEIC problem (1), the state trajectories of $\bar{{\varvec{e}}}(t) = {\varvec{{\mathcal {W}}}}(t){\varvec{x}}(t)-{\varvec{l}}(t)$ are given in Fig. 2b. As observed in Fig. 2b, all states of $\bar{{\varvec{e}}}$ converges to zero in any initial state. In Fig. 2c, all the residual errors $J_{E}$ of FCNN model (11) converge to zero within the range of $3.5{\text {-}}4{\text {s}}$. Combining with the analysis in Sect. 4, it can be concluded that the ${\varvec{x}}(t)$ presented in Fig. 2a simultaneously satisfies time-varying linear equations (i.e., ${\varvec{{\mathcal {W}}}}(t){\varvec{x}}(t) = {\varvec{l}}(t)$) and the inequality constraints (i.e., ${\varvec{x}}_1 \le {\varvec{x}}(t) \le {\varvec{x}}_2$). In other words, ${\varvec{x}}(t)$ presented in Fig. 2a can converge to the theoretical solution ${\varvec{x}}^{*}(t)$ of TLEIC problem (1) within finite time. Therefore, the feasibility and finite-time convergence of FCNN model (11) with linear activation function and $\xi _{1} = 1$ for TLEIC problem (1) is substantiated.

In order to verify the influence of different values of $\xi _{1}$ on the convergence performance of FCNN model (11), numerical simulations are carried out for $\xi _{1} = 5$ and $\xi _{1} = 50$, respectively. The relevant simulation results are displayed in Figs. 3 and 4.

As shown in Figs. 3a and 4a, all the state trajectories of ${\varvec{x}} (t)$ obtained by FCNN model (11) with linear activation function are within $[-0.2, 0.2]$. The state trajectories of $\bar{{\varvec{e}}}(t)$ in Figs. 3b and 4b both converge to zero. Besides, we can observe that the residual errors $J_{E}$ of FCNN model (11) with $\xi _{1} = 5$ converge to zero within the range of $0.75{\text {-}}0.85{\text {s}}$ in Fig. 3c. Similarly, in Fig. 4c, the residual errors of FCNN model (11) with $\xi _{1} = 50$ converge to zero within the range of $0.075{\text {-}}0.085{\text {s}}$. This indicates that the ${\varvec{x}}(t)$ presented in Figs. 3a and 4a simultaneously hold ${\varvec{{\mathcal {W}}}}(t){\varvec{x}}(t) = {\varvec{l}}(t)$ and ${\varvec{x}}_1 \le {\varvec{x}}(t) \le {\varvec{x}}_2$ true. Thus, the feasibility and finite-time convergence of FCNN model (11) with linear activation function for TLEIC problem (1) is substantiated again. Furthermore, the comparison of Figs. 2c, 3c and 4c shows that as the value of $\xi _{1}$ increases, the convergent rate of residual error $J_{E}$ can be improved and the convergent time can be shortened, that is, increasing $\xi _{1}$ enhances the convergence performance of the proposed FCNN model (11). Note that the value of $\xi _{1}$ should be selected appropriately for experimental or simulation purpose.

Fig. 5

Comparative results of residual errors $J_{E} = \Vert {\varvec{{\mathcal {K}}}}(t) {\varvec{z}}(t) - {\varvec{q}}(t) \Vert _2$ using the proposed FCNN model (11) and ZNN model for solving TLEIC problem (1) with different values of $\xi _{1}$ and $\beta _{1}$ when $\xi _{2} = 1$ is fixed. a $\xi _{1}=1$ and $\beta = 1$, b $\xi _{1}=5$ and $\beta = 5$, c $\xi _{1}=50$ and $\beta = 50$

5.2 Comparative Verification

For illustrate the superiority of the proposed FCNN model (11) for TLEIC problem (1), comparisons between ZNN model are stated in this subsection.

For comparison convenience, the design formula of ZNN is shown as

$$\begin{aligned} \dot{{\varvec{e}}}(t) = -\beta {\varvec{\varPhi }} \left( {\varvec{e}}(t) \right) \end{aligned}$$

and the following three activation functions is used to ZNN.

• 1) The hyperbolic-sine activation function (ZNN-h):

  $$\begin{aligned} \phi (e_{i}(t))=\frac{\exp {e_{i}(t)}-\exp {(-e_{i}(t))}}{2}. \end{aligned}$$

• 2) The linear activation function (ZNN-l):

  $$\begin{aligned} \phi (e_{i}(t))=e_{i}(t). \end{aligned}$$

• 3) The bisigmoid activation function (ZNN-bi):

  $$\begin{aligned} \phi (e_{i}(t))=\frac{1-\exp (-\alpha e_{i}(t))}{1+\exp (-\alpha e_{i}(t))}, \text{ with } \alpha >2. \end{aligned}$$

Note that $e_{i}(t)$ as the $i-$th element of ${\varvec{e}}(t)$. The relevant simulation results are displayed in Fig. 5.

Figure 5 presents the residual errors $J_{E} = \Vert {\varvec{{\mathcal {K}}}}(t) {\varvec{z}}(t) - {\varvec{q}}(t) \Vert _2$ of FCNN model (11) with linear activation function and ZNN model with above three activation functions (i.e., ZNN-h, ZNN-l, ZNN-bi). In addition, the value of $\xi _{2}$ and d/b are the same as defined in Sect. 5.1. The adjustable parameter $\xi _{1}$ and $\beta$ are simultaneously set as 1, 5, 50 in Fig. 5a, b, c, respectively. As observed in Fig. 5a, b, c, the residual errors of FCNN model (11) with linear activation function converge to zero within $3.5{\text {s}}$, $0.75{\text {s}}$ and $0.075{\text {s}}$, respectively, while at the same time, ZNN-h, ZNN-l and ZNN-bi converge slower. This comparison results indicate that the convergent time of FCNN model (11) is shorten than that of ZNN model. Furthermore, Table 1 shows the convergent accuracy of FCNN model (11) and ZNN model when residual errors converge to zero, which can be seen that the convergent accuracy of FCNN model (11) is better than that of ZNN-h, ZNN-l and ZNN-bi. Hence, the excellent convergence performance of FCNN model (11) with linear activation function as compared with ZNN-h, ZNN-l and ZNN-bi for solving TLEIC problem (1) is verified.

Table 1 Comparisons of convergent accuracy using the proposed FCNN model (11) with the ZNN model for TLEIC problem (1) solving

6 Application of FCNN Model on Redundant Manipulators

6.1 Problem Description

In this subsection, we demonstrate the application of the proposed FCNN model to trajectory planning of redundant manipulators. The corresponding inverse-kinematics problem is shown as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{J}}({\varvec{\theta }}(t)) \dot{{\varvec{\theta }}}(t)=\dot{{\varvec{r}}}_{d}(t) + f_{b}({\varvec{r}}_{d} - {\varvec{f}}({\varvec{\theta }})) \\ {\varvec{\theta }}^{-} \le {\varvec{\theta }}(t) \le {\varvec{\theta }}^{+} \\ \dot{{\varvec{\theta }}}^{-} \le \dot{{\varvec{\theta }}}(t) \le \dot{{\varvec{\theta }}}^{+} \end{array} \right. \end{aligned}$$

(27)

where ${\varvec{J}}({\varvec{\theta }}(t)) \in R^{m \times n}$ is the Jacobian matrix. ${\varvec{\theta }}(t) \in R^{n}$ is a joint-angle vector. $\dot{{\varvec{\theta }}}(t) \in R^{n}$ is a joint-velocity vector. Moreover, ${\varvec{\theta }}^{\pm } \in R^{n}$ and $\dot{{\varvec{\theta }}}^{\pm } \in R^{n}$ represents the constraints of ${\varvec{\theta }}(t)$ and $\dot{{\varvec{\theta }}}(t)$, respectively. ${\varvec{r}} _{d} \in R^{m}$ and ${\varvec{f}}({\varvec{\theta }}) \in R^{m}$ are the expected trajectory and the actual trajectory of the end effector, respectively. $f_{b}({\varvec{r}}_{d} - {\varvec{f}}({\varvec{\theta }}))$ is the feedback on the position, in which $f_{b} \in R$ (with $f_{b} > 0$) represents the feedback gain of the position.

Since the scheme (27) is established based on the velocity layer, the joint-angle constrains (i.e., ${\varvec{\theta }}^{-} \le {\varvec{\theta }}(t) \le {\varvec{\theta }}^{+}$) need to be converted into the following joint-velocity constrains [36]:

$$\begin{aligned} \varrho \left( {\varvec{\theta }}^{-}-{\varvec{\theta }}(t)\right) \le \dot{{\varvec{\theta }}} \le \varrho \left( {\varvec{\theta }}^{+}-{\varvec{\theta }}(t)\right) \end{aligned}$$

where large value of parameter $\varrho > 0$ may cause quick joint deceleration when a joint approaches its limits [5]. Then, by combining the above formula with $\dot{{\varvec{\theta }}}^{-} \le \dot{{\varvec{\theta }}}(t) \le \dot{{\varvec{\theta }}}^{+}$, the inequality constraints on $\dot{{\varvec{\theta }}}(t)$ can be transformed into

$$\begin{aligned} {\varvec{\vartheta }}^{-} \le \dot{{\varvec{\theta }}} \le {\varvec{\vartheta }}^{+} \end{aligned}$$

where the i-th element (with $i = 1, 2, \cdots , n$) in ${\varvec{\vartheta }}^{-}$ and ${\varvec{\vartheta }}^{+}$ can be expressed as

$$\begin{aligned} \begin{array}{l} \vartheta _{i}^{-} = \max \left\{ {\dot{\theta }}_{i}^{-}, \varrho \left( \theta _{i}^{-} - \theta _{i}\right) \right\} ,\\ \vartheta _{i}^{+} = \min \left\{ {\dot{\theta }}_{i}^{+}, \varrho \left( \theta _{i}^{+}-\theta _{i}\right) \right\} . \end{array} \end{aligned}$$

Furthermore, scheme (27) can be re-written as

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{J}}({\varvec{\theta }}(t)) \dot{{\varvec{\theta }}}(t)=\dot{{\varvec{r}}}_{d}(t) + f_{b} ({\varvec{r}}_{d} - {\varvec{f}}({\varvec{\theta }})) \\ {\varvec{\vartheta }}^{-} \le \dot{{\varvec{\theta }}} \le {\varvec{\vartheta }}^{+} \end{array} \right. \,. \end{aligned}$$

(28)

Considering the TLEIC problem (1) described in Sect. 2, which is similar to the form of scheme (28). That is, ${\varvec{\theta }}(t)$ corresponds to ${\varvec{x}}(t)$, ${\varvec{J}}({\varvec{\theta }}(t))$ corresponds to ${\varvec{{\mathcal {W}}}}(t)$, $\dot{{\varvec{r}}}_{d}(t) + f_{b} ({\varvec{r}}_{d} - {\varvec{f}}({\varvec{\theta }}))$ corresponds to ${\varvec{l}}(t)$, ${\varvec{\vartheta }}^{-}$ and ${\varvec{\vartheta }}^{+}$ correspond to ${\varvec{x}}_{1}$ and ${\varvec{x}}_2$ respectively. Hence, the FCNN model (11) proposed in this paper can be used to solve scheme (28) with

$$\begin{aligned} \begin{aligned} {\varvec{G}}(t)&= \left[ \begin{array}{cc} {\varvec{J}}({\varvec{\theta }}(t)) &{} {\varvec{0}} \\ {\varvec{U}} &{} 2{\varvec{V}}(t) \end{array} \right] , ~{\varvec{H}}(t) = \left[ \begin{array}{cc} \dot{{\varvec{J}}}({\varvec{\theta }}(t)) &{} {\varvec{0}} \\ {\varvec{0}} &{} {\varvec{0}} \end{array} \right] , \\ {\varvec{{\mathcal {K}}}}(t)&= \left[ \begin{array}{cc} {\varvec{J}}({\varvec{\theta }}(t)) &{} {\varvec{0}} \\ {\varvec{U}} &{} {\varvec{V}}(t) \end{array} ~\right] , ~~~{\varvec{z}}(t) = \left[ \begin{array}{cc} \dot{{\varvec{\theta }}}(t) \\ {\varvec{s}}(t) \end{array} \right] , \\ {\varvec{q}}(t)&= \left[ \begin{array}{cc} \dot{{\varvec{r}}}_{d}(t) + f_{b} ({\varvec{r}}_{d} - {\varvec{f}}({\varvec{\theta }})) \\ {\varvec{c}} \end{array} \right] . \end{aligned} \end{aligned}$$

To further illustrate the practical feasibility of the FCNN model (11), FCNN model (11) will be applied to the six-degree-of-freedom (six-DOF) planar manipulator and PUMA560 redundant manipulator.

Fig. 6

Computational results of six-DOF planar manipulator tracking circular trajectory with joint-angle constrains and joint-velocity constrains by the FCNN model (11) with $\xi _{1} =100$ and $\xi _{2} = 1$ under linear activation function. a Motion trajectory of the six-DOF planar manipulator, b End-effector trajectory, c End-effector tracking errors, d Trajectories of joint-angle, e Trajectories of joint-velocity

6.2 Six-DOF Planar Manipulator

In this simulation, the proposed FCNN model (11) with $\xi _{1} = 100$ and linear activation function is applied to the circular trajectory planning of the six-DOF planar manipulator with joint constraints. Other adjustable parameters $\xi _{2} = 1$, $d/b = 5/7$ and $f_{b} = 1$ in FCNN model (11). The initial joint-angles is set to ${\varvec{\theta }}(0) = [\pi /4; \pi /4; \pi /4; \pi /4; \pi /4; \pi /4]$. In addition, the specific upper and lower bounds of ${\varvec{\theta }}(t)$ and $\dot{{\varvec{\theta }}}(t)$ (i.e., $\theta ^{\pm }_{i}$ and ${\dot{\theta }}^{\pm }_{i}$) are given in Table 2. The entire period of motion in this simulation is $10{\text {s}}$. The relevant simulation results are displayed in Fig. 6.

Figure 6a presents the motion trajectory of the six-DOF planar manipulator tracking the circular trajectory. Figure. 6b shows the desired trajectory and the actual trajectory of the end-effector. As we can see from Fig. 6a, b, the actual trajectory of the end-effector coincides with the desired circular trajectory. In Fig. 6c, the tracking errors (i.e., $\varepsilon {\varvec{X}}$, $\varepsilon {\varvec{Y}}$) of the end-effector of six-DOF planar manipulator is shown. It can be seen that the maximum tracking error is not more than $3\times 10^{-5} {\text {m}}$. This illustrates that the end-effector of six-DOF planar manipulator can successfully track the desired circular trajectory with a small error. Furthermore, Fig. 6d, e show the state trajectories of ${\varvec{\theta }}(t)$ and $\dot{{\varvec{\theta }}}(t)$ of six-DOF planar manipulator. The maximum and minimum values of each ${\varvec{\theta }}(t)$ (i.e., $\max \theta _{i}$ and $\min \theta _{i}$) and $\dot{{\varvec{\theta }}}(t)$ (i.e., $\max {\dot{\theta }}_{i}$ and $\min {\dot{\theta }}_{i}$) are listed in Table 2. It can be seen that the maximum and minimum values of ${\varvec{\theta }}(t)$ and $\dot{{\varvec{\theta }}}(t)$ of the six-DOF planer manipulator are kept within the given joint constraints. In conclusion, these results verify the effectiveness of FCNN model (11) to the trajectory planning of the six-DOF planar manipulator with joint constraints. This further illustrates the capability of the proposed FCNN.

Table 2 Joint constrains used in the simulation of the six-DOF planar manipulator and the minimum and maximum of joint variables obtained by the FCNN model (11)

Fig. 7

Computational results of PUMA560 redundant manipulator tracking octagon trajectory with joint-angle constrains and joint-velocity constrains by the FCNN model (11) with $\xi _{1} =100$ and $\xi _{2} = 1$ under linear activation function. a Motion trajectory of the PUMA560 redundant manipulator, b End-effector trajectory, c End-effector tracking errors, d Trajectories of joint-angle, e Trajectories of joint-velocity

Table 3 Joint limits used in the simulation of the PUMA560 redundant manipulator and the minimum and maximum of joint variables obtained by the FCNN model (11)

Fig. 8

Comparative results of residual errors $J_{E} = \Vert {\varvec{{\mathcal {K}}}}(t) {\varvec{z}}(t) - {\varvec{q}}(t) \Vert _2$ using the proposed FCNN model (11) and ZNN model for trajectory planning of manipulator with joint limitations. a Residual errors in six-DOF planar redundant manipulator, b Residual errors in PUMA560 redundant manipulator

6.3 PUMA560 Redundant Manipulator

In this simulation, the proposed FCNN model (11) with $\xi _{1} = 100$ and linear activation function is applied to the octagon trajectory planning of the PUMA560 redundant manipulator with joint constraints, where the length of the octagon is 1. The values of $\xi _{2}$, d/b and $f_{b}$ are the same defined as Sect. 6.1. The initial joint-angles is set to ${\varvec{\theta }}(0) = [\pi /4; 0; 0; -\pi /4; \pi /4;-\pi /4]$. In addition, the limitations of joint-angles and joint-velocities (i.e., $\theta ^{\pm }_{i}$ and ${\dot{\theta }}^{\pm }_{i}$) are given in Table 3. Note that the entire period of motion in this simulation is $8{\text {s}}$. The relevant simulation results are displayed in Fig. 7.

Figure 7a presents the movement trajectory of the PUMA560 redundant manipulator. Figure 7b shows the actual motion trajectory and the expected octagonal trajectory of the end-effector. As can be seen from these two figures, the actual trajectory of the end-effector coincides with the desired octagonal trajectory. As observed in Fig. 7c, the maximum tracking error of the end-effector of PUMA560 redundant manipulator, i.e., max{$\varepsilon {\varvec{X}}$, $\varepsilon {\varvec{Y}}$, $\varepsilon {\varvec{Z}}$}, is less than $3.1\times 10^{-5}{\text {m}}$, which further verifies that the end-effector can successfully track the expected octagonal trajectory with minimal error. Subsequently, Figs. 7d, e show the state trajectories of ${\varvec{\theta }}(t)$ and $\dot{{\varvec{\theta }}}(t)$ of PUMA560 redundant manipulator. The maximum and minimum values of each ${\varvec{\theta }}(t)$ (i.e., $\max \theta _{i}$ and $\min \theta _{i}$) and $\dot{{\varvec{\theta }}}(t)$ (i.e., $\max {\dot{\theta }}_{i}$ and $\min {\dot{\theta }}_{i}$) are listed in Table 3. It can be seen that the ${\varvec{\theta }}(t)$ and $\dot{{\varvec{\theta }}}(t)$ in the PUMA560 redundant manipulator during movement are kept within the given joint constraints. In summary, these simulation results verify the effectiveness and practicability of FCNN model (11) for solving the trajectory planning problem of PUMA560 redundant manipulator with joint constraints.

To illustrate the excellent convergence performance of FCNN model (11), the residual errors $J_{E} = \Vert {\varvec{{\mathcal {K}}}}(t) {\varvec{z}}(t) - {\varvec{q}}(t) \Vert _2$ using FCNN model (11) with linear activation function and ZNN model with three activation functions (i.e., ZNN-h, ZNN-l, ZNN-bi) are carried out in Fig. 8. Note that the ZNN-h, ZNN-l and ZNN-bi are defined in Sect. 5. In addition, the adjustable parameter of $\beta$ is set as 100 in ZNN model. Figure 8a presents the residual errors $J_{E}$ of FCNN model (11) and ZNN model for the circular trajectory planning of six-DOF planar manipulator with joint constraints is shown. Figure 8b shows the residual errors for the octagon trajectory planning of the PUMA560 redundant manipulator with joint constraints. From these two figures, it can be seen that the residual errors $J_{E}$ of FCNN model (11) converge to zero within $0.04{\text {s}}$ and $0.048{\text {s}}$, respectively, while the convergent rate of ZNN-h, ZNN-l and ZNN-bi is slower at $t=0.04{\text {s}}$ and $t=0.048{\text {s}}$. These results illustrate that FCNN model (11) can solve the trajectory planning problem of manipulator with joint constraints in finite time, and the convergence performance of FCNN model (11) is better than that of ZNN-h, ZNN-l and ZNN-bi.

Above all, the conclusions obtained from the simulation results in Figs. 6, 7 and 8 can be summarized as follows:

• 1. The effectiveness and availability of FCNN model (11) for the trajectory planning of redundant manipulator with joint constraints is verified.

• 2. The convergence performance of FCNN model (11) with linear activation function is superior to ZNN model with hyperbolic activation function, linear activation function and bipolar sigmoid activation function for the trajectory planning of redundant manipulators with joint constraints.

7 Conclusion

For finding the solution of TLEIC, a FCNN model has been proposed in this paper. Specifically, by introducing a non-negative slack variable, the TLEIC is transformed into a class of time-varying linear equations. Then, the proposed FCNN model is used to solve the transformed equations. By using the Lyapunov stability theorem, the stability of the FCNN model (11) is proved concretely. Meanwhile, the convergent time of the FCNN model (11) with linear activation function is calculated, which proves its finite-time convergence. Compared with the ZNN model with three kinds of activation functions (i.e., ZNN-h, ZNN-l and ZNN-bi) in numerical simulation, the convergent speed, convergent time and convergent accuracy of the FCNN model (11) are significantly improved in solving TLEIC problem (1). Finally, the effectiveness and feasibility of the FCNN model (11) are further demonstrated through its application to two types of redundant manipulator with joint constraints. Further work may lie in the application of FCNN model (11) to a practical redundant manipulator, and the discrete-time form of the FCNN model (11) will be studied to solve the TLEIC.