1 Introduction

Support vector machine (SVM) [5, 27, 28] has been an excellent tool for classification and regression over the past decade as a modern machine learning approach, which enjoys strong theoretical foundations and successes in many real-world applications.

Although SVM owns better generalization classification ability compared with other machine learning methods like artificial neural network (ANN), its training cost is expensive, i.e., O(n 3), where n is the total size of training data. So far, many fast algorithms have been presented. Traditionally, SVM is trained by using decomposition techniques such as SMO [13, 23] , chunking [21], \(\hbox{SVM}^{\rm light}\) [11], and LIBSVM [3], which solve the dual problems by optimizing a small subset of the variables each iteration. Another kind of fast algorithm is the least squares SVM which was proposed by using equality constraints instead of inequality constraints [25]. All the above classifiers discriminate a sample by determining in which half space it lies. Mangasarian and Wild [19] first proposed a classification method named generalized eigenvalue proximal support vector machine (GEPSVM) by the proximity of the data to one of two nonparallel planes. Then Jayadeva, Khemchandani, and Chandra [10], proposed a twin support vector machine (TWSVM) classifier for classification in the spirit of GEPSVM. The formulation of TWSVM is very much similar to a classical SVM except that it aims at generating two nonparallel planes such that each plane is closer to one class and as far as possible from the other. TWSVM has become one of the popular methods because of its low computational complexity, see e.g. [8, 9, 15, 16].

As for support vector regression (SVR), there exist some corresponding fast algorithms such as SMO [24], LSSVR [26], smooth SVR [18], geometric method [1], heuristic training [29], and so on. All those methods for SVR have at least two groups of constraints, each of which ensures that more training samples locate within the given \(\epsilon\)-insensitive tube as far as possible. Recently, Peng [22] proposed a twin support vector regression (TSVR) in the spirit of TWSVM. The TSVR aims at generating two functions such that each one determines the \(\epsilon\)-insensitive down- or up-bound of the unknown regressor. For this purpose, it solves two smaller-sized quadratic programming problems (QPPs) instead of solving a large one as in the usual SVR. Although TSVR achieves good performance, it is less robust because the square of the 2-norm distance of the residuals is sensitive to the large errors. This fact motivates us to formulate TSVR as two linear programming problems by using the 1-norm distance. In order to distinguish our algorithm with that in [22], we term our algorithm as LPTSVR (linear programming TSVR) and the algorithm in [22] as QPTSVR (quadratic programming TSVR). The use of 1-norm distance in the LPTSVR as opposed to the square of the 2-norm in the QPTSVR leads to the robustness, which makes the LPTSVR own the better generalization ability. Further, the LPTSVR allows us to solve twin linear programs as opposed to twin quadratic programs in the QPTSVR. We conclude results in Sect. 5, which demonstrate that linear programs are much more computationally efficient than quadratic programs.

The outline of the paper is as follows. A brief introduction of SVRs is given in Sect. 2. Section 3 presents the LPTSVR, and we extend it to the nonlinear cases in Sect. 4. In Sect. 5, the performance of the LPTSVR is compared with other SVRs. Section 6 concludes the paper.

2 Brief introduction of SVRs

2.1 The SVR

Let the learning samples to be denoted by a set of row vectors A i \((i=1,\ldots,n)\), where \(A_i=(x_{i1},x_{i2},\ldots,x_{id})\). Let \(A=[A_1;A_2;\ldots;A_n]\) represent the vertical concatenation of the vectors A i . Let \(Y=[y_1;y_2;\ldots;y_n]\) denote the response vector of training data points.

The SVR seeks to estimate a linear function \(f(\user2{x})=\user2{w}^{\top}\user2{x}+b\) that tolerates a small error in fitting the given learning data, where \({\user2{w}\in {\mathbb{R}}^d}\) and \({b\in \mathbb{R}}\). This can be obtained by using the \(\epsilon\)-insensitive loss function, and any error smaller than \(\epsilon\) is ignored. Applying the idea of SVM, the function \(f(\user2{x})\) is made as flat as possible. The SVR can be formulated as the following QPP:

$$ \begin{array}{lll} \hbox{min} && \frac{1}{2}\user2{w}^{\top}\user2{w}+C(\user2{e}^{\top}{\varvec{\xi}}_1+\user2{e}^{\top}{\varvec{\xi}}_2)\\ \hbox{s.t.}&& Y-(A\user2{w}+\user2{e}b)\leq \epsilon\user2{e}+ {\varvec{\xi}}_1,\quad {\varvec{\xi}}_1\geq {\bf 0},\\ &&(A\user2{w}+\user2{e}b)-Y\leq \user2{e}\epsilon+{\varvec{\xi}}_2,\quad {\varvec{\xi}}_2\geq {\bf 0},\\ \end{array} $$
(1)

where C > 0 is the regularization parameter that balances the tradeoff between the fitting errors and the flatness of the function, \({{\varvec{\xi}}}_1\) and \( {{\varvec{\xi}}}_2\) are the slack vectors reflecting whether the samples locate into the \(\epsilon\)-tube or not, \(\user2{e}\) is the vector of ones of appropriate dimensions. The solution of (1) can be obtained by finding the saddle point of the Lagrange function. Then, the decision function is of the form

$$ f(\user2{x})=\sum_{i=1}^n (\alpha_{i}^{*}-\alpha_i)\user2{x}_i^{\top}\user2{x}+b, $$
(2)

where \({\varvec{\alpha}}, {\varvec{\alpha}}^{*}\) are Lagrange multipliers that satisfy \({\varvec{\alpha}}_i{\varvec{\alpha}}_{i}^{*}=0, \;i=1,\ldots,n.\)

The complexity of solving the dual QPP is O(n 3). As the number of training samples increases, the time needed to train the SVR estimator also increases.

2.2 The LSSVR

Recall that the SVR requires large training time as the training samples increase, Suyken et al. [26] proposed the least squares version of SVR termed as LSSVR to improve it. The formulation of LSSVR is as follows:

$$ \begin{array}{lll} \hbox{min}&& \frac{1}{2}\user2{w}^{\top}\user2{w}+\frac{C}{2}{\varvec{\xi}}^{\top}{\varvec{\xi}}\\ \hbox{s.t.}&& Y=A\user2{w}+\user2{e}b+ {\varvec{\xi}}. \end{array} $$
(3)

LSSVR finds the regression function by solving a set of n linear equations. Its computational complexity depends on the algorithm used for its solution. For example, the Gaussian elimination technique leads to a complexity of O(n 3), whereas for the conjugate gradient method, it is less than O(n 3). In comparison with the SVR, the LSSVR is not sparseness. In addition, it is less robust because of the sensitivity of sum squared error. In recent years, considerable attentions have been paid to these limitations, see e.g., [12, 14, 17, 30, 31].

2.3 The QPTSVR

The QPTSVR aims at finding two functions

$$ f_1(\user2{x})=\user2{w}_1^{\top}\user2{x}+b_1, \quad f_2(\user2{x})=\user2{w}_2^{\top}\user2{x}+b_2, $$
(4)

such that each function determines one of the \(\epsilon\)-insensitive down- or up-bound regressor. It is obtained by solving the following pair of QPPs

$$ \begin{array}{lll} \hbox{min}&& \frac{1}{2}(Y-\user2{e}\epsilon_1-(A\user2{w}_1+\user2{e}b_1))^{\top}(Y-\user2{e}\epsilon_1-(A\user2{w}_1+\user2{e}b_1))+C_1\user2{e}^{\top}{\varvec{\xi}}_1\\ \hbox{s.t.} &&Y-(A\user2{w}_1+\user2{e}b_1)\geq \user2{e}\epsilon_1-{\varvec{\xi}}_1,\quad {\varvec{\xi}}_1\geq {\bf 0}, \end{array} $$
(5)
$$ \begin{array}{lll} \hbox{min}&& \frac{1}{2}(Y+\user2{e}\epsilon_2-(A\user2{w}_2+\user2{e}b_2))^{\top}(Y+\user2{e}\epsilon_2-(A\user2{w}_2+\user2{e}b_2))+C_2\user2{e}^{\top}{\varvec{\xi}}_2\\ \hbox{s.t.} &&(A\user2{w}_2+\user2{e}b_2)-Y\geq \user2{e}\epsilon_2-{\varvec{\xi}}_2,\quad {\varvec{\xi}}_2\geq {\bf 0}, \end{array} $$
(6)

where C 1 and C 2 > 0 are regularization parameters. The end regressor is decided by the mean of these two functions:

$$ f(\user2{x})=\frac{1}{2}(f_1(\user2{x})+f_2(\user2{x}))=\frac{1} {2}(\user2{w}_1+\user2{w}_2)^{\top} \user2{x}+\frac{1}{2}(b_1+b_2). $$
(7)

The QPTSVR is comprised of a pair of QPPs such that each QPP determines the one of up- or down-bound function by using only one group of constraints compared with the standard SVR. Hence, the QPTSVR gives rise to two smaller-sized QPPs. As TWSVM, the QPTSVR is approximately four times faster than the SVR in theory.

3 The LPTSVR

Notice that the first term in the objective function of (5) or (6) is the sum of squared distances from the shifted function \(y=\user2{w}_1^{\top}\user2{x}+b_1+\epsilon_1\) or \(y=\user2{w}_2^{\top}\user2{x}+b_2-\epsilon_2\) to the training points. That is, the residuals between the real values and the predicted values are penalized by the square of the 2-norm, which is sensitive to the large errors. By replacing the square of the 2-norm \( \|Y-\user2{e}\epsilon_1-(A\user2{w}_1+\user2{e}b_1)\|^2_2 \) or \(\|Y+\user2{e}\epsilon_2-(A\user2{w}_2+\user2{e}b_2)\|^2_2\) in the quadratic program (5) or (6) with the 1-norm \( \|Y-\user2{e}\epsilon_1-(A\user2{w}_1+\user2{e}b_1)\|_1 \) or \(\|Y+\user2{e}\epsilon_2-(A\user2{w}_2+\user2{e}b_2)\|_1\), we obtain the LPTSVR as follows.

$$ \begin{array}{lll} \hbox{min}&& \nu_1\user2{e}^{\top}{\varvec{\xi}}_1+\|Y-\user2{e}\epsilon_1-(A\user2{w}_1+\user2{e}b_1)\|_1\\ \hbox{s.t.} &&Y-(A\user2{w}_1+\user2{e}b_1)\geq \user2{e}\epsilon_1-{\varvec{\xi}}_1,\quad {\varvec{\xi}}_1\geq {\bf 0}, \end{array} $$
(8)
$$ \begin{array}{lll} \hbox{min}&& \nu_2\user2{e}^{\top}{\varvec{\xi}}_2+\|Y+\user2{e}\epsilon_2-(A\user2{w}_2+\user2{e}b_2)\|_1\\ \hbox{s.t.} &&(A\user2{w}_2+\user2{e}b_2)-Y\geq \user2{e}\epsilon_2-{\varvec{\xi}}_2,\quad {\varvec{\xi}}_2\geq {\bf 0}, \end{array} $$
(9)

where ν1 and ν2 > 0 are regularization parameters. The slack vector \({\varvec{\xi}}_1\) or \({\varvec{\xi}}_2\) is introduced to measure the error wherever the distance is closer than \(\epsilon_1\) or \(\epsilon_2\).

We note that the term \(\|Y-\user2{e}\epsilon_1-(A\user2{w}_1+\user2{e}b_1)\|_1\) in (8) or \(\|Y+\user2{e}\epsilon_2-(A\user2{w}_2+\user2{e}b_2)\|_1\) in (9) is easily converted to a linear term \(\user2{e}^{\top}\user2{s}\) with the added constraint \(-\user2{s}\leq Y-\user2{e}\epsilon_1-(A\user2{w}_1+\user2{e}b_1)\leq \user2{s}\) or \(-\user2{s}\leq Y+\user2{e}\epsilon_2-(A\user2{w}_2+\user2{e}b_2)\leq \user2{s}\). Hence, the LPTSVR allows us to solve twin linear programs as opposed to quadratic programs. Further, the 1-norm distance is less sensitive to large errors. The use of 1-norm distance in the LPTSVR as opposed to the square of the 2-norm in the QPTSVR leads to the robustness to large noises.

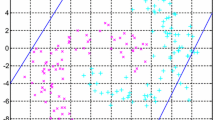
As a toy example, for data generated by \(y_i=x_i+\eta_i\) with x i being simulated uniformly in [0,1] and η being Gaussian noise N (0,0.012), we calculated the final regressors by the QPTSVR and the LPTSVR, respectively. For simplicity, we set \(\epsilon_1=\epsilon_2=0\). Moreover, we added large noises in the dataset to test the robustness of the two methods. Results are shown in Fig. 1. We can see from the plots that for the dataset without large noises, these two regressors almost overlap. However, for the dataset with large noises, the regressor calculated by the QPTSVR is drawn toward noises, while the regressor calculated by the LPTSVR is robust to noises.

Fig. 1
figure 1

Predictions of the QPTSVR with \(C_1=C_2=2^{-2}\) and the LPTSVR with \(\nu_1=\nu_2=2^{-2}.\) The left graph shows the regressors calculated on the dataset without large noises. In the right graph, the regressors are calculated on the dataset with large noises

Full size image

4 Kernelizing LPTSVR

In order to extend the linear LPTSVR to the nonlinear case, we consider the following kernel-generated functions instead of linear functions.

$$ f_1(\user2{x})=K(\user2{x}^{\top}, A^{\top})\user2{u}_1+b_1,\; f_2(\user2{x})=K(\user2{x}^{\top}, A^{\top})\user2{u}_2+b_2, $$
(10)

where \(K(\cdot, \cdot)\) is a kernel representing the inner product in the feature space \({\mathbb{H}}\), i.e., \(K(\user2{u}^{\top}, \user2{v})=\varphi(\user2{u})^{\top}\varphi(\user2{v})\) with \(\varphi(\cdot)\) being a nonlinear map from the input space R d into the feature space \({\mathbb{H}}\). We use \(K(A, B^{\top})\) to denote the kernel matrix with \(K_{ij}=K(A_i, B^{\top}_j)\).

We note that the linear functions (4) are recovered from (10) if we use the linear kernel \(K(\user2{x}^{\top}, A^{\top})=\user2{x}^{\top}A^{\top}\) and define \(\user2{w}_1=A^{\top}\user2{u}_1\) or \(\user2{w}_2=A^{\top}\user2{u}_2\). With this nonlinear kernel formulations, the mathematical programs for generating the nonlinear regressor become the following, upon kernelizing (8) and (9):

$$ \begin{array}{lll} \hbox{min}&& \nu_1\user2{e}^{\top}{\varvec{\xi}}_1+\user2{e}^{\top}\user2{s}_{1}\\ \hbox{s.t.}&&-\user2{s}_{1}\leq Y-\user2{e}\epsilon_1-(K(A, A^{\top})\user2{u}_1+\user2{e}b_1)\leq \user2{s}_1,\\ &&Y-(K(A, A^{\top})\user2{u}_1+\user2{e}b_1)\geq \user2{e}\epsilon_1-{\varvec{\xi}}_1, \\ && {\varvec{\xi}}_1\geq {\bf 0}, \end{array} $$
(11)
$$ \begin{array}{lll} \hbox{min}&& \nu_2\user2{e}^{\top}{\varvec{\xi}}_2+\user2{e}^{\top}\user2{s}_{2}\\ \hbox{s.t.}&& -\user2{s}_2\leq Y+\user2{e}\epsilon_2-(K(A,A^{\top})\user2{u}_2+\user2{e}b_2)\leq \user2{s}_2,\\ &&(K(A,A^{\top})\user2{u}_2+\user2{e}b_2)-Y\geq \user2{e}\epsilon_2-{\varvec{\xi}}_2,\\ && {\varvec{\xi}}_2\geq {\bf 0}. \end{array} $$
(12)

5 Experiments and discussion

To demonstrate the validity of the proposed LPTSVR, we compared it with the LSSVR and the QPTSVR on a collection of datasets, including a group of artificial datasets and seventeen benchmark datasets. All the regression methods were implemented on a PC with AMD 3600+(2.00 GHz) processor, 512 MB memory in Matlab 7.0 environment. As the machine learning tools, the performances of these algorithms depend on the choices of parameters. In our experiments, we set \(\nu_1=\nu_2\) and \(\epsilon_1=\epsilon_2\) in the LPTSVR, \(C_1=C_2\) and \(\epsilon_1=\epsilon_2\) in the QPTSVR to degrade the computational complexity of parameter selection. In order to evaluate the performance of the algorithms, the evaluation criteria are specified before presenting the experimental results. Let N be the number of testing samples, y i and \(\hat{y}_i\) be the real value and predicted value of sample \(\user2{x}_i\), respectively. Denote \(\bar{y}=\frac{1}{N}\sum_{i=1}^{N}y_i\) as the average value of \(y_1,\ldots, y_N\). We use the following criteria for algorithm evaluation.

  • RMSE: Root mean squared error, which is defined as \(\hbox{RMSE}=\sqrt{\frac{1}{N}\sum_{i=1}^{N}(\hat{y}_i-y_i)^2}\). It is commonly used as the deviation measurement between the real and predicted values. RMSE represents the fitting precision; the smaller RMSE is, the fitter the estimation is. However, when noises are also used as testing samples, too small value of RMSE probably speaks for overfitting of the regressor.

  • MAE: Mean absolute error, which is defined as \(\hbox{MAE}=\frac{1}{N}\sum_{i=1}^{N}|\hat{y}_i-y_i|\). MAE is also a popular deviation measurement between the real and predicted values.

  • SSE/SST [22]: Ratio between the sum squared error \(\hbox{SSE}=\sum_{i=1}^N (\hat{y}_i-y_i)^2\) and the sum squared deviation of testing samples \(\hbox{SST}=\sum_{i=1}^N (y_i-\bar{y})^2\). SSE is in fact a variant of RMSE. SST reflects the underlying variance of the testing samples. In most cases, small SSE/SST means good agreement between estimations and real values.

  • SSR/SST [22]: Ratio between interpretable sum squared deviation \(\hbox{SSR}=\sum_{i=1}^N (\hat{y}_i-\bar{y})^2\) and SST. SSR reflects the explanation ability of the regressor. The larger SSR is, the more statistical information it catches from testing samples. To obtain smaller SSE/SST usually accompanies an increase in SSR/SST. However, the extremely small value of SSE/SST is in fact not good, for it probably means overfitting of the regressor. Therefore, a good estimator should strike balance between SSE/SST and SSR/SST.

To compare the CPU time and accuracies of three algorithms, we used “quadprog.m” function to realize the QPTSVR and the “inv.m” function to implement the LSSVR. For the LPTSVR, we first applied the “linprog.m” function in Matlab to realize it. We found that the LPTSVR needed less time on moderate and large-scale datasets. However, for the small-scale datasets, it was not the case. In order to improve the speed, we employed Newton method for 1-norm SVM in [20] to speed up it. In addition, we normalized the training data into the closed span [0,1] and mapped back to the original space when we calculate accuracies of algorithms.

5.1 Artificial datasets

The regressions of sinc function \(y=\frac{\hbox{sin} \pi x}{\pi x}, \quad x\in [-5, 5]\) were tested to reflect the performance of the LPTSVR. Training data points were perturbed by some different kinds of noises, which include the Gaussian noises and the uniformly distributed noises. Specially, the following kinds of training samples \((x_i, y_i), i=1,\ldots, n\) were generated:

$$ y_i=\frac{\hbox{sin}\pi x_i}{\pi x_i}+\eta_i, \quad x\sim U[-5, 5],\quad \eta_i \sim N(0,0.15^2), $$
(13)
$$ y_i=\frac{\hbox{sin} \pi x_i}{\pi x_i}+\eta_i, \quad x\sim U[-5, 5],\quad \eta_i\sim N(0,0.3^2), $$
(14)
$$ y_i=\frac{\hbox{sin} \pi x_i}{\pi x_i}+\eta_i, \quad x\sim U[-5, 5],\quad \eta_i\sim U[0,0.15], $$
(15)
$$ y_i=\frac{\hbox{sin} \pi x_i}{\pi x_i}+\eta_i, \quad x\sim U[-5, 5],\quad \eta_i\sim U[0,0.3], $$
(16)

where N (0,d 2) represents the Gaussian random variable with zero means and variance d 2, and U[a, b] represents the uniformly random variable in [a, b].

In order to avoid of biased comparisons, for each kind of noises, we randomly generated ten independent groups of noisy samples which respectively consists of 350 training samples and 500 test samples. The test data are uniformly sampled from the objective sinc function without any noise. Table 1 shows the average accuracies of the LPTSVR, QPTSVR, and LSSVR with ten independent runs, in which types I, II, III, and IV represent the four different types of noises (13–16). It has been shown that the LPTSVR obtains the smallest RMSE and MAE among the three algorithms for three types of noises (types I, II, and IV). This indicates that the LPTSVR is robust to noises. Besides, the LPTSVR derives the smallest SSE/SST values for the first two types of noises and the largest SSR/SST values for the last two types of noises. Table 1 also compares the training time for these three algorithms. It has been shown that the LSSVR is the fastest learning method among them, whereas the LPTSVR is faster than the QPTSVR.

Table 1 Comparisons of LSSVR, QPTSVR, and LPTSVR on Sinc datasets with different types of noises
Full size table

5.2 Benchmark datasets

For further evaluation, we tested seventeen real-world benchmark datasets, including Boston Housing (BH), AutoMPG, Servo, Pyrimidines (Pyrim), Triazines, Concrete Slump (Con. S) from UCI repository [2], Concrete Compressive Strength (Con. CS), Pollution, Bodyfat from StatLib databaseFootnote 1, AutoPrice, Machine CPU (MCPU), Wisconsin Breast Cancer (Wis. BC), Diabetes from http://www.liaad.up.pt/~ltorgo/Regression/DataSets.html, MgFootnote 2, Chwirut1Footnote 3, OzoneFootnote 4, and Titanium Heat (TH) [6]. The Concrete Slump dataset has three output features. In our experiments, we merely used slump feature as the output.

First, we make the linear kernel comparisons of the LPTSVR, LSSVR, and QPTSVR. We evaluated the regression accuracy using 10-fold cross-validation. The optimal \(\epsilon\) values for the LPTSVR and QPTSVR were searched in the range {0.001, 0.01, 0.1, 0.2}, and the optimal regularization parameters C (or ν) for the three algorithms were selected over the range \(\{2^i|i=-7,\ldots,7\}\). Table 2 lists the experimental results of the three algorithms on fifteen benchmark datasets. It consists of the mean values of RMSE, MAE, SSE/SST, SSR/SST on each dataset, the standard deviation values of the four measures on each dataset, the computation time, and the optimal parameter values.

Table 2 Results of LSSVR (I), QPTSVR (II), and LPTSVR (III) on benchmark datasets with linear kernel
Full size table

Since the Friedman test with the corresponding post hoc tests is pointed out to be a simple, safe, and robust nonparametric test for comparison of more classifiers over multiple datasets [7], we use it to compare the performance of the three algorithms. Table 3 illustrates the average ranks of the three algorithms on RMSE, MAE, SSE/SST, and SSR/SST values. The computational process of the average rank of the three algorithms on RMSE values is shown in "Appendix" section as an example. First, we compare the RMSE performance of the three algorithms. We employ the Friedman test to check whether the measured average ranks are significantly different from the mean rank \(R_j\,=\,2\) expected under the null hypothesis:

$$ \begin{aligned} \chi^2_{F}&=\frac{12\times 15}{3\times 4}\left[(2.167^2+2.433^2+1.4^2)-\frac{3\times 4^2} {4}\right]=8.6307\\ F_{F}&=\frac{14\times 8.6307}{15\times 2- 8.6307}=5.6544 \end{aligned} $$

With three algorithms and 15 datasets, F F is distributed according to the F distribution with (2,28) degrees of freedom. The critical value of F(2,28) for \(\alpha\,=\,0.05\) is 3.340, so we reject the null hypothesis. We use the Nemenyi test for further pairwise comparison. According to [7], at \(p\,=\,0.10\), CD is \(2.052\sqrt{\frac{3\cdot4}{6\cdot 15}}=0.7493\). Since the difference between the LPTSVR and the QPTSVR is larger than 0.7493 (2.433 − 1.4 = 1.033 > 0.7493), we can identify that the performance of the LPTSVR is better than that of the QPTSVR. In the same way, we see that the performance of the LPTSVR is better than that of the LSSVR (2.167 − 1.4 = 0.767 > 0.7493). Similarly, we obtain that the F F value on MAE is 3.8160, which is larger than the critical value 3.340, so we reject the null hypothesis. From Table 3, we see that the LPTSVR performs significantly better than the QPTSVR (2.3 − 1.467 = 0.833 > 0.7493) and the LSSVR (2.233 − 1.467 = 0.766 > 0.7493). The F F value on SSE/SST is 1.5751, which is smaller than the critical value 3.340 (or 2.503, which is the critical value of F(2,28) for α = 0.10), so there is no significant difference between the three algorithms. For SSR/SST, the F F value is 3.3081 which is larger than 2.503, so we reject the null hypothesis. By the further post hoc test, we conclude that the performance of the QPTSVR is better than that of the LPTSVR.

Table 3 Average ranks of LSSVR, QPTSVR, and LPTSVR with linear kernel
Full size table

As for the computation time, the LSSVR spends on the least CPU time among the three algorithms, while the LPTSVR needs the less CPU time than the QPTSVR.

For the nonlinear case, the RBF kernel \(k(\user2{x}, \user2{z})=\exp(-\|\user2{x}-\user2{z}\|^2/\gamma)\) was chosen for all algorithm training. As the machine learning tools, the performance of algorithms seriously depends on the choice of parameters. As we know, the conventional exhaustive grid search method is prohibitively performed. So we take a simple variant instead, which may not find the same hyper-parameters as the traditional search method, but it can be very easily and efficiently implemented. In the experiments, we utilized the initial points \((C_0, \gamma_0),\,(C_0, \epsilon_0, \gamma_0)\) and \((\nu_0, \epsilon_0, \gamma_0)\) as the starting points for the LSSVR, QPTSVR, and LPTSVR, respectively. Then, we search the local optimal values. During the search process, when we find the optimal value for one parameter step by step, other parameters are fixed. From Ref. [4], we know that γ is a more important parameter compared to others. So we first fixed C (or ν) and \(\epsilon\) to search the optimal value for γ. As for the initial point, we may employ some techniques [4] to estimate it, but the computational complexity is expensive. Hence, we used the fixed point, say \(C_0 (or \nu_0)=2^{-3}, \epsilon_0=0.001, \gamma_0=2^{-3}\), as the initial point instead. The parameter γ was selected over the range \(\{2^i|i=-4,-3,\ldots,7\},\,C\) or ν was searched in the range \(\{2^i|i=-4,-3,\ldots,7\}\), and \(\epsilon\) was selected from the set {0.001, 0.01, 0.1, 0.2}. The experimental results are summarized in Table 4 which consists of the mean values of RMSE, MAE, SSE/SST, SSR/SST on each dataset, the standard deviation values of the four measures on each dataset, the computation time, and the optimal parameter values.

Table 4 Results of LSSVR (I), QPTSVR (II), and LPTSVR (III) on benchmark datasets with RBF kernel
Full size table

The average ranks of the three algorithms on four measures are shown in Table 5. We can calculate that the F F value on RMSE is 3.8011, which is larger than the critical value 3.340, so we reject the null hypothesis. It has been seen that the performance of the LPTSVR is better than those of the QPTSVR and LSSVR (2.2667 − 1.4667 = 0.8 > 0.7493). Also, we obtain that the F F value on MAE is 4.4487 and conclude that the LPTSVR performs significantly better than the QPTSVR (2.3 − 1.4333 = 0.8667 > 0.7493) and the LSSVR (2.2667 − 1.4333 = 0.8334 > 0.7493). The F F value on SSE/SST is 1.9899, which is smaller than the critical value 3.340 or 2.503, so there is no significant difference among the three algorithms on SSE/SST. For SSR/SST, the F F value is 13.8756, which is larger than 3.340, so we reject the null hypothesis. By the Nemenyi test, we can see that the QPTSVR performs best.

Table 5 Average ranks of LSSVR, QPTSVR, and LPTSVR with RBF kernel
Full size table

Besides, the LSSVR still spends on the least CPU time among the three algorithms, while the LPTSVR needs less CPU time than the QPTSVR.

6 Conclusion

In this paper, we have proposed an approach to data regression, termed LPTSVR. In the LPTSVR, we solve twin linear programming problems instead of quadratic programming problems as one does in the QPTSVR. This makes the LPTSVR robust and faster than the QPTSVR. The LPTSVR has been extended to nonlinear regression by using nonlinear kernel techniques. The experimental results show that the generalization of the LPTSVR compares favorably with the QPTSVR and LSSVR for both linear and nonlinear cases. Besides, the LPTSVR is also suitable for weighted learning by adjusting the parameters \(\epsilon_1\) and \(\epsilon_2\). However, as does the QPTSVR [22], the LPTSVR also loses sparsity. The further work includes finding a feature selection method for the LPTSVR which is capable of generating sparse solutions.