Feedforward neural network for blind equalization with PSK signals

Abstract

Most of the cost functions used for blind equalization are nonconvex and nonlinear functions of tap weights, when implemented using linear transversal filter structures. Therefore, a blind equalization scheme with a nonlinear structure that can form nonconvex decision regions is desirable. The efficacy of complex-valued feedforward neural networks for blind equalization of linear and nonlinear communication channels has been confirmed by many studies. In this paper we present a complex valued neural network for blind equalization with M-ary phase shift keying (PSK) signals. The complex nonlinear activation functions used in the neural network are especially defined for handling the M-ary PSK signals. The training algorithm based on constant modulus algorithm (CMA) cost function is derived. The improved performance of the proposed neural network in both, stationary and nonstationary environments, is confirmed through computer simulations.

1 Introduction

The adaptive channel equalization is an important task in practical implementation of efficient digital communication. The past few years have witnessed an increased interest in problems and techniques related to blind signal processing, especially blind equalization [1–10]. The classical methods of channel equalization rely on transmitting the training signal, known in advance by the receiver. The receiver adapts the equalizer so that its output closely matches the known reference (training) signal. For time-varying situations, the training signals have to be transmitted repeatedly. Inclusion of such signals sacrifices valuable channel capacity. Therefore, to reduce the overhead of transmission of training signals, the equalization without using the training signal, i.e., blind equalization is required.

Blind equalization techniques are either based on second-order statistics (SOS), or on higher order statistics (HOS). Bussgang blind equalization techniques [11] use higher order statistics in an implicit manner, as these methods rely on optimization of some cost function. The cost functions used in blind equalization are nonconvex and nonlinear functions of tap weights, when implemented using linear FIR filter structures. A linear, finite duration impulse response (FIR) filter structure, however, has a convex decision region [12], and hence, is not adequate to optimize such cost function. Therefore, a blind equalization scheme with a nonlinear structure that can form nonconvex decision region is desirable [13].

Neural Networks, often referred to as an emerging technology, have been used in many signal processing applications, for example, filtering, parameter estimation, signal detection, system identification, signal reconstruction, signal compression, time series estimation [14–17]. Neural networks have also been applied for blind equalization, and better results, as compared to linear filtering, have been reported [1–3, 6–10, 13]. However, most of these studies are limited to real valued signals and channel models. Therefore, the development of neural network-based equalization schemes is desirable for complex-valued channel models with high level signal constellations such as M-ary phase shift keying (PSK) and quadrature amplitude modulation (QAM). One such study of blind equalization schemes is available in [13], but is limited to M-ary QAM signal only, under stationary environment.

In general, complex data can be handled in two different ways. One way is to treat the real and imaginary parts of each complex data as two separate entities. In this case, the weights of two real-valued neural networks are updated independently. The other way is to assign complex values to the weights of neural network and update using a complex learning algorithm such as complex backpropagation algorithm (CBP). Many studies [13, 18] have shown that a complex-valued MLP yields more efficient structure than two real-valued MLPs.

The neural networks can be used to optimize any of the cost functions used for blind equalization. However, the Godard algorithm (also CMA) [19, 20] is considered to be the most successful among the HOS-based blind equalization algorithms. The Godard algorithm has many advantages when compared with other HOS-based Bussgang algorithms [12, 21]. Thus, in this paper, the complex-valued multiplayer feedforword neural networks for M-ary PSK signals are presented. The learning algorithms are based on the Godard or CMA cost functions. These blind equalization schemes yield lower mean-squared error and symbol error rate in comparison to linear FIR structures-based equalizers due to decorrelation performed by the nonlinearities of the activation functions.

The paper is organized as follows. In Sect. 2, the neural network model for M-ary PSK signals is described. The learning algorithm is presented in Sect. 3. The performance of neural network-based equalizer is described through simulation in stationary as well as in nonstationary environment, in Sect. 4. Finally, the conclusions are given in Sect. 5.

2 Neural network model

The blind equalization structure is described in Fig. 1. A signal sequence of independent and identically distributed (iid) data is transmitted through a linear channel with an impulse response h(t). The output of the channel is represented, as in [12], by

$$x(t) = {\sum\limits_{k = - \infty}^\infty {s_{k} h(t - kT) + \nu (t)}},$$

(1)

where {s _k } represents the data sequence which is sent over the channel with symbols spaced time T apart and ν(t) is additive white noise.

Fig. 1

Blind equalization structure in digital communication

The received signal is sampled by substituting t=NT in (1)

$$x(nT) = {\sum\limits_{k = - \infty}^\infty {s_{k} h[(n - k)T] + \nu (nT)}}.$$

(2)

In simplified form, sampled signal of (2) is described as

$$x(n) = {\sum\limits_{k = 0}^L {s_{k} h_{{n - k}} + \nu (n)}},$$

(3)

where the channel is modeled as an FIR filter of length L. x(n) and ν(n) represent the sampled channel output and the sampled noise, respectively.

The input to the equalizer is formed by N samples of channel output as

$${\mathbf{x}}(n) = [x(n),x(n - 1), \ldots, x(n - N + 1)]^{\rm T}. $$

(4)

The output of a linear FIR equalizer is expressed as

$$y(n) = {\mathbf{w}}^{H} {\mathbf{x}}(n),$$

(5)

where w is an N×1 vector representing the weights of the equalizer and y(n) is the output, which is obtained as a rescaled and phase-shifted version of the transmitted signal.

2.1 Structure

A three-layer complex-valued feedforward network for blind equalization is shown in Fig. 2. The network has N input nodes, H hidden layer nodes and one output node. The complex-valued weight w⁽¹⁾ _kl denotes the synaptic weight, connecting the output of node l of input layer to the input of neuron k in the hidden layer. w⁽²⁾ _k refers to the synaptic weight connected between neuron k of hidden layer and the output neuron.

Fig. 2

Complex-valued multilayer feedforward neural network equalizer

The input of the equalizer is formed by N samples of the received signal as given by (4) and represented for convenience as

$${\mathbf{x}}(n) = [x_{1} (n),x_{2} (n), \ldots, x_{N} (n)]^{\rm T}. $$

(6)

The activation sum net⁽¹⁾ _k (n) and the output u _k (n) of neuron k in the hidden layer are given as

$${\rm net}^{{(1)}}_{k} (n) = {\rm net}^{{(1)}}_{{k,R}} (n) + {\rm jnet}^{{(1)}}_{{k,I}} (n) = {\sum\limits_{l = 1}^N {w^{{(1)}}_{{kl}} (n)x_{l} (n) + \theta ^{{(1)}}_{k}}}(n)$$

(7)

and

$$u_{k} (n) = \varphi ^{{(1)}} ({\rm net}^{{(1)}}_{k} (n))\quad ;k = 1,2, \ldots,H,$$

(8)

where net⁽¹⁾_k,R (n) and net⁽¹⁾_k,I (n) are, respectively, the real and imaginary parts of the activation sum net⁽¹⁾ _k (n), at time n, and φ ⁽¹⁾ (.) represents the nonlinear activation function of neurons in hidden layer and θ ⁽¹⁾ _k (n) denotes the threshold of neuron k of the hidden layer.

For the neuron of the output layer, the activation sum and the output are expressed as

$${\rm net}^{{(2)}} (n) = {\rm net}^{{(2)}}_{\rm R} (n) + {\rm jnet}^{{(2)}}_{\rm I} (n) = {\sum\limits_{k = 1}^H {w^{{(2)}}_{k} (n)u_{k} (n) + \theta ^{{(2)}}}}(n)$$

(9)

and

$$y(n) = \varphi ^{{(2)}} ({\rm net}^{{(2)}} (n)),$$

(10)

where y(n) denotes the output of the equalizer, net⁽²⁾_{R (n)} and net⁽²⁾_{I (n)} are, respectively, the real and imaginary parts of the activation sum net⁽²⁾(n), at time n, and φ ⁽²⁾ (.) is the activation function of the neuron in the output layer.

2.2 Activation functions for M-ary PSK signals

In the present model of complex-valued neural blind equalizer, the activation functions are defined according to the M-ary signal constellation. The choice of activation function plays an important role in the performance of the blind equalizers. For QAM signal, complex-valued activation functions are studied in [13]. However, it has been found that the choice of different activation functions for the hidden and output layers can further improve the performance of the blind equalizers [22]. Here, also for PSK signals we consider different activation functions for the nodes of hidden and output layer.

• 1. For the neurons of hidden layer, the activation function φ⁽¹⁾ is described as

  $$\varphi ^{{(1)}} (z) = \varphi ^{{(1)}} (z_{\rm R}) + j\varphi ^{{(1)}} (z_{\rm I}),$$

  (11)

  where z_R and z_I are the real and imaginary parts of the complex quantity z, and φ⁽¹⁾ (.) is a function defined by

  $$\varphi ^{{(1)}} (x) = \alpha \tanh (\beta x),$$

  (12)

  while α and β are two real constants.

• 2. For the output layer node, the activation function is given by

  $$\begin{aligned} \varphi ^{{(2)}} (z) = & f_{1} ({\left| z \right|})\,\exp (jf_{2} (\angle z)) \\ = & f_{1} ({\left| z \right|})\,\cos (f_{2} (\angle z)) + jf_{1} ({\left| z \right|})\,\sin (f_{2} (\angle z)) \\ \end{aligned}, $$

  (13)

  where | z | and $\angle {\text{z}}$ denote the modulus and the angle of a complex quantity z. The functions f₁(.) and f₂(.) are defined as

  $$f_{1} ({\left| z \right|}) = a\tanh (b{\left| z \right|})$$

  (14)

  and

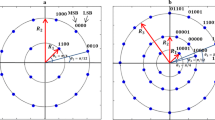
  $$f_{2} (\angle z) = \angle z - b\sin (m\angle z),$$

  (15)

  where b is a constant and m is the order of PSK signals. Figure 3a, b shows the plots of nonlinear activation functions defined in (12), (14) and (15).

From this figure, it can be seen that the activation functions have saturation regions around the symbol values of the PSK signal constellation shown in Fig. 6a. This multisaturation characteristic makes the network robust to noise. The complex-valued processing elements of output layers of the equalizers, defined by (14), (15), are illustrated in Fig. 4.

The properties of a suitable complex activation function are given in [13]. However, it can be noted that it is sufficient to optimize the filter design if the gradient of the cost function exists. The gradient is defined as

$$\nabla _{k} J = \frac{{\partial J}}{{\partial w_{{k{\rm R}}}}} + j\frac{{\partial J}}{{\partial w_{{k{\rm I}}}}};\quad k = 0,1,2\ldots,$$

(16)

where w_k,R and w_k,I denote the real and imaginary parts of k’th element w _k of the vector w. This gradient will exist if the activation functions of both hidden and output layers have the following first-order derivatives

$$\frac{{\partial \varphi _{\rm R} (z_{\rm R})}}{{\partial z_{\rm R}}},\frac{{\partial \varphi _{\rm R} (z_{\rm R})}}{{\partial z_{\rm I}}},\frac{{\partial \varphi _{\rm I} (z_{{\rm I})}}}{{\partial z_{\rm R}}}{\text{ and }}\frac{{\partial \varphi _{\rm I} (z_{\rm I})}}{{\partial z_{\rm I}}}, \quad {\text{for }} \varphi = \varphi ^{{(1)}} {\text{ and }}\varphi ^{{(2)}}.$$

The activation functions defined by (12) and (13) have the following useful properties:

• 1. The functions are nonlinear in both z_R and z_I

• 2. The first-order partial derivatives mentioned above are continuous and bounded.

• 3. Real and imaginary parts of the complex activation functions have same dynamic range.

• 4. Real and imaginary parts of the complex activation functions of the output layer are saturated according to the signal constellation.

With these properties, the gradient of the CMA cost function is obtainable for M-ary PSK signal, as the required partial derivative can be easily computed w.r.t. |z|

Fig. 3

a General nature of nonlinear functions (φ⁽¹⁾ and f₁) b Plot of nonlinear function f₂ (θ) for 8-PSK signal

3 Learning algorithm

In the task of blind equalization, the desired outputs are not available for training of the neural network. Therefore, the learning is unsupervised and is based on the minimization of a cost function. We obtain the update rules for the weights of neural networks by applying the gradient descent approach to minimize the CMA cost function. The updating rules are described as follows.

• (1) For the weights connected between hidden layer and output layer:

  $$w^{{(2)}}_{k} (n + 1) = w^{{(2)}}_{k} (n) + \eta \delta ^{{(2)}} (n)u^{*}_{k} (n),$$

  (17)

  where δ⁽²⁾ (n) is given as

  $$\delta ^{{(2)}} (n) = ({\left| {y(n)} \right|}^{2} - R_{2}){\left| {y(n)} \right|}(ab - \frac{b}{a}{\left| {y(n)} \right|}^{2})({\rm net}^{{(2)}} (n)/{\left| {{\rm net}^{{(2)}} (n)} \right|}).$$

  (18)

  In (18), the parameter R₂ depends on the statistical characteristics of the signal sequence, as defined in the Appendix, whereas constants a and b are chosen according to the channel outputs.

• (2) For the weights connected between input and hidden layer:

  $$w^{{(1)}}_{{kl}} (n + 1) = w^{{(1)}}_{{kl}} (n) + \eta \delta ^{{(1)}}_{k} (n)x^{*}_{l} (n),$$

  (19)

  where δ⁽¹⁾ _k (n) is given by

  $$\delta ^{{(1)}}_{k} (n) = \frac{{\delta ^{{(2)}} (n)}}{{{\rm net}^{{(2)}} (n)}}\{\varphi ^{{(1)\prime}} ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n))\operatorname{Re} (w^{{(2)}}_{k} (n){\rm net}^{{(2)*}} (n)) - \varphi ^{{(1)\prime}} ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))\operatorname{Im} (w^{{(2)}}_{k} (n){\rm net}^{{(2)*}} (n))\}. $$

  (20)

  Here u^* _k (n) and x^* _l (n) denote the complex conjugate of kth and lth elements of u(n) and x(n), respectively. η is the learning rate parameter while φ^(1)′(.) and φ ^(2)′(.) represent the derivatives of φ ⁽¹⁾ (.) and φ⁽²⁾ (.). The derivations of the update rules of (17), (18), (19), (20) are given in the Appendix.

4 Simulation

To observe the performance of complex-valued multilayer feedforward blind equalizer for M-ary PSK signals, three different complex channels are used. The first channel (CH-1) is the one used in [13], and its z transform is

$$\begin{aligned} H(z) =& (0.0410 + j0.0109) + (0.0495 + j0.0123)z^{{- 1}} + (0.0672 + j0.0170)z^{{- 2}} \\ & + (0.0919 + 0.0235)z^{{- 3}} + (0.7920 + j0.1281)z^{{- 4}} + (0.3960 + j0.0871)z^{{- 5}}\\ & + (0.2715 + j0.0498)z^{{- 6}} + (0.2291 + j0.0414)z^{{- 7}} + (0.1287 + j0.0154)z^{{- 8}}\\ & + (0.1032 + j0.0119)z^{{- 9}} \\ \end{aligned}.$$

(21)

The second channel (CH-2) is a multipath channel whose relative values of complex path gains and path delays are given in Table 1.

Table 1 Multipath channel

The continuous time multipath channel is described as

$$c(t) = {\sum\limits_i {g_{i} \delta (t - \tau _{i})}},$$

(22)

where g _i and τ _i are the path gain and path delay of ith path, respectively. For pulse shaping, a raised cosine pulse limited to a time duration 3T, where T is the sample period, is used with 10% roll off factor. The expression for combined channel is

$$h(t) = c(t) \oplus p(t) = {\sum\limits_i {g_{i} p(t - \tau _{i})}},$$

(23)

where p(t) is the raised cosine pulse and ⊕ denotes the convolution.

The discrete time channel is obtained by sampling the channel h(t) at baud rate. The sampled channel and its zeros are plotted in Fig. 5a, b and c, respectively.

Fig. 4

The complex-valued processing element for M-ary PSK signals

Fig. 5

Complex-valued sampled channel (CH-2). a The real part. b The imaginary part.c Zeros of the channel

The structures of the complex valued multilayer feedforward networks and the linear FIR equalizer along with initializations used in the simulation are given in Table 2. As in the case of linear FIR equalizer, where the length of the equalizer is required to be greater than the channel order, the number of nodes in the input layer of neural blind equalizer should also be greater than the channel length. To determine the channel order, the algorithms given in [23, 24] can be used. The parameters of the activation functions of hidden layer neurons are chosen according to the channel output. In this simulation η=0.00001. Higher value of learning rate parameter did not yield good convergence.

Table 2 Structural details of the blind equalizers used in simulation (a=2, b=0.5, α=4, β=0.4)

For the satisfactory convergence of CMA-based equalizers, the central tap of linear FIR equalizer is initialized as 1 and other taps are set to zero. The weights w⁽¹⁾ _ij and w⁽²⁾ _i are initialized by small random values, close to zero, except for the real parts of the central elements of the weights, i.e., w⁽¹⁾_58,R and w⁽²⁾_5,R. The weight w⁽¹⁾_58,R= 1 while w⁽²⁾_5,R is chosen according to the channel output and is 1.5.

The output of the channel CH-1 at 20 dB SNR is shown in Fig. 6b for 8-PSK signal. Figure 6c, d show the outputs of the linear FIR and neural network equalizers, respectively.

Fig. 6

a 8-PSK signal constellation. b Output of the channel CH-1 at 20 dB SNR. c Output of the linear equalizer for the channel CH-1. d Output of the neural network equalizer for the channel CH-1

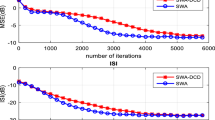
The MSE curves for the two equalizers are shown in Fig. 7a. The MSE curves are obtained by averaging 50 independent runs. The symbol error rate performance of these blind equalizers is illustrated in Fig. 7b. The difference between symbol error rates of linear and neural network equalizers is more at higher values of SNR.

Fig. 7

Performance of linear and neural network equalizers for channel CH-1. a MSE curves: (solid line) neural network equalizer; (dotted line) linear equalizer. b SER curves: (line with circle) linear filter; (line with asterisk) neural network equalizer

For the multipath channel CH-2, the MSE curves for the linear equalizer and the NN equalizer are given in Fig. 8a and the corresponding symbol error rate curves are plotted in Fig. 8b.

Fig. 8

Performance of linear and neural network equalizers for channel CH-2. a MSE curves: (solid line) neural network equalizer; (dotted line) linear equalizer. (b) SER curves: (line with circle) linear filter; (line with asterisk) neural network equalizer

It can be observed that in comparison with linear FIR equalizer, the NN equalizers achieve lower MSE and symbol error rate for stationary channels CH-1 and CH-2. The MSE of NN equalizer is less than the MSE of linear FIR equalizer by about 4 dB in the case of channel CH-1, and by about 2 dB for channel CH-2.

The performance of an adaptive system in nonstationary environment depends upon the tracking ability of the training algorithm that is employed [12]. However, in order to compare the performances of linear and neural blind equalizers, both trained by the same stochastic gradient method in nonstationary environment, the simulation of a nonstationary channel is presented here.

The nonstationary channel (CH-3) used for the simulation is shown in Fig. 9a. This channel incorporates both a sudden change and a gradual change in the environment. There is a fixed zero at z₁=0.5. After 3,000 iterations another zero which is a mobile zero, appears as given below:

$$z_{2} (n) = 1.6\exp \left(\frac{j2\pi}{3}\right) + 0.2\exp (j\pi (n - 3000)\,10^{{- 4}}).$$

(24)

The channel suddenly changes after n=3,000 and becomes a continuously varying medium. Figure 9b shows 1,000 samples of the output of this channel after n=5,000 at 20 dB SNR.

Fig. 9

a Zeros of the nonstationary channel; b output of the nonstationary channel at SNR=20 dB

For 8-PSK signal, the MSE plots of linear FIR and neural blind equalizers are shown in Fig. 10a. The MSE plots are obtained after correcting the phase shift of output symbols of the two equalizers. The symbol error rate curves shown in Fig. 10b are obtained by considering the outputs of the two equalizers after 10,000 iterations, without stopping the training. Again, the neural network equalizer gives lower MSE and symbol error rate as compared to the linear FIR filter.

Fig. 10

Performance of linear and neural network equalizer under nonstationary channel CH-3. aMSE curves (solid line): neural network equalizer; (dotted line) linear equalizer. b SER after 10,000 iterations: (line with circle) linear equalizer; (line with asterisk) neural network equalizer

5 Conclusions

In this paper, a complex-valued feedforward neural network, with complex activation functions having multisaturation characteristics, is applied for the blind equalization of complex communication channels with M-ary PSK signals. The learning rules of the complex-valued weights of the networks are based on the constant modulus algorithm (CMA). Comparison with linear FIR equalizers shows that the proposed neural equalizer is able to deliver better performance in terms of lower MSE and symbol error rate. The performance of these neural equalizers is also examined in nonstationary environment. The plots of MSE computed after correcting the phase shift of output symbols show that neural equalizers maintain lower MSE as compared to linear equalizers in nonstationary environment as well. The superior performance of the equalizer based on the neural network is attributed to its ability to form nonconvex decision regions and the decorrelation performed by the nonlinearities present in the node of the output layer. Since this nonlinear function used in the output node has been selected according to the signal constellation, this also makes the equalizer robust to noise. However, the improvement in the performance is obtained at the cost of increased computational complexity.

Appendix

The CMA cost function is expressed as

$$J(n) = \frac{1}{4}E{\left[ {{\left({{\left| {y(n)} \right|}^{2} - R_{2}} \right)}^{2}} \right]},$$

(25)

where

$$R_{2} = \frac{E[{\left| {s(n)} \right|}^{4} ]}{E[{\left| {s(n)} \right|}^{2} ]}.$$

Using the gradient descent technique, the weights of the neural network can be updated as

$$w^{{(2)}}_{k} (n + 1) = w^{{(2)}}_{k} (n) - \eta \nabla _{{w^{{(2)}}_{k}}} J(n)$$

(26)

and

$$w^{{(1)}}_{{kl}} (n + 1) = w^{{(1)}}_{{kl}} (n) - \eta \nabla _{{w^{{(1)}}_{{kl}}}} J(n),$$

(27)

where η is the learning rate parameter and the terms $\nabla_{{w^{(2)}_{k}}} J(n)$ and $\nabla _{{w^{(1)}_{{kl}}}} J(n)$ represent the gradients of the cost function J(n) defined by (25) with respect to the weights w⁽²⁾ _k and w⁽¹⁾ _kl , respectively.

Since the activation function of the output layer neuron for M-ary PSK signal is defined in terms of modulus and angle of the activation sum, the gradient of the CMA cost function with respect to the output layer weight w⁽²⁾ _k (n) is expressed as

$$\nabla _{{w^{{(2)}}_{k}}} J(n) = ({\left| {y(n)} \right|}^{2} - R_{2})\,{\left| {y(n)} \right|}\,{\left({ab - \frac{b}{a}{\left| {y(n)} \right|}^{2}} \right)}\frac{{\partial {\rm net}^{{(2)}} (n)}}{{\partial w^{{(2)}}_{k} (n)}}.$$

(28)

To obtain an expression for the partial derivative of (28), we use the relationship

$${\left| {{\rm net}^{{(2)}} (n)} \right|}^{2} = {\left({{\rm net}^{{(2)}}_{\rm R} (n)} \right)}^{2} + {\left({{\rm net}^{{(2)}}_{\rm I} (n)} \right)}^{2}. $$

(29)

On differentiating (29) with respect to w⁽²⁾ _k , we get

$$\begin{aligned} \frac{{\partial {\left| {{\rm net}^{{(2)}} (n)} \right|}}} {{\partial w^{{(2)}}_{k} (n)}} = & \frac{1} {{{\left| {{\rm net}^{{(2)}} (n)} \right|}}}{\left[ {{\rm net}^{{(2)}}_{\rm R} (n)\,\frac{{\partial {\rm net}^{{(2)}}_{\rm R} (n)}} {{\partial w^{{(2)}}_{k} (n)}} + {\rm net}^{{(2)}}_{\rm I} (n)\frac{{\partial {\rm net}^{{(2)}}_{\rm I} (n)}} {{\partial w^{{(2)}}_{k} (n)}}} \right]} \\ = & \frac{1} {{{\left| {{\rm net}^{{(2)}} (n)} \right|}}}{\left[ {{\rm net}^{{(2)}}_{\rm R} (n){\left( {\varphi ^{{(1)}} (net^{{(1)}}_{{k,{\rm R}}} (n)) - j\varphi ^{{(1)}} ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))} \right)} + {\rm net}^{{(2)}}_{\rm I} (n){\left( {\varphi ^{{(1)}} ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n)) + j\varphi ^{{(1)}} ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n))} \right)}} \right]} \\ = & \frac{{\varphi ^{{(1)*}} ({\rm net}^{{(1)}}_{k} (n)){\rm net}^{{(2)}} (n)}} {{{\left| {{\rm net}^{{(2)}} (n)} \right|}}} \\ \end{aligned} $$

(30)

On substituting (30) in (28), the expression for the gradient becomes

$$\nabla _{{w^{{(2)}}_{k}}} J(n) = \delta ^{{(2)}} (n) u^{*}_{k} (n)$$

(31)

where

$$\delta ^{{(2)}} (n) = {\left[ {{\left({{\left| {y(n)} \right|}^{2} - R_{2}} \right)}{\left| {y(n)} \right|}{\left({ab - \frac{b}{a}{\left| {y(n)} \right|}^{2}} \right)}} \right]}\frac{{{\rm net}^{{(2)}} (n)}}{{{\left| {{\rm net}^{{(2)}} (n)} \right|}}}.$$

(32)

Substitution of (31) in (26) along with (32) gives the update equation (17) with (18) for M-ary PSK signal.

In order to obtain the update equation for the weights {w⁽¹⁾ _kl }, we need the following gradient

$$\nabla _{{w^{{(1)}}_{{kl}}}} J(n) = {\left({{\left| {y(n)} \right|}^{2} - R_{2}} \right)}\,{\left| {y(n)} \right|}\,{\left({ab - \frac{b}{a}{\left| {y(n)} \right|}^{2}} \right)}\frac{{\partial {\left| {{\rm net}^{{(2)}} (n)} \right|}}}{{\partial w^{{(1)}}_{{kl}} (n)}}.$$

(33)

The partial derivative terms in (33) can be obtained by using (29)

$$\frac{{\partial {\left| {{\rm net}^{{(2)}} (n)} \right|}}}{{\partial w^{{(1)}}_{{kl}} (n)}} = \frac{1}{{{\left| {{\rm net}^{{(2)}} (n)} \right|}}}{\left[ {{\rm net}^{{(2)}}_{\rm R} (n)\frac{{\partial {\rm net}^{{(2)}}_{\rm R} (n)}}{{\partial w^{{(1)}}_{{kl}} (n)}} + {\rm net}^{{(2)}}_{\rm I} (n)\frac{{\partial {\rm net}^{{(2)}}_{\rm I} (n)}}{{\partial w^{{(1)}}_{{kl}}(n)}}} \right]},$$

(34)

where

$$\begin{aligned} \frac{{\partial {\rm net}^{{(2)}}_{\rm R} (n)}} {{\partial w^{{(1)}}_{{kl}} (n)}} = & w^{{(2)}}_{{k,{\rm R}}} (n){\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n)).(x_{{l,{\rm R}}} (n) - jx_{{l,{\rm I}}} (n)) \\ & - w^{{(2)}}_{{k,{\rm I}}} (n){\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))(x_{{l,{\rm I}}} (n) + jx_{{l,{\rm R}}} (n)) \\ \end{aligned} $$

(35)

and

$$\begin{aligned} \frac{{\partial {\rm net}^{{(2)}}_{\rm I} (n)}} {{\partial w^{{(1)}}_{{kl}} (n)}} = & w^{{(2)}}_{{k,{\rm R}}} (n){\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))(x_{{l,{\rm I}}} (n) + jx_{{l,{\rm R}}} (n)) \\ & + w^{{(2)}}_{{k,{\rm I}}} (n){\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n))(x_{{l,{\rm R}}} (n) - jx_{{l,{\rm I}}} (n)) \\ \end{aligned}. $$

(36)

Now the substitution of (35) and (36) in (34) and some simplification lead to

$$\frac{{\partial {\left| {{\rm net}^{{(2)}} (n)} \right|}}} {{\partial w^{{(1)}}_{{kl}} (n)}} = \frac{{x^{*}_{l} (n)}} {{{\left| {{\rm net}^{{(2)}} (n)} \right|}}}{\left( {{\varphi ^{(1)} }^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n))\,\operatorname{Re} [w^{{(2)}}_{k} (n){\rm net}^{{(2)*}} (n)] - j{\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))\,\operatorname{Im} [w^{{(2)}}_{k} (n){\rm net}^{{(2)*}} (n)]} \right)}. $$

(37)

Finally, by substituting (37) in (33), we get

$$\begin{aligned} \nabla _{{w^{{(1)}}_{{kl}} }} J(n) = & \delta ^{{(2)}} (n)x^{*}_{l} (n){\left( {{\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n))\,\operatorname{Re} [w^{{(2)}}_{k} (n){\rm net}^{{(2)*}} (n)] - j{\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))\,\operatorname{Im} [w^{{(2)}}_{k} (n)net^{{(2)*}} (n)]} \right)} \\ = & \delta ^{{(1)}}_{k} (n)x^{*}_{l} (n) \\ \end{aligned} $$

(38)

where

$$\delta ^{{(1)}}_{k} (n) = \frac{{\delta ^{{(2)}} (n)}}{{{\rm net}^{{(2)}} (n)}}{\left( {{\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm R}}} (n))\,\operatorname{Re} [w^{{(2)}}_{k} (n)net^{{(2)*}} (n)] - j{\varphi ^{(1)}} ^{\prime } ({\rm net}^{{(1)}}_{{k,{\rm I}}} (n))\,\operatorname{Im} [w^{{(2)}}_{k} (n){\rm net}^{{(2)*}} (n)]} \right)}.$$

Using (38) and (27), we get the update rule of (19) for M-ary PSK signal.