Identification of unbalance characteristics of rotating machinery using a novel optimization-based methodology

Abstract

In this study, a novel optimization-based method is proposed to determine the parameters of a rotating unbalance in a rotor-bearing system. For that purpose, the weighted sum of squared difference between the analytical and predicted unbalance response due to rotational unbalance is considered as the objective function. A hybrid algorithm integrating salp swarm algorithm and Nelder–Mead algorithms is presented for detecting unbalance magnitude and phase as the unbalance parameters. Parameters of the aforementioned optimization algorithm are determined systematically using the Taguchi design of experiments method. The efficiency of the proposed method is compared with various optimization algorithms in the literature. The optimization method is validated with different unbalances experimentally to consider the real-world conditions. The results show the superiority of the proposed hybrid algorithm in terms of the accuracy of the unbalance parameters and computational efficiency.

1 Introduction

Rotating machines have been widely used in industrial applications. Rotor unbalance is one of the primary sources of undesired vibration in rotating machinery, which can lead to catastrophic failures. Condition monitoring has been commonly used for monitoring a parameter of condition in machinery to identify a developing fault. Therefore, predicting the unbalance parameters in rotary machinery is an important capability that has been at the heart of research literature recently (Mohanty 2018; Torres Cedillo and Bonello 2014).

There have been many methods available in the literature to identify the unbalance parameters. Sanches and Pederiva (2016) proposed a model-based approach to identify the rotor unbalance and residual shaft bow, both theoretically and experimentally. In this study, the finite element method is used to derive the dynamic equations governing the system, and the correlation-based method is utilized to detect possible the faults. Similarly, Jalan and Mohanty (2009) employed a model-based method to detect fault of a rotor-bearing system in terms of its misalignment and unbalance under steady-state conditions. Kalman filter and recursive least square-based force identification methods were used by Shrivastava and Mohanty (2018) to detect the amplitude and the phase of unbalance in the rotor disk bearing systems. Zou et al. (2019) used augment Kalman filter (AKF) to identify unbalance load of rotor-bearing systems. The proposed method can well identify the unbalance parameters online and in real time. Linear and nonlinear regression models are used by Nauclér and Söderström (2010) to determine unbalance parameters. Similarly, the unbalance parameters of rotor-bearing systems using an algebraic method combined with an active control scheme are investigated by Arias-Montiel et al. (2014). A configuration consisting of two disks, which were asymmetrically placed along the shaft with a ball bearing at one end and active suspension at the other end, was considered as a case study. The least angle regression method is used by Chatzissavas and Dohnal (2015) in order to predict different fault modes. In this study, multi-fault identification method based on sparse vibration measurements is used when the machine operates under constant speed.

Deepthikumar et al. (2013) proposed a method to detect a distributed unbalance by utilizing a polynomial curve for modeling the eccentricity distribution using finite element models. Sergio Guillermo Torres Cedillo et al. (2019) introduced a noninvasive inverse problem method for the balancing of nonlinear squeeze-film damped (SFD) rotor dynamics applications. The SFD journal displacements are estimated from the vibration of the casing using identified inverse SFD models based on recurrent neural networks (RNNs). Model-based fault diagnosis (MFD) methods and quantification methods were analyzed by Lees et al. (2009). Tiwari and Chougale (2014) proposed an identification algorithm for the rotors that were fully levitated on active magnetic bearings (AMBs). Unbalance parameters on the supports of system are estimated by considering the problem as an inverse problem by Menshikov (2013). In this study, Tikhonov regularization method is employed to obtain the stable results. Pennacchi (2008, 2009) proposed the M-estimators for the identification of the excitation in mechanical systems. A novel method based on response polar plot analysis is proposed by Ocampo et al. (2017). In this study, a shaft system with two degrees of freedom and unequal principal moments of inertia is considered. Equivalent loads and vibration minimization methods are used for the unbalance identification in a SPECTRAQUEST MFS rotor system experimentally by Sudhakar and Sekhar (2011). In another study, Sekhar (2005) proposed a model-based method and reduced basis dynamic expansion to identify the crack and unbalance in the rotary systems simultaneously. The multi-fault detection in rotor-bearing systems based on vibration signal analysis is studied by Lal and Tiwari (2012). In this study, least squares technique is used to estimate the bearing and coupling dynamic parameters, and residual unbalances.

Nowadays, metaheuristics optimization algorithms are widely used in engineering problems as an alternative to classical optimization methods (Dey et al. 2020; Khalilpourazari and Khalilpourazary 2019; Li et al. 2020). In this regard, a combination of modal expansion method and metaheuristic optimization methods is used by Yao et al. (2018) to detect the axial location of the unbalance and phase for a rotor-bearing system with single and double disks. In this study, the ant lion optimization algorithm (ALO), simulated annealing (SA), and firefly optimization algorithm (FOA) are utilized to solve the inverse problem. The findings from this study were experimentally validated. Pavlenko et al. (2019a, b) developed a new method using artificial neural networks (ANN) to improve the quality of diagnosis in rotary machines. The proposed methodology was demonstrated successfully on turbo-pump units used in liquid rocket engines. In another work of Pavlenko et al. (2019a, b), computational and analytical methods were developed to improve the vibrational reliability of rotary systems by estimating the parameters of the dynamic state of turbomachines and realizing the virtual balancing procedure through ANN.

There has been an exponential increase in the development of metaheuristic algorithms in recent years (Abbasi et al. 2021a, b). For example, several swarm intelligence algorithms have been proposed to solve many engineering problems. Harris hawk optimization (HHO) (2019), inspired from the hunting behavior of Harris hawk birds, was one of the most recently developed algorithms. Applications of this algorithm to many engineering problems can be found in the literature. Abbassi et al. (2019) used HHO algorithm to minimize entropy generation in microchannel heat sinks. Mehta et al. (2019) demonstrated the application of the HHO algorithm to solve the optimum load dispatch problems. Engineering applications of the whale optimization algorithm (WOA) (Mirjalili and Lewis 2016) and the grasshopper optimization algorithm (GOA) (Saremi et al. 2017) have been reported extensively in the literature. Salp swarm algorithm (SSA) (Mirjalili et al. 2017) is a new global optimization algorithm that simulates the behaviors of salps during navigating and hunting. SSA has shown superior performance compared to other algorithms in several engineering problems. In these algorithms, tuning of the parameters to avoid stagnation in local optima is critical. Abbassi et al. (2019) proposed an efficient method for extracting the parameters of photovoltaic cells using the SSA algorithm. A novel hybrid metaheuristic chaotic salp swarm algorithm (CSSA) is proposed by Sayed et al. (2018) to enhance the convergence rate and accuracy of the SSA algorithm. Similarly, a new hybrid algorithm that combines the sine cosine algorithm and salp swarm algorithms is proposed (Singh et al. 2019) to increase the efficiency and convergence of algorithm by balancing the exploration and exploitation phases.

The aforementioned algorithms and methods were also used as part of condition monitoring in engineering applications. For example, damage and failures in engineering systems were determined using the inverse approach (Vakil-Baghmisheh et al. 2008; He and Hwang 2006; Firouzi et al. 2021a, 2021b). For that purpose, the weighted squared difference between the measured and calculated natural frequencies was considered as the objective function to predict the location and the depth of crack. This procedure was found effective for the detection and identification of cracks in mechanical systems. Moezi et al. (2015, 2018) and Firouzi et al. (2021a, 2021b) proposed several metaheuristic algorithms to identify the location and depth of a possible crack in the mechanical systems. Similarly, Moradi et al. (2011) used bees algorithm to estimate the location and depth of open edge cracks in Euler–Bernoulli beams. Modified version of PSO algorithm and self-adaptive fuzzy PSO are used by Jena et al. (2015a, b) to predict the crack parameters.

As it is of significant importance to determine the unbalance parameters in rotating machinery, there has been a variety of methods available in the literature. Even though the optimization methods were employed for this purpose (Yao et al. 2018), there is still room for improvement for the accurate determination of these parameters. The main aim of the research is to improve the accuracy of the unbalance parameters compared to the previous methods which may be needed for critical engineering applications. A hybrid salp swarm–Nelder–Mead (SSA–NM) algorithm is proposed, where the objective function is considered as the weighted squared difference between the analytical and predicted unbalance response in this study. Optimization parameters are tuned systematically using the Taguchi design of experiments (DOE) methods for fair comparison of the results. Besides, the comparison of the computational efficiency of the proposed algorithm with the recent optimization algorithms such as whale optimization algorithm (WOA), grasshopper optimization algorithm (GOA), salp swarm algorithm (SSA), and Harris hawk optimization (HHO) is made.

The organization of the remainder of the paper is as follows: Firstly, the mathematical models are explained in Sect. 2. Thereafter, the analysis methods used in this study are briefly described in Sect. 3. The proposed methodology and flowchart of the SSA–NM algorithm and the Taguchi design method are detailed in Sect. 4. The proposed method is demonstrated in two case studies in Sect. 5. The case studies are: 1) the rotor system with a single disk and 2) the rotor system with double disks. Finally, conclusions are presented in Sect. 6.

2 Research methodology

In this section, finite element models for the rotor system (Sect. 2.1), element stiffness and mass matrices for Euler–Bernoulli element (Sect. 2.2) and equation of motion (Sect. 2.3) describing the rotor system are presented in detail.

2.1 Finite element models

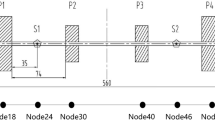
In this study, two case studies are considered: (1) single-disk rotor and (2) double-disk rotor system. The rotor system is modeled using the finite element method by discretizing the continuous rotor-bearing system as lumped masses and support points. Each rotor shaft is modeled as an Euler–Bernoulli beam element with constant cross section and material properties. This type of element has translational and rotational degrees of freedom per node in the both planes. The disk is modeled as a rigid mass, and the gyroscopic effects are taken into account. The bearings are represented by using translational spring and damper at the corresponding nodes. Single-disk and double-disk rotor systems are shown in Fig. 1a and b, respectively. There are 13 nodes for both cases. Rigid disk is lumped at node 9 for the single-disk system. Similarly, two disks are located at nodes 7 and 9 for double-disk configurations.

Fig. 1

Finite element model for rotor system with a single disk and b double disks

Equation of motion can be formulated in the standard matrix form as follows:

$$ \left[ M \right]_{52 \times 52}^{\left( s \right)} \left\{ {\ddot{\eta }} \right\}_{52 \times 1} + \left( {\left[ C \right]_{52 \times 52}^{\left( s \right)} - \omega \left[ G \right]_{52 \times 52}^{\left( s \right)} } \right) \left\{ {\dot{\eta }} \right\}_{52 \times 1} + \left[ K \right]_{52 \times 52}^{\left( s \right)} \left\{ \eta \right\}_{52 \times 1} = \left\{ f \right\}_{52 \times 1} $$

(1)

where $\left[ M \right]$, $\left[ C \right]$, $\left[ G \right]$, $\left[ K \right]$, $\left\{ \eta \right\}$ and $\left\{ f \right\}$ are global mass matrix, global damping matrix, global gyroscopic matrix, global stiffness matrix (including bearings stiffness), nodal displacement vector, and force vector, respectively. The global stiffness matrix is assembled considering the element stiffness matrix for each Euler–Bernoulli beam element. Since the geometry and material properties for each element are the same, the same element stiffness matrix is obtained. Similarly, the global mass matrix is obtained from the mass matrix for each element. In the assembly of the global mass matrix, the mass of the each disk is lumped and added to the proper location on the global mass matrix. The equations related to global mass, gyroscopic, and stiffness matrices are well known. For detailed information on the formulation, the reader is referred to (Tiwari 2017; Pavlenko et al. 2017, 2018). The nodal displacement vector is given in Eq. (2).

$$ \left\{ \eta \right\}_{52 \times 1} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{1} } \\ {\varphi_{y1} } \\ {\upsilon_{1} } \\ \end{array} } \\ {\varphi_{x1} } \\ \vdots \\ {u_{13} } \\ {\begin{array}{*{20}c} {\varphi_{y13} } \\ {\upsilon_{13} } \\ {\varphi_{x13} } \\ \end{array} } \\ \end{array} } \right\} $$

(2)

The gyroscopic matrix for each element is given in Eq. (3):

$$ \left[ G \right] = - \omega \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {I_{P} } \\ 0 & 0 & 0 & 0 \\ 0 & { - I_{P} } & 0 & 0 \\ \end{array} } \right] \left\{ {\begin{array}{*{20}c} {\dot{u}} \\ {\dot{\varphi }_{y} } \\ {\begin{array}{*{20}c} {\dot{\upsilon }} \\ {\dot{\varphi }_{x} } \\ \end{array} } \\ \end{array} } \right\} $$

(3)

$I_{P}$ is the polar mass moment of inertia. In next subsection, the details of the FE formulation of the models are described briefly.

2.2 FE formulation of Euler–Bernoulli Beam

In this section, the FE formulation, based on the Galerkin method, for the rotor-bearing system, is explained. The analysis is performed in the transverse plane, i.e., y–z plane, as shown in Fig. 2. For that purpose, the shaft is discretized into several FEs, and the formulation of an element at a distance z from the global coordinate system in the plane y–z is derived. Each node of the element has four degrees of freedom (DOFs): (1) u and υ are the translational displacement, and (2) $\varphi_{x}$ and $\varphi_{y}$ are the rotational displacement of the nodes. Therefore, this element has eight DOFs: ($u_{1}$,$\upsilon_{1}$,$\varphi_{x1}$, $\varphi_{y1}$, $u_{2}$, $\upsilon_{2}$, $\varphi_{x2}$, $\varphi_{y2}$), where subscripts 1 and 2 refer to the first and second nodes of the element. The displacement within the element can be expressed by using the appropriate shape functions as shown in Eq. (4).

$$ \upsilon^{{\left( {\text{e}} \right)}} \left( {z,t} \right) = \left[ {N\left( z \right)} \right] \left\{ {\eta \left( t \right)} \right\}^{{\left( {{\text{ne}}} \right)}} $$

(4)

Fig. 2

a FE discretization of the shaft and b DOFs of an element

$\left\lfloor {N\left( z \right)} \right\rfloor$ is a row vector containing the shape functions, which will be described later in this subsection. $\left\{ {\eta \left( t \right)} \right\}$ is the displacement vector containing translational and rotational displacement of the element, e and ne represent the element and node numbers of the element, respectively.

The displacement given in Eq. (4) is then substituted to the differential equation governing the Euler–Bernoulli beam, which is shown in Eq. (5). The resulting equation, which represents the residue (R^e), is shown in Eq. (6). The reader is referred to Tiwari (2017) for more detailed derivation by the application of Hamilton’s principle.

$$ EI_{xx} \frac{{\partial^{4} \upsilon \left( {z,t} \right)}}{{\partial z^{4} }} + \rho A\frac{{\partial^{2} \upsilon \left( {z,t} \right)}}{{\partial t^{2} }} = f\left( {z,t} \right) + f_{0} \left( t \right)\delta^{*} \left( {z - z_{0} } \right) $$

(5)

$$ R^{e} = EI_{xx} \frac{{\partial^{4} \upsilon }}{{\partial z^{4} }} + \rho A\frac{{\partial^{2} \upsilon }}{{\partial t^{2} }}^{\left( e \right)} - f\left( {z,t} \right) - f_{0} \left( t \right)\delta^{*} \left( {z - z_{0} } \right) $$

(6)

where $\delta^{*}$ is the direct delta function, $f\left( {z,t} \right)$ is the distributed external force, and $\rho$ is the density. The residue is then minimized over the element domain as given in Eq. (7):

$$ \mathop \smallint \limits_{0}^{L} N_{i} \left( z \right)R^{\left( e \right)} \,{\text{d}}z = 0;\quad i = 1,2, \ldots ,r $$

(7)

where r is the number of DOFs (r = 4 for this study). $N_{i}$ represents the ith shape function, while L is the element length.

The weak form of the finite element is obtained by solving Eq. (7):

$$ \begin{aligned} & \mathop \int \limits_{0}^{L} \rho AN_{i} \left( z \right)\frac{{\partial^{2} \upsilon^{\left( e \right)} }}{{\partial t^{2} }}{\text{d}}z + N_{i} \frac{\partial }{\partial z}\left( {EI_{xx} \frac{{\partial^{2} \upsilon^{\left( e \right)} }}{{\partial z^{2} }}} \right)\left| {\begin{array}{*{20}c} L \\ 0 \\ \end{array} - \frac{{{\text{d}}N_{i} }}{{{\text{d}}z}}\left( {EI_{xx} \frac{{\partial^{2} \upsilon^{\left( e \right)} }}{{\partial z^{2} }}} \right)} \right|\begin{array}{*{20}c} L \\ 0 \\ \end{array} \\ & \quad + \,\mathop \int \limits_{0}^{L} \frac{{{\text{d}}^{2} N_{i} }}{{{\text{d}}z}}EI_{xx} \frac{{\partial^{2} \upsilon^{\left( e \right)} }}{{\partial z^{2} }}{\text{d}}z - \mathop \smallint \limits_{0}^{L} N_{i} \left\{ {f\left( {z,t} \right) + f_{0} \left( t \right)\delta^{*} \left( {z - z_{0} } \right)} \right\}\,{\text{d}}z = 0,\quad i = 1,2, \ldots ,r \\ \end{aligned} $$

(8)

where the prime represents the partial derivative with respect to z. Then the proper shape function is derived.

2.3 Element stiffness and mass matrix

The element stiffness and mass matrices are obtained using the weak form and the shape functions.

The element stiffness matrix in terms of the parameters of the model is given by:

$$ \left[ K \right]^{\left( e \right)} = \frac{{EI_{xx} }}{{L^{3} }} \left[ {\begin{array}{*{20}c} {12} & { - 6L} & { - 12} & { - 6L} \\ { - 6L} & {4L^{2} } & {6L} & {2L^{2} } \\ { - 12} & { - 6L} & {12} & {6L} \\ { - 6L} & {4L^{2} } & {6L} & {4L^{2} } \\ \end{array} } \right] $$

(9)

Finally, the mass matrix is given by:

$$ \left[ M \right]^{\left( e \right)} = \frac{\rho AL}{{420}} \left[ {\begin{array}{*{20}c} {156} & { - 22L} & {54} & {13L} \\ { - 22l} & {4L^{2} } & { - 13L} & { - 3L^{2} } \\ {54} & { - 13L} & {156} & {22L} \\ {13L} & { - 3L^{2} } & {22L} & {4L^{2} } \\ \end{array} } \right] $$

(10)

The global assembly matrix is assembled using the element stiffness, mass matrix, and the connectivity information between the nodes of the FE model. For a more detailed explanation, the reader is referred to Tiwari (2017).

3 Analysıs methods

In this section, the analysis methods used in the proposed optimization algorithm are presented. More specifically, modal analysis is detailed in Sect. 3.1, the details of the unbalance response are given in Sect. 3.2. Finally, the bearing parameters used in the finite element model are explained in Sect. 3.3.

3.1 Modal analysis

A modal analysis is performed to determine the modes and mode shapes for the aforementioned cases. The modes and corresponding mode shapes for the first three modes are shown in Fig. 3 for the rotor system with the single disk and the double disks. The parameters of the analysis are summarized in Table 1. The comparison of the results shows that the addition of the second disk reduces the natural frequencies as a result of increased mass as expected. The addition of the second disk affects the mode shapes differently due to the fact that system stiffness in each direction such as transverse or vertical directions is different. Besides, the Campbell diagram and critical speed for these two cases are shown in Fig. 4 and Table 2, respectively. It is seen from Fig. 3, the first critical speeds for rotor system with single disk and double disk are 55.5 and 41.6 rad/s, also second critical speeds are 300.55 and 252 rad/s, respectively. The Campbell diagram shows the importance of including the gyroscopic effects clearly.

Fig. 3

Mode shapes (linear displacement) for the rotor system with single disk and double disk

Table 1 Parameters of the rotor-bearing systems

Fig. 4

Campbell diagram for two rotor systems

Table 2 Critical speed of rotor systems

3.2 Unbalance response analysis

In this section, a method based on an optimization algorithm is presented to determine the magnitude and phase of unbalance mass using an unbalance response. The unbalance response can be calculated for the rotor-bearing system, shown in Fig. 1, according to the formulation described in Sect. 2.

An unbalance with known magnitude in g mm and phase in degree is fixed to the disks. To obtain axial position of unbalance, a reference coordinate system, aligned with the y-axis at t = 0, is used to position the unbalance axially. The phase is measured with respect to this coordinate system. The angular speed, $\omega$, is in counterclockwise direction as shown in Fig. 5. The unbalance mass creates the vertical component of unbalance force with a magnitude of $m_{b} r_{b} \omega^{2} e^{j\varphi } e^{j\omega t}$, where $m_{b}$ is the unbalance mass and $r_{b}$ is the offset of the unbalance mass from the center of gravity of the disk. The force matrix is shown in Eq. (11), where the force due to unbalance mass is added to the proper location of the force vector.

$$ \left\{ {\overline{F}\left( \omega \right)} \right\} = \left\{ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \vdots \hfill \\ {m_{b} r_{b} \omega^{2} e^{j\varphi } } \hfill \\ \vdots \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right\} $$

(11)

Fig. 5

The position of the unbalance mass on the disk

The unbalance response due to unbalance force is calculated as given in Eq. (12):

$$ \begin{aligned} & - \omega^{2} \left[ M \right]\left\{ {\overline{\eta }} \right\} + \left( { \left[ C \right] j \omega - j\omega^{2} \left[ G \right] } \right)\left\{ {\overline{\eta }} \right\} + \left[ K \right]\left\{ {\overline{\eta }} \right\} = \left\{ {\overline{F}\left( \omega \right)} \right\} \\ & \left\{ {\overline{\eta }} \right\} = \left( { \left[ K \right] - \omega^{2} \left[ M \right] + \left[ C \right] j \omega - j\omega^{2} \left[ G \right] } \right)^{ - 1} \left\{ {\overline{F}\left( \omega \right)} \right\} \\ \end{aligned} $$

(12)

The matrices $\left[ M \right]$ and $\left[ K \right]$ contain real numbers, whereas force vector $\left\{ {\overline{F}} \right\}$ and corresponding displacement vector $\left\{ {\overline{\eta }} \right\}$ have complex terms.

3.3 Bearing parameters calculation

Bearings are the most commonly used components in rotating machinery. The hydrodynamic bearings are chosen as flexible support of rotor systems in this study. The empirical models of the hydrodynamic bearings are common in the literature. A simple representation of a hydrodynamic bearing is shown in Fig. 6. Lubrication fluid between the bearing and the shaft prevents metal-to-metal contact. This fluid acts as a direct coupler and affects the critical speed and unbalance response of the machinery.

Fig. 6

Schematic of a hydrodynamic bearing with linearized damping and stiffness coefficients

The analysis of hydrodynamic bearings can be performed theoretically by properly modeling the bearing fluid film. For modeling of a hydrodynamic bearing, the following assumptions are taken into account (Hamrock et al. 2004):

• 1. Film thickness is small compared with journal dimensions.

• 2. Inertia of fluid in film is negligible.

• 3. There is laminar flow in the bearing fluid film.

• 4. The fluid is a simple Newtonian liquid with its viscosity independent of the shear rate.

• 5. The viscosity and density of the fluid are constant throughout the bearing.

The governing equations that represent the dynamic behavior of hydrodynamic bearings were obtained by Reynolds (1886):

$$ \frac{\partial }{\partial s}\left( {h^{3} \frac{\partial p}{{\partial s}}} \right) + \frac{\partial }{\partial z}\left( {h^{3} \frac{\partial p}{{\partial z}}} \right) = 6\mu U\frac{\partial h}{{\partial s}} $$

(13)

where $s$ is the distance around the bearing circumference of the point under consideration measured from some arbitrary reference, $z$ is the position of the point in the axial direction, $h$ is the film clearance, $p$ is the lubricant pressure, $U$ is the tangential velocity of the journal surface, and $\mu$ is the dynamic viscosity of lubricant.

The variation of lubricant pressure in both the axial (z) and circumferential (s) direction can be found using Eq. (13). An approximate solution can be obtained by making the short bearing approximation. For the short bearing, eight parameters related to stiffness and damping coefficient can be calculated as below (Hamrock et al. 2004; McCallion 1970):

$$ \begin{aligned} k_{xy} & = \frac{{\pi \left\{ {\pi^{2} - 2\pi^{2} \varepsilon^{2} - \left( {16 - \pi^{2} } \right)\varepsilon^{4} } \right\}Q\left( \varepsilon \right)}}{{\varepsilon \sqrt {1 - \varepsilon^{2} } }} \\ k_{yx} & = \frac{{ - \pi \left\{ {\pi^{2} + \left( {32 + \pi^{2} } \right)\varepsilon^{2} + 2\left( {16 - \pi^{2} } \right)\varepsilon^{4} } \right\}Q\left( \varepsilon \right)}}{{\varepsilon \sqrt {1 - \varepsilon^{2} } }} \\ k_{yy} & = \frac{{4\left\{ {\pi^{2} + \left( {32 + \pi^{2} } \right)\varepsilon^{2} + 2\left( {16 - \pi^{2} } \right)\varepsilon^{4} } \right\}Q\left( \varepsilon \right)}}{{1 - \varepsilon^{2} }} \\ k_{xx} & = 4\left\{ {2\pi^{2} + \left( {16 - \pi^{2} } \right)\varepsilon^{4} } \right\}Q\left( \varepsilon \right) \\ c_{xx} & = \frac{{2\pi \sqrt {1 - \varepsilon^{2} } \left\{ {\pi^{2} + 2\left( {\pi^{2} - 8} \right)\varepsilon^{2} } \right\}Q\left( \varepsilon \right)}}{\varepsilon } \\ c_{yy} & = \frac{{2\pi \left\{ {\pi^{2} + 2\left( {24 - \pi^{2} } \right)\varepsilon^{2} + \pi^{2} \varepsilon^{4} } \right\}Q\left( \varepsilon \right)}}{{\varepsilon \sqrt {1 - \varepsilon^{2} } }} \\ c_{xy} & = c_{yx} = - 8\left\{ {\pi^{2} + 2\left( {\pi^{2} - 8} \right)\varepsilon^{2} } \right\}Q\left( \varepsilon \right) \\ Q\left( \varepsilon \right) & = \frac{1}{{\left\{ {\pi^{2} + \left( {16 - \pi^{2} } \right)\varepsilon^{2} } \right\}^{3/2} }}\quad \varepsilon = \frac{{e_{r} }}{{c_{r} }} \\ \end{aligned} $$

(14)

where $e_{r}$, $c_{r}$ are journal eccentricity and radial clearance, respectively. $\varepsilon$ is the eccentricity ratio, which can be determined from Eq. (15):

$$ S\left( \frac{L}{D} \right)^{2} = \frac{{\left( {1 - \varepsilon^{2} } \right)^{2} }}{{\pi \varepsilon \sqrt {\pi^{2} \left( {1 - \varepsilon^{2} } \right) + 16\varepsilon^{2} } }} $$

(15)

$$ S = \frac{\mu DLN}{W}\left( {\frac{R}{{c_{r} }}} \right)^{2} $$

(16)

where $S$ is Sommerfeld number, which is a non-dimensional number for hydrodynamic lubrication analysis. is load on the bearing, $D$ is the bearing bore, $R$ is journal radius, $L$ is length of bearing, $\mu$ is viscosity of lubricant, $N$ is the number of revolutions per second. The parameters (diameter and length of bearing, radial clearance, and viscosity of lubricant) are reported in Table 1. First, $S$ is calculated from the parameters of the bearing using Eq. (16). Then, is obtained using the relationship between S and given in Eq. (15). Once is determined, eight parameters of the bearing are calculated according to Eq. (14). Figure 7 shows the process of obtaining bearing parameters. The results of bearing parameters are summarized in Table 3:

Fig. 7

Process of obtaining bearing parameters

Table 3 Stiffness and coefficient of bearing with respect to speed of the rotor (Tiwari 2017)

4 Optimization methodology

4.1 Salp swarm algorithm

Salp swarm algorithm, which mimics the exploration and foraging behavior of salps deep in the sea, is proposed by Mirjalili et al. (2017). A group of salps moves unitedly, which is known as a salp chain. Salp chain would lead to better foraging and navigation. In the initialization step of the salp swarm algorithm, the community of salps is separated into two groups: followers and leaders. The position of leaders is updated according to Eq. (17):

$$ y_{j}^{1} = \left\{ {\begin{array}{*{20}l} {F_{j} + c_{1} \left( {\left( {ub_{j} - lb_{j} } \right)c_{2} + lb_{j} } \right)} \hfill & {\quad c_{3} \ge 0} \hfill \\ {F_{j} - c_{1} \left( {\left( {ub_{j} - lb_{j} } \right)c_{2} + lb_{j} } \right)} \hfill & {\quad c_{3} < 0} \hfill \\ \end{array} } \right. $$

(17)

where $y_{j}^{1}$ is the location of the best solution, which is the leader of salps and $F_{j}$ is the position of food source in the jth dimension, $ub_{j}$ and $lb_{j}$ are the upper and lower bounds in the jth dimension, respectively. c₁, c₂, and c₃ are randomly selected parameters. The parameters c₂ and c₃ are random numbers between 0 and 1. The parameter, c₁, is used to balance the exploration and exploitation phases of the algorithm and determined using Eq. (18):

$$ c_{1} = 2e^{{ - \left( \frac{4l}{L} \right)^{2} }} $$

(18)

where L is the maximum number of iterations, and l is the current iteration. Similarly, the location of followers is given by:

$$ y_{j}^{i} = \frac{1}{2}at^{2} + v_{0} t $$

(19)

where i ≥ 2, $y_{j}^{i}$ demonstrates the location of ith follower in jth dimension. In this equation, v₀ is the initial speed and t is time. a and v are calculated from Eq. (20):

$$ a = \frac{{v_{{{\text{final}}}} }}{{v_{0} }},\quad v = \frac{{y - y_{0} }}{t} $$

(20)

By considering v₀ = 0, and replacing $\Delta t$ with the iteration number, j, Eq. (19) is rewritten as follows:

$$ y_{j}^{i} = \frac{1}{2}\left( {y_{j}^{i} + y_{j}^{i - 1} } \right) $$

(21)

where i ≥ 2 and $y_{j}^{i}$ represents the location of ith follower salp in the jth dimension.

4.2 Proposed hybrid algorithm using Nelder–Mead

The SSA algorithm is a powerful algorithm that has led to superior results in many engineering problems. However, this algorithm has still drawbacks such as being trapped to local optimum and slow convergence. There is no one algorithm that works for every case according to no free lunch theorem (NFL). In the literature, it is shown that combining metaheuristics algorithms with the Nelder–Mead algorithm can lead to better convergence (Yıldız et al. 2019; Nelder and Mead 1965; Sarakhsi et al. 2016; Mesbahi et al. 2016). The Nelder–Mead simplex method (Nelder and Mead 1965) is effective in finding improved solutions. This algorithm has shown superiority over the other algorithms based on random search. Therefore, integrating the SSA and Nelder–Mead (NM) algorithms is proposed for enhancing these deficiencies.

The steps of the proposed hybrid algorithm are as follows: Firstly, the location and phase angle of the unbalance are obtained using the SSA algorithm. Secondly, the predicted phase and location are used as initial guesses for the Nelder–Mead algorithm to improve the accuracy and rate of convergence of the SSA algorithm. The flowchart of the proposed hybrid SSA–NM optimization algorithm is shown in Fig. 8.

Fig. 8

The flowchart of the SSA–NM algorithm

4.3 Optimization of unbalance response

In this subsection, the objective function for finding magnitude and phase of unbalance mass is presented. The objective function is considered as the weighted squared difference between the measured and calculated unbalance response as given in Eq. (22). Besides, the constraints are given in Eq. (23) in the negative null form. The former specifies the lower and upper bounds on the unbalance mass, while the latter is for specifying the lower and upper bounds on the phase angle.

$$ {\text{Cost}} \left( {m_{unb} , \varphi_{unb} } \right) = \mathop \sum \limits_{i} W_{i} \left( {\eta_{i}^{*} - \eta_{i} } \right)^{2} $$

(22)

$$ \begin{aligned} & 0 < m_{unb} < 500 \;{\text{g}}\,{\text{mm}} \\ & 0 < \varphi_{unb} < 360^{^\circ } \\ \end{aligned} $$

(23)

where $i$ is number of nodes, $W_{i}$ is the ith weighting factor, $\eta_{i}$, $\eta_{i}^{*}$ are the ith measured unbalance response of the unbalanced system, and the ith unbalance response estimated from the optimization algorithm, respectively. Weighting factor is considered $\frac{1}{i}$ for each node. The unbalance response related to each node is calculated according to Eq. (12). The optimization algorithm starts to find the optimal unbalance response, $\eta_{i}^{*}$, which is function of desired mass and phase of unbalance during selected iterations. Using more unbalance response related to modes in the objective function improves the accuracy of the optimization results. Eight test cases, as shown in Table 4, are considered with different magnitude of unbalance and phase angles for the rotor system with a single disk and double disks (Table 4). The magnitude of the unbalance is varied between 115 and 232 g mm. Similarly, the phase angles range between 30° and 225° in the test cases.

Table 4 Eight test cases

The displacement results are plotted against spin speed are plotted in Figs. 9 and 10 for the rotor systems with single disk and double disk, respectively. Besides, the displacement of node 7 and node 9 corresponding to the spin speed of 2000 rpm is summarized in Table 5. The variation of the results is due to the different magnitude and phase angles for the unbalance mass.

Fig. 9

Unbalance response for the rotor system with a single disk a test 1 and b test 2

Fig. 10

Unbalance response for the rotor with double disks a test 1 and b test 2

Table 5 Results for unbalance response due to the rotational unbalance for rotational speed of 2000 rpm

5 Taguchi design of experiment (DOE) method

As one of the objectives of the paper is to benchmark the accuracy and computational efficiency of the proposed method compared to four recent optimization algorithms, the optimization parameters are determined systematically. In this section, the details of the application of the Taguchi method are presented to tune the parameters of the proposed optimization algorithm. Design matrix consisting of orthogonal arrays is used to determine the best levels of the design factors by reducing the variance for the design of experiments in the Taguchi method. The essence of this method is to minimize the variance of the signal-to-noise ratio (S/N), which is considered as the objective function. Thus, this method enables us to gain insight into the effect of many design factors with a minimum number of experiments. The flowchart of the Taguchi DOE is shown in Fig. 11. The brief description of the five main steps is as follows:

• Phase 1 (Plan) The objective, measurement method, and main design factors are defined in this step.

• Phase 2 (Design) The noise factors, testing conditions, and objective functions are designed according to the factors and levels in the step.

• Phase 3 (Conducting) The design of the experiment matrix is conducted, and the results are generated in the third phase of the method.

• Phase 4 (Analysis) The results from the previous step are analyzed for determining the best design model. Various techniques such as S/N ratio are performed for analyzing the results based on the test condition.

• Phase 5 (Verification) The results from the DOE are verified by estimating how close the results match the actual performance. Besides, the expected improvement with the new design condition is estimated in the final step.

Fig. 11

The flowchart for the application of Taguchi method to tune the optimization parameters

The levels of the Taguchi method for the aforementioned optimization algorithms are presented in Table 6. Orthogonal arrays (OA) are used in this method to reduce the large number of experiments, which eventually reduce the computational time. For that purpose, the L25 array of Taguchi design of experiment method is used in this study (Roy 2001). The Taguchi method performs a sensitivity analysis to select a suitable level for each parameter. The sensitivity function (S/N ratio) is defined in Eq. (24):

$$ {\text{S/N ratio}} = - 10 \log \left[ {\sum \frac{{y_{i}^{2} }}{x}} \right] $$

(24)

Table 6 The levels of each optimization algorithm for Taguchi DOE method

where $y_{i}$ is the value of optimization objective function shown in Eq. (22) and $x$ is the number of repetitions of optimization method for solving the problem.

The results of the DOE study are shown in Fig. 12. The best parameters for case study 1 and case study 2 with the highest quality are reported in Tables 7 and 8, respectively.

Fig. 12

Taguchi design parameters for a GOA, b HHO, c WOA, and d SSA algorithms

Table 7 Optimization parameters used in case study 1

Table 8 Optimization parameters used in case study 2

6 Results and dıscussıon

In this section, the results of five algorithms are presented: (1) GOA, (2) WOA, (3) HHO, (4) SSA, and (5) SSA–NM. More specifically, the accuracy of the magnitude and phase of the unbalance is compared. Besides, the computational efficiency of each algorithm is discussed. For the demonstration purposes, two case studies are considered: (1) rotor system with a single disk and (2) rotor system with double disks. Considering the random and probabilistic nature of the optimization methods, all the algorithms are run ten times. The average of the results is then presented for accuracy and computational efficiency. The results for case studies 1 and 2 are presented in Sects. 5.1 and 5.2, respectively. The effect of rotor speed on identification methodology is examined in Sect. 5.3. The proposed methodology is demonstrated on a multi-disks in Sect. 5.4. Finally, the optimization method is applied to different unbalances experimentally to take into account the practical issues.

6.1 Case study 1: rotor system with a single disk

Eight tests are considered for the rotor-bearing system with different unbalance magnitudes and phase angles, as shown in Table 4. The unbalance response for each test is calculated according to the formulation outlined in Sect. 3.2. The aforementioned optimization algorithms are then used to determine the magnitude and phase of the aforementioned cases. The results for the rotor system with a single disk are summarized in Table 9.

Table 9 Optimization results for case study 1

The results indicate that all of the optimization algorithms are capable of predicting the phase of unbalance mass with very high accuracy for each test condition. However, the results on the magnitude of unbalance mass show some variation. The SSA algorithm is more accurate than GOA, WOA, and HHO algorithms. The results also indicate that the exploitation phase of SSA is more efficient than the exploration phase. This conclusion is supported by the fact that mere exploration does not guarantee the global optimum, and a proper balance between the exploration and exploitation phases is required. Therefore, a hybrid approach was used by integrating SSA and N–M algorithms. The Nelder–Mead algorithm is in considered as a deterministic class of optimization. One of the main advantages of this algorithm is its reliability, which means that it guarantees convergence. However, one important disadvantage of this algorithm is that it can cause local optima stagnation problem as the characteristics of deterministic optimization algorithms. On the other hand, SSA is known as one of the best algorithms available in the literature to avoid local optima stagnation in most of engineering problems. Local optima stagnation occurs when an optimization algorithm finds a local solution and considers it as the global optimum solution. A real search space usually has a large number of local solutions. Therefore, an optimization algorithm should be able to avoid them efficiently to determine the global optimum (Mirjalili et al. 2017). As a result, combining these two algorithms results in finding the optimal solution in term of best accuracy as shown in Table 8, the best results (i.e., the minimum value for the objective function or the most accurate prediction of magnitude and phase angle for the unbalance mass) are obtained from the application of the hybrid the SSA–NM algorithm. This indicates the success of the SSA–NM method in solving the optimization problem of unbalance mass detection. The performance of the Nelder–Mead algorithm depends on the initial guess from the application of the SSA algorithm to optimize the objective function.

Relative error between the optimization algorithm and actual values for each test is shown in Table 10. The results show that the SSA–NM algorithm is able to find the optimal solution exactly. The SSA algorithm has predicted the maximum error of 3.31% as the second best algorithm among the algorithms considered in this study.

Table 10 Relative error between actual and calculated value for magnitude and phase for case study 1

The aforementioned algorithms are compared on the convergence speed for the eight test cases in Fig. 13. The results indicate that the speed of convergence is improved significantly with the application of the SSA–NM algorithm.

Fig. 13

Objective function vs. iteration number for case study 1 a test 1, b test 2, c test 3, d test 4, e test 5, f test 6, g test 7, and h test 8

To mimic actual situation of these two study cases, different levels of noise are introduced and the results in terms of the accuracy are benchmarked with the other algorithms available in the literature. The optimization procedure was performed by using SSA–NM being the most accurate algorithm. The results and relative error results are reported in Table 11. The results show that maximum relative error is 0.4% on magnitude and 1.4% for the phase angle when there is 5% noise in the data. Therefore, the methodology is able to compete with methods in the literature.

Table 11 Optimization results for case study 1 with noise

6.2 Case study 2: rotor system with double disks

The proposed methodology is applied to the rotor system with double disks in this section. The number of variables in the objective function is changed to four to account for the addition of the second disk. For this case study, eight different test conditions are considered, as shown in Table 12. More variables in the optimization problems make it more difficult to converge. For instance, it is shown that for the rotor system with double disks, FOA (fruit fly algorithm) is not able to determine the unbalance parameters with the increase in the optimization variables (Yao et al. 2018).

Table 12 Optimization results for case study 2

Table 12 shows the result of optimization for double disks for solving the unbalance mass detection problem. Similar to case study 1, the performance of the SSA algorithm is better than GOA, WOA, and HHO algorithms on the prediction of the rotational unbalance mass. The improvement is attributed to: (1) the graduate movement of follower salps prevents the SSA algorithm from being trapped to local optima, and (2) the adaptive mechanism of SSA allows this algorithm to avoid local solutions and eventually finds an accurate estimation of the best solution. The proposed hybrid algorithm shows a superior performance in this problem. Similarly, the results on the relative error are presented in Table 13. The error related to the SSA–NM algorithm is zero. After that, SSA, HHO, GOA, and WOA have a minimum relative error, respectively. The results are also plotted in Fig. 14 to show the convergence of each algorithm. The results with the noise levels and the relative error on the magnitude and phase angle are summarized in Tables 14 and 15, respectively. The results show acceptable accuracy for detecting unbalance mass.

Table 13 Relative error for magnitude and phase for case study 2

Fig. 14

Objective function vs. iteration number for case study 2 a test 1, b test 2, c test 3, d test 4, e test 5, f test 6, g test 7, and h test 8

Table 14 Optimization results for case study 2 with noise

Table 15 Relative error for magnitude and phase for case study 2 with noise for SSA–NM algorithm

6.3 Effect of rotor speed on ıdentification process

One of the major concerns in the identification process is the effect of the rotor speed. The robustness of the developed methodology is investigated in terms of the rotor speed in this section. For that purpose, the unbalance response at multiple speeds for test 1 is used to identify the parameters of the unbalance for mutual verification. Similarly, different levels of noise as in case study 1 and 2 are considered in the analyses. The estimation of the unbalance parameters and the relative error between actual and estimated parameters corresponding to 0%, 1%, 3%, and 5% random noises for single disk and double disks cases are summarized in Tables 16 and 17, respectively. It is observed from Table 17, for the case study with single and double disks, the relative error considering the noise in the system is almost constant for the range of rotor speeds from 4000 to 12,000 rpm. The maximum relative error occurs for the rotor system with double disks where 5% noise is considered in the system. The simulation results demonstrate the robustness of the proposed methodology for the estimation of the rotational unbalance parameters.

Table 16 Effect of speed for finding unbalance For Test 1 and SSA–NM algorithm

Table 17 Relative error for different rotor speeds in Test 1 using SSA–NM algorithm

Table 18 shows the results of the aforementioned algorithms in the literature for identifying unbalance mass. The proposed optimization-based method has a higher accuracy than the other algorithms. More specifically, the maximum relative error on the magnitude and phase of unbalance mass for the majority of the eight cases is almost zero for the rotor system with a single and double disk. In the literature, various optimization methods have been tested only on one test case for the rotor system with double disk. In this study, the proposed algorithm has been compared with the aforementioned algorithms for eight test cases. As the results point out, the accuracy of the proposed algorithm is improved compared to the other algorithms in the literature, and the parameters can be calculated with high accuracy.

Table 18 Comparison of the proposed algorithm with previous research studies

The unbalance response of the rotor-bearing system is obtained from the proper sensors which is placed in the suitable place on the rotor. As it is seen in previous parts, this methodology successfully achieves the unbalanced parameters containing mass and radial distance needed for correction of unbalance in the system. The system can be balanced subjected to the condition that trial mass is kept at the specific radius, diametrically opposite to the disk eccentricity direction.

6.4 Verification of proposed method on a multi-disks case

In this part, a rotor-bearing system with multi-disks (four disks) is considered to challenge the proposed methodology for a complicated system. For this purpose, two disks are added to doubled-disk case: one disk at node 5 and the other one in node 3. Two unbalances are placed in disk 1 and disk 2 (node 9, 7) and the methodology is performed to identify the parameters of unbalances. Tests 1 and 4 are chosen with 5% level of noise at 4000 rpm speed of rotor. The results and related error for identification process are reported in Table 19. The results show little increment in errors in compared to single disk and double disks which is normal behavior for such complicated system. But these range of errors are acceptable for this system and the unbalances are estimated with good accuracy.

Table 19 Optimization results and relative error for multi-case disks with 5% noise for SSA–NM algorithm at 4000 rpm

6.5 Experimental validation

In this section, the rotor test rig and the way to obtain vibration response from the system is explained. When the system operates without any fault in the system, the vibration response is named as the response of the undamaged system. The vibration response is called the damaged response with the fault in the system. The residual vibration of the system is the difference between vibration responses of the undamaged and damaged system. The optimization process described in the previous sections is able to identify the unbalance parameters considering the residual vibration.

The rotor test rig used in this study is from IIT Guwahati and is shown in Fig. 15. The experimental setup consists of the shaft (diameter 10 mm and length 510 mm), a bush bearing, proximity sensors (eddy current displacement sensors: the probe sensitivity is 7874 V/m), and a motor speed control unit. The shaft has two detachable disks (placed at one-third of the shaft span) of 800 gm (with steel disks of inside diameter 10 mm, outside diameter 78 mm and thickness 25 mm) each mounted on it and having holes at different orientation at a distance 3 cm from disk center for addition of unbalances. The FEM model is created using 15 Timoshenko beam elements.

Fig. 15

The rotor test rig

As the first part of the model validation, an impulse test is performed on the test rig to compare the natural frequency of test rig and the FEM model. Displacement amplitude vs. frequency from this test is shown in Fig. 16. The first natural frequency of test rig and finite element model is 26 Hz and 24.93 Hz, respectively. The relative error is 4.3% due to conditions prevailing at bush bearings.

Fig. 16

a Displacement vs. time curve and b displacement amplitude vs. frequency curve for impulsive force applied in the rotor system

Two displacement sensors (eddy current sensor) are placed near two disks. The rotor runs at 900 rpm with and without the addition of the unbalance trials in the damaged rotor system. The displacement signals can be seen on the oscilloscope for left and right disks (named as left and right plane) and can be digitized for further processing. The vibrational response is as a result of the presence of residual unbalance, which is due to manufacturing tolerances, thermal distortion, as well as permanent bow. Permanent bow or residual bow can be produced in the shaft as a result of creep, and impulsive force. The effect of unbalance on the system is shown on displacement versus time curve, and orbit plot in Figs. 17 and 18, respectively.

Fig. 17

Displacement versus time curve at a left plane and b right plane with and without addition of trial unbalance at 900 rpm

Fig. 18

Orbit plot at a left plane and b right plane with and without addition of trial unbalance at 900 rpm

Total six tests for first case (one unbalance with two variables) and one test for second case (two unbalances with four variables) are designed to verify the proposed methodology. The response of these tests is measured and used in the unbalance identification algorithms. The rotor runs at 900 rpm and response of one sensor is used in the identification algorithm. The results for single and double unbalance cases are shown in Tables 20 and 21, respectively. The results show that the unbalance parameters including magnitude and phase can be identified by the proposed optimization methodology. The best result belongs to SSA–NM algorithm. For the single unbalance, the maximum and minimum relative errors of magnitude related to SSA–NM algorithm are 12.25% and 6.25%, respectively. Also maximum and minimum relative errors of phase related to SSA–NM algorithm are 6.8% and 0.12%, respectively. The relative errors related to double unbalance cases for magnitudes and phases are 13.19% and 17.94% and 6.51% and 14.65%, respectively, which is calculated by SSA–NM algorithm. The other algorithms identified the unbalance with huge errors that can be seen in Tables 20 and 21. As it is expected, the relative errors of double unbalances case are higher than the single unbalance case since the second case has more variables in comparison with the first case. Therefore, it is more challenging for the optimization algorithm to detect unbalances. In addition, the results demonstrate that the proposed methodology can identify the unbalances in the system with acceptable accuracy.

Table 20 Experimental results of the single unbalance in the system

Table 21 Experimental results of the double unbalances in the system

The balancing of the rotor system is carried out utilizing the balance masses estimated in Table 21. The balance masses are added at the respective planes, and the rotor system is operated at 900 rpm. The percentage reduction in displacement amplitude is shown in Table 22, i.e., found out to be 42% at the left plane location and 47% at the right plane location. The appreciable reduction in the dynamic response of the rotor system shows the effectiveness of the algorithm in the detection of the unbalances. The orbit plot of the rotor system at both balancing planes is shown in Fig. 19. It should be mentioned that to show the extent of balancing after addition of the balance mass, the residual shaft bow is removed from the responses in Fig. 19. The system is rotated at the low speed (250 rpm) and the displacement response due to shaft bow is obtained. (Contribution of the unbalance forces are less at lower speeds.) The 1× harmonics of low speed is subtracted from the 1× harmonics of the displacement responses at high speed to remove the bow effect. Then the orbit plot of the modified response is obtained that shows the vibrational amplitude due to unbalances only at 900 rpm.

Table 22 Balancing of the system with double unbalances for SSA–NM algorithm

Fig. 19

Orbit plot at a left plane and b right plane before and after balancing at 900 RPM

7 Conclusıons

A new methodology was proposed to identify the unbalance characteristics of rotating machinery based on the unbalance response. The objective function is considered as the weighted squared difference between the measured and the calculated unbalance responses. The proposed hybrid algorithm combines the power of the SSA algorithm to avoid local optima stagnation, and the reliability of the Nelder–Mead algorithm to find a more accurate solution for the rotational unbalance parameters. The performance of the proposed hybrid algorithm is compared to four algorithms in the literature. For a fair comparison of the results, the optimization parameters for all the algorithms are tuned systematically using the Taguchi method. The methodology is demonstrated on a rotor system with a single disk and double disks. The former has two design variables in the objective function, while the latter has four. The proposed methodology can determine the rotational unbalance parameters exactly for the rotor system with a single disk and double disks. For both case studies, the minimum and the maximum relative error between the optimized and actual values are 0% for the rotational unbalance mass and for the phase angle for the systems without any noise. The accuracy of the proposed method is much higher than the other algorithms considered in this case study. Moreover, this study shows that the proposed methodology can identify the parameters of the unbalance accurately for different rotor speeds in the presence of different noise levels. In addition, an experiment is conducted to verify the proposed method. The proposed algorithm is able to detect the unbalance characteristics with acceptable accuracy.

The research findings indicate that the new hybrid method has great potential to improve the accuracy of the solutions for engineering problems efficiently. Also, this methodology has high potential capabilities to combine with a suitable control system. With using active magnetic bearing in the system which can easily tune the stiffness and damping of the vibration, considering the magnitude of possible unbalances the unwanted vibration of the system can be simply reduced. Control application of such these methods will be the subject of our future research work.