An enhanced moth flame optimization with mutualism scheme for function optimization

Abstract

Nature-inspired meta-heuristics have demonstrated superior efficiency in the solution of complicated nonlinear optimization problems than conventional techniques. In this article, an enhanced moth flame optimization (EMFO) is designed using the mutualism phase from the symbiotic organism search (SOS) algorithm. The suggested approach is examined on 36 classical benchmark functions taken from literature. The outputs of EMFO are compared with the latest meta-heuristic algorithms and variants of the MFO algorithm. The comparison results indicate that our proposed method is competitive from the compared methods. Also, the Friedman rank test is used to evaluate the new algorithm’s efficiency, and it is found that the rank of EMFO is superior. Finally, EMFO is being applied to solve seven real-world problems, and the outcomes of the proposed algorithm were found to be satisfactory.

1 Introduction

Optimization is one of the main factors in both industrial purposes and the scientific research world. Many numerical and computational processes have been invented to clear up optimization issues in the last twenty years. However, with the aid of numerical methods, it is very complicated to resolve the problems which are non-convex, highly nonlinear, include a giant quantity of variables and constraints. To overcome the drawbacks, such as extra mathematical calculations, initial guess, and convergent problems in discrete optimization problems, a set of optimization algorithms known as meta-heuristics algorithms have been proposed in the latest decades, namely genetic algorithm (GA) (Holand 1992), particle swarm optimization (PSO) (Kennedy and Eberhart 1995), differential evolution (DE) (Storn and Price 1997), artificial bee colony (ABC) (Yi and He 2014), firefly algorithm (FA) (Yang 2009), cuckoo search algorithm (CS) (Gandomi et al. 2013), symbiotic organisms search (SOS) (Cheng and Prayogo 2014), JAYA algorithm (Arora and Singh 2015), butterfly optimization algorithm (BOA) (Mirjalili 2015), moth flame optimization (MFO) (Wang et al. 2015), monarch butterfly optimization (MBO) (Rao 2016), etc.

Nowadays, meta-heuristic algorithms are extensively used to solve engineering applications for their accessible mathematical operators, uncomplicated executions, and fewer chances to stick at local optimum solutions. Usually, these algorithms start with a randomly taken set of the initial solution and then run the process until the globally optimal solutions of the objective functions are obtained. Broadly we divide meta-heuristic algorithms into two classes, viz., single solution-based (SSB) methods and population-based (PB) methods. The SSB methods perform the search by single search representatives, and a group of search representatives is used in PB methods. Depending on single and social information, each solution’s position is renovated in PB methods. Moreover, various solutions can quickly check the whole search space; hence, better results are produced than SSB methods. The PB optimization methods are broadly grouped into four types: evolutionary algorithms, swarm intelligence (SI) algorithms, physical or chemical law-based algorithms and human-based algorithms. Apart from these algorithms, several algorithms have been proposed using mathematics concepts such as algebra and geometry. Some of such popular algorithms are sine cosine algorithm (SCA) (Mirjalili 2016), generalized convex approximation (GCA) (Chickermane and Gea 1996), nonlinear integer and discrete programming (NIDP) (Sandgren 1990), and the method of moving asymptotes (MMA) (Svanberg 1987).

The population-based optimization methods have two essential characteristics: diversification (exploration) and intensification (exploitation). Diversification refers to searching the entire space, representing the algorithm's capability in its global search competence. Exploitation refers to the quality of solutions in the course of iterations and shows the ability of a method in the local search and finding the best answer around an already seen potential solution. On the other hand, higher exploration causes a slow convergence rate for achieving a globally optimum solution. Higher exploitation causes convergence approaches to local optimum before key reaching global optima. Thus, a trade-off between these two factors is vital for an optimization algorithm to become efficient and robust.

In the last few decades, researchers have frequently modified several meta-heuristics (for example, improving algorithm formulae, parameters tuning of algorithms, hybridizing two or more algorithms, etc.). They have established other meta-heuristic methods to enhance the efficiency of the basic algorithms for solving complex and challenging scientific problems. They use commonly shared information among multiple agents, which is the main reason behind the popularity of meta-heuristic algorithms.

In the present article, MFO is considered to be thoroughly studied and analyzed. MFO is a swarm intelligence-based algorithm that was introduced in 2015 by Mirjalili (2015). MFOs inspiration came from the moth navigation technique in nature referred to as transverse orientation. The author of the MFO has proved that it has superior performance compared to the other popular meta-heuristic algorithms over twenty-nine benchmark functions. MFO has a solid ability to solve numerous challenging constrained and unknown search space problems, which is the main advantage of MFO among all other traditional algorithms.

Due to the advantages of MFO, such as faster convergence toward global solutions and a smaller number of algorithm-specific parameters, it has been enforced for several applications. Few of them are image segmentation (Muangkote et al. 2016), PID parameter optimization (Bourouba et al. 2018), economic load dispatch (ELD) problems (Babar et al. 2016), manufacturing industry optimization (Yidiz and Yidiz 2017), power load forecasting (Li et al. 2016a), solar energy devices (Allam and A, Eteiba MB, 2016), multilayer perceptron (Yamany et al. 2015), medical diagnoses (Wang et al. 2017), feature selection problem (Zawbaa et al. 2016), robust routing problem (Khan et al. 2018), unit commitment problem (Reddy et al. 2018), and optical network unit placement (Singh and Prakash 2017).

As a new PB optimization algorithm, however, MFO's performance is still required to improve in some direction, such as convergence rate and global optimum solution. Therefore, a lot of methods were proposed to enhance MFO's efficiency. In (Li et al. 2016b), the author developed a Levy flight operator, which increases population diversity, disrupts each moth's role, and enhances MFO convergence efficiency. Emary and Zawbaa (2016) added chaos parameter in the spiral equation to change the location for moths to improve MFO's efficiency to boost the basic MFO's. In (Apinantanakon and Sunat 2017), Apinantanakon and Sunat have introduced a new strategy named as opposition-based learning (OBL) to enhance the convergence speed of MFO. Elaziz et al. (2020) introduced a new method called OMFODE, by the combination of opposition-based learning and differential evolution (DE) which overcome the above limitations of the basic MFO algorithm. In (Singh and Salgotra 2018), three new techniques such as iteration division, Cauchy distribution function, and best flame technique have been used by authors to achieve a good trade-off between intensification and diversification. In (Li et al. 2018), the authors used two new techniques; one is flame generation technique by DE, and the other is dynamic guidance of flame. The obtained results outperform six modified MFO algorithms on CEC 2013 test suits concerning convergence rate and better solution. Savsani and Tawhid (2017) have proposed a multi-objective version of MFO by sorting non-dominated outcomes and crowding distance approach, which generates actual Pareto front and helps maintain diversity among the set of optimal results. Nanda and Multi-objective moth flame optimization (2016) have proposed multi-objective moth flame optimization by exploring and exploiting MFO algorithm, grid techniques, and non-dominated solutions for generating the Pareto front and finding the solutions of a multi-objective problem.

In recent times, meta-heuristics and hybrid meta-heuristics have played a significant role in the research field. Hybridization is used to solve complex optimization problems due to the combination of two to three individual meta-heuristics algorithms. It is also helpful for improving the meta-heuristics algorithm with additional techniques for better improvement in results, run-time, or both. Some of the hybrid methods of MFO have been developed by different authors, such as Bhesdadiya et al. (2017) proposed an algorithm by integrating PSO and MFO, which enhance the diversification search during solving high complex design problems and showed superiority in solving unconstrained optimization problems. In (Khalilpourazari and Khalilpourazary 2019), the author developed a modified algorithm of MFO by the mixture of water cycle algorithm (WCA) and MFO noted as WCMFO. Here MFO increases the exploitation, and WCA improves the diversification of WCMFO. Also, it has been used in solving constrained optimization problems. To overcome the premature convergence problem of MFO, Wu et al. (2018) proposed a new MFO algorithm which combines chaotic operator crisscross strategy in MFO. Kamalpathi et al. (2018) developed a new hybrid algorithm by the mixture of fuzzy logic control (FLC) and MFO algorithm and have been used to solve torque tap problem of the BLDC engine. In this literature, MFO has been used to control the minimum line stream harmonics and voltage in a motor system. In contrast, FLC has been used to increase the MFO’s efficiency by improving the MFO update position. Sarma et al. (2017) combined two algorithms named MFO and GSA and applied them to determine the degree of food rottenness problem, minimizing monetary losses due to food and storage. Also, to disable the shortcomings of the original MFO algorithm like low-quality solutions and slow convergence, Sayed and Hassanien (2018) developed another new algorithm by combining simulated annealing (SA) MFO algorithm. Recently, Li et al. (2021) developed a high-quality improvement in the MFO algorithm named ODSMFO to overcome the demerits of the MFO algorithm. The author added the OBL mechanism and DE algorithm to obtain good quality solution and diversity enhancement, respectively, then used an enhanced local search technique based on shuffled frog leaping algorithm (SFLA) to improve global search ability and finally applied death mechanism to eliminate individuals with low fitness value. Shan et al. (2021) proposed double adaptive weight mechanism for stabilization of MFO algorithm (WEMFO). The main goal of the WEMFO is to enhance the search capability and maintain a good trade-off between diversification and intensification of the classic MFO algorithm. The authors used two weights to adjust the search strategy adaptively in a different phase of the algorithm. Then, the efficiency of the proposed WEMFO was measured by applying it to train kernel extreme learning machines (KELM) and several engineering problems. Khan et al. (2021) used the strength of the MFO algorithm in an integrated power plant system containing a stochastic window (SW). The authors combined active set algorithm (ASA), interior point algorithm (IPA), and sequential quadratic programming (SQP) with MFO algorithm and developed three hybrid techniques named MFO-ASA, MFO-IPA, and MFO-SQP to solve economic load dispatch (ELD) problem and ELD including stochastic wind (ELD-SW). Pelosi et al. (2020) introduced an enhanced version of the basic MFO algorithm named improved moth flame optimization (IMFO) to reduce the shortcomings of the MFO algorithm, such as convergence speed and global searchability. They added a weight factor to the proposed algorithm to maintain equilibrium between local search and global search. Ma et al. (2021) introduced an improved version of the MFO algorithm developed to overcome the basic MFO algorithm's issues, such as slow convergence and convergence to a local minimum. The inertia weight of the diversity feedback control and the small probability mutation factor (added after the position update phase) is embedded in the proposed exploration balancing (and exploitation) and optimization performance algorithm. Zhao et al. (2020) proposed improved population-based techniques named improved MFO algorithm in which mutation operator and linear search techniques are used for position updating of original MFO algorithm and OBL strategy for a flame generation. Kigsirisin and Miyauchi (2021) proposed a method that is derived from the MFO algorithm named alternative binary MFO (BAMFO) to solve unit commitment (UC) problems. The main disadvantage of the MFO algorithm is a prefixed flame strategy responsible for stocking at a local optimum. In this proposed BAMFO, the authors introduced four flame generation strategies instead of following the predetermined flame strategy of the basic MFO algorithm. After that, a repair strategy was submitted to solve the UC problem. Tumar et al. (2020) developed a modified MFO algorithm named EBMFO (enhanced binary moth flame optimization algorithm) for the prediction of software faults by using adaptive synthetic sampling (ADASYN). In this literature, the original MFO algorithm's transformation to binary MFO algorithm has been discussed and then proposed the upgraded version named EBMFO algorithm. Spare and Mini (2021a) offered a new version of the MFO algorithm, namely the Emulous mechanism based multi-objective MFO algorithm (EMMFO). In this literature, pairwise competitions between the moths have been used to update the position of the moth in each iteration. Zhang et al. (2020) invented a new novel called improved multi-objective optimization and have been applied to solve the cascade reservoir model. In short, the proposed method is called R-IMOMFO, and the formulation has three phases. In the first phase, the authors of the literature first improved the basic MFO algorithm by adding three mechanisms (position update method, flame population update strategy, and inspiration of the moth linear flight path) to overcome the local stagnation and enhance the MFO algorithm. In the second phase, R-domination (with three reference points) technique has been used to distinguish the solution in Pareto domination. Finally, five new algorithms have been generated by integrating different evolutionary algorithms and multi-objective mechanisms to verify the performance of both IMFO and R-domination. Dabba et al. (2021) developed a modified version of the MFO algorithm named mutual information maximization-modified moth flame algorithm (MIM-MFA) and then applied it to solve gene selection in microarray data classification by the help of MIM. Kadry et al. (2021) proposed a new technique by using Kapur’s threshold image segmentation and modified MFO algorithm and then applied it to remove the tumor section from the clinical-grade MRI slices recorded with Flair and T2 modalities. The suggested algorithm has experimented on benchmark images of BRAINIX and TCIA-GBM. The experimental results proved the superiority against the T2 modality. Spare and Mini embedded (Sapre and Mini 2021b) a new algorithm named differential moth flame optimization algorithm (DMFO) and applied it to reduce wireless sensor networks' problems (WSNs) with mobile sink. Dash et al. (2020) applied Jaya-based MFO (JMFO) and basic MFO algorithm in IEEE network to minimize the loss transmission through an efficient position of FACTS devices. Two compensators named TCSC and SVC are used in IEE 14 AND IEE 30 bus system as a fitness function for MFO and JMFO algorithm. Gupta et al. (2020) developed a higher version of the MFO algorithm named modified MFO (MMFO) and applied it for suitable feature selection problems. Suja (2021) developed a modified algorithm to improve the performance and reduce the power quality issues for smart grid (SG) systems. The name of the modified MFO algorithm is Leavy flight MFO (LMFO) algorithm. The suggested method helps in getting better optimal solutions with respect to the objectives of SG systems.

Apart from the above modifications on MFO algorithm, various researchers have worked on other efficient meta-heuristic algorithms to enhance their performances. Some of those works are given below:

Asghari et al. (2021) developed two-hybrid methods named chaotic-based hybrid whale and PSO by integrating PSO with WOA (in short CWP) and multiswarm version of CWP (in short MCWP) which integrate MFO with improved WOA by using various chaotic maps and roulette wheel selection operator. Asghari et al. (2021) introduced another hybrid method named chaotic GWO and WOA (CGWW) by combining GWO with WOA to overcome the shortcomings of the both algorithm and developed an efficient algorithm. At first, the authors modified WOA and then integrate it with GWO. After that, chaotic maps have been applied to the hybrid GWO and WOA for enhancement of diversification and intensification. Gharehchopogh and Gholizadeh (2019) proposed a comprehensive survey on whale optimization algorithm and its application. The author provided an updated review version of the recently proposed whale optimization algorithm. They added various variants, improved and hybrid version of WOA with its application in various paths, including image processing, networks, engineering, task scheduling, and other engineering applications. Masdar and Zangakani introduced (Masdari and Zangakani 2020) an extensive survey on proactive virtual machine placement approaches, they split it into various categories such as simulation software, workload data, power management method, evaluation parameters, and prediction factor according to their applied forecasting methods. Masdar et al. (2017) developed another survey paper on PSO-based scheduling algorithms in cloud computing. They presented a deep analysis of the task and workflow scheduling scheme on PSO for the cloud environment and provided the classification based on the type of PSO algorithms. Masdar et al. (2019) introduced a new modified version of artificial bee colony algorithm named chaotic discrete version of an artificial bee colony (CDABC) with the help of chaotic maps. The author applied this algorithm to organize the lifetime of wireless sensor networks (WSNs) by choosing appropriate nodes. Nama et al. (2020a) proposed a novel hybrid meta-heuristic algorithm by combining teaching–learning-based optimization (TLBO) algorithm and quadratic approximation (QA), where the QA technique is applied to improve the global, as well as local search capability of the proposed algorithm. Nama et al. (2017a) proposed a new hybrid algorithm named hybrid symbiosis organisms search (HSOS) by integrating symbiosis organisms search (SOS) algorithm with simple quadratic interpolation (SQI), which helps in enhancing the robustness of the algorithm. Sharma et al. (2021) introduced a novel hybrid butterfly optimization algorithm named MPBOA, where the BOA is combined with mutualism and parasitism phases of the SOS algorithm to enhance the search behavior of BOA, which ensures a better trade-off between the global and local search of the proposed MPBOA algorithm. Sharma and Saha (2021) introduced a powerful hybrid algorithm named BOSCA by combining SCA with BOA, which helps stabilize the global exploration and local exploitation ability of the proposed algorithm. Chakraborty et al. (2021a) introduced a powerful hybrid meta-heuristic algorithm named WOAmM. The mutualism phase from the SOS algorithm is modified and integrated with WOA to alleviate premature convergence's inherent drawback. Chakraborty et al. (2021b) introduced a new hybrid method named SHADE-WOA by integrating modified WOA with success history-based adaptive differential evolution (SHADE). The main goal of this hybrid method is to reduce the shortcomings of both algorithms and guide both algorithms to explore and exploit in the search space and helps obtain good quality of solutions.

Another standard SI (Swarm Intelligence)-based algorithm is SOS, created in 2014 by Cheng and Prayogo. SOS comprises three, namely mutualism, commensalism, and parasitism process. Out of these three stages, the SOS phase of mutualism and commensalism describes enhancing the SOS algorithm's local exploitation potential. In contrast, the phase of parasitism deals with improving the algorithm's exploration capability. The results obtained from three versions of SOS with some combinations of benefit factors and adaptive benefit factors showed that it achieves a better trade-off between intensification and diversification in search space. From (Gandomi et al. 2013), it can be concluded that SOS is a powerful algorithm in terms of efficiency and solving numerous complicated real-life problems, which makes it a powerful algorithm as compared to other traditional algorithms. SOS has some advantages as it mimics common parameters like maximum number of feature evaluation and population size, has good capacity for exploitation with commensalism and mutualism processes, and has capacity for discovery by integrating mutation and cloning into the parasitism system.

Due to the above advantages, SOS has been applied in solving numerous engineering optimization problems. Few of them have been found in the literature which are given in Kavousi-Fard et al. (2015); Nama et al. 2016) and (Verma et al. 2017). Lots of modifications have been developed to improve SOS performance for various characteristics and structures of the problem. The details of these modifications have discussed in Nama et al. (2017b), Kumar et al. (2019) and Tejani et al. (2019), etc.

Though the MFO versions mentioned above have proved the most beneficial enhancements in their efficiency, they may also be caught at local optima and fail to generate excessive-performance flames and low convergence charge when engaged in solving a complex optimization problem. Recently, in m-MBOA (Sharma et al. 2020), the creator utilized the SOS mutualism step in the exploration section of BOA to decorate the overall performance of the original BOA algorithm. To tackle these problems and motivated by way of the above works, in this article, a novel expanded MFO (namely, EMFO) has been added in order to improve the performance of original MFO similarly by using adding the mutualism section of SOS with the simple MFO algorithm. The effectiveness of the proposed EMFO algorithm has been examined on a set of 36 benchmark take a look at functions from the literature, and also, the acquired outcomes have been in contrast with some ultra-modern optimization algorithms and determined that EMFO performs higher than the different meta-heuristic optimization algorithms.

The rest of the present article is designed as follows: A short summery on MFO algorithm is shown in Sect. 2. The mutualism phase is proposed in Sect. 3. The proposed EMFO algorithm and computational complexity of the proposed method are shown in Sect. 4 and Sect. 5, respectively. The simulation results and performance are presented in Sect. 6. Further in Sect. 6, a brief detail on benchmark functions, statistical test, convergence analysis, and comparison with variants of MFO algorithm are presented. The application of real-world problem is shown in Sect. 7 and at the end, conclusions are discussed in Sect. 8.

2 Moth flame optimization

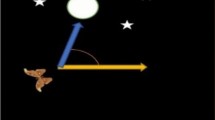
Moths are insects and belong to the class of Arthropoda. The navigation techniques of moths are unique, which attracts researchers to think about it. Moths travel in the night with the help of the moonlight, and for navigation, moths utilize a transverse orientation mechanism. Through crosswise inclination, they fly using moonbeam by keeping a fixed tendency toward the moon for a long journey in a straight path. The efficiency of direction depends on the distance of flame, i.e., when the distance between them decreases, the moth moves in a helix path around the flame which connects the moth to the flame. Using these behaviors of moth and mathematical modeling, the MFO algorithm was developed by Mirjalili in 2015.

2.1 MFO algorithm

In basic MFO, all moths are expressed as a set of candidate’s solutions and their position is expressed as a vector of decision variables. Let us consider the following matrix for moths

$$ X = \left[ {\begin{array}{*{20}c} {X_{1} } \\ {X_{2} } \\ \vdots \\ {X_{N} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{1,1} } & {x_{1,2} } & \cdots & {x_{1,n - 1} } & {x_{1,n} } \\ {x_{2,1} } & \ddots & \cdots & \cdots & {x_{2,n} } \\ \vdots & \cdots & \ddots & \cdots & \vdots \\ { x_{N - 1,1} } & \cdots & \cdots & \ddots & {x_{N - 1,n} } \\ {x_{N,1} } & {x_{N,2} } & \cdots & {x_{N, n - 1} } & {x_{N,n} } \\ \end{array} } \right] $$

(1)

where $X_{i} = \left[ {x_{i,1} , x_{i,2} , \ldots , x_{i,n} } \right]$, $i \in \left\{ {1, 2, \ldots ,N} \right\}$. N indicates moths’ number at initial population and n as variable numbers.

Now the fitness vector of moth is shown in below

$$ {\text{Fit}}\left[ X \right] = \left[ {\begin{array}{*{20}c} {{\text{Fit}}[X_{1} ]} \\ {{\text{Fit}}[X_{2} ]} \\ \vdots \\ {Fit[X_{n} ]} \\ \end{array} } \right] $$

(2)

The second key point of the MFO is flame matrix. Here the size of both moth’s matrix (X) and flame matrix (FM) are same as each moth flies around the corresponding flame.

$$ {\text{FM}} = \left[ {\begin{array}{*{20}c} {{\text{FM}}_{1} } \\ {{\text{FM}}_{2} } \\ \vdots \\ {{\text{FM}}_{N} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\text{Fm}}_{1,1} } & {{\text{Fm}}_{1,2} } & \cdots & {{\text{Fm}}_{1,n - 1} } & {{\text{Fm}}_{1,n} } \\ {{\text{Fm}}_{2,1} } & \ddots & \cdots & \cdots & {{\text{Fm}}_{2,n} } \\ \vdots & \cdots & \ddots & \cdots & \vdots \\ {{\text{Fm}}_{N - 1,1} } & \cdots & \cdots & \ddots & {{\text{Fm}}_{N - 1,n} } \\ {{\text{Fm}}_{N,1} } & {{\text{Fm}}_{N,2} } & \cdots & {{\text{Fm}}_{N - 1} } & {{\text{Fm}}_{N,n} } \\ \end{array} } \right] $$

(3)

Also, the fitness vector of flame matrix is stored in following matrix, i.e.,

$$ {\text{Fit}}\left[ {{\text{FM}}} \right] = \left[ {\begin{array}{*{20}c} {{\text{Fit[FM}}_{1} {]}} \\ {{\text{Fit[FM}}_{2} {]}} \\ M \\ {{\text{Fit[FM}}_{n} {]}} \\ \end{array} } \right] $$

(4)

Here Fit [$*$] is a candidate solution’s fitness function. In fact, MFO has two important component one is moth and other is flame, where moth moves through the respective flame to achieve suitable outcomes and the best outcomes acquired by the moth is known as flame. As the moth moves in a spiral manner; therefore, the author of MFO has defined a spiral function called logarithmic spiral function in order to create a spiral path which is represent in following equation.

$$ { }x_{i}^{K + 1} = { }\left\{ {\begin{array}{*{20}c} {\delta_{i} \cdot e^{{{\text{bt}}}} \cdot \cos \left( {2\pi t} \right) + {\text{Fm}}_{i} , i \le N \cdot {\text{FM}}} \\ {\delta_{i} \cdot e^{{{\text{bt}}}} \cdot \cos \left( {2\pi t} \right) + {\text{Fm}}_{i} , i \ge N \cdot {\text{FM}}} \\ \end{array} } \right. $$

(5)

where $\delta_{i} = \left| {x_{i}^{K} - {\text{Fm}}_{i} } \right|$, i.e., the distance between the ith moth Mi and its specific flame Fi; b is a constant to recognize the shape of the search for helix flight shape; t be any random number between -1 and 1 referring to how much closer the moth is to its specific flame. Illustration 1 represents that a moth flies toward its flame in a helix manner, with a distinct value of t in a one-dimensional manner. An adjustable course of action has been suggested to lessen the variable (t) value over the repetition, which enhance the effectiveness of both exploration and exploitation in first and last iterations, respectively.

$$ a_{1} = - 1 + {\text{current}}_{{{\text{iter}}}} \left( {\frac{ - 1}{{{\text{max}}_{{{\text{iter}}}} }}} \right) $$

(6)

$$ t = \left( {a_{1} - 1} \right) \times r + 1 $$

(7)

where ${\text{max}}_{{{\text{iter}}}}$ represents the number of maximum iterations, $a_{1}$ be the convergence constant decreases from − 1 to − 2 linearly proving that both diversification and intensification occurs in MFO algorithm. Each moth must renovate its position to just one flame to bypass local minima. Flames are sorted and modified in each iteration according to the fitness value. First, moth changes its location according to the first flame and last moth as per the last. However, this positioning can harm the exploitation of best solutions for N-flame positions. To overcome this issue, the number of flames (N.FM) is reduced over the iteration can be obtained by the following formula

$$ {\text{N}} \cdot {\text{FM}} = {\text{round}}\left( {{\text{N}} \cdot {\text{FM}}_{{\text{Lst it}}} - {\text{crnt}} \cdot {\text{it}}\frac{{\left( {{\text{N}} \cdot {\text{FM}}_{{\text{Lst it}}} - 1} \right)}}{{\max {\text{it}}}}} \right) $$

(8)

where both the flame number and last iteration flame number are denoted by N.FM and ${\text{N}} \cdot {\text{FM}}_{{\text{Lst it}}}$, respectively. Figures 1 and 2 represent the moths place corresponding to the first and last iterations of the method and spiral movement of moth around the flame, respectively. The details about MFO are described in Mirjalili (2015).

Fig. 1

Position of moths

Fig. 2

Spiral movement of moth

3 Symbiotic organisms search algorithm

SOS belongs to the SI-based design algorithm that has been invented by Cheng and Prayogo and can be used for a number of real problems. It copies the interdependency between various species to grow in a habitat as an individual solution in a community. The efficiency and sturdiness of SOS are standard and practically reasonable with respect to both benchmark and real-life problems. It haphazardly produces the first community by initializing N organisms and then using the three-way techniques like mutualism, commensalism, and parasitism phases new solutions are modernized. We have only merged the mutualism step of SOS in our proposed algorithm which is summarized in below.

When in nature, two different species get benefit from their interaction then it is called mutualism. Let us take two species $X_{i}$ and $X_{j}$ from the ecosystem where $X_{i}$ interacts with randomly selected species $X_{j}$ to create new solutions by using Eqs. (7) and (8):

$$ X_{{i^{{{\text{new}}}} }} = X_{i} + r\left[ {0,1} \right] \times \left( {X_{b} - \left( {\frac{{X_{i} + X_{j} }}{2}} \right) \times {\text{Ben}}_{{F_{1} }} } \right) $$

(9)

$$ X_{{j^{{{\text{new}}}} }} = X_{j} + r\left[ {0,1} \right] \times \left( {X_{b} - \left( {\frac{{X_{i} + X_{j} }}{2}} \right) \times {\text{Ben}}_{{F_{2} }} } \right) $$

(10)

where ${\text{r}}\left[ {0,1} \right]$ be a random number lying in the range $\left[ {0,1} \right]$, $X_{b}$ be the best ecosystem organism, ${\text{Ben}}_{{F_{1} }}$ and ${\text{Ben}}_{{F_{2} }}$ are the benefit factors whose value is either 1 or 2. These factors indicate the level of benefit to each organism, and mutual vector, i.e., $\left( {{{X_{i} + X_{j} } \mathord{\left/ {\vphantom {{X_{i} + X_{j} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)$, implies the characteristics relationship between $X_{i}$ and $X_{j}$. $X_{{i^{{{\text{new}}}} }}$ and $X_{{j^{{{\text{new}}}} }}$ will then be compared to $X_{i}$ and $X_{j}$ to select the best solution for each pair. In mutualism, new solutions are created on the basis of $X_{b}$.

4 Proposed method

The main motto of any meta-heuristic algorithm is to handle the balance between exploration and exploitation. We know that excessive exploration is the reason for losing optimal solutions because it spends more time searching the uninteresting regions. On the other hand, extreme exploitation is the main reason for premature convergence as the population rapidly lacks diversity. So, better performance of any algorithm is achieved when it maintains stability between diversification and intensification. In basic MFO, the parameter value t supports diversification and intensification. The power of the exponent factor ‘t’ gives a better clarification about exploration and exploitation. We know that the next position of the moth is obtained from the spiral Eq. 5. In this equation, t defines the next moth’s location relative to the flame. When t =  − 1, the next position moth is nearest, and t = 1 represents the farthest moth’s position regarding the flame. Therefore, exploration and exploitation occur when any moth’s next position belongs to the space to moth and flame and does not belong to the space, respectively. We observe that the sorting procedure of the best moth produces flames, and in other side position of moths are updated to the flame, leading to an imperfection in MFO and a reason for losing the promising individuals in the search space. Due to the more exploitation of basic MFO, some best solutions are stuck at local optima. To escape these solutions, we applied a simple step called the mutualism step of SOS in MFO, which is very effective in maintaining a balance between diversification and intensification in the search space and accelerates the speed of the solution. In mutualism phase, two candidate solutions update their position with the help of the best solution and thus they help themselves to find new solutions as the second candidate solution is chosen randomly and use of best solution confirms that the strategy also helps the solutions to find the nearby solutions of already existed best solution. For these benefits of mutualism strategy, Sharma et al. (2020), Chakraborty et al. (2021a), Wang et al. (2020), Tan et al. (2020), and Nama et al. (2017b) have applied mutualism scheme to various algorithms to enhance the performances of those algorithms to produce efficient algorithms. Our proposed methodology is called EMFO with the goal of maximizing population diversity against premature convergence and accelerating convergence speeds, i.e., this framework is useful to create a good balance between the diversification and intensification ability of MFO. We start the algorithm in the similar manner like MFO, and then, we apply mutualism phase (Eqs. 11 and 12) for position updating, i.e., in mutualism phase, we take two organisms (here organism means moths) from the population for updating the position of each moth in each iteration and share information with another randomly chosen moth to update their respective positions in the search space. The formulation of mutualism phase is presented below:

$$ X_{{i^{{{\text{new}}}} }}^{K + 1} = X_{i }^{K} + r\left[ {0,1} \right] \times \left( { X_{b }^{K} - \left( {\frac{{ X_{i }^{K} + X_{j }^{K} }}{2}} \right) \times {\text{Ben}}_{{F_{1} }} } \right) $$

(11)

$$ X_{{j {\text{new}}}}^{K + 1} = X_{j }^{K} + r\left[ {0,1} \right] \times \left( { X_{b }^{K} - \left( {\frac{{ X_{i }^{K} + X_{j }^{K} }}{2}} \right) \times {\text{Ben}}_{{F_{2} }} } \right) $$

(12)

where$X_{j }^{K}$ is randomly chosen another solution and $X_{{i^{{{\text{new}}}} }}^{K + 1}$, $X_{{j {\text{new}}}}^{K + 1}$ are new updated populations. ${\text{Ben}}_{{F_{1} }}$ and $Ben_{{F_{2} }}$ are benefit factor w.r.t $X_{i }^{K}$ and $X_{j }^{K}$ whose value is randomly considered as 1 or 2. Also, we plot a graph between the values of t with respect to the iterations in Fig. 3 for EMFO which provides the better value for t as compared to MFO. Due to the above characteristics, the proposed approach could provide superior performance over MFO and maintains good balance between exploration and exploitation.

Fig. 3

Comparison between EMFO and MFO w.r.t the parameter value t

The main EMFO steps can simply be shown in Algorithm 1 and summarized in below.

Step 1: Initialize all parameters such as number of populations, maximum iteration, and function evaluation randomly.

Step 2: Apply the sorting procedure to the both moth matrix and flame matrix w.r.t the fitness value and update number of flames using Eqs. 8.

Step 3: Update r and t using Eqs. 6 and 7.

Step 4: Update moths position w.r.t corresponding flame using Eq. 5.

Step 5: Update the new solution by using Eqs. 11 and 12 and then find the fitness value of the new solutions. Best fitness gives the optimum value.

Step 6: If it does not satisfy the stopping criteria then go to 2nd step until to get the best fitness value.

5 Computational complexity of EMFO

Complexity of any algorithm is a function which provides the running time or space with respect to input size. This is of two kinds: One is complexity of space and other is time complexity. The process of finding a formula for total space that will be required toward execution of the algorithm is referred as space complexity. Also, process of finding a formula for total time required for successful execution of algorithm is known as time complexity. The complexity of EMFO also depends on initialization of moth position (Ŧ_IMP), evaluation of moth position (Ŧ_EMP), searching of spiral flight (Ŧ_SSF), flame generation (Ŧ_FG), and position updating in mutualism phase Ŧ (_MP). Let maximum iterate number, variable number, and moths’ number are denoted by I, D, and N, respectively. Here we will use time complexity for the comparison of both EMFO and MFO algorithm. According to the quicksort algorithm, computational complexity for sorting N-flame and N-moth are lying between 3Nlog3NI and (3 N)²I toward worst and best case

Hence, time complexity for EMFO with respect to worst case is O [NI (D + N)]. Also, from Mirjalili (2015), the time complexity of MFO for the worst case is O [NI (D + N)]. Therefore, both MFO and EMFO has same complexity.

6 Results and discussion

This section includes a brief note on the benchmark functions and several discussions on the obtained results of both unimodal and multimodal benchmark functions. In Sect. 6.1, details of the benchmark functions are discussed. In Sect. 6.2, the experimental setup of our proposed method has been discussed. In Sect. 6.3, a comparison of EMFO with basic MFO and other evolutionary algorithms has been discussed. Friedmann rank test and convergence analysis of benchmark functions are presented in Sects. 6.4 and 6.5, respectively. In subsection 6.6, a comparison of EMFO with six variants of the MFO algorithm is presented with statistical measurement.

6.1 Benchmark functions

Every new meta-heuristic algorithm's performance must be validated and compared with other existing meta-heuristic algorithms over a good set of test functions. Thus, benchmark functions play an essential role in terms of reliability, verification, and efficiency of the algorithms. These test functions have been carefully selected from Jamil and Yang (2013) and are presented in Appendix 1. To validate our proposed EMFO algorithm, 36 benchmark functions have been selected and split into two parts, namely unimodal benchmark functions and multimodal benchmark functions.

The selected unimodal functions (from F1 to F15) include only one local optimum value called the global minimum value of the corresponding unimodal function. Unimodal functions are helped in validating the exploitation capability of the stochastic optimization algorithm. Therefore, these functions are optimized by those meta-heuristic algorithms which have better exploitation capability.

In the chosen multimodal functions (from F16 to F36), many local minimum values are associated with these functions and harder to solve than unimodal functions as sometimes solutions of these functions are stuck at local optima and are not escaped. Also, the difficulty level of multimodal functions rises with the number of dimensions, search area, and local optima value. Due to the ability to search new places, these functions test the exploration ability of meta-heuristic algorithms.

6.2 Experimental setup

The code of the proposed algorithm is written and implemented using MATLAB R2015a on a computer with an Intel i5 processor, 8 GB of RAM with Windows 2010 operating system. At most, 10,000 iterations are in use as a basis to stop our proposed algorithm. There are different ways to stop the algorithm, such as maximum number of iterations achieved, a fixed error tolerance value, maximum use of CPU time, and maximum number of iterations having zero improvements. Each function was repeated for 30 runs and rounded up two digits after the decimal to produce more minor statistical errors and statistically significant output.

We put down the mean (M) and standard deviation (SD) of EMFO with other algorithms for collation. One particular union of variables was used for EMFO in the copy of both unimodal and multimodal benchmark functions to fulfill this criterion. The powers exponent constant b is equal to 1 and t varies from − 1 to 1, and the population size is 50.

6.3 Experimental results of benchmark functions

In this subsection, the obtained simulation result of our proposed EMFO has been compared with other six meta-heuristics MFO, SOS, PSO, DE, JAYA, and BOA, on 36 benchmark functions including both unimodal and multimodal functions and are presented in subsection 6.3.1 and 6.3.2, respectively. Also, in subsection 5.3.3, it has been compared with other five popular and latest algorithm namely ABC, GA, FA, MBO, and CS.

6.3.1 Discussion on unimodal functions

The means and the standard deviations for optimized unimodal functions along with EMFO and other six algorithms are provided in Table 1. It is evident from the table that EMFO offered the least values compared to different algorithms. EMFO algorithm provides the best results for F1, F2, F3, F5, F7, F8, F9, F11, F13, and F14. It provides the second best results for functions F6 and F10 and inferior results for F4, F12, and F15. Therefore, our proposed approach can be assumed to be a superior algorithm to others.

Table 1 Comparison of unimodal functions with MFO, SOS, PSO, JAYA, DE, and BOA

6.3.2 Discussion on multimodal functions

In Table 2, functions F16 to F36 have been investigated under multimodal function optimization. It can be clear that for functions F16, F17, F18, F19, F20, F26, F27, F29, F30, F31, F32, F34, and F35, EMFO possess superior result than other algorithms. For functions F23, F28, and F36, EMFO offers the second highest results and for rest five functions it is inferior than other algorithms. Hence, it can be concluded that EMFO is a superior algorithm as compared to the six other algorithms in respect of the optimization of multimodal functions.

Table 2 Comparison of multimodal functions with MFO, SOS, PSO, JAYA, DE, and BOA

The number of cases where EMFO’s mean performance is better than, similar to, and worse than the other six algorithms is shown in Table 3. From Table 3, we noticed that EMFO works better than MFO, SOS, PSO, DE, BOA, and JAYA in 16, 20, 27, 26, 21, and 33 benchmark functions, respectively, similar results can be seen in 15, 10, 2, 3, 9, and 0 occasions, respectively, and worse values are achieved in 5, 6, 7, 7, 6, and 3 benchmark functions, respectively. The mathematical formulation of the 36 benchmark functions with dimension, range of the variables, and optimum value are shown in Appendix 1.

Table 3 Performance assessment of EMFO compared to MFO, SOS, PSO, DE, BOA, and JAYA on 36 benchmark functions

6.3.3 Discussion on other evolutionary algorithms

The simulation results including mean and standard deviations of EMFO, ABC, GA, FA, MBO, and CS

are presented in Table 4 for validating the performance of EMFO algorithm over 20 benchmark functions containing both unimodal (F1 to F12) and multimodal functions (F16 to F23). These benchmark functions are taken from Appendix 1. Except EMFO all results of other algorithms are taken from the reference (Kigsirisin and Miyauchi 2021). From Table 4, it is clear that for functions F1, F2, F3, F5, F6, F7, F9, F10, F12, F13, F14, F16, F17, and F21, EMFO has the best results as compared to other algorithms and for rest six functions EMFO offers second, third, and fourth best results. Therefore, it can be concluded that EMFO is a competitive algorithm as compared to other meta-heuristic algorithms.

Table 4 Comparison of EMFO with ABC, GA, FA, MBO, and CS

6.4 Friedman rank test

Milton (1937) developed a variable (non-parametric) statistical test called the Friedman test. It is used for the treatment of differences across numerous trials of the test. It ranks each row (or block) together and considers the value by columns. In this paper, for each benchmark function, the Friedman test is used from the average performance of algorithms. We use IBM-SPSS software for finding the middle rank. From Table 5, it is concluded that rank of EMFO can be seen that the rank of EMFO is least which indicates it is best among the rest methods.

Table 5 Statistical analysis (Friedman rank test)

6.5 Convergence analysis

To collate the convergence rate of EMFO with other algorithms, some of the convergence graphs compared with DE, PSO, JAYA, BOA, WOA, SOS, and MFO for few benchmark functions such as F1 (Sphere), F2 (Cigar function), F4 (Rosenbrock function), F5 (Schwefel1.2 function), F6 (Schwefel2.21 function), F7 (Schwefel2.22 function), F16 (Bohachevsky function), F17 (Ackley function), and F18 (Griewank Function) are presented in Fig. 4. In these figures, both the number of iterations and fitness evaluations are presented in horizontal and vertical axis, respectively, and the curves were plotted with dimensional size 100. EMFO has rapid convergence as compared to the other methods concerning the worldwide optima. On the other hand, the convergence rate of other compared optimization algorithms is moderate due to being stuck in neighborhood optima. For F4, converging to the global optima is tough for optimization problems as it is placed in a small canyon. However, the proposed EMFO achieves this global optimum within hundred dimensions. Therefore, the proposed EMFO reveals its high convergence rate equipped with other optimization methods.

Fig. 4

Convergence graph of benchmark functions for DE, PSO, JAYA, BOA, WOA, SOS, MFO, and EMFO

6.6 Comparison with some of the variants of MFO algorithm

In this subsection, comparison evaluation has been done in with six MFO variants such as LMFO (Li et al. 2016b), OMFO (Apinantanakon and Sunat 2017), MFO3 (Soliman et al. 2016), WCMFO (Khalilpourazari and Khalilpourazary 2019), ODSMFO (Li et al. 2021), and WEMFO (Shan et al. 2021). The simulation outcomes of EMFO together with six MFO variants for 20 benchmark functions including both unimodal (F1 to F12) and multimodal functions (F16 to F23) are presented in Table 6. These benchmark functions are taken from Appendix 1. All the results are evaluated using Matlab 2015(a). The mean (M) and standard deviation of EMFO with other variants of the MFO algorithm are presented in Table 6.

Table 6 Comparison of EMFO with other variants of MFO algorithm

From Table 6, it can be observed that our proposed EMFO algorithm achieved more than 85% best results for all groups of benchmark problems as compared to the variants of MFO algorithms but it provides seventy percent best results when compared with WCMFO and WEMFO algorithm. Also, the number of occasions of superiority, similarity, and inferiority is presented in Table 7. From Table 7, we noticed that EMFO works better than OMFO, LMFO, MMFO3, WCMFO, ODSMFO, and WEMFO in 15, 17, 14, 14, 20, and 12 benchmark functions, respectively, similar results can be seen in 3, 1, 3, 0, 0, and 3 occasions, respectively, and worse values are achieved in 2, 2, 3, 6, 0, and 5 benchmark functions, respectively.

Table 7 Performance assessment of EMFO compared to MFO, SOS, PSO, DE, BOA, and JAYA on 20 benchmark functions

6.6.1 Statistical analysis

Friedman is used to analyze the performance of proposed EMFO algorithm. In this paper, for each benchmark function Friedman test is used from the average performance of algorithms. We use IBM-SPSS software for finding the average rank. The outcomes of the Friedman rank test between EMFO with OMFO, LMFO, MMFO3, WCMFO, ODSMFO, and WEMFO for 20 benchmark functions is shown in Table 8. From Table 8, it is clearly visible that EMFO obtains least rank among other algorithms at 1% relevant.

Table 8 Friedman rank test on variants of MFO algorithm

6.6.2 Convergence analysis

To collate the convergence rate of EMFO with other algorithms, some of the convergence graphs compared with OMFO, LMFO, MMFO3, WCMFO, ODSMFO, and WEMFO for few benchmark functions such as F1 (Sphere), F2 (Cigar function), F6 (Schwefel 2.21 function), F7 (Schwefel2.22 function), F9 (Matyasa function), F16 (Bohachevsky function), F17 (Ackley function), F18 (Griewank Function), and F20 (Schaffer function) are presented in Fig. 5. In these figures, both the iteration and objective function value are presented in horizontal and vertical axes, respectively, and the curves were plotted with dimensional size 100. EMFO has rapid convergence as compared to the other methods concerning the worldwide optima. On the other hand, the convergence rate of other compared optimization algorithms is moderate due to being stuck in neighborhood optima. However, the proposed EMFO achieves this global optimum within hundred dimensions. Therefore, the proposed EMFO reveals its high convergence rate as compared to other variants of MFO.

Fig. 5

Convergence graph of benchmark functions for variants of MFO and proposed EMFO

7 Description of real-world problems

Seven real-world problems (RWP) such as optimal capacity of gas production problem, gear train design problem, cantilever beam design problem, minimize I-beam vertical deflection problem, welded beam design problem, three-bar truss design problem, and car-side crash design problem have been considered and solved by our proposed EMFO algorithm and discussed in following section. Appendix 2 shows the mathematical formulation of all the above problem.

7.1 RWP-1: optimal capacity of gas production problem

This problem is taken from Gandomi (2014). To measure the efficiency, EMFO has been tested by solving gas production problem. The experimental result of this problem is presented in Table 9 and compared with other algorithms, namely DE, GSA, and hybrid DE-GSA. It is clear that, the efficiency of our proposed work superior than other algorithms which is indicated by bold face in Table 9.

Table 9 Comparison performance of EMFO with MFO, DE, gravitation search algorithm (GSA), and DE-GSA for gas production problem

7.2 RWP-2: gear train design problem

It belongs to the branch of mechanical engineering and its target is to minimize the gear ratio for a set of four train gears (Połap 2017). It has four variables and has no constraint. The variables range are taken as constraints. The layout of the above problem is presented in Fig. 6.

Fig. 6

Gear train design problem

The efficiency of EMFO has been tested by solving the above problem and the obtained result compared with other eight meta-heuristic algorithms which is taken from Nama et al. 2020b and presented in Table 10. Table 10 confirms that EMFO algorithm produces superior results compared to the other algorithms.

Table 10 Comparison results of EMFO with different algorithms on gear train design problem

7.3 RWP-3: cantilever beam design problem

It comprises five hollow elements with square-shaped cross section. The beam is constant in thickness and each element has a single variable, so that five structural parameters are linked to it, as shown in Fig. 7. Figure 7 usually requires a vertical load on the free end of a beam (node 6) and a stable beam side (node 1) support. There is also one constraint of vertical displacement that does not violate the final optimal setup. The efficiency of EMFO has been tested by EMFO and compared with the other methods found in the literature (Kigsirisin and Miyauchi 2021), namely GCA-II, MMA, GCA-I, SOS, CS, and ALO. In Table 11, the bold face indicates that EMFO shows better performance for this problem.

Fig. 7

Cantilever beam design

Table 11 Comparison results of EMFO with different algorithms on cantilever beam design problem

7.4 RWP-4: minimize I-beam vertical deflection problem:

Out of the various structural problems, one of the important problems is I-beam vertical deflection. To minimize the vertical deflection of an I-beam is the main objective of this problem also stress constraints and cross-sectional area simultaneously satisfied under given loads. The figure of the problem is shown in Fig. 8.

Fig. 8

I-beam deflection

In Table 12, the optimum value obtained by MFO, SOS, SSA, ARSM, improved ARSM, SaISOS, CS, and EMFO for I-beam vertical deflection problem are presented and except EMFO, all the results are taken from Gandomi et al. (2011). It can be seen that EMFO outperforms than other algorithms. Therefore, we can conclude that EMFO has better efficiency, searching capability, and robustness in terms of solving real-world problems.

Table 12 Comparison of EMFO with ARSM, Improved ARSM, SOS, MFO, SSA, and SAISOS on I-beam vertical deflection problem

7.5 RWP-5: welded beam design problem

The problem of WB design is an important problem among all structural design issues, and it has been solved by different researchers. Fig. 9 shows the WB's schematic figure. From Fig. 9 and Appendix 2, it is clear that the beam has seven constraints and four variables. The slogan of this issue is to maximize WB's total cost with respect to the constraints of bending stress, shear stress, end deflection, and overhang load, respectively (P).

Fig. 9

Welded beam design problem

The optimization results of EMFO with other algorithms found in the literature are shown in Table 13. Our proposed EMFO algorithm found global optimum of 1.8011 within 50,000 function evaluations, i.e., it requires 1000 iterations. In Table 13 except EMFO all the other results are taken from Sapre and Mini 2021b and from Table 13, the bold face indicates that the obtained result of EMFO is superior to other algorithms found by the researchers.

Table 13 Comparison results of EMFO with different algorithms

7.6 RWP-6: three-bar truss design problem

Three-bar truss design problem is a structural optimization problem in civil engineering field. This problem is used due to its complex constrained search space (Gandomi et al. 2013; Sadollah et al. 2013). In addition to achieve minimum weight, two parameters of this design problem have been manipulated with respect to the constraints, namely buckling, stress, and deflection. The mathematical formulation and various components of the three-bar truss design problem are presented in Appendix 2 and Fig. 10, respectively.

Fig. 10

Three-bar truss design problem

This design problem is solved by using our proposed EMFO algorithm and compared with DEDS, MBA, Tsa, PSO-DE and CS algorithms in the literature (Mirjalili 2015) and the compared results including optimal variable and optimal weights are shown in Table 14. From Table 14, it can be concluded that our proposed EMFO algorithm is superior as compared to other three algorithms.

Table 14 Comparison performance of EMFO with other algorithms for three-bar truss problem

7.7 RWP-7: car-side impact design problem

This problem was initially proposed by Gu and Wang (2016). The car is exposed to a side impact on the foundation of the European Enhanced Vehicle Safety Committee (EEVC) procedures. The objective is to minimize the car's total weight using eleven mixed variables while maintaining safety performance according to the standard. These variables represent the thickness and material of critical parts of the vehicle. The 8th and 9th variables are discrete, and these are material design variables, while the rest are continuous and represent thickness design variables.

The symbols are used here to represent the variables thickness of B-pillar inner, the thickness of B-pillar reinforcement, the thickness of floor side inner, the thickness of cross members, the thickness of door beam, the thickness of door beltline reinforcement, consistency of roof rail, the material of B-pillar inner, the material of floor side inner, barrier height, and barrier hitting position, respectively. The problem is subjected to ten inequality constraints. The car-side impact design is considered a real case of a mechanical optimization problem with mixed discrete and continuous design variables.

This problem is solved by the proposed EMFO algorithm and compared with the other algorithms such as ABC, PSO, MFO, ALO, ER-WCA, GWO, WCA, MBA, SSA, and WOA found in the literature (Yildiz et al. 2020). The compared results are presented in Table 15. From Table 15, it can be concluded that the proposed EMFO has achieved the superior best solution compared to the other algorithms. The mathematical formulation and schematic diagram are presented in Appendix 2 and Fig. 11, respectively.

Table 15 Comparison performance of EMFO with other algorithms for car-side crash problem

Fig. 11

Car-side Image

8 Conclusion

In order to the above discussions, we can conclude that the intensification ability of EMFO is remarkable as can be observed from the results of unimodal functions optimization. It provides the satisfactory results for 90% of the benchmark functions. The diversification ability of EMFO is also impressive as can be observed from its better performance than other meta-heuristic algorithms. The EMFO can handle better trade-offs between global search and local search. Thus, it has vast scope for modification and future work.

This paper acquaints with the upgraded version of MFO called EMFO, which improves the MFO algorithm by the help of the interdependency step. To examine the performance of EMFO, several demonstrations have applied to the benchmark functions. The obtained results have been compared with the basic algorithms such as MFO, SOS, PSO, DE, BOA, JAYA, and with variants of the MFO algorithm. Also, validating the proposed EMFO was used to solve seven engineering design problems, which yield superior results than other popular algorithms. The results proved that the EMFO algorithm could use the better global optimum in the optimization phase, leading to rapid convergence. Further, the mutualism phase also allows the EMFO to avoid premature convergence and local optimum. Hence, we conclude that the proposed EMFO has convinced itself to be an encouraging method for solving engineering applications and real-life problems.

Appendices

Appendix 1

See Tables

Table 16 Mathematical formulation of unimodal functions

16,

Table 17 Mathematical formulation of multimodal functions

17 and

Table 18 Mathematical formulation of multimodal functions

18.

Appendix 2

• a. Optimal capacity of gas production problem

  $$ {\text{Min }}f\left( x \right) = 61.8 + 5.72 \times x_{1} \times 0.2623 \times \left[ {\left( {40 - x_{1} } \right) \times \ln \frac{{x_{2} }}{200}} \right]^{ - 0.85} + 0.087 \times \left( {40 - x_{1} } \right) \times \ln \frac{{x_{2} }}{200} + 700.23 \times x_{2}^{ - 0.75} $$
  $$ {\text{s.t}}.\;x_{1} \ge 17.5, x_{2} \ge 200, 17.5 \le x_{1} \le 40, 300 \le x_{2} \le 600; $$

• b. Gear train design problem

  $$ {\text{Minimize}}\;f\left( {\vec{x}} \right) = \left[ {\frac{1}{6.931} - \frac{{x_{3} x_{2} }}{{x_{1} x_{4} }}} \right]^{2} , $$
  $$ {\text{Subjected to }}12\; \le x_{1} , x_{2} , x_{3} , x_{4} \le 60, $$
  $$ {\text{Where}}\;\vec{x} = \left[ {x_{1} x_{2} x_{3} x_{4} } \right] = \left[ {n\alpha \; n\beta \; n\gamma \; n\delta } \right]. $$

• c. Cantilever beam design problem

  $$ {\text{Minimize}}\;f\left( {\vec{x}} \right) = 0.06224\left( {x_{1} + x_{2} + x_{3} + x_{4} + x_{5} } \right), $$
  $$ {\text{Subjected to}}: \, h(\vec{x}) = \frac{61}{{x_{1}^{3} }} + \frac{37}{{x_{2}^{3} }} + \frac{19}{{x_{3}^{3} }} + \frac{7}{{x_{4}^{3} }} + \frac{1}{{x_{5}^{3} }} \le 1, $$
  $$ {\text{Where}}\;0.01 \le x_{1} , x_{2} , x_{3} , x_{4} , x_{5} \le 100. $$

• d. I- beam vertical deflection problem

  $$ {\text{Minimize}}\;f\left( {\vec{x}} \right) = \frac{5000}{{\frac{{2t_{f} \left( {h - t_{f} } \right)^{2} }}{2} + \frac{{t_{w} *\left( {h - 2t_{f} } \right)}}{12} + \frac{{bt_{f}^{3} }}{6}}} $$

  Subjected to the cross-sectional area (< 300 cm²).

  $$ x_{1} = t_{w} *\left( {h - 2t_{f} } \right) + 2*b*t_{w} \le 300, $$

  The stress constraint (where allowable bending stress of the beam is 56 KN/CM²)

  $$ x_{2} = \frac{{15*b*10^{3} }}{{\left( {h - 2t_{f} } \right)*t_{w}^{3} + 2t_{w} *b^{3} }} + \frac{{18*h*10^{4} }}{{\left( {h - t_{f} } \right)^{3} *t_{w} + 2b\left( {4t_{f}^{2} + 3h\left( {h - 2t_{f} } \right)} \right)t_{w} *b^{3} }} \le 56 $$
  $$ {\text{Provided}}\;0.9 \le t_{f} , t_{w} \le 5,{ }10 \le b \le 50\;{\text{ and }}\;10 \le h \le 80 $$

• e. Welded beam design problem

  $$ {\text{Minimize}}\;f\left( {{\vec{\text{x}}}} \right) = f\left( {h, l, t, b} \right) = f\left( {{\text{x}}_{1} ,{\text{ x}}_{2} ,{\text{ x}}_{3} ,{\text{ x}}_{4} } \right) = {\text{A}}x_{2} x_{1}^{2} + Bx_{4} x_{3} \left( {C + x_{2} } \right). $$
  $$ {\text{Subjected to}}\;h_{1} \left( x \right) = \tau_{\max } - \tau \left( x \right) \ge 0 $$
  $$ h_{2} \left( x \right) = \sigma_{\max } - \sigma \left( x \right) \ge 0 $$
  $$ h_{3} \left( x \right) = \delta_{max} - \delta \left( x \right) \ge 0 $$
  $$ h_{4} \left( x \right) = x_{4} - x_{1} \ge 0 $$
  $$ h_{5} \left( x \right) = P_{c} \left( x \right) - P \ge 0 $$

  where A = 1.10471; B = 0.04811; C = 14.0

  $\tau_{\max } = 13600$ psi; $\sigma_{\max } =$ 30000psi; $\delta_{\max }$ = 0.25in;

  $$ \tau \left( x \right) = \sqrt {\left( {\tau^{\prime}\left( x \right)} \right)^{2} + \left( {\frac{{l\tau^{\prime\prime}\left( x \right)}}{{\sqrt {0.25\left( {x_{2}^{2} + \left( {x_{1} + x_{3} } \right)^{2} } \right)} }} + \left( {\tau^{\prime\prime}\left( x \right)} \right)^{2} } \right)} $$
  $$ \sigma \left( x \right) = \frac{50400}{{x_{4} x_{3}^{2} }} $$
  $$ P_{c} \left( x \right) = 64746x_{3} \left( {1 - 0.0282346x_{3} } \right)x_{4}^{3} $$
  $$ \delta \left( x \right) = \frac{2.1952}{{x_{4} x_{3}^{3} }} $$
  $$ \tau^{\prime}\left( x \right) = \frac{6000}{{\sqrt 2 x_{2} x_{1} }} $$
  $$ \tau^{\prime\prime}\left( x \right) = \frac{{6000\left( {0.5x_{2} + 14} \right)\sqrt {0.25\left( {x_{2}^{2} + \left( {x_{1} + x_{3} } \right)^{2} } \right)} }}{{2\left\{ {0.707x_{1} x_{2} \left( {\frac{{x_{2}^{2} }}{12} + 0.25\left( {x_{1} + x_{3} } \right)^{2} } \right)} \right\}}} $$
  $$ {\text{Range of variables}}\;0.125 \le x_{1} \le 5 $$
  $$ 0.1 \le x_{2} ,x_{3} \le 10 $$
  $$ 0.1 \le x_{4} \le 5 $$

  Parameters A = 1.10471; B = 0.04811; C = 14.0

  $\tau_{\max } = 13600$ psi; $\sigma_{\max } =$ 30000psi; $\delta_{\max }$ = 0.25in;

  E = 30 $\times 10^{6}$ psi G = 12 $\times 10^{6}$ psi.

  P = 6000 lb.

  L = 14in.

• f. Three-bar truss problem

  $$ \vec{\user2{k}} = \left\{ {k_{1} , k_{2} , } \right\} $$

  Objective function

  $$ {\text{Min}} \cdot f\left( k \right) = L\left\{ {k_{2} + 2\sqrt 2 k_{1} } \right\} $$

  Subject to

  $$ h_{1} \left( k \right) = \frac{{k_{2} }}{{2k_{2} k_{1} + \sqrt 2 k_{1}^{2} }} P - \sigma \le 0, $$
  $$ h_{2} \left( k \right) = \frac{{k_{2} + \sqrt 2 k_{1} }}{{2k_{2} k_{1} + \sqrt 2 k_{1}^{2} }} P - \sigma \le 0, $$
  $$ h_{3} \left( k \right) = \frac{1}{{k_{1} + \sqrt 2 k_{2} }}P - \sigma \le 0, $$

  where

  $$ 0 \le k_{1} ,k_{2} \le 1,\;{\text{and}} $$
  $$ P = 2, L = 100 \& \sigma = 2 $$

• g. Car-side crash design problem

  $$ \vec{\user2{a}} = \left\{ {a_{1} ,\user2{ }a_{2} ,a_{3} ,\user2{ }a_{4} ,\user2{ }a_{5} ,\user2{ }a_{6} ,\user2{ }a_{7} ,a_{8} ,a_{9} ,\user2{ }a_{10} ,a_{11} } \right\} $$

Objective function

$$ Min \; f\left( a \right) = 1.98 + 4.90 a_{1} + 6.67 a_{2} + 6.98 a_{3} + 4.01 a_{4} + 1.78 a_{5} + 2.73 a_{7} , $$

Subject to

$$ \begin{aligned} h_{1} \left( a \right) & = 1.16 - 0.3717 a_{2} a_{4} - 0.00931 a_{2} a_{10} - 0.484 a_{3} a_{9} \\ & + 0.01343 a_{6} a_{10 } \le 1, \\ \end{aligned} $$

$$ \begin{aligned} h_{2} \left( a \right) & = 0.261 - 0.0159 a_{1} a_{2} - 0.188 a_{1} a_{8} - 0.019 a_{2} a_{7} + 0.0144 a_{3} a_{5} + 0.0008757 a_{5} a_{10} \\ & + 0.080405 a_{6} a_{9} + 0.00139 a_{8} a_{11} + 0.00001575 a_{10} a_{11} \le 0.32, \\ \end{aligned} $$

$$ \begin{aligned} h_{3} \left( a \right) & = 0.214 + 0.00817 a_{5} - 0.131 a_{1} a_{8} - 0.0704 a_{1} a_{9} + 0.03099 a_{2} a_{6} - 0.018 a_{2} a_{7} + 0.0208 a_{3} a_{8} \\ & + 0.121 a_{3} a_{9} - 0.00364 a_{5} a_{6} + 0.0007715 a_{5} a_{10} - 0.0005354 a_{6} a_{10} + 0.00121 a_{8} a_{11} \le 0.32, \\ \end{aligned} $$

$$ h_{4} \left( a \right) = 0.074 - 0.061 a_{2} - 0.163 a_{3} a_{8} + 0.001232 a_{3} a_{10} - 0.166 a_{7 } a_{9} + 0.227 a_{2}^{2} \le 0.32, $$

$$ \begin{aligned} h_{5} \left( a \right) & = 28.98 + 3.818 a_{3} - 4.2 a_{1} a_{2} + 0.0207 a_{5} a_{10} + 6.63 a_{6} a_{9} \\ & - 7.7 a_{7} a_{8} + 0.32 a_{9} a_{10} \le 32, \\ \end{aligned} $$

$$ h_{6} \left( a \right) = 33.86 + 2.95 a_{3} + 0.1792 a_{10} - 5.05 a_{1} a_{2} - 11.0 a_{2} a_{8} - 0.0215 a_{5} a_{10} - 9.98 a_{7} a_{8} + 22.0 a_{8} a_{9} \le 32, $$

$$ \user2{ }h_{7} \left( a \right) = 46.36 - 9.9 a_{2} - 12.9 a_{1} a_{8} + 0.1107 a_{3} a_{10} \le 32, $$

$$ \begin{aligned} h_{8} \left( a \right) & = 4.72 - 0.5 a_{4} - 0.19 a_{2} a_{3} - 0.0122 a_{4} a_{10} + 0.009325 a_{6} a_{10} \\ & + 0.000191 a_{11}^{2} \le 4, \\ \end{aligned} $$

$$ \begin{gathered} h_{9} \left( a \right) = 10.58 - 0.674 a_{1} a_{2} - 1.95 a_{2} a_{8} + 0.02054 a_{3} a_{10} - \hfill \\ 0.0198 a_{4} a_{10} + 0.028 a\left( 6 \right) a\left( {10} \right) \le 9.9, \hfill \\ \end{gathered} $$

$$ h_{10} \left( a \right) = 16.45 - 0.489 a_{3} a_{7} - 0.843 a_{5} a_{6} + 0.0432 a_{9} a_{10} - 0.0556 a_{9} a_{11} - 0.000786 a_{11}^{2} \le 15.7, $$

where

$$ 0.5 \le a_{i} \le 1.5, i = 1, 2, 3, 4, 5, 6, 7 $$

$$ a_{8} ,a_{9} \in \left( {0.192, 0.345} \right), $$

$$ - 30 \le a_{10} , a_{11} \le 30. $$