Cubic fuzzy Heronian mean Dombi aggregation operators and their application on multi-attribute decision-making problem

Abstract

This paper contributes to cubic aggregation operator and applications in decision-making problem. In this paper, we use Dombi operational laws and Heronian mean operators, to develop a new concept of cubic fuzzy Heronian mean Dombi aggregation operators, i.e., cubic fuzzy Heronian mean Dombi aggregation (CFHMDA), cubic fuzzy weighted Heronian mean Dombi aggregation (CFWHMDA), cubic fuzzy geometric Heronian mean Dombi aggregation (CFGHMDA), and cubic fuzzy weighted geometric Heronian mean Dombi aggregation (CFWGHMDA) operators. The proposed operators are not deal single aspect, but also deal with the relation between multi-aspects making them more effectively solving decision-making (MADM) problems. We proposed a new algorithm to solve a multi-attribute decision-making problem based on the developed operators. Finally, we solved a MADM problems with the cubic fuzzy Heronian mean Dombi aggregation operators.

1 Introduction

In daily life, we are facing a decision-making problem which is a very important issue in the management of companies, for example, a company wants the most suitable supplier to make a strong supply root. Construction Company wants to choose a suitable site for construction to get better result for completing its project. A bus traveling company wants to estimate routes and select the suitable one and invite the other companies. In ancient times, decision-making methods attracted the researcher interest in every field of life. Furthermore, owing to the difficulties in decision-making, problems emerge in daily life. Decision-making problem options have to be calculated from multi-perspectives in its place and selecting only one before defining the most suitable option. Hence, (MADM) problems have invited the scholars to think about these issues (Shi et al. 2018; Xing et al. 2018; Xu et al. 2018; Mao et al. 2018; Wang et al. 2018; Yu et al. 2018; Zhang et al. 2017; Li et al. 2018a, b). Nevertheless, the decision-making information and selecting suitable values in MADM are a very big issue recently for several causes. The decision-making of concrete problems has many difficulties of denoting attribute data very closely, the other point which is influenced by factors such decision-makers personal experience and mental skills and sensitivity, and for an expert in decision-making it is very difficult to utilize all the information about the decision. Hence, assign attribute cost is urgent and correct which is to be needed. In the last few years, scholars have been working day and night to find a way to describe uncertain information and some theories about them. Zadeh (1965) is one of them. He presented affective tools called, fuzzy set (FS), to solve decision-making problems. Since his foundation, FS made a huge change in the field of mathematics. Afterward, Atanassov (1986) explained more FSs and corrected its defects, the work of Atanassov is called an intuitionistic fuzzy set (IFS), which shows us about the membership and non-membership degree. As IFSs have many good points to solve the problems of unclear information and values, they compile the scholars to find some solution for them. The notation of the intuitionistic fuzzy weighted averaging aggregation (IFWA) operators was introduced by Xu (2007), and Xu and Yager (2006). The notation of intuitionistic fuzzy Bonferroni mean operators was (IFBMO) introduced by the Wang and Liu (2012), Zhang (2017), and Xu and Yager (2011) and their simplest forms, etc. Arqub et al. (2017) defined some application of reproducing kernel algorithm for solving second-order, two-point fuzzy boundary value problems. Patel et al. (2015) introduced a novel methodology toward a trusted environment in mashup web applications. Notation of intuitionistic fuzzy Maclaurin symmetric mean operators is (IFMSM) proposed by Xia et al. (2013) and Qin and Liu (2014) in order to show relationship between multi attributes. Al-Janabi et al. (2020) developed an innovative synthesis of deep learning techniques (DCapsNet & DCOM) for generation electrical renewable energy from wind energy. Alkaim and Al-Janabi (2019) defined a multi-objectives optimization to gas flaring reduction from oil production. Al-Janabi et al. (2020) introduced a new method for prediction of air pollution based on intelligent computation. Al-Janabi and Alkaim (2020) defined a nifty collaborative analysis to predicting a novel tool (DRFLLS) for missing values estimation. Al-Janabi et al. (2015) proposed design and evaluation of a hybrid system for detection and prediction of faults in electrical transformers. Liu and Li (2017) defined some Muirhead mean operators for intuitionistic fuzzy numbers and their applications to group decision making. Arqub and Al-Smadi (2020) developed some fuzzy conformable fractional differential equations, which is the extended approach and new numerical solutions. Arqub et al. (2016) proposed the numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method.

1.1 Motivation and limitation

IFSs have a good advantage to explain decision information in MADM problems for decision-makers. Nevertheless, IFS has many defects that are not used in many circumstances for experts in decision-making to given facts. In the IFSs, one of the key points is that the unknown power is to ignore it, for example when experts in decision-making take an IFN (0.2, 0.3) is denoted his estimation on a positive attribute. Formerly, the unknown value of the experts in decision making is 1–0.2–0.3. In actual MADM, the degree of the unknown should not be found by itself and should be proposed by decision-makers. Suppose when the degree of membership and the degree of non-membership are found then the degree of the unknown is also found. For this purpose, decision-makers take some values 0.2 is the membership, 0.3 is the non-membership, the experts in decision making are not clear about the value is 0.1,  then the experts in decision making represent resulted value as (0.2, 0.1, 0.3),  which is not contained in IFSs. For the solution of these problems. Hence, the inherent fuzziness information with a great effort to solve this. IFSs incorporated fuzzy inference systems were presented by Le et al. (2017) to improve their presentation. Commonly saying, MADM methods are of two types. The first type in decision-making is old way decision-making. The old way is related to cubic fuzzy information in MADM problems. A second type is a form of aggregation observation operators, in which we used the aggregation for multi-attribute values into a single one and choose the best one. For a piece of good and suitable aggregation information, for a cubic fuzzy number (CFNs) (Fahmi et al. 2018) proposed some geometric operators with triangular cubic linguistic hesitant fuzzy number and their application in group decision making.

Thus, in MADM problems these operators have been very strongly used in CFNs, and there are few boundaries first of all cubic fuzzy numbers consists of algebraic operational laws for cubic fuzzy operators. Nowadays, DTT (Dombi 1982) is very powerful gears in aggregation and used in many processes of aggregation in single-valued neutrosophic information (Chen and Ye 2017), hesitant fuzzy information (He 2018), and intuitionistic fuzzy information (Liu et al. 2018). So, it is important to extend CFNs to DTT and their basic operational rules. Therefore, all the cubic fuzzy aggregation is not interrelated to each other between CFNs. However, attributes are more practical and MADM issues are interrelated, which means the interrelationship among the attribute values should be considered when it is aggregate. Nowadays, a large number of aggregation gears that can be proposed such interrelationship between aggregated variables have been come to models, such as the Heronian mean (HM) (Sykora 2009) Bonferroni mean (BM) (Bonferroni 1950). In the literature (Yu and Wu 2012), the expert has suggested why HM and has certain meliorist on BM. Therefore, in this article we work on HM and GHM are the important aggregation information procedure for combining CFNs based on DTT. So, we introduced for MADM a new procedure within the range of CFSs.

In this article, we presented new rules for the CFNs based on DTT; to present a new cubic fuzzy Dombi Heronian mean operators for the aggregation of CFNs and introduced a innovative style to decision making. In this way, the different sections of this paper are consisting of under. (1) Contain several elementary definitions of CFSs, DTT, HM, and GHM. (2) Contain propose a group of CFHMDA notation is cubic fuzzy Heronian mean Dombi aggregation operators. (3) Contain an algorithm for MADM problems with cubic fuzzy information. (4) We presented proof and numerical examples to verify the proposed method and the last result of this article.

2 Preliminaries

This section provides the basic concept and definition of fuzzy set and cubic sets.

Definition 1

(Zadeh 1965) Let $F\ne \phi$. Then, a fuzzy set E over F is defined by,

$$\begin{aligned} E=\{\left\langle \xi _{\alpha }(y)/y\right\rangle |y\in F\}, \end{aligned}$$

(2.1)

where $\xi _{\alpha }$ is called membership function of E and is denoted by $\xi _{\alpha }:F\rightarrow [0,1]$. For each $y\in F$, the value $\mu _{\alpha }(y)$ represents the degree of y belonging to the fuzzy set E.

Definition 2

(Atanassov1986) Let $F\ne \phi$, then a cubic set C in F is defined as follows,

$$\begin{aligned} C=\left\{ \left\langle y,\xi _{\alpha }(y),\gamma _{\alpha }(y)\right\rangle |y\in F\right\} , \end{aligned}$$

(2.2)

so $\xi _{\alpha }(y)$ is an IVF set in E and $\gamma (y)$ is a fuzzy set in E. A cubic set $C_{1}=\left\{ \left\langle y,\xi _{\alpha }(y),\gamma _{\alpha }(y)\right\rangle |y\in E\right\}$ is simply denoted by $C=\left\langle \xi _{\alpha },\gamma _{\alpha }\right\rangle ,$ and $C^{E}$ is denoted by the combination of all cubic sets in E. A cubic set $C=\left\langle \xi _{\alpha },\gamma _{\alpha }\right\rangle$ in which $\xi _{\alpha }(y)=0$ and $\gamma _{\alpha }(y)=1$(resp $\xi _{\alpha }(y)=1$ and $\gamma _{\alpha }(y)=0)\forall y\in E$ is denoted by 0 (resp 1).

A cubic set $C_{2}=\left\{ \left\langle y,\xi _{\beta }(y),\gamma _{\beta }(y)\right\rangle |y\in E\right\}$ is simply represented by $C=\left\langle \xi _{\beta },\gamma _{\beta }\right\rangle$ denoted by $C^{E}$ the combination of all cubic sets in E. A cubic set $C=\left\langle \xi _{\beta },\gamma _{\beta }\right\rangle$ in which $\xi _{\beta }(y)=0$ and $\gamma _{\beta }(y)=1$(resp $\xi _{\beta }(y)=0$ and $\gamma _{\beta }(y)=1)\forall$ $y\in E$ is denoted by 0 (resp 1).

Definition 3

[?] Let $E=\phi$. A cubic set $\beta =\left\langle \xi _{\alpha }(y),\gamma _{\alpha }(y)\right\rangle$ in E is said to be internal cubic set if $\xi _{\alpha }^{-}(y)\le \gamma _{\alpha }(y)\le \xi _{\alpha }^{+}(y)$ for all $y\in E.$

Definition 4

[?] Let $E=\phi$. A cubic set $\beta =\left\langle \xi _{\alpha }(y),\gamma _{\alpha }(y)\right\rangle$ in E is said to be an external cubic set if $\ \gamma _{\alpha }(y)\notin (\xi _{\alpha }^{-}(y),\xi _{\alpha }^{+}(y))$ for all $y\in E.$

Definition 5

[?] Let $C_{1}=\left\{ \left[ \xi _{\alpha }^{-},\xi _{\alpha }^{+} \right] ;\gamma _{\alpha }\right\}$ and $C_{2}=\left\{ [\xi _{\beta }^{-},\xi _{\beta }^{+}];\gamma _{\beta }\right\}$ be two cubic fuzzy sets (CFSs). Then, the operations on cubic fuzzy sets (CFSs) are defined as follows:

• (a) $C_{1}\subseteq C_{2}$ iff for all $\alpha ,\beta \in C$

  $$\begin{aligned} \xi _{\alpha }^{-}\ge & {} \xi _{\beta }^{-},\xi _{\alpha }^{+}\ge \xi _{\beta }^{+}{} \ and\gamma _{\alpha }\le \gamma _{\beta } \\ \xi _{\alpha }^{-}\le & {} \xi _{\beta }^{-},\xi _{\alpha }^{+}\le \xi _{\beta }^{+}{} \ \text {and}{} \ \gamma _{\alpha }\ge \gamma _{\beta } \end{aligned}$$

• (b) $C_{1}\cap _{T,T^{*}}C_{2}=\left\langle T\left[ \xi _{\alpha }^{-},\xi _{\beta }^{-}\right] ,T\left[ \xi _{\alpha }^{+},\xi _{\beta }^{+} \right] ,T\left[ \gamma _{\alpha },\gamma _{\beta }\right] \right\rangle .$

• (c) $C_{1}\cup _{T,T^{*}}C_{2}=\left\langle T\left[ \xi _{\alpha }^{-},\xi _{\beta }^{-}\right] ,T\left[ \xi _{\alpha }^{+},\xi _{\beta }^{+} \right] ,T\left[ \gamma _{\alpha },\gamma _{\beta }\right] \right\rangle .$

Hence, any pair $(T,T^{*})$ can be used; T represent a t-norm, and $T^{*}$ denote a t-conorm.

To compare any two CFNs, firstly we introduced the concept of score function.

Definition 6

(Wei2017) Let a cubic number $C=\left\{ \left[ \xi _{\alpha }^{-},\xi _{\alpha }^{+}\right] ; \gamma _{\alpha }\right\}$, then a score function S of C can be defined as;

$$\begin{aligned} S(C)=\frac{\xi _{\alpha }^{-}+\xi _{\alpha }^{+}-\gamma _{\alpha }}{3}. \end{aligned}$$

(2.3)

Definition 7

(Dombi1982) Let $\lambda$ $\ge 0$ and $y,z\in [0,1].$ The DTT are defined as follows;

$$\begin{aligned} T_{D,\lambda }(y,z)=\frac{1}{1+\left( \left( \frac{1-y}{y}\right) ^{\lambda }+\left( \frac{1-z}{z}\right) ^{\lambda }\right) ^{1/\lambda }}, \end{aligned}$$

(2.4)

and

$$\begin{aligned} T_{D,\lambda }^{*}(y,z)=1-\frac{1}{1+\left( 1+\left( \frac{y}{1-y} \right) ^{\lambda }+\left( \frac{z}{1-z}\right) ^{\lambda }\right) ^{1/\lambda }}, \end{aligned}$$

(2.5)

is consist on the notation (DTT) Dombi t-norm and t-conorm, we propose some new rules for CFNs.

Definition 8

[?] Let $C_{1}=\left\{ [\xi _{\alpha }^{-},\xi _{\alpha }^{+}];\gamma _{\alpha }\right\}$ and $C_{2}=\left\{ [\xi _{\beta }^{-},\xi _{\beta }^{+}];\gamma _{\beta }\right\}$ be a cubic numbers. Then,

$$\begin{aligned}&c_{1}\oplus _{D}c_{2}\\&\quad =\left\{ \begin{array}{c} \left[ 1-\frac{1}{1+\left( \left( \frac{\xi _{\alpha }^{-}}{1-\xi _{\alpha }^{-}}\right) ^{\lambda }+\left( \frac{\xi _{\beta }^{-}}{1-\xi _{\beta }^{-} }\right) ^{\lambda }\right) ^{1/\lambda }},1-\frac{1}{1+\left( \left( \frac{ \xi _{\alpha }^{+}}{1-\xi _{\alpha }^{+}}\right) ^{\lambda }+\left( \frac{ \xi _{\beta }^{+}}{1-\xi _{\beta }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ \frac{1}{1+\left( \left( \frac{1-\gamma _{\alpha }}{\gamma _{\alpha }} \right) ^{\lambda }+\left( \frac{1-\gamma _{\beta }}{\gamma _{\beta }} \right) ^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \\&c_{1}\otimes _{D}c_{2}\\&\quad =\left\{ \begin{array}{c} \left[ \frac{1}{1+\left( \left( \frac{1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}}\right) ^{\lambda }+\left( \frac{1-\xi _{\beta }^{-}}{\xi _{\beta }^{-} }\right) ^{\lambda }\right) ^{1/\lambda }},\frac{1}{1+\left( \left( \frac{ 1-\xi _{\alpha }^{+}}{\xi _{\alpha }^{+}}\right) ^{\lambda }+\left( \frac{ 1-\xi _{\beta }^{+}}{\xi _{\beta }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{\left( \left( \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }} \right) ^{\lambda }+\left( \frac{\gamma _{\beta }}{1-\gamma _{\beta }} \right) ^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \\&{pc}=\left\{ \begin{array}{c} \left[ 1-\frac{1}{1+\left( p\left( \frac{\xi _{\alpha ^{-}}}{1-\xi _{\alpha ^{-}}}\right) ^{\lambda }\right) ^{1/\lambda }},1-\frac{1}{1+\left( p\left( \frac{\xi _{\beta }^{-}}{1-\xi _{\beta }^{-}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ \frac{1}{1+\left( p\left( \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }} \right) ^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \\&{pc}^{*}=\left\{ \begin{array}{c} \left[ 1-\frac{1}{\left( p\left( \frac{\xi _{\alpha }^{+}}{1-\xi _{\alpha }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }},1-\frac{1}{1+\left( p\left( \frac{\xi _{\beta }^{+}}{1-\xi _{\beta }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ \frac{1}{1+\left( p\left( \frac{\gamma _{\beta }}{1-\gamma _{\beta }}\right) ^{\lambda }\right) } \end{array} \right\} \\&c^{p}=\left\{ \begin{array}{c} \left[ \frac{1}{1+\left( p\left( \frac{1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}}\right) ^{\lambda }\right) ^{1/\lambda }},\frac{1}{1+\left( p\left( \frac{1-\xi _{\beta }^{-}}{\xi _{\beta }^{-}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{1+\left( p\left( \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }} \right) ^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \\&c^{q}=\left\{ \begin{array}{c} \left[ \frac{1}{1+\left( q\left( \frac{1-\xi _{\alpha }^{+}}{\xi _{\alpha }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }},\frac{1}{1+\left( q\left( \frac{1-\xi _{\beta }^{+}}{\xi _{\beta }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{1+\left( q\left( \frac{\gamma _{\beta }}{1-\gamma _{\beta }} \right) ^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \end{aligned}$$

3 Heronian mean

Definition 9

(Sykora 2009) Let the series of crisp numbers is $y_{i}(i=1,2,\ldots ,k)$, if

$$\begin{aligned} {\text {HM}}^{p,q}(y_{1},y_{2},\ldots ,y_{k})= & {} \left( \frac{2}{k(k+1)}\underset{i=1}{ \overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }}y_{i}^{p}y_{j}^{q} \right) ^{\frac{1}{p+q}}, \end{aligned}$$

(3.1)

$$\begin{aligned} {\text {GHM}}^{p,q}(y_{1},y_{2},\ldots ,y_{k})= & {} \frac{1}{p+q}\prod \limits _{{\ddot{\imath }} =1}^{k}\prod \limits _{j=1}^{k}\left( py_{i}+qy_{j}\right) ^{\frac{2}{k(k+1)}},\nonumber \\ \end{aligned}$$

(3.2)

where p, q be a positive numbers, then ${\text {HM}}^{p,q}, {\text {GHM}}^{p,q}$ is called Heronian mean (HM) and geometric Heronian mean (GHM) operators. In this unite, we discuss HM to cubic fuzzy Heronian mean Dombi aggregation (CFHMDA) operators.

4 The cubic fuzzy Heronian mean Dombi aggregation (CFHMDA) operator

In this section, we generalized the aggregation operator of cubic number by using the Heronian mean and Dombi T-norm and D-T-conorm. We define the cubic fuzzy Heronian mean Dombi aggregation operators.

Definition 10

Let p, q be positive numbers and $c_{i}=\langle \left[ \xi _{\alpha i},\xi _{\beta i}\right] ;\gamma _{i}\rangle (i=1,2,\ldots ,k)$ be a collection of cubic numbers and $\lambda \ge 0$. Then, the cubic fuzzy Heronian mean Dombi aggregation (CPHMDA) operator is defined as;

$$\begin{aligned}&{\text {CPFDHM}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\nonumber \\&\quad =\left( \frac{2}{k(k+1)}\underset{i=1}{ \overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }}c_{i}^{p}\otimes c_{j}^{q}\right) ^{\frac{1}{p+q}}. \end{aligned}$$

(4.1)

Theorem 1

Let p, q be positive numbers and $c_{i}=\langle \left[ \xi _{\alpha i},\xi _{\beta i}\right] ;\gamma _{i}\rangle (i=1,2,\ldots ,k)$ be a collection of cubic numbers and $\lambda \ge 0$. Then, the cubic fuzzy Heronian Mean Dombi aggregation (CFHMDA)operator is defined as,

Proof

According to definition, we have;

$$\begin{aligned} c_{i}^{p}= & {} \left\{ \begin{array}{c} \left[ \frac{1}{1+\left( p\left( \frac{1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}}\right) ^{\lambda }\right) ^{1/\lambda }},\frac{1}{1+\left( p\left( \frac{1-\xi _{\beta }^{-}}{\xi _{\beta }^{-}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{1+\left( p\left( \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }} \right) ^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \ \\ c_{j}^{q}= & {} \left\{ \left[ \frac{1}{1+\left( q\left( \frac{1-\xi _{\alpha }^{+} }{\xi _{\alpha }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }},\frac{1}{ 1+\left( q\left( \frac{1-\xi _{\beta }^{+}}{\xi _{\beta }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] \right. ; \\&\quad \left. 1-\frac{1}{1+\left( q\left( \frac{ \gamma _{\beta }}{1-\gamma _{\beta }}\right) ^{\lambda }\right) ^{1/\lambda } }\right\} \end{aligned}$$

Let

$$\begin{aligned} \frac{1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}}= & {} A_{i},\frac{1-\xi _{\alpha }^{+}}{\xi _{\alpha }^{+}}=A_{j},\frac{1-\xi _{\beta }^{-}}{\xi _{\beta }^{-}}=B_{i},\frac{1-\xi _{\beta }^{+}}{\xi _{\beta }^{+}}=B_{j}, \\ \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }}= & {} C_{i},\frac{\gamma _{\beta } }{1-\gamma _{\beta }}\acute{=}C_{j}, \end{aligned}$$

Then, we have,

$$\begin{aligned}&c_{i}^{p}\otimes _{D}c_{j}^{q}=\left\{ \begin{array}{c} \left[ \frac{1}{1+(pA_{i}^{\lambda }+qA_{j}^{\lambda })^{1/\lambda }},\frac{1 }{1+\left( pB_{i}^{\lambda }+qB_{j}^{\lambda }\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{1+\left( pC_{i}^{\lambda }+qC_{j}^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \\&\underset{j=i}{\overset{k}{\sum }}c_{i}^{p}\otimes _{D}c_{j}^{q}\\&\quad =\left\{ \begin{array}{c} \left[ 1-1/1+\left( \underset{j=i}{\overset{k}{\sum }}\frac{1}{ (pA_{i}^{\lambda }+qA_{j}^{\lambda })}\right) ^{1/\lambda },1-1/\left( 1+\left( \underset{j=i}{\overset{k}{\sum }}\frac{1}{(pB_{i}^{\lambda }+qB_{j}^{\lambda })}\right) ^{1/\lambda }\right) \right] ; \\ 1/1+\left( \underset{j=i}{\overset{k}{\sum }}\frac{1}{pC_{i}^{\lambda }+qC_{i}^{\lambda }}\right) ^{1/\lambda } \end{array} \right\} \\&\underset{i=1}{\overset{k}{\sum }}\underset{j=i}{\overset{k}{\sum }} c_{i}^{p}\otimes _{D}c_{j}^{q}=\left\{ \begin{array}{c} \left[ \begin{array}{c} 1-1/1+\left( \underset{i=1}{\overset{k}{\sum }}\underset{j=i}{\overset{k}{ \sum }}\frac{1}{(pA_{i}^{\lambda }+qA_{j}^{\lambda })}\right) ^{1/\lambda }, \\ 1-1/\left( 1+\left( \underset{i=1}{\overset{k}{\sum }}\underset{j=i}{\overset{k}{\sum }}\frac{1}{(pB_{i}^{\lambda }+qB_{j}^{\lambda })}\right) ^{1/\lambda }\right) \end{array} \right] ; \\ 1/\left( 1+\left( \underset{i=1}{\overset{k}{\sum }}\underset{j=i}{\overset{k }{\sum }}\frac{1}{pC_{i}^{\lambda }+qC_{i}^{\lambda }}\right) ^{1/\lambda }\right) \end{array} \right\} \\&\qquad \qquad \qquad \qquad \qquad \qquad \left( \frac{2}{k(k+1)}\underset{i=1}{\overset{k}{\sum }}\underset{j=i}{ \overset{k}{\sum }}c_{i}^{p}\otimes _{D}c_{j}^{q}\right) ^{\frac{1}{p+q}} \\&=\left\{ \begin{array}{c} \left[ \begin{array}{c} 1/\left( 1+\left( \left( \frac{k(k+1)}{2(p+q)}\right) 1\times \left( \underset{i=1}{\overset{k}{\sum }}\underset{j=i}{\overset{k}{\sum }}\frac{1}{ pA_{i}^{\lambda }+qA_{j}^{\lambda }}\right. \right) ^{1/\lambda }\right) , \\ 1/\left( 1+\left( \left( 1+\left( \left( \frac{k(k+1)}{2(p+q)}\right) 1\times \left( \underset{i=1}{\overset{k}{\sum }}\underset{j=i}{\overset{k}{\sum }} \frac{1}{pB_{i}^{\lambda }+qB_{j}^{\lambda }}\right. \right) ^{1/\lambda }\right) \right) \right) \end{array} \right] ; \\ 1-1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\left( \left( \underset{i=1}{\overset{k}{ \sum }}\underset{j=i}{\overset{k}{\sum }}\frac{1}{pC_{i}^{\lambda }+qC_{i}^{\lambda }}\right. \right) ^{1/\lambda }\right) \right) \end{array} \right\} \end{aligned}$$

Now, putting the value back we have;

$$\begin{aligned}&{\text {CFHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k}) \\&\qquad =\left\{ \begin{array}{c} \left[ \begin{array}{c} 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\overset{k}{\sum }} \underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{1-\xi _{\alpha }^{-} }{\xi _{\alpha }^{-}}\right) ^{\lambda }+q\left( \frac{1-\xi _{\alpha }^{+}}{ \xi _{\alpha }^{+}}\right) ^{\lambda }}\right) ^{1/\lambda }\right) , \\ 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\overset{k}{\sum }} \underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{1-\xi _{\beta }^{-} }{\xi _{\beta }^{-}}\right) ^{\lambda }+q\left( \frac{1-\xi _{\beta }^{+}}{ \xi _{\beta }^{+}}\right) ^{\lambda }}\right) ^{1/\lambda }\right) \end{array} \right] ; \\ 1-1/\left( 1+\left( \left( 1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\overset{k}{\sum }}\underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }}\right) ^{\lambda }+q\left( \frac{\gamma _{\beta }}{1-\gamma _{\beta }}\right) } \right. \right) ^{1/\lambda }\right) \right) \end{array} \right\} \end{aligned}$$

This is the completing proof of ${\text {CFHMDA}}^{p,q}.$ $\square$

Moreover, the CFHMDA operators satisfy the below properties

Theorem 2

(Idempotency). Let $c_{i}=\left\langle \left[ \xi _{\alpha i}^{-},\xi _{\beta i}^{+}\right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,k)$ are the collection of CNs, if $c_{i}(i=1,2,\ldots ,k)$ are equal, that is $c_{i}=c=\left\langle \left[ \xi _{\alpha }^{-},\xi _{\alpha }^{+}\right] ;\gamma _{\alpha }\right\rangle .$ Then,

$$\begin{aligned} {\text {CFHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{n}) \end{aligned}$$

(4.2)

Proof

Let ${\text {CFHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})=(\xi _{\alpha }^{-},\xi _{\alpha }^{+},\gamma _{\alpha }),$ we will prove that $CFHMDA^{p,q}(c_{1},c_{2},\ldots ,c_{k})=\langle \left[ \xi _{\alpha }^{-},\xi _{\alpha }^{+}\right] ;\gamma _{\alpha }\rangle ,$ since $c_{i}=c=\left\langle \left[ \xi _{\alpha }^{-},\xi _{\alpha }^{+}\right] ;\gamma _{\alpha }\right\rangle ,$ and $c_{j}=c=\left\langle \left[ \xi _{\alpha }^{-},\xi _{\alpha }^{+}\right] ;\gamma _{\alpha }\right\rangle ,$ we have,

$$\begin{aligned} \xi _{\alpha }^{-}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{ \overset{k}{\sum }}\underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{ 1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}}\right) ^{\lambda }+q\left( \frac{ 1-\xi _{\alpha }^{+}}{\xi _{\alpha }^{+}}\right) ^{\lambda }}\right) ^{1/\lambda }\right) \\= & {} 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\overset{k}{\sum }} \underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{1-\xi }{\xi } \right) ^{\lambda }+q\left( \frac{1-\xi }{\xi }\right) ^{\lambda }}\right) ^{1/\lambda }\right) \\= & {} 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\overset{k}{\sum }} \underset{j=i}{\overset{k}{\sum }}\frac{1}{\left( \frac{1-\xi }{\xi }\right) ^{\lambda }\left( p+q\right) }\right) ^{1/\lambda }\right) \\= & {} 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\overset{k}{\sum }} \underset{j=i}{\overset{k}{\sum }}\frac{k(k+1)}{2\left( \frac{1-\xi }{\xi } \right) ^{\lambda }\left( p+q\right) }\right) ^{1/\lambda }\right) \\= & {} 1/\left( 1+\left( \frac{1-\xi }{\xi }\right) ^{\lambda }\right) ^{1/\lambda }=\xi \end{aligned}$$

Again, for $\xi _{\alpha }^{+}$

$$\begin{aligned} \xi _{\alpha }^{+}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{ \overset{k}{\sum }}\underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{ 1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}}\right) ^{\lambda }+q\left( \frac{ 1-\xi _{\alpha }^{+}}{\xi _{\alpha }^{+}}\right) ^{\lambda }}\right) ^{1/\lambda }\right) \\= & {} 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\overset{k}{\sum }} \underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{1-\xi }{\xi } \right) ^{\lambda }+q\left( \frac{1-\xi }{\xi }\right) ^{\lambda }}\right) ^{1/\lambda }\right) \\= & {} 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\overset{k}{\sum }} \underset{j=i}{\overset{k}{\sum }}\frac{k(k+1)}{2\left( \frac{1-\xi }{\xi } \right) ^{\lambda }\left( p+q\right) }\right) ^{1/\lambda }\right) \\= & {} 1/\left( 1+\left( \frac{1-\xi }{\xi }\right) ^{\lambda }\right) ^{1/\lambda }=\xi \end{aligned}$$

Similarly, for $\gamma \alpha ,$

$$\begin{aligned} \gamma _{\alpha }= & {} 1-1/\left( 1+\left( \left( 1+(\frac{k(k+1)}{2(p+q)} \times 1/\underset{i=1}{\overset{k}{\sum }}\underset{j=i}{\overset{k}{\sum }} \frac{1}{p\left( \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }}\right) ^{\lambda }+q\left( \frac{\gamma _{\beta }}{1-\gamma _{\beta }}\right) } \right) ^{1/\lambda }\right) \right) \\= & {} 1-1/\left( 1+\left( \left( 1+(\frac{k(k+1)}{2(p+q)}\times 1/\underset{i=1}{\overset{k}{\sum }}\underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{ \gamma }{1-\gamma }\right) ^{\lambda }+q\left( \frac{\gamma }{1-\gamma } \right) }\right) ^{1/\lambda }\right) \right) \\= & {} 1-1/\left( 1+\left( \left( 1+(\frac{k(k+1)}{2(p+q)}\times 1/\underset{i=1}{\overset{k}{\sum }}\underset{j=i}{\overset{k}{\sum }}\frac{1}{\left( \frac{ \gamma }{1-\gamma }\right) ^{\lambda }\left( p+q\right) }\right) ^{1/\lambda }\right) \right) \\= & {} 1-1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\overset{k}{\sum } }\underset{j=i}{\overset{k}{\sum }}\frac{k(k+1)}{2\left( \frac{\gamma }{ 1-\gamma }\right) ^{\lambda }\left( p+q\right) }\right) ^{1/\lambda }\right) \\= & {} 1-1/\left( 1+\left( \left( \frac{\gamma }{1-\gamma }\right) ^{\lambda }\right) ^{1/\lambda }\right) =\gamma \end{aligned}$$

Hence, proved. $\square$

Theorem 3

(Monotonicty) Let $c_{i}=\left\langle \left[ \xi _{i}^{-},\xi _{i}^{+}\right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,k)$ and $c_{i}^{*}=\left\langle \left[ \xi _{i}^{-^{*}},\xi _{i}^{+*}\right] ;\gamma _{i}^{*}\right\rangle (i=1,2,\ldots ,k)$ be two CNs, if $c_{i}\le c_{i}^{*},$ for all i, then,

$$\begin{aligned} {\text {CFHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\le {\text {CFHMDA}}^{p,q}(c_{1}^{*},c_{2},\ldots ,c_{k}^{*}) \nonumber \\ \end{aligned}$$

(4.3)

Proof

Let ${\text {CFHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})=\left\langle \left[ \xi _{i}^{-},\xi _{i}^{+}\right] ;\gamma _{i}\right\rangle$ and ${\text {CFHMDA}}^{p,q}(c_{1}^{*},c_{2}^{*},\ldots ,c_{k}^{*})=\left\langle \left[ \xi _{i}^{-^{*}},\xi _{i}^{+*}\right] ;\gamma _{i}^{*}\right\rangle ,$ since $\xi _{i}\le \xi _{i}^{*},$ then we have;

$$\begin{aligned} \ \frac{1-\xi _{i}}{\xi _{i}}\ge & {} \frac{1-\xi _{i}^{*}}{\xi _{i}^{*}} \\ \frac{1-\xi _{j}}{\xi _{j}}\ge & {} \frac{1-\xi _{j}^{*}}{\xi _{j}^{*} } \end{aligned}$$

Thereafter,

$$\begin{aligned}&\ \left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\times 1/\overset{k}{\sum }} \underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{1-\xi _{i}}{\xi _{i} }\right) ^{\lambda }+q\left( \frac{1-\xi _{j}}{\xi _{j}}\right) ^{\lambda }} \right) ^{1/\lambda } \\&\quad \ge \left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\times 1/\overset{k}{\sum } }\underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{1-\xi _{i}^{*} }{\xi _{i}^{*}}\right) ^{\lambda }+q\left( \frac{1-\xi _{j}^{*}}{\xi _{j}^{*}}\right) ^{\lambda }}\right) ^{1/\lambda } \end{aligned}$$

And,

$$\begin{aligned}&1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\times 1/\overset{k}{\sum }} \underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{1-\xi _{i}}{\xi _{i} }\right) ^{\lambda }+q\left( \frac{1-\xi _{j}}{\xi _{j}}\right) ^{\lambda }} \right) ^{1/\lambda }\ \\&\quad \le \left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\times 1/\overset{k}{\sum } }\underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{1-\xi _{i}^{*} }{\xi _{i}^{*}}\right) ^{\lambda }+q\left( \frac{1-\xi _{j}^{*}}{\xi _{j}^{*}}\right) ^{\lambda }}\right) ^{1/\lambda } \\&1/(1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\times 1/\overset{k}{\sum } }\underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{1-\xi _{i}}{\xi _{i}}\right) ^{\lambda }+q\left( \frac{1-\xi _{j}}{\xi _{j}}\right) ^{\lambda }}\right) ^{1/\lambda }\ \\&\quad \le 1/(1+\left( \frac{k(k+1)}{2(p+q)}\underset{i=1}{\times 1/\overset{k}{ \sum }}\underset{j=i}{\overset{k}{\sum }}\frac{1}{p\left( \frac{1-\xi _{i}^{*}}{\xi _{i}^{*}}\right) ^{\lambda }+q\left( \frac{1-\xi _{j}^{*}}{\xi _{j}^{*}}\right) ^{\lambda }}\right) ^{1/\lambda } \end{aligned}$$

which means $\xi \le \xi ^{*},$ similarly, we can also prove remaining result like this. $\square$

Theorem 4

(Boundedness) Let $c_{i}=\left\langle \left[ \xi _{i}^{-},\xi _{i}^{+}\right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,n)$ be a collection of CNs , if $c_{1}^{+}=\left\langle \left[ (\max )\xi _{i}^{-},(\min )\xi _{i}^{+}\right] ;(\min )\gamma _{i}\right\rangle$ and $c_{2}^{-}=\left\langle \left[ (\min )\xi _{i}^{-},(\max )\xi _{i}^{+}\right] ;\right.$$\left. (\max )\gamma _{i}\right\rangle .$ Then,

$$\begin{aligned} \ c_{2}^{-}\le {\text {CFHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\le c_{1}^{+} \end{aligned}$$

(4.4)

Proof

From theorem, we have;

$$\begin{aligned} {\text {CFHMDA}}^{p,q}(c_{2}^{-},c_{2}^{-},\ldots ,c_{k}^{-})= & {} c_{2}^{-}, \\ {\text {CFHMDA}}^{p,q}(c_{1}^{+},c_{1}^{+},\ldots ,c_{k})= & {} c_{1}^{+}. \end{aligned}$$

Thereafter

$$\begin{aligned}&{\text {CFHMDA}}^{p,q}(c_{2}^{-},c_{2}^{-},\ldots ,c_{k}^{-})\\&\quad \le {\text {CFHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\\&\quad \le {\text {CFHMDA}}^{p,q}(c_{1}^{+},c_{1}^{+},\ldots ,c_{k}) \end{aligned}$$

Therefore, we get

$$\begin{aligned} c_{2}^{-}\le {\text {CFHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\le c_{1}^{+}\\ \end{aligned}$$

$\square$

5 The cubic fuzzy weighted Heronian mean Dombi aggregation (CFWHMDA) operator

Definition 11

Let $p,q\ge 0$ and $c_{i}=\left\langle \left[ \xi _{i}^{-},\xi _{i}^{+} \right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,k)$ be a collection of CNs. If

$$\begin{aligned}&{\text {CFWHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\ \nonumber \\&\qquad =\left( \frac{2}{k(k+1)}\overset{k}{ \underset{i=1}{\sum }}\underset{j=i}{\overset{k}{\sum }}\left( {\hat{w}} _{i}c_{i}\right) ^{p}\otimes _{D}\left( {\hat{w}}_{j}c_{j}\right) ^{q}\right) ^{\frac{1}{p+q}}, \nonumber \\ \end{aligned}$$

(5.1)

so the weighted vector is $\ {\hat{w}}=({\hat{w}}_{1},{\hat{w}}_{2},\ldots ,{\hat{w}} _{n})^{T}$ of $c_{i}$ $(i=1,2,\ldots ,k)$ where ${\hat{w}}\in [0,1],$ $\sum _ {i=1}^{n} \ {\hat{w}}_{i}=1.$ Then, ${\text {CFWHMDA}}^{p,q}$ is the cubic fuzzy weighted Heronian mean Dombi Aggregation operator.

Theorem 5

Let $p,q\ge 0$ and $c_{i}=\left\langle \left[ \xi _{i}^{-},\xi _{i}^{+} \right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,k)$ is a combination of CNs. The aggregated value CFWHMDA is still a CNs and,

$$\begin{aligned}&{\text {CFWHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k}) \\&\quad =\left\{ \begin{array}{c} \left[ \begin{array}{c} 1/1+\left( \frac{k(k+1)}{2(p+q)}\times 1/\left( \underset{i=1}{\overset{k}{ \sum }}\overset{k}{\underset{j=i}{\sum }}1/\left( \frac{p}{{\hat{w}}_{i}\left( \frac{\xi _{\alpha }^{-}}{1-\xi _{\alpha }^{-}}\right) ^{\lambda }}+\frac{q}{ {\hat{w}}_{j}\left( \frac{\xi _{\alpha }^{+}}{1-\xi _{\alpha }^{+}}\right) } \right) \right) \right) ^{1/\lambda }, \\ 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\times 1/\left( \underset{i=1}{ \overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }}1/\left( \frac{p}{{\hat{w}}_{i}\left( \frac{\xi _{\beta }^{-}}{1-\xi _{\beta }^{-}}\right) ^{\lambda }} +\frac{q}{{\hat{w}}_{j}\left( \frac{\xi _{\beta }^{+}}{1-\xi _{\beta }^{+}} \right) }\right) \right) \right) ^{1/\lambda }\right) \end{array} \right] ; \\ 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\times 1/\left( \underset{i=1}{ \overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }}1/\left( \frac{p}{{\hat{w}}_{i}\left( \frac{^{\gamma _{\alpha }}}{1-\gamma _{\alpha }}\right) ^{\lambda }}+\frac{q}{{\hat{w}}_{j}\left( \frac{\gamma _{\beta }}{1-\gamma _{\beta }}\right) }\right) \right) \right) ^{1/\lambda }\right) \end{array} \right\} \end{aligned}$$

Proof

According to given definition, we have,

$$\begin{aligned} {\hat{w}}_{i}c_{i}= & {} \left\{ \begin{array}{c} \left[ 1-\frac{1}{1+\left( {\hat{w}}_{i}\left( \frac{\xi _{\alpha }^{-}}{1-\xi _{\alpha }^{-}}\right) ^{\lambda }\right) ^{1/\lambda }},1-\frac{1}{1+\left( {\hat{w}}_{i}\left( \frac{\xi _{\beta }^{-}}{1-\xi _{\beta }^{-}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{1+\left( {\hat{w}}_{i}\left( \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }}\right) ^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \\ {\hat{w}}_{j}c_{j}= & {} \left\{ \begin{array}{c} \left[ 1-\frac{1}{1+\left( {\hat{w}}_{j}\left( \frac{\xi _{\alpha }^{+}}{1-\xi _{\alpha }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }},1-\frac{1}{1+\left( {\hat{w}}_{j}\left( \frac{\xi _{\beta }^{+}}{1-\xi _{\beta }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{1+\left( {\hat{w}}_{j}\left( \frac{\gamma _{\beta }}{1-\gamma _{\beta }}\right) ^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \end{aligned}$$

Let

$$\begin{aligned}&\frac{\xi _{\alpha }^{-}}{1-\xi _{\alpha }^{-}} =A_{i},\frac{\xi _{\alpha }^{+}}{1-\xi _{\alpha }^{+}}=A_{j},\frac{\xi _{\beta }^{-}}{1-\xi _{\beta }^{-}}=B_{i},\frac{\xi _{\beta }^{+}}{1-\xi _{\beta }^{+}}\\&\quad =B_{j},\frac{ \gamma _{\alpha }}{1-\gamma _{\alpha }}=C_{i}, \frac{\gamma _{\beta }}{1-\gamma _{\beta }} =C_{j} \end{aligned}$$

Then,

$$\begin{aligned}&({\hat{w}}_{i}c_{i})^{p}\\&\quad =\left\{ \left[ \frac{1}{1+\left( p/{\hat{w}} _{i}A_{i}^{\lambda }\right) ^{1/\lambda }},\frac{1}{1+\left( p/{\hat{w}} _{i}B_{i}^{\lambda }\right) ^{1/\lambda }}\right] ;\frac{1}{1+\left( p/{\hat{w}}_{i}C_{i}^{\lambda }\right) ^{1/\lambda }}\right\} \\&({\hat{w}}_{j}c_{j})^{q}\\&\quad =\left\{ \left[ \frac{1}{1+\left( q/{\hat{w}} _{j}A_{j}^{\lambda }\right) ^{1/\lambda }},\frac{1}{1+\left( q/{\hat{w}} _{j}B_{j}^{\lambda }\right) ^{1/\lambda }}\right] ;\frac{1}{1+\left( q/{\hat{w}}_{j}C_{j}^{\lambda }\right) ^{1/\lambda }}\right\} \end{aligned}$$

Thereafter,

$$\begin{aligned}&({\hat{w}}_{i}c_{i})^{p}\otimes _{D}({\hat{w}}_{j}c_{j})^{q}\\&\quad =\left\{ \begin{array}{c} \left[ \frac{1}{1+\left( p/{\hat{w}}_{i}A_{i}^{\lambda }+q/{\hat{w}} _{j}A_{j}^{\lambda }\right) ^{1/\lambda }},\frac{1}{1+\left( p/{\hat{w}} _{i}B_{i}^{\lambda }+q/{\hat{w}}_{j}B_{j}^{\lambda }\right) ^{1/\lambda }} \right] \\ ;\frac{1}{1+\left( p/{\hat{w}}_{i}C_{i}^{\lambda }+q/{\hat{w}}_{j}C_{j}^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \end{aligned}$$

And

$$\begin{aligned}&\frac{2}{k(k+1)}\underset{i=1}{\overset{k}{\sum }}\overset{k}{\underset{j=i }{\sum }}({\hat{w}}_{i}c_{i})^{p}\otimes _{D}({\hat{w}}_{j}c_{j})^{q} \\&\quad =\left\{ \begin{array}{c} \left[ \begin{array}{c} 1-1/\left( 1+\left( \frac{2}{k\left( k+1\right) }\underset{i=1}{\overset{k}{ \sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{\left( p/{\hat{w}} _{i}A_{i}^{\lambda }+q/{\hat{w}}_{j}A_{j}^{\lambda }\right) }\right) ^{1/\lambda }\right) , \\ 1-1/\left( 1+\left( \frac{2}{k\left( k+1\right) }\underset{i=1}{\overset{k}{ \sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{(p/{\hat{w}} _{i}B_{i}^{\lambda }+q/{\hat{w}}_{j}B_{j}^{\lambda })}\right) ^{1/\lambda }\right) \end{array} \right] ; \\ 1-1/\left( 1+\left( \frac{2}{k\left( k+1\right) }\underset{i=1}{\overset{k}{ \sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{(p/{\hat{w}} _{i}C_{i}^{\lambda }+q/{\hat{w}}_{j}C_{j}^{\lambda })}\right) ^{1/\lambda }\right) \end{array} \right\} \end{aligned}$$

Furthermore,

$$\begin{aligned}&\left( \frac{2}{k(k+1)}\underset{i=1}{\overset{k}{\sum }}\overset{k}{ \underset{j=i}{\sum }}({\hat{w}}_{i}c_{i})^{p}\otimes _{D}({\hat{w}} _{j}c_{j})^{q}\right) ^{\frac{1}{p+q}} \\&\quad =\left\{ \begin{array}{c} \left[ \begin{array}{c} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) }\times 1/\underset{i=1}{ \overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{\left( p/{\hat{w}}_{i}A_{i}^{\lambda }+q/{\hat{w}}_{j}A_{j}^{\lambda }\right) }\right) ^{1/\lambda }\right) , \\ 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) }\underset{i=1}{\overset{k }{\sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{(p/{\hat{w}} _{i}B_{i}^{\lambda }+q/{\hat{w}}_{j}B_{j}^{\lambda })}\right) ^{1/\lambda }\right) \end{array} \right] ; \\ 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) }\underset{i=1}{\overset{k }{\sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{(p/{\hat{w}} _{i}C_{i}^{\lambda }+q/{\hat{w}}_{j}C_{j}^{\lambda })}\right) ^{1/\lambda }\right) \end{array} \right\} , \end{aligned}$$

Now, putting values back, then we have,

$$\begin{aligned}&\left( \frac{2}{k(k+1)}\underset{i=1}{\overset{k}{\sum }}\overset{k}{ \underset{j=i}{\sum }}({\hat{w}}_{i}c_{i})^{p}\otimes _{D}({\hat{w}} _{j}c_{j})^{q}\right) ^{\frac{1}{p+q}} \\&\quad =\left\{ \begin{array}{c} \left[ \begin{array}{c} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) }\times 1/\left( \overset{k}{ \underset{i=1}{\sum }}\underset{j=i}{\overset{k}{\sum }}1/\left( \frac{p}{_{{\hat{w}} _{i}\left( \frac{\xi _{\alpha }^{-}}{1-\xi _{\alpha }^{-}}\right) ^{\lambda }}}+\frac{q}{{\hat{w}}_{j}\left( \frac{\xi _{\alpha }^{+}}{1-\xi _{\alpha }^{+} }\right) ^{\lambda }}\right) \right) \right) ^{1/\lambda }\right) , \\ 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) }\times 1/\left( \overset{k}{ \underset{i=1}{\sum }}\underset{j=i}{\overset{k}{\sum }}1/\left( \frac{p}{{\hat{w}} _{i}\left( \frac{\xi _{\beta }^{-}}{1-\xi _{\beta }^{-}}\right) ^{\lambda }}+ \frac{q}{{\hat{w}}_{j}\left( \frac{\xi _{\beta }^{+}}{1-\xi _{\beta }^{+}} \right) ^{\lambda }}\right) \right) \right) ^{1/\lambda }\right) \end{array} \right] ; \\ 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) }\times 1/\left( \underset{i=1}{ \overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }1/}\left( \frac{p}{{\hat{w}} _{i}\left( \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }}\right) ^{\lambda }}+ \frac{q}{{\hat{w}}_{j}\left( \frac{\gamma _{\beta }}{1-\gamma _{\beta }} \right) ^{\lambda }}\right) \right) \right) ^{1/\lambda }\right) \end{array} \right\} \end{aligned}$$

This is the complete proof . $\square$

Moreover, CFWHMDA having below properties:

Theorem 6

(Monotonicty) Let $c_{i}=\left\langle \left[ \xi _{i}^{-},\xi _{i}^{+}\right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,k)$ and $c_{i}^{*}=\left\langle \left[ \xi _{i}^{-^{*}},\xi _{i}^{+*}\right] ;\gamma _{i}^{*}\right\rangle (i=1,2,\ldots ,k)$ be two CNs, if $c_{i}\le c_{i}^{*},$ for all i,then,

$$\begin{aligned} {\text {CFHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\le {\text {CFHMDA}}^{p,q}(c_{1}^{*},c_{2}^{*},\ldots ,c_{k}^{*}). \nonumber \\ \end{aligned}$$

(5.2)

Theorem 7

(Boundedness) Let $c_{i}=\left\langle \left[ \xi _{i}^{-},\xi _{i}^{+}\right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,k)$ be a collection of CNs, if $c_{1}^{+}=\left\langle \left[ (\xi _{(\max )}^{+},\xi _{(\min )}^{+}\right] ;\gamma _{(\min )}\right\rangle$ and $c_{2}^{-}=\left\langle \left[ \xi _{(\min )}^{-},\xi _{(\max )}^{-}\right] ;\gamma _{(\max )}\right\rangle ,$ where $\lambda >0$

$$\begin{aligned} \xi _{(\max )}^{+}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\max )\xi _{i}^{-}}{(\max )\xi _{i}^{-}}\right) \right. \right. \\&\left. \left. \times 1/\left( \overset{k}{\underset{i=1}{\sum }}\underset{j=i}{\overset{k}{\sum } }1/\left( \frac{p}{_{{\hat{w}}_{i}}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) \\ \xi _{(\min )}^{+}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\min )\xi _{i}^{+}}{(\min )\xi _{i}^{+}}\right) \right. \right. \\&\left. \left. \times 1/\left( \overset{k}{\underset{i=1}{\sum }}\underset{j=i}{\overset{k}{\sum } }1/\left( \frac{p}{{\hat{w}}_{i}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) \\ \gamma _{(\min )}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\min )\gamma _{i}}{(\min )\gamma _{i}}\right) \right. \right. \\&\left. \left. \times 1/\left( \underset{i=1}{\overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }1/}\left( \frac{p}{{\hat{w}}_{i}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) \\ \xi _{(\min )}^{-}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\min )\xi _{i}^{-}}{(\min )\xi _{i}^{-}}\right) \right. \right. \\&\left. \left. \times 1/\left( \overset{k}{\underset{i=1}{\sum }}\underset{j=i}{\overset{k}{\sum } }1/\left( \frac{p}{_{{\hat{w}}_{i}}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) \\ \xi _{(\max )}^{-}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\max )\xi _{i}^{+}}{(\max )\xi _{i}^{+}}\right) \right. \right. \\&\left. \left. \times 1/\left( \overset{k}{\underset{i=1}{\sum }}\underset{j=i}{\overset{k}{\sum } }1/\left( \frac{p}{{\hat{w}}_{i}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) , \\ \gamma _{(\max )}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\max )\gamma _{i}}{(\max )\gamma _{i}}\right) \right. \right. \\&\left. \left. \times 1/\left( \underset{i=1}{\overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }1/}\left( \frac{p}{{\hat{w}}_{i}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) \end{aligned}$$

Then,

$$\begin{aligned} c^{-}\le {\text {CFWHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\le c^{+} \end{aligned}$$

(5.3)

Cubic fuzzy geometric Heronian mean Dombi aggregation (CFGHMDA) operator

Definition 12

Let a series of crisp numbers is $y_{i}(i=1,2,\ldots ,n)$ and p, q be a positive numbers. If

$$\begin{aligned} {\text {GHM}}^{p,q}(y_{1},y_{2},\ldots ,y_{k})=\frac{1}{p+q}\underset{i=1}{\overset{k}{ \prod }}\overset{k}{\underset{j=i}{\prod }}(py_{i}+qy_{j})^{\frac{2}{k(k+1) }} \nonumber \\ \end{aligned}$$

(5.4)

this is the geometric Heronian mean (GHM) operator.

In this section, we discuss cubic fuzzy geometric Heronian mean Dombi aggregation (CFGHMDA) operators.

6 The cubic fuzzy geometric Heronian mean Dombi aggregation (CFGHMDA) operator

Definition 13

Let p, q be a positive numbers and $c_{i}=(c_{1},c_{2},\ldots ,c_{n})$ be a collection of CNs and $\lambda>$ 0. If,

$$\begin{aligned}&{\text {CFHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\nonumber \\&\quad =\frac{1}{p+q}\overset{k}{\underset{i=1}{ \prod }}\underset{j=i}{\overset{k}{\prod }}(pc_{i}\oplus _{D}qc_{j})^{ \frac{2}{k(k+1)}} \end{aligned}$$

(6.1)

the ${\text {CFGHMDA}}^{p,q}$ is the notation of cubic fuzzy Heronian mean Dombi aggregation operator.

Theorem 8

Let p, q be a positive number and $c_{i}=(c_{1},c_{2},\ldots ,c_{k})$ be a collection of CNs and $\lambda >0$ . The resultant value of aggregation CFGHMDA is still a CNs and

Proof

According to given definition, we have:

$$\begin{aligned} {pc}_{i}= & {} \left\{ \begin{array}{c} \left[ \frac{1}{1+\left( p\left( \frac{1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}}\right) ^{\lambda }\right) ^{1/\lambda }},\frac{1}{1+\left( p\left( \frac{1-\xi _{\beta }^{-}}{\xi _{\beta }^{-}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{1+\left( p\left( \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }} \right) ^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \\ {qc}_{j}= & {} \left\{ \begin{array}{c} \left[ \frac{1}{1+\left( p\left( \frac{1-\xi _{\alpha }^{+}}{\xi _{\alpha }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }},\frac{1}{1+\left( p\left( \frac{1-\xi _{\beta }^{+}}{\xi _{\beta }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{1+\left( p\left( \frac{\gamma \beta }{1-\gamma _{\beta }}\right) ^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \end{aligned}$$

Let

$$\begin{aligned}&\frac{1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}} = A _{i},\frac{1-\xi _{\alpha }^{+}}{\xi _{\alpha }^{+}}=A_{j},\frac{1-\xi _{\beta }^{-}}{\xi _{\beta }^{-}}\\&\quad =B_{i},\frac{1-\xi _{\beta }^{+}}{\xi _{\beta }^{+}}=B_{j}, \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }}=C_{i},\frac{\gamma \beta }{ 1-\gamma _{\beta }}=C_{j}, \end{aligned}$$

then,

$$\begin{aligned}&({pc}_{i}\oplus _{D}{qc}_{j})\\&\quad =\left\{ \begin{array}{c} \left[ \frac{1}{1+\left( pA_{i}^{\lambda }+qA_{j}\right) ^{1/\lambda }}, \frac{1}{1+\left( pB_{i}^{\lambda }+qB_{j}\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{1+\left( pC_{i}^{\lambda }+qC_{j}\right) ^{1/\lambda }} \end{array} \right\} \\&\overset{k}{\underset{i=1}{\prod }}\underset{j=i}{\overset{k}{\prod }} ({pc}_{i}\oplus _{D}{qc}_{j})\\&\quad =\left\{ \begin{array}{c} \left[ \begin{array}{c} \left( 1-\left( 1/\left( 1+\underset{i=1}{\overset{k}{\sum }}\overset{k}{ \underset{j=i}{\sum }}\frac{1}{1+\left( pA_{i}^{\lambda }+qA_{j}^{\lambda }\right) }\right) \right) ^{1/\lambda }\right) , \\ \left( 1-\left( 1/\left( 1+\underset{i=1}{\overset{k}{\sum }}\overset{k}{ \underset{j=i}{\sum }}\frac{1}{1+\left( pB_{i}^{\lambda }+qB_{j}^{\lambda }\right) }\right) \right) ^{1/\lambda }\right) \end{array} \right] ; \\ \left( 1/\left( 1+\underset{i=1}{\overset{k}{\sum }}\overset{k}{\underset{j=i }{\sum }}\frac{1}{1+\left( pC_{i}^{\lambda }+qC_{j}^{\lambda }\right) } \right) \right) ^{1/\lambda } \end{array} \right\} \end{aligned}$$

Then,

$$\begin{aligned}&\frac{1}{P+q}\overset{k}{\underset{i=1}{\prod }}\underset{j=i}{\overset{k}{\prod }}({pc}_{i}\oplus _{D}{qc}_{j})^{\frac{2}{k(k+1)}} \\&\quad =\left\{ \begin{array}{c} \left[ \begin{array}{c} 1/\left( 1+\frac{k(k+1)}{2(p+q)}\times 1/\left( \underset{i=1}{\overset{k}{ \sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{1+\left( pA_{i}^{\lambda }+qA_{j}^{\lambda }\right) }\right) \right) ^{1/\lambda }, \\ 1/\left( 1+\frac{k(k+1)}{2(p+q)}\times 1/\left( \underset{i=1}{\overset{k}{ \sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{1+\left( pB_{i}^{\lambda }+qB_{j}^{\lambda }\right) }\right) \right) ^{1/\lambda } \end{array} \right] ; \\ 1-\left( 1/\left( 1+\frac{k(k+1)}{2(p+q)}\times 1\left( \underset{i=1}{ \overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{1+\left( pC_{i}^{\lambda }+qC_{j}^{\lambda }\right) }\right) \right) \right) \end{array} \right\} \end{aligned}$$

putting values of (A, B, C)

$$\begin{aligned}&{\text {CFGHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k}) \\&\quad =\left\{ \begin{array}{c} \left[ \begin{array}{c} 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\times 1/\left( \underset{i=1}{ \overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{1+\left( p\left( \frac{1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}}\right) ^{\lambda }+q\left( \frac{1-\xi _{\alpha }^{+}}{\xi _{\alpha }^{+}}\right) ^{\lambda }\right) }\right) \right) \right) ^{1/\lambda }, \\ 1/\left( 1+\frac{k(k+1)}{2(p+q)}\times 1\left( \underset{i=1}{\overset{k}{ \sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{1+\left( p\left( \frac{ 1-\xi _{\beta }^{-}}{\xi _{\beta }^{-}}\right) ^{\lambda }+q\left( \frac{ 1-\xi _{\beta }^{+}}{\xi _{\beta }^{+}}\right) ^{\lambda }\right) }\right) \right) ^{1/\lambda } \end{array} \right] ; \\ 1-\left( 1/\left( 1+\frac{k(k+1)}{2(p+q)}\times 1\underset{i=1}{\overset{k}{ \sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{1+\left( p\left( \frac{ \gamma _{\alpha }}{1-\gamma _{\alpha }}\right) ^{\lambda }+q\left( \frac{ \gamma \beta }{1-\gamma _{\beta }}\right) ^{\lambda }\right) }\right) \right) ^{1/\lambda } \end{array} \right\} \end{aligned}$$

This is the complete proof of${\text {CFGHMDA}}^{p,q}.$ $\square$

Moreover, CFGHMDA has the following properties.

Theorem 9

(Idempotency) Let $c_{i}=\left\langle \left[ \xi _{\alpha i}^{-},\xi _{\beta i}^{+}\right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,k)$ are the collection of CNs if $c_{i}(i=1,2,\ldots ,k)$ are equal, that is $c_{i}=c=\left\langle \left[ \xi _{\alpha }^{-},\xi _{\alpha }^{+}\right] ;\gamma _{\alpha }\right\rangle ,$then,

$$\begin{aligned} {\text {CFGHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})=c_{1} \end{aligned}$$

(6.2)

Theorem 10

(Monotonicty) Let $c_{i}=\left\langle \left[ \xi _{i}^{-},\xi _{i}^{+}\right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,k)$ and $c_{i}^{*}=\left\langle \left[ \xi _{i}^{-^{*}},\xi _{i}^{+*}\right] ;\gamma _{i}^{*}\right\rangle (i=1,2,\ldots ,k)$ be two CNs ,if $c_{i}\le c_{i}^{*},$ for all i, then

$$\begin{aligned}&{\text {CFHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\nonumber \\&\quad \le {\text {CFGHMDA}}^{p,q}(c_{1}^{*},c_{2}^{*},\ldots ,c_{k}^{*}) \end{aligned}$$

(6.3)

Theorem 11

(Boundedness) Let $c_{i}=\left\langle \left[ \xi _{i}^{-},\xi _{i}^{+}\right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,k)$ be a collection of CNs, if $c_{1}^{+}= \left\langle \left[ (\max )\xi _{i}^{-},\right. \right. \left. \left. (\min )\xi _{i}^{+}\right] ;(\min )\gamma _{i}\right\rangle$ and c$_{2}^{-}=\left\langle \left[ (\min )\xi _{i}^{-},(\max )\xi _{i}^{+}\right] ;(\max )\gamma _{i}\right\rangle .$ Then,

$$\begin{aligned} c_{2}^{-}\le {\text {CFGHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\le c_{1}^{+} \end{aligned}$$

(6.4)

7 The cubic fuzzy weighted geometric Heronian mean Dombi aggregation (CPFDWGHM) operator

Definition 14

Let p, q be positive numbers and $c_{i}=([\xi _{\alpha }^{-},\xi _{\alpha }^{+}];\gamma _{\alpha })(i=1,2,\ldots ,k)$ be a collection CNs. If

$$\begin{aligned}&{\text {CFWGHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\nonumber \\&\quad =\frac{1}{p+q}\underset{i=1}{\overset{k}{\prod }}\overset{k}{\underset{j=i}{\prod }}(\left( pc_{i}\right) ^{{\hat{w}} _{i}}\oplus _{D}\left( qc_{j}\right) ^{{\hat{w}}_{j}})^{\frac{1}{k(k+1)}} \end{aligned}$$

(7.1)

so the weight vector ${\hat{w}}=({\hat{w}}_{1},{\hat{w}}_{2},\ldots ,{\hat{w}}_{n})^{T}$ is of $c_{i}(i=1,2,\ldots ,k),$ satisfy ${\hat{w}}_{1}\in [0,1],\sum _{i=1}^{n}{\hat{w}}_{i}=1,$ the ${\text {CFWGHMDA}}^{p,q}$ is called the cubic fuzzy weighted geometric Heronian mean Dombi aggregation (CFWGHMDA) operator .

Theorem 12

Let p, q be a positive numbers and $c_{i}=(c_{1},c_{2},\ldots ,c_{k})$ be a combination of CNs and $\lambda >0$. The aggregated value by CFWGHMDA is still a CNs and

$$\begin{aligned}&{\text {CFWGHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k}) \\&\quad =\left\{ \begin{array}{c} \left[ \begin{array}{c} 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\times 1/\left( \underset{i=1}{ \overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }}1/\left( \frac{p}{{\hat{w}}_{i}\left( \frac{\xi _{\alpha }^{-}}{1-\xi _{\alpha ^{-}}}\right) ^{\lambda }}+\frac{q}{{\hat{w}}_{j}\left( \frac{\xi _{\alpha }^{+}}{1-\xi _{\alpha }^{+}} \right) ^{\lambda }}\right) \right) \right) ^{1/\lambda }\right) , \\ 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\times 1/\left( \underset{i=1}{ \overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }}1/\left( \frac{p}{{\hat{w}}_{i}\left( \frac{\xi _{\beta }^{-}}{1-\xi _{_{\beta }^{-}}}\right) ^{\lambda }}+\frac{q}{{\hat{w}}_{j}\left( \frac{\xi _{\beta }^{+}}{1-\xi _{\beta }^{+}}\right) ^{\lambda }}\right) \right) \right) ^{1/\lambda }\right) \end{array} \right] ; \\ 1/\left( 1+\left( \frac{k(k+1)}{2(p+q)}\times 1/\left( \underset{i=1}{ \overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }}1/\left( \frac{p}{{\hat{w}}_{i}\left( \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }}\right) ^{\lambda }} +\frac{q}{{\hat{w}}_{j}\left( \frac{\gamma \beta }{1-\gamma _{\beta }}\right) ^{\lambda }}\right) \right) \right) ^{1/\lambda }\right) \end{array} \right\} \end{aligned}$$

Proof

According to definition, we have

$$\begin{aligned} {pc}_{i}= & {} \left\{ \begin{array}{c} \left[ 1-\frac{1}{1+\left( p\left( \frac{1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}}\right) ^{\lambda }\right) ^{1/\lambda }},1-\frac{1}{1+\left( p\left( \frac{1-\xi _{\beta }^{-}}{\xi _{\beta }^{-}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{1+\left( p\left( \frac{\gamma _{\alpha }}{1-\gamma _{\alpha }} \right) ^{\lambda }\right) ^{1/\lambda }}\end{array} \right\} , \\ {qc}_{j}= & {} \left\{ \begin{array}{c} \left[ 1-\frac{1}{1+\left( p\left( \frac{1-\xi _{\alpha }^{+}}{\xi _{\alpha }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }},1-\frac{1}{1+\left( p\left( \frac{1-\xi _{\beta }^{+}}{\xi _{\beta }^{+}}\right) ^{\lambda }\right) ^{1/\lambda }}\right] ; \\ 1-\frac{1}{1+\left( p\left( \frac{\gamma _{\beta }}{1-\gamma _{\beta }} \right) ^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} . \end{aligned}$$

Let

$$\begin{aligned}&\frac{1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}}=A_{i,}\frac{1-\xi _{\alpha }^{+}}{\xi _{\alpha }^{+}}=A_{j},\frac{1-\xi _{\beta }^{-}}{\xi _{\beta }^{-} }\\&\quad =B_{i},\frac{1-\xi _{\beta }^{+}}{\xi _{\beta }^{+}}=B_{j},\frac{1-\gamma _{\alpha }}{\gamma _{\alpha }}=C_{i},\frac{1-\gamma _{\beta }}{\gamma _{\beta }}=C_{j} \\&\left( {pc}_{i}\right) ^{{\hat{w}}_{i}}\ \\&\quad =\left\{ \left[ 1-\frac{1}{1+\left( p/ {\hat{w}}_{i}A_{i}^{\lambda }\right) ^{1/\lambda }},1-\frac{1}{1+\left( p/{\hat{w}}_{i}B_{i}^{\lambda }\right) ^{1/\lambda }}\right] ;\right. \\&\quad \left. 1 -\frac{1}{1+\left( p/ {\hat{w}}_{i}C_{i}^{\lambda }\right) ^{1/\lambda }}\right\} \\&\left( {qc}_{j}\right) ^{{\hat{w}}_{j}}\\&\quad =\left\{ \begin{array}{c} \left[ 1-\frac{1}{1+\left( q/{\hat{w}}_{j}A_{j}^{\lambda }\right) ^{1/\lambda } },1-\frac{1}{1+\left( q/{\hat{w}}_{j}B_{j}^{\lambda }\right) ^{1/\lambda }} \right] ; \\ 1-\frac{1}{1+\left( q/{\hat{w}}_{j}C_{j}^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \\&\left( \left( {pc}_{i}\right) ^{{\hat{w}}_{i}}\oplus _{D}\left( qc_{j}\right) ^{{\hat{w}} _{j}}\right) \\&\quad =\left\{ \begin{array}{c} \left[ \frac{1}{1+\left( p/{\hat{w}}_{i}A_{i}^{\lambda }+q/{\hat{w}} _{j}A_{j}^{\lambda }\right) ^{1/\lambda }},\frac{1}{1+\left( p/{\hat{w}} _{i}B_{i}^{\lambda }+q/{\hat{w}}_{j}B_{j}^{\lambda }\right) ^{1/\lambda }} \right] ; \\ \frac{1}{1+\left( p/{\hat{w}}_{i}C_{i}^{\lambda }+q/{\hat{w}}_{j}C_{j}^{\lambda }\right) ^{1/\lambda }} \end{array} \right\} \\&\frac{2}{k(k+1)}\underset{i=1}{\overset{k}{\prod }}\overset{k}{\underset{ j=i}{\prod }}(\left( pc_{i}\right) ^{{\hat{w}}_{i}}\oplus _{D}\left( qc_{j}\right) ^{{\hat{w}}_{j}}) \\&\quad =\left\{ \begin{array}{c} \left[ \begin{array}{c} 1-1/\left( 1+\left( \frac{2}{k\left( k+1\right) }\underset{i=1}{\overset{k}{ \sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{\left( p/{\hat{w}} _{i}A_{i}^{\lambda }+q/{\hat{w}}_{j}A_{j}^{\lambda }\right) }\right) ^{1/\lambda }\right) , \\ 1-1/\left( 1+\left( \frac{2}{k\left( k+1\right) }\underset{i=1}{\overset{k}{ \sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{(p/{\hat{w}} _{i}B_{i}^{\lambda }+q/{\hat{w}}_{j}B_{j}^{\lambda })}\right) ^{1/\lambda }\right) \end{array} \right] ; \\ 1-1/\left( 1+\left( \frac{2}{k\left( k+1\right) }\underset{i=1}{\overset{k}{ \sum }}\overset{k}{\underset{j=i}{\sum }}\frac{1}{(p/{\hat{w}} _{i}C_{i}^{\lambda }+q/{\hat{w}}_{j}C_{j}^{\lambda })}\right) ^{1/\lambda }\right) \end{array} \right\} \end{aligned}$$

Furthermore,

Table 1 The cubic fuzzy decision matrix

Now putting values back,

$$\begin{aligned}&\left[ \frac{2}{k(k+1)}\underset{i=1}{\overset{k}{\prod }}\overset{k}{ \underset{j=i}{\prod }}(\left( pc_{i}\right) ^{{\hat{w}}_{i}}\oplus _{D}\left( qc_{j}\right) ^{{\hat{w}}_{j}})\right] ^{\frac{1}{p+q}} \\&\quad =\left\{ \begin{array}{c} \left[ \begin{array}{c} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) }\times 1/\left( \overset{k}{ \underset{i=1}{\sum }}\underset{j=i}{\overset{k}{\sum }}1/\left( \frac{p}{_{{\hat{w}} _{i}\left( \frac{1-\xi _{\alpha }^{-}}{\xi _{\alpha }^{-}}\right) ^{\lambda }}}+\frac{q}{{\hat{w}}_{j}\left( \frac{1-\xi _{\alpha }^{+}}{\xi _{\alpha }^{+} }\right) ^{\lambda }}\right) \right) \right) ^{1/\lambda }\right) , \\ 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) }\times 1/\left( \overset{k}{ \underset{i=1}{\sum }}\underset{j=i}{\overset{k}{\sum }}1/\left( \frac{p}{{\hat{w}} _{i}\left( \frac{1-\xi _{\beta }^{-}}{\xi _{\beta }^{-}}\right) ^{\lambda }}+ \frac{q}{{\hat{w}}_{j}\left( \frac{1-\xi _{\beta }^{+}}{\xi _{\beta }^{+}} \right) ^{\lambda }}\right) \right) \right) ^{1/\lambda }\right) \end{array} \right] ; \\ 1/\left( 1+ \left( \frac{k(k+1)}{2\left( p+q\right) }\times 1/\left( \overset{k}{\underset{i=1}{\sum }}\overset{k}{\underset{j=i}{\sum }1/}\left( \frac{p}{{\hat{w}} _{i}\left( \frac{1-\gamma _{\alpha }}{\gamma _{\alpha }}\right) ^{\lambda }}+ \frac{q}{{\hat{w}}_{j}\left( \frac{1-\gamma _{\beta }}{\gamma _{\beta }} \right) ^{\lambda }}\right) \right) \right) ^{1/\lambda }\right) \end{array} \right\} \end{aligned}$$

Thus, this is the required proof of the theorem. $\square$

The CFWGHMDA satisfies the below properties.

Theorem 13

(Monotonicty) Let $c_{i}=\left\langle \left[ \xi _{i}^{-},\xi _{i}^{+}\right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,k)$ and $c_{i}^{*}=\left\langle \left[ \xi _{i}^{-^{*}},\xi _{i}^{+*}\right] ;\gamma _{i}^{*}\right\rangle (i=1,2,\ldots ,k)$ be two CNs, if $c_{i}\le c_{i}^{*},$ for all i, then

$$\begin{aligned}&{\text {CFWGHMDA}}^{p,q}(c_{1},c,\ldots ,c_{k})\nonumber \\&\quad \le {\text {CFWGHMDA}}^{p,q}(c_{1}^{*},c_{2}^{*},\ldots ,c_{k}^{*}) \end{aligned}$$

(7.2)

Theorem 14

(Boundedness) Let $c_{i}=\left\langle \left[ \xi _{i}^{-},\xi _{i}^{+}\right] ;\gamma _{i}\right\rangle (i=1,2,\ldots ,k)$ be a collection of CNs, if c$_{1}^{+}=\left\langle \left[ (\xi _{(\max )}^{+},\xi _{(\min )}^{+}\right] ;\gamma _{(\min )}\right\rangle$ and $c_{2}^{-}= \left\langle \left[ \xi _{(\min )}^{-},\xi _{(\max )}^{-}\right] ;\gamma _{(\max )}\right\rangle ,$ where $\lambda >0$

$$\begin{aligned} \xi _{(\max )}^{+}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\max )\xi _{i}^{-}}{(\max )\xi _{i}^{-}}\right) \right. \right. \\&\quad \left. \left. \times 1/\left( \overset{n}{\underset{i=1}{\sum }}\underset{j=i}{\overset{n}{\sum } }1/\left( \frac{p}{_{{\hat{w}}_{i}}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) , \\ \xi _{(\min )}^{+}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\min )\xi _{i}^{+}}{(\min )\xi _{i}^{+}}\right) \right. \right. \\&\quad \left. \left. \times 1/\left( \overset{n}{\underset{i=1}{\sum }}\underset{j=i}{\overset{n}{\sum } }1/\left( \frac{p}{{\hat{w}}_{i}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) , \\ \gamma _{(\min )}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\min )\gamma _{i}}{(\min )\gamma _{i}}\right) \right. \right. \\&\quad \left. \left. \times 1/\left( \underset{i=1}{\overset{n}{\sum }}\overset{n}{\underset{j=i}{\sum }1/}\left( \frac{p}{{\hat{w}}_{i}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) . \\ \xi _{(\min )}^{-}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\min )\xi _{i}^{-}}{(\min )\xi _{i}^{-}}\right) \right. \right. \\&\quad \left. \left. \times 1/\left( \overset{k}{\underset{i=1}{\sum }}\underset{j=i}{\overset{k}{\sum } }1/\left( \frac{p}{_{{\hat{w}}_{i}}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) \\ \xi _{(\max )}^{-}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\max )\xi _{i}^{+}}{(\max )\xi _{i}^{+}}\right) \right. \right. \\&\quad \left. \left. \times 1/\left( \overset{k}{\underset{i=1}{\sum }}\underset{j=i}{\overset{k}{\sum } }1/\left( \frac{p}{{\hat{w}}_{i}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) , \\ \gamma _{(\max )}= & {} 1/\left( 1+\left( \frac{k(k+1)}{2\left( p+q\right) } \times \left( \frac{1-(\max )\gamma _{i}}{(\max )\gamma _{i}}\right) \right. \right. \\&\quad \left. \left. \times 1/\left( \underset{i=1}{\overset{k}{\sum }}\overset{k}{\underset{j=i}{\sum }1/}\left( \frac{p}{{\hat{w}}_{i}}+\frac{q}{{\hat{w}}_{j}}\right) \right) \right) ^{1/\lambda }\right) . \end{aligned}$$

Then,

$$\begin{aligned} \ c^{-}\le {\text {CFWGHMDA}}^{p,q}(c_{1},c_{2},\ldots ,c_{k})\le c^{+} \end{aligned}$$

(7.3)

8 A models for cubic fuzzy aggregation operators with MADM

In this article, we discuss cubic fuzzy aggregation operators to MADM. Suppose ${\hat{w}}=({\hat{w}}_{1},{\hat{w}}_{2},\ldots ,{\hat{w}}_{n})$ be the weighting vector of the attribute $C_{j}\ (j=1,2,\ldots ,n)$, satisfying ${\hat{w}}_{j}\in [0,1],{{\sum _{j=1}^{n}}}=1.I=\{I_{1},I_{2},\ldots ,I_{m} \}$ be a set of alternatives and $C=\{C_{1},C_{2},\ldots ,C_{n}\}$ be a set of attribute for decision making the decision-makers committee are decide over alternatives, for criteria C, the members of committee are required to use CFNs to show best one result, which can be represented as $\beta _{ij}=\langle [\xi _{\alpha _{ij}}^{-},\xi _{\alpha ij}^{+}];\gamma _{\alpha ij}\rangle$ $(i=1,2,\ldots ,m;j=1,2,\ldots ,n)$. So, $F=(\beta _{ij})_{m\times n}$ is the decision matrix.

Here, we apply the CFHMDA, CFWHMDA, CFGHMDA, and CFGWHMDA operators to the MADM problems.

• Step 1 We use the decision information given in a formula $F=(\beta _{ij})_{m\times n}$ to remove the different attribute types. The decision should be normalized:

  $$\begin{aligned} \beta _{ij}=\left\{ \begin{array}{c} \langle [\xi _{\alpha _{ij}}^{-},\xi _{\alpha ij}^{+}];\gamma _{\alpha ij}\rangle ,C_{j}\in S_{1} \\ \langle [\xi _{\beta _{ij}}^{-},\xi _{\beta ij}^{+}];\gamma _{\beta ij}\rangle ,C_{j}\in S_{2} \end{array} \right\} , \end{aligned}$$

  (8.1)

where $S_{1}$ represents the benefit attribute and $S_{2}$ represents the cost attribute.

• Step 2 Utilizing the CFHMDA, CFWHMDA, CFGHMDA, and CFWGHMDA operators;

  $$\begin{aligned} C_{i}= & {} {\text {CFHMDA}}(c_{i1},c_{i2},\ldots ,c_{in}) \\ C_{i}= & {} {\text {CFWHMDA}}(c_{i1},c_{i2},\ldots ,c_{in}) \end{aligned}$$

Table 2 The aggregated results of the ERP systems by the CFHMDA, CFWHMDA, CFGHMDA, and CFWGHMDA operators

or

The CFWHMDA and CFWGHMDA operator:

$$\begin{aligned} C_{i}= & {} {\text {CFGHMDA}}(c_{i1},c_{i2},\ldots ,c_{in}) \\ C_{i}= & {} {\text {CFWGHMDA}}(c_{i1},c_{i2},\ldots ,c_{in}) \end{aligned}$$

to aggregate all the given information. Then, we obtained all values of $C_{i}(i=1,2,\ldots ,m)$ of alternatives.

• Step 3 Compute the score function of alternatives $I_{i}(1,2,3,4,5)$.

• Step 4 Give ranking to the alternatives according to the scores.

• Step 5 Using CFHMDA, CFWHMDA, CFGHMDA, and CFWGHMDA operators to aggregate the given alternatives $(I_{1},I_{2},I_{3},I_{4},I_{5})$ where $p=1,q=2$ and $\lambda =(1,2,3,4,5,6,7,8,9,10)$.

• Step 6 End

9 Numerical example

In this unite, we using a numerical example for decision-making problems to show the uses of the developed methods. Let a company decide to impose ERP (enterprise resource planning) system. About ERP dealer and systems collecting all suitable information, the experts committee choose $I_{i}(i=1,2,\ldots ,5)$ five possible alternatives as investors. The organization members are some external experts in decision-making. The team selects five attribute $C_{i}(i=1,2,\ldots ,5)$. To evaluate the alternatives: (1) function and technology $C_{1}$, (2) strategic fitness $C_{2}$ (3) vendor’s ability $C_{3}$ (4) vendor’s reputation $C_{4}$ (5) vendor’s growth analysis $C_{5}$. The experts committee is to use CFNs to make the original decision matrix.

$C_{i}$ are five attribute, and $I_{i}$ are five alternatives ${\hat{w}} =(0.2,0.15,0.15,0.25,0.25)^{T}$ is the weight vector of them. Now, let $p=1,q=1,k=5$ and $\lambda =2,$ so we aggregate the five CFNs solution as below(Tables 1, 2, 3 and 4).

are five CNs, $p=1,q=2,k=5$ and $\lambda =2,$ so the aggregation of the five CFNs. The solution is as below.

Table 3 The score values of the ERP system

Table 4 Ordering of the ERP systems

Table 5 Score values of alternatives using CFHMDA operator

9.1 Sensitivity analysis

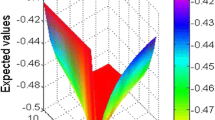
The versatility of the proposed approach is expressed in two aspects. Firstly, it is based in DTT, so that the information aggregation process is also flexible. Second, it is based on HM, which has two important parameters and plays a key role in the outcome of the decision. It is therefore possible to obtain various scores of alternatives and rating orders with regard to parameters $\lambda$. In the following, we will analyze the effect of the parameters on the results. We let $p=1$ and $q=2$ be a fixed set assign and investigate the influence of $\lambda$ on the different aggregation operators. Details can be found in Tables 5, 6, 7 and 8.

1) Using CFHMDA operator to aggregate the given alternatives $(I_{1},I_{2},I_{3},I_{4},I_{5})$ where $p=1,q=2$ and $\lambda =(1,2,3,4,5,6,7,8,9,10).$ So,

2) Using CFWHMDA operator to aggregate the given Alternatives $(I_{1},I_{2},I_{3},I_{4},I_{5})$ where $p=1,q=2$ and $\lambda =(1,2,3,4,5,6,7,8,9,10).$ So,

Table 6 Score values of alternatives using CFWHMDA operator

3) Using CFGHMDA operator to aggregate the given Alternatives $(I_{1},I_{2},I_{3},I_{4},I_{5})$ where $p=1,q=2$ and $\lambda =(1,2,3,4,5,6,7,8,9,10).$ So,

Table 7 Score values of alternatives using CFGHMDA operator

4) Using CFGWHMDA operator to aggregate the given alternatives $(I_{1},I_{2},I_{3},I_{4},I_{5})$ where $p=1,q=2$ and $\lambda =(1,2,3,4,5,6,7,8,9,10).$ So,

Table 8 Score values of alternatives using CFGWHMDA operator

Form Tables 5, 6, 7, and 8, we can find out that different scores of alternatives can be derived with respect to different parameter $\lambda$. This characteristic illustrates the flexibility of the proposed method and operators. In real MADM problems, the values of alternatives can be determined by decision-makers according to actual needs. In Tables 5, 6, 7, and 8, we investigate the individual effect of the parameter $\lambda$ on the score function and ranking results, i.e., we let p or q be a fixed value and investigate the influence of another parameter $\lambda$ on the ranking results. As we can see from Tables 5, 6, 7, and 8, different scores and ranking results can be obtained with the change of $\lambda$. Additionally, it can be noticed that alternative ranking is different with the change of parameters $\lambda$, the best alternatives are always $I_{4}$. This feature demonstrates the robustness of the proposed method. It is worth pointing out that in the above discussion, we used the proposed aggregation operators to aggregate decision-makers’ preference information. In the following, we investigate the influence of parameter $\lambda$ on the scores and ranking orders in the proposed operators. Analogously, we assign the different values to the parameter $\lambda$ and the corresponding scores of alternatives and ranking orders are derived. Details can be found in Tables 5, 6, 7, and 8.

In this section, we investigate the influence of the parameter on the scores and ranking orders. Results illustrate the flexibility and powerfulness of the proposed method. Moreover, the proposed method exhibits high robustness in the process of information aggregation and MADM. Thus, the proposed method is sufficient to deal with practical MADM problems.

10 Conclusions

Nowadays, the cubic fuzzy set (CFs) has developed very popular than an intuitionistic fuzzy set (IFS) and it proceeds good decision-makers objectivity steps into suppositions. This paper consists of specific steps on cubic fuzzy aggregation (CFA) operators based on DTT. First, for (CFNs) we proposed the operational laws on the rules of (DTT) notation of Dombi t-conorm and t-norm. So, the recently developed cubic fuzzy operations and HM to CFs. We write in detail and introduced the CFHMDA, CFWHMDA, CFGHMDA, and CFWGHMDA operators. The defined operators for aggregation did not show the relationship between CFNs, but process the given data very will. For MADM problems, we developed a new method with the cubic fuzzy information. An enterprise resource planning provides suitable numerical examples for the proposed method. We also find out the effect of the result of the decision based on recently introduced the cubic fuzzy aggregation operators. Then, we compare our work to others existing work for finding their mistakes and for future progress to make him correct. In the future, we will continue our struggle to investigate more aggregation operators and finding out more and more methods related to our topic.