1 Introduction

Various real-world optimization problems can be described as multi-objective optimization problems (MOPs), e.g., optimal power flow problem (Medina et al. 2014), economic emission unit commitment problem (Trivedi et al. 2015), vehicle routing problem with stochastic demands (Gee et al. 2016), metal rolling control (Hu et al. 2019a). A MOP contains more than one objective and they often conflict with each other. There is usually no solution can achieve the optimum for all objectives at the same time. That means, the optimal solution of a MOP is a set of trade-off solutions rather than a single one.

Without loss of generality, a MOP can be described as follows:

$$\begin{aligned} \begin{aligned}&\min \ F(x)=(f_1(x),f_2(x),\ldots ,f_M(x))^T,\\&\hbox {s.t.}\quad {x}\in \varOmega ^{D}, \end{aligned} \end{aligned}$$
(1)

where \(x=(x_1,x_2,\ldots x_N)^T, N\) is the scale of the solution set, \(x_i=(x_i^{1},\ldots ,x_i^{D})\) for all \(i=1,\ldots ,N\) is one of the solutions with D-dimensional decision variables in the decision space \(\varOmega ^{D}\), and \(\varOmega ^{D}=\prod _{i=1}^D [a_i,b_i]\subset R^D, M\) is the number of objective functions and the mapping function \(F: \varOmega ^{D}\rightarrow R^{M}\) defines M- objective functions in the objective space \(R^{M}\). When \(M>3\), the MOP is called many-objective optimization problems (MaOPs). Multi-objective evolutionary algorithms (MOEAs) are demonstrated to be suitable for handling kinds of MOPs.

Over the past two decades, most MOEAs have been proposed, such as SPEA (Zitzler and Thiele 1999), NSGAII (Deb et al. 2002), SPEA2 (Zitzler et al. 2001), ASMiGA (Nag et al. 2015). These algorithms evaluate individuals by using Pareto dominance, which evaluate the fitness together with a diversity maintenance as a secondary criterion and perform well in two or three objectives optimization. However, the performance of the algorithm drops sharply when the number of objectives increases. Because almost all individuals in the population are non-dominated solutions. The degenerated selection pressure makes the Pareto-dominance-based algorithms fail to solve MaOPs (Purshouse and Fleming 2007).

Apart from those Pareto-dominance-based MOEAs, it has been an increasing interest in decomposition-based approach to solving MOPs and MaOPs. Decomposition-based approaches decompose MOPs or MaOPs into a number of scalar subproblems and optimize them simultaneously, such as MOEA/D (Zhang and Li 2007), MOEA-TPN (Jiang and Yang 2016), NSGAIII (Deb and Jain 2014). In this type of algorithm, the setting of weight vectors of aggregation functions plays a key role in the performance (Fan et al. 2019). In other words, weight vectors with different shapes produce different optimization results (Ishibuchi et al. 2017). Some efforts have been made to adjust weight vectors dynamically, the detailed introduction will be given in Sect. 2.2.

Besides, the used aggregation method and the setting of reference points have also some effects on the performance of algorithms (Wang et al. 2017b). In study Wang et al. (2017a), the dynamic reference point was adopted through the adjustment of \(\epsilon \), which can strike a good balance between exploitation and exploration. In a recent study RPEA (Liu et al. 2017), according to the information of the current population, a series of reference points including several local ideal points and a global ideal point with good performances in convergence and distribution were continuously generated to guide the evolution. Literature (Liu et al. 2010) utilized a monotonic increasing function, in order to transform each objective function into a hyperplane in the original objective function space and ensure the non-dominance solutions are close to it. However, it cannot work well when solve complex problems with disconnected subregions, a sharp peak and a long tail.

In addition to the above two methods, indicator-based methods for multi-objective optimization have also been studied, such as hypervolume estimation algorithm for multi-objective optimization (HypE) (Bader and Zitzler 2011) and R2MOPSO (Li et al. 2015a). The optimization process is guided according to the indicators values in this category of algorithms. Although such methods have sound theoretical support, the heavy computational complexity is a fatal flaw.

Some other algorithms can be viewed as the hybrid of different mechanisms, e.g., MOEA/DD (Li et al. 2015b) used the Pareto-dominance-based fitness evaluation and the MOEA/D framework. R2HMOPSO (Wei et al. 2018) mixed three methods above. Stable matching model (STM) was introduced to coordinate the selection process (Li et al. 2014). Some studies (Ying et al. 2017; Yuan et al. 2016; Hu et al. 2017, 2019b) made efforts on the balance of convergence and diversity, which is a difficulty in multi-objective and many-objective optimization.

Given the above considerations, the evenly distributed weight vectors are not suitable for complex Pareto fronts (PFs), so a new optimizer including the adaptive adjustment of weight vectors and the balance of convergence and diversity is considered in this paper. Based on this, a self-adaptive weight vector adjustment strategy for decomposition-based multi-objective differential evolution algorithm (AWDMODE) is proposed in this work. The main properties of AWDMODE can be summarized as follows.

  1. (1)

    At the initialization phase, three weight vectors with different shapes (line, concave, convex) are generated, so as to facilitate adaptive processing of optimization problems with different shapes of PFs.

  2. (2)

    Not only the shapes of PFs, but also the scope of PFs are considered in AWDMODE. When the algorithm runs to a certain degree, the weight vectors are adjusted in the searched space according to the information of the current population. The purpose of this strategy is to make weight vectors more relevant to the PFs and ensure the guidance of weight vectors becomes more accurate and effective.

  3. (3)

    A parameter \(\xi \) is introduced to balance the convergence and diversity, different \(\xi \) guides the algorithm to choose different environment selection strategies. In the early stage of the optimization, the main task of AWDMODE is to enhance convergence. In order to accelerate the convergence rate, a self-learning strategy is adopted. In this strategy, the solutions in lower dominance level are close to that in higher dominance level. When the algorithm reaches a certain degree of convergence, the main task of evolution is increasing diversity. The coordinated switching of the two environmental selection ensures better convergence and distribution of the final solution set.

In the remainder of this paper, Sect. 2 reviews the related work. Then, the proposed AWDMODE is outlined in detail in Sect. 3. Thereafter, the simulation results on a set of test instances are presented and the analysis is given in Sect. 4. Finally, Sect. 5 concludes this paper and provides suggestions on possible opportunities for future research.

2 Background and related work

2.1 Decomposition methods

Three scalar functions were introduced in original MOEA/D framework: (1) the weighted sum; (2) the weighted Tchebycheff function; and (3) the penalty-based boundary intersection (PBI) function. A set of uniformly spread weight vectors is generated, i.e., \(W=\{w_{1},w_{2},\ldots ,w_{N}\}\), where \(w_{i}=(w_{i}^{1},w_{i}^{2},\ldots ,w_{i}^{M})\) for all \(i=1,\ldots ,N\). The MOP in Eq. (1) is decomposed into N scalar subproblems by these weight vectors and the subproblems are optimized simultaneously.

  1. (1)

    Weighted Sum (WS) approach In this approach, the aggregate function is written as

    $$\begin{aligned} \min \ g^{ws}(x_i|w_i)=\sum _{j=1}^{M} w_i^jf_j(x_i), \end{aligned}$$
    (2)

    where \(i=1,\ldots N\). This approach works well to solve the problems with convex PF. However, it cannot obtain the entire PF and the effect is slightly poor for nonconvex PFs.

  2. (2)

    Tchebycheff approach The corresponding aggregate function formula is defined as:

    $$\begin{aligned} \min \ g^{te}(x\mid w,z^*)=\displaystyle {\max _{1\le {i}\le {M}}}\{w_i|f_i(x)-z_i^*|\}, \end{aligned}$$
    (3)

    where \(z^*=(z_1^{*},z_2^{*},\ldots ,z_M^{*})^{T}\) is a reference point, and \(z_i^{*}=min\{f_i(x)\mid x\in \varOmega ^{D}\}\), \(i=1,2,\ldots ,M, w_i\) corresponding to the i-th subproblem.

  3. (3)

    Penalty-based boundary intersection (PBI) approach In this approach, the i-th subproblem is defined in the form

    $$\begin{aligned} \min \ g^{pbi}(x|w_i,z^{*})=d_1+\theta d_2, \end{aligned}$$
    (4)

    where \(\theta \) is penalty parameter and \(d_1, d_2\) are defined as follows:

    $$\begin{aligned} \begin{aligned}&d_1=\frac{|(f(x)-z^{*})^Tw|}{\Vert w\Vert }, \\&d_2=\Vert f(x)-z^{*}-d_1\frac{w}{\Vert w\Vert } \Vert . \end{aligned} \end{aligned}$$
    (5)

    Different decomposition methods produce great influence on the performance of algorithm (Lee et al. 2014). Here, Tchebycheff decomposition method is adopted in this paper.

2.2 Related work

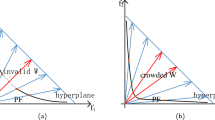
The weight vectors play a fundamental role in MOEA/D, while the evenly distributed weight vectors are not suitable for complex PFs, especially for the PFs with a long tail and a sharp peak. In study Ishibuchi et al. (2017), the experimental results illustrated that the distribution of weight vectors should be adjusted to the shape and the size of the PF. There are several related works on the improvement of weight vectors of MOEA/D.

In MOEA/D-AWA (Qi et al. 2014), WS-transformation was proposed as a new weight vectors initialization method. According to the current optimal solution set periodically, an adaptive weight vector adjustment (AWA) strategy was designed to adjust the distribution of the weight vectors. Besides, MOEA/D-AWA divides the whole optimization procedure into two phases to balance convergence and diversity. When dealing with MOPs with discrete PFs, the biggest challenge is how to identify sparse regions and true discrete regions. Therefore, vicinity distance is used to evaluate the sparsity of the solutions in the current non-dominated set, then new subproblems are added into the real sparse regions. This strategy demonstrates that MOEA/D-AWA is great potential for solving complex problems with disconnected subregions, a sharp peak or a long tail.

Similarly, in MOEA/D-TPN (Jiang and Yang 2016), a two-phase strategy (TP) is employed. During the first stage, convergence is as important as diversity in optimization, and at the end of the first stage, the algorithm identifies the geometric shape of the PF. Then, according to the geometric shape (convex or concave), the algorithm adjusts weight vectors and decides whether or not to allocate computational resources to unsolved subproblems. In MOEA/D-TPN, it is important to identify extreme solutions and add solutions in extreme regions.

In RVEA (Cheng et al. 2016), the angle-penalized distance (APD) is designed dynamically to balance convergence and diversity in MaOPs. The algorithm focus on convergence in the early stage and puts the main position to improve the diversity in the late stage of the optimization. During the optimization, the distribution of the reference vectors is adjusted according to the ranges of different objective functions. RVEA normalizes the reference vectors rather than the objective functions to ensure a uniform distribution of the candidate solutions in the objective space. However, a possible situation is that more than one reference vector associates with a same candidate solution, which may cause the sparse areas in objective space.

Pareto-adaptive weight vectors (\(pa\lambda \)) MOEA/D (Jiang et al. 2011) was proposed to adjust uniform automatically according to geometrical characteristics of PF. The initial weight vectors of \(pa\lambda \)-MOEA/D are generated by mixture uniform design (MUD) to obtain an arbitrary number of weight vectors. The algorithm identifies the geometrical characteristics (concave or convex) of the Pareto front by calculating the hypervolume value, and then, weight vectors are adjusted automatically to scatter or assemble weight vectors. \(pa\lambda \)-MOEA/D assumes that PF is symmetric, which is a challenging problem for handling asymmetric PF.

Different from the above improvement methods, weight vectors in PICEA-w (Wang et al. 2015) are adaptively modified in a coevolutionary manner with the candidate solutions during the search. In PICEA-w, candidate solutions are ranked by each of the weighted aggregate function, and a ranking matrix is created, then the fitness of candidate solutions is calculated based on this matrix. The weights are coevolved with the candidate solutions toward an optimal distribution. This strategy makes the algorithm less sensitive to the geometry of the problem. Nevertheless, the key factor affecting the performance of the algorithm is the generation mechanism of offspring.

From another perspective, a monotonic increasing function is utilized in T-MOEA/D to transform the objective functions into a new function, which makes the curve shape of the candidate solutions close to the unit hyperplane in the original objective function space (Liu et al. 2010). The algorithm can achieve good distribution with fixed weight mode. However, the algorithm may be less effective in dealing with MaOPs and the MOPs with discrete Pareto front.

To overcome the drawback of fixed weight, many improvements have been attempted on adjusting weights adaptively in decomposition- based algorithms. However, there is less research on PF with different axis ranges, such as WFG series test functions. Therefore, to address such PFs, a self-adaptive weight vector adjustment strategy for decomposition-based multi-objective differential evolution algorithm is proposed.

3 The proposed algorithm: AWDMODE

This section proposes a novel algorithm called multi-objective differential evolution algorithm by decomposition with adaptive weight vectors (AWDMODE). In the following paragraphs, the implementation details of each component in AWDMODE will be explained step-by-step.

3.1 General framework

The pseudocode of the proposed method is shown in Algorithm 1. The AWDMODE shares a common framework that is employed by many evolutionary algorithms. In the first part, an initial population P is formed by generating N individuals randomly, then their fitness values are calculated and the reference point \(z^*\) is acquired. Next, weight vectors with three different shapes (line, concave, convex) are generated and one of them is chosen as the original weight vectors. During the process of iteration and update, an adaptive weight vector is introduced to ensure a uniform distribution on PF. Then, differential evolution operators are performed to obtain an offspring population Q and neighborhood is updated similar to that of MOEA/D-DE. Finally, elitism strategy is adopted to select N best solutions based on the weight vectors for survival. It can be seen that there are three key operators in AWDMODE: generation of weight vectors (line 4), adaptive adjustment of weight vectors (line 8) and selection of elite individuals (line 12). In the following subsections, the above key operators will be described in detail.

figure a

3.2 Generate weight vector

The weight vector plays a crucial role in decomposition-based optimization algorithms, and affects the performance of the algorithm. It is worth mentioning that the evenly distributed weight vectors are not suitable for complex PFs, especially for the PFs that have a long tail and a sharp peak. Hence, three different shapes (line, concave, convex) are generated in advance at the initialization phase of the proposed algorithm, in order to solve different PFs.

figure b
Fig. 1
figure 1

The weight vectors with different \(\alpha \)

Full size image

As described in Algorithm 2, weight vectors are generated according to the method in MOEA/D, and these vectors are treated as a basic weight and called \(line-weight\) in this paper (lines 1–2), i.e., \(W.line=(w_1,w_2,\ldots ,w_N)\). It is well-known that the weight vectors of \(line-weight\) are a series of discrete points evenly distributed in \(f_1+f_2+\cdots +f_M=1\). Based on this, \(convex-weight\) can be generated through the following equation:

$$\begin{aligned} W.convex=(W.line)^{\alpha }, \end{aligned}$$
(6)

where \(\alpha \) is a parameter to determine the curvature of the weight vectors. Then, \(concave-weight\) is the symmetrical mapping of \(convex-weight\) on \(f_1+f_2+\cdots +f_M=1\).

In Fig. 1a, there are several convex weight vectors generated by Eq. (6) with different \(\alpha \), where \(N=20,M=2\). It can be observed from Fig. 1a, the curvature of the curve is changed with different \(\alpha \). The larger \(\alpha \), the greater the curvature. The curvature of \(\alpha =2\) is large, and the curvature of \(\alpha =1.5\) is small, which does not improve the guidance of the population significantly. Intuitively, \(\alpha =1.75\) is set in this paper, which is more suitable for distinguishing different PFs. The detailed analysis is described in Sect. 4.5.2.

Fig. 2
figure 2

MOEA/D with original weight vectors

Full size image
Fig. 3
figure 3

MOEA/D with adjusted weight vectors

Full size image

3.3 Adaptive weight vector

In this study, not only the shape of the PFs, but also the scope of the PFs is considered. Weight vectors are adjusted adaptively by making full use of information provided by the current population. The detailed procedure is given in Algorithm 3.

figure c

When the algorithm goes to a certain degree (40% maximum function evaluation times), AWDMODE adjusts adaptively the weight vectors every 30 generations (line 1 in Algorithm 3). First of all, the shape of PF should be identified in order to choose suitable type of weight vectors. The fitness values are normalized by the following formula:

$$\begin{aligned} Fit\_normal=\frac{Fit-Fit_{min}}{Fit_{max}-Fit_{min}} \quad , \end{aligned}$$
(7)

where the \(Fit_{max}\) and \(Fit_{min}\) are the maximum and minimum of the fitness values (line 3 in Algorithm 3), respectively. The mean of the \(Fit\_normal\) is calculated to judge the bumpiness of the PF. It is worth noting that C is a scaling parameter and it is set to 1 in this paper because the population is normalized in the previous steps. During the optimization process, the fault tolerance is set to 5%. That means, when the average fitness value of the population (i.e., \(mean\_Fit\) in Algorithm 3) is between (\(1-0.05\)) and (\(1+0.05\)), the \(line-weight\) vector is adopted. If \(mean\_Fit\) is greater than (\(1+0.05\)), then the shape of the current population is considered as concave. If \(mean\_Fit\) is less than (\(1-0.05\)), then the shape of the current population is considered as convex. Then, the suitable weight vectors are chosen and adopted in the later optimization. Finally, the weight vectors are enlarged or reduced according to the maximum of the Fit.

To demonstrate the effectiveness of adjusting weights more intuitively, Figs. 2 and 3 show the results of MOEA/D on WFG3, WFG4, WFG10 with different weight vectors. In Fig. 2, the different range on each objective results in uneven distribution of the solutions. After adopting the improved weight vectors in this paper, it is obvious that the distribution is increased on different PF shapes in Fig. 3. The purpose of this study is to make weights more relevant to the PFs, so that the guidance of weight vectors becomes more accurate and effective.

figure d

3.4 Environment selection

Environmental selection mechanism is an important factor that affects the convergence or diversity of an algorithm. However, for a MOP with complex Pareto fronts, classic decomposition-based scheme cannot work well in balancing the convergence and diversity. Previous research shows that the number of non-dominated solutions in archive can reflect the progress of the algorithm to some extent (Fan et al. 2018). The completion-checking factor \(\xi \) is adopted to make up for the insufficiency of traditional decomposition-based algorithms. Algorithm 4 shows the environmental selection procedure.

In the early stages of optimization, the main task of the algorithm is to speed up the convergence so that the solution set can converge to the true PF as soon as possible. First of all, non-dominated-sorting operation is executed to measure the current process of the algorithm. When there are less non-dominated solutions in the archive, dominance-based approach is adopted to accelerate convergence. Not only the solutions in the first dominance level, but also the solutions in other dominance levels are also used to construct a new archive. The solutions at the other dominance level move to the first level until N solutions are obtained (lines 5–11 in Algorithm 4). That means the individuals at low dominance levels move one by one toward the first front (lines 2–3 in Algorithm 5). If the new solution dominates the old one, then the new solution survives(lines 4–6 in Algorithm 5). Through this self-learning method between individuals, the convergence rate of the entire population can be accelerated. The detailed steps are reflected in Algorithm 5.

figure e

In the second phase of the algorithm, the main task is improving distribution. Every solution is associated with weight vectors according to the distance just like that in NSGAIII (Deb and Jain 2014) (line 13 in Algorithm 4). For each weight vector, there is one solution which associates with it to ensure the distribution of the algorithm (lines 14–17 in Algorithm 4). For an arbitrary weight vector \(w_i\), there are three scenarios. The first scenario is that only one solution is associated with \(w_i\). In this case, this solution is selected as a candidate solution and added to the archive (lines 1–2 in Algorithm 6). In the second case, there are more than one solution associated with \(w_i\). At this time, among the solutions associated with \(w_i\), the solution with the smallest aggregation function value (\(g^{te}\)) is selected as a candidate solution and added to the archive (lines 3–4 in Algorithm 6). If there is more than one solution with the smallest aggregation function value, one of the solutions is chosen at random. The last case is that there is no solution associated with \(w_i\). At this time, the solution closest to \(w_i\) is selected as a candidate solution and added to the archive (lines 5–6 in Algorithm 6). It should be noted that at the beginning of the second phase, some dominating solutions may be retained in the archive.

figure f

Actually, dominance-based approach can work well when the number of objectives is small. As the number of objectives increases, the performance of the algorithm plummets. Therefore, \(\xi \) is set by Eq. (8):

$$\begin{aligned} \xi =\frac{1}{(M-1)^2}, \end{aligned}$$
(8)

where M is the number of objectives. More details of the sensitivity of parameter of \(\xi \) can be found in Sect. 4.5.1.

4 Experimental studies

To benchmark the performance of AWDMODE, four competitor MOEAs are considered: NSGAII (Deb et al. 2002), R2MOPSO (Li et al. 2015a), RVEA (Cheng et al. 2016) and MOEA/D-STM (Li et al. 2014). Besides, in order to reflect the effectiveness of adaptive weighting strategies, AWDMODE with the original weight (the weight vectors adopted in MOEA/D (Zhang and Li 2007) is also compared in the following experiment, which is denoted as AWDMODE0.

4.1 Test instance

WFG1-WFG10 (Huband et al. 2006) are used in this study. The PFs of WFG test problems are irregular, being discontinued or mixed, and are scaled with different ranges in each objective. The WFG parameter k (position parameter) is set to 18 and the number of decision variables D is set to 32, i.e., the WFG parameter l (distance parameter) is 14, where \(l=D-k\) for each test instance. In this work, 2-, 3- and 4-objective of these problems are focused.

4.2 Performance metric

In this paper, the widely used performance metric hypervolume (HV) (Zitzler and Thiele 1999) is adopted to evaluate the performance of all compared algorithms, which can assess convergence and diversity of obtained solutions. Pareto solution set with higher HV value has better convergence and diversity. Hypervolume metric is computed as follows:

$$\begin{aligned} HV(S)=Leb( \cup _{x \in S}[f_1(x),R_1]\times \cdot \cdot \cdot \times [f_M(x),R_M]),\nonumber \\ \end{aligned}$$
(9)

where set S is the obtained non-dominated solutions, Leb(S) is the Lebesgue measure of S. \(R = (R_1,\ldots , R_M)^T\) is a reference point which is dominated by any point in the set S. In this experiment, R is set to \((3,\ldots ,2M+1)^T\) for M-objective test instances.

4.3 Parameter settings

Each algorithm is performed for 20 runs independently on each test instance, the detailed parameter settings are summarized as follows.

Reproduction operators: The mutation probability \(pm = 1/D\), distribution index \(\eta _m=20\). For the DE operator, probability is used to select in the neighborhood: \( \delta = 0.9, CR = 1.0\), and \(F = 0.5\) as recommended in MOEA/D-DE (Li and Zhang 2009).

Population size and stopping condition: \(N = 100\) for bi-objective test instances, 210 for the three-objective ones and 286 for the four-objective ones. Function evaluations, i.e., \(FEs=100000, 210000, 286000\) for 2-, 3-,4-objective instances respectively.

Neighborhood size: \(\hbox {T} = 20\).

4.4 Experimental results

Tables 1, 2 and 3 show the mean and standard deviation (SD) of HV performance metric for six algorithms, where AW refers to AWDMODE, AW0 represents the algorithm with the original weight vectors AWDMODE0 and STM represents MOEA/D-STM. In these tables, the best results of the mean or standard deviation for each test function are marked as bold face. In addition, the Wilcoxon rank sum test is adopted to compare the results obtained by AWDMODE and those by five compared algorithms at a significance level of 0.05, which examined that whether the HV mean values obtained by AWDMODE are different from that obtained by the other algorithms statistically. Namely, when p value (p) is bigger than 0.05, it means that the compared HV values are similar in statistics. The bold italics in tables show that there is no significant difference between AWDMODE and the contrastive algorithms. In these tables, the better/similar/worse (\(+/=/-\)) denote that the performance of AWDMODE is significantly better than, equivalent to, or worse than that of the compared algorithms on all test functions.

Table 1 HV values on WFG1-10 (\(M=2\))
Full size table
Table 2 HV values on WFG1-10 (\(M=3\))
Full size table
Table 3 HV values on WFG1-10 (\(M=4\))
Full size table

AWDMODE0 employs a set of evenly distributed weights, which faces difficulties on the problems with complex PF whose geometry is not similar to a hyperplane. The distribution of solutions for those problems is poor because the performance of AWDMODE0 is guided by the evenly distributed weights.

For bi-objective optimization problems, as shown in Table 1, AWDMODE is the most effective algorithm which obtains the most of the best results. RVEA performs very competitively to AWDMODE and it performs best on WFG1, WFG4 and WFG10. NSGAII performs well when the number of objectives is small. The performance of R2MOPSO is poor than that of its competitors. It may result from the update mechanism of the particle swarm algorithm is not suitable for dealing with complex PF like WFG test instances. The proposed AWDMODE obtains significantly better performance than the other algorithms on WFG2, WFG3 and WFG7-9, and shows clear improvements over AWDMODE0, R2MOPSO and MOEA/D-STM on almost all of 10 test instances.

Table 2 gives results of all the WFG test instances with three-objective optimization problems. It is clear that AWDMODE performs best, presenting a clear advantage over the other five algorithms on the majority of the test instances. AWDMODE performs best on WFG3, WFG5-9 comparing with other algorithms, while RVEA outperforms other algorithms on WFG1, WFG2 and WFG10. It is demonstrated that AW0, R2MOPSO and MOEA/D-STM obtain relatively poor performance compared with their counterparts. This phenomenon may be due to the particularity of the WFG series test problems. Uniform distribution of weight vectors cannot guarantee a good distribution of the obtained solutions on true PF. Obviously, performance of NSGAII in three-objective optimization problems is worse than that in the bi-objective. The reason for this can be the reduction in selection pressure mentioned in the introduction. On WFG5, WFG6 and WFG10, the final solutions by four algorithms are plotted in Fig. 4. It is evident that AWDMODE obtains the best distribution and is able to approximate the boundary parts well.

As can be seen from Table 3, NSGAII obtains weaker performance than AWDMODE and RVEA. This verifies the fact to some extent that the performance of the dominance-based algorithms declines in solving MaOPs. Figure 5 depicts the parallel coordinate plots, where the horizontal axis represents the number of objective functions and the vertical axis denotes the value of the objective functions. The different colors in these figures represent different solutions. It can be observed from Fig. 5 that AWDMODE gains good distribution along the Pareto front on WFG1, WFG6 and WFG8.

Fig. 4
figure 4

Pareto front on WFG5, WFG6, WFG10 with three-objective

Full size image
Fig. 5
figure 5

Pareto front on WFG1, WFG6, WFG8 with 4-objective

Full size image
Fig. 6
figure 6

Variation of HV-metric value on WFG1-10 with two-objective

Full size image
Fig. 7
figure 7

Variation of HV-metric value on WFG1-10 with three-objective

Full size image
Fig. 8
figure 8

Variation of HV-metric value on WFG1-10 with 4-objective

Full size image

To compare the convergence speed of the algorithms, the evolution of the mean HV-metric values obtained by five algorithms is plotted in Figs. 6, 7 and 8. Obviously, all the algorithms obtain a fast convergence performance on the test functions. It can be observed that AWDMODE performs remarkably better than other algorithms on the most of test problems. These results show clearly that AWDMODE is capable to solve the problems with complicated PF.

Table 4 HV values on WFG1-10 with different \(\xi \) (\(M=2\))
Full size table
Table 5 HV values on WFG1-10 with different \(\xi \) (\(M=3\))
Full size table
Table 6 HV values on WFG1-10 with different \(\xi \) (\(M=4\))
Full size table

4.5 Parameter analysis

4.5.1 Sensitivity of performance to the parameter \(\xi \)

As mentioned above, the performance of dominance-based algorithms plummets with the number of objectives increases. Actually, they can work well when the number of objectives is small. Therefore, the completion-checking factor \(\xi \) is adopted in environmental selection mechanism, i.e., Sect. 3.4. To verify the effectiveness of this strategy, different \(\xi \) values are examined on all the WFG test problems with 2-, 3-, 4-objectives. For simplicity, function evaluations are set to \(N*700\), and the same settings for other parameters in Sect. 4.3 are used.

Tables 4, 5 and 6 collect all the HV comparison results for AWDMODE with the different \(\xi \) values. In Table 4, the algorithm performance can be seen of 2-objective test functions. At first, when the value of \(\xi \) increases, the algorithm performance shows a good trend, that is, the HV value increases with the increase of \(\xi \). However, the algorithm performance degrades as \(\xi \) continues to increase. In other words, \(\xi =1\) is the best choice for 2-objective test functions. In Table 5, the HV value for \(\xi = 0.25\) is clearly better than that with the other \(\xi \) values. Than means, \(\xi =0.25\) is the best choice for 3-objective test functions. In Table 6, it can be found that the performance with small value is significantly better than that of large \(\xi \) value. Thus, \(\xi =0.11\) is the most promising choice for 4-objective test functions.

As a result, it is unreasonable to set \(\xi \) to a fixed value for solving optimization problems with different objective numbers. Instead, the value of \(\xi \) should be adaptively adjusted when handling different problems. Therefore, for most of the test problems adopted in this paper, the setting of \(\xi \) can be summarized as Eq. (8).

Fig. 9
figure 9

The optimal results of different \(\alpha \) values on all WFG functions for HV values

Full size image

4.5.2 Sensitivity of performance to the parameter \(\alpha \)

As mentioned in Sect. 3.2, \(\alpha \) is a parameter that controls the curvature. The larger \(\alpha \) value, the greater the curvature. To obtain a more appropriate value, different \(\alpha \) values on WFG test suites are executed with 2-, 3-, 4-objective. The same settings for other parameters in Sect. 4.3 are used. Due to the small difference in values, the further statistical analysis is conducted to facilitate more intuitive observation of the results.

Figure 9 plots the optimal results of different \(\alpha \) values on WFG functions for HV values. For example, \(\alpha =2\) gains the best result on 2-objective WFG1, \(\alpha =1\) obtains the best performance on 3- and 4-objective WFG1. It can be clearly observed that the performance of \(\alpha =1\) and \(\alpha =1.75\) is outstanding on most issues.

Table 7 records the comparison summary of AWDMODE on the WFG test problems with different \(\alpha \) values. The best performance is outperformed when \(\alpha =1.75\), which indicates 1.75 is an appropriate value to adopt in this paper.

5 Conclusions and future work

In this paper, a self-adaptive weight vector adjustment strategy for decomposition-based multi-objective differential evolution algorithm is proposed, termed as AWDMODE. In AWDMODE, weight vectors with different shapes (line, concave, convex) are predefined. Then, the weight vector is adaptively adjusted according to the shape of the PFs. Besides, a parameter \(\xi \) is introduced to balance the convergence and diversity of the algorithm, and self-learning strategy is adopted to accelerate the convergence rate. Four state-of-the-art algorithms are compared with AWDMODE, namely NSGAII (dominance-based), R2MOPSO (indicator-based), RVEA and MOEA/D-STM. Experimental studies are performed on WFG1-WFG10 with 2-, 3-, 4-objective problems, respectively. In order to verify the effectiveness of adaptive weight adjustment strategy, the algorithm with the original weight vectors also participates in the experiment, termed AWDMODE0. Experimental results indicate that AWDMODE can obtain well-converged and evenly distributed approximated PFs for MOPs with complex PFs, especially with irregular PFs or the PFs with different ranges in each objective.

Table 7 The comparison summary of AWDMODE on the WFG test problems with different \(\alpha \) values
Full size table

Although AWDMODE shows great potential in handling complicated test instances, there are still some limitations. In our future work, we may concentrate on dealing with the PFs with discontinuous regions and reducing the computational cost of adjusting weight vectors in MaOPs.