1 Introduction

Multi-criteria decision making (MCDM) has become a hot research issue for a long time (Chen et al. 1992; Ribeiro 1996; Wei 2008; Jiang et al. 2018). Up to now, various methods and approaches have been developed to study this problem, such as TOPSIS (García-Cascales and Lamata 2012; Tsaur 2011), VIKOR (Opricovic and Tzeng 2004, 2007; Sayadi et al. 2009), evidential reasoning-based approach (Yager 1992; Deng and Jiang 2018; Xu and Deng 2018), and analytic hierarchy process (AHP) (Saaty 1980), fuzzy-based method (Zhang et al. 2017; Xu and Yager 2008; Fei et al. 2017; Nie et al. 2011), etc. (Jiang et al. 2017a; Zheng and Deng 2018b). Besides, game theory, as a tool to study agent’s behaviors in competitive environment (Wang et al. 2017, 2016; Deng et al. 2016; Xu et al. 2018), is also widely used in the field of MCDM (Aplak and Türkbey 2013; Peldschus and Zavadskas 2005; Aplak and Sogut 2013; Yang et al. 2013; Liu et al. 2017a; Kang et al. 2017). Among them, the AHP method has attracted widely attention due to its ability in uniting both qualitative and quantitative factors in decision-making process. In the classical AHP model, the relative importance between elements, also called preference relation between elements, is represented in a pairwise comparison matrix.

Generally, the multiplicative preference relation (Saaty 1980) satisfying \(a_{ij} \times a_{ji} = 1\) is often employed in the AHP method. Meanwhile, other types of preference relations are also existing. One is called fuzzy preference relation satisfying \(r_{ij} + r_{ji} = 1\). A fuzzy preference relation (Tanino 1984; Herrera-Viedma et al. 2004, 2007; Xu 2007) provides another way to construct a decision matrix of pairwise comparisons based on linguistic values given by experts. However, the conventional fuzzy preference relation is on the basis of complete and certain information. It is unable to deal with the cases involving incompleteness and uncertainty. In order to overcome this deficiency, in reference (Deng et al. 2014b) a concept of D numbers preference relation was proposed which extends the fuzzy preference relation by using D numbers, where the tool of D numbers (Deng et al. 2014a, b; Deng 2012) provides a new representation to express the uncertain information by extending Dempster–Shafer theory (Dempster 1967; Shafer 1976; Denoeux 2013; Antoine et al. 2014; Zheng et al. 2017; Zheng and Deng 2018a; Yager 2014; Yang and Xu 2013; Yager and Liu 2008). Based on the concept of D numbers preference relation, a D-AHP method (Deng et al. 2014b) has been proposed for MCDM problems, and the D-AHP method extends the traditional AHP method in theory.

In the proposed D-AHP method, the derived results about the ranking and priority weights of alternatives are impacted by the credibility of providing information. A parameter \(\lambda \) is used to express the credibility of information, and its value is associated with the cognitive ability of experts. If the comparison information used in the decision-making process is provided by an authoritative expert, \(\lambda \) will take a smaller value. If the comparison information comes from an expert whose judgment is with low belief, \(\lambda \) takes a higher value. As suggested in Deng et al. (2014b), a feasible scheme is shown as follows.

$$\begin{aligned} \lambda = \left\{ {\begin{array}{l@{\quad }l} {\left\lceil {\underline{\lambda }}\right\rceil }, &{} \text {The information is with high credibility} \\ {n,} &{} \text {The information is with medium credibility} \\ {{n^2} / 2,} &{} \text {The information is with low credibility} \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(1)

where \({\underline{\lambda }}\) represents lower bound of \(\lambda \), and \(\left\lceil {\underline{\lambda }} \right\rceil = \min \{ k \in \mathbb {Z}| k \geqslant {\underline{\lambda }}\}\), and n is the number of alternatives. For instance, \(\left\lceil {\underline{\lambda }}\right\rceil = 2\) if \({\underline{\lambda }} = 1.58\). In previous study (Deng et al. 2014b), the D-AHP method has been successfully used to solve a supplier selection problem, but the credibility of providing information is not further and deeply studied. In this paper, the credibility of information is focused to investigate its impact on the decision-making results when applying the D-AHP method to a MCDM problem. Three cases, namely information with high credibility, medium credibility and low credibility, are taken into consideration, respectively. The results show that the credibility of information slightly impacts the ranking of alternatives, but the priority weights of alternatives are influenced in a relatively obvious degree. The explanation and reasonability for the results are well displayed in this paper.

The remainder of this paper is organized as follows. A brief introduction about D numbers is presented in Sect. 2. Then the D-AHP method is given in Sect. 3. After that, a case study considering the credibility of information in the D-AHP method is presented in Sect. 4. Finally, conclusions are given in Sect. 5.

2 D numbers

The tool of D numbers (Deng et al. 2014a, b; Deng 2012) is a new representation for uncertain information, which can be seen as an extension of basic probability assignment (BPA) in Dempster–Shafer theory (Dempster 1967; Shafer 1976; Jiang and Zhan 2017) for uncertainty modeling and handling (Jiang and Wang 2017; Deng et al. 2017; Zhang et al. 2018). At present, it has been used in some fields, for example supplier selection (Deng et al. 2014b), environmental impact assessment (Deng et al. 2014a), failure mode and effects analysis (Liu et al. 2014, 2018; Jiang et al. 2017b). D numbers overcome a few of existing deficiencies (i.e., exclusiveness hypothesis and completeness constraint; refer to Deng et al. 2014a, b for more details) in Dempster–Shafer theory and is very effective in representing various types of uncertainties. Some basic concepts about D numbers are given as follows.

Definition 1

Let \(\Theta \) be a nonempty set \(\Theta = \{ F_1 ,F_2 , \ldots ,F_N \}\) satisfying \(F_i \ne F_j\) if \(i \ne j\), \(\forall i,j = \{ 1, \ldots , N\}\) , a D number is a mapping formulated by

$$\begin{aligned} D: 2^{\Theta } \rightarrow [0,1] \end{aligned}$$
(2)

with

$$\begin{aligned} \sum \limits _{B \subseteq \Theta } {D(B) \le 1} \quad \hbox {and} \quad D(\emptyset ) = 0 \end{aligned}$$
(3)

where \(\emptyset \) is the empty set and B is a subset of \(\Theta \).

If \(\sum \nolimits _{B \subseteq \Theta } {D(B) = 1}\), the information expressed by the D number is said to be complete; if \(\sum \nolimits _{B \subseteq \Theta } {D(B) < 1}\), the information is said to be incomplete.

For a discrete set \(\Theta = \{b_1, b_2, \ldots , b_i, \ldots , b_n\}\), where \(b_i \in R\) and \(b_i \ne b_j\) if \(i \ne j\), a special form of D numbers can be expressed by Deng et al. (2014a, b)

$$\begin{aligned}&D(\{ b_1 \} ) = v_1, D(\{ b_2 \} ) = v_2, \ldots , D(\{ b_i \} )\nonumber \\&\qquad = v_i, \ldots , D(\{ b_n \} ) = v_n \end{aligned}$$
(4)

or simply denoted as \(D = \{(b_1, v_1), (b_2, v_2), \ldots , (b_i, v_i), \ldots , (b_n, v_n) \}\), where \(v_i > 0\) and \(\sum \nolimits _{i = 1}^n {v_i } \le 1\). Some properties of this form of D numbers are introduced as follows.

Remark 1

Permutation invariability. If there are two D numbers that \(D_1 = \{(b_1, v_1), \ldots , (b_i, v_i), \ldots , (b_n, v_n) \}\) and \(D_2 = \{ (b_n, v_n), \ldots , (b_i, v_i), \ldots , (b_1, v_1)\}\), then \(D_1 \Leftrightarrow D_2\).

Remark 2

For a D number \(D = \{(b_1, v_1), (b_2, v_2), \ldots , (b_i, v_i), \ldots , (b_n, v_n) \}\), the integration representation of D is defined as

$$\begin{aligned} I(D) = \sum \limits _{i = 1}^n {b_i v_i } \end{aligned}$$
(5)

where \(b_i \in R\), \(v_i > 0\) and \(\sum \nolimits _{i = 1}^n {v_i } \le 1\). For the sake of simplification, the integration representation of a D number is called its I value.

3 D-AHP method

3.1 D numbers preference relation

Preference relation (Xu 2007) which is usually denoted as pairwise comparison matrix is a classical means to express expert’s subjective knowledge. Generally, there are two types of preference relations: multiplicative preference relation satisfying \(a_{ij} \times a_{ji} = 1\) and additive preference relation, also called fuzzy preference relation, satisfying \(r_{ij} + r_{ji} = 1\). A reciprocal fuzzy preference relation can be conveniently represented by an \(n \times n\) matrix \(R = [r_{ij}]_{n \times n}\), being \(r_{ij} = \mu _R (A_i, A_j) \forall i,j \in \{ 1,2, \ldots ,n\}\), namely (Tanino 1984; Herrera-Viedma et al. 2004, 2007)

$$\begin{aligned} R = \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {} &{}{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {A_1 } &{} {A_2 } &{} \cdots &{} {A_n } \\ \end{array}} \\ {\begin{array}{l} {A_1 } \\ {A_2 } \\ \vdots \\ {A_n } \\ \end{array}} &{} {\left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {r_{11} } &{}\quad {r_{12} } &{}\quad \cdots &{}\quad {r_{1n} } \\ {r_{21} } &{}\quad {r_{22} } &{}\quad \cdots &{}\quad {r_{2n} } \\ \vdots &{} \quad \vdots &{} \quad \ddots &{}\quad \vdots \\ {r_{n1} } &{}\quad {r_{n2} } &{} \quad \cdots &{}\quad {r_{nn} } \\ \end{array}} \right] } \\ \end{array} \end{aligned}$$
(6)

where (1) \(r_{ij} \ge 0\); (2) \(r_{ij} + r_{ji} = 1, \; \forall i,j \in \{ 1,2, \ldots ,n\}\); (3) \(r_{ii} = 0.5,\; \forall i \in \{ 1,2, \ldots ,n\}\). \(r_{ij}\) denotes the preference degree of alternative \(A_i\) over alternative \(A_j\), where \(r_{ij} = 0\) means that \(A_j\) is absolutely preferred to \(A_i\), \(r_{ij} < 0.5\) that \(A_j\) is preferred to \(A_i\) to some degree, \(r_{ij} = 0.5\) that there is indifferent between \(A_i\) and \(A_j\). On the contrary, \(r_{ij} > 0.5\) means that \(A_i\) is preferred to \(A_j\) to some degree, \(r_{ij} = 1\) implies that \(A_i\) is absolutely preferred to \(A_j\).

Fig. 1
figure 1

Procedure to obtain the ranking and priority weights of alternatives based on a D numbers preference relation (Deng et al. 2014b)

Full size image

However, the original fuzzy preference relation can be only constructed on the basis of complete and certain information. It is unable to deal with the cases that involve incomplete and uncertain information. In order to overcome the deficiency, in the literature (Deng et al. 2014b) we proposed the concept of D numbers preference relations which extends the fuzzy preference relations by using D numbers. The D numbers preference relation is formulated by

$$\begin{aligned} R_D = \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {} &{} {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {A_1 \; } &{} {A_2 \; } &{} \cdots &{} {A_n } \\ \end{array}} \\ {\begin{array}{lc} {A_1 } \\ {A_2 } \\ \vdots \\ {A_n } \\ \end{array}} &{} {\left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {D_{11} } &{}\quad {D_{12} } &{}\quad \cdots &{}\quad {D_{1n} } \\ {D_{21} } &{}\quad {D_{22} } &{}\quad \cdots &{}\quad {D_{2n} } \\ \vdots &{} \quad \vdots &{}\quad \ddots &{}\quad \vdots \\ {D_{n1} } &{}\quad {D_{n2} } &{}\quad \cdots &{}\quad {D_{nn} } \\ \end{array}} \right] } \\ \end{array} \end{aligned}$$
(7)

where \(D_{ij} = \{(b^1_{ij}, v^1_{ij}), (b^2_{ij}, v^2_{ij}), \ldots , (b^p_{ij}, v^p_{ij}), \cdots \}\), \(D_{ji} = \lnot D_{ij} {=} \{(1-b^1_{ij}, v^1_{ij}), (1-b^2_{ij}, v^2_{ij}), \ldots , (1-b^p_{ij}, v^p_{ij}), \cdots \}, \forall i,j \in \{ 1,2, \ldots ,n\}\), and \(b_{ij}^p \in [0,1]\), \(v_{ij}^p > 0\), \(\sum \nolimits _p {v_{ij}^p } = 1\). Obviously, \(D_{ii} = \{(0.5, 1.0)\} \;\; \forall i \in \{ 1,2, \ldots ,n\}\) in \(R_D\). Because the D numbers preference relation can be represented in the form of matrix, herein, the corresponding matrix is called D numbers preference matrix, abbreviated as D matrix.

3.2 Solution for a D numbers preference relation

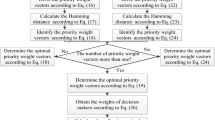
Once a D numbers preference relation about alternatives has been constructed, a key problem is how to obtain the ranking and priority weights of alternatives based on the D numbers preference relation. In Deng et al. (2014b), we studied the solution for D numbers preference relation. The procedure of the solution is shown in Fig. 1.

  • Step 1 At first, the D numbers preference relation \(R_D\) is converted to an I values matrix \(R_I\) by using Eq.(5).

  • Step 2 At second, let us construct a probability matrix \(R_p\) based on \(R_I\), where \(R_p\) represents the preference probability between each pair of alternatives.

  • Step 3 At third, in terms of \(R_p\), a triangular probability matrix \(R_p^T\) is derived, with the assist of local information if necessary. Based on \(R_p^T\), the ranking of alternatives can be obtained.

  • Step 4 At fourth, a triangulated I values matrix \(R_I^T\) is generated based on \(R_I\) and \(R_p^T\); then, the weights of alternatives can finally calculated by means of \(R_I^T\).

Please refer to the literature (Deng et al. 2014b) for more details. In the following, a numerical example is given to simply exhibit this procedure.

Example 1

Assume there are four proposals \(P_1\), \(P_2\), \(P_3\), \(P_4\) for building a power station. The pairwise comparisons among the four proposals are given in Table 1.

In order to obtain the ranking of all proposals and priority weigh of each one, the solution shown in Fig. 1 is utilized. Here the detailed process is omitted, but some important intermediate outcomes are given as follows.

$$\begin{aligned} R_I = \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {0.50} &{}\quad {0.80} &{}\quad {0.60} &{}\quad {0.55} \\ {0.20} &{}\quad {0.50} &{}\quad {0.80} &{}\quad {0.48} \\ {0.40} &{}\quad {0.20} &{}\quad {0.50} &{}\quad {0.90} \\ {0.45} &{}\quad {0.12} &{}\quad {0.10} &{}\quad {0.50} \\ \end{array}} \right] \end{aligned}$$
(8)
$$\begin{aligned} R_p = \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 &{}\quad 1 &{}\quad 1 &{} \quad 1 \\ 0 &{}\quad 0 &{} \quad 1 &{} \quad 0.95 \\ 0 &{} \quad 0 &{}\quad 0 &{} \quad 1 \\ 0 &{}\quad 0.05 &{}\quad 0 &{}\quad 0 \\ \end{array}} \right] \end{aligned}$$
(9)
$$\begin{aligned} R_p^T = \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0.95 \\ 0 &{}\quad 0 &{} \quad 0 &{}\quad 1 \\ 0 &{} \quad 0.05 &{}\quad 0 &{}\quad 0 \\ \end{array}} \right] \end{aligned}$$
(10)
$$\begin{aligned} R_I^T = \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {0.50} &{}\quad {0.80} &{}\quad {0.60} &{}\quad {0.55} \\ {0.20} &{} \quad {0.50} &{}\quad {0.80} &{}\quad {0.68} \\ {0.40} &{} \quad {0.20} &{}\quad {0.50} &{}\quad {0.90} \\ {0.45} &{} \quad {0.32} &{} \quad {0.10} &{}\quad {0.50} \\ \end{array}} \right] \end{aligned}$$
(11)
Table 1 Pairwise comparisons among four proposals in the form of D numbers preference relation
Full size table

According to \(R_p^T\), the ranking of proposals can be derived: \(P_1 \succ P_2 \succ P_3 \succ P_4\). In \(R_I^T\), the elements above and alongside the main diagonal, namely (0.8, 0.8, 0.9), indicate the weight relationship of proposals. Because \(R_I^T(1,2) = 0.8\), \(R_I^T(2,3) = 0.8\), \(R_I^T(3,4) = 0.9\), the weights of proposals, indicated by \(w_1\), \(w_2\), \(w_3\) and \(w_4\), meet the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} \lambda (w_1 - w_2 ) = 0.8 - 0.5 \\ \lambda (w_2 - w_3 ) = 0.8 - 0.5 \\ \lambda (w_3 - w_4 ) = 0.9 - 0.5 \\ w_1 + w_2 + w_3 + w_4 = 1 \\ \lambda > 0 \\ w_i \ge 0,\quad \forall i \in \{ 1,2,3,4\} \\ \end{array} \right. \end{aligned}$$
(12)

By solving Eq.(12), we have

$$\begin{aligned} \left\{ \begin{array}{l} w_1 = 1/4 + 0.475/\lambda \\ w_2 = 1/4 + 0.175/\lambda \\ w_3 = 1/4 - 0.125/\lambda \\ w_4 = 1/4 - 0.525/\lambda \\ \end{array} \right. ,\quad \lambda \in [2.1, + \infty ) \end{aligned}$$
(13)

where parameter \(\lambda \) expresses the credibility of information. If the comparison information is provided by an authoritative expert, \(\lambda \) takes a smaller value; if the comparison information comes from an expert whose judgment is with low belief, \(\lambda \) takes a higher value. The decline of \(\lambda \) means the decrease in expert’s cognitive ability to slight difference, which will lead that the weights of proposals are gradually closing to each others. Figure 2 shows the weight of each proposal with the change in \(\lambda \). It is easy to find that the difference among weights of proposals declines with the increase in \(\lambda \). In Deng et al. (2014b), a scheme is suggested to determine the value of \(\lambda \) as follows.

$$\begin{aligned} \lambda = \left\{ {\begin{array}{l@{\quad }l} {\left\lceil {\underline{\lambda }} \right\rceil ,} &{} \text {The information is with high credibility} \\ {\;\; n,} &{} \text {The information is with medium credibility} \\ {{n^2} / 2,} &{} \text {The information is with low credibility} \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(14)

Based on this scheme, the weights of these proposals are obtained, as shown in Table 2.

Fig. 2
figure 2

Weights of proposals with the change in \(\lambda \)

Full size image
Table 2 Weights and ranking of proposals in Example 1
Full size table

3.3 Hierarchical structure of D-AHP method

Based on the concept of D numbers preference relation, in Deng et al. (2014b) a D-AHP method has been proposed to extend the traditional AHP method. The hierarchical structure of D-AHP method is shown in Fig. 3. In the D-AHP, the critical point, obtaining the priority weights of alternatives based on the D numbers preference relation in each hierarchy, is solved by using the solution shown in Sect. 3.2. The determination of final priority weight of each alternative is a recursive integration layer by layer, as shown in Table 3.

Fig. 3
figure 3

Hierarchical structure of D-AHP method (Deng et al. 2014b)

Full size image
Table 3 Integration of each level’s weights in D-AHP (Deng et al. 2014b)
Full size table

4 Case study considering the credibility of information

As mentioned above, in the D-AHP the critical issue is to calculate the priority weights in each D numbers preference relation. But the setting of information’s credibility, i.e., \(\lambda \), has an impact on the results within the framework of D-AHP method. In previous study, the sensitivity analysis of \(\lambda \) is not discussed. In this section, we will use an illustrative example to exhibit the impact of information’s credibility on the final outcomes.

In the literature, Chen and Chao (2012) gave an example of supplier selection about an electronic company in southern Taiwan. In that paper, the authors have given detailed data about the example; please refer to Chen and Chao (2012) to get the data. In the example, there are four alternatives: \(X_1\), \(X_2\), \(X_3\) and \(X_4\). The structure of multi-criteria for supplier selection is displayed in Fig. 4. Based on those given data in Chen and Chao (2012), the ranking and priority weights of alternatives can be obtained by using the D-AHP method under different credibility of information, as shown in Tables 4, 5 and 6.

Fig. 4
figure 4

Structure of multi-criteria for supplier selection (Chen and Chao 2012)

Full size image
Table 4 Result of D-AHP method when the information is with high credibility
Full size table
Table 5 Result of D-AHP method when the information is with medium credibility
Full size table
Table 6 Result of D-AHP method when the information is with low credibility
Full size table

From the tables, the ranking of alternatives is

$$\begin{aligned} X_3 \mathop \succ \limits _{0.072} X_1 \mathop \succ \limits _{0.153} X_2 \mathop \succ \limits _{0.030} X_4, \end{aligned}$$
(15)

if the information is considered to be highly credible. The ranking is

$$\begin{aligned} X_3 \mathop \succ \limits _{0.0} X_1 \mathop \succ \limits _{0.061} X_2 \mathop \succ \limits _{0.014} X_4, \end{aligned}$$
(16)

if the information is considered to be moderately credible. The ranking is

$$\begin{aligned} X_1 \mathop \succ \limits _{0.002} X_3 \mathop \succ \limits _{0.030} X_2 \mathop \succ \limits _{0.007} X_4, \end{aligned}$$
(17)

if the information is considered to have low credibility. As can be found from these results, the rankings of alternatives are basically same in the situations of high credibility and medium credibility. In these two situations, the best alternative is \(X_3\), and the worst alternative is \(X_4\). Compared with the situation of information with medium credibility which yields two best alternatives \(X_3\) and \(X_1\), the information with high credibility is more effective in distinguishing \(X_3\) and \(X_1\), which reflects the assumption that high credibility shows the information has better cognitive ability. Besides, the differences among the obtained weights are relatively big in the two situations. The ranking of alternatives given by high or medium credibility is the same with the results given in the literature (Chen and Chao 2012) that is \(X_3 \mathop \succ \limits _{0.01} X_1 \mathop \succ \limits _{0.11} X_2 \mathop \succ \limits _{0.03} X_4\).

Now let us consider the situation of low credibility. In the situation, superficially the best alternative is \(X_1\) and the worst alternative is \(X_4\). But specifically, because their weights are \(w_1 = 0.268\), \(w_3 = 0.266\), \(w_2 = 0.236\) and \(w_4 = 0.229\), respectively, the gap between \(w_1\) and \(w_3\) is very small, i.e., \(w_1 - w_3 = 0.002\). Also, the gap between \(w_2\) and \(w_4\) is still very small, i.e., \(w_2 - w_4 = 0.007\). Conversely, the gap between \(w_3\) and \(w_2\) is relatively big, i.e., \(w_3 - w_2 = 0.030\). So, these alternatives are actually divided into two groups, namely superior suppliers \(\{X_1, X_3\}\) and inferior suppliers \(\{X_2, X_4\}\), when the credibility of information is low. From this point of view, qualitatively the result in the situation of low credibility is basically consistent with that in the situations of medium credibility and high credibility.

Such sensitivity analysis shows that as a whole these results, derived from the information whether it is high or medium or low credibility, are reasonable. And the results are consistent, although these situations have different discriminative capability in the differences of alternatives’ weights. When the information is considered to be lowly credible, which means that experts do not clearly distinguish the alternatives, so the differences among derived weights of alternatives are small. With the increase in information’s credibility (\(\lambda \) becomes lower), the slight differences among alternatives’ weights can be distinguished due to the improvement of experts’ cognitive capability. As a result, the priority weights of suppliers present relatively obvious difference, as shown in the situation of high credibility. Thus, the impact of information’s credibility in the D-AHP method on the results of ranking alternatives has been illustrated clearly.

5 Conclusions

In this paper, the MCDM problem has been studied by using our previous proposed D-AHP method, where the credibility of providing information is numerically analyzed. Regarding the value of parameter \(\lambda \) that associates with the cognitive ability of experts, it takes a smaller value if the comparison information is provided by an authoritative expert which means the information is with higher credibility, while it takes a higher value if the comparison information comes from an expert whose judgment is with low belief that implies the information is with lower credibility. The results show that the credibility of information slightly impacts the ranking of alternatives, and the priority weights of alternatives have been influenced in a relatively obvious degree. In the future research, the criteria for measuring the credibility of information will be studied.