An intuitionistic view of the Dempster–Shafer belief structure

Abstract

We discuss the Dempster–Shafer belief theory and describe its role in representing imprecise probabilistic information. In particular, we note its use of intervals for representing imprecise probabilities. We note in fuzzy set theory that there are two related approaches used for representing imprecise membership grades: interval-valued fuzzy sets and intuitionistic fuzzy sets. We indicate the first of these, interval-valued fuzzy sets, is in the same spirit as Dempster–Shafer representation, both use intervals. Using a relationship analogous to the type of relationship that exists between interval-valued fuzzy sets and intuitionistic fuzzy sets, we obtain from the interval-valued view of the Dempster–Shafer model an intuitionistic view of the Dempster–Shafer model. Central to this view is the use of an intuitionistic statement, pair of values, (Bel(A) Dis(A)), to convey information about the value of a variable lying in the set A. We suggest methods for combining intuitionistic statements and making inferences from these type propositions.

1 Introduction

The Dempster–Shafer theory provides a well-established structure for the representation of imprecise information about the value of uncertain variable (Dempster 1966; Shafer 1976; Zadeh Zadeh1986; Smets 1988, 1990; Yager 1992; Smets and Kennes 1994; Yager et al. 1994; Denoeux 1998, 1999; Yager 1999, 2001; Ferson et al. 2002; Dempster 2008; Yager and Liu 2008). Using this theory, the probability that a variable lies in a set is expressed as an interval. Here, we are allowing for imprecision in our knowledge of probabilities. This type of situation is often referred second order uncertainty. A similar example of second order uncertainty occurs in fuzzy set theory. In this case, we have imprecision in our knowledge of the membership grades of a fuzzy set. Two approaches have been developed in the domain of fuzzy sets for the representation of imprecise membership. These two approaches are interval-valued fuzzy sets (Karnik and Mendel 2001; Mendel and Bob John 2002; Mendel et al. 2006; Mendel and Wu 2010; Mizumoto and Tanaka 1976; Rickard et al. 2010) and intuitionistic fuzzy sets (Atanassov 1986, 2012; Bustince and Burrillo 1996; Pasi et al. 2005; Szmidt and Kacprzyk 2001; Xu and Yager 2009; Yager 2009). In the interval-valued approach, the imprecision in membership grade is captured by the use of an interval. In the intuitionistic approach, the imprecision is captured by the use of two values, support for membership and support against, which do not necessarily sum to one as in the case of the standard fuzzy set.

What is clear is that the representation of the imprecision used in the Dempster–Shafer model is in the same spirit as the interval-valued membership grades of fuzzy sets. Here, our objective is to provide a view of the Dempster–Shafer structure using a framework in the spirit of the intuitionistic approach of fuzzy set theory. The accomplishment of this objective is greatly aided by the known underlying relationship between interval-valued fuzzy sets and intuitionistic fuzzy sets (Atanassov and Gargov 1989; Cornelis et al. 2003; Deschrijver and Kerre 2003). Using the basic principal of this relationship, we are able to go very naturally from the classic interval-valued view of the imprecision in Dempster–Shafer theory to an intuitionistic view of the imprecision in Dempster–Shafer theory.

We note that in (Dymova and Sevastjantov 2010a, b, 2012), Dymova and Sevastjantov look at some connections between intuitionistic fuzzy sets and Dempster–Shafer belief structures; however, their focus and interest was different than ours. In Dymova and Sevastjantov (2010a, b, 2012), the authors focus on the problem of multi-criteria decision making in situations in which the criteria satisfactions are expressed in terms of intuitionistic membership grades. They are interested in using Dempster–Shafer theory to help provide decision making tools for comparing the interval satisfactions. Our focus is on the representation of information about an uncertain variable and on understanding the comparable ways we can provide this information using intervals, as in the belief approach and pairs of values as in the intuitionistic approach.

2 Belief structures and imprecise information

A Dempster–Shafer belief structure (Yager and Liu 2008; Liu and Yager 2008) provides a generalization of a probability distribution that can be used to model the case when we have imprecise information about the probability distribution. We note an even more general approach to modeling imprecise probabilities is that introduced by Walley (1982, 2000). Formally, a Dempster–Shafer belief structure $m$ on a space X is defined via a collection of non-empty subsets of ${X},{F}_{1}, \ldots ,{F}_{q}$, called focal elements and a mapping ${m}({F}_{j} ) \in \left( {0, {1}} \right]$ such that $\sum _{j={1}} ^qm( {F_j }) = {1}.$ Here, $m(F_{j})$ is known as the weight associated with $F_{j}$. It is specifically required that ${m}(\emptyset )=0$.

One interpretation of the D–S belief structure is that we have a variable V that can take its value in the space X. Instead of assigning a probability $p_{j}$ to each $x_{j}$ in X, we allocate an amount of probability, $m(F_{j})$, to be distributed among the elements in $F_{j}$ without specifically assigning it to any of the elements. When the probability in $m(F_{j})$ is allocated in this manner, this introduces an imprecision in our knowledge.

Two important concepts associated with Dempster–Shafer structures are plausibility and belief (Shafer 1976). We recall for any subset A of X

$$\begin{aligned} {Pl}({A})=\sum \limits _{j_{,\;} A\cap F_j \ne \emptyset } {m(F_j )} \;=\;\sum \limits _{j=1}^q {m(F_j )\mathrm{Poss}[A/F_j ]} \end{aligned}$$

$$\begin{aligned} \text{ Bel }({A})&= \sum \limits _{j,\;F_j \subseteq A} {m(F_j )\;} =\sum \limits _{j=1}^q {m(F_j )\mathrm{Cert}(A/F_j } )\\&= \sum \limits _{j=1}^q {m(F_j )(1-\mathrm{Poss}(\overline{A} /F_j )}\\&= 1-\sum \limits _{j=1}^q {m(F_j )\mathrm{Poss}(\overline{A} /F_j )}\end{aligned}$$

We recall that $\text{ Poss }[{A}/{F}_{j} ]=\text{ Max }_{x} [\text{ Min }({A}({x}),{F}_{j} ({x}))]$ and $\text{ Cert }[{A}/{F}_{j} ] =\mathrm{Min}_x [\mathrm{Max}(A(x), \bar{F}_j (x))]=1-\mathrm{Poss}(\bar{A}/F_j )$ and A(x) and $F_{j}(x)$ is the degree of membership of x in the respective sets. In the case where the associated sets are fuzzy sets, a number of approaches other than the above have been suggested in the literature (Yen 1990, 1992; Flaminio et al. 2013).

We note $\text{ Bel }({A})={ 1 }-\mathrm{Pl}( {\overline{A} })$. It is easily shown that these are actually measures (Yager 1999) on the space X

$$\begin{aligned} \text{ Pl }:{ 2}^{X}&\rightarrow \left[ {0,{ 1}} \right] {\text{ where }}\, \mathrm{Pl}(\emptyset )=0, \text{ Pl }({X})={ 1 \,\mathrm{and\,}}\\&\mathrm{Pl} ({A})\ge \text{ Pl }({B}) \text{ if } \,A \supseteq {B} \end{aligned}$$

$$\begin{aligned} \text{ Bel }:{ 2}^{X}&\rightarrow \left[ {0,{ 1}} \right] \text{ where } \text{ Bel }(\emptyset )=0, \text{ Bel }( {X})=0 \text{ and } \\&\text{ Bel } ({A})\ge \text{ Bel }({B}) { \mathrm{if}\, A}\supseteq {B}. \end{aligned}$$

These concepts are used to define the upper and lower probability bounds of the imprecise probability of A. Here, Bel(A) is the lower probability, denoted $P^{-}(A)$, and plausibility is the upper probability, denoted $P^{+}(A)$. Thus here, the probability P(A) lies in an interval, ${P}({A})\in \left[ {{\mathrm{Bel}}( {A}), \mathrm{Pl}({A})} \right] .$ We note $\left[ {\mathrm{Bel}({A}),\mathrm{Pl}( {A})} \right]$ is a sub-interval the unit interval, [0, 1].

A related situation occurs in what is called type two fuzzy sets (Mizumoto and Tanaka 1976). In this environment, we have imprecise membership grades associated with a fuzzy set. A particular example of a type two fuzzy subset is the so-called interval-value fuzzy set studied in great detail by Mendel (Mendel and Bob John 2002; Mendel et al. 2006; Mendel and Wu 2010). In this case, if F is an interval-valued fuzzy subset of the space X then F(x), the membership grade of the element x in F is a subset of the unit interval ${F}( {x})=[{F}_{\mathrm{L}} ( {x}),{F}_\mathrm{U} ({x})]$.

A related formulation for imprecise membership grades of a fuzzy set $F$ was introduced by Atanassov (1986, 2012), these are called intuitionistic membership grades. Here, we associate with $F(x)$, the membership of $x$ in $F$, not an interval, but a pair of values $\langle {F}_\mathrm{Y} ({x}),{F}_\mathrm{N} ({x})\rangle$. In this formulation, $F_\mathrm{Y}(x)$ is called the degree of support for membership and $F_\mathrm{N}(x)$ is called the degree of support against membership. Both ${F}_\mathrm{Y}(x)$ and ${F}_\mathrm{N} ({x})\in \left[ {0,1} \right]$ and it is required that ${F}_\mathrm{Y} (x)+{F}_\mathrm{N} ( x)\le {1}.$ Here, $\langle {F}_\mathrm{Y} (x), {F}_\mathrm{N} ( {x})\rangle$ can be referred to as an intuitionistic statement about the membership of $x$ in $A$.

A relationship was shown to exist between these two representations of imprecise fuzzy membership grades (Deschrijver and Kerre 2003; Cornelis et al. 2003). In particular, the interval-valued membership grade [$F_\mathrm{L}(x)$, $F_\mathrm{U}(x)$] was seen to be equivalent to an intuitionistic membership grade pair $\langle {F}_\mathrm{Y} (x), {F}_\mathrm{N} (x)\rangle$ where ${F}_\mathrm{L} (x) = F_\mathrm{Y} (x)$ and ${F}_\mathrm{N} (x) ={1 }-F_\mathrm{U} (x).$

The analogy between the imprecise interval-valued membership grade of a fuzzy set $F(x) \in [F_\mathrm{L} (x), F_\mathrm{U} (x)]$ and the imprecise interval-valued probability of the belief structure $P(A) \in \left[ {\text{ Bel }(A), \text{ Pl }(A)} \right]$ inspires us to consider an intuitionistic representation of the interval associated with the probability of the set $A$, $P(A)$. If we follow this analogy, we get an intuitionistic representation of the imprecise value associated with the probability of A as $\langle \text{ Bel }(A),{1}- \text{ Pl }(A)\rangle$. We further see that $\text{ Bel }(A)=1- \text{ Pl }({\overline{A}}) =1-\sum \nolimits _{j=} \mathrm{Poss} [\bar{A}/F_j )m(F_j )$ and ${1} - \text{ Pl }(A)=1-\sum \nolimits _{j=1} ^n\mathrm{Poss}\left[ {A/F_j } \right) m( {F_j }).$ Here, we shall refer to $1 - \mathrm{Pl}(A)$ as the degree of disbelief of A and denote it as $\text{ Dis }(A)=1-\text{ Pl }(A).$

Using this here, we then have a pair $\langle \mathrm{Bel}(A), \mathrm{Dis}(A)\rangle$ where $\text{ Bel }(A)=1- \text{ Pl }( {\overline{A} })$ and Dis($A$) = $1 - \mathrm{Pl}(A)$. Thus, Bel($A$) is the belief that the value of the variable $V$ lies in $A$ and Dis($A$) is the belief that the value of variable does not lie in $A$. We note that $\text{ Bel }( A)+ \text{ Dis }(A)\le {1}.$ We shall refer to $\langle \mathrm{Bel}(A), \mathrm{Dis}(A)\rangle$ as an intuitionistic statement about finding $V$ in $A$ and use the notational convenience $\mathrm{IS}(A) = \langle \mathrm{Bel}(A), \mathrm{Dis}(A)\rangle$ to indicate an intuitionistic statement about finding $V$ in the set $A$.

We note that Dis is not a measure, actually it has complementary properties of a measure (Wang and Klir 1992). $\text{ Dis }:{2}^{X}\rightarrow \left[ {0,{ 1}} \right]$ is such (1) Dis($X$) = 0, (2) $\text{ Dis }(\emptyset )={ 1}$ and (3) $\text{ Dis }( {A})\ge \text{ Dis }( B) \text{ if }\, A\subseteq B$.

We note that in the framework of using the plausibility and belief to represent imprecise probability where $\mathrm{Bel}(A) = P_\mathrm{L}(A)$ and $\mathrm{Pl}(A) = P_\mathrm{U}(A)$, we can represent $\text{ Prob }(A)\in [P_{\text{ L }} (A),P_{\text{ U }} (A)],$ as a pair $\langle P_\mathrm{L}(A)$, $1 - P_\mathrm{U}(A)\rangle$. Here, we can think of $P_\mathrm{L}(A)$ as the guaranteed probability of $A$. We can think of $1 - P_\mathrm{U}(A)$ as the degree of improbability of $A$. We observe that $P_{\text{ L }} (A) + (1 - P_{\text{ U }} (A))\le 1$.

3 Characterizing features of imprecise information

Given an intuitionist statement $\mathrm{IS}(A)$ = $\langle \mathrm{Bel}(A), Dis(A)\rangle$ representing our knowledge about finding the value of $V$ in $A$, we can associate with this characterizing features related to the $quality$ of the information it contains. The first feature is the $commitment$

$$\begin{aligned} \text{ Com }(A)= \text{ Bel }(A)+ \text{ Dis }(A) \end{aligned}$$

The stronger the commitment, the better the information. Values of $\mathrm{Com}(A) < 1$ indicate some indecisiveness regarding the allocation between Bel($A$) and Dis($A$). The second feature is what we shall refer to clarity we define this as

$$\begin{aligned}&\text{ Clarity } ( A)\\&\quad =\frac{1}{\mathrm{Com}(A)}\left[ {\text{2 } \text{ Max }( {\text{ Bel }(A), \text{ Dis }(A)})- \text{ Com }(A)} \right] \\&\text{ Clarity } ( A)=\frac{2\;\mathrm{Max}[\mathrm{Bel}(A),\;\mathrm{Dis}(A)]}{\mathrm{Com}(A)}\;-\;1 \end{aligned}$$

We see that when $\mathrm{Bel}(A) = \mathrm{Dis}(A) = \frac{1}{2}\mathrm{Com}(A)$ then Clarity $=$ 0. We see that when one of the Bel($A$) $=$ 1 or Dis($A$) $=$ 1 then Max[Bel($A$), Dis($A$)] $=$ 1 and $\mathrm{Com}(A) = 1$ then $\mathrm{Clarity}(A)= 1$. Thus, $\mathrm{Clarity}(A) \in [0, 1]$. The larger the value of the clarity the more the distinction regarding the support for $V$ lying in $A$ and the support for $V$ not lying in $A$.

We note that

$$\begin{aligned} \frac{1}{2}\text{ Com }(A)\le \text{ Max }( {\text{ Bel }( A), \text{ Dis } (A)})\le \text{ Com }(A) \end{aligned}$$

More generally if $\mathrm{Bel}(A) = \mathrm{Dis}(A) = a$ then $\mathrm{Clarity} (A) = \frac{1}{2a}(2a - 2a) = 0$. Thus, the minimal clarity occurs when $\mathrm{Bel}(A) = \mathrm{Dis}(A)$. Also, note that $\mathrm{Bel}(A) = \mathrm{Dis}(A)$ corresponds to the case $\mathrm{possibility}(A) = \mathrm{possibility}(\text{ not }\,\bar{A}) = 1$ in the framework of possibility theory, and this is known to be a case of total ignorance, so clarity is (a sort of) the converse of ignorance.

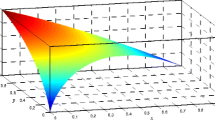
In Fig. 1, we illustrate the connection between $\mathrm{Dis}(A), \mathrm{Bel}(A), \mathrm{Com}(A) \,\mathrm{and} \,\mathrm{Clarity}(A)$.

Fig. 1

Relationship between properties

Another interesting special case occurs when the probability that $V$ lies in $A$ is precisely known, $\text{ Prob }( A)=\alpha .$ Here, $\text{ Bel }(A)=\alpha$ and $\text{ Pl }(A)=\alpha$ and thus $\text{ Dis }(A)={ 1 }-\text{ Pl }(A)={ 1 }-\alpha .$ In this case, $\text{ Com }(A)={ 1 }-\alpha +\alpha ={ 1}$, we have full commitment. In this case, we get, however, that $\text{ Clarity }( A) = \text{2Max }[({1 }-\alpha ),\alpha ]-{ 1}.$ We see this plotted as a function of $\alpha$ in Fig. 2. Thus, this takes its minimal value, least clarity, when $\alpha = 0.5$ and it increases as either $\alpha$ decreases or increases from 0.5. It attains maximum clarity when we have a probability $\alpha$ of either 1 or 0.

Fig. 2

Clarity as function of $\alpha$

In the preceding when we know the probability of $A$ is $\alpha$, we have $\mathrm{Pl}(A) - \mathrm{Bel}(A) = 0$. Consider now the case where $\mathrm{Pl}(A) - \mathrm{Bel}(A) = \beta$. Here,

$$\begin{aligned}&{1 }-( {\text{ Pl }(A)- \text{ Bel }(A)})={ 1 }-\beta \\&{1 }- \text{ Pl }(A)+ \text{ Bel }(A)={ 1 }-\beta \\&\text{ Dis }(A)+ \text{ Bel }(A)={ 1 }-\beta \end{aligned}$$

Thus, the sum of the belief and disbelief is equal to the complement of the imprecision, $\beta$. In this case,

$$\begin{aligned}&\text{ Clarity } ({A})\\&\quad =\frac{1}{\mathrm{Com}(A)}\left[ {\text{2 } \text{ Max }( {\text{ Bel }(A), \text{ Del }(A)})- \text{ Com }(A)} \right] \\&\quad =\frac{2\mathrm{Max}[\mathrm{Bel}(A),\;\mathrm{Del}(A)]}{1-\beta } -{1} \end{aligned}$$

We observe that this is maximized by making Max[Bel($A$), Dis($A$)] as large as possible. Furthermore, we note a symmetry between belief and disbelief. We get this maximum when either one of the two is as large as possible. Since Dis($A$) $+$ Bel(A) $= 1 - \beta$ thus clarity comes by maximizing the difference between belief and disbelief, making $[\mathrm{Dis}(A) - \mathrm{Bel}(A)]$ as big as possible. Here, then, if we have $\mathrm{Bel}(A) = 1 - \beta$ and $\mathrm{Dis}(A) = 0$ then we get maximal Clarity and we have $\text{ Clarity }(A)={ 2}\frac{1-\beta }{1-\beta } -{ 1 }={ 1}.$ On the other hand, the minimal occurs when $\text{ Bel }( A)= \text{ Dis }(A)=\frac{1}{2}({1 }-\beta ).$ In this case, $\mathrm{Max}[\mathrm{Dis}(A), \mathrm{Bel}(A)] = (1 - \beta )$ and we get that $\mathrm{Clarity}(A) = 0$.

It is important to emphasize that the Clarity and Commitment are measuring different things. We recall that $\mathrm{Dis}(A) + \mathrm{Bel}(A)$ is what we called the commitment. We observe that the complement of commitment

$$\begin{aligned} {1} - \text{ Com }(A)&= { 1 }-( {\text{ Dis }(A)+ \text{ Bel }(A)})=( {{1}- \text{ Dis }( A)})\\&- \text{ Bel }(A)= \text{ Pl }(A)- \text{ Bel }(A) \end{aligned}$$

is a kind of measure of imprecision or hesitancy. On the other hand, the

$$\begin{aligned} \text{ Clarity }(A)=\frac{2\mathrm{Max}[\mathrm{Bel}(A),\mathrm{Dis}(A)]}{\mathrm{Comp}(A)}-1 \end{aligned}$$

is related to how the total committed value is distributed between the Belief and Disbelief. The more unequally we distribute the committed value the more clarity.

We note that we can alternatively express the clarity as

$$\begin{aligned} \text{ Clarity }( A)=\frac{\mathrm{Max}[\mathrm{Bel}(A),\mathrm{Dis}(A)]}{\mathrm{Ave}[\mathrm{Bel}(A),\mathrm{Dis}(A)]} -{ 1} \end{aligned}$$

$$\begin{aligned} \text{ where } \text{ Ave }\left[ {\text{ Bel }(A), \text{ Dis }(A)} \right] =\frac{\mathrm{Bel}(A)+\mathrm{Dis}(A)}{2}. \end{aligned}$$

We observe that if $\mathrm{Com}(A) = 1\,\, \mathrm{then} \, \mathrm{Clarity}(A) =2\mathrm{Max}[\mathrm{Bel}(A), \mathrm{Dis}(B)] - 1$. In this case, the measure of clarity has properties related to the DeLuca and Termini measure of fuzziness (DeLuca and Termini 1972; Yager 1979, 1980). Actually, it is the complement of the DeLuca and Termini measure of fuzziness. We see this if we denote $F(z)= \mathrm{Clarity}(A)$ where $z = \mathrm{Max}[\mathrm{Bel}(A), \mathrm{Dis}(A)]$. If we consider $1 - F(z)$ we get the DeLuca and Termini properties

• (1) If $z = 1$, then $1 -F(z) = 0$.

• (2) $1 -F(z)$ attains its maximum value if $z = \mathrm{Max}(\mathrm{Del}(A), \mathrm{Del}(B)] = 0.5$, in this case, we get $1 - F(z) = 1$.

• (3) Since $z = \mathrm{Max}[\mathrm{Bel}(A), \mathrm{Dis}(A)] \ge 0.5$ then $1 - F(z)$ increases as $z$ increases.

Thus, we see that the Clarity is related to fuzziness, the Clarity is the complement to fuzziness.

4 Entailment of Dempster–Shafer belief structures

In 1986, Yager introduced the idea of entailment associated with D–S belief structures. Consider we have the knowledge that $P(A) \in R_{1} = [a_{1}, b_{1}]$. Here, we have that $P(A)$ lies in the interval $[a_{1}, b_{1}]$. Assume $R_{2} = [a_{2}, b_{2}]$ is another interval such that $a_{2}\le a_{1}$ and $b_{2} \, \ge b_{1}$. What is clear is that we can say that $P(A)\in [a_{2}, b_{2}]$. Thus, while the knowledge $P(A) \in R_{2}$ is less informative than $P(A) \epsilon R_{1}$ it is still a true statement. Thus, given that $P(A) \in R_{1}$ we can infer that $P(A) \in R_{2}$. We can go for the smaller range to the wider range. Here, we say $R_{1}$ entails $R_{2}$, the truth of $R_{1}$ implies the truth of $R_{2}$, we denote this $R_{1}\vert - R_{2}$.

Let us look at the idea of entailment from an intuitionistic perspective. Consider two ranges $R_{1}(A) = [a_{1}, b_{1}]$ and $R_{2}(A) = [a_{2}, b_{2}]$ such that $a_{1} \, \ge a_{2}$ and $b_{1} \, \le b_{2}$, $R_{1} \, \subseteq R_{2}$. So, here, starting with $R_{1}$, we can always infer $R_{2}$. Let us look at the associated intuitionistic representation. Here, we have ${\mathrm{IS}}_{1}{(A)} = \langle {a}_{1}, 1 - {b}_{1}\rangle$ and ${\mathrm{IS}}_{2}{(A)} = \langle {a}_{2},(1 - {b}_{2})\rangle$. In the first case, $\mathrm{Bel}_{1}(A) = a_{1}$ and $\mathrm{Dis}_{1}(A) = 1- b_{1}$ while in the second case, $\mathrm{Bel}_{2}(A) = a_{2}$ and $\mathrm{Dis}_{2}(A) = 1 - b_{2}$. We further see that $\mathrm{Bel}_{1}(A)= a_{1} \ge a_{2} = \mathrm{Bel}_{2}(A)$ and $\mathrm{Dis}_{1}(A) = 1 - b_{1}\ge 1 - b_{2} = \mathrm{Dis}_{2}(A)$. Here, we see that in the case of IS$_{2}(A)$, we have reduced the values associated with both the belief and disbelief. Thus, starting with a statement $\langle \mathrm{Bel}_{1}(A), \mathrm{Dis}_{1}(A)\rangle$, we can always infer $\langle \mathrm{Bel}_{2}(A), \mathrm{Dis}_{2}(A)\rangle$ where $\mathrm{Bel}_{2}(A) \le \mathrm{Bel}_{1}(A)$ and Dis$_{2}(A) \le \mathrm{Dis}_{1}(A)$. Then, here, we have reduced our commitment with respect to our belief and disbelief. Thus, inference from the intuitionistic perspective is simply a matter of reducing the belief and disbelief.

Thus, we see that starting with a Bel/Dis pair $\langle \mathrm{Bel}_{1}, \mathrm{Dis}_{1}\rangle$ we can infer a pair $\langle \mathrm{Bel}_{2}, \mathrm{Dis}_{2}\rangle$ so that Bel$_{2} \le \mathrm{Bel}_{1}$ and Dis$_{2}\le \mathrm{Dis}_{1}$ while this always results in a reduction in commitment the situation with respect to clarity is not as well behaved. Thus, if $\mathrm{Bel}_{1} \ge \mathrm{Dis}_{1}$ the clarity is $\mathrm{Bel}_{1}- \mathrm{Dis}_{1}$. Assume now we infer $\langle \mathrm{Bel}_{2}, \mathrm{Dis}_{2}\rangle$ where Dis$_{ 2 }\le$ Dis$_{1}$ but Bel$_{1} = \mathrm{Bel}_{2}$ then we get a clarity of $\mathrm{Bel}_{1}- \mathrm{Dis}_{2} \ge \mathrm{Bel}_{1} - \mathrm{Dis}_{1}$ we have increased the clarity. On the other hand, if $\mathrm{Dis}_{1} = \mathrm{Dis}_{2}$ and $\mathrm{Bel}_{2} \le \mathrm{Bel}_{1}$ but still $\mathrm{Bel}_{2} \ge \mathrm{Dis}_{2}$ then we get a clarity of $\mathrm{Bel}_{2} - \mathrm{Dis}_{1} \le \mathrm{Bel}_{1} - \mathrm{Dis}_{2}$ we have reduced clarity.

In 1986, Yager provides a more general framework extending the idea of entailment to belief structures. Assume $m_{1}$ and $m_{2}$ are two D–S belief structures on $X$ such that for all subsets $A$ of $X$, we have $R_{1}(A) \subseteq R_{2}(A)$. What is clear is that if we know $m_{1}$ to be a correct representation of our knowledge then we can infer that $m_{2}$ is also correct. In this case, we say $m_{1}$ entails $m_{2 }$ and we write $m_{1} \, \vert - m_{2}$. We further note that in this case, $m_{1}$ provides more information but still $m_{2}$ is not wrong. We see that in going for $m_{1}$ to $m_{2}$, we have essentially reduced our committed with regard to our belief and disbelief associated with our information.

On the other hand, we observe that if $m_{1}$ entails $m_{2}$, $m_{1} \, \vert - m_{2}$, then for any $A$ since $R_{1}(A)\subseteq R_{2}(A) m_{2}$ is less constraining that $m_{1}$. The belief structure $m_{2}$ is less restrictive.

In Yager (1986), we provided a form for an entailment principle for Dempster–Shafer structures that says the following. Assume $m$ is a belief structure with focal elements $A_{1}, {\ldots } A_{P}$ and $m(A_{i}) = a_{i}$. Let another $m_{1}$ be a belief structure with focal elements $B_{11}, B_{12}, {\ldots }, B {1n(1)}, B_{21}, {\ldots }, B_{2n(2)},\dots B_{Pr1}, {\ldots }B_{pn(P)}$ with $A_{i} \, \supseteq B_{ij}$ for all $j = 1$ to $n(i)$ and $\sum$ $_{j=1}^{n(j)}m_{2}(B_{ij}) = a_{1}$ then $m_{1} \, \vert - m$. Then, from $m_{1}$ we can entail $m$. Furthermore, $m$ is less constraining and less informed than $m_{1}$. The justification of this form for the entailment principle is the fact given the relationship between the focal elements in $m$ and $m_{1}$ it can be shown that for any subset $E$ we have $R_{1}(E) \subseteq R(E)$.

5 Providing intuitionistic information

The ability to provide the information about the uncertainty associated with a variable using an intuitionistic type expression of the knowledge may be useful for some information providers. Consider the situation in which an expert provides information about the value of a variable $V$ lying in a subset $A$ of the domain $X$ in terms of an intuitionistic statement $\mathrm{IS}(A)=\,\langle \mathrm{Bel}(A),\mathrm{Dis}(A)\rangle$. With this statement, they are saying their belief that the variable $V$ lies in $A$ is Bel($A$) and their disbelief is Dis($A$). In providing this type of information, there are just a few constraints. The first is that if $A = X$, then we must have $\mathrm{Bel}(X) = 1$ and $\mathrm{Dis}(X) = 0$, $\mathrm{IS}(X) = \langle 1,0\rangle$. For $A=\emptyset$, we must have $\langle 0, 1\rangle$, $\text{ Bel }(\emptyset )=0$ and $\text{ Dis }(\emptyset )={ 1}.$ Finally, for any other set $A$, all that are required is $\mathrm{Bel}(A) + \mathrm{Dis}(A) \le 1$. Thus, this is very convenient and comfortable way for a informant to express information about the value of a variable. The following example illustrates such a situation. We have just heard a lecture from very interesting young scholar and a colleague asks my opinion as to whether he is “over 21”. As I am uncertain I provide the following information my Belief that he is over 21 is 0.6 and my Disbelief is 0.2.

Consider now we are providing the information IS($A) = \langle \mathrm{Bel}(A), \mathrm{Dis}(A)\rangle =\langle a, b\rangle$ about the value of some variable $V$. Here, we are saying that our belief that $V$ lies in $A$ is $a$ and our disbelief is $b$.

Consider now a Dempster–Shafer belief structure $m$ with focal elements $F_{1} = A, F_{2}= \overline{A}$ and $F_{3} = X$ where $m(F_{1}) = \mathrm{Bel}(A) = a$, $m(F_{2}) = \mathrm{Dis}(A) = b$ and $m(F_{3}) = 1 - (\mathrm{Dis}(A)+ \mathrm{Bel}(A)) = 1- a -b$. Conceptually, we see $1- (\mathrm{Dis}(A) + \mathrm{Bel}(A))$ as the amount non-committed. We see for this belief structure $m$, we have

$$\begin{aligned} \text{ Pl }_{m} ({A})&= \sum _{j={1}}^{\text{3 }}m( {F_j})\mathrm{Poss}\left[ {A/F_j } \right] \\&= a+( {{1}-( {b +a})})={ 1 }-b \end{aligned}$$

$$\begin{aligned} {\text{ Pl }}_{m} ( {\overline{A} })&= \sum \limits _{j=1}^n {m(F_j )\mathrm{Poss}[\bar{A}/F_j ]} \\&= b+( {{1}-( {b +a})})={ 1 }-a \end{aligned}$$

In this case, Bel$_{m}(A) = 1 - \mathrm{Pl}_{m}(\overline{A} ) = a$ and Dis($A) = 1 - \mathrm{Pl}_{m}(A) = b$. Here, then, we have the IS$_{m}(A) =$ $\langle a, b\rangle$. Thus, $m$ correctly conveys the provided information. Thus, $m$ is an appropriate representation of the knowledge in the preceding intuitionistic statement $\mathrm{IS}(A)=\,\langle \mathrm{Bel}(A), \mathrm{Dis}(A)\rangle =\langle a, b\rangle$.

We provide a theorem generalizing the preceding.

Theorem 1

Any belief structure $m_{1}$ that satisfies IS$_{m1}(A) =\langle a, b\rangle$ must have the following focal elements

• (i) A collection of focal elements $F_{j} \,\subseteq A$ whose total weight is $a$.

• (ii) A collection of focal elements $F_{j} \,\subseteq \,\overline{A}$ whose total weight is $b$.

• (iii) A collection of focal $F_{j}$ so that $F_{j} \cap {A}\ne \emptyset$ and $F_{j} \,\not \subset A$ whose total weight is $1 - (b + a)$.

Proof

Consider now any belief structure $m_{1}$ that satisfies $\mathrm{IS}_{m1}(A) =\, \langle a, b\rangle$. Let us denote its focal elements as $F_{1}, {\ldots }, F_{q}$ and their weights as $m_{1}(F_{j})$. We observe that we can partition this collection of focal elements into three categories:

• (1) Those that are contained in $A, F_{i} \,\subseteq A$. Let these be $F_{1}, {\ldots }, F_{r}$.

• (2) Those that intersect $A$ but are not contained in $A, F_{r + 1}, {\ldots } F_{P}$.

• (3) Those which does not intersect $A$, those contained in $\overline{A}$, $F_{P + 1}, {\ldots }, F_{q}$.

Here, then,

$$\begin{aligned} \mathrm{Pl}_{m_1 } ({A})&= \sum _{j={1}}^q \mathrm{Poss}\left[ {A/F_j } \right] m_{1} ( {F_j })\\&= \sum \limits _{j,F_j \cap A\ne \emptyset } {m_1 (F_j )} =\sum _{j={1}} ^Pm_{1} ( {F_j }) \end{aligned}$$

From the fact that IS$_{m1}(A) = \langle a, b\rangle$ where $b = 1 - \mathrm{Pl}_{m_1 }(A)$, we have $\mathrm{Pl}_{m_1 } (A) = 1 - b$ and hence, $\sum _{j=1}^{p}m_{1}(F_{j}) = 1 - b$. In addition, $\mathrm{Bel}_{m_1 } (A) = \sum \nolimits _{j,\;F_j \subseteq A} {m_1 (F_j )} =\sum$ $_{j=1}^{r}m_{1}(F_{j}) = a$.

Furthermore, we note that

$$\begin{aligned} {1}-b&= \sum _{j={1}} ^Pm_{1} ( {F_j }) =\sum _{j={1}} ^rm_{1} ( {F_j })+ \sum _{j=r+{1}} ^Pm_{1} ( {F_j })\\&= a+ \sum _{j=r+{1}} ^Pm_{1} ( {F_j }) \end{aligned}$$

Thus, we see that

$$\begin{aligned} \sum _{j=r+{1}} ^Pm_{1} ( {F_j })={ 1 }-( {{b}+{ a}})={ 1 }-{ b }-{ a} \end{aligned}$$

Since

$$\begin{aligned}&{1 }=\sum _{j={1}} ^qm_{1} ( {F_j })=\sum _{j={1}} ^rm_{1} ( {F_j })+\sum _{j=r+{1}} ^Pm_{1} ( {F_j })\\&\qquad +\sum _{j=P+{1}} ^qm_{1} ( {F_j })={ a }+( {{1}-{b }-{ a}}) +\sum _{j=P+{1}}^qm_{1} ( {F_j }) \end{aligned}$$

thus, we see that $\sum$ $_{j=P+1}^{q}m_{1}(F_{j}) = b$.

Recall our belief structure m with $m(A) = a, m(\overline{A} ) = b$ and $m(X) = 1 - (b + a)$. We observe that all $F_{j}$ for $j = 1$ to $r$ are such $F_{j}\subseteq A$, all $F_{j}$ for $j = r + 1$ to $p$ are such that $F_{j}\subseteq \, \overline{A}$ and all $F_{j}$ for $j = p + 1$ to $q$ are such that $F_{j} \, \subseteq X$ then from the entailment principle we can infer $m_{1}\,\vert -m$. Thus, all belief structures that satisfy $\mathrm{IS}(A) =\,\langle a, b\rangle$ entail $m$, hence $m$ is the least restrictive belief structure that satisfies $\mathrm{IS}(A) =\, \langle a, b\rangle$. Thus, implementing the knowledge $\langle \mathrm{Bel}(A), \mathrm{Dis}(A)\rangle \,=\,\langle a, b\rangle$ by $m$ is the most appropriate representation as it assumes no additional information.

Let $B$ be another subset of $X$. We see that $B$ can have one of three different possible relationships with $A$.

• (1) $B_{1} \,\subseteq A$

• (2) ${B}_{2} \cap {A}=\emptyset$

• (3) ${B}_{3} \cap {A}\ne \emptyset \,\text{ but }\, {B}_{3} \not \subset A$

Using the belief structure $m$ described above, we see that

• (1) For $B_{1} \,\subseteq A$, we have

  $$\begin{aligned} \mathrm{{Pl}}_{m} ({B}_{1} )&\le { 1 }-{ b} \\ {\text{ Pl }}_{m} ( {\overline{B} _1 })&\ge \sum \limits _{j=1}^3 {m(F_j )\mathrm{Poss}(\bar{B}_1 /F_j )}\\&= { b}+( {{1}-({{b}+{ a}})})={ 1 }-{ a} \end{aligned}$$

  Thus, $\text{ Pl }_{m} ({B}_{1} )={ 1 }-{b}^*$ where ${b}^*\ge { b}$ and $\text{ Pl }_{m} ({\overline{B} _1 })={ 1 }-{a}^*$ where ${a}^*\le { a}.$ Here, then $\text{ IS }_{m} ({B}_{1} )\,=\,\langle \text{ Bel }({B}_{1} ), \text{ Dis }({B}_{1} )\rangle$ = $\langle ({1 }- \text{ Pl }_{m} ( {\overline{B} }),{1 }- \text{ Pl }_{m} ({B})\rangle$ = $\langle {a}^*,{ b}^*\rangle$. Thus, here, we essentially decrease our belief and increase our disbelief

• (2) For ${A}\cap {B}_{2} =\emptyset$, we have

  $$\begin{aligned} \text{ Pl }_{m} ({B}_{2} )&= { a\,\mathrm{Poss}}({B}_{2} /{A})+{ b\,\mathrm{Poss}}({B}_{2} /\overline{A} )\\&+( {{1}-({{a}+{ b}})})\text{ Poss }({B}_{2} /{X})\\&= 0+{b }+({1 }-({{a}+{b}})={1}-{a} \\ \text{ Pl }_{m} ( {\overline{B}}_2 )&= {a\,\mathrm{Poss}}({\overline{B}}_{2} /{A})+{ b\,\mathrm{Poss}}( {\overline{B}}_{2}/{\overline{A}})\\&+{1}-({{a}+{b}}) \text{ Poss } ( {\overline{B}}_{2} /{X})\\&= { a}+{ b }+( {{1}-{a}+{b}})={1} \end{aligned}$$

  Here, then IS$_{m}(B _{2})$ = $\langle 0, a\rangle$

• (3) ${B}_{3} \cap {A}\ne \emptyset \,\text{ but } B_{3} \not \subset A$

  $$\begin{aligned} \text{ Pl }_{m} (B_{3} )&= { a\,\mathrm{Poss}}({B}_{3} /{A})+{ b\,\mathrm{Poss}}({B}_{3} /{\overline{A}} )\\&+({{1}-({{a}+{b}})}) \text{ Poss }({B}_{3} /{X})\\&= {a}+{b}+({1}-( {{a}+{b}})={ 1} \\ \text{ Pl }_{m} ( {\overline{B} })&= { a\,\mathrm{Poss}}( {\overline{B}}_{3} /A) +{ b\,\mathrm{Poss}}({\overline{B}}_3 /\overline{A}\\&+({1 }-({a } +{ b})\text{ Poss })( {\overline{B}}_3 /{X})\\&= { a}+{b}+( {1 }-{a}-{b})={ 1} \end{aligned}$$

  Here, we see IS($B_{3}$) = (0, 0). $\square$

6 Credibility of intuitionistic statements

In many situations, information provided in a decision process can have some associated degree of credibility. In one case, this can be a reflection of how confident the supplier is in his judgment. In other cases, it could be an external judgment about the competence of the supplier. Here, we are interested in modeling this type of qualification. Given a piece of evidence of the form of an intuitionistic statement about finding the value of the variable $V$ in $A$, $IS(A)\,=\,\langle \mathrm{Bel}(A), \mathrm{Dis}(A)\rangle \,=\,\langle a, b\rangle$ we now consider the case where the provided information has an associated degree of credibility $\alpha \in [0,1]$. To reflect this credibility in our modeling of the information provided, we use the idea of discounting introduced by Shafer (1976). Consider now the belief structure $m$ with focal elements, $F_{1} = A$, $F_{2}=\overline{A}$ and $F_{3} = X$ in which $m(F_{1}) = a$, $m(F_{2}) = b$ and $m(X) = 1 - (a + b)$. The effect of discounting this belief structure by $\alpha$ results in a new belief structure $m_{1}$ with the same focal elements, $F = A_{1}, F_{2} = \overline{A}$ and $F_{3} = X$, however, in the case of $m_{1}$, we have $m_{1}(F_{1})=\alpha a, m_{2}(E_{2})=\alpha b$ and $m_{2}(X) = 1- \alpha (b + a)$. Consider now the object $\langle \mathrm{Bel}_{1}(A),\mathrm{Dis}_{1}(A)\rangle \,=\,\langle a_{1}, b_{1}\rangle$ associated with this new belief structure. Here,

$$\begin{aligned} \text{ Pl }_{1} ({A})&= \sum _{j={1}} ^{3}m_{1} ( {F_j })\mathrm{Poss}( {A/F_j })\\&= \alpha {a }+({1 }-\alpha ) ( {{b}+{a}})={1 }-\alpha {b} \end{aligned}$$

From this, we get Dis$_{1} (A) = 1 - \mathrm{Pl}_{1}(A) = \alpha b$. Furthermore,

$$\begin{aligned} \text{ Pl }_{1} ( {\overline{A} })&= \sum \limits _{j=1}^3 {m_1 (F_j)\mathrm{Poss}(\bar{A}/F_j )}=\alpha {b } \\&+({1 }-\alpha )( {{b}+{a}})={ 1 }-\alpha {a} \end{aligned}$$

From this we get then $\text{ Bel }_{1} ( {A})={ 1 }-\text{ Pl }_{1} ( {\overline{A} }) =\alpha {a}.$

The effect of discounting is to induce a new piece of effective information $\langle \alpha \mathrm{Bel}(A),\alpha \mathrm{Dis}~(A)\rangle$ = $\langle \alpha a, \alpha b\rangle$. Thus, the effect of associating a degree of credibility $\alpha$ with our information $\langle \mathrm{Bel}(A), \mathrm{Dis}(A)\rangle$ is simply to reduce each Bel and Dis proportionally by $\alpha$. We see if $\alpha = 0$ then we get $\langle 0, 0\rangle$ which corresponds to the belief structure with one focal element $X$. It is the belief structure corresponding to no information.

7 Combining multiple pieces of information

Consider now the situation when we have multiple pieces of information, $\langle \mathrm{Bel}_{1}(A_{1}),\mathrm{Dis}_{1}(A_{1})\rangle$ = $\langle a_{1}, b_{1}\rangle$ and $\langle \mathrm{Bel}_{2}(A_{2}), \mathrm{Dis}_{2}(A_{2})\rangle$ = $\langle a_{2}, b_{2}\rangle$. We can represent this information using belief structures. Here, then, we have two belief structures, $m_{1}$ and $m_{2}$, generated from our expert opinions. Here, $m_{1}$ has focal elements $A_{1}$, $\overline{A} _{1 }$ and $X$ with $m_{1}(A_{1}) = a_{1}$, $m_{1}(\overline{A} _{1}) = b_{1}$ and $m_{1}(X) = 1 - (a_{1} + b_{1})$. For $m_{2}$, we have focal elements $A_{2}, \overline{A} _{2 }$ and $X$ with $m_{2}(_{2}) = a_{2}, m_{2}(\overline{A} _{2}) = b_{2}$ and $m_{2}(X) = 1 - (a_{1} + b_{2})$. A notable way to combine these is to use the Dempster’s rule (Dempster 1967, 1968, 2008). The Dempster’s rule can be seen to be a two-step process. In the first step we form subsets, $F_{j}$, by taking the conjunction of all pairs consisting of a focal element from each of the being combined. We also associate with each a preliminary weight, $w(F_{j})$ which is the product of the weights of the focal elements being combined to form $F_{j}$. We denote these preliminary weights as $w(F_{j})$. In the second step, we obtain as the focal elements of the combined belief structure $m$ all the ${F}_{j} \ne \emptyset$. We then obtain the weights of the focal elements by dividing their preliminary weights by the sum of the preliminary associated with the ${F}_{j} \ne \emptyset$. This second step is called normalization. In the following, we illustrate the implementation of the first step for the case of $m_{1}$ and $m_{2 }$ given above.

$$\begin{aligned} \begin{array}{l@{\quad }l} {F}_{1} ={ A}_{1} \cap {A}_{2} &{} {w}({F}_{1} )={ a}_{1}\cdot {a}_{2} \\ {F}_{2} ={ A}_{1} \cap \overline{A} _{2} &{} {w}({F}_{2} )={ a}_{1}\cdot {b}_{2} \\ {F}_{3} ={ A}_{1} \cap {X }={ A}_{1} &{} {w}({F}_{3} )={ a}_{1}({1 }-({a}_{2} +{ b}_{2} )) \\ {F}_{4} =\overline{A} _{1} \cap {A}_{2} &{} {w}({F}_{4} )={ b}_{1}\cdot {a}_{2} \\ {F}_{5} =\overline{A} _{1} \cap \;\overline{A} _2 &{} {w}({F}_{5} )={ b}_{1}\cdot {b}_{2} \\ {F}_{6} =\overline{A} _{1} \cap {X }=\overline{A} _{1} &{} {w}({F}_{6} )={b}_{1} ({1}-({a}_{2} +{ b}_{2} )) \\ {F}_{7} ={ X}\cap {A}_{2} ={A}_{2} &{} {w}({F}_{7})=({1}-({a}_{1} +{ b}_{2} ))\cdot {a}_{2}\\ {F}_{8} ={ X}\cap \overline{A} _{2} =\overline{A} _{2} &{} \text{ w }({F}_{8} )=({1 }-({a}_{1} +{ b}))-{b}_{2} \\ {F}_{9} ={ X}\cap {X }={ X} &{} {w}({F}_{9} )=({1 }-({a}_{1} +{ b}_{1} ))({1 }-({a}_{2} +{ b}_{2} )) \\ \end{array} \end{aligned}$$

Going on to the second step, the normalization requires more knowledge about sets $A_{1}$ and $A_{2}$.

We now consider the special case where $A_{1} = A_{2} = A$, both pieces knowledge are with respect to the same set. Here,

$$\begin{aligned} \begin{array}{l@{\quad }l} {F}_{j} &{}\quad {w}({F}_{j}) \\ {F}_{1} ={ A} &{}\quad { a}_{1} \cdot {a}_{2} \\ {F}_{2} =\emptyset &{}\quad {a}_{1} \cdot {b}_{2} \\ {F}_{3} ={ A} &{}\quad {a}_{1} ({1 }-({a}_{2} +{ b}_{2} )) \\ {F}_{4} =\emptyset &{}\quad {b}_{1} \cdot {a}_{2} \\ {F}_{5} ={\overline{A}} &{}\quad {b}_{1}\cdot {b}_{2} \\ {F}_{6} ={\overline{A}} &{}\quad {b}_{1} ({1 }-({a}_{2} +{ b}_{2} )) \\ {F}_{7} ={ A} &{}\quad { a}_{2} ({1 }-({a}_{1} +{ b}_{1} )) \\ {F}_{8} ={\overline{A}} &{}\quad {b}_{2} ({1 }-({a}_{1} +{ b}_{1} )) \\ {F}_{9} ={ X } &{}\quad ({1 }-({a}_{1} +{ b}_{1} )({1 }-({a}_{2} +{ b}_{2} )) \\ \end{array} \end{aligned}$$

Let us now combine and rename these as follows

$$\begin{aligned} \begin{array}{ll} {H}_{1} &{}={ A}\, \mathrm{and}\, {w}({H}_{1} )={a}_{1} \cdot {a}_{2} +({a}_{1} ({1}-({a}_{2} +{ b}_{2})) \\ &{}\quad +{ a}_{2} ({1 }-({a}_{1} +{ b}_{1} ))\\ {H}_{2} &{}={\overline{A}}\, \mathrm{and}\, {w}({H}_{2} )={ b}_{1} \cdot {b}_{2} +{ b}_{1} ({1 }-({a}_{2} +{b}_{2} ))\\ &{}\quad +{ b}_{2} ({1 }-({a}_{1} +{ b}_{1} ))\\ {H}_{3} &{}={ X}\, \mathrm{and}\, {w}({H}_{3} )=({1}-({a}_{1} +{ b}_{1} ))({1 }-({a}_{2}+{ b}_{2} )) \\ {H}_{4} &{}=\emptyset \, \mathrm{and}\, {w}({H}_{4} )={a}_{1}{b}_{2} +{ a}_{2} {b}_{1} \\ \end{array} \end{aligned}$$

We now perform the appropriate normalization required in the use of the Dempster’s rule (Shafer 1976) to get a belief structure $m$ as a result of combining $m_{1}$ and $m_{2}$. The belief structure $m$ has focal elements $A$, $\overline{A}$ and $X$ where

$$\begin{aligned} {m}( {A})=\frac{a_1 \cdot a_2 \;+\;a_1 (1-a_2 -b_2 )\;+\;a_2 (1-a_1 -b_1 )}{1\;-\;(a_1 b_2 \;+\;a_2 b_1 )} \end{aligned}$$

$$\begin{aligned} {m}( {\overline{A} })=\frac{b_1 b_2 + b_1 (1-a_2 -b_2 )+b_2 (1-a_1 -b_1 )}{1-(a_1 b_2 +a_2 b_1 )} \end{aligned}$$

$$\begin{aligned} {m}( {X})=\frac{(1\;-\;a_1 \;-\;b_1 )(1\;-\;a_{2\;} -\;b_2 )}{1\;-\;(a_1 b_2 \;+\;a_2 b_1 )} \end{aligned}$$

An important point to emphasize is that the structure of the belief structure $m$ is the same as the two original belief structures, it has focal elements $A$, $\overline{A}$ and $X$. From this we can conclude that all the information needed for generating $m$ is contained in the single intuitionistic statement $\langle \mathrm{Bel}_{m}(A), \mathrm{Dis}_{m}(A)\rangle$ = $\langle a, b\rangle$. Let us see the relationship between $a$ and $b$ and the original pieces of information $\langle \mathrm{Bel}_{1}(A_{1}), \mathrm{Dis}_{1}(A_{1})\rangle$ = $\langle a_{1}, b_{1}\rangle$ and $\langle \mathrm{Bel}_{2}(A_{2}), \mathrm{Dis}_{2}(A_{2})\rangle$ = $\langle a_{2}, b_{2}\rangle$.

In the following, we use the notation $T_{1} = a_{1} + b_{1}$ and $T_{2} = a_{2} + b_{2}$.

Here, then $\text{ Dis }_{m}({A})={ 1 }-\text{ Pl }_{m} ({A})={ 1 }-\frac{1-a_1 a_2 +a_1 (1-T_2 )+a_2 (1-T_1 )+(1-T_1 )(1-T_2 )}{1-(a_1 b_2 +a_2 b_2 )}$ after some arithmetic manipulation, we get

$$\begin{aligned} \text{ Dis }_{m} ({A})={1}-\frac{1-b_1 -b_2 +b_2 b_1 }{1\;-\;(a_1 b_2 \;+\;b_1 a_2 )}\\ ={ 1 }-\frac{(1-b_1 )(1-b_2 )}{1\;-\;(a_1 b_2 \;+\;b_1 a_2 )} \end{aligned}$$

Here, we see that

$$\begin{aligned} \text{ Dis }_{m} ( {A})&= { 1 }-\frac{(1-\mathrm{Dis}_1 (A)(1-\mathrm{Dis}_2 (A))}{1\;-\;(a_1 b_2 \;+\;b_1 a_2 )}\\&= 1\;-\;\frac{Pl_1(A)\;Pl_2 (A)}{1\;-\;(a_1 b_2 \;+\;b_1 a_2 )} \end{aligned}$$

Furthermore, we observe that

$$\begin{aligned}&\text{ Bel }_{m} ( {A})={ 1 }- \text{ Pl }_{m} ( {\overline{A}})\\&\quad ={ 1 }\!-\!\frac{b_1 b_2 \!+\!b_2 (1-T_2 )\!+\!b_2 (1-T_1 )\!+\!(1-T_1 )(1-T_2 )}{1-(a_1 b_2 +b_1 a_2 )} \end{aligned}$$

$$\begin{aligned} \text{ Bel }_{m} ( {A})={ 1 }-\frac{(1-\mathrm{Bel}_1 (A))(1-\mathrm{Bel}_2 (A))}{1-(a_1 b_2 +b_1 a_2 )} \end{aligned}$$

Returning to our example of the young scholar who gave the lecture, my colleague at the lecture indicates that he disagrees with me. He says his belief that the lecturer was over 21 is 0 and his disbelief that the lecturer was over 21 is 0.9. Having just been exposed to Dempster’s he suggests we now use the Dempster rule to combine the two opinions. Here, we have $a_{1} = 0.6$ and $b_{1} = 0.2$ and $a_{2} = 0$ and $b_{2} = 0.9$ from these using the formulas above, we obtain the combined beliefs and disbeliefs, $a$ and $b$, as

$$\begin{aligned} a=1-\frac{(1-a_1 )(1-a_2 )}{1-(a_1 b_2 +b_1 a_2 )}=1-\frac{0.4}{1-(0.6*0.9)}=0.13 \end{aligned}$$

$$\begin{aligned} b=1-\frac{(1-b_1 )(1-b_2 )}{1-(a_1 b_2 +b_1 a_2 )}=1-\frac{0.8*0.1}{1-(0.6*0.9)}=0.82 \end{aligned}$$

8 Conclusion

We introduced the Dempster–Shafer belief theory and described its role in representing imprecise probabilistic information. We noted its use of intervals for representing imprecise probabilities. We noted that in fuzzy set theory, there are two related approaches used for representing imprecise membership grades, interval-valued fuzzy sets and intuitionistic fuzzy sets. We showed that the first of these, interval-valued fuzzy sets, is in the same spirit as Dempster–Shafer representation, both use intervals. Using a relationship analogous to the type of relationship that exists interval-valued fuzzy sets and intuitionistic fuzzy sets, we obtained from the interval-valued view of the Dempster–Shafer model an intuitionistic view of the Dempster–Shafer model. Central to this view is the use of an intuitionistic statement, pair of values, (Bel($A$) Dis($A$)), to convey information about the value of a variable lying in the set $A$. We suggested methods for combining intuitionistic statements and making inferences from these type propositions.