1 Introduction

Efficiency and productivity measurement of organizations have attracted extensive attention in recent years. DEA is a nonparametric method with multiple inputs and outputs for evaluating the performance of commercial units; furthermore, it is a mathematical method for measuring relative efficiency of DMUs. CCR model is one of the fundamental models in DEA, which was initially proposed by Charnes et al. (1978). Since then, due to the extensive use of DEA in various problems, several models have been presented in this regard. Many researchers assume that the input and output data are constant and without change, while in practice, the input and output data are mainly random fuzzy (Ra-Fu). So far, various methods have been presented for solving DEA problems with fuzzy data (Zhu 2003; Wu et al. 2006). Zadeh (1978) defined the possibility theory for fuzzy sets as a mathematical framework in modeling.

Fig. 1
figure 1

Density functions of SN distribution for \(\delta \)s difference

Full size image

A normal distribution is a continuous distribution which is extremely important in statistics because of its behavior. It has numerous characteristics which increase the applicability. In their previous studies on DEA models with random fuzzy data, researchers have assumed that input and output variables follow a normal distribution (Tavana et al. 2012, 2013a, b; Khanjani et al. 2014a, b, 2017), while this may not be true in the real world and data may be slightly skewed and asymmetric. Therefore, if an asymmetrical distribution has similar characteristics to a normal one, it can play a major role in data analysis.

One of these distributions is the skew-normal (SN) distribution, first introduced by Azzalini (1985) and widely considered by other researchers. This distribution has a skewness regulation parameter which, if set to 0, can result in a normal distribution. Thus, a SN distribution also includes a normal distribution. In random fuzzy environments, inputs and outputs are random fuzzy, and such data cannot be directly applied in DEA models because they lead to incorrect conclusions. In the present paper, it was assumed that the input and output variables were random fuzzy and followed a skew-normal distribution with a fuzzy mean and a fuzzy cutoff level. Accordingly, the models were presented in possibility–probability and necessity–probability states and, finally, the proposed models were investigated in two numerical examples.

The rest of this paper is organized as follows. In the next section, the normal-skewed distribution and primary fuzzy definitions will be introduced. Section (2) presents some models in possibility–probability and necessity–probability states in the presence of the skew-normal distribution. In Sect. (4), the models presented in the previous section will be expressed in one numerical example, and finally, Sect. (5) includes the discussion and conclusion.

2 Preliminaries

In this section, we first review some basic definitions of fuzzy sets (Dubois and Prade 1978; Klir and Yuan 1995; Zimmermann 2001) followed by several definitions associated with fuzzy random variables (FRVs) (Kwakernaak 1978; Liu and Liu 2002, 2003) and the SN distribution (Azzalini 1985; Azzalini and Capitano 1999).

Definition 1

SN Distribution: A random variable Z is said to have a standard SN distribution with real parameters \(\delta \), denoted by \(Z\sim \mathrm{SN}\left( \delta \right) \), if its probability density function (pdf) is given by

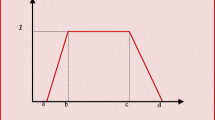
$$\begin{aligned} f_{Z} \left( z \right) =2\phi \left( z \right) {\varPhi }\left( {\delta z} \right) , \end{aligned}$$
(1)

where \(\phi \) and \(\varPhi \) are the pdf and cumulative distribution function (cdf) of standard normal distribution, respectively. The shape parameter \(\delta \) is called skewness control parameter. The pdf (1) for \(\delta >0\) is skewness to right, \(\delta <0\) skewness to left and, also, if \(\delta =0\) then it is symmetric and is transformed into standard normal distribution. The pdf (1) for \(\delta \)s difference is drawn in Fig. 1.

With transformation \(W=\mu +\sigma Z,\mu \in \mathfrak {R},\sigma >0\) pdf of random variable W with location parameter \(\mu \), scale parameter \(\sigma \) and skew parameter \(\delta \) (henceforth called the \(W\sim \mathrm{SN}\left( {\mu ,\sigma ^{2},\delta } \right) \) distribution) is:

$$\begin{aligned} f_{W} \left( w \right) =\frac{2}{\sigma }\phi \left( {\frac{w-\mu }{\sigma }} \right) \varPhi \left( {\delta \left( {\frac{w-\mu }{\sigma }} \right) } \right) . \end{aligned}$$
(2)

If \(W\sim \mathrm{SN}\left( {\mu ,\sigma ^{2},\delta } \right) \), then mean and variance are as follows:

$$\begin{aligned} {\mathbb {E}}\left( W \right) =\mu +\sigma \mu _z ,\,{\mathbb {V}}\left( W \right) =\sigma ^{2}\left( {1-\mu _{z}^{2} } \right) , \end{aligned}$$
(3)

where \(\mu _{z} =\sqrt{\frac{2}{\pi }}\upgamma \) and \(\upgamma =\frac{\delta }{\sqrt{1+\delta ^{2}}}\), see Azzalini (1985).

Definition 2

Let U be a universe set. A fuzzy set \({\tilde{A}}\) of U is defined by a membership function \(\mu _{\tilde{A}} \left( x \right) \rightarrow \left[ {0,1} \right] \), where \(\mu _ {\tilde{A}} \left( x \right) \), \(\forall x\in U\), indicates the degree of membership of A to U.

Definition 3

The \(\alpha \)-cut of fuzzy set \({\tilde{A}} \), \( {\tilde{A}}_{\alpha } \), is the crisp set \({\tilde{A}}_{\alpha } =\left\{ {x\left| {\mu _{\tilde{A}} } \left( x \right) \ge \alpha \right. } \right\} \). The support of \({\tilde{A}}\) is the crisp set Sup\(\, {\tilde{A}} =\left\{ {x\left| {\mu _{\tilde{A}} } \left( x \right) \ge 0 \right. } \right\} \).

Definition 4

\({\tilde{\hbox {A}}} \) is a fuzzy number if and only if \({\tilde{A}}\) is normal and convex fuzzy subset of the set of real numbers.

Definition 5

A fuzzy number of L–R type is denoted by \(\tilde{A} = {\left( {m,\alpha ,\beta } \right) _{LR}}\) and its membership function can be expressed as

$$\begin{aligned} \mu _{\tilde{A}}\left( t \right) = \left\{ {\begin{array}{ll} L\left( {\frac{{m - x}}{\alpha }} \right) &{} \quad x \le m,\\ R\left( {\frac{{x - m}}{\beta }} \right) &{} \quad x \ge m. \end{array}} \right. \end{aligned}$$
(4)

where L and R are the left and right functions, respectively, and \(\alpha \) and \(\beta \) are the (nonnegative) left and right spreads, respectively.

Definition 6

The \(\alpha \)-cut, \(\alpha \in \left[ {0~,~1} \right] \), of a L–R type fuzzy number \({\tilde{A}}\) is a closed interval as follows

$$\begin{aligned} A_{\alpha }= & {} \left\{ {x\left| {{\mu _{ {\tilde{A}} }}\left( x \right) \ge \alpha } \right. } \right\} = \left[ {A_{\alpha }^{L}\,, A_{\alpha }^{R}} \right] \nonumber \\= & {} \left[ {m - {L^{ - 1}}\left( \alpha \right) ,~m + {R^{ - 1}}\left( \alpha \right) } \right] \end{aligned}$$
(5)

where \(A_{\alpha }^{L}\) and \(A_{\alpha }^{R}\) are the left and right extreme points, respectively.

Definition 7

Let \(\left( \Omega ,A,\Pr \right) \) be probability space where \(\Omega \) is a sample space, A is the s-algebra of subset of \(\Omega \) and \(\Pr \) is a probability measure on \(\Omega \), and \(F\left( R \right) \) be the set of all fuzzy numbers in the set of real numbers R. Generally, F involves the normal convex fuzzy subsets. Thus, a fuzzy random variable (FRV) is a mapping function \(\xi :\Omega \rightarrow F\) such that for any Borel set B of \({\mathcal {R}}\), and

Definition 8

Let \(\xi =\left( {\xi _{1} ,\xi _{2} ,\ldots ,\xi _{n} } \right) \) be a fuzzy random vector, and \(f:\mathfrak {R}^{n}\rightarrow \mathfrak {R}\) be a continuous function, then \(f\left( \xi \right) \) is FRV.

Definition 9

Given a universe set U, let P (U) be a power set of U. \(\left( {U,P\left( U \right) ,\mathrm{Pos}} \right) \) . The triple \(\left( {U,P\left( U \right) ,\mathrm{Pos}} \right) \) is called a possibility space where Pos is a possibility measure defined on \(P\left( U \right) \). For any set A and B, the properties of the possibility measure are presented as

  1. a.

    \(\mathrm{Pos}\left( \emptyset \right) =0\) and \(\mathrm{Pos}\left( U \right) =1\);

  2. b.

    Monotonicity; \(A\subset B\) implies \(\mathrm{Pos}\left( A \right) \le \mathrm{Pos}\left( B \right) \) for any \(A,B\in P\left( U \right) \);

  3. c.

    Subadditivity; \(\mathrm{Pos}\left( {A\cup B} \right) +\mathrm{Pos}\left( {A\cap B} \right) \le \mathrm{Pos}\left( A \right) +\mathrm{Pos}\left( B \right) \) for any \(A,B\in P\left( U \right) \).

The necessity measure of A, denoted by Nec(A), is also defined on \(P\left( U \right) \) as \(\mathrm{Nec}\left( A \right) =1-\mathrm{Pos}\left( {A^{c}} \right) \) where \(A^{c}\) is a complement set of A. For any set A and B, the properties of the necessity measure are presented as,

  1. a.

    \(\mathrm{Nec}\left( \emptyset \right) =0\) and \(\mathrm{Nec}\left( U \right) =1\);

  2. b.

    \(\mathrm{Pos}\left( A \right) \ge \mathrm{Nec}\left( A \right) ;\)

  3. c.

    Monotonicity; \(A\subset B\) implies \(\mathrm{Nec}\left( A \right) \le \mathrm{Nec}\left( B \right) \);

  4. d.

    Subadditivity; \(\mathrm{Nec}\left( {A\cup B} \right) +\mathrm{Nec}\left( {A\cap B} \right) \ge \mathrm{Nec}\left( A \right) +\mathrm{Nec}\left( B \right) \).

3 DEA with random fuzzy data

In this section, the CCR model of DEA with random fuzzy data will be generalized. This model will be presented with possibility–probability and necessity–probability constraints with the possibility level and fuzzy necessity.

In the general state, the probability level might be inaccurate and indefinite. In this section, a DEA model with a fuzzy threshold level will be generalized; in fact, it is assumed that \({\tilde{\delta }}\) is a fuzzy number.

3.1 Possibility–probability CCR model in the presence of SN distribution with Fuzzy threshold level

In this section, we evaluate the performance of decision-making units (DMUs) with random fuzzy inputs and outputs. Assume that we have n DMUs such that all DMUs are independent from one another for the ith random fuzzy input, \( i=1,2,\ldots ,m\) and the rth random fuzzy output, \(r=1,2,\ldots ,s. \) Also, assume \( \tilde{\bar{x}}_{ij}{\sim } \mathrm{CSN}_{1,1} \left( x_{ij} ,\sigma _{ij}^{2} ,\delta _{ij} ,0,\sigma _{ij}^{2} \right) \) in which there are \(\bar{x}_{ij} =\left( {x_{ij}^{\alpha } ,x_{ij}^{m_{1}} ,x_{ij}^{m_{2}} ,x_{ij}^{\beta } } \right) _{LR} \) per \( j=1,2,\ldots ,n,\) and \( \tilde{\bar{y}}_{rj}{\sim } \mathrm{CSN}_{1,1} \left( \bar{y}_{rj} ,\tau _{rj}^{2} ,\varepsilon _{rj} ,0,\tau _{rj}^{2} \right) \), in which there are \(\tilde{\bar{x}}_{ij} =\left( {x_{ij}^{\alpha } ,x_{ij}^{m_{1}} ,x_{ij}^{m_{2}} ,x_{ij}^{\beta }} \right) _{LR} \). Let us assume that \({\tilde{\delta }} \) is illustrated as in \({\tilde{\delta }} =\left( {\delta ^{\alpha },\delta ^{m_{1} },\delta ^{m_{2} },\delta ^{\beta }} \right) \); then, the CCR model with possibility–probability constraints will be as model (6):

$$\begin{aligned}&\max \, \varphi \nonumber \\&\mathrm{s.t.}\nonumber \\&\mathrm{Pos}\left[ \Pr \left( \varphi \le \mathop \sum \limits _{r=1}^{s} u_r \tilde{\bar{y}}_{rp} \right) \ge \tilde{\delta }\right] \ge \gamma ,\nonumber \\&\mathrm{Pos}\left[ \Pr \left( \mathop \sum \limits _{i=1}^m \nu _{i} \tilde{\bar{x}}_{ip} \le 1\right) \ge \tilde{\delta }\right] \ge \gamma ,\nonumber \\&\mathrm{Pos}\left[ \Pr \left( \mathop \sum \limits _{i=1}^m \nu _{i} \tilde{\bar{x}}_{ip} \ge 1\right) \ge \tilde{\delta } \right] \ge \gamma ,\nonumber \\&\mathrm{Pos}\left[ \Pr \left( \mathop \sum \limits _{r=1}^s u_r \tilde{\bar{y}}_{rj} -\mathop \sum \limits _{i=1}^{m} \nu _{i} \tilde{\bar{x}}_{ij} \le 0\right) \ge \tilde{\delta }\right] \ge \nonumber \\&\quad \gamma ,j=1,\ldots ,n\nonumber \\&u_{r} ,\nu _{i} \ge 0,r=1,\ldots ,s,i=1,\ldots ,m. \end{aligned}$$
(6)

where \(\tilde{\bar{x}}_{ij} \) and \(\tilde{\bar{y}}_{rj} \) have a closed skew-normal distribution with fuzzy mean and \( \tilde{\delta }\) is a fuzzy threshold level. To convert this model into a definite model, the following theorem is used.

Theorem 1

Assume that \(\tilde{\bar{\lambda }}_{1} \) and \(\tilde{\bar{\lambda }}_{2} \) are two independent random fuzzy numbers with a closed skew-normal distribution as \(\tilde{\bar{\lambda }}_1 {{\sim }} \mathrm{CSN}\big (\bar{\mu }_{1},\sigma _{1}^{2},\delta _{1},0, \sigma _{1}^{2} \big )\) and \(\tilde{\bar{\lambda }}_{2} {\sim } \mathrm{CSN}\big ( \bar{\mu }_{2},\sigma _{2}^{2},\delta _{2},0,\sigma _{2}^{2} \big )\). Then, the means will be as \(\bar{\mu }_1 =\left( {\lambda _{1}^{\alpha } ,\lambda _{1}^{m_{1} },\lambda _{1}^{m_{2} },\lambda _{1}^{\beta }} \right) _{LR} \) and \(\bar{\mu }_{2} =\left( {\lambda _{2}^{\alpha } ,\lambda _{2}^{m_{1} },\lambda _{2}^{m_{2} },\lambda _{2}^{\beta } } \right) _{LR}; \) thus, we have:

  1. (a)

    If \(\mathrm{Pos}\left[ {\Pr }\left( \tilde{\bar{\lambda }}_1 \le \tilde{\bar{\lambda }}_2 \right) \ge \tilde{\delta } \right] \ge \alpha \) is true, then:

    $$\begin{aligned}&\left( {\lambda _1^{m_1 } -\lambda _2^{m_2 } +L^{-1}\left( \alpha \right) \left( {\lambda _1^\alpha +\lambda _2^\beta } \right) } \right) \nonumber \\&\quad +\,\left( {\sqrt{\sigma _1^2 +\sigma _2^2 }} \right) {\varPsi }^{-1}\left( {\delta ^{m_1 }-L^{-1}\left( \alpha \right) \delta ^{\alpha }} \right) \le 0, \end{aligned}$$
    (7)

    where

    $$\begin{aligned} \mathop \int \limits _{-\infty }^{{\varPsi }^{-1}\left( {\delta ^{m_1 }-L^{-1}\left( \alpha \right) \delta ^{\alpha }} \right) } f_\Delta \left( \delta \right) \mathrm{d}\delta =\delta ^{m_1 }-L^{-1}\left( \alpha \right) \delta ^{\alpha }. \end{aligned}$$
  2. (b)

    If \(\mathrm{Nec}\left[ {\Pr }\left( \tilde{\bar{\lambda }}_1 \le \tilde{\bar{\lambda }}_2 \right) \ge \tilde{\delta }\right] \ge \alpha \) is true, then:

    $$\begin{aligned}&\left( {\lambda _1^{m_2 } -\lambda _2^{m_{1 }} +R^{-1}\left( {1-\alpha } \right) \left( {\lambda _2^\alpha +\lambda _1^\beta } \right) } \right) \nonumber \\&\quad +\,\left( {\sqrt{\sigma _1^2 +\sigma _2^2 }} \right) {\varPsi }^{-1}\left( {\delta ^{m_2 }+R^{-1}\left( \alpha \right) \delta ^{\beta }} \right) \le 0. \end{aligned}$$
    (8)

where

$$\begin{aligned} \mathop \int \limits _{-\infty }^{{\varPsi }^{-1}\left( {\delta ^{m_2 }+R^{-1}\left( \alpha \right) \delta ^{\beta }} \right) } f_{\Delta } \left( \delta \right) \mathrm{d}\delta =\delta ^{m_2 }+R^{-1}\left( \alpha \right) \delta ^{\beta } \end{aligned}$$
Table 1 Parameters of inputs SN distribution
Full size table

Note: Normal case of this theorem introduced by Tavana et al. (2013a, b).

Proof

Assume that \(\tilde{\bar{\lambda }}_1 \) and \(\tilde{\bar{\lambda }}_2 \) are two independent random fuzzy numbers with a closed skew-normal (CSN) distribution as \(\tilde{\bar{\lambda }}_1 {\sim } \mathrm{CSN}\left( {\tilde{\mu }}_1,\sigma _{1}^{2},\delta _{1} ,0,\sigma _{1}^{2} \right) \) and \(\tilde{\bar{\lambda }}_2 {\sim } \mathrm{CSN}\left( {\tilde{\mu }}_2,\sigma _{2}^{2} ,\delta _{2},0,\sigma _{2}^{2} \right) \); thus, \(\tilde{\bar{h}} =\tilde{\bar{\lambda }} _{1} -\tilde{\bar{\lambda }}_{2} \)will have a closed skew-normal distribution with the following parameters:

$$\begin{aligned} {\mu }_{\tilde{{\bar{\mathrm{h}}}}}= & {} E\left[ {\tilde{\bar{\lambda }}_{1} -\tilde{\bar{\lambda }}_{2} } \right] = \bar{\mu }_{1} -\bar{\mu }_{2} \\= & {} \left( {\lambda _{1}^{\alpha } +\lambda _{2}^{\beta } ,\lambda _{1}^{m_{1} } -\lambda _{2}^{m_{2} } ,\lambda _{1}^{m_{2} } -\lambda _{2}^{m_{1} } ,\lambda _{1}^{\beta } +\lambda _{2}^{\alpha } } \right) \\ \sigma _{\tilde{\bar{h}}}^{2}= & {} Var\left[ {\tilde{\bar{\lambda }}_{1} -\tilde{\bar{\lambda }}_{2} } \right] =\sigma _{1}^{2} +\sigma _{2}^{2} \\ D^{*}= & {} \frac{1}{\sigma _{1}^{2} +\sigma _{2}^{2} }\left[ {{\begin{array}{l} {\delta _1 \sigma _1^2 } \\ {-\delta _2 \sigma _2^2 } \\ \end{array} }} \right] \\ \nu ^{*}= & {} \left[ {0,0} \right] ^{{\prime }} \\ {\Delta }^{*}= & {} \left[ {{\begin{array}{ll} {\sigma _{1}^{2} +\delta _{1}^{2} \sigma _{1}^{2} -\frac{\delta _{1}^{2} \sigma _{1}^{4} }{\sigma _{1}^{2} +\sigma _{2}^{2} }}&{} {\frac{\delta _{1} \delta _{2} \sigma _{1}^{2} \sigma _{2}^{2} }{\sigma _{1}^{2} +\sigma _{2}^{2} }} \\ {\frac{\delta _{1} \delta _{2} \sigma _{1}^{2} \sigma _{2}^{2} }{\sigma _{1}^{2} +\sigma _{2}^{2} }}&{} {\sigma _{2}^{2} +\delta _{2}^{2} \sigma _{2}^{2} -\frac{\delta _{2}^{2} \sigma _{2}^{4} }{\sigma _{1}^{2} +\sigma _{2}^{2} }} \\ \end{array} }} \right] \end{aligned}$$

The CSN distribution \(\tilde{\bar{h}}\) with mean fuzzy parameters is as follows:

$$\begin{aligned} f\left( \tilde{\bar{h}}\right)= & {} c\phi \left( \tilde{\bar{h}};{\mu }_{\tilde{{\bar{\mathrm{h}}}}} ,\sigma _{\tilde{\bar{h}}}^{2} \right) \varPhi _{2} \left( {D^{*}\left( \tilde{\bar{h}}-{\mu }_{\tilde{{\bar{\mathrm{h}}}}} \right) ;\nu ^{*},{\Delta }^{*}} \right) . \\ c^{-1}= & {} \varPhi _{2} \left( {0;\nu ^{*},{\Delta }^{*}+D^{*}\sigma _{\tilde{\bar{h}}}^{2} D^{*}} \right) \end{aligned}$$

So that in this state and in \(c^{-1}=2^{-2}\),

By changing the variable \(W=\frac{\tilde{\bar{h}} -\mu _{\tilde{\bar{h}}}}{\sigma _{\tilde{\bar{h}}}}\), we will have the following equation:

$$\begin{aligned}&\left[ {P\left( {\tilde{\bar{h}}\le 0} \right) } \right] _{\alpha }\\&\quad =\left\{ \mathop \int \limits _{-\infty }^{\frac{-\mu _{\tilde{\bar{h}}}}{\sigma _{\tilde{\bar{h}}}}} f\left( w \right) \mathrm{d}w\left| {\mu _{\tilde{\bar{h}}}} \in \left( {\mu _{\tilde{\bar{h}}}} \right) _{\alpha } ; \mathop {\int }\limits _{-\infty }^{+\infty } f\left( w \right) \mathrm{d}w=1 \right. \right\} \\&\quad =\left\{ {{\varPsi }\left( \frac{-\mu _{\tilde{\bar{h}}}}{\sigma _{\tilde{\bar{h}}}} \right) \left| \mu _{\tilde{\bar{h}}}\in \left( \mu _{\tilde{\bar{h}}}\right) _{\alpha } ;\mathop {\int } \limits _{-\infty }^{+\infty } f\left( w \right) \mathrm{d}w=1 \right. } \right\} \end{aligned}$$
Table 2 Parameters of outputs SN distribution
Full size table

And \({\varPsi }\) is the cumulative distribution function (CDF) of the standard closed skew-normal distribution of variable W. Also, \(\varPsi \) is an additive continuous function. Using the definition of \(\alpha \)-cut, we will have the following equation:

$$\begin{aligned}&\left[ {P\left( {\tilde{\bar{\lambda }}}_1 \le {\tilde{\bar{\lambda }}}_2 \right) } \right] _{\alpha } =\left[ {{\varPsi }\left( {\frac{-\mu _{\tilde{\bar{h}}}}{\sigma _{\tilde{\bar{h}}}}} \right) _\alpha ^R ,{\varPsi }\left( {\frac{-\mu _{\tilde{\bar{h}}} }{\sigma _{\tilde{\bar{h}}}} } \right) _{\alpha }^{L} } \right] _{\alpha }\\&\mathrm{Pos}\left[ \Pr \left( {\tilde{\bar{\lambda }}}_1 \le {\tilde{\bar{\lambda }}}_{2} \right) \ge {\tilde{\delta }} \right] \ge \alpha \Rightarrow \left[ {\Pr \left( {{\tilde{\bar{\lambda }}}_1 \le {\tilde{\bar{\lambda }}}_2 } \right) } \right] _{\alpha }^{R} \ge \left( {\tilde{\delta }} \right) _{\alpha }^{L}\\&{\varPsi }\left( {\frac{-\mu _{\tilde{\bar{h}}} }{\sigma _{{\tilde{{\bar{h}}}} } }} \right) _{\alpha }^{L} \ge \left( {\tilde{\delta } } \right) _{\alpha }^{L} \Leftrightarrow \left( {\mu _{{\tilde{{\bar{h}}}} } } \right) _{\alpha }^{L} +\sigma _{{\tilde{{\bar{h}}}} } {\varPsi }^{-1} \left( {\left( {\tilde{\delta } } \right) _{\alpha }^{L} } \right) \le 0 \end{aligned}$$

where

$$\begin{aligned} \left( {\mu _{{\tilde{{\bar{h}}}} } } \right) _{\alpha }^{L}= & {} \lambda _{1}^{m_{1} } -\lambda _{2}^{m_{2} } +L^{-1}\left( \alpha \right) \left( {\lambda _{1}^{\alpha } +\lambda _{2}^{\beta } } \right) \\ \sigma _{{\tilde{{\bar{h}}}} }= & {} \sqrt{\sigma _{1}^{2} +\sigma _{2}^{2} }\\ \left( {\tilde{\delta } } \right) _\alpha ^{L}= & {} \delta ^{{m}_{1} }-L^{-1}\left( \alpha \right) \delta ^{\alpha } \end{aligned}$$

Proof of the second part is similar to the first part.\(\square \)

Now, let us assume that there are n DMUs with m inputs and s outputs as follows:

$$\begin{aligned}&{\tilde{{\bar{x}}}}_{ij} {\sim } \mathrm{CSN}_{1,1} \left( {{\bar{x}}_{ij} ,\sigma _{ij}^{2} ,\delta _{ij} ,0,\sigma _{ij}^{2} } \right) ,{\bar{x}}_{ij} \\&\quad =\left( {x_{ij}^{\alpha } ,x_{ij}^{{m}_{1} } ,x_{ij}^{{m}_{2} } ,x_{ij}^{\beta } } \right) _{LR}\\&{\tilde{{\bar{y}}}}_{rj} {\sim } \mathrm{CSN}_{1,1} \left( {{\bar{y}}_{rj} ,\tau _{rj}^{2} ,\varepsilon _{rj} ,0,\tau _{rj}^{2} } \right) ,{\bar{y}}_{rj} \\&\quad =\left( {y_{rj}^{\alpha } ,y_{rj}^{{m}_{1} } ,y_{rj}^{{m}_{2} } ,y_{rj}^{\beta } } \right) _{LR} \end{aligned}$$

Using the above theorem on the constraints of model (6), the following definite model will be obtained:

$$\begin{aligned}&\max \,\varphi \nonumber \\&\mathrm{s.t.}\nonumber \\&\quad \varphi -\mathop \sum \limits _{r=1}^{s} u_{r} \left( {y_{rp}^{{m}_{2} } -L^{-1}\left( \gamma \right) y_{rp}^{\beta } } \right) +\sigma _{p} \left( u \right) {\varPsi }^{-1}\left( \delta \right) _{\gamma }^{L} \le 0,\nonumber \\&\quad \mathop \sum \limits _{i=1}^{m} \nu _{i} \left( {x_{ip}^{{m}_{1} } -L^{-1}\left( \gamma \right) x_{ip}^{\alpha } } \right) +\sigma _{p} \left( \nu \right) {\varPsi }^{-1}\left( \delta \right) _{\gamma }^{L} \le 1,\nonumber \\&\quad \mathop \sum \limits _{i=1}^{m} \nu _{i} \left( {x_{ip}^{{m}_{1} } +L^{-1}\left( \gamma \right) x_{ip}^\alpha } \right) -\sigma _p \left( \nu \right) {\varPsi }^{-1}\left( \delta \right) _\gamma ^L \ge 1,\nonumber \\&\quad \mathop \sum \limits _{r=1}^{s} u_{r} y_{rj}^{{m}_{1} } -\mathop \sum \limits _{i=1}^{m} \nu _{i} x_{ij}^{{m}_{2} } -L^{-1}\left( \gamma \right) \left( {\mathop \sum \limits _{r=1}^s u_r y_{rj}^\alpha +\mathop \sum \limits _{i=1}^m \nu _i x_{ij}^\beta } \right) \nonumber \\&\qquad +\,\sigma _j \left( {u,\nu } \right) {\varPsi }^{-1}\left( \delta \right) _\gamma ^L \le 0,j=1,\ldots ,n,\nonumber \\&\qquad \quad u_r ,\nu _i ,\sigma _p \left( u \right) ,\sigma _p \left( \nu \right) ,\sigma _j \left( {u,\nu } \right) \nonumber \\&\qquad \ge 0,r=1,\ldots ,s;i=1,\ldots ,m;j=1,\ldots , n \end{aligned}$$
(9)

And \(\left( \delta \right) _{\gamma }^{L} \) is the lower bound of \(\upgamma \)-cutoff of the following range:

$$\begin{aligned} {\tilde{\delta }} =\left[ {\left( \delta \right) _{\gamma }^{L} ,\left( \delta \right) _{\gamma }^{R} } \right]= & {} \left[ {\delta ^{{m}_{1} }-L^{-1}\left( \gamma \right) {\delta }^{\alpha },\delta ^{{m}_{2} }+R^{-1}\left( \gamma \right) \delta ^{\beta }} \right] ,\\ \sigma _{p} \left( u \right)= & {} \sqrt{\mathop \sum \limits _{r=1}^{m} u_{r}^{2} \tau _{rp}^{2} },\\ \sigma _{p} \left( \nu \right)= & {} \sqrt{\mathop \sum \limits _{i=1}^{m} \nu _{i}^{2} \sigma _{ip}^{2} },\\ \sigma _{j} \left( {u,\nu } \right)= & {} \sqrt{\mathop \sum \limits _{r=1}^{m} u_{r}^{2} \tau _{rj}^{2} +\mathop \sum \limits _{i=1}^{m} \nu _{i}^{2} \sigma _{ij}^{2} },j=1,\ldots ,n. \end{aligned}$$

By changing the variables of \(\left( {\theta _{p}^{o} } \right) ^{2}=\left( {\sigma _{p} \left( u \right) } \right) ^{2}\), \(\left( {\theta _{p}^{I} } \right) ^{2}=\left( {\sigma _{p} \left( \nu \right) } \right) ^{2}\) and \(\left( {\lambda _{j} } \right) ^{2}=\left( {\sigma _{j} \left( {u,\nu } \right) } \right) ^{2}\), the following second-order programming will be obtained.

Table 3 Possibility–probability scores of the DMUs with their fuzzy thresholds
Full size table
Table 4 Necessity–probability scores of the DMUs with their fuzzy thresholds
Full size table
Table 5 Possibility–probability scores of the DMUs with their fuzzy thresholds and normal distribution
Full size table
Table 6 Necessity–probability scores of the DMUs with their fuzzy thresholds and normal distribution
Full size table
$$\begin{aligned}&\max \, \varphi \nonumber \\&\mathrm{s.t.}\nonumber \\&\quad \varphi -\mathop \sum \limits _{r=1}^{s} u_{r} \left( {y_{rp}^{m_{2} } -L^{-1}\left( \gamma \right) y_{rp}^{\beta } } \right) {+}\theta _{p}^{o} {\varPsi }^{-1}\left( {\delta ^{{m}_{1} }-L^{-1}\left( \gamma \right) \delta ^{\alpha }} \right) \le 0,\nonumber \\&\quad \mathop \sum \limits _{i=1}^m \nu _i \left( {x_{ip}^{m_1 } -L^{-1}\left( \gamma \right) x_{ip}^\alpha } \right) +\theta _{p}^{I} {\varPsi }^{-1}\left( {\delta ^{{m}_{1} }-L^{-1}\left( \gamma \right) \delta ^{\alpha }} \right) \le 1,\nonumber \\&\quad \mathop \sum \limits _{i=1}^{m} \nu _{i} \left( {x_{ip}^{{m}_{1} } +L^{-1}\left( \gamma \right) x_{ip}^{\alpha } } \right) -\theta _{p}^{I} {\varPsi }^{-1}\left( {\delta ^{{m}_{1} }-L^{-1}\left( \gamma \right) \delta ^{\alpha }} \right) \ge 1,\nonumber \\&\quad \mathop \sum \limits _{r=1}^{s} u_{r} y_{rj}^{{m}_{1} } -\mathop \sum \limits _{i=1}^{m} \nu _{i} x_{ij}^{m_{2} } -L^{-1}\left( \gamma \right) \left( {\mathop \sum \limits _{r=1}^{s} u_{r} y_{rj}^{\alpha } +\mathop \sum \limits _{i=1}^{m} \nu _{i} x_{ij}^{\beta } } \right) \nonumber \\&\qquad +\,\lambda _{j} {\varPsi }^{-1}\left( {\delta ^{{m}_{1} }-L^{-1}\left( \gamma \right) \delta ^{\alpha }} \right) \le 0,j=1,\ldots ,n,\nonumber \\&\quad \left( {\theta _p^o } \right) ^{2}=\mathop \sum \limits _{r=1}^m u_r^2 \tau _{rp}^{2},\nonumber \\&\quad \left( {\theta _p^I } \right) ^{2}=\mathop \sum \limits _{i=1}^m \nu _i^2 \sigma _{ip}^{2},\nonumber \\&\quad \left( {\lambda _j } \right) ^{2}=\mathop \sum \limits _{r=1}^m u_{r}^{2} \tau _{rj}^{2} +\mathop \sum \limits _{i=1}^{m} \nu _{i}^{2} \sigma _{ij}^{2},\nonumber \\&\quad u_{r} ,\nu _{i} ,\theta _{p}^{o} ,\theta _{p}^{I} , \lambda _{j} \ge 0,r=1,\ldots ,s;i=1,\ldots ,m;j=1,\ldots , n.\nonumber \\ \end{aligned}$$
(10)

Definition 10

DMU is called efficient at probability level \(\upgamma \) and fuzzy possibility level \(\tilde{\delta } \) if the objective function of model (10) is equal to or bigger than 1; otherwise, it is called inefficient.

3.2 Necessity–probability CCR model in the presence of SN distribution with Fuzzy threshold level

In this section, the CCR model with necessity–probability constraints and fuzzy threshold level will be generalized in order to evaluate the DMUs. Therefore, the CCR model with necessity–probability constraints in the presence of SN distribution with fuzzy level \(\tilde{\delta } =\left( {\delta ^{\alpha },\delta ^{m_1 },\delta ^{m_2 },\delta ^{\beta }} \right) \) is as follows:

$$\begin{aligned}&\max \, \varphi \nonumber \\&\mathrm{s.t.}\nonumber \\&\quad \mathrm{Nec}\left[ {\Pr \left( \varphi \le \mathop \sum \limits _{r=1}^{s} u_{r} {\tilde{{\bar{y}}}}_{rp} \right) \ge \tilde{\delta } } \right] \ge \gamma ,\nonumber \\&\quad \mathrm{Nec}\left[ {\Pr \left( \mathop \sum \limits _{i=1}^{m} \nu _{i} {\tilde{{\bar{x}}}}_{ip} \le 1\right) \ge \tilde{\delta } } \right] \ge \gamma ,\nonumber \\&\quad \mathrm{Nec}\left[ {\Pr \left( \mathop \sum \limits _{i=1}^{m} \nu _i {\tilde{{\bar{x}}}}_{ip} \ge 1\right) \ge \tilde{\delta } } \right] \ge \gamma ,\nonumber \\&\quad \mathrm{Nec}\left[ {\Pr \left( \mathop \sum \limits _{r=1}^{s} u_{r} {\tilde{{\bar{y}}}}_{rj} -\mathop \sum \limits _{i=1}^{m} \nu _{i}{\tilde{{\bar{x}}}}_{ij} \le 0\right) \ge \tilde{\delta } } \right] \nonumber \\&\qquad \ge \gamma ,j=1,\ldots ,n,\nonumber \\&\quad u_r ,\nu _i \ge 0,r=1,\ldots ,s,i=1,\ldots ,m. \end{aligned}$$
(11)

Again, let us consider the assumption of the previous section, a summary of which is as follows:

$$\begin{aligned}&{\tilde{{\bar{x}}}}_{ij} {\sim } \mathrm{CSN}_{1,1} \left( {{\bar{x}}_{ij} ,\sigma _{ij}^2 ,\delta _{ij} ,0,\sigma _{ij}^2 } \right) ,{\bar{x}}_{ij} \\&\quad =\left( {x_{ij}^\alpha ,x_{ij}^{m_1 } ,x_{ij}^{m_2 } ,x_{ij}^\beta } \right) _{LR},\\&{\tilde{{\bar{y}}}}_{rj} {\sim } \mathrm{CSN}_{1,1} \left( {{\bar{y}}_{rj} ,\tau _{rj}^2 ,\varepsilon _{rj} ,0,\tau _{rj}^2 } \right) ,{\bar{y}}_{rj} \\&\quad =\left( {y_{rj}^\alpha ,y_{rj}^{m_1 } ,y_{rj}^{m_2 } ,y_{rj}^\beta } \right) _{LR}. \end{aligned}$$

By applying the second part of Theorem 1 and solving the CCR model with necessity–probability constraints with fuzzy probability level, the following definite model is obtained:

$$\begin{aligned}&\max \,{\bar{\varphi }}\nonumber \\&\mathrm{s.t.}\nonumber \\&\quad {\bar{\varphi }} -\mathop \sum \limits _{r=1}^{s} u_{r} \left( {y_{rp}^{{m}_{2} } +R^{-1}\left( {1-\gamma } \right) y_{rp}^{\beta } } \right) \nonumber \\&\qquad +\rho _{p}^{o} {\varPsi }^{-1}\left( {\delta ^{{m}_{2} }+R\left( \gamma \right) \delta ^{\beta }} \right) \le 0,\nonumber \\&\quad \mathop \sum \limits _{i=1}^{m} \nu _{i} \left( {x_{ip}^{{m}_{2} } +R^{-1}\left( {1-\gamma } \right) x_{ip}^{\beta } } \right) \nonumber \\&\qquad +\rho _{p}^{I} {\varPsi }^{-1}\left( {\delta ^{{m}_{2} }+R\left( \gamma \right) \delta ^{\beta }} \right) \le 1,\nonumber \\&\quad \mathop \sum \limits _{i=1}^{m} \nu _{i} \left( {x_{ip}^{{m}_{1} } +R^{-1}\left( {1-\gamma } \right) x_{ip}^\beta } \right) \nonumber \\&\qquad -\rho _{p}^{I} {\varPsi }^{-1}\left( {\delta ^{{m}_{2} }+R\left( \gamma \right) \delta ^{\beta }} \right) \ge 1,\nonumber \\&\quad \mathop \sum \limits _{r=1}^{s} u_{r} y_{rj}^{{m}_{1} } \nonumber \\&\quad -\mathop \sum \limits _{i=1}^{m} \nu _{i} x_{ij}^{{m}_{2} } +R^{-1}\left( {1-\gamma } \right) \left( {\mathop \sum \limits _{r=1}^{s} u_{r} y_{rj}^{\beta } +\mathop \sum \limits _{i=1}^m \nu _i x_{ij}^\alpha } \right) \nonumber \\&\qquad +\,h_j{\varPsi }^{-1} \left( {\delta ^{m_2 }+R\left( \gamma \right) \delta ^{\beta }} \right) \le 0, j=1,\ldots ,n,\nonumber \\&\quad \left( {\rho _p^o } \right) ^{2}=\mathop \sum \limits _{r=1}^{m} u_{r}^{2} \tau _{rp}^{2}\nonumber \\&\quad \left( {\rho _p^I } \right) ^{2}=\mathop \sum \limits _{i=1}^{m} \nu _{i}^{2} \sigma _{ip}^{2}\nonumber \\&\quad \left( {h_j } \right) ^{2}=\mathop \sum \limits _{r=1}^{m} u_{r}^{2} \tau _{rj}^{2} +\mathop \sum \limits _{i=1}^{m} \nu _{i}^{2} \sigma _{ij}^{2}\nonumber \\&\quad u_{r} ,\nu _{i} ,\theta _{p}^{o} ,\theta _{p}^{I} ,\lambda _{j} \ge 0, r=1,\ldots ,s;\nonumber \\&\qquad i=1,\ldots ,m;j=1,\ldots , n \end{aligned}$$
(12)

And \({\varPsi }\) is the cumulative distribution function (CDF) of the standard closed skew-normal distribution.

Definition 11

DMU is called efficient at probability level \(\upgamma \) and fuzzy necessity level \(\tilde{\delta } \) if the objective function of model (12) is equal to or bigger than 1; otherwise, it is called inefficient.

We should note that although we used this models in the paper, we could alternatively use the envelopment models.

4 Numerical examples

In this paper, we developed the possibility–probability and necessity–probability DEA models with Ra-Fu parameters in presence of SK distribution with fuzzy thresholds. We provide a numerical example to illustrate the applications of models.

In this section, we will provide an example and compares the results of the efficiency of DMUs when inputs and outputs are normal distributed or SN distribution. Suppose that 25 DMUs with three inputs and five outputs. All these data are stochastic, and also, inputs and outputs for different DMUs are independent. These data are given in Tables 1 and 2.

By using the data of Tables 1 and 2, we apply model (10) and model (12) the results with what is obtained from solving the models with input orientation. The computational results of models (10) and (12) are presented in Tables 3 and 4. Information of Table 3 is the results of efficiency and slacks of DMUs with real distribution of data (SN distribution).

We used \(\tilde{\delta } =\left( {0.1,0.1,0.1} \right) \) for \(=0.1\), 0.3 and 0.9 and for fixed \(\gamma =0.5\) and three fuzzy numbers for \(\tilde{\delta } =\left\{ {\left( {0.1,0.1,0.1} \right) ,\left( {0.1,0.3,0.1} \right) ,\left( {0.1,0.7,0.1} \right) } \right\} \) such that \(\left( {0.1,0.1,0.1} \right) \le \left( {0.1,0.3,0.1} \right) \le \left( {0.1,0.7,0.1} \right) \). The results derived from model (10) are given in Table 3. As given in Table 3, for \(\tilde{\delta } =\left( {0.1,0.1,0.1} \right) \) and \(=0.1\), 0.3, 0.5 and 0.9, DMUs 5 and 14 have the highest and lowest scores. The results of the model (12) in Table 4 are lower compared to the results of the model (10) in Table 3. The efficiency of model (12) is less than the efficiency of model (10); when \(\gamma =0.5\) is fixed and \(\tilde{\delta } \) is increased, the score of model (12) is decreased.

If skewness control parameter equals to zero, we have normal distribution. Using normal data, we fit the models in normal mode (Tavana et al. 2013a, b). Results are presented in Tables 5 and 6. The results of Table 5 show that DMUs 1 and 2 are efficient, but in Table 3 these DMUs are inefficient. DMU 14 with real distribution of data in Table 3 is efficient, whereas with unsuitable choice of distribution it is inefficient. The results show that an inefficient DMU may be wrongly diagnosed as an efficient DMU and vice versa.

5 Discussion and conclusion

In the classic DEA theory, it is assumed that the data are definite. The nonparametric programming method in DEA is so popular due to its simplicity and applicability. The use of DEA in recent years in various fields including economy, operational research, statistics, marketing, and public services has led to completely new results; furthermore, the use of DEA as a powerful tool for evaluating the performance of DMUs with the applied programs has resulted in a new challenge. The real input data were mostly vague, random, and/or fuzzy, and the outputs were the same. In a real problem, we may face the two random and fuzzy states simultaneously. In previous works, it has been assumed that the random fuzzy data follow a normal distribution so that if the fitness of this distribution is not suitable for the data, it will lead to incorrect conclusions. However, in the present paper, it was assumed that the input and output variables were random fuzzy and followed a SN distribution; furthermore, the possibility–probability and necessity–probability models were fitted with the conditions that the use of the skew-normal distribution in random fuzzy state instead of the previous method would be more general and better. In other words, this method embraced the previous methods in a specific state. The advantage of this theorem was also represented in two numerical examples.