Fuzzy chance-constrained data envelopment analysis: a structured literature review, current trends, and future directions

Abstract

Fuzzy data envelopment analysis (FDEA) is one of the most applicable approaches for performance assessment of peer decision making units under ambiguity which is evolving rapidly and gaining popularity under uncertain data envelopment analysis field. The goal of this paper is to review some FDEA models based on applied possibility, necessity, credibility, general fuzzy measures and chance-constrained programming to deal with data ambiguity. The study presents a comprehensive and structured literature review of fuzzy chance-constrained data envelopment analysis (FCCDEA) studies including 87 studies from 2000 to 2020. The main contributions of this research include the following details: (1) Review of fuzzy chance-constrained programming, (2) Survey of FCCDEA models based on different fuzzy measures, (3) Analysis of FCCDEA applications and features, (4) Classification of FCCDEA studies from modeling and uncertainty type viewpoints, (5) Bibliometric analysis of FCCDEA literature, and (6) Extraction of main research gaps and guidelines for future research directions.

1 Introduction

Performance appraisal is one of the most important decision-making issues in various areas of application and real-world problems. Data envelopment analysis (DEA) is a powerful and popular mathematical programming approach for performance measurement. DEA was presented by Charnes et al. (1978) for the first time and it is originated from Farrell’s (1957) research for performance assessment of peer decision making units (DMUs) in the presence of multiple crisp inputs and outputs. However, for many real cases, most of the times, the observed values of inputs and/or outputs of DEA models are tainted by ambiguity (Hatami-Marbini et al., 2011). Data ambiguity can be the result of the absence or lack of knowledge about data, non-obtainable data, expert based information, linguistic terms, and unquantifiable data.

The conventional DEA models cannot be applied for performance evaluation and ranking DMUs in the presence of imprecise and vague data (Emrouznejad & Tavana, 2014). As a result, it is essential and important to develop DEA models for eliminating this issue, otherwise, the efficiency score and ranking of the DMUs may become unreliable and invalid (Peykani et al., 2020). Accordingly, in recent years, many researchers proposed variants of uncertain data envelopment analysis (UDEA) models by employing uncertain programming approaches.

Fuzzy chance-constrained data envelopment analysis (FCCDEA) is one of the popular and applicable approaches that can handle fuzzy data and linguistic terms. The FCCDEA approach is the result of the integration of DEA models, fuzzy mathematical programming (FMP) and chance-constrained programming (CCP). Given the importance and growing trend of FCCDEA field, in this paper, a comprehensive and structured literature review of fuzzy chance-constrained DEA researches is presented. The current study covers 87 studies of FCCDEA field from 2000 to 2020 and concludes with suggestions about the directions for further researches in this field. The main contributions of this literature review can be summarized as follows:

• The relations of fuzzy chance-constrained programming (FCCP) are introduced.

• FCCDEA modeling is explained based on different optimistic-pessimistic attitudes.

• Literature is classified according to the features and applications of FCCDEA studies.

• FCCDEA studies are categorized according to the type of uncertainty and FCCP approaches.

• Bibliometric analysis, beneficial statistical information and main research gaps are extracted.

• Future research directions are suggested through a comprehensive literature review.

The rest of this paper is organized as follows. The fundamentals and backgrounds of data envelopment analysis will be presented in Sect. 2. The background of fuzzy measures for measuring fuzzy events based on chance-constrained programming will be explained in Sect. 3. Fuzzy chance-constrained DEA modeling will be discussed in Sect. 4. Then, a comprehensive literature review of FCCDEA studies will be presented in Sect. 5. Finally, conclusions and some directions for future research are given in Sect. 6.

2 Data envelopment analysis (DEA)

Data envelopment analysis is one of the prominent non-parametric techniques for performance measurement, benchmarking and ranking of the peer DMUs. This technique is widely applied in many real-life problems and applications (Emrouznejad & Yang, 2018; Hosseinzadeh Lotfi et al., 2020). In term of modeling, the data envelopment analysis models are categorized according to four characteristics including (1) Projection Construction, (2) Model Form, (3) Model Orientation, and (4) Returns to Scale (RTS). The explanation of these characteristics is summarized as follows:

• Projection Construction The radial projection (RP) construction implies that the DEA optimizes all inputs or outputs of a DMU at a certain proportion. However, in the non-radial projection (NRP) construction, the DEA reduces inputs or increases outputs non-proportionally.

• Form The multiplier forms (M-F) and envelopment form (E-F) of conventional DEA models are modeled based on the concept of relative efficiency and production possibility set (PPS), respectively.

• Orientation DEA models are classified into the input-oriented, output-oriented, and non-oriented methods. In the input-oriented (I-O) models, the possible proportional reduction of inputs is fixed. In the output-oriented (O-O) models, the possible proportional increase in the outputs is considered, while the inputs are fixed. In the non-oriented (N-O) DEA models, the inputs are decreased and the outputs are increased, simultaneously.

• Returns to Scale RTS denotes the proportional changes in outputs per change in inputs, including constant returns to scale (CRS), variable returns to scale (VRS), non-increasing returns to scale (NIRS), and non-decreasing returns to scale (NDRS).

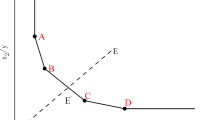
The graphical presentation of DEA characteristics classification is introduced in Fig. 1: Also, the orientation types, production possibility set, and efficient frontier (EF) under the different returns to scale assumptions are depicted in Fig. 2.

Fig. 1

Background of DEA modeling

Fig. 2

PPS under different RTS assumptions and the orientation types

To get acquainted with DEA modeling, assume that there are $n$ homogenous decision-making units $DMU_{j} \left( {j = 1,...,n} \right)$ each consuming $m$ inputs $x_{{ij}} \left( {i = 1,...,m} \right)$ and producing $s$ outputs $y_{{rj}} (r = 1,...,s)$. Here, the subscript $o$ refers to the DMU under consideration. Moreover, the non-negative weights $v_{i} (i = 1,...,m)$ and $u_{r} (r = 1,...,s)$ are assigned to inputs and outputs, respectively. Also, the free sign variable $w$ allows the change of scale and non-negative variables $\lambda _{j} (j = 1,...,n)$ are employed in production possibility set formulation.

After introducing the indices, parameters and decision variables that will be employed in DEA modeling, the basic and popular DEA models under different characteristics will be presented in the following. Charnes et al. (1978) proposed the first DEA model that based on the CRS assumption and called the CCR (Charnes-Cooper-Rhodes) model. The variants of CCR model are presented as follows:

CCR (M-F & I-O)		CCR (M-F & O-O)
${\text{Max}}\quad \sum\limits_{{r = 1}}^{s} {y_{{ro}} u_{r} }$	(1)	${\text{Min}}\quad \sum\limits_{{i = 1}}^{m} {x_{{io}} v_{i} }$	(2)
${\text{S}}.{\text{t}}.\quad \,\,\sum\limits_{{i = 1}}^{m} {x_{{io}} v_{i} } = 1$		${\text{S.t.}}\quad \,\,\sum\limits_{{r = 1}}^{s} {y_{{ro}} u_{r} } = 1$
$\quad \quad \,\,\,\sum\limits_{{r = 1}}^{s} {y_{{rj}} u_{r} } - \sum\limits_{{i = 1}}^{m} {x_{{ij}} v_{i} } \le 0,\,\quad \forall j$		$\quad \quad \,\,\,\sum\limits_{{r = 1}}^{s} {y_{{rj}} u_{r} } - \sum\limits_{{i = 1}}^{m} {x_{{ij}} v_{i} } \le 0,\quad \forall j$
$\quad \quad \,\,\,v_{i} ,\,u_{r} \ge 0,\quad \forall i,r$		$\quad \quad \,\,\,v_{i} ,\,u_{r} \ge 0,\quad \forall i,r$

CCR (E-F & I-O)		CCR (E-F & O-O)
${\text{Min}}\quad \Theta$	(3)	${\text{Max}}\quad \Phi$	(4)
${\text{S.t.}}\quad \,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} x_{{ij}} } \le \Theta x_{{io}} ,\quad \forall i$		${\text{S.t.}}\quad \,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} x_{{ij}} } \le x_{{io}} ,\quad \forall i$
$\quad \quad \,\,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} y_{{rj}} } \ge y_{{ro}} ,\quad \forall r$		$\quad \quad \,\,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} y_{{rj}} } \ge \Phi y_{{ro}} ,\quad \forall r$
$\quad \quad \,\,\,\lambda _{j} \ge 0,\quad \forall j$		$\quad \quad \,\,\,\lambda _{j} \ge 0,\quad \forall j$

Then, Banker et al. (1984) developed CCR model based on the VRS assumption and called the BCC (Banker-Charnes-Cooper) model. The CCR and BCC models are radial projection constructs. The variants of BCC model are presented as follows:

BCC (M-F & I-O)		BCC (M-F & O-O)
${\text{Max}}\quad \sum\limits_{{r = 1}}^{s} {y_{{ro}} u_{r} } + w$	(5)	${\text{Min}}\quad \sum\limits_{{i = 1}}^{m} {x_{{io}} v_{i} } - w$	(6)
${\text{S.t.}}\quad \,\,\sum\limits_{{i = 1}}^{m} {x_{{io}} v_{i} } = 1$		${\text{S.t.}}\quad \,\,\sum\limits_{{r = 1}}^{s} {y_{{ro}} u_{r} } = 1$
$\quad \quad \,\,\,\sum\limits_{{r = 1}}^{s} {y_{{rj}} u_{r} } - \sum\limits_{{i = 1}}^{m} {x_{{ij}} v_{i} } + w \le 0,\quad \forall j$		$\quad \quad \,\,\,\sum\limits_{{r = 1}}^{s} {y_{{rj}} u_{r} } - \sum\limits_{{i = 1}}^{m} {x_{{ij}} v_{i} } + w \le 0,\quad \forall j$
$\quad \quad \,\,\,v_{i} ,\,u_{r} \ge 0,\quad \forall i,r$		$\quad \quad \,\,\,v_{i} ,\,u_{r} \ge 0,\quad \forall i,r$

BCC (E-F & I-O)		BCC (E-F & O-O)
${\text{Min}}\quad \Theta$	(7)	${\text{Max}}\quad \Phi$	(8)
${\text{S.t.}}\quad \,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} x_{{ij}} } \le \Theta x_{{io}} ,\quad \forall i$		${\text{S.t.}}\quad \,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} x_{{ij}} } \le x_{{io}} ,\quad \forall i$
$\quad \quad \,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} y_{{rj}} } \ge y_{{ro}} ,\quad \forall r$		$\quad \,\quad \,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} y_{{rj}} } \ge \Phi y_{{ro}} ,\quad \forall r$
$\quad \quad \,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} } = 1$		$\,\,\quad \quad \sum\limits_{{j = 1}}^{n} {\lambda _{j} } = 1$
$\quad \quad \,\lambda _{j} \ge 0,\quad \forall j$		$\quad \quad \,\lambda _{j} \ge 0,$

Charnes et al., (1985b) proposed the non-radial DEA model by considering 3simultaneously both input minimization and output maximization and called the additive (ADD) model. The variants of ADD model are presented as follows:

ADD (M-F & CRS)		ADD (M-F & VRS)
${\text{Max}}\quad \sum\limits_{{r = 1}}^{s} {y_{{ro}} u_{r} } - \sum\limits_{{i = 1}}^{m} {x_{{io}} v_{i} }$	(9)	${\text{Max}}\quad \sum\limits_{{r = 1}}^{s} {y_{{ro}} u_{r} } - \sum\limits_{{i = 1}}^{m} {x_{{io}} v_{i} } + w$	(10)
${\text{S.t.}}\quad \,\,\sum\limits_{{r = 1}}^{s} {y_{{rj}} u_{r} } - \sum\limits_{{i = 1}}^{m} {x_{{ij}} v_{i} } \le 0,\quad \forall j$		${\text{S.t.}}\quad \,\,\sum\limits_{{r = 1}}^{s} {y_{{rj}} u_{r} } - \sum\limits_{{i = 1}}^{m} {x_{{ij}} v_{i} } + w \le 0,\quad \forall j$
$\quad \quad \,\,\,u_{r} \ge 1,\quad \forall r$		$\quad \quad \,\,\,u_{r} \ge 1,\quad \forall r$
$\quad \quad \,\,\,v_{i} \ge 1,\quad \forall i$		$\quad \quad \,\,\,v_{i} \ge 1,\quad \forall i$

ADD (E-F & CRS)		ADD (E-F & VRS)
${\text{Min}}\quad \sum\limits_{{i = 1}}^{m} {\delta _{i}^{ - } } + \sum\limits_{{r = 1}}^{s} {\delta _{r}^{ + } }$	(11)	${\text{Min}}\quad \sum\limits_{{i = 1}}^{m} {\delta _{i}^{ - } } + \sum\limits_{{r = 1}}^{s} {\delta _{r}^{ + } }$	(12)
${\text{S.t.}}\quad \,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} x_{{ij}} } + \delta _{i}^{ - } = x_{{io}} ,\quad \forall i$		${\text{S.t.}}\quad \,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} x_{{ij}} } + \delta _{i}^{ - } = x_{{io}} ,\quad \forall i$
$\quad \quad \,\,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} y_{{rj}} } - \delta _{r}^{ + } = y_{{ro}} ,\quad \forall r$		$\quad \quad \,\,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} y_{{rj}} } - \delta _{r}^{ + } = y_{{ro}} ,\quad \forall r$
$\quad \quad \,\,\,\lambda _{j} ,\,\delta _{i}^{ - } ,\,\delta _{r}^{ + } \ge 0,\quad \forall j,r,i$		$\quad \quad \,\,\,\sum\limits_{{j = 1}}^{n} {\lambda _{j} } = 1$
		$\quad \quad \,\,\,\lambda _{j} ,\, \delta _{i}^{ - } ,\, \delta _{r}^{ + } \ge 0,\quad \forall j,r,i$

The multiplier and envelopment forms of conventional DEA are the dual linear programming problem to each other (Cooper et al., 2011).

3 Fuzzy chance-constrained programming (FCCP)

Zadeh (1978) suggested that in fuzzy linear programming, fuzzy coefficients can be viewed as fuzzy variables and constraints can be considered as fuzzy events (Inuiguchi et al., 1993). Accordingly, by integrating the chance-constrained programming (CCP) proposed by Charnes and Cooper (1959) and fuzzy measures such as possibility, necessity, credibility, and general, the chances of occurrence of fuzzy events can be measured. The goal of this section is to introduce the preliminaries, principles and relations of fuzzy chance-constrained programming (FCCP) approach under triangular and trapezoidal fuzzy variables.

The membership function of triangular fuzzy variable (TRFV) $\tilde{\alpha }=(\alpha _{1} ,\,\alpha _{2} ,\,\alpha _{3} ),\,\alpha _{1} < \alpha _{2} < \alpha _{3}$ and trapezoidal fuzzy variable (TLFV) $\tilde{\beta } = (\beta _{1} , \, \beta _{2} , \, \beta _{3} , \, \beta _{4} ), \, \beta _{1} < \beta _{2} < \beta _{3} < \beta _{4}$ are proposed in Eqs. (13) and (14), respectively:

TFV
$\mu (x) = \left\{ \begin{gathered} \frac{{x - \alpha _{1} }}{{\alpha _{2} - \alpha _{1} }}, \, \quad if \, \alpha _{1} \le x \le \alpha _{2} ; \hfill \\ \frac{{\alpha _{3} - x}}{{\alpha _{3} - \alpha _{2} }},\quad if \, \alpha _{2} \le x \le \alpha _{3} ; \hfill \\ 0,\quad \quad \quad \,\,\,\,\,otherwise. \hfill \\ \end{gathered} \right.$	(13)
$\mu (x) = \left\{ \begin{gathered} \frac{{x - \beta _{1} }}{{\beta _{2} - \beta _{1} }},\quad \,if \, \beta _{1} \le x \le \beta _{2} \, ; \hfill \\ 1,\quad \quad \quad \,\,\,\,\,if \, \beta _{2} \le x \le \beta _{3} \, ; \hfill \\ \frac{{\beta _{4} - x}}{{\beta _{4} - \beta _{3} }},\quad if \, \beta _{3} \le x \le \beta _{4} \, ; \hfill \\ 0,\quad \quad \quad \,\,\,\,otherwise \, . \hfill \\ \end{gathered} \right.$	(14)

TRFV and TLFN are the most popular and applicable fuzzy number in fuzzy mathematical literature and they are special kind of LR fuzzy variable (Xu & Zhou, 2011). The membership function curve of TRFN and TLFN are shown in Fig. 3.

Fig. 3

The representation of fuzzy number. (A) Triangular membership function, (B) Trapezoidal membership function

In the following of this section, by considering $\tilde{\alpha }$, $\tilde{\beta }$, and $\gamma$ as a TRFN, TLFN, and crisp number, respectively, all relations will be introduced.

3.1 Possibility measure

Let the triple $\left( {\Psi , \, \Omega \left( \Psi \right), \, Pos} \right)$ be a possibility space where $\Psi$ is the universe and non-empty set containing all possible events, $\Omega \left( \Psi \right)$ is the power set of $\Psi$, and Pos is a possibility measure (Zadeh, 1978). The properties of the possibility (Pos) measure are presented as follows:

• $Pos\left\{ \emptyset \right\} = 0, \, Pos\left\{ \Psi \right\} = 1$

• $\forall \, H \, \in \, \Omega \left( \Psi \right) \, \Rightarrow { 0} \le \, Pos\left\{ H \right\} \, \le 1$

• $Pos\left\{ { \cup _{k} H_{k} } \right\} = Sup_{k} \left( {Pos\left\{ {H_{k} } \right\}} \right)$

• $\forall \, H, \, Q \, \in \, \Omega \left( \Psi \right),H \subseteq Q \, \Rightarrow \, Pos\left\{ H \right\} \, \le \, Pos\left\{ Q \right\}$

• $\forall \, H, \, Q \, \in \, \Omega \left( \Psi \right) \, \Rightarrow \, Pos\left\{ {H \cup Q} \right\} + Pos\left\{ {H \cap Q} \right\} \, \le \, Pos\left\{ H \right\} + Pos\left\{ Q \right\}$

The Pos measure of fuzzy events $\left\{ {\tilde{\alpha } \le \gamma } \right\}$, $\left\{ {\tilde{\alpha } \ge \gamma } \right\}$, $\left\{ {\tilde{\beta } \le \gamma } \right\}$ and $\left\{ {\tilde{\beta } \ge \gamma } \right\}$ are shown in Eqs. (15) to (18), respectively:

POS measure
$Pos\left\{ {\tilde{\alpha } \le \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {0,\quad \quad \quad \quad if\,\alpha _{1} \ge \gamma ;} \\ {\frac{{\gamma - \alpha _{1} }}{{\alpha _{2} - \alpha _{1} }},\quad\quad\, \,if\,\alpha _{1} \le \gamma \le \alpha _{2} ;} \\ {1,\quad \quad \quad\,\,\,\,\, if\,\alpha _{2} \le \gamma ;} \\ \end{array} } \right.$	(15)
$Pos\left\{ {\tilde{\alpha } \ge \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {1,\quad \quad \quad if\,\gamma \le \alpha _{2} ;} \\ {\frac{{\alpha _{3} - \gamma }}{{\alpha _{3} - \alpha _{2} }},\quad \, \, \, if\,\alpha _{2} \le \gamma \le \alpha _{3} ;} \\ {0,\quad \quad \quad if\,\alpha _{3} \le \gamma .} \\ \end{array} } \right.$	(16)
$Pos\left\{ {\tilde{\beta } \le \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {0,\quad \quad \,\,\,\,\, if\,\beta _{1} \ge \gamma ;} \\ {\frac{{\gamma - \beta _{1} }}{{\beta _{2} - \beta _{1} }},\quad \,if\,\beta _{1} \le \gamma \le \beta _{2} ;} \\ {1,\quad \,\,\,\, \quad if\,\beta _{2} \le \gamma ;} \\ \end{array} } \right.$	(17)
$Pos\left\{ {\tilde{\beta } \ge \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {1,\quad \quad \quad if\,\gamma \le \beta _{3} ;} \\ {\frac{{\beta _{4} - \gamma }}{{\beta _{4} - \beta _{3} }},\quad\,\, if\,\beta _{3} \le \gamma \le \beta _{4} ;} \\ {0,\quad \quad \,\,\,\,if\,\beta _{4} \le \gamma .} \\ \end{array} } \right.$	(18)

According to the Pos measure and CCP, the deterministic counterparts and equivalent crisp ones of fuzzy chance constraints under desired confidence level $\xi$ are presented in Eqs. (19) to (22) as follows:

POS measure
$Pos\left\{ {\tilde{\alpha } \le \gamma } \right\} \ge \xi \, \Leftrightarrow \, \left( {1 -\xi } \right) \, \alpha _{1} + \left( \xi \right) \, \alpha _{2} \le \gamma$	(19)
$Pos\left\{ {\tilde{\alpha } \ge \gamma } \right\} \ge \xi \, \Leftrightarrow \, \left( \xi \right) \, \alpha _{2}\, { + }\,\left( {1 -\xi } \right) \, \alpha _{3} \ge \gamma$	(20)
$Pos\left\{ {\tilde{\beta } \le \gamma } \right\} \ge \xi \, \Leftrightarrow \, \left( {1 -\xi } \right) \, \beta _{1} + \left( \xi \right) \, \beta _{2} \le \gamma$	(21)
$Pos\left\{ {\tilde{\beta } \ge \gamma } \right\} \ge \xi \, \Leftrightarrow \, \left( \xi \right) \, \beta _{3} \,{ + }\,\left( {1 -\xi } \right) \, \beta _{4} \ge \gamma$	(22)

The Pos measure indicates the most optimistic possibility occurrence level of fuzzy events. As a result, the Pos measure is applied in situations where the decision maker (DM) takes an optimistic viewpoint.

3.2 Necessity measure

The necessity measure of a fuzzy event $H \, \in \, \Omega \left( \Psi \right)$ is defined on $\left( {\Psi , \, \Omega \left( \Psi \right), \, Pos} \right)$ as $Nec\left\{ H \right\} = 1 - Pos\left\{ {H^{C} } \right\}$, where $\left\{ {H^{C} } \right\}$ is the complement of $\left\{ H \right\}$ (Dubois & Prade, 1978, 1988). The properties of the necessity (Nec) measure are presented as follows:

• $Nec\left\{ \emptyset \right\} = 0, \, Nec\left\{ \Psi \right\} = 1$

• $\forall \, H \, \in \, \Omega \left( \Psi \right) \, \Rightarrow { 0 } \le \, Nec\left\{ H \right\} \, \le 1$

• $Nec\left\{ { \cap _{k} H_{k} } \right\} = Inf_{k} \left( {Nec\left\{ {H_{k} } \right\}} \right)$

• $\forall \, H, \, Q \, \in \, \Omega \left( \Psi \right),H \subseteq Q \, \Rightarrow \, Nec\left\{ H \right\} \, \le \, Nec\left\{ Q \right\}$

• $\forall \, H, \, Q \, \in \, \Omega \left( \Psi \right) \, \Rightarrow \, Nec\left\{ {H \cup Q} \right\} + Nec\left\{ {H \cap Q} \right\} \, \ge \, Nec\left\{ H \right\} + Nec\left\{ Q \right\}$

• $\forall \, H \, \in \, \Omega \left( \Psi \right),Pos\left\{ H \right\} < 1 \, \Rightarrow \, Nec\left\{ H \right\} = 0$

• $\forall \, H \, \in \, \Omega \left( \Psi \right),Nec\left\{ H \right\} > 0 \, \Rightarrow \, Pos\left\{ H \right\} = 1$

The Nec measure is the dual of Pos measure. The Nec measure of fuzzy events $\left\{ {\tilde{\alpha } \le \gamma } \right\}$, $\left\{ {\tilde{\alpha } \ge \gamma } \right\}$, $\left\{ {\tilde{\beta } \le \gamma } \right\}$ and $\left\{ {\tilde{\beta } \ge \gamma } \right\}$ are shown in Eqs. (23) to (26), respectively:

NEC measure
$Nec\left\{ {\tilde{\alpha } \le \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {0,\quad \quad \quad if\,\gamma \le \alpha _{2} ;} \\ {\frac{{\gamma - \alpha _{2} }}{{\alpha _{3} - \alpha _{2} }},\quad \,\, if\,\alpha _{2} \le \gamma \le \alpha _{3} ;} \\ {1,\quad \quad \quad if\,\alpha _{3} \le \gamma .} \\ \end{array} } \right.$	(23)
$Nec\left\{ {\tilde{\alpha } \ge \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {1,\quad \quad \quad if\,\alpha _{1} \ge \gamma ;} \\ {\frac{{\alpha _{2} - \gamma }}{{\alpha _{2} - \alpha _{1} }},\quad \,\, if\,\alpha _{1} \le \gamma \le \alpha _{2} ;} \\ {0,\quad \quad \quad if\,\alpha _{2} \le \gamma ;} \\ \end{array} } \right.$	(24)
$Nec\left\{ {\tilde{\beta } \le \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {0,\quad \quad \quad if\,\gamma \le \beta _{3} ;} \\ {\frac{{\gamma - \beta _{3} }}{{\beta _{4} - \beta _{3} }},\quad \,\,if\,\beta _{3} \le \gamma \le \beta _{4} ;} \\ {1,\quad \quad \,\,\,\,\,if\,\beta _{4} \le \gamma .} \\ \end{array} } \right.$	(25)
$Nec\left\{ {\tilde{\beta } \ge \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {1,\quad \quad \quad if\,\beta _{1} \ge \gamma ;} \\ {\frac{{\beta _{2} - \gamma }}{{\beta _{2} - \beta _{1} }},\quad \,\,\, if\,\beta _{1} \le \gamma \le \beta _{2} ;} \\ {0,\quad \quad \,\,\,\,\, if\,\beta _{2} \le \gamma ;} \\ \end{array} } \right.$	(26)

According to the Nec measure and CCP, the deterministic counterparts and equivalent crisp ones of fuzzy chance constraints under desired confidence level $\xi$ are presented in Eqs. (27) to (30) as follows:

NEC measure
$Nec\left\{ {\tilde{\alpha } \le \gamma } \right\} \ge \xi \, \Leftrightarrow \, \left( {1 -\xi } \right) \, \alpha _{2} + \left( \xi \right) \, \alpha _{3} \le \gamma$	(27)
$Nec\left\{ {\tilde{\alpha } \ge \gamma } \right\} \ge \xi \, \Leftrightarrow \, \left( \xi \right) \, \alpha _{1} \,{ + }\,\left( {1 -\xi } \right) \, \alpha _{2} \ge \gamma$	(28)
$Nec\left\{ {\tilde{\beta } \le \gamma } \right\} \ge \xi \, \Leftrightarrow \, \left( {1 -\xi } \right) \, \beta _{3} + \left( \xi \right) \, \beta _{4} \le \gamma$	(29)
$Nec\left\{ {\tilde{\beta } \ge \gamma } \right\} \ge \xi \, \Leftrightarrow \, \left( \xi \right) \, \beta _{1} { + }\left( {1 -\xi } \right) \, \beta _{2} \ge \gamma$	(30)

According to the pessimistic viewpoint of the Nec measure, decision maker (DM) can be employed Nec measure instead of Pos measure in order to an allude risk (Xu & Zhou, 2011). It must be emphasized that Pos and Nec are two standards and well-known fuzzy measures that are wieldy applied in fuzzy chance-constrained programming models.

3.3 Credibility measure

The credibility measure of a fuzzy event $H \, \in \, \Omega \left( \Psi \right)$ is defined on $\left( {\Psi , \, \Omega \left( \Psi \right), \, Pos} \right)$ as $Cr\left\{ H \right\} = 0.5 \, \left( {Pos\left\{ H \right\} + Nec\left\{ H \right\}} \right)$. In other words, credibility measure is the average of Pos and Nec measures (Liu & Liu, 2002). The properties of the credibility (Cr) measure are presented as follows:

• $Cr\left\{ \emptyset \right\} = 0, \, Cr\left\{ \Psi \right\} = 1$

• $\forall \, H \, \in \, \Omega \left( \Psi \right) \, \Rightarrow { 0 } \le \, Cr\left\{ H \right\} \, \le 1$

• $\forall \, H \, \in \, \Omega \left( \Psi \right) \, \Rightarrow \, Cr\left\{ H \right\} + Cr\left\{ {H^{C} } \right\} = 1$

• $\forall \, H, \, Q \, \in \, \Omega \left( \Psi \right),H \subseteq Q \, \Rightarrow \, Cr\left\{ H \right\} \, \le \, Cr\left\{ Q \right\}$

• $\forall \, H, \, Q \, \in \, \Omega \left( \Psi \right) \, \Rightarrow \, Cr\left\{ {H \cup Q} \right\} \, \le \, Cr\left\{ H \right\} + Cr\left\{ Q \right\}$

• $\forall \, H \, \in \, \Omega \left( \Psi \right) \, \Rightarrow \, Pos\left\{ H \right\} \ge Cr\left\{ H \right\} \ge Nec\left\{ H \right\}$

It should be underlined that the Cr measure is self-dual and it capable to be supported a compromise attitude of the DM over both extremes (Liu & Liu, 2002). The Cr measure of fuzzy events $\left\{ {\tilde{\alpha } \le \gamma } \right\}$, $\left\{ {\tilde{\alpha } \ge \gamma } \right\}$, $\left\{ {\tilde{\beta } \le \gamma } \right\}$ and $\left\{ {\tilde{\beta } \ge \gamma } \right\}$ are shown in Eqs. (31) to (34), respectively:

CR measure
$Cr\left\{ {\tilde{\alpha } \le \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {0,\quad \quad \quad \quad \,if\,\alpha _{1} \ge \gamma ;} \\ {\frac{{\gamma - \alpha _{1} }}{{2\,(\alpha _{2} - \alpha _{1} )}},\quad\, \,\,\, if\,\alpha _{1} \le \gamma \le \alpha _{2} } \\ {\frac{{\gamma + \alpha _{3} - 2\alpha _{2} }}{{2\,(\alpha _{3} - \alpha _{2} )}},\quad\, \,if\,\alpha _{2} \le \gamma \le \alpha _{3} ;} \\ {1,\quad \quad \quad\, \,\,\,\ if\,\alpha _{3} \le \gamma .} \\ \end{array} } \right.$	(31)
$Cr\left\{ {\tilde{\alpha } \ge \gamma } \right\} = \left\{ {\begin{array}{*{20}c} {1,\quad \quad \, if\,\alpha _{1} \ge \gamma ;} \\ {\frac{{2\alpha _{2} - \alpha _{1} - \gamma }}{{2\,(\alpha _{2} - \alpha _{1} )}},\quad if\,\alpha _{1} \le \gamma \le \alpha _{2} ;} \\ {\frac{{\alpha _{3} - \gamma }}{{2\,(\alpha _{3} - \alpha _{2} )}},\quad \,\,\,if\,\alpha _{2} \le \gamma \le \alpha _{3} ;} \\ {0,\quad \quad if\,\alpha _{3} \le \gamma .} \\ \end{array} } \right.$	(32)
$Cr\left\{ {\tilde{\beta } \le \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {0,\quad \,\,\,\, \quad \quad if\,\beta _{1} \ge \gamma ;} \\ {\frac{{\gamma - \beta _{1} }}{{2\,(\beta _{2} - \beta _{1} )}},\quad \, if\,\beta _{1} \le \gamma \le \beta _{2} ;} \\ {0.5,\quad \quad\, \,\,\,if\,\beta _{2} \le \gamma \le \beta _{3} ;} \\ {\frac{{\gamma + \beta _{4} - 2\beta _{3} }}{{2\,(\beta _{4} - \beta _{3} )}}\,\,\,\,\,\,\, if\,\beta _{3} \le \gamma \le \beta _{4} ;} \\ {1,\quad \quad \quad\, if\,\beta _{4} \le \gamma .} \\ \end{array} } \right.$	(33)
$Cr\left\{ {\tilde{\beta } \ge \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {1,\quad \quad \quad \quad if\,\beta _{1} \ge \gamma ;} \\ {\frac{{2\beta _{2} - \beta _{1} - \gamma }}{{2\,(\beta _{2} - \beta _{1} )}},\quad \,\, if\,\beta _{1} \le \gamma \le \beta _{2} ;} \\ {0.5,\quad \quad \quad if\,\beta _{2} \le \gamma \le \beta _{3} ;} \\ {\frac{{\beta _{4} - \gamma }}{{2\,(\beta _{4} - \beta _{3} )}},\quad \,\,if\,\beta _{3} \le \gamma \le \beta _{4} ;} \\ {0,\quad \quad \quad \,\,\,\,if\,\beta _{4} \le \gamma .} \\ \end{array} } \right.$	(34)

According to the Cr measure and CCP, the deterministic counterparts and equivalent crisp ones of fuzzy chance constraints under desired confidence level $\xi$ are presented in Eqs. (35) to (38) as follows:

CR measure
$Cr\left\{ {\tilde{\alpha } \le \gamma } \right\} \ge \xi \, \Leftrightarrow \, \left\{ \begin{gathered} \left( {1 - 2\xi } \right) \, \alpha _{1} + \left( {2\xi } \right) \, \alpha _{2} \le \gamma ,\quad \quad \quad if \, \xi \le 0.5; \hfill \\ \left( {2 - 2\xi } \right) \, \alpha _{2} + \left( {2\xi - 1} \right) \, \alpha _{3} \le \gamma ,\quad \,\,if \, \xi > 0.5. \hfill \\ \end{gathered} \right.$	(35)
$Cr\left\{ {\tilde{\alpha } \ge \gamma } \right\} \ge \xi \, \Leftrightarrow \,\left\{ \begin{gathered} \left( {2\xi } \right)\,\alpha _{2} + \left( {1 - 2\xi } \right)\,\alpha _{3} \ge \gamma ,\quad \quad \quad if\,\,\xi \le 0.5; \hfill \\ \left( {2\xi - 1} \right)\,\alpha _{1} + \left( {2 - 2\xi } \right)\,\alpha _{2} \ge \gamma ,\quad \,\,\,if\,\,\xi > 0.5. \hfill \\ \end{gathered} \right.$	(36)
$Cr\left\{ {\tilde{\beta } \le \gamma } \right\} \ge \xi \Leftrightarrow \left\{ \begin{gathered} \left( {1 - 2\xi } \right)\,\beta _{1} + \left( {2\xi } \right)\,\beta _{2} \le \gamma ,\quad \quad \quad if\,\xi \le 0.5; \hfill \\ \left( {2 - 2\xi } \right)\,\beta _{3} + \left( {2\xi - 1} \right)\,\beta _{4} \le \gamma ,\quad \,\,if\,\xi > 0.5. \hfill \\ \end{gathered} \right.$	(37)
$Cr\left\{ {\tilde{\beta } \ge \gamma } \right\} \ge \xi \Leftrightarrow \left\{ \begin{gathered} \left( {2\xi } \right)\,\beta _{3} + \left( {1 - 2\xi } \right)\,\beta _{4} \ge \gamma ,\quad \quad \quad if\,\xi \le 0.5; \hfill \\ \left( {2\xi - 1} \right)\,\beta _{1} + \left( {2 - 2\xi } \right)\,\beta _{2} \ge \gamma ,\quad \,\,\,if\,\xi > 0.5. \hfill \\ \end{gathered} \right.$	(38)

As it can be seen from Eqs. (35) to (38), for the confidence level $\xi$ greater or less than 0.5, an equivalent crisp of fuzzy chance constraints based on Cr measure is different.

3.4 General fuzzy measure

The general fuzzy measure of a fuzzy event $H \, \in \, \Omega \left( \Psi \right)$ is defined on $\left( {\Psi , \, \Omega \left( \Psi \right), \, Pos} \right)$ as $GF\left\{ H \right\} = Nec\left\{ H \right\} + \left( \dag \right) \, \left( {Pos\left\{ H \right\} - Nec\left\{ H \right\}} \right) = \left( \dag \right)Pos\left\{ H \right\} + \left( {1 - \dag } \right)Nec\left\{ H \right\}$ (Xu & Zhou, 2011, 2013). In other words, general fuzzy measure is equal to the convex combination of Pos and Nec. The properties of the general fuzzy (GF) measure are presented as follows:

• $GF\left\{ \emptyset \right\} = 0, \, GF\left\{ \Psi \right\} = 1$

• $\forall \, H \, \in \, \Omega \left( \Psi \right) \, \Rightarrow { 0 } \le \, GF\left\{ H \right\} \, \le 1$

• $\forall \, H \, \in \, \Omega \left( \Psi \right),\dag \le 0.5 \, \Rightarrow { 0 } \le GF\left\{ H \right\} + GF\left\{ {H^{C} } \right\} \le 1$

• $\forall \,H\, \in \,\Omega \left( \Psi \right),\,\dag \ge 0.5 \Rightarrow 1 \le GF\left\{ H \right\} + GF\left\{ {H^{C} } \right\} \le 2$

• $\forall \, H, \, Q \, \in \, \Omega \left( \Psi \right),H \subseteq Q \, \Rightarrow \, GF\left\{ H \right\} \, \le \, GF\left\{ Q \right\}$

• $\forall \, H, \, Q \, \in \, \Omega \left( \Psi \right),\dag \ge 0.5 \, \Rightarrow \, GF\left\{ {H \cup Q} \right\} \, \le \, GF\left\{ H \right\} + GF\left\{ Q \right\}$

• $\forall \, H \, \in \, \Omega \left( \Psi \right) \, \Rightarrow \, Pos\left\{ H \right\} \ge GF\left\{ H \right\} \ge Nec\left\{ H \right\}$

The GF measure $\dag \, \left( {0 \le \dag \le 1} \right)$ is the optimistic-pessimistic parameter to determine the attitude of a DM. The GF measure of fuzzy events $\left\{ {\tilde{\alpha } \le \gamma } \right\}$, $\left\{ {\tilde{\alpha } \ge \gamma } \right\}$, $\left\{ {\tilde{\beta } \le \gamma } \right\}$ and $\left\{ {\tilde{\beta } \ge \gamma } \right\}$ are shown in Eqs. (39) to (42), respectively:

GF measure
$GF\left\{ {\tilde{\alpha } \le \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {0,\quad \qquad \quad \quad \quad \quad \quad if\,\alpha _{1} \ge \gamma ;} \\ {\dag \left( {\frac{{\gamma - \alpha _{1} }}{{\alpha _{2} - \alpha _{1} }}} \right),\quad \qquad \quad \,\,\,\,if\,\alpha _{1} \le \gamma \le \alpha _{2} ;} \\ {\dag + (1 - \dag )\left( {\frac{{\gamma - \alpha _{2} }}{{\alpha _{3} - \alpha _{2} }}} \right),\quad if\,\alpha _{2} \le \gamma \le \alpha _{3} ;} \\ {1,\quad \quad \,\quad \quad \quad \quad \quad \,\,\,if\,\alpha _{3} \le \gamma .} \\ \end{array} } \right.$	(39)
$GF\left\{ {\tilde{\alpha } \ge \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {1,\quad \quad \,\quad \quad \quad \quad \quad \quad if\,\alpha _{1} \ge \gamma ;} \\ {\dag + (1 - \dag )\left( {\frac{{\alpha _{2} - \gamma }}{{\alpha _{2} - \alpha _{1} }}} \right),\quad \,if\,\alpha _{1} \le \gamma \le \alpha _{2} ;} \\ {\dag \left( {\frac{{\alpha _{3} - \gamma }}{{\alpha _{3} - \alpha _{2} }}} \right),\quad \quad \quad \quad \,\,\,\,\,\,if\,\alpha _{2} \le \gamma \le \alpha _{3} ;} \\ {0,\quad \quad \quad \quad \quad \quad \quad \,\,\,\,\,if\,\alpha _{3} \le \gamma .} \\ \end{array} } \right.$	(40)
$GF\left\{ {\tilde{\beta } \le \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {0,\qquad \qquad \quad \quad \quad \quad if\,\beta _{1} \ge \gamma ;} \\ {\dag \left( {\frac{{\gamma - \beta _{1} }}{{\beta _{2} - \beta _{1} }}} \right),\quad \quad \qquad \,\,\,\,\,\,if\,\beta _{1} \le \gamma \le \beta _{2} ;} \\ {\dag ,\,\,\,\,\,\, \qquad \quad \quad \quad \quad \quad if\,\beta _{2} \le \gamma \le \beta _{3} ;} \\ {\dag + (1 - \dag )\left( {\frac{{\gamma - \beta _{3} }}{{\beta _{4} - \beta _{3} }}} \right),\quad if\,\beta _{3} \le \gamma \le \beta _{4} ;} \\ {1,\quad \,\,\,\,\, \quad \quad \quad \qquad \quad \,if\,\beta _{4} \le \gamma .} \\ \end{array} } \right.$	(41)
$GF\left\{ {\tilde{\beta } \ge \gamma } \right\} = \left\{ {\begin{array}{*{20}l} {1,\quad \quad \quad \quad \quad \quad \quad \quad \quad \,if\,\beta _{1} \ge \gamma ;} \hfill \\ {\dag + (1 - \dag )\left( {\frac{{\beta _{2} - \gamma }}{{\beta _{2} - \beta _{1} }}} \right),\quad \quad \,\,if\,\beta _{1} \le \gamma \le \beta _{2} ;} \hfill \\ {\dag ,\quad \quad \quad \quad \quad \quad \quad \quad \quad if\,\beta _{2} \le \gamma \le \beta _{3} ;} \hfill \\ {\dag \left( {\frac{{\beta _{4} - \gamma }}{{\beta _{4} - \beta _{3} }}} \right),\,\quad \quad \quad \quad \quad \,\,\,\,\, if\,\beta _{3} \le \gamma \le \beta _{4} ;} \hfill \\ {0,\quad \quad \quad \quad \quad \quad \quad \quad \quad if\,\beta _{4} \le \gamma .} \hfill \\ \end{array} } \right.$	(42)

According to the GF measure and CCP, the deterministic counterparts and equivalent crisp ones of fuzzy chance constraints under desired confidence level $\xi$ for both conditions of $\xi$ greater or less than $\dag$, are presented in Eqs. (43) to (46) as follows:

GF measure
$GF\left\{ {\tilde{\alpha } \le \gamma } \right\} \ge \xi \Leftrightarrow \left\{ {\begin{array}{*{20}l} {\left( {\frac{{\dag - \xi }}{\dag }} \right)\alpha _{1} + \left( {\frac{\xi }{\dag }} \right)\,\alpha _{2} \le \gamma ,\,\,\quad \quad \quad \quad if\,\xi \le \dag ;} \\ {\left( {\frac{{1 - \xi }}{{1 - \dag }}} \right)\,\alpha _{2} + \left( {\frac{{\xi - \dag }}{{1 - \dag }}} \right)\,\alpha _{3} \le \gamma ,\qquad \quad \,\,if\,\xi > \dag .} \\ \end{array} } \right.$	(43)
$GF\left\{ {\tilde{\alpha } \ge \gamma } \right\} \ge \xi \Leftrightarrow \left\{ {\begin{array}{*{20}l} {\left( {\frac{\xi }{\dag }} \right)\,\alpha _{2} + \left( {\frac{{\dag - \xi }}{\dag }} \right)\,\alpha _{3} \ge \gamma ,\quad \quad \quad \quad if\,\xi \le \dag ;} \\ {\left( {\frac{{\xi - \dag }}{{1 - \dag }}} \right)\,\alpha _{1} + \left( {\frac{{1 - \xi }}{{1 - \dag }}} \right)\,\alpha _{2} \ge \gamma ,\,\,\,\quad \quad \,\,\,if\,\xi > \dag .} \\ \end{array} } \right.$	(44)
$GF\left\{ {\tilde{\beta } \le \gamma } \right\} \ge \xi \Leftrightarrow \left\{ {\begin{array}{*{20}l} {\left( {\frac{{\dag - \xi }}{\dag }} \right)\,\beta _{1} + \left( {\frac{\xi }{\dag }} \right)\,\beta _{2} \le \gamma ,\quad \,\, \quad \quad \quad if\,\xi \le \dag ;} \\ {\left( {\frac{{1 - \xi }}{{1 - \dag }}} \right)\,\beta _{3} + \left( {\frac{{\xi - \dag }}{{1 - \dag }}} \right)\,\beta _{4} \le \gamma ,\quad \qquad \,\,if\,\xi > \dag .} \\ \end{array} } \right.$	(45)
$GF\left\{ {\tilde{\beta } \le \gamma } \right\} \ge \xi \Leftrightarrow \left\{ {\begin{array}{*{20}l} {\left( {\frac{\xi }{\dag }} \right)\,\beta _{3} + \left( {\frac{{\dag - \xi }}{\dag }} \right)\,\beta _{4} \ge \gamma ,\quad \quad \quad \quad if\,\xi \le \dag ;} \\ {\left( {\frac{{\xi - \dag }}{{1 - \dag }}} \right)\,\beta _{1} + \left( {\frac{{1 - \xi }}{{1 - \dag }}} \right)\,\beta _{2} \ge \gamma ,\qquad \quad if\,\xi > \dag .} \\ \end{array} } \right.$	(46)

It should be noted that in special cases, if the $\dag$ is set equal to 1, 0 and 0.5, the GF measure is converted to Pos, Nec and Cr measures, respectively (Xu & Zhou, 2013). The main characteristics of Pos, Nec, Cr and GF measures as well as FCCDEA models can be summarized in Fig. 4:

Fig. 4

The attitude of fuzzy measures

As it can be seen in Fig. 4, in the GF measure only by setting $\dag$, the desired attitude of DM can be achieved. As a result, in recent years, the popularity and applicability of GF measure is increasing among researchers and it is wieldy used in real-world problems under fuzzy environment.

4 Fuzzy chance-constrained data envelopment analysis (FCCDEA)

In this section, fuzzy chance-constrained DEA models are proposed which are based on possibility, necessity, credibility and general fuzzy approaches. It is noteworthy that the FCCDEA models will be presented based on the basic DEA model, i.e., CCR (M-F & I-O) model. Moreover, with respect to the generality of trapezoidal fuzzy number, data uncertainty is intended to be in all inputs and outputs under trapezoidal distribution $\tilde{x} = \left( {x^{{(1)}} , \, x^{{(2)}} , \, x^{{(3)}} , \, x^{{(4)}} } \right) \, x^{{(1)}} < x^{{(2)}} < x^{{(3)}} < x^{{(4)}}$ and $\tilde{y} = \left( {y^{{(1)}} , \, y^{{(2)}} , \, y^{{(3)}} , \, y^{{(4)}} } \right) \, y^{{(1)}} < y^{{(2)}} < y^{{(3)}} < y^{{(4)}}$. Accordingly, in the first step, to deal with the uncertainty of inputs and outputs, Model (1) is converted to Model (47) as follows:

Uncertain DEA
${\text{Max}}\quad \Delta$	(47)
${\text{S.t.}}\quad \,\sum\limits_{{r = 1}}^{s} {\tilde{y}_{{ro}} u_{r} } \ge \Delta$
$\quad \quad \,\,\sum\limits_{{i = 1}}^{m} {\tilde{x}_{{io}} v_{i} } \le 1$
$\quad \quad \,\,\sum\limits_{{r = 1}}^{s} {\tilde{y}_{{rj}} u_{r} } - \sum\limits_{{i = 1}}^{m} {\tilde{x}_{{ij}} v_{i} } \le 0,\quad \forall j$
$\quad \quad \,\,v_{i} , \, u_{r} \ge 0,\quad \forall i,r$

The optimal solution of Model (47) is equal to Model (1) (for more details see Peykani et al., 2018a, b). Then, in the second step, in order to deal with uncertainty of fuzzy chance constraints in uncertain DEA model and convert them to their equivalent crisp values, suitable fuzzy measure and chance-constrained programming in form of FCCP can be used as follows:

FCCDEA
${\text{Max}}\quad \Delta$	(48)
${\text{S.t.}}\quad \mathop {Measure}\limits_{{\left( {Pos, \, Nec, \, Cr, \, GF} \right)}} \, \left\{ {\sum\limits_{{r = 1}}^{s} {\tilde{y}_{{ro}} u_{r} } \ge \Delta } \right\} \ge \, \xi$
$\quad \,\,\,\,\,\mathop {Measure}\limits_{{\left( {Pos, \, Nec, \, Cr, \, GF} \right)}} \, \left\{ {\sum\limits_{{i = 1}}^{m} {\tilde{x}_{{io}} v_{i} } \le 1} \right\} \ge \, \xi$
$\quad \,\,\,\,\,\mathop {Measure}\limits_{{\left( {Pos, \, Nec, \, Cr, \, GF} \right)}} \, \left\{ {\sum\limits_{{r = 1}}^{s} {\tilde{y}_{{rj}} u_{r} } - \sum\limits_{{i = 1}}^{m} {\tilde{x}_{{ij}} v_{i} } \le 0} \right\} \ge \, \xi ,\quad \forall j$
$\quad \,\,\,\,\,v_{i} , \, u_{r} \ge 0,\quad \forall i,r$

4.1 Possibility-based FCCDEA (PFCCDEA)

According to the Pos approach and using Eqs. (21) and (22), the PFCCDEA model is proposed as Model (49):

PFCCDEA
${\text{Max}}\quad \Delta _{{ \, {\text{POS}}}}$	(49)
${\text{S.t.}}\quad \,\,\sum\limits_{{r = 1}}^{s} {\left( {\left( \xi \right)y_{{ro}}^{{(3)}} + \left( {1 - \xi } \right)y_{{ro}}^{{(4)}} } \right)u_{r} } \ge \Delta _{{ \, {\text{POS}}}}$
$\quad \quad \,\,\,\sum\limits_{{i = 1}}^{m} {\left( {\left( {1 - \xi } \right)x_{{io}}^{{(1)}} + \left( \xi \right)x_{{io}}^{{(2)}} } \right)v_{i} } \le 1$
$\quad \quad \,\,\,\sum\limits_{{r = 1}}^{s} {\left( {\left( {1 -\xi } \right)y_{{rj}}^{{(1)}} + \left( \xi \right)y_{{rj}}^{{(2)}} } \right)u_{r} } - \sum\limits_{{i = 1}}^{m} {\left( {\left( \xi \right)x_{{ij}}^{{(3)}} + \left( {1 - \xi } \right)x_{{ij}}^{{(4)}} } \right)v_{i} } \le 0,\quad \forall j$
$\quad \quad \,\,\,v_{i} , \, u_{r} \ge 0,\quad \forall i,r$

4.2 Necessity-based FCCDEA (NFCCDEA)

According to the Nec approach and using Eqs. (29) and (30), the NFCCDEA model is proposed as Model (50):

NFCCDEA
${\text{Max}}\quad \Delta _{{ \, {\text{NEC}}}}$	(50)
${\text{S.t.}}\quad \,\,\sum\limits_{{r = 1}}^{s} {\left( {\left( \xi \right)y_{{ro}}^{{(1)}} + \left( {1 - \xi } \right)y_{{ro}}^{{(2)}} } \right)u_{r} } \ge \Delta _{{ \, {\text{NEC}}}}$
$\quad \quad \,\,\,\sum\limits_{{i = 1}}^{m} {\left( {\left( {1 - \xi } \right)x_{{io}}^{{(3)}} + \left( \xi \right)x_{{io}}^{{(4)}} } \right)v_{i} } \le 1$
$\quad \quad \,\,\,\sum\limits_{{r = 1}}^{s} {\left( {\left( {1 -\xi } \right)y_{{rj}}^{{(3)}} + \left( \xi \right)y_{{rj}}^{{(4)}} } \right)u_{r} } - \sum\limits_{{i = 1}}^{m} {\left( {\left( \xi \right)x_{{ij}}^{{(1)}} + \left( {1 - \xi } \right)x_{{ij}}^{{(2)}} } \right)v_{i} } \le 0,\quad \forall j$
$\quad \quad \,\,\,v_{i} , \, u_{r} \ge 0,\quad \forall i,r$

4.3 Credibility-based FCCDEA (CFCCDEA)

According to the Cr approach and using Eqs. (37) and (38), the CFCCDEA model is proposed as Model (51). It is noteworthy that that in the Cr approach, an equivalent crisp of fuzzy chance constraints for the $\xi$ greater or less than 0.5, is different. As a result, a binary variable $\Upsilon$ and a sufficient big number ${\rm M}$ are employed in Model (51), for the linearization of incompatible constraints.

CFCCDEA
${\text{Max}}\quad \Delta _{{ \, {\text{CR}}}}$	(51)
${\text{S.t.}}\quad\,\, \sum\limits_{{r = 1}}^{s} {\left( {\left( {2\xi } \right)y_{{ro}}^{{(3)}} + \left( {1 - 2\xi } \right)y_{{ro}}^{{(4)}} } \right)u_{r} } \ge \Delta _{{\rm {CR}}} - {\rm M}\Upsilon$
$\quad \quad \,\,\,\sum\limits_{{r = 1}}^{s} {\left( {\left( {2\xi - 1} \right)y_{{ro}}^{{(1)}} + \left( {2 - 2\xi } \right)y_{{ro}}^{{(2)}} } \right)u_{r} } \ge \Delta _{{\rm {CR}}} - {\rm M}\left( {1 - \Upsilon } \right)$
$\quad \quad \,\,\sum\limits_{{i = 1}}^{m} {\left( {\left( {1 - 2\xi } \right)x_{{io}}^{{(1)}} + \left( {2\xi } \right)x_{{io}}^{{(2)}} } \right)v_{i} } \le 1 + {\rm M} \, \Upsilon$
$\quad \quad \,\,\sum\limits_{{i = 1}}^{m} {\left( {\left( {2 - 2\xi } \right)x_{{io}}^{{(3)}} + \left( {2\xi - 1} \right)x_{{io}}^{{(4)}} } \right)v_{i} } \le 1{ + }{\rm M} \, \left( {1 - \Upsilon } \right)$
$\quad \quad \,\,\sum\limits_{{r = 1}}^{s} {\left( {\left( {1 - 2\xi } \right)y_{{rj}}^{{(1)}} + \left( {2\xi } \right)y_{{rj}}^{{(2)}} } \right)u_{r} } - \sum\limits_{{i = 1}}^{m} {\left( {\left( {2\xi } \right)x_{{ij}}^{{(3)}} + \left( {1 - 2\xi } \right)x_{{ij}}^{{(4)}} } \right)v_{i} } \le {\rm M}\Upsilon ,\quad \forall j$
$\quad \quad \,\,\sum\limits_{{r = 1}}^{s} {\left( {\left( {2 - 2\xi } \right)y_{{rj}}^{{(3)}} + \left( {2\xi - 1} \right)y_{{rj}}^{{(4)}} } \right)u_{r} } - \sum\limits_{{i = 1}}^{m} {\left( {\left( {2\xi - 1} \right)x_{{ij}}^{{(1)}} + \left( {2 - 2\xi } \right)x_{{ij}}^{{(2)}} } \right)v_{i} } \le {\rm M}\,\left( {1 - \Upsilon } \right),\quad \forall j$
$\quad \quad \,\,\xi \le 0.5 + {\rm M} \, \Upsilon$
$\quad \quad \,\,\xi > 0.5 - {\rm M} \, \left( {1 -\Upsilon } \right)$
$\quad \quad \,\,\Upsilon \, \in \left\{ {0,1} \right\}$
$\quad \quad \,\,v_{i} , \, u_{r} \ge 0,\quad \forall i,r$

4.4 General fuzzy-based FCCDEA (GFCCDEA)

According to the GF approach and using Eqs. (45) and (46), the GFCCDEA model is proposed as Model (52):

GFCCDEA
${\text{Max}}\quad \Delta _{{ \, {\text{GF}}}}$	(52)
${\text{S.t.}}\quad \,\,\sum\limits_{{r = 1}}^{s} {\left( {\left( {\frac{\xi }{\dag }} \right)y_{{ro}}^{{(3)}} + \left( {\frac{{\dag - \xi }}{\dag }} \right)y_{{ro}}^{{(4)}} } \right)u_{r} } \ge \Delta _{{ \, {\text{GF}}}} - {\rm M} \, \Upsilon$
$\quad \quad \,\,\sum\limits_{{r = 1}}^{s} {\left( {\left( {\frac{{\xi - \dag }}{{1 - \dag }}} \right)y_{{ro}}^{{(1)}} + \left( {\frac{{1 - \xi }}{{1 - \dag }}} \right)y_{{ro}}^{{(2)}} } \right)u_{r} } \ge \Delta _{{ \, {\text{GF}}}} - {\rm M} \, \left( {1 - \Upsilon } \right)$
$\quad \quad \,\,\sum\limits_{{i = 1}}^{m} {\left( {\left( {\frac{{\dag - \xi }}{\dag }} \right)x_{{io}}^{{(1)}} + \left( {\frac{\xi }{\dag }} \right)x_{{io}}^{{(2)}} } \right)v_{i} } \le 1 + {\rm M} \, \Upsilon$
$\quad \quad \,\,\sum\limits_{{i = 1}}^{m} {\left( {\left( {\frac{{1 - \xi }}{{1 - \dag }}} \right)x_{{io}}^{{(3)}} + \left( {\frac{{\xi - \dag }}{{1 - \dag }}} \right)x_{{io}}^{{(4)}} } \right)v_{i} } \le 1{ + }{\rm M} \, \left( {1 - \Upsilon } \right)$
$\quad \quad \,\,\sum\limits_{{r = 1}}^{s} {\left( {\left( {\frac{{\dag - \xi }}{\dag }} \right)y_{{rj}}^{{(1)}} + \left( {\frac{\xi }{\dag }} \right)y_{{rj}}^{{(2)}} } \right)u_{r} } - \sum\limits_{{i = 1}}^{m} {\left( {\left( {\frac{\xi }{\dag }} \right)x_{{ij}}^{{(3)}} + \left( {\frac{{\dag - \xi }}{\dag }} \right)x_{{ij}}^{{(4)}} } \right)v_{i} } \le {\rm M} \, \Upsilon ,\quad \forall j$
$\quad \quad \,\,\sum\limits_{{r = 1}}^{s} {\left( {\left( {\frac{{1 - \xi }}{{1 - \dag }}} \right)y_{{rj}}^{{(3)}} + \left( {\frac{{\xi - \dag }}{{1 - \dag }}} \right)y_{{rj}}^{{(4)}} } \right)u_{r} } - \sum\limits_{{i = 1}}^{m} {\left( {\left( {\frac{{\xi - \dag }}{{1 - \dag }}} \right)x_{{ij}}^{{(1)}} + \left( {\frac{{1 - \xi }}{{1 - \dag }}} \right)x_{{ij}}^{{(2)}} } \right)v_{i} } \le {\rm M} \, \left( {1 - \Upsilon } \right),\quad \forall j$
$\quad \quad \,\,\xi \le \dag + {\rm M} \, \Upsilon$
$\quad \quad \,\,\xi > \dag - {\rm M} \, \left( {1 -\Upsilon } \right)$
$\quad \quad \,\,\Upsilon \, \in \left\{ {0,1} \right\}$
$\quad \quad \,\,v_{i} , \, u_{r} \ge 0,\quad \forall i,r$

Similar to CFCCDEA model, by applying a binary variable $\Upsilon$ and a sufficient big number M, the linearization of incompatible constraints for the $\xi$ greater or less $\dag$ than are made in Model (52). In the GFCCDEA model only by setting $\dag$, the desired attitude of DM can be achieved. In special cases, if the optimistic-pessimistic parameter $\dag$ is set equal to 1, 0 and 0.5, GFCCDEA model can be converted to PFCCDEA, NFCCDEA, and CFCCDEA models, respectively (for more detail see Peykani et al., 2019a, b, c). Also, for the optimistic-pessimistic parameter $\dag$, efficiency scores of DMUs decrease while the confidence level $\xi$ increases. Additionally, as shown in Fig. 4, by increasing optimistic-pessimistic parameter $\dag$, the attitudes of DM are changed from pessimistic to optimistic viewpoint in order to measure the chances of occurrence of fuzzy events.

The efficiency scores of DMUs under crisp (certain) data are less than or equal to one. But in uncertain DEA especially FCCDEA model, this relation may be violated. As a result, by calculating the efficiency scores of DMUs for the same optimistic-pessimistic attitude, the DMUs can be classified under FCCDEA approach as follows:

• A DMU is ultra-efficient ($\Theta ^{{ + + }}$) if its efficiency scores $\Delta ^{*}$ for all confidence levels $\xi$ are greater than or equal to one.

• A DMU is marginal-efficient ($\Theta ^{ + }$) if its efficiency scores $\Delta ^{*}$ for some of confidence levels $\xi$are greater than or equal to one.

• A DMU is inefficient ($\Theta ^{ - }$) if its efficiency scores $\Delta ^{*}$ for all confidence levels $\xi$ are less than one.

At the end of this section, it is worthwhile to mention that fuzzy chance-constrained DEA models can be presented based on other basic DEA models and characteristics in a similar manner.

5 A Structured literature review of fuzzy chance-constrained DEA

In this section, a comprehensive and structured literature review of FCCDEA studies will be presented. Accordingly, a systematic and comprehensive search is done in different database including Web of Science (WoS), Scopus, and Google Scholar as well as popular publishers such as Elsevier, Springer, Wiley-Blackwell, Taylor & Francis, Sage, Wolters Kluwer, Emerald, Inderscience, and IEEE.

The search strategy of the paper is illustrated in Fig. 5. According to the Fig. 5, the aforementioned keywords were searched in “Title, Abstract, Keywords” of documents belonging to WoS, Scopus, and Google Scholar databases. Then, duplicate documents are eliminated and grey literature is excluded. Finally, 87 relevant researches were found in FCCDEA literature from 2000 to 2020.

Fig. 5

Research methodology and search strategy

5.1 Bibliometric analysis of FCCDEA literature

In the first step, the bibliometric information of fuzzy chance-constrained DEA Literature is presented in Table 1. It should be noted that in this section, the research code of each FCCDEA study is employed for reference in all tables.

Table 1 The fuzzy chance-constrained DEA studies

The statistical information of fuzzy chance-constrained DEA studies including the quantity of researches per year, the growing trend of FCCDEA field, and distribution of publication type, are presented in Fig. 6:

Fig. 6

Bibliometric Information of FCCDEA Literature (A) Distribution of Studies per Year, (B) Distribution of Publication Type

According to the Fig. 6, the FCCDEA studies have increased rapidly in the last decade and the growing trend is expected for literature of FCCDEA in the future. In order to examine the place of the FCCDEA field among journals, the most influential journals in the fuzzy chance-constrained DEA literature are introduced in Table 2:

Table 2 The top publishing journals contributing to the FCCDEA literature

As it can be seen in Table 2, numerous articles of FCCDEA literature have been published in top-tier journals, which this point indicates on the importance, applicability, and attractiveness of this area.

At the end of bibliometric analysis, statistics based on top contributing affiliations in FCCDEA literature is introduced. Accordingly, Fig. 7 presents the most influential countries/territories as well as organizations/institutions along-with their number of FCCDEA publications:

Fig. 7

Top contributing affiliations in FCCDEA literature. (A) Countries/Territories, (B) Organizations/Institutions

According to the Fig. 7, top 5 contributing countries in FCCDEA area are Iran, China, USA, Thailand, and Canada, respectively. Also, top 5 contributing university in FCCDEA field are Islamic Azad University (IAU), Iran University of Science and Technology (IUST), Hebei University, La Salle University, and Beihang University, respectively.

5.2 A Survey of features and applications of FCCDEA researches

In the second step, all 87 fuzzy chance-constrained DEA studies are examined according to their perspectives, number of DMUs, number of inputs and outputs, uncertainty type of data, the research objective, the research feature, and the research application which the results are introduced in Table 3:

Table 3 The features, objectives, and applications of FCCDEA studies

As is seen in Table 3, most of the research applies fuzzy chance-constrained DEA approach in real-world application and this point demonstrates the applicability of FCCDEA field. The analysis of applications in FCCDEA literature indicated that most researches address assessments in the fields of banking (9 researches), health care (7 researches), supply chain (7 researches), and financial market (5 researches) in order to performance measurement of DMUs under uncertainty environment. Moreover Fig. 8 shows the frequency analysis of data uncertainty type in FCCDEA literature:

Fig. 8

Distribution of data uncertainty type

It should be explained that the application of mixed uncertainty to demonstrate an uncertain parameter is becoming more and more popular among researchers.

5.3 Analysis of FCCDEA studies in terms of modeling

In the third step, fuzzy chance-constrained DEA studies are classified according to the type of FCCDEA models including basic DEA model, projection construction, form, orientation, RTS, the uncertain data, fuzzy measures, hybrid uncertain programming approaches and class of proposed FCCDEA model which are reported in Table 4. Moreover, the statistical information of FCCDEA models is presented in Fig. 9:

As can be seenin Table 4 and Fig. 9, most studies presented fuzzy chance-constrained DEA model based on input-oriented multiplier CCR (M-F & I-O) model. Also, the most commonly used uncertain measures in FCCDEA literature are possibility and credibility, respectively.

Table 4 The classification of FCCDEA models

Fig. 9

Statistical information of RDEA models. (A) Basic model, (B) Model type, (C) Model form, (D) Model orientation, (E) Model return to scale, (F) Uncertain data, (G) Hybrid uncertain programming approach, (H) FCCDEA model class, (I) Uncertain measure

6 Conclusions and future research directions

The integration of data envelopment analysis method and fuzzy chance-constrained programming in context of FCCDEA, is one of the applicable and effective approach that wieldy employed for performance measurement of DMUs under data ambiguity. Accordingly, this paper introduced a comprehensive literature review of fuzzy chance-constrained DEA. Moreover, all FCCDEA studies are analyzed and classified according to several aspects and factors such as bibliometric information, the features and objectives of the FCCDEA model, real-world application and case study, basic DEA model, characteristics of DEA modeling, type of uncertainty, and uncertain measures.

Now, pursuant to the classification, observations, and discussions of previous sections, the research fronts in FCCDEA field will be proposed to guide future researches. The following areas are suggested for future researches:

• Adjustable Fuzzy Data Envelopment Analysis (AFDEA) Presenting FCCDEA approach based on general fuzzy measure for handling all attitudes of DM only by setting an adjustable optimistic-pessimistic parameter (for more details see Xu & Zhou, 2011, 2013; Peykani et al., 2019a, b, c).

• Fuzzy Network Data Envelopment Analysis (FNDEA) Proposing fuzzy network chance-constrained DEA approach for performance assessment and ranking of homogeneous DMUs with network structure such as two-stage, series, parallel, and mixed (for more details seeKao & Hwang, 2008; Chen et al., 2009; Kao, 2014, 2017; Peykani et al., 2021).

• Robust Possibilistic Data Envelopment Analysis (RPDEA) Extending FCCDEA models based on robust possibilistic programming to endogenously adjust the confidence level of each fuzzy chance constraints (for more details see Pishvaee et al., 2012; Pishvaee & Khalaf, 2016; Peykani et al., 2018a, b).

• Z-Number Data Envelopment Analysis (ZNDEA) Introducing fuzzy chance-constrained DEA approach based on Z-number instead of classical fuzzy number in order to improve reliability of uncertain data (for more details see Zadeh, 2011; Azadeh & Kokabi, 2016; Mohtashami & Ghiasvand, 2020).

• Fuzzy Dynamic Data Envelopment Analysis (FDDEA) Dynamic efficiency evaluation of DMUs under fuzzy panel data using dynamic data envelopment analysis (DDEA), Malmquist productivity index (MPI), and window data envelopment analysis (WDEA) approaches (for more details see Färe & Grosskopf, 1992; Charnes et al., 1985a; Mariz et al., 2018).

In addition to the above suggestions, FCCDEA models can be proposed in the presence of negative data, undesirable factor, non-discretionary factor, dual-role factor. Finally, the most valuable suggestion and direction for future researches would be to employ existing or extended fuzzy chance-constrained DEA models in real-world problems and applications.