Parameter identification of chaotic systems using a shuffled backtracking search optimization algorithm

Abstract

An accurate mathematical model has a vital role in controlling and synchronization of chaotic systems. But generally in real-world problems, parameters are mixed with mismatches and distortions. This paper proposes two simple but effective estimation methods to detect the unknown parameters of chaotic models. These methods focus on improving the performance of a recently proposed evolutionary algorithm called backtracking search optimization algorithm (BSA). In this research firstly, a new operator to generate initial trial population is proposed. Then a group search ability is provided for the BSA by proposing a shuffled BSA (SBSA). Grouping population into several sets can provide a better exploration of search space, and an independent local search of each group increases exploitation ability of the BSA. Also new proposed operator to generate initial trial population, by providing a deep search, increases considerably the quality of solutions. The superiority of the proposed algorithms is investigated on parameter identification of 10 typical chaotic systems. Practical experiences and nonparametric analysis of obtained results show that both of the proposed ideas to improve performance of original BSA are very effective and robust so that the BSA by aforementioned ideas produces similar and promising results over repeated runs. A considerably better performance of proposed algorithms based on average of objective functions demonstrates that the proposed ideas can evolve robustness and consistence of BSA. A comparison of the proposed algorithms in this study with respect to other algorithms reported in the literature confirms a considerably better performance of proposed algorithms.

1 Introduction

Chaos is a common feature in nonlinear dynamical systems. Nonlinear systems which have chaos feature are highly sensitive to initial conditions so that a small change in initial conditions of dynamic system yields widely diverging outcomes. It causes an infinite number of unstable periodic motions, so behavior of nonlinear systems becomes unpredictable and complex to be analyzed. Chaotic behavior exists in many real-world systems and phenomena such as biological systems, for example chaotic behavior in the population growth or in epileptic brain seizures, ecological systems, for example chaotic model for hydrology, economic and financial systems, for example improving economic models, transportation and traffic systems, for example traffic forecasting, chemical reactions, for example peroxidase–oxidase reaction and electrical engineering, for example chaotic oscillators. However, all the aforementioned systems and phenomena are stochastic and even unpredictable, but they are actually deterministic in nature and they can be predicted and controllable by natural laws if mathematical models of them are successfully constructed.

The traditional trend of analyzing and understanding chaos has already evolved a new phase in investigation: controlling and utilizing chaos where detecting the unstable periodic orbits and estimating the unknown parameters of the chaos are of vital importance (Gao et al. 2013). So for controlling and synchronization of chaotic systems, a mathematical model is vital. Since such models have been applied in definite chaotic systems with predetermined system parameters, however, there generally exist parameter mismatches and distortions in real-world problems. Therefore, this topic has become popular among the researchers, and numerous scientific studies have been proposed to overcome this drawback by suggesting novel solution (Wang and Xu 2011).

Parameter estimation of chaotic systems can be modeled as a multidimensional optimization problem after defining an appropriate fitness function. Since in this problem, the structure of system model is known in advance, the optimization methods should optimize a fitness function which is a difference between output of the true system and the estimated model under the same inputs. By this modeling, a variety of optimization methods can be applied on it to extract its unknown parameters. This issue has been becoming topic of many researches during the past two decades (Konnur 2003; Park and Kwon 2005; Zaher 2008; Yu et al. 2009; Sun et al. 2009; Li et al. 2011). The original parameters of a chaotic system are not easy to estimate because of the unstable dynamic of the chaotic system. Meanwhile, it is very difficult for traditional mathematical methods to identify the true values of those parameters to achieve global optimization, since there are lots of local optima in the landscape of the goal function. Nowadays, the development of effective approaches for solving parameter estimation is still a hot topic with significance in both academic and engineering fields (Wang and Xu 2011).

Tendency of recent researches for parameter estimation of chaotic systems has been propelled to heuristic algorithms especially with stochastic search techniques such as evolutionary algorithms (EAs). The EAs have a prominent advantage over other types of numerical methods. They only require information about the objective function itself, which can be either explicit or implicit. Other accessory properties such as differentiability or continuity are not necessary. As such, they are more flexible in dealing with a wide spectrum of problems (Brest et al. 2006).

A wide variety of EAs are progressively being applied on parameter estimation of chaotic systems in recent years such as differential evolution (DE) (Tang et al. 2012; Gao et al. 2014), particle swarm optimization (PSO) (Yuan and Yang 2012; Chen et al. 2014), biogeography-based optimization (BBO) (Wang and Xu 2011; Lin 2014) and artificial bee colony (Gao et al. 2012; Hu et al. 2015).

One of the very recently proposed population-based EAs is the backtracking search optimization algorithm (BSA) (Civicioglu 2013). Civicioglu (2013) in an attempt to develop a simpler and more effective search algorithm and to mitigate the effects of problems that are frequently encountered in EAs, such as excessive sensitivity to control parameters, premature convergence, and slow computation, proposed the BSA. It has only a single control parameter which the BSA is not oversensitive to the initial value of this parameter. By employing a memory, this algorithm allows to take advantage of experiences gained from previous generations when it generates a trial preparation. After Civicioglu (2013), only one another improved version of this algorithm was proposed in different literature. Lin (2015) proposed an opposition-based version of BSA for parameter identification of hyperchaotic systems. This new version of BSA is trying to increase the diversity of initial population and to accelerate the convergence speed. The current research is an attempt to provide a grouping and parallel search ability for the BSA algorithm. This idea was borrowed from shuffled frog leaping algorithm (SFLA) (Eusuff and Lansey 2003). Based on this idea, a population is divided into several groups and then each of these groups tries to evolve itself using a BSA evolutionary process. After a predefined repetition of this evolutionary process, all groups are shuffled together and new groups are made and this process is repeated again. Grouping population into several sets can provide a better exploration of search space, and an independent local search increases exploitation ability of BSA. Also a possibility of rebuilding groups with new members causes participating each of members in previous experience of all other members. Another concept to evolve exploitation ability of BSA in this research is to propose a new operator to generate initial trial population. This new operator provides a deep search around found promising areas.

The rest of the paper is organized as follows. In the next section, chaotic systems and dynamic equations of employed typical systems are described. In Sect. 3, the BSA is briefly presented. In Sect. 4, the utilized strategy to improve the BSA is discussed. The simulation results are presented and analyzed in Sect. 5. Section 6 concludes the paper.

2 Chaotic systems

In this section firstly, the chaotic systems are briefly described. Then problem of parameter identification of chaotic systems is formulated as an optimization problem. In the last part of this section, dynamic equations of 10 typical chaotic systems are described.

2.1 Chaotic system description and problem formulation

Generally, chaotic systems are nonlinear deterministic systems. Those display complex, noisy-like and unpredictable behaviors. The sensitive dependency on both initial conditions and parameter variations is a prominent characteristic of chaotic behavior. A general form for chaotic systems is given as follows (Jiang et al. 2015):

$$\begin{aligned} \dot{x}(t)=f(x(t), x(t-\tau ), x_0 , \theta ) \end{aligned}$$

(1)

where $x(t)=[x_1 (t) , x_2 (t),\ldots ,x_n (t) ]^\mathrm{T} \in R^{n}$ denotes the state vectors of chaotic system, $\dot{x}(t)$ denotes the derivative of the state vector x(t), $x(t-\tau )$ denotes delay vector ($\tau$ is the delay), $x_0 =[x_{01} , x_{02},\ldots ,x_{0n} ]^\mathrm{T}$ is the initial vector, and $\theta =\left[ {\theta _1, \theta _2,\ldots ,\theta _m} \right] ^\mathrm{T}\in R^{m}$ are unknown parameters, and suppose the form of nonlinear vector function $f: R^{n}\times R^{m}\rightarrow R^{n}$ is known and f is continuously differentiable.

Since the structure of system model is known in advance, the estimated system can be depicted as follows:

$$\begin{aligned} \dot{\hat{{x}}}(t)=f(\hat{{x}}(t), \hat{{x}}(t-\hat{{\tau }}), x_0 , \hat{{\theta }}) \end{aligned}$$

(2)

where $\hat{{x}}(t)=[\hat{{x}}_1 (t) , \hat{{x}}_2 (t),\ldots ,\hat{{x}}_n (t) ]^\mathrm{T} \in R^{n}$ denotes the state vectors, $\hat{{\tau }}$ and $\hat{{\theta }}=\left[ {\hat{{\theta }}_1 ,\hat{{\theta }}_2,\ldots ,\hat{{\theta }}_m } \right] ^\mathrm{T}\in R^{m}$ are the identification of unknown parameter $\tau$ and $\theta$, respectively.

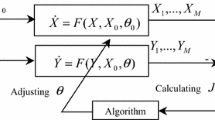
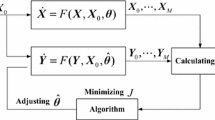
The basic principle of parameter estimation is to compare the output of the true system and the estimated model under the same inputs and to adjust the parameters $\theta =\left[ {\theta _1 ,\theta _2,\ldots ,\theta _m } \right] ^\mathrm{T}\in R^{m}$ for minimizing a predefined error function for a number of given samples, e.g., the following sum square error (SSE) function.

$$\begin{aligned} \hbox {SSE}=\sum _{k=1}^L {\left\| {x(k)-\hat{{x}}(k)} \right\| ^{2}} \end{aligned}$$

(3)

where $\hat{{x}}(k)$ is the output of the model with estimated parameters, L denotes the total number of sampling points, and $\left\| { . } \right\|$ represents the Euclidean norm of vectors. So in an overall view, the problem of parameters identification for a chaotic system to be solved using an optimization method can be formulated as follows:

$$\begin{aligned}&{\min }\,J=\sum _{k=1}^L {\left\| {x(k)-\hat{{x}}(k)} \right\| ^{2}}\nonumber \\&\hbox {subject\,to} \,\left\{ {\begin{array}{l} \dot{x}(t)=f(x(t), x(t-\tau ), x_0 , \theta ) \\ \dot{\hat{{x}}}(t)=f(\hat{{x}}(t), \hat{{x}}(t-\hat{{\tau }}), x_0 , \hat{{\theta }}) \\ L_i \le \hat{{\theta }}_i \le U_i i=1,\ldots , m \\ \hat{{\tau }}_{{\min }} \le \hat{{\tau }}\le \hat{{\tau }}_{{\max }} \\ \end{array}} \right. \end{aligned}$$

(4)

$(\hat{{\theta }}, \hat{{\tau }})$ is decision vector, and the optimization goal is to minimize J. $L_i$ and $U_i$ correspond to the upper and lower boundary of $\hat{{\theta }}_i$, respectively. Also $\hat{{\tau }}_{{\min }}$ and $\hat{{\tau }}_{{\max }}$ are the upper and lower boundary of $\hat{{\tau }}$, respectively (Jiang et al. 2015).

The parameter estimation of chaotic systems is not easy because of the unstable dynamic of the chaotic systems. Moreover, due to multiple variables in the problem and multiple local search optima in the landscape of the objective functions, traditional optimization can easily trap in local optima. Nowadays, the development of effective approaches for solving parameter identification is still an active research subject with significance in both academic and engineering fields (Wang and Xu 2011). So this research proposes two new versions of BSA for efficiently solving this problem.

2.2 Dynamic equations of typical chaotic systems

This section describes dynamic equations of 10 typical chaotic systems. To the best our knowledge, most of the papers applied on parameter identification of chaotic systems employed at most three systems to investigate their proposed methods. This research to provide a better investigation about performance of proposed algorithms uses 10 typical chaotic systems. Also since characteristics of all systems such as number of unknown parameters, dynamic range of parameters, initial conditions and number of samples are definite, so theses sets of typical chaotic systems can be used as a criterion to investigate and compare performance of different algorithms in the future researches.

Example 1

Lorenz chaotic system.

$$\begin{aligned} \dot{x}_1 (t)= & {} \theta _1 (x_2 (t)-x_1 (t)) \nonumber \\ \dot{x}_2 (t)= & {} \theta _2 x_1 (t)-x_2 (t)-x_1 (t)x_3 (t) \nonumber \\ \dot{x}_3 (t)= & {} x_1 (t)x_2 (t)+\theta _3 x_3 (t) \nonumber \\ x_1 (0)= & {} {0.1}, x_2 (0)={0.}1 x_3 (0)={0.1} \nonumber \\ t= & {} 1,2,\ldots , 100 \end{aligned}$$

(5)

where the parameters to be estimated are $\left[ {\theta _1 ,\theta _2, \theta _3 } \right]$. In this example, the real system parameters are assumed to be $\left[ {\theta _1, \theta _2, \theta _3 } \right] =\left[ {{10,28,2.6667}} \right]$. In addition, the searching ranges are set as follows: $5\le \theta _1 \le 15$, $20\le \theta _2 \le 30$ and $0.1\le \theta _3 \le 10$.

Example 2

Chen chaotic system.

$$\begin{aligned} \dot{x}_1 (t)= & {} \theta _1 (x_2 (t)-x_1 (t)) \nonumber \\ \dot{x}_2 (t)= & {} \theta _4 x_1 (t)-x_1 (t)x_3 (t)+\theta _3 x_2 (t) \nonumber \\ \dot{x}_3 (t)= & {} x_1 (t)x_2 (t)-\theta _2 x_3 (t) \nonumber \\ x_1 (0)= & {} -9, x_2 (0)=-5, x_3 (0)=14 \nonumber \\ t= & {} 1,2,\ldots , 100 \end{aligned}$$

(6)

where the parameters to be estimated are $\left[ {\theta _1, \theta _2, \theta _3, \theta _4 } \right]$. In this example, the real system parameters are assumed to be $\left[ {\theta _1 ,\theta _2, \theta _3, \theta _4 } \right] =\left[ {{35}, {3}, {28}, {-7}} \right]$. In addition, the searching ranges are set as follows: $30\le \theta _1 \le 40$, $0.1\le \theta _2 \le 10$, $20\le \theta _3 \le 30$ and $-10\le \theta _4 \le -0.1$.

Example 3

Rossler chaotic system.

$$\begin{aligned} \dot{x}_1 (t)= & {} -x_2 (t)-x_3 (t) \nonumber \\ \dot{x}_2 (t)= & {} x_1 (t)+\theta _1 x_2 (t) \nonumber \\ \dot{x}_3 (t)= & {} \theta _2 +x_1 (t)x_3 (t)-\theta _3 x_3 (t) \nonumber \\ x_1 (0)= & {} {0.5}, x_2 (0)={1.5}, x_3 (0)={0.1} \nonumber \\ t= & {} 1,2,\ldots , 100 \end{aligned}$$

(7)

where the parameters to be estimated are $\left[ {\theta _1, \theta _2, \theta _3 } \right]$. In this example, the real system parameters are assumed to be $\left[ {\theta _1, \theta _2, \theta _3} \right] =\left[ {{0.5}, {0.2}, {10}} \right]$. In addition, the searching ranges are set as follows: $0.1\le \theta _1 \le 1$, $0.1\le \theta _2 \le 1$ and $5\le \theta _3 \le 15$.

Example 4

Arneodo chaotic system.

$$\begin{aligned} \dot{x}_1 (t)= & {} x_2 (t) \nonumber \\ \dot{x}_2 (t)= & {} x_3 (t) \nonumber \\ \dot{x}_3 (t)= & {} -\theta _1 x_1 (t)-\theta _2 x_2 (t)-\theta _3 x_3 (t)+\theta _4 x_1^3 (t) \nonumber \\ x_1 (0)= & {} -0.2, x_2 (0)=0.5, x_3 (0)=0.2 \nonumber \\ t= & {} 1,2,\ldots , 100 \end{aligned}$$

(8)

where the parameters to be estimated are $\left[ {\theta _1, \theta _2, \theta _3, \theta _4} \right]$. In this example, the real system parameters are assumed to be $\left[ {\theta _1, \theta _2, \theta _3, \theta _4} \right] =\left[ {{-5.5}, {3.5}, {0.8}, {-1.0}} \right]$. In addition, the searching ranges are set as follows: $-6\le \theta _1 \le -5$, $2\le \theta _2 \le 5$, $0.1\le \theta _3 \le 1$ and $-1.5\le \theta _4 \le -0.5$.

Example 5

Duffing chaotic system.

$$\begin{aligned} \dot{x}_1 (t)= & {} x_2 (t) \nonumber \\ \dot{x}_2 (t)= & {} x_1 (t)-x_1^3 (t)-\theta _1 x_2 (t)+\theta _2 \cos (\theta _3 t) \nonumber \\ x_1 (0)= & {} {0.21}, x_2 (0)={0.31} \nonumber \\ t= & {} 1,2,\ldots , 100 \end{aligned}$$

(9)

where the parameters to be estimated are $\left[ {\theta _1, \theta _2, \theta _3} \right]$. In this example, the real system parameters are assumed to be $\left[ {\theta _1, \theta _2, \theta _3} \right] =\left[ {{0.15}, {0.31}, {1}} \right]$. In addition, the searching ranges are set as follows: $0.1\le \theta _1 \le 1$, $0.1\le \theta _2 \le 1$ and $0.1\le \theta _3 \le 2$.

Example 6

Genesio-Tesi chaotic system.

$$\begin{aligned} \dot{x}_1 (t)= & {} x_2 (t) \nonumber \\ \dot{x}_2 (t)= & {} x_3 (t) \nonumber \\ \dot{x}_3 (t)= & {} -\theta _1 x_1 (t)-\theta _2 x_2 (t)-\theta _3 x_3 (t)+\theta _4 x_1^2 (t) \nonumber \\ x_1 (0)= & {} -0.1, x_2 (0)=0.5, x_3 (0)=0.2 \nonumber \\ t= & {} 1,2,\ldots , 100 \end{aligned}$$

(10)

where the parameters to be estimated are $\left[ {\theta _1, \theta _2, \theta _3, \theta _4} \right]$. In this example, the real system parameters are assumed to be $\left[ {\theta _1, \theta _2, \theta _3, \theta _4} \right] =\left[ {{1.1} , {1.1} , {0.45} , {1.0}} \right]$. In addition, the searching ranges are set as follows: $1\le \theta _1 \le 2$, $1\le \theta _2 \le 2$, $0.1\le \theta _3 \le 1$ and $0.1\le \theta _4 \le 1.5$.

Example 7

Financial chaotic system.

$$\begin{aligned} \dot{x}_1 (t)= & {} x_3 (t)+x_1 (t)(x_2 (t)-\theta _1 ) \nonumber \\ \dot{x}_2 (t)= & {} 1-\theta _2 x_2 (t)-x_1^2 (t) \nonumber \\ \dot{x}_3 (t)= & {} -x_1 (t)-\theta _3 x_3 (t) \nonumber \\ x_1 (0)= & {} {2}, x_2 (0)={-1}, x_3 (0)={1} \nonumber \\ t= & {} 1,2,\ldots , 100 \end{aligned}$$

(11)

where the parameters to be estimated are $\left[ {\theta _1, \theta _2, \theta _3} \right]$. In this example, the real system parameters are assumed to be $\left[ {\theta _1, \theta _2, \theta _3} \right] =\left[ {{1} , {0.1}, {1}} \right]$. In addition, the searching ranges are set as follows: $0.5\le \theta _1 \le 1.5$, $0.01\le \theta _2 \le 1$ and $0.5\le \theta _3 \le 1.5$.

Example 8

Lu chaotic system.

$$\begin{aligned} \dot{x}_1 (t)= & {} \theta _1 (x_2 (t)-x_1 (t)) \nonumber \\ \dot{x}_2 (t)= & {} x_2 (t)-x_1^2 (t) \nonumber \\ \dot{x}_3 (t)= & {} x_1 (t)x_2 (t)-\theta _2 x_3 (t) \nonumber \\ x_1 (0)= & {} 0.2, x_2 (0)={0.5}, x_3 (0)={0.3} \nonumber \\ t= & {} 1,2,\ldots , 100 \end{aligned}$$

(12)

where the parameters to be estimated are $\left[ {\theta _1, \theta _2, \theta _3} \right]$. In this example, the real system parameters are assumed to be $\left[ {\theta _1, \theta _2, \theta _3} \right] =\left[ {36 , {3} , 20} \right]$. In addition, the searching ranges are set as follows: $30\le \theta _1 \le 40$, $0.1\le \theta _2 \le 10$ and $15\le \theta _3 \le 25$.

Example 9

Chuas oscillator chaotic system.

$$\begin{aligned} \dot{x}_1 (t)= & {} \theta _1 (x_2 (t)-x_1 (t)+\theta _4 x_1 (t)-W(x_4 (t))x_1 (t)) \nonumber \\ \dot{x}_2 (t)= & {} x_1 (t)-x_2 (t)+x_3 (t) \nonumber \\ \dot{x}_3 (t)= & {} -\theta _2 x_2 (t)-\theta _3 x_3 (t) \nonumber \\ \dot{x}_4 (t)= & {} x_1 (t) \nonumber \\ W(x_1 (t))= & {} \left\{ {\begin{array}{l} \theta _5 : \left| {x_1 (t)} \right| <1 \\ \theta _6 : \left| {x_1 (t)} \right| >1 \\ \end{array}} \right. \nonumber \\ x_1 (0)= & {} {0.8}, x_2 (0)={0.05}, x_3 (0)={0.007}, x_4 (0)={0.6} \nonumber \\ t= & {} 1,2,\ldots , 100 \end{aligned}$$

(13)

where the parameters to be estimated are $\left[ {\theta _1, \theta _2, \theta _3, \theta _4, \theta _5} \right]$. In this example, the real system parameters are assumed to be $\left[ {\theta _1, \theta _2, \theta _3, \theta _4, \theta _5, \theta _6 } \right] =\left[ {10.725} , {10.593} , {0.268} , {-0.7872} , {-1.1726} \right]$. In addition, the searching ranges are set as follows: $5\le \theta _1 \le 10$, $10\le \theta _2 \le 20$, $0.1\le \theta _3 \le 1$, $0.1\le \theta _4 \le 2$, $0.3\le \theta _5 \le 3$ and $0.1\le \theta _6 \le 1$.

Example 10

Henon chaotic system.

$$\begin{aligned} \dot{x}_1 (t)= & {} x_2 (t)+1-\theta _1 x_1^2 (t) \nonumber \\ \dot{x}_2 (t)= & {} \theta _2 x_1 (t) \nonumber \\ x_1 (0)= & {} {0.8}, x_2 (0)={0.5} \nonumber \\ t= & {} 1,2,\ldots , 100 \end{aligned}$$

(14)

where the parameters to be estimated are $\left[ {\theta _1, \theta _2} \right]$. In this example, the real system parameters are assumed to be $\left[ {\theta _1, \theta _2 } \right] =\left[ {{1.4}, {0.3}} \right]$. In addition, the searching ranges are set as follows: $1\le \theta _1 \le 3$ and $0\le \theta _2 \le 2$.

Figure 1 shows the phase portraits of aforementioned systems to show their chaotic behavior.

3 Backtracking search optimization algorithm

Backtracking search optimization algorithm (BSA) is a new population-based EA which uses well-known operators of genetic algorithms (GAs) in a new structure. In addition to these operators, i.e., selection, mutation and crossover, several unique mechanisms are inserted in BSA such as a memory in which it stores a population from a randomly chosen previous generation. Based on Civicioglu (2013), the BSA has five main steps including: initialization, selection-I, mutation, crossover and selection-II. These five steps are formulated as follows:

Fig. 1

Phase portraits of chaotic systems: a Lorenz, b Chen, c Rossler, d Arneodo, e Duffing, f Genesio-Tesi, g Financial, h Lu, i Chuas, j Henon

(1) Initialization

The BSA starts with a random initial sampling of individuals within the search space using a uniform distribution:

$$\begin{aligned} { POP}_{i,j}= & {} U({ low}_j, { up}_j ) \nonumber \\ \hbox {for} \; i= & {} 1,\ldots , N_{\mathrm{pop}} , j= 1,\ldots , N \end{aligned}$$

(15)

where $N_{\mathrm{pop}}$ and N are population size and function dimension, respectively, and U is the uniform distribution operator. Also $[{ low}_j , { up}_j ]$ is variables’ predefined interval boundaries.

(2) Selection-I

The BSA calculates the search direction by defining the historical population ${ oldPOP}$. The initial historical population is generated as follows:

$$\begin{aligned} { oldPOP}_{i,j}= & {} U({ low}_j , { up}_j ) \nonumber \\ \hbox {for} \; i= & {} 1,\ldots , N_{\mathrm{pop}} , j= 1,\ldots , N \end{aligned}$$

(16)

In BSA an option is provided to redefine ${ oldPOP}$ at the beginning of each iteration through the ‘if-then’ rule in Eq. (17):

$$\begin{aligned} \hbox {if}\; a<b\; \hbox {then}\; { oldPOP}={ POP}{\backslash } a,b=U(0,1) \end{aligned}$$

(17)

Equation (17) provides a memory for BSA. It ensures that BSA designates a population belonging to a randomly selected previous generation as the historical population and remembers this historical population until it is changed. After ${ oldPOP}$ is determined, a randomly change in the order of the individuals in ${ oldPOP}$ is performed using Eq. (18)

$$\begin{aligned} { oldPOP}={ permuting(oldPOP)} \end{aligned}$$

(18)

The permuting function used in Eq. (18) is a random shuffling function.

(3) Mutation

In this stage of algorithm, an initial form of trial population ${ mutPOP}$ is generated using Eq. (19)

$$\begin{aligned} { mutPOP}={ POP}+F \cdot ({ oldPOP-POP}) \end{aligned}$$

(19)

where F is a control parameter, and ${ (oldPOP-POP)}$ can be considered as amplitude of the search direction matrix. This amplitude is controlled using control parameter of F. Because of using the historical population to calculate the search direction matrix, BSA generates a trial population, taking partial advantage of its experiences from previous generations.

In Eq. (19), a trial point is generated by a differential operator. This operator propels the position of current population toward the corresponding members in the historical population. To provide a faster convergence, this research proposes a new operator by inspiring from mutation operators of DE algorithm, to generate initial trial population:

$$\begin{aligned}&\hbox {for}\; i= 1 \,to\, N_{\mathrm{pop}} \nonumber \\&\quad { mutPOP}_i ={ POP}_i +F \cdot ({ POPbest-POP}_i )\nonumber \\&\quad +\,F \cdot ({ oldPOP}_i -{ POP}_i)\nonumber \\&\hbox {end\,for} \end{aligned}$$

(20)

where ${ POP}_i$ and ${ oldPOP}_i$ are ith member of population and historical population, respectively. ${ POPbest}$ is the best member of population found so far.

Fig. 2

Steps of SBSA

(4) Crossover

After generation of an initial form of trial population ${ mutPOP}$, the final form of the trial population ${ trialPOP}$ is generated in the BSA’s crossover procedure. Trial individuals with better fitness values for the optimization problem are used to evolve the target population individuals. BSA’s crossover process has two steps. The first step calculates a random binary integer-valued matrix (${ map}$) of size ${N_\mathrm{pop}}\times N$ that indicates the individuals of ${ trialPOP}$ to be manipulated by using the relevant individuals of ${ POP}$. Based on this strategy, if ${ map}_{i,j} =1$, where $i= 1,\ldots , N_{\mathrm{pop}}$ and $j= 1,\ldots , N$, ${ trialPOP}$ is updated with ${ trialPOP}_{i,j} =POP_{i,j}$.

Some individuals of the trial population ${ trialPOP}_{i,j}$ obtained may exceed the lower and upper bounds of search space. Hence, the second step is designed to update these infeasible solutions with randomly generated individuals as in Eq. (15).

(5) Section-II

After generation of final form of candidate members, in the selection-II stage and according to a one-to-one spawning strategy and greedy selection, the individuals in ${ trialPOP}$ that have better fitness values are used to update the corresponding individuals in ${ POP}$. So value of cost function in the point ${ trialPOP}_i$, where $i= 1,\ldots , N_{\mathrm{pop}}$, is evaluated, and while $f({ trialPOP}_i )<f({ POP}_i)\,\,{ POP}_i$ is replaced with ${ trialPOP}_i$; otherwise, no replacement occurs. Moreover, if the best individual of ${ POP}$ (${ POPbest}$) has a better fitness value than the global minimum value obtained so far by BSA, the global minimizer is replaced by ${ POPbest}$, and the global minimum value is replaced by the fitness value of ${ POPbest}$.

4 Shuffled backtracking search optimization

The concept of group search has been used in some EAs such as shuffled complex evolution (SCE) (Duan et al. 1993), SFLA and shuffled DE (SDE) (Ahandani et al. 2010). These algorithms have a same structure. The main trait of them is a grouping search ability to provide some parallel attempts to obtain promising areas based on participating each member in previous experience of all other members. These algorithms have three main stages: partitioning, local search and shuffling. They begin with a population of points distributed randomly throughout the feasible search space. Then in partitioning stage, population is partitioned into several parallel groups. The different groups, which can be perceived as a set of parallel cultures, perform a local search independently using an evolutionary process to continuously evolve their quality for a defined maximum number of iteration. Then in shuffling stage, all evolved complexes are combined together into a single population and the stopping criteria are checked that if are not met the partitioning, local search and shuffling process are continued. The main difference of these algorithms is related their employed evolutionary strategy in local search stage. For example, the SCE, the SFL and the SDE use Nelder–Mead simplex search, PSO and DE, respectively.

This research employs a same approach to improve the original BSA by proposing a shuffled BSA (SBSA). The SBSA has a same structure in comparison with SCE, SFL and SDE algorithms; only the SBSA uses a BSA algorithm to evolve independently member of groups. So the SBSA merges the strengths of original BSA with group search ability. In the SBSA, to make groups on the assumption that partitioning m groups, each containing n members, after sorting of population in a decreasing order in terms of function evaluation, member ranking 1 goes to group 1, member ranking 2 goes to group 2,..., member ranking m goes to group m, then second member of each subset is assigned as: member ranking $(m+1)$ goes to group 1, member ranking $(m+2)$ goes to group 2,..., member ranking $(m+m)$ goes to group m. This process continues to assign all members into groups. Steps of the SBSA with m groups, n members of each group and $k_{\max }$ defined iteration number of evolutionary process are shown in Fig. 2. In this algorithm, ${ Group}_i$ and ${ oldGroup}_i$ denote ith group and historical group, respectively. ${ mutGroup}_i$ is trial members of ith group, ${ mapGroup}_i$ is binary integer-valued matrix of ith group, and ${ POPbest}$ is the best member found so far. Also a, b, c and d are random numbers with uniform distribution selected randomly in [0,1].

Table 1 Statistical results of different versions of BSA on Lorenz chaotic system (Note Zero value on this example means a number smaller than 1.0e−27)

Table 2 Statistical results of different versions of BSA on the literature on Chen chaotic system

Table 3 Statistical results of different versions of BSA on Rossler chaotic system (Note Zero value on this example means a number smaller than 1.0E−33)

Table 4 Statistical results of different versions of BSA on Arneodo chaotic system

Table 5 Statistical results of different versions of BSA on Duffing chaotic system

Table 6 Statistical results of different versions of BSA on Genesio-Tesi chaotic system

Table 7 Statistical results of different versions of BSA on Financial chaotic system (Note Zero value on this example means a number smaller than 1.0e−30)

Table 8 Statistical results of different versions of BSA on Lu chaotic system (Note Zero value on this example means a number smaller than 1.0e−30)

5 Computational results

In this section, different experiments are carried out to assess the performance of proposed algorithm. These experiments are designed to identify or estimate parameters of a wide variety of chaotic systems. A plenty of experiments were performed to give sufficiently good results for different problems, and the obtained values to set parameters of the BSA and the SBSA are as follows: $N_{\mathrm{pop}} = 24$, $m= 4$, $n= 6$ and $k_{{\max }} = 10$. Also control parameters of BSA, i.e., F is considered a random number in the range of [0,2] and ${ rate}_{{ mix}}$ is considered equal to 1 as proposed in Civicioglu (2013).

Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18 show how good our proposed algorithms are. Three different versions of BSA are proposed here and are compared against original BSA. In all comparisons, the original BSA which uses Eq. (13) to generate initial trial point is called here BSA1, and the original BSA which uses Eq. (14) to generate initial trial point is called here BSA2. Also the proposed SBSA with Eq. (13) to generate initial trial point is called here SBSA1 and the proposed SBSA with Eq. (14) to generate initial trial point is called here SBSA2. In addition, typical simulation results (including the convergent processes of objective value) are presented for the different chaotic systems with Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. For all problems, the statistical simulation results of 50 independent runs are reported, where “Best”, “Mean” and “Variance” denote values of unknown parameters in the best run, mean values of unknown parameters in all runs and the variance of values of unknown parameters, respectively. Also “Best-SSE”, “Mean-SSE” and “Variance-SSE” denote the best found SSE value, mean of the best SSE values and variance of found SSE values in all independent runs, respectively. Also “Success Rate” denotes percent of successful runs. In this research, a run is called successful if its corresponding SSE reaches less than 0.01. Also a fixed value of function evaluations equal to $5000\times N$ is considered as termination criterion. The best results in tables are presented in a bold face.

5.1 Simulation about Lorenz system

Table 1 shows the statistical results of different methods for the Lorenz chaotic system. The obtained results of these tables show that all algorithms are consistent and they converge to the true values as accurately as possible. Figure 3 shows the convergence of J corresponding to a typical run for the Lorenz chaotic system. An interesting observation from these curves is that all algorithms reach to vicinity of true values of parameters in early number of function evaluations.

5.2 Simulation about Chen system

Table 2 shows the statistical results of different methods for the Chen chaotic system. It can be seen that the SBSA2 outperforms other algorithms in terms of all considered aspects. The SBSA2 obtains the best minimum and mean of SSE values. The second-best results are related to the BSA2. The SBSA1 beside two aforementioned algorithms obtains a success rate of 100. These results demonstrate that both of the proposed ideas to improve BSA, i.e., grouping search and new operator, to generate initial trial point are effective to evolve the original BSA. Comparatively, the performances of original BAS, i.e., BSA1, are the worst among the four algorithms. Figure 4 shows the convergence of J corresponding to a typical run for the Chen chaotic system. From these curves, it is clear that the BSA2 and SBSA2 can achieve the best results with a high solution accuracy. So results of Table 2 and Fig. 4 demonstrate better effectiveness and robustness of the BSA2 and SBSA2 than the other two algorithms for parameter identification of the Chen chaotic system.

5.3 Simulation about Rossler system

Table 3 shows the statistical results of different methods for the Rossler chaotic system. Based on results of this table, all algorithms obtain a complete success rate. Also it can be seen that the BSA2 has the best performance in terms of Best-SSE and the SBSA2 obtains the best Mean-SSE. Also the BSA1 obtains again the worst Mean-SSE value among all algorithms. Figure 5 shows the convergence of J corresponding to a typical run for the Rossler chaotic system. The obtained curves of Fig. 5 show the fast convergence speed of algorithms. So results of Table 3 and Fig. 5 demonstrate better effectiveness and robustness of the BSA2 and SBSA2 than the other two algorithms for parameter identification of the Rossler chaotic system.

5.4 Simulation about Arneodo system

Table 4 shows the statistical results of different methods for the Arneodo chaotic system. As obtained in previous tables, the BSA2 and SBSA2 are again two superior algorithms on this system. The BSA1 obtains the best results, and the SBSA2 has the second-best performance. The SBSA1 has a better Best-SSE than the BSA1, but the BSA1 obtains a less Mean-SSE than the SBSA1. Figure 6 shows the convergence of J corresponding to a typical run for the Arneodo chaotic system. These curves show that the BSA2 and SBSA2 have faster convergence speed than the other two algorithms. So results of Table 4 and Fig. 6 demonstrate better effectiveness and robustness of the BSA2 and SBSA2 than the other two algorithms for parameter identification of the Arneodo chaotic system.

5.5 Simulation about Duffing system

Table 5 shows the statistical results of different methods for the Duffing chaotic system. It can be seen that all the results got by SBSA2 are consistent and it has the best performance. The second-best performance is related to the BSA2. Among all algorithms, only the SBSA2 and BSA2 have a success rate of 100. Also the original BSA1 is the worst among the four algorithms. Figure 7 shows the convergence of J corresponding to a typical run for the Duffing chaotic system. These curves confirm the obtained results of Table 5 about a better performance of the proposed algorithms in this research. The SBSA2 converges quickly and detects optimums in a few iterations.

5.6 Simulation about Genesio-Tesi system

Table 6 shows the statistical results of different methods for the Genesio-Tesi chaotic system. As obtained from aforementioned experiments, it is seen from the results of this table that the BSA2 and SBSA2 outperform two other algorithms. The BSA2 and SBSA2 have a complete success rate. The SBSA2 obtains the best Best-SSE, and the BSA2 has the best Mean-SSE. Also the SBSA1 has a better performance than the original BSA1. Figure 8 shows the convergence of J corresponding to a typical run for the Genesio-Tesi chaotic system. The trajectories of J during the evolutionary procedure confirm a better performance of the BSA2 and SBSA2. They converge quickly and detect optimums in a few iterations.

5.7 Simulation about financial system

Table 7 shows the statistical results of different methods for the Financial chaotic system. The obtained results on this system make confidence about superior performance of the SBSA2 and BSA2 methods. Among four algorithms, only the two algorithms converge to optimum point as accurately as possible in all runs. After them, the SBSA1 has the second-best results and the BSA1 is has the worst performance; however, it has a success rate of 100. Figure 9 shows the convergence of J corresponding to a typical run for the Financial chaotic system. From Fig. 9, it is clear that the all algorithms have a quick convergence toward optimum value.

5.8 Simulation about Lu system

Table 8 shows the statistical results of different methods for the Lu chaotic system. According to obtained results on this chaotic system, only the BSA1 cannot achieve a success rate of 100. However, the BSA1 beside BSA2 obtains the best Best-SSE value. Also the SBSA2 has the best Mean-SSE, and the BSA1 has the worst Mean-SSE. Figure 10 shows the convergence of J corresponding to a typical run for the Lu chaotic system. These curves depict the evolving processes of fitness value for all the algorithms. It is clear that the all algorithms have a quick convergence toward optimum value.

5.9 Simulation about Chuas system

Table 9 shows the statistical results of different methods for the Chuas chaotic system. This system has five unknown parameters to be estimated, and the obtained results show that it is very difficult to be solved. Table 9 highlights the efficiency and robustness of the proposed algorithms here. The SBSA2 and BSA2 have a considerably better performance in terms of all considered aspects than two another algorithms. The SBSA1 and BSA1 cannot obtain any success rate on this system. Results of this table demonstrate that the proposed operator to generate initial trial point is very effective to evolve performance of BSA and SBSA. Figure 11 shows the convergence of J corresponding to a typical run for the Chuas chaotic system. It is clear that the SBSA2 and BSA2 can achieve good results, whereas the SBSA1 and BSA1 get stuck on local minimums.

5.10 Simulation about Henon system

Table 10 shows the statistical results of different methods for the Henon chaotic system. This system has two unknown parameters to be estimated, and it is not difficult to be solved. All algorithms have a success rate of 100, and among all algorithms, the SBSA2 converges to optimum point as accurately as possible in all runs. Figure 12 shows the convergence of J corresponding to a typical run for the Henon chaotic system. From Fig. 12, it is clear that the all algorithms have a quick convergence toward optimum value.

Table 9 Statistical results of different versions of BSA on Chuas chaotic system

Table 10 Statistical results of different versions of BSA on Henon chaotic system (Note Zero value on this example means a number smaller than 1.0e−28)

Table 11 Ranks based on Best-SSE for the algorithms over the set of 10 chaotic systems

Table 12 Ranks based on Mean-SSE for the algorithms over the set of 10 chaotic systems

Table 13 Wilcoxon test applied over the obtained results of Tables 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 in terms of the best run (Best-SSE) and average of all runs (Mean-SSE)

To provide an overall consequence from Tables 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 about performance of algorithms on aforementioned 10 chaotic systems, Tables 11 and 12 show rank of each algorithm based on Best-SSE and Mean-SSE for the algorithms over the set of 10 chaotic systems, respectively. According to results of Tables 11 and 12, the SBSA2 obtains rank 1 on 7 and 8 problems based on Best-SSE and Mean-SSE, respectively. Also the BSA2 obtains rank 1 on 6 and 4 problems based on Best-SSE and Mean-SSE, respectively. It also obtains rank 2 on 4 and 6 other problems based on Best-SSE and Mean-SSE, respectively. The SBSA1 obtains rank 1 on 3 and 1 problems based on Best-SSE and Mean-SSE, respectively. It also obtains rank 3 on 3 and 8 other problems based on Best-SSE and Mean-SSE, respectively. The BSA1 obtains rank 1 on 4 and 1 problems based on Best-SSE and Mean-SSE, respectively. It also obtains rank 4 on 3 and 8 other problems based on Best-SSE and Mean-SSE, respectively.

A nonparametric analysis over the obtained results from Tables 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 using the Wilcoxon signed-rank test with $\alpha =0.05$ in terms of best run (Best-SSE) and average of all runs (Mean-SSE) is provided in Table 13.

Pairwise comparisons of Table 13 show that the BSA2 has a significant difference with respect to the BSA1 and SBSA1 in terms of Best-SSE. Also the SBSA2 considerably outperforms the BSA1 in terms of Best-SSE. Also difference of BSA2 and SBSA2 based on this test is not significant; however, this test confirms a better performance of SBSA2. Also based on Mean-SSE, BSA2 and SBSA2 have a significantly better performance than two other algorithms. Also this test confirms a better Mean-SSE performance of the SBSA2 than the BSA2; however, this difference is not significant.

Table 14 A comparison for the algorithms over the set of 10 chaotic systems based on average of running time (Note Time values in this table are in terms of seconds)

Table 15 Comparison among results of BSA2 and SBSA2 and results of Ho et al. (2010) on Chen chaotic system (Note Zero value on this example means a number smaller than 1.0e−30)

Table 16 Comparison among results of BSA2 and SBSA2 and results of Ho et al. (2010) on Lu chaotic system (Note Zero value on this example means a number smaller than 1.0e−30)

Table 17 Comparison among results of BSA2 and SBSA2 and results of Ho et al. (2010) on Rossler chaotic system (Note Zero value on this example means a number smaller than 1.0e−33)

Table 18 Comparison among results of BSA2 and SBSA2 and results of Tang et al. (2012) on Lu chaotic system (Note Zero value on this example means a number smaller than 1.0e−30)

Table 4 compares algorithms over the set of 10 chaotic systems based on average of running time.

Based on results of time comparison, since all algorithms have a same stopping criterion, i.e., a fixed value of function evaluation, there is not a significantly difference among running time of them. Also Table 14 clearly shows that the proposed ideas in this study to evolve the performance of original BSA are not more time-consuming than the original structure or operators of BSA.

From Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14 and Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12, the following results are observed: (i) both of the proposed ideas to improve performance of original BSA, i.e., group search ability and new operator, to generate initial trial population are effective. (ii) A considerably better performance of the SBSA2 and BSA2 based on Mean-SSE demonstrates that the proposed ideas can evolve robustness and consistence of algorithm. (iii) Inserting a new operator to generate initial trial population considerably makes better exploitation ability of original BSA algorithm so that the BSA2 could find solutions with a high accuracy. (iv) By providing a group search ability for the BSA algorithm and presenting the SBSA, the exploration ability of original BSA was improved. Also by inserting a new operator to generate initial trial population, exploitation ability of SBSA was evolved. So by combining these two concepts, we can see that the SBSA2 has the best performance among four algorithms.

5.11 Comparison with results reported in the literature

In this section, a comparison between the proposed algorithms in this research, i.e., BSA2 and SBSA2, and some other algorithms reported in the different literature to solve parameter identification of chaotic systems is performed. Ho et al. (2010) proposed an improved DE algorithm, named the Taguchi-sliding-based DE algorithm (TSBDEA), to solve the problem of parameter identification for Chen, Lü and Rossler chaotic systems. The TSBDEA combines the DE with the Taguchi-sliding-level method (TSLM). The TSLM is used as the crossover operation of the DEA. Then, the systematic reasoning ability of the TSLM is provided to select the better offspring to achieve the crossover and consequently enhance the DE. Based on Ho et al. (2010), sampling time is 0.0005 s for Chen and Lü systems, the sampling time is 0.001 s for Rossler system, and the total sampling number L is 100 for all three systems. Also number of function evaluations for Chen and Lü systems is considered equal to 10,000, and for the Rossler system, it is considered equal to 12,000. They used mean square error (MSE) as cost function as follows:

$$\begin{aligned} {\min } \, J=\frac{1}{L} \sum _{k=1}^L {\left\| {x(k)-\hat{{x}}(k)} \right\| ^{2}} \end{aligned}$$

(21)

Values of parameters for BSA2 and SBSA2 are same to those of considered in aforementioned experiments; only to provide a better comparison, size of initial population is considered equal to 16. Tables 15, 16 and 17 show this comparison. The obtained results demonstrate that the BSA2, SBSA2 and TSBDEA obtain the best results. They converge to optimal solution in all trial runs. Thus, it can be concluded that the BSA2, SBSA2 and TSBDEA can give a more effective and robust way for estimating the true parameters than the DE.

Tang et al. (2012) applied the DE to search the optimal parameters of commensurate fractional-order chaotic systems when orders are known and unknown. They applied the DE on Lu and Volta chaotic systems and compared the obtained results with GA. Sampling time is 0.005 and 0.0005 s for Lü and Volta systems, respectively, and the total sampling number, L, is 100 for both of them. Also number of function evaluations for these systems is considered equal to 10,000. Tables 18 and 19 compare results of BSA2 and SBSA2 in respect to results reported in Tang et al. (2012) when orders of chaotic systems are known. From these tables, it can be seen that the BSA2 and SBSA2 obtained the best results with respect to the DE and GA so that their estimated parameters are accurately same as the true parameter values, but there exist certain errors between the average results of DE and the true parameter values. Also, none of the results obtained by GA are the same as the true parameter values.

Hu et al. (2015) proposed a hybrid artificial bee colony (HABC) algorithm for identification of uncertain fractional-order chaotic systems. Fractional-order Economic and Rössler chaotic systems are selected to test the performance. Instead of MSE in Eq. (21), the following objective function is defined in Hu et al. (2015) which is a sum square error (SSE) function:

$$\begin{aligned} {\min }\, J=\sum _{k=1}^N {\left\| {X(k)-\hat{{X}}(k)} \right\| ^{2}} \end{aligned}$$

(22)

To calculate the objective function, the number of samples is set as 300 and the step size is 0.01. The parameters of HABC algorithm are set as follows: Population size is 100, maximum cycle number of iterations are set as 50 for fractional-order economic chaotic system and 100 for fractional-order Rössler chaotic systems, respectively, the control parameter (limit) is 15, and the maximum number of chaotic iteration $N = 300$. The algorithm is executed 15 times for each example, and all runs are terminated after the predefined maximum cycle number of iterations is reached.

Fig. 3

A comparison among convergence speed of BSA1, BSA2, SBSA1 and SBSA2 for a typical simulation by Lorenz chaotic system

In the first part of comparison study in Hu et al. (2015), the HABC was compared against two other versions of ABC, i.e., GABC and EABC on fractional-order Economic chaotic system. Table 20 shows the obtained results of the SBSA2 and the BSA2 against results of aforementioned algorithms. From the simulations results of the fractional-order Economic system, it can be concluded that the BSA2 outperforms all other algorithms based on all considered aspects. Also SBSA2 has a better performance than the GABC, the EABC and the HABC in terms of all criteria, except in comparison with the HABC in terms of Best-SSE.

In the second part of comparison study in Hu et al. (2015), the HABC was compared against three other EAs, i.e., GA, DE and PSO on fractional-order Rössler chaotic system. Table 21 shows the obtained results of the SBSA2 and the BSA2 against results of aforementioned algorithms. Table 21 clearly confirms a considerable better performance of the SBSA2 and the BSA2 in comparison with HABC, GA, DE and PSO. In this table, the BSA2 has the best performance in terms of all considered aspects and the SBSA2 obtains the second-best performance.

Fig. 4

A comparison among convergence speed of BSA1, BSA2, SBSA1 and SBSA2 for a typical simulation by Chen chaotic system

Fig. 5

A comparison among convergence speed of BSA1, BSA2, SBSA1 and SBSA2 for a typical simulation by Rossler chaotic system

Fig. 6

A comparison among convergence speed of BSA1, BSA2, SBSA1 and SBSA2 for a typical simulation by Arneodo chaotic system

Fig. 7

A comparison among convergence speed of BSA1, BSA2, SBSA1 and SBSA2 for a typical simulation by Duffing chaotic system

Fig. 8

A comparison among convergence speed of BSA1, BSA2, SBSA1 and SBSA2 for a typical simulation by Genesio-Tesi chaotic system

Fig. 9

A comparison among convergence speed of BSA1, BSA2, SBSA1 and SBSA2 for a typical simulation by Financial chaotic system

Fig. 10

A comparison among convergence speed of BSA1, BSA2, SBSA1 and SBSA2 for a typical simulation by Lu chaotic system

Fig. 11

A comparison among convergence speed of BSA1, BSA2, SBSA1 and SBSA2 for a typical simulation by Chuas chaotic system

Fig. 12

A comparison among convergence speed of BSA1, BSA2, SBSA1 and SBSA2 for a typical simulation by Henon chaotic system

In an overall view, the obtained results of comparison study against results reported in Ho et al. (2010), Tang et al. (2012) and Hu et al. (2015) in Tables 15, 16, 17, 18, 19, 20 and 21 show a considerably better performance of our proposed algorithms. These results confirm efficiency and robustness of two improved versions of BSA than the pure BSA. Also we can conclude that the proposed algorithms in this research can obtain more accurate solutions than the results of other algorithm reported in compared literature.

Table 19 Comparison among results of BSA2 and SBSA2 and results of Tang et al. (2012) on Volta chaotic system (Note Zero value on this example means a number smaller than 1.0e−34)

Table 20 Comparison among results of BSA2 and SBSA2 and results of Hu et al. (2015) on Economic chaotic system when orders are unknown (Note Zero value on this example means a number smaller than 1.0e−32)

Table 21 Comparison among results of BSA2 and SBSA2 and results of Hu et al. (2015) on Rossler chaotic system when orders are unknown (Note Zero value on this example means a number smaller than 1.0e−32)

6 Conclusions

A mathematical model has a vital role in controlling and synchronization of chaotic systems. But generally in real-world problems, parameters are mixed with mismatches and distortions. So presentation of scientific approaches to overcome this drawback is a popular topic. This research proposed two effective ideas to improve performance of BSA. Firstly to provide a faster convergence and a deep search, a new operator to generate initial trial population was proposed. Then a group search ability was provided for the BSA by proposing a SBSA. In the SBSA, a population is divided into several groups and each of groups tries to evolve itself using a BSA evolutionary process. Groping population into several sets provided a better exploration of search space and an independent local search of each groups increased exploitation ability of BSA. Also new proposed operator to generate initial trial population by providing a deep search increased satisfactorily solution quality. To measure efficiency of proposed algorithm with respect to their original versions, they were applied for parameter estimation of 10 typical chaotic systems. The obtained results and nonparametric analysis of them demonstrated that both of the proposed ideas were very effective and robust so that the BSA by aforementioned ideas produced similar and promising results over repeated runs. The BSA with group search ability and new proposed operator called SBSA2 due to a better exploration and a deep exploitation had the best performance among all algorithms. Also the second-best results were related to a BSA with only new proposed operator called BSA2 due to providing a deep search of found promising areas. In the final part of comparison study, a comparison of the proposed algorithms in this study with respect to other algorithms reported in the literature confirmed a considerably better performance of our proposed algorithms.