A hybrid artificial bee colony algorithm for parameter identification of uncertain fractional-order chaotic systems

Abstract

It is an important issue to estimate parameters of uncertain fractional-order chaotic systems in nonlinear science. In this paper, fractional orders as well as systematic parameters of fractional-order chaotic systems are all considered as independent variables. Firstly, the parameter estimation problem is transformed into a multi-dimensional function optimization problem. And in the meantime, an effective hybrid artificial bee colony algorithm is proposed to deal with the parameter estimation problem. Numerical simulations are conducted on two typical fractional-order chaotic systems to test the effectiveness of the proposed method. The experiments’ results show that the proposed approach for identification of uncertain fractional-order chaotic systems is a successful and promising method with higher calculation accuracy and faster convergence speed.

1 Introduction

During the past years, the applications of fractional calculus in aspects of science and engineering [1–5] have been drawn increasing attentions. This happens because it has been recently found that several physical problems, such as electrical capacitors [6], viscoelastic material [7], economic systems [8], transmission lines [9] and neurons [10], can be more accurately described by fractional differential equations. And a number of numerical methods are available for numerical solutions of fractional differential equations [4, 11]. Therefore, in recent years, considerable attentions have been attracted to make use of the great potential of fractional calculus in physics [3], electrical circuit theory [12] and control systems [13]. In particular, a significant role is played in chaos control theory, where many control methods have been devised for fractional-order chaotic systems under the conditions of known fractional orders and systematic parameters [14, 15]. But unfortunately, in the real world, the fractional orders and systematic parameters of fractional-order chaotic systems cannot be exactly known. Even worse, it is difficult to achieve control and identify the parameters of the fractional-order chaotic systems with unknown fractional orders and systematic parameters. Therefore, it is crucial for us to identify the fractional orders and systematic parameters of the uncertain fractional-order chaotic systems beforehand if the parameters are unknown.

The process to get the exact values of unknown fractional orders and systematic parameters for the uncertain fractional-order chaotic systems is called system inversion mechanism [16]. Up to now, there have been some approaches in system inversion of fractional-order chaotic systems [16–20]. Among the above literatures, two basic methods are mainly contained. One is synchronization method [17], which is based on the the stability analysis of fractional-order systems and the control methods. This concept was firstly proposed by Parlitz [21], and then, it has been extensively studied in many other papers concerning the parameter identification of uncertain chaotic systems [22, 23], but the design of both the controller and the updating law of parameter identification is still a hard task with techniques and sensitivities depending on the considered system. The other is the optimization method which is a non-classical way using artificial intelligent algorithms. In the second method, the unknown parameters are considered as independent variables and parameter estimation is converted into a function optimization problem via a functional extrema model. Compared with the first method, the optimization method is not sensitive to the considered systems and easy to implement, and thus, it is more applicable. To the best of our knowledge, facing to the second method, particle swarm optimization [18, 19] and differential evolution [16, 20] have been sufficiently investigated to identify the uncertain fractional-order chaotic systems.

Recently, great interests have emerged in evolutionary algorithms, such as particle swarm optimization (PSO) [24], genetic algorithm (GA) [25], differential evolution (DE) [26] and artificial bee colony (ABC) algorithm [27]. Particularly, the ABC algorithm is a useful computation technique developed by Karaboga in 2005 based on simulating the foraging behavior of honeybee swarm. A set of experimental results on function optimization [28–30] show that ABC algorithm is competitive with some population-based algorithms, although it uses less control parameters than others, such as PSO and DE. Actually, apart from the maximum cycle number (MCN) and population size number (SN), a standard DE has at least two control parameters (crossover rate, scaling factor) and a basic PSO has three control parameters (cognitive and social factors, inertia weight). Also, limit values for the velocities $v_{max}$ have a significant effect on the performance of PSO. However, the ABC algorithm has only one control parameter (limit) apart from MCN and SN. Therefore, with the nice characteristics, the ABC algorithm has been applied to solve continuous, constrained, large-scale, multi-modal and multi-dimensional optimization problems in many different fields, such as training neural networks [31], electrical engineering [32], control engineering [33] and image processing [34], etc.

As mentioned above, the ABC algorithm is a competitive population-based algorithm which has many wonderful properties [29, 30]. Due to its easy implementation and quick convergence, nowadays, the ABC algorithm has received a lot of attentions and wide applications in different continuous optimization problems [31–36]. Particularly, in Ref. [35], a hybrid Taguchi-chaos of multi-level immune and the ABC algorithm is employed to identify the integer-order Lorenz system. In Ref. [36], a novel ABC algorithm with space contraction is presented for unknown parameter identification and time delays of integer-order chaotic systems. However, as far as we know, for the parameter identification of uncertain fractional-order chaotic systems, little research has been done through the ABC algorithm. And this application area is relatively new for the ABC algorithm in contrast with that of PSO [18, 19] and DE [16, 20].

However, so far, there is no specific algorithm to achieve the best solution for all optimization problems. Namely, as far as most algorithms are concerned, it is difficult to simultaneously balance the ability of exploitation and exploration for all the optimization problems. In other words, most algorithms are difficult to have a better performance in the aspects of convergence speed and convergence precision for all optimization problems at the same time. Therefore, in this paper, to further enhance the exploration and the exploitation abilities, a hybrid artificial bee colony (HABC) algorithm is put forward. In the proposed HABC algorithm, to enhance the global convergence, when producing the initial population and scout bees, both chaotic system and opposition-based learning method are employed. At the same time, to keep the ability of exploitation and exploration well balanced, two new searching equations are proposed to generate the new candidate solutions. In addition, the ratio between employed and onlooker bees is changed to have a better searching performance. The HABC algorithm is further used for parameter identification of uncertain fractional-order chaotic systems via a functional extrema model. Numerical simulations are performed on two typical fractional-order chaotic systems and statistically compared with some typical existing ABC-based algorithms and some other population-based algorithms. As a result, compared to some ABC-based algorithms and other typical population-based algorithms, the simulation results demonstrate the good performance and the superiority of the HABC algorithm. Thus, it can be a promising candidate for parameter estimation of uncertain fractional-order chaotic systems.

The rest of the paper is organized as follows. In Sect. 2, some preliminaries are introduced, including the Caputo fractional-order derivative and the standard ABC algorithm. Section 3 gives a problem formulation. The HABC algorithm is proposed in sufficient details in Sect. 4. Simulations in Sect. 5 are made to estimate two typical fractional-order chaotic systems. Finally, conclusions are drawn in Sect. 6.

2 Preliminaries

2.1 Caputo fractional-order derivative

There are several definitions of fractional-order derivatives. The three best-known definitions are the Grunwald–Letnikov, Riemann–Liouville and Caputo definitions [4]. In particular, Caputo fractional-order derivative owns same initial conditions with classical integer-order derivatives, which is well understood in physical situations and more applicable to real-world problems. Thus, we introduce the Caputo fractional-order derivative in this paper.

Definition 1

(Caputo fractional-order derivative) The Caputo fractional-order derivative of order $\alpha >0$ for a function $f(t)\in C^{n+1}([t_{0},+\infty ),R)$ is defined as

$$\begin{aligned} _{t_{0}}D^{\alpha }_{t}f(t)=\frac{1}{\Gamma (n-\alpha )} \int ^{t}_{t_{0}}\frac{f^{(n)}(\tau )}{(t-\tau )^{\alpha +1-n}}\,\, d\tau , \end{aligned}$$

(1)

where $\Gamma (\cdot )$ denotes the gamma function and n is a positive integer such that $n-1<\alpha \le n$.

The Laplace transform of the Caputo fractional-order derivative is

$$\begin{aligned}&\mathcal {L}\left\{ _{t_{0}}D^{\alpha }_{t}f(t); s\right\} =s^{\alpha }F(s)-\sum ^{n-1}_{k=0}s^{\alpha -k-1}f^{(k)}(t_{0}),\\&\qquad \qquad \quad n-1<\alpha \le n. \end{aligned}$$

where $\mathcal {L}\{\cdot \}$ denotes the Laplace transform, s is the variable in Laplace domain, and F(s) is the Laplace transform of f(t).

Property 1

When C is any constant, $_{t_{0}}D^{\alpha }_{t}C=0$ holds.

Property 2

For constants $\mu$ and $\nu$, the linearity of Caputo fractional-order derivative is described by

$$\begin{aligned} _{t_{0}}D^{\alpha }_{t}(\mu f(t)+\nu g(t))=\mu ~ _{t_{0}}D^{\alpha }_{t}f(t)+\nu ~ _{t_{0}}D^{\alpha }_{t}g(t). \end{aligned}$$

2.2 The standard artificial bee colony algorithm

The ABC algorithm proposed by Karaboga [27–30] in 2005 is a competitive optimization technique which simulates the intelligent foraging behavior of honeybee swarm. In the standard ABC algorithm, the artificial bee colony includes three kinds of bees: employed bees, onlooker bees and scout bees. In reality, half of the colony consists of employed bees, and the rest of the colony represents onlooker bees. As a matter of fact, the number of employed bees is equal to the number of onlooker bees and equal to the number of food sources or solutions as well.

Among them, the employed bees are responsible for searching available food sources and gathering required information. At the same time, they also pass their food information to onlooker bees through dancing in the nearby hive. Thereafter, onlooker bees incline to select a better food source according to its fitness; that is, the more food amount the food source has, the more likely the corresponding food source is chosen. Then, the onlooker bees continue to further search a new food source around the chosen food sources. In addition, if the food amount of the new food source found by an onlooker bee is more than that of the previous one, the employed bee’s food source position is replaced by the new one in its memory. Meanwhile, a so-called parameter trial, which is used to record the number to determine whether the employed bee’s food source position should be replaced, is set to zero when the employed bee’s food source position is replaced, else the trial parameter is going to be plus one in the employed bee’s memory. As a result, if the number of trial exceeds a predetermined number of cycles, the employed bee’s food source is abandoned by its employed bee. Then, the employed bee becomes a scout bee and starts to search for a new food source in the vicinity of the hive.

In a word, the standard ABC algorithm is an iteration optimization technique similar to other population-based algorithms. The units of the standard ABC algorithm can be described as follows:

2.2.1 Initialization of the population

The initial population of solutions is filled with D-dimensional real-valued vectors which are generated randomly (i.e., food sources), and the size of the initial population is set as SN, where SN denotes the size of employed bees. Let $X_{i}=(x_{i,1},x_{i,2},\ldots ,x_{i,D})$ represents the ith food source in the population, and then, each food source is generated as follows:

$$\begin{aligned} x_{i,j}=x_{{min},j}+rand(0,1)(x_{{max},j}-x_{{min},j}), \end{aligned}$$

(2)

where $i=1,2,\ldots ,SN$, $j=1,2,\ldots ,D$. D is the dimension of the searching space. $x_{{min},j}$ and $x_{{max},j}$ are the lower and upper bounds for the dimension j in respect. These food sources are randomly assigned to the employed bees, and their fitness are evaluated accordingly.

2.2.2 The employed bee phase

At this stage, for each position of the employed bee’s food source $X_{i}$, a new food source position $V_{i}$ is generated via the equation as follows:

$$\begin{aligned} v_{i,j}=x_{i,j}+\phi _{i,j}(x_{i,j}-x_{k,j}), \end{aligned}$$

(3)

where $k=1,2,\ldots ,SN$ and $j=1,2,\ldots ,D$. k and j are randomly generated, and k must be different from i. $\phi _{i,j}$ is a random number in $[-1,1]$. The above explanation implies that the other components of $V_{i}$ except for dimension j are as same as the ones of $X_{i}$.

Then, a greedy selection is made between $X_{i}$ and $V_{i}$. That is, once $V_{i}$ is obtained, it will be evaluated and compared with $X_{i}$. If the fitness of $V_{i}$ is equal to or better than that of $X_{i}$, $V_{i}$ will replace $X_{i}$ and correspondingly become a member of the population. Otherwise, $X_{i}$ is retained.

2.2.3 Calculating probability values referred to the probabilities selection

After finishing the update process, employed bees share their nectar amount information, which is related to the food sources, with the onlooker bees in the nearby hive. An onlooker bee evaluates the nectar information taken from all employed bees and chooses a food source through a probability value $p_{i}$, which is calculated by

$$\begin{aligned} p_{i}=\frac{\hbox {fit}_{i}}{\sum \nolimits ^{SN}_{j=1}\hbox {fit}_{j}}, \end{aligned}$$

(4)

where $\hbox {fit}_{i}$ denotes the fitness value of solution $X_{i}$. It is obvious that the higher the fitness value of solution $X_{i}$ is, the higher the probability of selecting the ith food source corresponding to solution $X_{i}$ is. Besides, the fitness value $fit_{i}$ is defined as

$$\begin{aligned} \hbox {fit}_{i}= \left\{ \begin{array}{lll} \frac{1}{1+f(X_{i})},&{} \quad \hbox {if}\quad &{} f(X_{i})\ge 0,\\ 1+|f(X_{i})|, &{} \quad \hbox {if} \quad &{} f(X_{i})<0, \end{array} \right. \end{aligned}$$

(5)

where $f(X_{i})$ represents the objective function value of the decision vector $X_{i}$.

2.2.4 The onlooker bee phase

Based on the probability value $p_{i}$ calculated by Eq. (4), each onlooker bee randomly chooses a food source corresponding to the solution $X_{i}$ with a probability value $p_{i}$. Thereafter, it makes a modification (i.e., $V_{i}$) around the chosen food source by Eq. (3). Similar to the phase of employed bees, the greedy selection mechanism is applied to select a better solution between the solutions $X_{i}$ and $V_{i}$.

2.2.5 The scout bee phase

If the food source position corresponding to the solution $X_{i}$ is not improved continuously in the honeybee’s memory within certain time (limit), which is recorded by the parameter trial, then the corresponding employed bee will abandon the food source and becomes a scout bee. The scout bee produces a new food source randomly as Eq. (2).

3 Problem formulation

Consider the following fractional-order chaotic system

$$\begin{aligned} _{0}D^{\alpha }_{t}Y(t)=f(Y(t),Y_{0},\theta ), \end{aligned}$$

(6)

where $Y(t)=(y_{1}(t),y_{2}(t),\ldots ,y_{n}(t))^{T} \in R^{n}$ denotes the state vector, $Y_{0}=Y(0)$ denotes the initial value, $\theta =(\theta _{1},\theta _{2},\ldots ,\theta _{n})^{T}$ denotes the set of original systematic parameters, $\alpha =(\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}) (0<\alpha _{i}<1, i=1,2,\ldots ,n)$ is the fractional derivative orders, and $f(Y(t),Y_{0},\theta )=(f_{1}(Y(t)$, $Y_{0},\theta )$, $f_{2}(Y(t),Y_{0},\theta ),\ldots ,f_{n}(Y(t),Y_{0},\theta ))^{T}$.

The corresponding estimated system can be written as

$$\begin{aligned} _{0}D^{\tilde{\alpha }}_{t}\tilde{Y}(t)=f(\tilde{Y}(t),Y_{0},\tilde{\theta }), \end{aligned}$$

(7)

where $\tilde{Y}(t)=(\tilde{y}_{1}(t),\tilde{y}_{2}(t),\ldots ,\tilde{y}_{n}(t))^{T}\!\in \! R^{n}$ is the state vector of the estimated system, $\tilde{\theta }\!=\! (\tilde{\theta }_{1}, \tilde{\theta }_{2},\ldots ,\tilde{\theta }_{n})^{T}$ is a set of estimated systematic parameters, and $\tilde{\alpha }=(\tilde{\alpha }_{1},\tilde{\alpha }_{2},\ldots ,\tilde{\alpha }_{n})^{T}$ is the estimated fractional orders. Besides, systems (6) and (7) have the same initial conditions $Y_{0}$.

In general, to identify the fractional-order chaotic system (6), it can be transformed into a functional extrema model as

$$\begin{aligned} J(\tilde{\alpha },\tilde{\theta })=arg \ {\underset{(\tilde{\alpha },\tilde{\theta })\in \Omega }{min}} \ F =arg\ {\underset{(\tilde{\alpha },\tilde{\theta })\in \Omega }{min}} \sum ^{N}_{k=1}\Vert Y_{k}-\tilde{Y}_{k}\Vert _{2},\nonumber \\ \end{aligned}$$

(8)

where $k=1,2,\ldots ,N$ is the sampling time point and N denotes the length of data used for parameter estimation. $Y_{k}$ and $\tilde{Y_{k}}$, respectively, denote the state vector of the original system (6) and the estimated system (7) at time kh. h is the step size employed in the predictor–corrector approach for the numerical solutions of fractional differential equations [11]. $\Vert \cdot \Vert$ is Euclid norm. $\Omega$ is the searching area admitted for parameters $\tilde{\theta }$, where the fractional orders $\tilde{\alpha }$ are considered as special variables. The parameter identification of system (6) can be achieved by searching suitable $\tilde{\theta }$ and $\tilde{\alpha }$ in the searching space $\Omega$ such that the objective function (8) is minimized. In other words, the main task is to find the best combination of the independent variables $\tilde{\alpha }$ and $\tilde{\theta }$ for the objective function.

4 HABC algorithm

In this section, a hybrid artificial bee colony algorithm (HABC) is proposed. Firstly, chaotic opposition-based population initialization is employed to initialize the population, which can guide the population toward the more promising areas and spread it as much as possible over the searching space. Secondly, to keep the balance between exploitation and exploration abilities better, two new searching equations are proposed to generate new candidate solutions on employed bees phase and onlooker bees phase, respectively. Then, the idea of changing the ratio of employed and onlooker bees is adopted. Finally, chaotic opposition-based searching method on scout bees phase is used again. The details are described in the following subsections.

4.1 Chaotic initialization based on circle map

Owing to the characteristics of the certainty, ergodicity and pseudo-randomness, the chaotic map is suitable to initialize the population for the purpose of increasing the population diversity and achieve high-quality solution, which is called chaos optimization algorithm $({\textit{COA}})$ [37].

Particularly, in Ref. [37], Yang reveals the inherent mechanism of high efficiency and superior performance of ${\textit{COA}}$, from new respects of both the probability distribution property and search speed of chaotic sequences generated by different chaotic maps. And the statistical property and search speed of chaotic sequences are presented by the probability density function $({\textit{PDF}})$ and the Lyapunov exponent $({\textit{LE}})$ in respect. Among the eight chaos maps mentioned in Ref. [37], it is found that the circle map makes a better performance than others in many aspects. Its equation is written as

$$\begin{aligned} z_{n+1}=\left( z_{n}+\Omega -\frac{K}{2\pi }\sin (2\pi z_{n})\right) \hbox {mod} \ 1, \end{aligned}$$

(9)

where z is chaotic variable and the parameters K and $\Omega$ can be thought of as strength of nonlinearity and externally applied frequency, respectively. The circle map produces much unexpected behavior with the change of parameters.

Thus, in this paper, the circle map is used to initialize the population and the parameters are chosen as $\Omega =0.5$, $K=2$. At the same time, according to Ref. [38], using the opposition-based population initialization instead of the random initialization can achieve better initial solutions and then accelerate convergence speed. Therefore, in the phase of population initialization, an opposition-based learning method and a chaos optimization algorithm are combined to generate initial population. The pseudo-code of the proposed chaotic initialization is given in Algorithm 1 shown below.

Remark 1

Algorithm 1 is also used by the scout bees to discover a new food source.

4.2 Two modified solution searching equations

In order to achieve satisfying performance, all of the population-based optimization algorithms have to balance two contradictory aspects of their performances: exploration and exploitation. In the optimization algorithms, the exploration represents the ability to search the various unknown regions in the solution space to discover the global optimum, while the exploitation stands for the ability to take advantages of the information of the previous solutions to discover better solutions. That is, to achieve good performance on optimization problem, the two abilities must be well balanced. However, the solution searching equation of the standard ABC algorithm is selected to generate new candidate solutions based on the information of previous solutions. It is good at exploration but poor at exploitation [39], which result in some challenging problems, such as slow convergence speed when dealing with those unimodal problems.

To improve the performance of the standard ABC algorithm, one effective research trend is to investigate searching equations. So far, a variety of searching equations have been put forward [39–43]. The most representative one is GABC proposed by Zhu and Kwong [39]. In this method, in order to improve the exploitation and make full use of the information of the global best (gbest) solution to guide the search of candidate solution, a modified searching equation enlightened by PSO is suggested as follows:

$$\begin{aligned} v_{i,j}=x_{i,j}+\phi _{i,j}(x_{i,j}-x_{k,j})+\psi _{i,j}(x_{best,j}-x_{i,j}),\nonumber \\ \end{aligned}$$

(10)

where the third term in the right-hand side of Eq. (10) is a new added term called gbest term, $x_{best,j}$ is the jth element of the global best solution, and $\psi _{i,j}$ is a uniform random number in [0, 1.5]. Nevertheless, based on the experimental results shown in Ref. [39], it can be found that the improvement of the algorithm is not notable. Hence, to further develop the performance of the ABC algorithm, two improved searching equations are proposed as

$$\begin{aligned} v_{i,j}= & {} x_{r1,j}+\lambda (x_{i,j}-x_{r1,j})+\mu (x_{best,j}-x_{r1,j}), \end{aligned}$$

(11)

$$\begin{aligned} v_{i,j}= & {} x_{best,j}+p_{i}(x_{i,j}-x_{best,j})+\nu (x_{r1,j}-x_{r2,j}),\nonumber \\ \end{aligned}$$

(12)

where $x_{best,j}$ is the jth element of the global best solution. Similar to PSO algorithm, $x_{i,j}$ denotes the jth element of the best previous solution of the ith employed bee (i.e., local-best position or its experience). r1 and r2 are distinct integers randomly selected from $\{1,2,\ldots ,SN\}$ and are also different from i and best. $j\in \{1,2,\ldots ,n\}$ is a randomly chosen index. $p_{i}$ represents the current probability of the ith employed bee. $\lambda$, $\mu$ are random numbers in the range [0, 1] and $\nu$ is a random number in the range $[-1,1]$.

In Eq. (11), with the first term, the new candidate solution is generated around $X_{r1}$ which is a randomly selected individual from the population. The randomly selected individual $X_{r1}$ can bring more information to the searching equation and avoid trapping into the local optimum, which contributes to improving the exploration ability. Besides, although the guidance of $X_{best}$ is not used in the first term, Eq. (11) can also take full advantages of $x_{i,j}$ and $X_{best}$ in the latter two terms to drive the new candidate solution toward the current best solution, which can guarantee its convergence speed. So the last two terms of Eq. (11) make a contribution to developing the exploitation ability. As a whole, Eq. (11) can balance the exploration and exploitation well. But, due to the guidance of $X_{r1}$ in the first term, Eq. (11) place more emphasis on the exploration. According to [27], on the employed bee phase, the searching process focuses on the exploration which is consistent with emphasis of Eq. (11). Therefore, Eq. (11) is chosen as the searching equation for the employed bees.

From Eq. (12), owing to the first term, the new candidate solution is generated around $X_{best}$ which represents the current global best solution. The current probability is added in the second term to make full use of the information of the current population to further improve the exploitation. Therefore, the first two terms is good for the development of exploitation ability. In addition, to keep balance in corresponding to the first two terms in Eq. (12), the third term is introduced to improve the diversity of the population. To sum up, Eq. (12) may be beneficial to not only the convergence but also the diversity of the population. However, since the the guidance of $X_{best}$ in the first term, Eq. (12) pays more attention to the exploitation. According to Ref. [27], the onlooker bee phase lays stress on the exploitation which is in accordance with the emphasis of Eq. (12). Therefore, Eq. (12) is employed as the searching equation for the onlooker bees.

4.3 The change in the ratio of employed and onlooker bees

In standard ABC algorithm, half of the colony is composed of employed bees and the rest half is composed of onlooker bees, originally proposed by Karaboga and Basturk in Ref. [27]. That is, the ratio between the employed bees and onlooker bees is $\{1{:}1\}$. In Ref. [44], the ratio between two types of bees was changed as $\{$1:1, 1:2, 1:3, 1:4, 2:1, 3:1, 4:1, 2:2, 2:3, 3:2$\}$, respectively. From the simulation results in Ref. [44], it was shown that in some cases, the high ratio of onlooker bees had better effect on the new algorithm when compared to high ratio of employed bees, while in some cases, the high ratio of employed bees had better performance with respect to high ratio of onlooker bees. In a word, different ratios between onlooker and employed bees has better performance in contrast to the standard ABC algorithm. Particularly, a higher number of onlooker bees performs better results. Therefore, the ratio of employed and onlooker bees in this paper is taken as {1:4}.

4.4 The framework of HABC algorithm

In view of the above, the pseudo-code of the HABC algorithm is given below:

4.5 A novel parameter estimation scheme

Now, with the above HABC algorithm, the problem of parameter estimation for fractional-order chaotic systems is converted into that of nonlinear function optimization.

Then, the procedure of the new method is outlined in the following pseudo-code:

5 Simulations

To demonstrate the effectiveness of the proposed scheme, two typical fractional-order chaotic systems (namely fractional-order economic and Rössler systems) are selected to test the performance. The simulations are implemented using MATLAB 7.1 on Intel(R) Core(TM) i5-3470 CPU, 3.2 GHz with 4 GB RAM. To calculate the objective function, the number of samples is set as 300 and the step size is 0.01. The parameters of HABC algorithm are set as follows: population size (SN) is 100; maximum cycle number of iterations (MCN) are set as 50 for fractional-order economic system and 100 for fractional-order Rössler systems, respectively; the control parameter (limit) is 15, and the maximum number of chaotic iteration $N=300$. For the parameters of DE algorithm, according to Ref. [26], the scaling factor $F=0.5$ is usually a good choice. If the parameter F is smaller, the population may converge prematurely. On the contrary, the convergence speed decreases. Besides, about the crossover rate CR, a large CR often speeds up convergence. However, from a certain value upwards, the convergence speed may decrease or the population may also converge prematurely. A good choice for the crossover rate is a value between ${\textit{CR}}=0.3$ and ${\textit{CR}}=0.9$. In the following experiments, the parameters of DE are selected as: $F=0.5, \textit{CR}=0.7$. For PSO, empirical results have shown that a inertia weight $w=0.7298$ and cognitive and social factors with $c1=c2=1.49618$ provide good convergent behavior [24, 45]. So in the following simulation, the parameters for PSO are set as: $w=0.7298, c1=c2=1.49618$. Besides, according to Ref. [46], the best parameter setting for GA is $c_{r}=0.8, m_{u}=0.1$, where $c_{r}$ is the crossover rate and $m_{u}$ is the mutation rate. In order to eliminate the difference of each experiment, the algorithm is executed 15 times for each example, and all runs are terminated after the predefined maximum cycle number of iterations is reached. The HABC algorithm is compared with some existing typical ABC-based algorithms and other typical population-based algorithms (e.g., PSO, DE and GA) separately. To make a fair comparison, the searching spaces of the parameters are the same for all algorithms.

5.1 Comparison with some typical ABC-based algorithms

In this subsection, the performance on the search ability of the HABC algorithm is compared with some typical ABC-based algorithms, including the standard ABC, GABC [39] and EABC [43] algorithms. The basic parameter settings are the same as the HABC algorithm. Besides, based on the above parameter settings, just considering the influence of the population size (SN) on the time complexity, for the HABC algorithm proposed in Sect. 4 in a single iteration, the time complexity can be analyzed as follows: The time complexity of the employed bees searching around their neighbors is $O(0.2*SN)$; the time complexity for calculating the fitness values is $O(0.2*SN)$; the time complexity for calculating the probability values is $O(0.2*SN)$; the worst time complexity for the onlooker bees to select the nectar sources is $O(0.8*SN*0.2*SN)$;

the worst time complexity for updating the best nectar source is $O(0.2*SN)$; the worst time complexity for the scout bees to replace bad nectar source is $O(0.2*SN)$. Therefore, for one iteration, the worst time complexity is: $O(0.2*SN)+O(0.2*SN)+O(0.2*SN)+O(0.8\, * SN * 0.2*SN)+O(0.2*SN)+O(0.2*SN)$, and it can be simplified as $O(0.16*SN^{2})$. Thus, the worst time complexity for the HABC algorithm is $O(HABC)=O(0.16*SN^{2})$. Similarly, the time complexity for the standard ABC algorithm introduced in Sect. 2.2 is $O(ABC)=O(0.25*SN^{2})$; the time complexity for the GABC [39] and EABC [43] algorithms is $O(0.25*SN^{2})$ as well. Obviously, the time complexity of HABC algorithm is smaller than those of standard ABC, GABC and EABC algorithms. Then, simulations are done to synchronize the fractional-order economic system.

Example 1

Fractional-order economic system [16, 47, 48] described as:

$$\begin{aligned} \left\{ \begin{array}{l} _{0}D^{\alpha _{1}}_{t}x(t)=z(t)+(y(t)-a)x(t),\\ _{0}D^{\alpha _{2}}_{t}y(t)=1-by(t)-x^{2}(t),\\ _{0}D^{\alpha _{3}}_{t}z(t)=-x(t)-cz(t), \end{array} \right. \end{aligned}$$

(13)

when $(a,b,c)=(1,0.1,1)$, $(\alpha _{1},\alpha _{2},\alpha _{3})=(0.90,0.85,0.95)$ and initial point is $(2,-1,1)$, system (13) is chaotic. To show the performance of HABC algorithm clearly and for ease of representation in figures, the true values of fractional orders $\alpha _{1},\alpha _{2}$ and systematic parameter a are randomly assumed as unknown parameters which need to be estimated. The searching spaces of the unknown parameters and orders are set as $(\alpha _{1},\alpha _{2}, a)$ $\in$ $[0.1,1.4]\times [0.1,1.4]\times [0.5,1.5]$.

The corresponding objective function can be chosen as

$$\begin{aligned} F(\tilde{\alpha }_{1},\tilde{\alpha }_{2},\tilde{a})=\sum ^{N}_{k=1}\Vert Y_{k}-\tilde{Y}_{k}\Vert _{2}, \end{aligned}$$

(14)

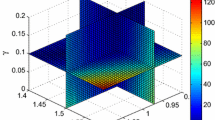
therefore, the problem of inversion for the chaotic systems (13) is transformed into that of nonlinear function optimization (14). In particular, the smaller F is, the better combination of parameters $(\alpha _{1},\alpha _{2},a)$ is. Figure 1 shows the distribution of the objective function value for the fractional-order economic system (13). As viewed from different colors in Fig. 1, it is obviously seen that the objective function values are smaller in the vicinity of the point $(\alpha _{1},\alpha _{2},a)=(0.90,0.85,1.00)$ than those in other places.

Fig. 1

Distribution of the objective function values for fractional-order economic system (13) with $(\alpha _{3},b,c)=(0.95,0.1,1)$

The statistical results of the best, the mean and the worst estimated parameters with corresponding relative error values over 15 independent runs are shown in Table 1. From Table 1, it can be easily found that the estimated values generated by HABC algorithm are closer to the true parameter values, which indicates that it is more accurate than the standard ABC, GABC and EABC algorithms. Besides, it can also be clearly seen that the relative error values obtained by HABC algorithm and marked with black are all smaller than those of the standard ABC, GABC, EABC algorithms, which can further prove that the HABC algorithm has higher calculation accuracy. What’s more, the best objective function values obtained by HABC algorithm is better than those obtained by the comparison algorithms.

Table 1 Simulation results of various algorithms for system (13) over 15 independent runs

The evolutionary curves of the parameters and objective function values estimated by various algorithms are shown in Figs. 2, 3 and 4 in a single run. Figures 2, 3 and 4 show that convergence processes of the parameters and objective function values of HABC algorithm are much better than other algorithms. The estimated parameters can be earlier close to the true values than comparison algorithms. The corresponding relative error values and objective function values obtained by HABC algorithm decline faster than other algorithms. In one word, it can be concluded that HABC algorithm has a better search ability with a smaller time complexity.

Fig. 2

Estimated parameter values with some ABC-based algorithms on fractional-order economic system (13)

Fig. 3

Relative error values with some ABC-based algorithms on fractional-order economic system (13)

Fig. 4

Best objective function values with some ABC-based algorithms

5.2 Comparison with some other typical population-based algorithms

To further test the effectiveness of the proposed scheme, the proposed HABC algorithm is mainly compared with the well-known PSO, DE and GA algorithms in this subsection. Similar to the analysis of the time complexity in Sect. 5.1, here the population size (${\textit{SN}}$) is only considered to have an influence on the time complexity. For the PSO algorithm, the time complexity can be obtained as follows: The time complexity for the initialization of the particle swarm is O(SN); the time complexity for calculating the fitness values is O(SN); the time complexity for updating the individual extreme value is O(SN); the time complexity for selecting the best individual extreme value is O(SN); the time complexity for updating the velocities and positions is O(SN). Therefore, the worst time complexity of PSO algorithm for one iteration is: $O(SN)+O(SN)+O(SN)+O(SN)+O(SN)$, which can be simplified as $O(PSO)=O(SN)$. For the DE algorithm, the time complexity mainly depends on the time complexities of mutation operation (O(SN)), crossover operation (O(SN)) and selecting operation (O(SN)). Therefore, the time complexity of DE algorithm for one iteration is $O(DE)=O(SN)$. Similar to the DE algorithm, the time complexity of GA algorithm is mainly determined by the time complexities of roulette wheel selection operation ($O(SN^{2})$), crossover operation (O(SN)) and mutation operation (O(SN)). Thus, the time complexity of the GA algorithm can be regarded as $O(GA)=O(SN^{2})$. In a word, it can be concluded that $O(GA)\simeq O({\textit{HABC}})>O({\textit{PSO}})\simeq O({\textit{DE}})$. Then, simulations are conducted to identify the fractional-order Rössler system.

Example 2

Fractional-order Rössler system [16, 47, 49] described as:

$$\begin{aligned} \left\{ \begin{array}{ll} _{0}D^{\alpha _{1}}_{t}x(t)=-(y(t)+z(t)),\\ _{0}D^{\alpha _{2}}_{t}y(t)=x(t)+ay(t),\\ _{0}D^{\alpha _{3}}_{t}z(t)=b+z(t)(x(t)-c), \end{array} \right. \end{aligned}$$

(15)

when $(a,b,c)=(0.5,0.2,10)$, $(\alpha _{1},\alpha _{2},\alpha _{3})=(0.90,0.85,0.95)$ and initial point is (0.5, 1.5, 0.1), system (15) is chaotic. Similarly, to show the performance of HABC algorithm clearly and for ease of representation in figures, the fractional orders $\alpha _{1},\alpha _{2},\alpha _{3}$ are randomly selected as unknown parameters to be estimated in this example. The searching spaces of the unknown parameters are set as $(\alpha _{1},\alpha _{2},\alpha _{3})\in [0.4,1.4]\times [0.4,1.4]\times [0.4,1.4]$. The distribution of the objective function value for the fractional-order Rössler system (15) is shown in Fig. 5.

Fig. 5

Distribution of the objective function values for fractional-order Rössler system (15) with $(a,b,c)=(0.5,0.2,10)$

The statistical results in terms of the best, the mean and the worst estimated parameters by various algorithms over 15 independent runs are listed in Table 2. From Table 2, it can be seen that the HABC algorithm has more accurate results than those of PSO, DE and GA algorithms. Figures 6, 7 and 8 depict the convergence profile of the evolutionary processes of the estimated parameters and the objective function values. From the figures, it can be seen that HABC algorithm can still converge to the optimal solution more rapidly and accurately than other algorithms.

Fig. 6

Estimated parameter values with some other population-based algorithms on fractional-order Rössler system (15)

Fig. 7

Relative error values with some other population-based algorithms on fractional-order Rössler system (15)

Fig. 8

Best objective function values with some other population-based algorithms on fractional-order Rössler system (15)

Table 2 Simulation results of various algorithms for system (15) over 15 independent runs

In addition, from the aspect of the time complexity, it can be clearly seen that under the same level of time complexity with the GA algorithm, the HABC algorithm has faster convergence speed and higher calculation accuracy in estimating the unknown fractional-order system (15). Besides, although the time complexity of HABC algorithm is higher than those of PSO and DE algorithms, its better search ability in convergence speed and accuracy could compensate for this shortcoming to some extent.

6 Conclusions

In this paper, a novel parameter estimation scheme based on a hybrid artificial bee colony (HABC) algorithm is proposed to identify the unknown fractional-order chaotic systems from the point of optimization. The hybrid algorithm is improved in terms of population initialization, searching equation and the ratio between employed and onlooker bees. In order to verify the optimization capabilities of the HABC algorithm, two typical fractional-order chaotic systems are chosen to test the performance. Compared with some ABC-based algorithms and some other population-based algorithms, the estimated results demonstrate the strong capabilities and the effectiveness of the proposed algorithm. It is shown that, for the given parameter configurations and maximum number of iterations, the HABC algorithm could estimate the unknown fractional-order chaotic systems more rapidly, more accurately and more stably. The proposed method can avoid the design of parameter update law in synchronization analysis of the fractional-order chaotic systems with unknown parameters. In general, the proposed HABC algorithm is a feasible, effective and promising method for parameter estimation of unknown fractional-order chaotic systems. Furthermore, although this paper mainly concentrates on the parameters estimation problem of uncertain fractional-order chaotic systems, the proposed method is also a useful tool for the study of various numerical optimization problems in physics and other related areas.