1 Introduction

It is a well-known fact that humans while choosing their control actions use their experience for dealing with variety of situations. The quality of control action taken by them significantly improves as they gain more knowledge and experience. Then, a human who has been trained with a set of control and identification-related tasks when presented with a new task (belonging to same category) is found to generate efficient actions (close to optimal) by utilizing the previously acquired knowledge.

To have above kind of effectiveness and efficiency in a machine, it must be equipped with the following components:

  1. 1.

    Collection of mathematical models representing the plants, controller or identification.

  2. 2.

    To have best possible configuration involving these components (along with sensors) so that the desired objective is achieved.

  3. 3.

    Learning algorithm which can make the controller and other components present in the configuration to generate the desired responses.

Above three components are deemed fundamental in order to make machine to behave like humans and learn from its own experience. In any control setting, a designer (human) is provided with the plant, environment and the control objectives and he is required to design and implement an appropriate controller. If he has dealt with similar situation before, then it will not be very difficult for him. But, most of the times the knowledge about the dynamics of given plant is poorly known or unknown which makes the job of designer more difficult. In such scenarios, we require an intelligent tool which can approximate the plant’s dynamics and then with the help of this identification tool the control algorithm can be formulated. Neural networks are found to be very useful in performing both the identification and control tasks. In this paper, they are used as a part of adaptive dynamic programming scheme for identification and control of nonlinear dynamical systems.

Various effective techniques have been applied for the development of the learning systems (Bhuvaneswari et al. 2009; Castillo and Melin 2003; Aguilar-Leal et al. 2016; Man et al. 2011; Tutunji 2016). Problems like optimization and optimal control can be solved using a tool known as dynamic programming (DP). But, it suffers from a well-known problem of curse of dimensionality (Bellman 1957; Dreyfus and Law 1977). The solution of Hamilton–Jacobi–Bellman (HJB) equation is an optimal cost function only when certain good number of analytic conditions is met. However, it is very difficult to obtain HJB equation solution theoretically, excluding systems such as linear systems which satisfy some very good conditions like quadratic utility and zero targets. So much progress have been made for dealing with the problem of curse of dimensionality by developing a system, called as critic, in order to approximate the cost function defined in the dynamic programming (Balakrishnan and Biega 1996; Jin et al. 2007; Hendzel and Szuster 2011). The strategic utility function or cost-to-go function (which in dynamic programming refers to the Bellman’s equation function) is approximated by the critic neural network (Xiao et al. 2015). Adaptive dynamic programming is developed from the combination of dynamic programming and artificial neural network (ANN) (Zhang et al. 2014; Song et al. 2013). ANNs are characterized of having strong learning potential, ability to approximate any nonlinear function and able to adapt according to situation (Srivastava et al. 2002, 2005; Singh et al. 2007). ADP has number of synonyms including adaptive critic designs (Prokhorov et al. 1997), approximate dynamic programming (Al-Tamimi et al. 2008; Werbos 1992), neuro-dynamic programming (Bertsekas and Tsitsiklis 1995), neural-dynamic programming (Si and Wang 2001) and reinforcement learning (Bertsekas 2011). Dynamic programming provides an optimal control strategy using Bellman equation for nonlinear dynamical systems (Yang et al. 2014). Adaptive critic designs (ACDs) are generally composed of neural networks and have the capability of doing optimization over time in the presence of uncertainties like disturbances etc.

In the literature, a number of different types of critics have been proposed. For example, Q-learning system was developed by Watkins and Dayan (1992). On the other hand, Werbos have developed systems that are capable of approximating the dynamic programming (Werbos 1992). He proposed a family of ACDs by doing the fusion of reinforcement learning and an adaptive dynamic programming. Using the idea of ADP, Abu-Khalaf and Lewis (2005), Vrabie and Lewis (2009) and Vamvoudakis and Lewis (2010) have investigated the continuous-time nonlinear optimal control problems. Traditional supervised learning neural networks are unable to develop an optimal controller since the effects of the series of sequential control actions taken can only be seen at the end of the sequence (Lewis and Vrabie 2009).

In Liu et al. (2013), the authors have used ANN to implement critic and action network. But in simulation, they have not tested their algorithm under disturbance signal and parameter variation effects. In paper Ni and He (2013), an internal goal structure was introduced in the ADP scheme for providing the internal goal/reward representation. In Liu et al. (2014), decentralized control strategy using online optimal learning approach was developed to ensure the stability of interconnected nonlinear systems. Further in Liu and Wei (2014), the solution of infinite horizon optimal control problem of nonlinear systems was developed using a new discrete-time policy iteration based on ADP. In Jiang and Jiang (2014), authors have proposed a method by combining techniques such as back stepping, small gain-theorem for nonlinear systems with the ADP. In Gao and Jiang (2015), authors have developed optimal controller by converting the problem of output regulation into a global robust optimal stabilization problem using the non-model based ADP scheme. In Dong et al. (2016), a novel event-triggered ADP scheme is developed for solving the optimal control problem for nonlinear systems. Authors in Song et al. (2016) developed a new off-policy action-critic structure for compensating the effects of disturbances on the nonlinear systems. In Yang et al. (2016), authors have developed a guaranteed cost neural tracking control algorithm based on ADP for the class of continuous-time matched uncertain nonlinear systems. In their algorithm, they have introduced a discount factor and transformed the guaranteed cost tracking control problem into an optimal tracking control problem. In Gao et al. (2016), authors have used policy iteration and value iteration methods to develop data-driven output-feedback control policies based on ADP. In Zhu et al. (2016), the authors have proposed an iterative ADP-based method to solve the continuous-time, unknown nonlinear zero-sum game with only online data. In Wang et al. (2016), the authors have designed a data-based adaptive critic for the optimal control of nonlinear continuous systems based on ADP.

In most of the literature available, no papers exist (to the best of our knowledge) that have carried out the comparative analysis between the algorithm they have developed in their papers and the GD algorithm. This comparative analysis is carried out in our present paper. Further, most papers have not shown robustness in the simulations. Also, many papers have not utilized the concept of adaptive learning rate which actually helps in getting the faster convergence of weights to their respective desired values. The contributions and novelties of our paper are summarized below.

1.1 Novelties and contributions of the paper

  1. 1.

    Compared the performance of LS algorithm with that of available gradient descent (GD) algorithm.

  2. 2.

    Dynamics of plants were assumed unknown in order to have the control over effects like parameter variation, disturbances and lack of knowledge about the dynamics of the plant. This is achieved by using the NN-based identifier.

  3. 3.

    Adaptive learning rate is used to ensure the faster learning and convergence of weights to their desired values.

  4. 4.

    Robustness of LS algorithm is checked against both parameter variation and disturbance signals effects.

The optimal control law is obtained by using an adaptive critic method in which two ANNs which are action neural network (whose output is a control signal to the plant) and critic neural network (approximate action network cost function) and their parameters (weights) undergo change during training. These two neural networks provide an approximation to the Hamilton–Jacobi–Bellman equation which is associated with the theory of optimal control (Song et al. 2010). The adaption process starts with a random non-optimal control action generated by the action neural network which gets improved with the subsequent iterations. Critic neural network guides the action neural network in adjusting its parameters (weights). Now coming to the problem of identification and control. If the system is linear time invariant (LTI), then identification of its dynamics are straightforward using conventional methods (Ljung 1998), but in reality almost every system is nonlinear. So, intelligent tools like neural network, which themselves are nonlinear, are used to approximate their dynamics (Petrosian et al. 2000). They do not require the information of the type of nonlinearity present in the system. The type of control done in this paper is indirect adaptive control. In this type of control, the parameters of controller continue to change (update) in real time depending upon the current mathematical model of the plant identified by the neural-based identification model. In case of direct control, parameters of controller are updated directly solely on the basis of trajectory error without requiring the intermediate step of identification (Lilly 2011).

Fig. 1
figure 1

Structure of proposed scheme (color figure online)

Full size image

Rest of the paper is organized as follows: Sect. 2 contains the mathematical formulation and structure of proposed scheme. In Sect. 3, the weights update equations are derived for all the three neural networks using gradient descent (GD) principle. It is followed by Sect. 4 which contains Lyapunov stability (LS) method-based derivation of weight update equations. Section 5 contains the mathematical formulation of adaptive learning rate. Section 6 contains simulation results. It contains 3 numerical examples on which the proposed scheme based on both LS and GD methods is applied. Robustness against parameter variation and disturbance signal is also tested. Section 7 includes the contribution and achievements of this paper. Section 8 contains the conclusion.

2 Preliminaries: structure of proposed scheme and its mathematical formulation

The performance index (cost function) for adjusting weights of action neural network is defined as

$$\begin{aligned} E_\mathrm{a}(k)=\frac{1}{2}[J(k)]^2 \end{aligned}$$
(1)

where J(k) represents critic neural network output at kth instant, and it is defined as

$$\begin{aligned} J(k)=\sum ^{\infty }_{k=i}{\gamma ^{k-i}U(k)} \end{aligned}$$
(2)

Here U(k) is the output of utility function which is defined as

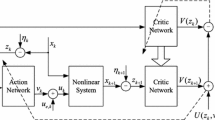
$$\begin{aligned} U(k)=\frac{1}{2}[e(k)]^2 \end{aligned}$$
(3)

\(\gamma \) represents the discount factor with its values lying in \(0<\gamma \le 1\). The objective is to generate the control signal sequence from the output of action neural network so as to minimize J(k) value. This refers to the optimality principle for the discrete-time systems. So, if by any strategy we are able to generate control sequence which makes J(k) value closer to or equal to zero, then it will also make value of U(k) closer to or equal to zero. If that happens, then output of plant will follow the desired trajectory. The structure of the proposed scheme, which is based on adaptive dynamic programming, is shown in Fig. 1. The components present inside the broken red line box are action neural network, utility function and the critic neural network. The dynamics of the plant under consideration are assumed unknown, so a separate artificial neural network (ANN)-based identification model is set up in parallel to the plant. TDL denotes the tapped delay lines and has delayed values of its input signal as its output. The output of this ANN identification model is represented by N(k). The desired trajectory is denoted by r(k). The input to the utility function is the error between the desired trajectory value and plant’s output. Thus, trajectory error is

$$\begin{aligned} e(k)=r(k)-y(k) \end{aligned}$$
(4)
Fig. 2
figure 2

General structure of artificial neural network

Full size image

The output of utility function acts as an input to the critic neural network, which implements Eq. 2. The performance index for critic neural network is defined as

$$\begin{aligned} E_\mathrm{c}(k)=\frac{1}{2}[e_\mathrm{c}(k)]^2 \end{aligned}$$
(5)

where

$$\begin{aligned} e_\mathrm{c}(k)=J(k-1)-U(k)-\gamma J(k) \end{aligned}$$
(6)

If \(e_\mathrm{c}(k)\) is zero, then Eq. 6 implies

$$\begin{aligned} J(k-1)=U(k)+\gamma J(k) \end{aligned}$$
(7)

or it can be written as

$$\begin{aligned} \begin{aligned} J(k-1)&= U(k)-\gamma [U(k+1)+\gamma J(k+1)]\\&= \sum ^{\infty }_{m=k}{\gamma ^{m-k}U(k)}\\ \end{aligned} \end{aligned}$$
(8)

The important thing to note in Eq. 8 is that if we are able to minimize the error defined in Eq. 6 by doing training of the critic neural network, then estimate of the cost function defined in Eq. 2 will be given by critic neural network output. Basically, in the proposed scheme, all three neural networks undergo online training simultaneously. The critic neural network output gets minimized by adjusting the weights of action neural network. This adjustment will happen during the online training. If this happens, then e(k) becomes closer to zero. Since output of utility function depends upon e(k) so if value of U(k) approaches zero, then value of J(k) will also approach to zero. In general, the output of a good critic network should not be negative if U(k) is nonnegative. This will be possible when U(k) is defined equal to the square of error in tracking control problems (Visnevski 1997).

2.1 How the proposed scheme works?

The performance index for updating the action neural network weights is actually the function of output of critic neural network as \(E_\mathrm{a}(k)=\frac{1}{2}[J(k)]^2\). Thus, if we are able to reduce the output of critic neural network to zero, then there will not be any need to update the weights of action network. Now it is interesting to see when the output of critic neural network becomes zero? From the Fig. 1, we can see that the input of critic neural network is actually the output of utility function, U(k), where U(k) is the function of its own input signal e(k) as \(U(k)=\frac{1}{2}[e(k)]^2\). The error, e(k), represents the difference between the desired external input r(k) and the output of the plant y(k), and our objective is to have y(k) follows r(k). Now if the weights of the action neural network are updated in the correct direction, then a correct control signal will be generated by the action neural network (as its output) and will make the plant to produce output equal to that of external input r(k). When this happens, e(k) becomes zero which makes the output of utility function and the critic neural network zero. This is the desired objective. Now to have the weights to be updated in the right direction, we need a learning algorithm (weight adjustment method). In this paper, LS-based weight updating algorithm is developed which is implemented and compared with that of GD-based algorithm. Action, critic and utility functions are the components of the ADP scheme which are being utilized to implement the adaptive control. Also, the other important component in the control scheme is the NN-based identification model (identifier). As the training progress, the identifier learns the dynamics of the plant in the form of its own weight values. The identifier is needed as we need the value of jacobian (which is \(\frac{\partial y(k)}{\partial u_\mathrm{c}(k)}\approx \frac{\partial N(k)}{\partial u_\mathrm{c}(k)}\)). The value of this derivative is obtained with the help of the NN-based identifier mathematical model (which is the mathematical equation of NN-based identifier).

3 Weights adjustment algorithm for ADP using gradient descent (GD) principle

In this section, recursive update equations are derived using gradient descent principle for adjusting the weights of action and critic neural networks and ANN identification model (identifier). Single hidden layer is taken in all these three neural networks with single neuron in the output layer and 20 neurons in the hidden layer. A general artificial neural network is shown in Fig. 2. Though the structure of ANN is available in the literature, it is drawn again in an expanded form in order to show the various signals present in it, how they are processed and to show the various symbols used for denoting these signals. It will provide the clarity on how the chain rule is to be applied while back propagating the output error to the hidden layers during the derivation of update equations for the input–output weight vectors.

3.1 Update equations for action neural network weights

The performance index for action neural network is already defined in Eq. 1. Let \(W_{2\mathrm{a}}(k)\) and \(W_{1\mathrm{a}}(k)\) denote output and input weight vectors, respectively, in action neural network at any kth instant and let \(W_{1\mathrm{c}}(k)\) and \(W_{2\mathrm{c}}(k)\) denote input and output weight vectors, respectively, in critic neural network. Let \(V_{1\mathrm{c}}(k)\) and \(V_{2\mathrm{c}}(k)\) denote induced fields for hidden neurons and output neuron, respectively, in the critic neural network and \(S_{1\mathrm{c}}(k)\) and \(S_{1\mathrm{a}}(k)\) denote output of hidden neurons in critic and action neural network, respectively. The induced fields of hidden and output neurons in action neuron network are denoted by \(V_{1\mathrm{a}}(k)\) and \(V_{2\mathrm{a}}(k)\), respectively. The activation functions used for hidden and output neuron in action, critic neural network and ANN identifier are hyperbolic tangent and purelin (linear with slope equal to 1), respectively. To obtain the update equations for the weights in action neural network, the performance index is differentiated with respect to respective weights of action neural network. Let y(k) denote output of the plant. On differentiating \(E_\mathrm{a}(k)\) with respect to output weight vector, we will have the following weight update equation:

$$\begin{aligned} \begin{aligned} W_{2\mathrm{a}}(k+1)= {}&W_{2\mathrm{a}}(k)+\eta J(k)W_{2\mathrm{c}}(k)\left( 1-(S^2_{1\mathrm{c}}(k))\right) \\&\times W_{1\mathrm{c}}(k)e(k)\frac{\partial N(k)}{\partial u_\mathrm{c}(k)}S_{1\mathrm{a}}(k) \end{aligned} \end{aligned}$$
(9)

where \(\eta \) denotes a learning rate and its value lies between (0, 1]. Since the dynamics (mathematical model) of the plant are assumed to be unknown, the value of the jacobian will be given by ANN identifier as it captures the dynamics of the plant during the online training. The identification procedure requires knowledge of the structure of unknown plant and its order because structure of identification model is chosen same as that of plant. Let N(k) denote output of ANN identification model. Then, the value of jacobian is calculated as

$$\begin{aligned} \frac{\partial y(k)}{\partial u_\mathrm{c}(k)}\approx \frac{\partial N(k)}{\partial u_\mathrm{c}(k)} \end{aligned}$$
(10)

Similarly, update equation for input weight vector of action neural network is:

$$\begin{aligned} W_{1a}(k+1)= & {} {} W_{1a}(k)+\eta J(k)W_{2c}(k)\left( 1-(S_{1c}(k))^2\right) \nonumber \\&\times W_{1c}(k)e(k)\frac{\partial N(k)}{\partial u_\mathrm{c}(k)}W_{2a}(k)\nonumber \\&\times \left( 1-\left( S^2_{1a}(k)\right) \right) r(k) \end{aligned}$$
(11)

3.2 Update equations for critic neural network weights

The performance index for critic neural network is already defined in Eq. 5. Differentiating it with respect to output weights of critic neural network, we will get the following input weights update equation

$$\begin{aligned} W_{2\mathrm{c}}(k+1)=W_{2\mathrm{c}}(k)+\eta e_\mathrm{c}(k)[-\gamma ]S_{1\mathrm{c}}(k) \end{aligned}$$
(12)

Following the same procedure, the update equation for input weight vector of critic neural network can be written as

$$\begin{aligned} W_{1\mathrm{c}}(k+1)= & {} W_{1\mathrm{c}}(k)\nonumber \\&+\,\eta e_{\mathrm{c}}(k)[-\gamma ]W_{2\mathrm{c}}(k)\left( 1-(S_{1\mathrm{c}}(k))^2\right) U(k)\nonumber \\ \end{aligned}$$
(13)

3.3 Update equations for ANN identification model weights

The performance index defined for ANN identification model is

$$\begin{aligned} E_\mathrm{i}(k)=\frac{1}{2}[e_\mathrm{i}(k)]^2 \end{aligned}$$
(14)

where

$$\begin{aligned} e_\mathrm{i}(k)=y(k)-N(k) \end{aligned}$$
(15)

Let \(W_{21}(k)\) and \(W_{1\mathrm{i}}(k)\) denotes output and input weight vectors of ANN identifier. Using chain rule, the update equation for the adjustments of output weight vector of ANN identifier is

$$\begin{aligned} \begin{aligned} W_{2\mathrm{i}}(k+1)= {}&W_{2\mathrm{i}}(k)+\eta \frac{\partial E_\mathrm{i}(k)}{\partial y(k)}\frac{\partial y(k)}{\partial u_\mathrm{c}(k)}\frac{\partial u_\mathrm{c}(k)}{\partial W_{2\mathrm{i}}(k)}\\&\\ \end{aligned} \end{aligned}$$
(16)

and update equation for input weight vector is

$$\begin{aligned} \begin{aligned} W_{1\mathrm{i}}(k+1)={}&W_{1\mathrm{i}}(k)+\eta \frac{\partial E_\mathrm{i}(k)}{\partial y(k)}\frac{\partial y(k)}{\partial u_\mathrm{c}(k)}\frac{\partial u_\mathrm{c}(k)}{\partial S_{1\mathrm{i}}(k)}\\&\times \frac{\partial S_{1\mathrm{i}}(k)}{\partial V_{1\mathrm{i}}(k)}\frac{\partial V_{1\mathrm{i}}(k)}{\partial W_{1\mathrm{i}}(k)}\\ \end{aligned} \end{aligned}$$
(17)

4 Lyapunov stability (LS) criterion-based weight learning algorithm

To remove the shortcomings of the GD-based update equations like instability or stucking in local minima (Denaï et al. 2007), Lyapunov stability criterion is now used to derive the weights update equations. In Lyapunov stability method, we initially choose a scalar function \(V_{rm L}(X)\), where X denotes its argument vector, which is a positive definite function (Chen 2011) for all initial conditions of its arguments except when all of them are simultaneously equals to zero. Now, system is said to be asymptotic stable if both conditions described by Eqs. 18 and 19 are met

$$\begin{aligned} V_\mathrm{L}(X)>0\quad {\hbox {for}}~{\hbox {all}}~ X~{\hbox {except}}~X=0 \end{aligned}$$
(18)

and

$$\begin{aligned} \frac{{\hbox {d}}V_\mathrm{L}(X)}{{\hbox {d}}t}= {\hbox {negative}}~{\hbox {definite}}\quad {\hbox {for}}~{\hbox {all}}~ X \end{aligned}$$
(19)

If both these conditions are met, then system is asymptotic stable. To lay the foundation for the weight learning algorithm, let us express the generalized form of weight update equation as:

$$\begin{aligned} W_\mathrm{g}(k+1)=W_\mathrm{g}(k)-\eta \Delta W_\mathrm{g}(k) \end{aligned}$$
(20)

where \(W_\mathrm{g}(k)\) represents a generalized weight vector (which denotes input–output weights of all three neural networks in the scheme). Let \(E_\mathrm{g}(k)\) be a generalized performance/cost function which denotes \((E_\mathrm{a}(k)\), \(E_\mathrm{c}(k)\) and \(E_\mathrm{i}(k))\) and is a function of generalized error, \({\hat{e}}(k)\), that represents \((e_\mathrm{c}(k)\), \(e_\mathrm{a}(k)\) and \(e_\mathrm{i}(k))\). This generalized performance function is defined as

$$\begin{aligned} E_\mathrm{g}(k)=\frac{1}{2}({\hat{e}}(k))^2 \end{aligned}$$
(21)

then \(\Delta W_\mathrm{g}(k)\) according to GD principle is given as

$$\begin{aligned} \Delta W_\mathrm{g}(k)=\frac{\partial E_\mathrm{g}(k)}{\partial W_\mathrm{g}(k)} \end{aligned}$$
(22)

or

$$\begin{aligned} \Delta W_\mathrm{g}(k)=\frac{\partial E_\mathrm{g}(k)}{\partial {\hat{e}}(k)}\frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)} \end{aligned}$$
(23)

As Eq. 23 may get into the problem of local minima, we choose Lyapunov function as

$$\begin{aligned} V_\mathrm{L}(k)=\frac{1}{2}[({\hat{e}}(k))^2+(W_\mathrm{g}(k))^2] \end{aligned}$$
(24)

This is a positive definite function. Since we are working in discrete domain, the second condition for asymptotic stability can be written as:

$$\begin{aligned} \Delta V_\mathrm{L}(k)=V_\mathrm{L}(k+1)-V_\mathrm{L}(k)\le 0 \end{aligned}$$
(25)

Now, we will try to prove Eq. 25 which in turn gives us the condition on \(\Delta W_\mathrm{g}(k)\). It is obvious that \(\Delta k\rightarrow 1\) as we are working in discrete environment. So, Eq. 25 can be written as

$$\begin{aligned} \begin{aligned} \Delta V_\mathrm{L}(k)={}&\frac{1}{2}[({\hat{e}}(k+1))^2+(W_\mathrm{g}(k+1))^2]\\&-\, \frac{1}{2}[({\hat{e}}(k))^2+(W_\mathrm{g}(k))^2]\\ \end{aligned} \end{aligned}$$
(26)

On writing similar nature terms together, we will get

$$\begin{aligned} \begin{aligned} \Delta V_{L}(k)={}&\frac{1}{2}[{\hat{e}}(k+1)^2-{\hat{e}}(k))^2]\\&+\,\frac{1}{2}[(W_\mathrm{g}(k+1))^2-(W_\mathrm{g}(k))^2]\\ \end{aligned} \end{aligned}$$
(27)

or

$$\begin{aligned} \begin{aligned} \Delta V_{L}(k)={}&\frac{1}{2}[{\hat{e}}(k+1)+{\hat{e}}(k)][{\hat{e}}(k+1)-{\hat{e}}(k)]\\&+\,\frac{1}{2} [W_\mathrm{g}(k+1)+W_\mathrm{g}(k)][W_\mathrm{g}(k+1)-W_\mathrm{g}(k)]\\ \end{aligned} \end{aligned}$$
(28)

Let \(\Delta {\hat{e}}(k)={\hat{e}}(k+1)-{\hat{e}}(k)\) and \(\Delta W_\mathrm{g}(k)= \big \{W_\mathrm{g}(k+1)-W_\mathrm{g}(k)\big \}\) so using them in Eq. 28 we will get

$$\begin{aligned} \begin{aligned} \Delta V_{L}(k)={}&\frac{1}{2}\Delta {\hat{e}}(k)[\Delta {\hat{e}}(k)+2{\hat{e}}(k)]\\&+\, \frac{1}{2}\Delta W_\mathrm{g}(k)[\Delta W_\mathrm{g}(k)+2W_\mathrm{g}(k)]\\ \end{aligned} \end{aligned}$$
(29)

On rearrangement of terms, Eq. 29 can be written as

$$\begin{aligned} \begin{aligned} \Delta V_{L}(k)={}&\frac{1}{2}[\Delta W_\mathrm{g}(k)]^2\left[ 1+\left[ \frac{\Delta {\hat{e}}(k)}{\Delta W_\mathrm{g}(k)}\right] ^2\right] \\&+\Delta W_\mathrm{g}(k)\left[ W_\mathrm{g}(k)+{\hat{e}}(k)\left[ \frac{\Delta {\hat{e}}(k)}{\Delta W_\mathrm{g}(k)}\right] \right] \end{aligned} \end{aligned}$$
(30)

For a very small change, Eq. 30 can be written as

$$\begin{aligned} \Delta V_{L}(k)= & {} \frac{1}{2}[\Delta W_\mathrm{g}(k)]^2\left[ 1+\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] ^2\right] \nonumber \\&+\Delta W_\mathrm{g}(k)\left[ W_\mathrm{g}(k)+{\hat{e}}(k)\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] \right] \end{aligned}$$
(31)

Theorem

For Lyapunov function, \(V_{L}(k)=\frac{1}{2}[({\hat{e}}(k))^2+(W_\mathrm{g}(k))^2]>0\), the condition \( \Delta V_{L}(k)\le 0\) is satisfied if and only if

$$\begin{aligned} \Delta W_\mathrm{g}(k)=-\frac{\left\{ W_\mathrm{g}(k)+{\hat{e}}(k)\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] \right\} }{1+\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] ^2} \end{aligned}$$
(32)

Stability Proof

From Eq. 31 , let

$$\begin{aligned} \Delta V_{L}(k)= & {} \frac{1}{2}[\Delta W_\mathrm{g}(k)]^2\left[ 1+\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] ^2\right] \nonumber \\&+\Delta W_\mathrm{g}(k)\left[ W_\mathrm{g}(k)+{\hat{e}}(k)\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] \right] =-\frac{1}{2}z\nonumber \\ \end{aligned}$$
(33)

where z must have a positive or zero value in order for condition, \(\Delta V_{L}(k)\le 0\), to hold. So Eq. 33 becomes

$$\begin{aligned} \Delta V_{L}(k)&{=}&\frac{1}{2}[\Delta W_\mathrm{g}(k)]^2\left[ 1{+}\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] ^2\right] \nonumber \\&+\,\Delta W_\mathrm{g}(k)\left[ W_\mathrm{g}(k){+}{\hat{e}}(k)\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] \right] {+}\frac{1}{2}z=0\nonumber \\ \end{aligned}$$
(34)

Consider a general quadratic equation

$$\begin{aligned} ax^2+bx+c=0 \end{aligned}$$
(35)

The roots of the quadratic equation are given by

$$\begin{aligned} d_1=\frac{-b+\sqrt{b^2-4ac}}{2a}\quad {\hbox {and}}\quad d_2=\frac{-b-\sqrt{b^2-4ac}}{2a} \end{aligned}$$
(36)

Comparing Eq. 34 with Eq. 35, it can be easily seen that \(\Delta W_\mathrm{g}(k)\) acts as x in Eq. 35 and values of a, b and c in Eq. 34 are : \(a=\frac{1}{2}\left[ 1+\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] ^2\right] \) , the value of b is equal to \(b=\left[ W_\mathrm{g}(k)+{\hat{e}}(k)\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] \right] \) and \(c=\frac{1}{2}z\). To have single unique solution of quadratic equation, the term \(\sqrt{b^2-4ac}\) must be equal to zero. Putting values of a, b and c in \(\sqrt{b^2-4ac}=0\), we get

$$\begin{aligned} \sqrt{\left[ W_\mathrm{g}(k)+{\hat{e}}(k)\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] \right] ^2-\left[ 1+\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] ^2\right] z}=0 \end{aligned}$$
(37)

Squaring both sides, we will get

$$\begin{aligned} \left[ W_\mathrm{g}(k)+{\hat{e}}(k)\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] \right] ^2-\left[ 1+\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] ^2\right] z=0 \end{aligned}$$
(38)

z comes out to be

$$\begin{aligned} z=\frac{\left[ W_\mathrm{g}(k)+{\hat{e}}(k)\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] \right] ^2}{\left[ 1+\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] ^2\right] } \end{aligned}$$
(39)

Since \(z\ge 0\), it means

$$\begin{aligned} \frac{\left[ W_\mathrm{g}(k)+{\hat{e}}(k)\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] \right] ^2}{\left[ 1+\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] ^2\right] }\ge 0 \end{aligned}$$
(40)

So, the unique root of Eq. 34 will be given as

$$\begin{aligned} \Delta W_\mathrm{g}(k)=\frac{-b}{2a}=\frac{-\left[ W_\mathrm{g}(k)+{\hat{e}}(k)\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] \right] }{\left[ 1+\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] ^2\right] } \end{aligned}$$
(41)

Hence, Eq. 32 is proved. Substituting \(\Delta W_\mathrm{g}(k)\) value from Eqs. 41 to 20, we get

$$\begin{aligned} W_\mathrm{g}(k+1)=W_\mathrm{g}(k)+\eta \frac{\left[ W_\mathrm{g}(k)+{\hat{e}}(k)\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] \right] }{\left[ 1+\left[ \frac{\partial {\hat{e}}(k)}{\partial W_\mathrm{g}(k)}\right] ^2\right] } \end{aligned}$$
(42)

Eq. 42 is the Lyapunov stability-based weight update equation for the adjustment of input–output weight vectors of all three neural networks of ADP scheme.

Figure 3 shows a flowchart which depicts step-by-step detailed procedure of training for adjusting all three neural networks weights.

Fig. 3
figure 3

Flowchart for weights adjustment training

Full size image

5 Adaptive learning rate

It is a well-known fact that the speed of training and convergence behavior depends upon number of factors like number of hidden neurons chosen, number of hidden layers used and the value of learning rate \(\eta \). In most of the cases, if the value of \(\eta \) is chosen very small, then number of iterations required to reach the optimal values of weight vectors will be exceedingly large. On the other hand, large value of \(\eta \) may leads to instability in the system or weights may oscillate during the iterations around the desired values. So, instead of choosing \(\eta \) to be constant if it is adjusted at each instant [thus making constant \(\eta \) to function of time instant \(\eta (k)\)], then it is known as adaptive (dynamic) learning rate. A number of methods have been proposed in the literature for adaptive adjustment of \(\eta (k)\). Becker and Le Cun (1988) showed that second derivatives of the error provide value of the curvature of error. This value can then be used to determine \(\eta (k)\) value dynamically in order to decrease the online training time. Franzini et al. (1987) utilized the concept of error surface curvature in which direction cosine of error derivative vector evaluated at instant k and \(k-1\) is employed to adjust the learning rate. In this paper, we propose a weighted vector average (of only output weight vectors of critic, action and identification neural networks) of direction cosine of successive incremental weighted vectors at several instants. Thus, each weight element in output weight vectors will be having adjustable \(\eta (k)\). Only output weight vector is chosen with adjustable \(\eta (k)\) because only for them the precise value of error is available. Input weight vectors in all three neural networks are adjusted with constant \(\eta \). This constant \(\eta \) value is taken to be 0.025 in all the simulation examples of this paper. Let \(\Delta W^{G}_\mathrm{o}(k)\) denote generalized adjustment output weight vector in all three identification models. During the learning (training), the change occurred in \(\Delta W^{G}_\mathrm{o}(k)\) between any two successive instants follows the steepest direction in order to reduce the cost function. If there occurs no change (or little change) in the direction between the two successive instants, then it implies that error surface local shape is relatively unchanged and in such case increasing the value of \(\eta (k)\) may increase the speed of minimization. On the other hand, if the current instant direction is very different from the previous instant direction, then it suggests error surface have quite complex local shape, then assigning \(\eta (k)\) with a smaller value may avoid the instability or overshooting problem. We propose to utilize the direction cosine of present \(\Delta W^{G}_\mathrm{o}(k)\) and several previously calculated \(\Delta W^{G}_\mathrm{o}(k)\) for adjusting the \(\eta (k)\). Then, \(\eta (k)\) is defined to be the weighted average of \(L+1\) successive incremental output weight vectors, where L is a positive integer and its value is set by us. In this paper, we used \(L=1\). The dynamic learning rate is then defined as

$$\begin{aligned} \begin{aligned} \eta (k)={}&\frac{\alpha _0\Delta W^{G}_\mathrm{o}(k)\Delta W^{G}_\mathrm{o}(k-1)}{\left\| \Delta W^{G}_\mathrm{o}(k)\right\| \left\| \Delta W^{G}_\mathrm{o}(k-1)\right\| }+\cdots \\&+\frac{\alpha _\mathrm{L}\Delta W^{G}_\mathrm{o}(k-L)\Delta W^{G}_\mathrm{o}(k-L-1)}{\left\| \Delta W^{G}_\mathrm{o}(k-L)\right\| \left\| \Delta W^{G}_\mathrm{o}(k-L-1)\right\| } \end{aligned} \end{aligned}$$
(43)

Further, the coefficients in Eq. 43 are assigned value as

$$\begin{aligned} \alpha _j=\frac{\beta }{e^j}~~~~~(j=0,1,2\ldots ,L) \end{aligned}$$
(44)

So, from the Eq. 44 it can be concluded that \(\alpha _0> \alpha _1> \alpha _2\cdots > \alpha _\mathrm{L}\). Value of \(\beta \) in Eq. 44 is evaluated as

$$\begin{aligned} \beta =\frac{1}{\sum ^{L}_{j=1}{e^{-j}}} \end{aligned}$$
(45)

6 Simulation results

Three nonlinear dynamical systems (plants) are used to test the ADP-based identification and control by using both gradient descent (GD)- and Lyapunov stability (LS)-based weight updating algorithms. The corresponding responses were compared, and it is found that the responses obtained with LS algorithm are better than those obtained with GD-based learning algorithm. The dynamics of plants considered are assumed to be unknown while carrying out the simulation study. In each example, the online training of each neural network is shown and the corresponding comparison of responses of plant with reference trajectory is plotted. The main objective of learning algorithm is to adjust the weights of all three neural networks in such a way that output of plant follows the reference trajectory signal r(k). After that, ADP is further tested with a different reference trajectory (whose values fall in the same domain as of initial trajectory values for which the system earlier underwent training) just to ensure that NNs get properly trained. Finally, the scheme is also tested against parameter variation and disturbance signal.

6.1 Example 1

Consider a nonlinear dynamical system described by the following difference equation (Narendra and Parthasarathy 1990)

$$\begin{aligned} y(k+1)=F[y(k),y(k-1)]+r(k) \end{aligned}$$
(46)

where

$$\begin{aligned} F[y(k),y(k-1)]=\frac{y(k)y(k-1)[y(k)+\lambda ]}{1+y^2(k)+y^2(k-1)} \end{aligned}$$
(47)

which is assumed to be unknown and parameter \(\lambda \) is equal to 0.05. Assuming system described by Eq. 46 is controllable and possess bounded-input bounded-output stability (BIBO), our aim is then to generate a control sequence so that output of the plant follows the desired trajectory r(k). The response of plant without control is shown in Fig. 4 when the desired trajectory signal \(r(k)={\hbox {sin}}(\frac{2\pi k}{240})\) is applied to it. From the figure, it can be noted that the response of plant (dotted red curve) is not following the desired trajectory (solid blue curve) and the reason for this is its own dynamics (plant).

Fig. 4
figure 4

Response of plant without ADP control (Example 1) (color figure online)

Full size image

So, proposed scheme, as shown in Fig. 1 is setup. Since F is unknown, to identify it following ANN-based identification model is set up in parallel to it

$$\begin{aligned} N(k+1)=N[y(k),y(k-1)]+u_\mathrm{c}(k) \end{aligned}$$
(48)

The series-parallel identification structure is used in which output(s) of the plant will be used to compute the next value of identification model. Since BIBO stability is assumed in the plant, all the signals in the ANN identification model will also remain bounded. The value of \(\gamma \) is selected to be 0.43. All three neural networks undergo training simultaneously. The response of ANN identification model at the end stages of learning is shown in Fig. 5. It can be seen from the figure that response of identification model (broken red line) due to Lyapunov stability (LS)-based learning algorithm is closer to the output of plant (solid blue line) than the response obtained (solid golden color line) due to gradient descent (GD) weight updating learning algorithm. As the online training progressed, response of plant continues to improve because weights of all three neural networks continues to update (improve). Figure 6 shows the response of plant during the final stages of training under the action of ADP scheme [where r(k) got replaced by \(u_\mathrm{c}(k)\) in Eq. 46 during controller action].

Fig. 5
figure 5

Response of ANN identification model (Example 1) (color figure online)

Full size image
Fig. 6
figure 6

Response of plant under ADP controller action (Example 1)

Full size image
Fig. 7
figure 7

Response of plant under ADP controller action with a different desired trajectory signal (validation) (Example 1) (color figure online)

Full size image

From the figure, it is seen that the response of plant, when ADP neural networks trained with LS algorithm, is following more closely the desired trajectory signal than the response obtained through GD-based learning algorithm. This shows that weights of each neural network in the proposed scheme reaches to their desired values (and hence can be freeze (stored)). Now, ADP with its final weights is tested (or validation) by taking a different desired trajectory signal

$$\begin{aligned} r(k) = \left\{ \begin{array}{ll} {\hbox {sin}}\left( \frac{2\pi k}{250}\right) + 0.2sin\left( \frac{2\pi k}{25}\right) &{}\quad \text{ if }~~ k \le 1000 \\ 1 &{} \quad \text{ if }~~ 1000<x \le 1500\\ {\hbox {sin}}\left( \frac{2\pi k}{125}\right) &{}\quad \text{ if }~~ 1500<x \le 2000\\ \end{array} \right\} \end{aligned}$$
(49)

Fig. 7 shows the response of plant under ADP scheme when above desired trajectory signal is used.

From the figure, it is again seen that the response of plant (continuous red line) obtained with LS algorithm is better than that (continuous golden line) obtained with GD-based learning. Since the weights are frozen after the training, the value of J(k) must be closer to zero. Figure 8 shows the plot of J(k) with LS- and GD-based ADP learning. The instantaneous mean square error (MSE) plot is shown in Fig. 9. It can be seen that the MSE remains close to zero all the time except at the instants when reference trajectory is changed. At these instants, a rise in MSE can be seen, but they quickly reduce to zero, which shows the robustness of the proposed scheme.

The response of critic neural network with LS learning is much smoother and closer to zero as compared to response obtained through GD-based weight learning. The response of critic neural network shows that weights of each neural network have reached to their optimum values. Figure 10 shows the average mean square error (MSE) using e(k) for different learning rates (i.e., the fixed learning rate for input weight vectors in all three neural networks is changed to different values) with LS and GD weight learning algorithm. From the bar graph, it is clear that average MSE in case of LS-based learning remains smaller than the GD-based weight learning for different learning rates (\(\gamma \) value was kept constant).

Fig. 8
figure 8

Response of critic neural network (Example 1)

Full size image
Fig. 9
figure 9

Instantaneous mean square error (MSE) (Example 1)

Full size image
Fig. 10
figure 10

Average MSE with LS and GD weight learning algorithm (Example 1)

Full size image

6.1.1 Performance testing against disturbance signal

The disturbance signal of magnitude 2.5 is added in identification model output at \(k=11{,}000\)th instant. The corresponding MSE plot with respect to \(e_\mathrm{i}(k)\) is shown in Fig. 11. From the figure, it can be seen that MSE (broken black line) with LS method reduces very quickly again to zero value after the effect of disturbance signal as compared to MSE drop (continuous blue line) obtained with GD method. So, we can write robustness order with respect to disturbance signal for two training algorithms as LS > GD.

Fig. 11
figure 11

Instantaneous MSE plot at disturbance signal instant (Example 1) (color figure online)

Full size image

6.2 Performance testing against parameter variation

Parameter \(\lambda \) of given plant is changed from its actual value 0.05 to 2 at \(k=10{,}000\)th instant. The corresponding variation in MSE is shown in Fig. 12. From the MSE plot, we can see that MSE response recovered very quickly with LS method as compared to GD method. This again shows the robustness order of training methods as LS > GD.

Fig. 12
figure 12

Instantaneous MSE plot at parameter variation instant (Example 1)

Full size image

6.3 Example 2

In this example, following nonlinear difference equation describes the BIBO stable dynamical system (Narendra and Parthasarathy 1990)

$$\begin{aligned} y(k+1)=G[y(k)]+r^3(k) \end{aligned}$$
(50)

where the nonlinear part

$$\begin{aligned} G[y(k)]=\frac{y(k)}{1+y^2(k)} \end{aligned}$$
(51)

is assumed to be unknown. Symbol r(k) denotes desired trajectory and is given as

$$\begin{aligned} r(k)={\hbox {cos}}\left( \frac{2\pi k}{240}\right) +0.2{\hbox {cos}}\left( \frac{k}{10}\right) \end{aligned}$$
(52)

The ANN identification model is chosen as

$$\begin{aligned} N(k+1)=N\left[ y(k)\right] ++r^3(k) \end{aligned}$$
(53)

The response of plant without ADP scheme is shown in Fig. 13. From the figure, it is clearly seen that the output of plant is not following the desired trajectory signal, so ADP scheme is again set up and the online training of all three neural networks is initiated. The value of \(\gamma \) is set to 0.43. Again, 20 neurons are used in the hidden layers for all three neural networks. The final stage plant output under ADP action is shown in Fig. 14. It is clear from the figure that response of plant (red line) with weights trained by LS algorithm is much closer to reference trajectory (blue line) than the response obtained with GD-based learning (green line). The response of ANN identification model during the final stages of online training is shown in Fig. 15. In this example also, we have obtained a better response from ANN identification model when its weights are updated through LS-based learning as compared to GD-based weight updating equations. Now, again it is time to test the neural networks (NNs) with updated weights by considering some different desired trajectory signal. The new desired trajectory is chosen as

$$\begin{aligned} r(k) = \left\{ \begin{array}{ll} {\hbox {cos}}\left( \frac{2\pi k}{250}\right) + 0.2{\hbox {sin}}\left( \frac{2\pi k}{25}\right) &{} \quad \text{ if }~~ k \le 500\\ 0.6{\hbox {sin}}\left( \frac{k}{120}\right) + 0.4{\hbox {cos}}\left( \frac{k}{21}\right) &{} \quad \text{ if }~~ 500\le x \le 900\\ {\hbox {sin}}\left( \frac{2\pi k}{125}\right) &{} \quad \text{ if }~~ 900<x \le 2000\\ \end{array} \right\} \end{aligned}$$
(54)
Fig. 13
figure 13

Plant response without control (Example 2)

Full size image
Fig. 14
figure 14

Plant response with ADP control (Example 2) (color figure online)

Full size image
Fig. 15
figure 15

ANN-based identification model output (Example 2)

Full size image

The plant response under ADP action corresponding to above external trajectory input is shown in Fig. 16. The response of plant obtained with LS method is very much closer to the desired trajectory than that obtained with GD-based method. This again shows the superiority of weights update equations obtained through LS method over the equations obtained through GD-based method. The response of critic neural network, J(k), is shown in Fig. 17. It is again seen that the critic response with LS method all the time remains close to zero as compared to response obtained through GD-based method. The average MSE bar chart corresponding to different learning rates, \(\eta \), is shown in Fig. 18 (where \(\gamma \) value was kept constant). From the figure, it is clear that average MSE in case of LS learning is much smaller than that obtained through GD-based weight update equations.

Fig. 16
figure 16

ADP-based plant output (validation) (Example 2)

Full size image
Fig. 17
figure 17

Critic neural network output (Example 2)

Full size image
Fig. 18
figure 18

Average MSE with different learning rates (Example 2)

Full size image

6.3.1 Testing of performance against disturbance signal

A disturbance signal of magnitude 3.1 is added in identification model output at \(k=37{,}000\)th instant.

Fig. 19
figure 19

Forced rigid pendulum

Full size image

Figure 19 shows the corresponding variation in MSE plot at the instant of disturbance signal. In this case also, MSE response with LS method is found to be better (as it reduces again to zero in a very short time after the inclusion of disturbance signal in the system) as compared to MSE response obtained with GD method. Thus, order of robustness against disturbance signal can be written as LS > GD.

6.4 Example 3

In this example, a forced rigid pendulum is considered. Its differential dynamical equation is given as in Lilly (2011)

$$\begin{aligned} I\ddot{\psi }=-M_\mathrm{g}L{\hbox {sin}}\psi -B\dot{\psi }+\tau \end{aligned}$$
(55)

The above equation is discretized with sampling period \(T=0.01\) s, and the corresponding difference equation is

$$\begin{aligned} \begin{aligned} \psi (k+2)={}&2\psi (k+1)-\psi (k)-32.66T^2{\hbox {sin}}(\psi (k))\\&-\,0.2T(\psi (k+1)-\psi (k))+T^222.22\tau (k)\\ \end{aligned} \end{aligned}$$
(56)
Fig. 20
figure 20

Instantaneous MSE when disturbance signal is added (Example 2)

Full size image
Fig. 21
figure 21

Open loop response of forced rigid pendulum (Example 3) (color figure online)

Full size image

\(\tau (k)\) represents the external control torque applied to the shaft at the attached point to the pendulum so that it follows the desired input trajectory signal. Figure 20 shows the forced pendulum (Lilly 2011). The values taken for various parameters in the pendulum model are mass: \(M=0.5\) kg, coefficient of friction at attached point: \(B=0.009\,\frac{{\hbox {kg}}\cdot {\hbox {m}}}{{\hbox {s}}^2}\), acceleration due to gravity: \(g=9.8\,\frac{{\hbox {m}}}{{\hbox {s}}^2}\) and length of mass less shaft: \(L=0.3\) m and moment of inertia: \(I=ML^2\). The open loop response of pendulum without controller action corresponding to desired input trajectory signal, \(r(k)=0.3{\hbox {sin}}(\pi kT)\), is shown in Fig. 21. From the figure, it can be clearly seen that the pendulum output (solid red line) is not following the desired input trajectory signal (solid blue line). Hence, ADP configuration as shown in Fig. 1 is set up. The value of \(\gamma \) is set to 0.27. Since the dynamics of pendulum are assumed to be unknown, ANN-based identification model is set up. The structure of series parallel identification model is chosen as

$$\begin{aligned} N(k+2)=N\left[ \psi (k+1), \psi (k)\right] +T^222.22\tau (k) \end{aligned}$$
(57)

The response of forced pendulum with LS- and GD-based learning algorithm is shown in Fig. 22. It can be seen from the figure that response due to LS-based weight learning is closer to reference trajectory as compared to response obtained with GD-based weight learning. The striking difference is in the number of iterations used in both the techniques. In LS-based method, only 400 iterations are used, whereas in GD-based method 1200 iterations were used to train the weights. A total of 1000 samples were used in every iteration during the training. This large difference in the number of iterations shows the superiority of the LS-based training over the GD-based training. Figure 23 shows the bar chart in which the comparison is shown in terms of average mean square error (MSE) by taking different learning rates. It can be easily seen that average MSE in the case of LS-based training is much less than that obtained with GD-based training. This again shows that LS-based weight update equation is more powerful than that obtained with GD-based learning method. So, from the 3 numerical examples simulated in this paper it can be easily concluded that weight update equation derived using LS-based method is more powerful than that obtained with GD-based method.

Fig. 22
figure 22

Response of Pendulum with ADP action (Example 3)

Full size image
Fig. 23
figure 23

Average MSE with different learning rates (Example 3)

Full size image

7 Contributions and achievements of this paper

  1. 1.

    Recursive weight update equations are developed using the powerful concept of Lyapunov stability criterion. The results so obtained are superior than those obtained through gradient descent based weight learning method. The benefit of using LS-based weight update equations is that it guarantees the stability of the system, and there is no fear of stucking in the minima (which may occur in case of GD-based weight update equations).

  2. 2.

    Though the dynamics of plants under consideration are assumed to be unknown, the proposed scheme is able to provide successfully the optimal trajectory control of unknown nonlinear dynamical systems.

  3. 3.

    Adaptive learning rate is employed in the weight update equation which ensures that in less number of iterations weights will reach to their optimal values.

  4. 4.

    In case of robustness also, LS-based method performed better than GD-based method.

  5. 5.

    The training of all three neural networks are done online which makes the proposed scheme more viable to be used in the real-time control applications. One such real-time example of forced pendulum is successfully controlled in this paper.

8 Conclusion

Recursive weight update equations for the proposed ADP scheme are derived using Lyapunov stability (LS) method, and the results so obtained were compared with the update equations using gradient descent (GD) principle. Both methods are able to provide the satisfactory results, but the responses obtained through LS method are improved and better than those obtained through GD method. The inclusion of adaptive learning rate has made the proposed learning algorithm more stronger. Also, in the presence of parameter variation and disturbance signal the performance of proposed scheme is found to be better with LS method as compared to the performance obtained with GD method. The models of plants considered in numerical simulation study are assumed to be unknown since there is always a possibility of lack of information about the dynamics of the plant and the presence of uncertainties like parameter variations and disturbance signals. Hence, in order to deal with these problems, a separate ANN identification model is set up which, during the online training, captures all these features. All three neural networks, namely critic neural network, action neural network and ANN identification model, which are employed in the ADP scheme, are able to successfully perform their respective functions (approximating the cost function, as a controller and as an identification model respectively), and simulation results obtained support these claims.