1 Introduction

Nowadays, neural network (NN) is extensively adopted to tackle unknown dynamics on account of its omnipotent approximation and learning capabilities [1,2,3]. And adaptive neural control (ANC) is established for a major category of nonlinear systems satisfying matching conditions by means of the adaptive technology [4,5,6,7]. These schemes are effectively developed to more common nonlinear systems with different structures [9,10,11,12,13,14], including pure feedback and strict feedback, by employing the backstepping method [8]. Moreover, ANC has been also successfully applied to various industrial systems [15,16,17,18]. Notice that ANC is motivated from the learning ability of human beings. As such, ANC should have the ability: acquiring experience knowledge of a changing environment, then reusing the experience knowledge to facilitate their work efficiency [19]. However, the ANC methods mentioned above pay little attention to neural learning ability, thereby still requiring to online training neural networks for similar control objectives. The major cause lies in the great challenge on the testification of the persistent excitation (PE) condition for closed-loop nonlinear systems. Hereafter, the neural learning issue was gradually developed as reinforcement learning [20,21,22] and adaptive dynamic programming [23,24,25], in which the PE condition is often presupposed to be met. To remove this restriction, a dynamic learning (DL) approach has been presented in [26] to accomplish the neural learning ability for closed-loop unknown system dynamics based on any recurrent reference orbit. This method has been extensively developed in theory [27,28,29,30,31] and practical engineering applications [32,33,34].

Compared to plentiful results of the aforementioned nonlinear systems in continuous-time form, the discrete-time (DT) counterpart is relatively few even though digital technology has been generally applied in industrial production [35,36,37,38,39,40]. The main reason lies in the following challenges: (1) The difference of the DT Lyapunov function is nonlinear, which makes the stability analysis more severe; (2) the controller design may encounter noncausal problems for the strict-feedback form, and (3) the existing framework and stability results cannot achieve the experience knowledge learning of unknown dynamics in the system. Some exclusive efforts have been made to solve these challenges [41,42,43,44,45]. To be more specific, for strict-feedback nonlinear systems (SFNSs) in DT case, an n-step predictor technology has been cleverly proposed in [41] to work out tracking control. Such a technology has been further developed to pure-feedback systems [42, 43] and multiinput-multioutput systems [44]. Based on a useful stability result of linear time-varying (LTV) systems in DT case subject to time delays, a novel DL strategy has been established in [46] to accomplish the learning control for DT SFNSs. It is worth pointing out that the n-step forward predictor technology brings about the n-step delay that exists in the NN weight updating law, which would lead to the complex weight storage, and the difficult knowledge reuse. Subsequently, a new ANC framework was proposed in [45] to avoid the time delay of weight updating laws by the variable substitution, instead of the n-step predictor. Unfortunately, this new framework cannot be directly used to solve neural DL because of the huge challenge on the exponentially convergent verification of neural weights. Particularly, unlike the continuous-time case, it is very difficult for DT SFNSs to construct the weight estimate error system as LTV system without delays, not to mention the exponential convergence of such a LTV system.

Inspired by the above discussion, this paper is to develop a new yet effective technology to handle the DL issue of SFNSs in DT form. To achieve such an objective, we construct a new auxiliary error estimator in this paper, and then a novel weight updating law is constructed based on the variable substitution framework. The developed approach can ensure the expected control performance and the exponential convergence of weight estimates. Specially, every convergent weight can be stored as a constant, which is easily stored and reused. As a result, the presented learning strategy facilitates the transient tracking performance and reduces the time/space complexity. To further clarify, the following contributions are listed:

  1. (1)

    A new auxiliary error estimator is subtly designed to estimate the system tracking error by the constant characteristic of the ideal value of the estimated weight;

  2. (2)

    A novel neural weight update law is constructed by the estimator error, instead of the traditional tracking error, which not only avoids time delay [16, 41, 42, 46, 50], but also guarantees every weight converges exponentially to its unique ideal value;

  3. (3)

    A novel learning controller is designed based on the simple storage and usage rules of the converged weights, which achieves the good control performance with small overshoot, fast convergence and little computation burden.

The rest of the paper is organized as follows. Section 2 gives the problem formulation and preliminaries. In Sect. 3, a novel dynamic learning control strategy is designed for a class of DT SFNSs by a new error estimator, which guarantee the closed-loop stability, the exponential convergence of estimated NN weights and the precise identification of unknown system dynamics. And then, the learning constant weights are stored and reused to design a static neural learning controller, which achieves the improved tracking control performance with less space complexity, better transient performance and less energy consumption. These advantages are illustrated in Sect. 4 by a simulation comparison. The conclusions are shown in Sect. 5.

Notation: General notations are used throughout this paper. The estimated variable is denoted by \(\hat{(\cdot )}\), and the estimation error is denoted by \(\tilde{(\cdot )}\). \(I_{m}\) denotes the \(m\times m\) identity matrix. The m-dimensional Euclidean space is denoted by \(R^m\). The recurrent orbit being made up of \(\Upsilon (k)\) is represented by \(\varphi (\Upsilon (k))\).

2 Problem formulation

Consider the DT SFNSs as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{\chi }_{i}(k+1)}= f_{i}({{\bar{\chi }}}_{i}(k))+g_{i}({{\bar{\chi }}}_{i}(k)){{\chi }_{i+1}(k)}\\&{{\chi }_{n}(k+1)}= f_{n}({{\bar{\chi }}}_{n}(k))+g_{n}({{\bar{\chi }}}_{n}(k)){u(k)}\\&{{y}(k)}={{\chi }_{1}(k)} \end{aligned}\right. \end{aligned}$$
(1)

where \(i=1,2,\ldots , n-1\), \(y(k)\in R\), \(\bar{\chi }_{j}(k) = [{\chi _1}(k),\ldots ,{\chi _j}(k)]^T\) \(\in R^j\) and \(u(k)\in R\) represent, severally, system output, state and input, \(f_{j}({\bar{\chi }}_{j}(k))\in R\) represent the unknown smooth nonlinear functions, and \(g_{j}({{\bar{\chi }}}_{j}(k))\in R\) stand for the known smooth functions, in which \(j=1,2,\ldots , n\).

Assumption 1 [41] \({g_{i}({{\bar{\chi }}}_{i}(k))}\) satisfies \({0<\underline{g}_{i}}\le |{g_{i}({{\bar{\chi }}}_{i}(k))}|\) \(\le {\overline{g}}_{i}\), in which \({\underline{g}_{i}}\) and \({{\overline{g}}_{i}}\) are two constants with \(i=1,2,\ldots ,n\).

Our main control objective is to construct a novel DL control strategy for DT SFNSs (1) with Assumption 1 such that: (1) the output signal y(k) can trace the recurrent tracking trajectory \(y_d(k)\); (2) NN weights can converge to their optimal values which is independent of the time sequence; (3) the converged weights can be easily expressed and reused for the amelioration of tracking control performance.

2.1 RBF NNs

2.1.1 Omnipotent approximation ability

Radial basis function (RBF) NNs [47] are adopted to tackle the unknown function \(\varpi {(\Upsilon (k))}\) as

$$\begin{aligned} \left. \begin{aligned} \varpi {(\Upsilon (k))}{=}W^{*T}{\Theta (\Upsilon (k))}+\epsilon (\Upsilon (k)),\forall {\Upsilon (k)}\in {\Omega _{\Upsilon }} \end{aligned}\right. \nonumber \\ \end{aligned}$$
(2)

in which \(m>1\) stands for NN node number, \(\Omega _{\Upsilon }\) denotes a compact set, \(W^*\in {R^m}\) stands for the desired weight vector, the DT NN input vector is denoted by \(\Upsilon (k)\subset {R^q}\). \(\epsilon (\Upsilon (k))\) denotes the approximation error which satisfies \(|{\epsilon (\Upsilon (k))}|\le {\epsilon ^*}\), in which \(\epsilon ^*>0\) denotes a tiny constant. \(\Theta (\Upsilon (k))=[\Theta _1(\Upsilon (k)),\Theta _2(\Upsilon (k)),\ldots ,\Theta _m(\Upsilon (k))]^T\in {R^m}\) stands for the activation function vector with \({\Theta _i(\Upsilon (k))}=\exp [-(\Upsilon (k)-\nu _{i})^T\) \((\Upsilon (k)-\nu _{i})/\ell _{i}^2]\), where \(\ell _i\) and \(\nu _{i}=[\nu _{i1},\nu _{i2},\ldots ,\nu _{iq}]^T\) are, respectively, the width and the center of NN.

2.1.2 Localized approximation ability

Reference [26] shows that the RBF NN owns the capacity of localized approximation. Particularly, for each recurrent signal \(\Upsilon (k)\in \Omega _{\Upsilon }\), by employing the neurons near \(\Upsilon (k)\), we have

$$\begin{aligned} \left. \begin{aligned} \varpi {(\Upsilon (k))}=W_{\xi }^{*T}{\Theta _{\xi }(\Upsilon (k))}+\epsilon _{\xi }(\Upsilon (k)) \end{aligned}\right. \end{aligned}$$
(3)

where \({W_{\xi }^*}\in R^{m_{\xi }}\) with \(m_{\xi }<m\) stand for neural weights closing to the recurrent orbit \(\varphi (\Upsilon (k))\) which is composed of NN inputs \(\Upsilon (k)\), the corresponding activation function and approximation error are, respectively, \({\Theta _{\xi }(\Upsilon (k))}=[{\Theta _{1\xi }(\Upsilon (k))},\) \(\ldots , {\Theta _{j\xi }(\Upsilon (k))}]^T\in {R^{m_{\xi }}}\), and \(\epsilon _{\xi }(\Upsilon (k))\). Due to the localized approximation ability, the term \(|{\epsilon _{\xi }(\Upsilon (k))}|\) is also arbitrarily small.

2.1.3 PE and exponential stability

Definition 1

[48] A DT sequence \(\Theta (\Upsilon (k))\) is regarded as PE if we can find positive constants \(k_0\), \(k_1\) and \(k_2\) such that

$$\begin{aligned} \left. \begin{aligned} \sum _{k=k_0}^{k_0+k_1-1}\Theta (\Upsilon (k))\Theta ^{T}(\Upsilon (k))\ge {k_2}{I}. \end{aligned}\right. \end{aligned}$$
(4)

Lemma 1

[48] Suppose that the neural input \(\Upsilon (k)\) maintains in a compact set \(\Omega _{\Upsilon }\) and is recurrent. Then, \(\Theta _{\xi }(\Upsilon (k))\) meets the PE condition for the recurrent sub-vector \(\Theta _{\xi }(\Upsilon (k))\) being made up of the activation function vector \(\Theta (\Upsilon (k))\) near \(\varphi (\Upsilon (k))\).

2.2 Exponential convergence of DT LTV systems

Consider the following DT LTV systems

$$\begin{aligned} \left. \begin{aligned} \eta (k+1)=C(k)\eta (k)+\delta (k) \end{aligned}\right. \end{aligned}$$
(5)

in which the system matrix is denoted by \(C(k) \in R^{m\times m}\), the system state is denoted by \(\eta (k) \in R^m\), and a bounded disturbance is \(\delta (k)\in R^{m}\).

Lemma 2

[48] Considering the LTV system in DT case (5), suppose that \(C(k) = {I_n} - \Gamma H(k){H^T}(k)\), \(H^T(k)\Gamma {H(k)}<2\), and \(\Vert \delta (k)\Vert \) represents an adequately small value, where \(H(k)\in R^{m}\) stands for a time-varying vector, and \(\Gamma \in R^{m\times m}\) represents a constant positive definite symmetric matrix. \(\eta (k)\) can converge exponentially to a tiny vicinity around origin if H(k) satisfies the PE condition.

3 DL control for DT strict-feedback system

A novel DL control strategy will be designed in this part for a class of DT SFNSs by using a new error estimator, so that NN weights can exponentially converge to a tiny vicinity of their desired values, and the unknown dynamics of the system can be precisely approximated by experienced neural networks with converged constant weights. To achieve such a goal and avoid the traditional causality contradiction, this paper firstly employs the variable substitution framework [45], and then the error estimator is cleverly designed to guarantee the exponential convergence of NN weights based on the exponential convergence theory of LTV systems in DT case. The overall scheme block diagram is shown in Fig. 1.

Fig. 1
figure 1

Overall scheme block diagram of the DL control strategy

Full size image

To begin with, define the following error variables:

$$\begin{aligned} \left. \begin{aligned} {z_i}(k) = {\chi _i}(k) - {\tau _{i - 1}}(k),~~i = 1,2,\ldots ,n \end{aligned}\right. \end{aligned}$$
(6)

where \({y_d}(k)\in R\) is the given reference trajectory, \({\tau _0}(k)={y_d}(k)\), and \({\tau _i}(k)\in R\) stands for the virtual controller.

Step 1: From (1) and (6), we have

$$\begin{aligned} \left. \begin{aligned} {z_1}(k + 1) =&{f_1}({{{\bar{\chi }}}_1}(k))+{g_1}({{{\bar{\chi }}}_1}(k)){\chi _2}(k) - {y_d}(k + 1)\\ =&{g_1}({{{\bar{\chi }}}_1}(k))\bigg [ {\tau _1}(k)+{z_2}(k)\\&\quad + \frac{{{f_1}({{{\bar{\chi }}}_1}(k)) - {y_d}(k + 1)}}{{{g_1}({{{\bar{\chi }}}_1}(k))}}\bigg ]. \end{aligned}\right. \end{aligned}$$
(7)

The virtual controller \({\tau _1}(k)\) is constructed as

$$\begin{aligned} \left. \begin{aligned} {\tau _1}(k) = {\rho _1}({\bar{\chi }_1}(k)) + \frac{{{y_d}(k + 1)}}{{{\iota _1}({{{\bar{\chi }}}_1}(k))}} \end{aligned}\right. \end{aligned}$$
(8)

in which \({\rho _1}({{{\bar{\chi }}}_1}(k)) = - \frac{{{f_1}({{\bar{\chi }}_1}(k))}}{{{g_1}({{{\bar{\chi }}}_1}(k))}}\) and \({\iota _1}({{\bar{\chi }}_1}(k)) = {g_1}({{{\bar{\chi }}}_1}(k))\).

Substituting (8) into (7) yields

$$\begin{aligned} \left. \begin{aligned} {z_1}(k + 1) = {g_1}({{\bar{\chi }}_1}(k)){z_2}(k). \end{aligned}\right. \end{aligned}$$
(9)

Step i (\(2\le i\le n-1\)): It follows from (1) and (6) that

$$\begin{aligned} \left. \begin{aligned} {z_i}(k + 1) =&{g_i}({\bar{\chi }_i}(k))\bigg [{z_{i + 1}}(k) + {\tau _i}(k) \\&+ \frac{{{f_i}({{{\bar{\chi }}}_i}(k))}}{{{g_i}({{{\bar{\chi }}}_i}(k))}}- \frac{{{\tau _{i - 1}}(k + 1)}}{{{g_i}({{{\bar{\chi }}}_i}(k))}}\bigg ]. \end{aligned}\right. \end{aligned}$$
(10)

Based on (1), we get that \({\chi }_{i}(k+1)\) is a nonlinear function of \(\bar{\chi }_{i+1}(k)\). Then, define the one-step predictor as

$$\begin{aligned} \left. \begin{aligned} {\chi _i}(k + 1) \buildrel \textstyle .\over = {\vartheta _i}({{\bar{\chi }}_{i + 1}}(k)),i = 1,2,\ldots ,n - 1. \end{aligned}\right. \end{aligned}$$
(11)

where \( {\vartheta _i}({{\bar{\chi }}_{i + 1}}(k))=f_{i}({\bar{\chi }}_{i}(k))+g_{i}({{\bar{\chi }}}_{i}(k)){{\chi }_{i+1}(k)}\), and \(\bar{\chi }_{i+1}(k) = [{\chi _1}(k),\ldots ,{\chi _j}(k),{\chi _{j+1}}(k),]^T\) \(\in R^{j+1}\).

To show how to deal with the causal contradiction issue, the expression of \({\tau _1}(k + 1)\) is first given. According to (8) and (11), we have

$$\begin{aligned} \left. \begin{aligned} {\tau _1}(k + 1) =&\, {\rho _1}({{{\bar{\chi }}}_1}(k + 1)) + \frac{{{y_d}(k + 2)}}{{{\iota _1}({{{\bar{\chi }}}_1}(k + 1))}}\\ =&\, {\rho _1}({\vartheta _1}({{{\bar{\chi }}}_2}(k))) + \frac{{{y_d}(k + 2)}}{{{\iota _1}({\vartheta _1}({{{\bar{\chi }}}_2}(k)))}}. \end{aligned}\right. \end{aligned}$$
(12)

From (12), the problem of causal contradiction can be avoided by converting the future signal \({\chi }_1(k + 1)\) into a function of \({{y_d}(k + 2)}\) and \({{{\bar{\chi }}}_2}(k)\). Subsequently, by employing recursive design methods, it can be concluded that

$$\begin{aligned} \left. \begin{aligned} {\tau _{i - 1}}(k + 1)&= {\rho _{i - 1}}({{\bar{\vartheta }} _{i - 1}}({{\bar{\chi }}_i}(k))) \\ {}&\quad + \frac{{{y_d}(k + i)}}{{{\iota _{i - 1}}({{{\bar{\vartheta }} }_{i - 1}}({{{\bar{\chi }}}_i}(k)))}} \end{aligned}\right. \end{aligned}$$
(13)

in which \({{\bar{\vartheta }} _{i - 1}}({{\bar{\chi }}_i}(k)) = [{\vartheta _1}({{\bar{\chi }}_2}(k)),\ldots ,{\vartheta _{i - 1}}({{\bar{\chi }}_i}(k))]^T \in R^{i-1}\).

Based on (10) and (13), one can establish the virtual controller law \({\tau _i}(k)\) as

$$\begin{aligned} \left. \begin{aligned} {\tau _i}(k) = {\rho _i}({{\bar{\chi }}_i}(k)) + \frac{{{y_d}(k + i)}}{{{\iota _i}({{\bar{\chi }}_i}(k))}} \end{aligned}\right. \end{aligned}$$
(14)

where

$$\begin{aligned} \Bigg \{ \left. \begin{aligned} {\rho _i}({{{\bar{\chi }}}_i}(k)) =&- \frac{{{f_i}({{\bar{\chi }}_i}(k))}}{{{g_i}({{{\bar{\chi }}}_i}(k))}} + \frac{{{\rho _{i - 1}}({{{\bar{\vartheta }} }_{i - 1}}({{{\bar{\chi }}}_i}(k)))}}{{{g_i}({{\bar{\chi }}_i}(k))}}\\ {\iota _i}({{{\bar{\chi }}}_i}(k)) =&{g_i}({{{\bar{\chi }}}_i}(k)){\iota _{i - 1}}({{{\bar{\vartheta }} }_{i - 1}}({{{\bar{\chi }}}_i}(k))). \end{aligned}\right. \end{aligned}$$
(15)

By (10) and (14), we have

$$\begin{aligned} \left. \begin{aligned} {z_i}(k + 1) = {g_i}({{\bar{\chi }}_i}(k)){z_{i + 1}}(k). \end{aligned}\right. \end{aligned}$$
(16)

Step n: Using the same analysis, we obtain

$$\begin{aligned} {z_n}(k + 1){} & {} = {g_n}({\bar{\chi }_n}(k)) \nonumber \\{} & {} \quad \times \bigg [\frac{{{f_n}({{{\bar{\chi }}}_n}(k))}}{{{g_n}({{\bar{\chi }}_n}(k))}} - \frac{{{\tau _{n - 1}}(k + 1)}}{{{g_n}({{\bar{\chi }}_n}(k))}}+u(k)\bigg ].\nonumber \\ \end{aligned}$$
(17)

From (6) and (14), we know that \(z_n(k)\) is unavailable because \(\tau _{n-1}(k) \) contains an unknown nonlinear function \(\rho _i(\bar{\chi }_i(k))\). To construct an effective neural learning controller u(k), the following recursive process is used in this paper by combining (9), (16) and (17)

$$\begin{aligned} \left. \begin{aligned} {z_1}(k + n) = \iota (k + n - 1)[ F(\Upsilon (k))+u(k)] \end{aligned}\right. \end{aligned}$$
(18)

where \(\iota (k + n - 1) = {g_1}({{\bar{\chi }}_1}(k + n - 1)){g_2}({\bar{\chi }_2}(k + n - 2))\cdots \) \({g_n}({{\bar{\chi }}_n}(k)) \in R\) is the known smooth nonlinear function, \(\Upsilon (k) = [{\chi _1}(k),{\chi _2}(k),\dots ,{\chi _n}(k),{y_d}(k + n)]^T \in R^{n+1}\), and \(F(\Upsilon (k))\) is defined as

$$\begin{aligned} F(\Upsilon (k)) =-{\rho _n}({{{\bar{\chi }}}_n}(k))+\frac{{{y_d}(k + n)}}{{\iota _n}({{{\bar{\chi }}}_n}(k))} \end{aligned}$$

in which \({\rho _n}({{{\bar{\chi }}}_n}(k))=-\frac{{{f_n}({{\bar{\chi }}_n}(k))}}{{{g_n}({{{\bar{\chi }}}_n}(k))}} + \frac{{{\rho _{n - 1}}({{{\bar{\vartheta }} }_{n - 1}}({{{\bar{\chi }}}_n}(k)))}}{{{g_n}({{\bar{\chi }}_n}(k))}}\), \({\iota _n}({{{\bar{\chi }}}_n}(k)) = {g_n}({{\bar{\chi }}_n}(k)){\iota _{n - 1}}({{{\bar{\vartheta }} }_{n - 1}}({{\bar{\chi }}_n}(k)))\). It can be easily obtained from Assumption 1 that \(\iota (k + n - 1) \) is bounded.

Since \( F(\Upsilon (k))\) is unknown, then by adopting the RBF NN given in (2), one has

$$\begin{aligned} \left. \begin{aligned} F(\Upsilon (k)) = {W^{*T}}\Theta (\Upsilon (k)) + \varepsilon (k). \end{aligned}\right. \end{aligned}$$
(19)

Then, the NN controller is developed as

$$\begin{aligned} \left. \begin{aligned} u(k) = - {\hat{W}^T}(k)\Theta (\Upsilon (k)) \end{aligned}\right. \end{aligned}$$
(20)

in which \({{\hat{W}}}(k)\) denotes the estimate of \({W^*}\). Substituting (20) into (18) yields

$$\begin{aligned} \left. \begin{aligned} {z_1}(k + n)\, {=}\, \iota (k + n - 1)[ - {{\tilde{W}}^T}(k)\Theta (\Upsilon (k)) + \varepsilon (k)] \end{aligned}\right. \nonumber \\ \end{aligned}$$
(21)

where \({\tilde{W}}(k)={\hat{W}}(k)-W^{*}\), which is the weight estimation error.

It can be seen from (21) that there exists \({n-1}\)-step delay between \(\tilde{W}(k)\) and \(z_1(k+n)\). Such a phenomenon may cause the delay in the neural weight updating law, thereby preventing the exponential convergence of weight estimates. To solve such a problem, a new auxiliary error estimator is designed in this paper. Firstly, error dynamic equation (18) is rewritten as

$$\begin{aligned} \left. \begin{aligned} {z_1}(k + 1) = \iota (k)[u({k_1}) + F(\Upsilon ({k_1}))] \end{aligned}\right. \end{aligned}$$
(22)

where \({k_1} = k - n + 1\).

Subsequently, design the following error estimator

$$\begin{aligned} \left. \begin{aligned} {{\hat{z}}_1}(k + 1) = \iota (k)[u({k_1}) + {{\hat{W}}^T}(k)\Theta (\Upsilon ({k_1}))]. \end{aligned}\right. \end{aligned}$$
(23)

Define the estimation error \({{\tilde{z}}_1}(k) = {{\hat{z}}_1}(k) - {z_1}(k)\). From (22) and (23), one has

$$\begin{aligned} \left. \begin{aligned} {{\tilde{z}}_1}(k + 1) = \iota (k)[{{\tilde{W}}^T}(k)\Theta (\Upsilon ({k_1})) - \varepsilon ({k_1})]. \end{aligned}\right. \end{aligned}$$
(24)

It is easily seen from (24), we have canceled the time delay between \({{\tilde{z}}_1}(k + 1) \) and \({\tilde{W}}(k)\). Based on the auxiliary estimation error, the neural weight updating law is skillfully constructed as

$$\begin{aligned} \left. \begin{aligned} {\hat{W}}(k + 1) = {\hat{W}}(k) - \Gamma \Theta (\Upsilon ({k_1})){{\tilde{z}}_1}(k + 1) \end{aligned}\right. \end{aligned}$$
(25)

where the design parameter \(\Gamma \) satisfies \(\Gamma =\Gamma ^T > 0\), and \( \lambda _{\max }(\Gamma ) =r\). Noting that \(\tilde{W}(k)={\hat{W}}(k)-W^{*}\), one has

$$\begin{aligned} \left. \begin{aligned} {\tilde{W}}(k + 1) = {\tilde{W}}(k) - \Gamma \Theta (\Upsilon ({k_1})){{\tilde{z}}_1}(k + 1). \end{aligned}\right. \end{aligned}$$
(26)

Remark 1

By using the constant characteristic of the ideal value of the estimated weight, a new auxiliary error estimator is subtly designed to estimate the system tracking error. Notice that two principles should be satisfied to achieve the exponential convergence of NN weights \(\hat{W}(k)\): (1) the neural weight updating law is implementable; (2) the error system \(\tilde{W}(k+1)\) can be converted into LTV system (5) in DT case. It is observed that \(z_n(k)\) is unavailable in this paper due to the unknown virtual control \(\tau _{n-1}\). Although \(z_1(k)\) is available, there is no connection between \(z_1(k)\) and \(\tilde{W}(k)\). As such, the use of \(z_1(k)\) cannot derive the LTV form of the weight estimate error system. To solve such a difficulty, auxiliary error estimator (23) is cleverly designed. Subsequently, estimation error system (24) is designed to construct the relationship between \(\tilde{z}_1(k + 1)\) and \(\tilde{W}(k)\). Moreover, since \(\tilde{z}_1(k + 1)\) is available, this paper creatively uses \(\tilde{z}_1(k + 1)\), instead of the traditional \(z_1(k+1)\), to design weight updating law \(\hat{W}(k+1)\), which makes two principles mentioned above be met. In addition, if we use \(\tilde{z}_1(k + 1)\) to design a neural weight updating law, each weight component of the estimated weight vector converges to one value instead of multiple values. Therefore, the convergent weights can be easily stored as constant weights.

Theorem 1

Consider the closed-loop system being made up of SFNSs (1), actual control input (20), error estimator (23) as well as weight update law (25). Then, we can prove that: (1) \(z_1(k)\) converges to the desired tiny vicinity around origin; (2) the estimated weights vector \({{\hat{W}}}(k)\) converges exponentially to the tiny vicinity of the desired weights vector \(W ^*\); (3) the unknown dynamics \(F(\Upsilon (k))\) is precisely approximated by the constant neural network \(\bar{W}^T\Theta (\Upsilon (k))\) with the converged weights \(\bar{W}\) expressed by

$$\begin{aligned} \left. \begin{aligned} {\bar{W}} = \textrm{mean}_{k \in [{k_i},{k_j}]}{\hat{W}}(k) \end{aligned}\right. \end{aligned}$$
(27)

where \({\textrm{mean}_{k \in [{k_i},{k_j}]}}{\hat{W}}(k) = \frac{1}{{{k_j} - {k_i} + 1}}\sum \nolimits _{k = {k_i}}^{{k_j}} {\hat{W}(k)}\), and \([{k_i},{k_j}] \) with \(k_j>k_i\) represents a time segment of steady-state process.

Proof: This proof will be divided into two parts. The first part will be used to complete the goal (1) of Theorem 1, and the goals (2) and (3) will be achieved in the second part.

(1) Let the Lyapunov function as

$$\begin{aligned} \left. \begin{aligned} V(k) = {{\tilde{W}}^T}(k){\Gamma ^{ - 1}}{\tilde{W}}(k) + \frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k) \end{aligned}\right. \end{aligned}$$
(28)

in which \({\bar{\iota }}>0\) is the upper bound of \(\iota (k)\). Subsequently, we have

$$\begin{aligned} \Delta V(k)= & {} {{\tilde{W}}^T}(k + 1){\Gamma ^{ - 1}}{\tilde{W}}(k + 1) - {{\tilde{W}}^T}(k){\Gamma ^{ - 1}} \nonumber \\{} & {} \times {\tilde{W}}(k)+ \frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k + 1) - \frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k). \end{aligned}$$
(29)

For convenience, let \(\Theta (k) = \Theta (\Upsilon (k))\). Substituting (26) into (29), we can get

$$\begin{aligned} \left. \begin{aligned} \Delta V(k) =&\frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k + 1) - \frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k)- 2{{\tilde{W}}^T}(k)\Theta ({k_1}){{{\tilde{z}}}_1} \\ {}&(k + 1) + {\Theta ^T}({k_1})\Gamma \Theta ({k_1}){{{\tilde{z}}}^2}_1(k + 1)\\ =&\frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k + 1) - 2\Big [\frac{{{{\tilde{z}}_1}(k + 1)}}{{\iota (k)}}+ \varepsilon ({k_1})\Big ]{{{\tilde{z}}}_1}\\ {}&(k + 1)- \frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k)+ {\Theta ^T}({k_1})\Gamma \Theta ({k_1}){{{\tilde{z}}}^2}_1(k + 1)\\ \le&- \frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k + 1) - \frac{1}{{\bar{\iota }}}{\tilde{z}}_1^2(k) - 2\varepsilon ({k_1}){{{\tilde{z}}}_1}(k +1)\\&+ {\Theta ^T}({k_1})\Gamma \Theta ({k_1}){{\tilde{z}}^2}_1(k + 1). \end{aligned}\right. \end{aligned}$$

Based on this fact \(\left\| \Theta (k)\right\| ^{2}\le l\) [49] and Young’s inequality, one obtains

$$\begin{aligned} \left. \begin{aligned} \Delta V(k) \le&- \frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k + 1) - \frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k) + \frac{{r{\tilde{z}}_1^2(k + 1)}}{{{\bar{\iota }}}}\\&+ \frac{{{\bar{\iota }}{\varepsilon ^2}({k_1})}}{r} + rl{{{\tilde{z}}}^2}_1(k + 1)\\ =&- \frac{{1 - r - rl{\bar{\iota }}}}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k + 1) - \frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k) \\ {}&\quad + \frac{{\bar{\iota }{\varepsilon ^2}({k_1})}}{r} \end{aligned}\right. \end{aligned}$$

where r is a positive constant. By selecting \(r < \frac{1}{{1 + l{\bar{\iota }}}}\) and using \(|\varepsilon (k)| \le {\bar{\varepsilon }} \) yields

$$\begin{aligned} \left. \begin{aligned} \Delta V(k) \le - \frac{1}{{{\bar{\iota }}}}{\tilde{z}}_1^2(k) + \frac{{{\bar{\iota }}{{\bar{\varepsilon }}^2}}}{r}. \end{aligned}\right. \end{aligned}$$
(30)

Formula (30) implies \(\Delta V(k) \le 0\), if

$$\begin{aligned} \left. \begin{aligned} |{{\tilde{z}}_1}(k)| > \frac{{{\bar{\iota }}{\bar{\varepsilon }} }}{{\sqrt{r} }}. \end{aligned}\right. \end{aligned}$$
(31)

From (30), it can be seen that for a small constant \({\mu _1} > \frac{{{\bar{\iota }}{\bar{\varepsilon }} }}{{\sqrt{r} }}\), we can find a integer \(\textrm{M}>0\), so that for each \(k>\textrm{M}\), \(|{\tilde{z}_1}(k)| < {\mu _1}\) holds. Further, we have \(|{{\tilde{z}}_1}(k + 1)| < {\mu _1}\) when \(k>\textrm{M}\).

According to (24), we have that \({\tilde{W}^T}(k)\Theta ({k_1}) = \frac{{{{{\tilde{z}}}_1}(k + 1)}}{{\iota (k)}} + \varepsilon ({k_1})\). Because \(\iota (k)\) is bounded, there is a small constant \({\mu _2} = {\textrm{O}_2}({\bar{\varepsilon }} )\), so that for each \(k>\textrm{M}\), \(| {{\tilde{W}}^T}(k)\Theta ({k_1})| < {\mu _2}\), i.e., \(| {{\tilde{W}}^T}(k+n)\Theta (k)| < {\mu _2}\)) holds.

By (26), we can get

$$\begin{aligned} \begin{aligned} {\tilde{W}}(k+n) =&{\tilde{W}}(k+n-1) - \Gamma \Theta (k){{{\tilde{z}}}_1}(k+n)\\ =&{\tilde{W}}(k) - \Gamma \sum \limits _{i = 1}^{n} {\Theta (k - n + i){{{\tilde{z}}}_1}} (k + i). \end{aligned} \nonumber \\ \end{aligned}$$
(32)

When \( k>\textrm{M}\), \({\tilde{W}}(k+n)\) is in the close vicinity of \({\tilde{W}}(k)\), because \(|{{\tilde{z}}_1}(k)| < {\mu _1}\), for \(\forall k > \textrm{M}\), where n is a finite real number. Then, according to \(| {{\tilde{W}}^T}(k+n)\Theta (k)| < {\mu _2},\forall k > \textrm{M}\) and (21), we know that there is a tiny constant \({\mu _3} = {\textrm{O}_3}({\bar{\varepsilon }} )\), so that for \(k>\textrm{M}\), \(|{z_1}(k+n) |< {\mu _3}\). Hence, \({z_1}(k)\) converges to a tiny vicinity of origin.

Based on (9), one has \({z_2}(k +n- 1) = \frac{1}{{{g_1}({{{\bar{\chi }}}_1}(k +n- 1))}} {z_1}(k+n)\). Noting that \({g_1}({{\bar{\chi }}_1}(k+n - 1))\) is bounded, there exists a small constant \({\mu _4} = {\textrm{O}_4}({\bar{\varepsilon }} )\), so that for each \(k>\textrm{M}\), \(|{z_2}(k+n - 1) |< {\mu _4}\) holds. As a result, \({z_2}(k)\) is tiny small. Similarly, on the basis of (16), it is easy to conclude that \({z_i}(k),~i = 3,\ldots ,n\), is also tiny small.

(2) In light of Theorem 1, \({z_1}(k)\) at time \(\textrm{M}\) is extremely small. Since \({y_d}(k)\) is recurrent and \({z_1}(k) = {\chi _1}(k) - {y_d}(k)\), it is obvious that \({\chi _1}(k)\) is recurrent. By (1), one has \({\chi _2}(k) = \frac{{{\chi _1}(k + 1) - {f_1}({{{\bar{\chi }}}_1}(k))}}{{{g_1}({{{\bar{\chi }}}_1}(k))}}\), which indicates that \({\chi _2}(k)\) is recurrent. In the same way, from (1), it is not difficult to deduce that for \(k > \textrm{M}\), \({\chi _i}(k)\) are also recurrent signals with \(i = 1,2,\ldots ,n\).

\(\varphi (\Upsilon (k))\) is the trajectory of NN input variables \(\Upsilon (k)\) starting from time \(\textrm{M}\). From Lemma 1, the recurrent sub-vector \({\Theta _\xi }(\Upsilon (k))\) meets the PE condition along the recurrent orbit \(\varphi (\Upsilon (k))\). Moreover, in light of (26), we get

$$\begin{aligned} \left. \begin{aligned} {{\tilde{W}}_\xi }(k + 1) = {A_\xi }(k){{\tilde{W}}_\xi }(k) + \delta _{\xi }(k) \end{aligned}\right. \end{aligned}$$
(33)

where

$$\begin{aligned} {A_{\xi }}(k) = {I_\xi } - \Gamma \iota (k){\Theta _\xi }({k_1}){\Theta ^T_\xi }({k_1}), \end{aligned}$$
$$\begin{aligned} \delta _{\xi }(k) = \Gamma \iota (k)S_\xi ^T({k_1}){\varepsilon _\xi }({k_1}) \end{aligned}$$

By choosing an appropriate parameter matrix \(\Gamma \), we have \(\iota (k){\Theta _\xi }({k_1})\Gamma {\Theta _\xi }^T({k_1}) < 2{I_\xi }\) holds. Combining the small perturbation \(\delta _{\xi }(k)\) and the PE condition of \({\Theta _\xi }({k_1})\), we can prove from Lemma 2 that \({{\tilde{W}}_\xi }(k)\) exponentially converges to a tiny vicinity around origin. This means that along \(\varphi (\Upsilon (k))\), \({\hat{W}_\xi }(k)\) can converge exponentially to a tiny vicinity of the desired weight \({W^*}\). On the other hand, the weight estimates \({{\hat{W}}_{{\bar{\xi }} }}(k)\) distant from the recurrent trajectory, remain nearly unchanged due to the smaller value \({\Theta _{{\bar{\xi }} }}(k)\). As such, when we select the initial values \({\hat{W}}(0) = \cdots = {\hat{W}}(n) = 0\), the weight estimates \({{\hat{W}}_{{\bar{\xi }} }}(k)\) will remain at zero. Based on the above analysis, every weight estimate can converge to a constant, which is expressed as

$$\begin{aligned} \left. \begin{aligned} {\bar{W}} = mea{n_{k \in [{k_i},{k_j}]}}{\hat{W}}(k) \end{aligned}\right. \end{aligned}$$
(34)

where \([{k_i},{k_j}],{k_j}> {k_i} > M\) denotes the time quantum after the transient process.

Subsequently, along \(\varphi (\Upsilon (k))\), we can obtain

$$\begin{aligned} F(\Upsilon (k))= & {} {\hat{W}} ^T(k){\Theta }(\Upsilon (k)) + {\varepsilon _{1}}(k) \nonumber \\= & {} \bar{W}^T{\Theta }(\Upsilon (k)) + {\varepsilon _2}(k) \end{aligned}$$
(35)

where \(|{\varepsilon _2}(k)| < \varepsilon \) is very small.

Remark 2

It should be pointed out that the traditional n-step predictor scheme is widely employed in the existing results [16, 41, 42, 46, 50] to convert system (1) into the n-step predictor system. Such a method results in weight updating law with n-step delays, i.e., \({\hat{W}}(k + 1) = {\hat{W}}(k-n+1) - \Gamma \Theta (\Upsilon ({k-n+1})) z_1(k + 1)\), which may make \(\hat{W}(k)\) converge to multiple different values based on time sequence, and further increases the difficulty of knowledge storage and reuse [46]. To solve this problem, the auxiliary error estimator \(\hat{z}_1(k + 1)\) in (23) is designed by replacing \({{\hat{W}}^T}({k_1})\Theta (\Upsilon ({k_1}))\) with \({\hat{W}^T}(k)\Theta (\Upsilon ({k_1}))\). Subsequently, the weight updating law \({\hat{W}}(k + 1) \) in (25) is designed on the basis of the estimation error \(\tilde{z}_1(k + 1)\) instead of the traditional tracking error \(z_1(k + 1)\), which is free from time delay. Based on the new weight updating law, it is easy to verify from Lemma 2 that \(\hat{W}(k)\) converges to a constant value \(\bar{W}\), which reduces the space complexity and simplifies knowledge reuse.

By adopting the trained RBF NN \(\bar{W}^T \Theta (\Upsilon (k))\), we can develop the following static neural controller

$$\begin{aligned} \left. \begin{aligned} u(k) =- {\bar{W}^T}\Theta (\Upsilon (k)). \end{aligned}\right. \end{aligned}$$
(36)

Controller (36) is employed to obtain the elevated tracking performance for the similar tracking objective.

Corollary 1

Consider the closed-loop system being made up of SFNSs (1) and actual control input (36) constructed using the constant weights shown in (34). The tracking error can converge to the expected tiny vicinity around origin for the similar reference trajectory \({y_d}(k)\).

Proof: Let the Lyapunov function as:

$$\begin{aligned} \left. \begin{aligned} V_{1}(k) = \frac{1 }{{{\bar{\iota }}}^2}z_1^2(k)\\ \end{aligned}\right. \end{aligned}$$
(37)

By (22), (35), and (36), we get

$$\begin{aligned} \Delta V_{1}(k)= & {} \frac{1 }{{{\bar{\iota }}}^2}z_1^2(k+1)-\frac{1 }{{{\bar{\iota }}}^2}z_1^2(k) \nonumber \\= & {} -\frac{1 }{{{\bar{\iota }}}^2}z_1^2(k)+\frac{1 }{{{\bar{\iota }}}^2}\iota ^2(k)\varepsilon ^2_{2}(k_{1}) \nonumber \\\le & {} -\frac{1 }{{{\bar{\iota }}}^2}z_1^2(k)+\varepsilon ^2. \end{aligned}$$
(38)

From (38), it can be seen that for a small constant \({\mu _5} > \frac{ \varepsilon }{{\bar{\iota }}}\), there exists a positive integer \(K_{1}\), so that for any \(k>K_{1}\), \(|{z_1}(k)|< {\mu _5}\) holds. As a result, it is easy to demonstrate that \({z_1}(k)\) converges to a tiny vicinity around origin.

Remark 3

It is should be pointed out that the variable substitution approach has been put forward in [45] to tackle the causality contradiction. By combining this approach and a new auxiliary error estimator, a novel weight updating law is constructed in our paper to guarantee the exponential convergence of NN weights. Compared with the existing result [45], the proposed scheme can fulfil knowledge acquirement and storage of NN weights and reuse the stored constant weights for the high-performance control with less space complexity, better transient performance and less energy consumption.

4 Simulation study

Consider the following DT SFNS [45]:

$$\begin{aligned} \left. \begin{aligned} {\chi _1}(k + 1) =&{g_1}({\chi _1}(k)){\chi _2}(k)+{f_1}({\chi _1}(k))\\ {\chi _2}(k + 1) =&{g_2}({{{\bar{\chi }}}_2}(k))u(k)+{f_2}({{{\bar{\chi }}}_2}(k)) \end{aligned}\right. \end{aligned}$$
(39)

where \({f_1}({\chi _1}(k)) \!= \!\frac{{\chi _1^2(k)}}{{\chi _1^2(k)+1}}\), \({f_2}({{\bar{\chi }}_2}(k)) \!=\! \frac{{0.2{\chi _1}(k) - 0.6{\chi _2}(k)}}{{1 + \chi _1^2(k) + \chi _2^2(k)}} +{\chi _2}(k)\), \({g_1}({\chi _1}(k)) =0.2\sin ({\chi _1}(k))+ 0.5 \), and \({g_2}({\bar{\chi }_2}(k)) =\) \( 0.8\cos ({\chi _1}(k))+1 \) with \({{\bar{\chi }}_2}(k) = [{\chi _1}(k),{\chi _2}(k)]^T\).

The tracking trajectory \({y_d}(k)\) is derived from the following Henon system shown in (40):

$$\begin{aligned} \left. \begin{aligned} {\chi _{d,1}}(k + 1) =&{\chi _{d,2}}(k)\\ {\chi _{d,2}}(k + 1) =&1.4p - \frac{{\chi _{d,2}^2(k)}}{p} + 0.3{\chi _{d,1}}(k) \end{aligned}\right. \end{aligned}$$
(40)

where \({y_d}(k) = {\chi _{d,1}}(k)\), and \(p = 1\).

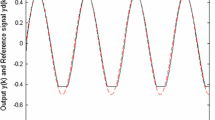
First, in the simulation, select initial states and design parameters as follows: \(\bar{\chi }_2(0) = [\chi _{1}(0), \chi _{2}(0)]^T={[0,0]^T}\), \({\chi _d}(0)\) \( = [\chi _{d,1}(0), \chi _{d,2}(0)]^T={[0,0]^T}\), \(\hat{W}(0)=0\), \(\Gamma =0.3I\). Moreover, the center \(\nu _i\) is equally spaced over \([-2.1,2.1] \times [-7,4.5]\) \( \times [-2.1,2.1]\), and the corresponding widths \(\ell _i=[0.375,0.625,\) \(0.375]^T\), the number of nodes is 5400. Besides, \(\bar{W}\) is designed as \(\bar{W}=\frac{1}{100}\sum _{k=4901}^{5000}\hat{W}(k)\). Simulation results are displayed in Figs. 2, 3, 4, 5, 6, and 7. The tracking error is exhibited in Fig. 2 by using ANC strategy (20). Figures 3 and 4 display the recurrent feature of \(\chi _2(k)\) and the boundedness of controller u(k), respectively. Figure 5 shows that \(\hat{W}(k)\) indeed converges exponentially to a tiny vicinity of their desired value. From Fig. 6, we know that the RBF NN can accurately approximate \(F(\Upsilon (k))\). The simulation comparison of tracking performance is given in Fig. 7 between ANC (20) and static neural control (SNC) (36). By Fig. 7, we can see that the transient tracking performance is vastly improved by employing the stored experience weights \(\bar{W}\).

Then, simulation experiments are carried out compared with the existing schemes. For same DT SFNS (39) and the desired tracking signal in (40), simulation shows the results of previous learning control (PLC) scheme, which refers to the literature [46]. Such a simulation is to exhibit the advantages of the estimator-based leaning control (LC) scheme proposed in this paper by comparing it with PLC scheme [46].

Fig. 2
figure 2

Tracking performance by using adaptive neural controller

Full size image
Fig. 3
figure 3

System state \(\chi _{2}(k)\)

Full size image
Fig. 4
figure 4

System control input u(k)

Full size image
Fig. 5
figure 5

Partial NN weights convergence of \(\hat{W}(k)\)

Full size image
Fig. 6
figure 6

System dynamics \(F(\Upsilon (k))\) and RBF NN \({{\hat{W}}^T}(k)\Theta (k)\)

Full size image
Fig. 7
figure 7

Tracking error comparison between ANC and SNC

Full size image
Fig. 8
figure 8

Partial NN weights convergence of PLC in [46]

Full size image
Fig. 9
figure 9

Partial NN weights convergence of LC

Full size image
Table 1 Comparisons between PLC in [46] and the new LC
Full size table

The constant NN weights are calculated as

$$\begin{aligned} \left. \begin{array}{l} {{{\bar{W}}}_{\textrm{PLC},1}} = \frac{1}{{50}}\sum \nolimits _{{k^1} = 4991}^{4999} {{{{\hat{W}}}_\textrm{PLC}}} ({k^1})\\ {{{\bar{W}}}_{\textrm{PLC},2}} = \frac{1}{{50}}\sum \nolimits _{{k^2} = 4992}^{5000} {{{{\hat{W}}}_\textrm{PLC}}} ({k^2}) \end{array}\right. \end{aligned}$$
(41)

where time sequences \(k^1\) and \(k^2\) are chosen, respectively, as

$$\begin{aligned} \left. \begin{aligned} \left\{ {{k^1}|{k^1} = 4991,4993,4995,\ldots } \right\} \end{aligned}\right. \end{aligned}$$

and

$$\begin{aligned} \left. \begin{aligned} \left\{ {{k^2}|{k^2} = 4992,4994,4996,\ldots } \right\} . \end{aligned}\right. \end{aligned}$$

In the simulation, choose initial states and design parameters as follows: \(\bar{\chi }_{\textrm{PLC},2}(0) = [\chi _{\textrm{PLC},1}(0), \chi _{\textrm{PLC}, 2}(0)]^T={[0,0]^T}\), \({\chi _{d,\textrm{PLC}}}(0) = [\chi _{d,\textrm{PLC}1}(0), \chi _{d,\textrm{PLC}2}(0)]^T={[0,0]^T}\), \(\hat{W}_\textrm{PLC}(0)=0\), \(\Gamma _\textrm{PLC}=0.2I\). The centers \(\nu _{i, j }, j=1,2\) of NNs are evenly spaced on \([-3,3] \times [-8,5] \times [-3,3]\) and \([-3,3] \times [-8,5] \times [-8,5]\). The corresponding widths are

$$\begin{aligned} \left. \begin{aligned} \ell _{i,j }=[0.625,0.625,0.625]^T, j=1 \end{aligned}\right. \end{aligned}$$

and

$$\begin{aligned} \left. \begin{aligned} \ell _{i,j }=[0.625,0.625,1]^T, j=2. \end{aligned}\right. \end{aligned}$$

And the numbers of nodes are 5239 and 6851, respectively. Compared to the PLC, it is demonstrated from Figs. 8 and  9 that in the LC scheme proposed in this paper, the NN weights converge to a fixed value. For the same NN weight, the LC scheme only needs to store one value, while the PLC scheme needs to store two values. Therefore, LC scheme reduces the overhead of system storage space, especially when the system order is higher, the cost saving is more obvious. Moreover, Table 1 shows that LC scheme reduces the computation time with smaller mean absolute error.

In addition, the scheme proposed in this paper is compared with that in the existing work [51]. The simulation parameters of PLC scheme in [51] are set to be consistent with the scheme in this paper, and the simulation results are shown in Fig. 10 and Table 2. Figure 10 shows that each weight of the NN weight vector in PLC scheme [51] converges to two values instead of one. According to Table 2, although the computation time of our LC scheme is slightly larger, its mean absolute error is reduced significantly. Moreover, for the same number of neural nodes, our LC scheme reduces the system storage space by 50%.

Fig. 10
figure 10

Partial NN weights convergence of PLC in [51]

Full size image
Table 2 Comparisons between PLC in [51] and the new LC
Full size table

5 Conclusions

A new neural DL approach was proposed for a class of DT SFNSs in this article. By combining the variable substitution method and the new auxiliary error dynamic estimator, a novel NN updating law was proposed to guarantee that neural weight estimates exponentially converged to a tiny vicinity of their desired values, which avoids n-step delays of weight update and simplifies weight knowledge reuse. The converged constant weights were stored as experience knowledge and reemployed to establish a static LC strategy. Such a controller achieved the improvement of control performance due to the avoidance of online update of NN weights.