1 Introduction

Nowadays, fractional calculus theory is widely used as a superb tool for handling nonlinear real issues in applied mathematics, engineering and physics including fluid mechanics, electrical circuits, diffusion, damping laws, relaxation processes and mathematical biology Klimek (2001), Laskin (2000), Klafter et al. (2011), Ortigueira (2010), El-Ajou et al. (2015), Liu and Burrage (2011), Magin (2006), Tarasov (2011). The fractional calculus topic plays a critical and serious role to describe a complex dynamical behavior in tremendous scope of applications fields, helps to understand the nature of the models deeper more than the integer-order derivatives as well as simplifies the controlling design without any loss of hereditary behaviors and explain even more complex structures.

However, mathematical modeling of nonlinear systems is a major challenge for contemporary scientists. The Rabinovich–Fabrikant system is one of the nonlinear realism chaotic models that consist of three coupled ordinary differential equations due to Mikhail Rabinovich and Anatoly Fabrikant in their work on waves of non-equilibrium substances Rabinovich and Fabrikant (1979), which is described as follows:

$$\begin{aligned} x^{\prime }(t)= & {} y(z+x^{2}-1)+ax, \nonumber \\ y^{\prime }(t)= & {} x(3z-x^{2}+1)+ay, \\ z^{\prime }(t)= & {} -2z(b+xy),\nonumber \end{aligned}$$
(1)

where a and b are real finite constant that control the evolution of this model. Anyhow, these types of problems are of great importance in many branches of mathematics and physics. Therefore, they received special attention of scientists and researchers Agrawal et al. (2012), Liu et al. (2010), Srivastava et al. (2014), Kolebaje et al. (2013).

On the other hand, we know that there is no classical method to handle the nonlinear FDEs and provide explicit solutions due to the complexities of fractional calculus involving these equations. For this reason, we need a reliable numerical approach to obtain the coefficients of the fractional series form solution to such models. In this paper, we intend the application of MsGDTM to provide approximate form solution for a class of nonlinear FDEs included some well-known fractional Rabinovich–Fabrikant equations. This approach has several advantages for dealing directly with suggested chaotic model: It needs a few iterations to get high accuracy, it is very simple for obtaining analytical approximate solution in rapidly convergent formulas over a long time interval, it also gives significantly information in providing continuous representation of these approximations and it has the ability for solving other problems appearing in several scientific fields Al-Smadi et al. (2015), Momani et al. (2014), Al-Smadi et al. (2017), Al-Smadi et al. (2016).

The structure of this article is organized as follows: In the next section, necessary details and preliminaries about the fractional calculus theory are briefly provided. Description of the MsGDTM in order to construct and predict series form solution for fractional Rabinovich–Fabrikant model is presented in Sect. 4. In Sect.  5.1, the stability analysis is also discussed. In Sect.  5.2, numerical simulations are given to verify the validity and performance of the present method. This paper ends with some concluding remarks.

2 Mathematical preliminaries

In this section, basic preliminaries, concepts and notations of fractional integrals and derivatives are introduced. Also, we adopt the Caputo fractional derivative sense which is a modification of Riemann–Liouville sense because the initial conditions that defined during the formulation of the system are similar to those conventional conditions of integer order. For more details about the mathematical properties of FDEs, we refer to Caputo (1967), Podlubny (1999), Millar and Ross (1993), Mainardi (2010).

Definition 1

A real-valued function \(\psi (x,t),\) \(x\,{\in }\, \mathcal {R},\) \(t\,{>}\,0\) is said to be in the space \(C_{\mu },\) \(\mu \,{\in }\, \mathcal {R},\) if there exists a real number \(q\,{>}\,\mu \) such that \(\psi (x,t)\,{=}\,t^{q}\psi _{1}(x,t),\) where \(\psi _{1}(x,t)\,{\in }\, C(\mathcal {R}\times [0,\infty ))\), and it is said to be in the space \(C_{\mu }^{m}\) if \(\frac{\partial ^{m}}{\partial t^{m}}\psi (x,t)\,{\in }\, C_{\mu },\) \(m\,{\in }\, \mathcal {N}.\)

Definition 2

For a function \(\psi (x,t)\,{\in }\, C_{\mu },\) \(\mu \,{\ge }\, {-1}\), the Riemann–Liouville integral operator of order \(\alpha \,{\ge }\, 0\) is defined as

$$\begin{aligned}&J_{t}^{\alpha }\psi (x,t)\nonumber \\&\quad =\left\{ \begin{array}{ll} \frac{1}{\varGamma (\alpha )}\int _{0}^{t}(t-\zeta )^{\alpha -1}\psi (x,\zeta )\text {d}\zeta , &{} \quad \alpha >0,0<\zeta <t, \\ \psi (x,t), &{} \quad \alpha =0. \end{array} \right. \nonumber \\ \end{aligned}$$
(2)

Consequently, for \(\psi (x,t)\,{\in }\, C_{\mu },\) \(\mu \,{\ge }\, {-1},\) \(\alpha ,\beta \,{\ge }\, 0,\) \(c\,{\in }\, \mathbb {R}\) and \(\gamma \,{>}\, {-1}\), the operator \(J_{t}^{\alpha }\) has the following properties:

  1. 1.

    \(J_{t}^{\alpha }J_{t}^{\beta }\psi (x,t)=J_{t}^{\alpha +\beta }\psi (x,t)=J_{t}^{\beta }J_{t}^{\alpha }\psi (x,t),\)

  2. 2.

    \(J_{t}^{\alpha }c=\dfrac{c}{\varGamma (\alpha +1)}t^{\alpha },\)

  3. 3.

    \(J_{t}^{\alpha }t^{\gamma }=\dfrac{\varGamma (\gamma +1)}{\varGamma (\alpha +\gamma +1)}t^{\alpha +\gamma }.\)

Now, we introduce a modified fractional differential operator \(D_{t}^{\alpha }\) proposed by Caputo (1967) as follows

$$\begin{aligned} D_{t}^{\alpha }\psi (x,t)= & {} J_{t}^{m-\alpha }\psi ^{(m)}(x)\frac{1}{\varGamma (m-\alpha )}\nonumber \\= & {} \int _{0}^{x}(x-\eta )^{m-\alpha -1}\psi ^{(m)}(\eta )\text {d}\eta ,\quad t\ge 0, \end{aligned}$$
(3)

for \(m-1\,{<}\,\alpha \,{\le }\, m,\) \(m\,{\in }\, \mathbb {N},\) \(t\,{\le }\, x\) and \(\psi (x)\,{\in }\, C_{-1}^{m}.\)

Definition 3

The Caputo time-fractional derivative operator of order \(\alpha \,{>}\,0\) is defined as

$$\begin{aligned}&D_{t}^{\alpha }\psi (x,t)=\frac{\partial ^{\alpha }\psi (x,t)}{\partial t^{\alpha }}\nonumber \\&\quad =\left\{ \begin{array}{ll} J_{t}^{m-\alpha }\left( \frac{\partial ^{m}\psi (x,t)}{\partial t^{m}} \right) , &{} \quad 0\le m-1<\alpha <m, \\ \frac{\partial ^{m}\psi (x,t)}{\partial t^{m}}, &{} \quad \alpha =m\in \mathcal {N}, \end{array} \right. \end{aligned}$$
(4)

where m is the smallest integer that exceeds \(\alpha .\)

Lemma 1

Podlubny (1999) If \(m-1\,{<}\,\alpha \,{\le }\, m,\) \(m\,{\in }\, \mathcal {N},\) \(\psi (x,t)\,{\in }\, C_{\gamma }^{m},\) and \(\gamma \,{\ge }\, -1\), then \(D_{t}^{\alpha }J_{t}^{\alpha }\psi (x,t)\,{=}\,\psi (x,t),\) and \(J_{t}^{\alpha }D_{t}^{\alpha }\psi (x,t)\,{=}\,\psi (x,t)-\sum \nolimits _{k=0}^{m-1}\frac{\partial ^{k}\psi (x,0^{+})}{\partial t^{k}}\frac{t^{k}}{k!},\) where \(t\,{>}\,0\).

3 Description of the multistep GDT approach

To illustrate this purpose, consider the following system of fractional differential equations

$$\begin{aligned}&D_{t_{0}}^{\alpha _{i}}y_{i}(t)=f_{i}(t,y_{1}(t),y_{2}(t),\ldots ,y_{n}(t)), \nonumber \\&\quad i=1,2,\ldots ,n, \ t_{0}\le t\le T, \end{aligned}$$
(5)

with the initial conditions

$$\begin{aligned} y_{i}(t_{0})=d_{i},\quad i=1,2,\ldots ,n, \end{aligned}$$
(6)

where \(0\,{<}\,\alpha _{i}\,{\leqslant }\, 1,\) \(d_{i}\) \(\left( i\,{=}\,1,2,\ldots ,n\right) \) are real finite constant, \(f_{i}:\left( \left[ t_{0},T\right] \times \mathbb {R} ^{n}\right) \,{\rightarrow }\, \mathbb {R}^{n}, \) and \(D_{*}^{\alpha _{i}}\) is the Caputo fractional derivative of order \(\alpha _{i}.\)

Prior to applying the multistep approach, we defined the generalized differential transform of f(t) as follows

$$\begin{aligned} F(k)=\frac{1}{\varGamma (k\alpha +1)}\left[ \frac{\text {d}^{k\alpha }f(t)}{\text {d}t^{k\alpha }}\right] _{t=t_{0}}. \end{aligned}$$
(7)

According to the GDTM that described in Momani et al. (2007), Ertürk et al. (2008), Odibat et al. (2010), the mth approximate series form solution of fractional initial value problem (FIVP) (5) and (6) can be given by

$$\begin{aligned} y_{i}(t)=\sum \limits _{k=0}^{m}\varPsi _{i}(k)(t-t_{0})^{k\,\alpha _{i}},\quad t\in [t_{0},T], \end{aligned}$$
(8)

where \(\varPsi _{i}(k)\) satisfies the following recurrence relation

$$\begin{aligned}&\frac{\varGamma ((k+1)\alpha _{i}+1)}{\varGamma (k\alpha _{i}+1)}\varPsi _{i}(k+1)\nonumber \\&\quad =F_{i}(k,\varPsi _{1},\varPsi _{2},\ldots ,\varPsi _{n}),\quad i=1,2,\ldots ,n, \end{aligned}$$
(9)

in which \(F_{i}(k,\varPsi _{1},\varPsi _{2},\ldots ,\varPsi _{n})\) denotes the differential transformed function of \( f_{i}(t,y_{1},y_{2},\ldots ,y_{n})\) with initial data \(\varPsi _{i}(t_{0})\,{=}\,d_{i},\) \(i\,{=}\,1,2,\ldots ,n.\)

By dividing the interval \([t_{0},T]\) into M subintervals \([t_{j-1},t_{j}],\) \(j\,{=}\,1,2,\ldots ,M,\) of equal step size, \(h\,{=}\,(T-t_{0})/M\) and nodes \(t_{i}\,{=}\,t_{0}+j\,h\). Then, by applying the GDTM over the first subinterval \([t_{0},t_{1}]\), we obtain approximate series solution in the form

$$\begin{aligned} y_{i,1}(t)=\sum \limits _{k\ =\ 0}^{l}\varPsi _{1}(k)(t-t_{0})^{k\alpha _{i}}, \quad t\in [t_{0},t_{1}], \end{aligned}$$

with initial data \(y_{i,1}(t_{0})\,{=}\,d_{i},\) \(i\,{=}\,1,2,\ldots ,n\). However, using the initial conditions \(y_{i,j}(t_{j-1})\,{=}\,y_{i,j-1}(t_{j-1}),\) for \(j\ge 2,\) at each subinterval \([t_{j-1},t_{j}]\) and then applying the GDTM to system (5) in order to obtain approximate series solutions \(y_{i,j}(t)\) as follows

$$\begin{aligned} y_{i,j}(t)=\sum \limits _{k\ =\ 0}^{l}\varPsi _{j}(k)(t-t_{j-1})^{k\alpha _{i}}, \quad t\in [t_{j-1},t_{j}]. \end{aligned}$$

This procedure can be repeated till generate a sequence of approximate series solutions \(y_{i,j}(t),\) \(j\,{=}\,1,2,\ldots ,M,\) \(i\,{=}\,1,2,\ldots ,n.\) Therefore, the multistep approximate series solution of FVIP (5) and (6) will be given by

$$\begin{aligned} y_{i}(t)=\sum \limits _{j\text { }=\ 1}^{M}\chi _{\upsilon }y_{i,j}(t),\quad i=1,2,\ldots ,n, \end{aligned}$$
(10)

where

$$\begin{aligned} \chi _{v}=\left\{ \begin{array}{c} 1, \quad t\in [t_{j-1},t_{j}],\\ 0, \quad t\notin [t_{j-1},t_{j}]. \end{array} \right. \end{aligned}$$

The idea behind multistep approach is that approximate series solution which is obtained more valid and accurate during a long time as well as converges for wide time regions Ertürk and Momani (2010), Odibat and Shawagfeh (2007), Odibat and Momani (2008). It is worth noting that if the step size \(h\,{=}\,T\), then the multistep approach reduces to the classical sense. Nevertheless, the multistep algorithm is powerful for investigating approximate series solution of various kinds of such systems and very simple for computational performance for all values of h. However, we apply the following time step-size control algorithm according the multistep approach:

  1. 1.

    One gives the admissible local error \(\delta \,{>}\,0\) and chooses the order N of the multistep scheme.

  2. 2.

    From calculations, the values \(\varPsi _{j}(k)\) \((j\,{=}\,1,2,\ldots ,N)\) are known for every solution component j.

  3. 3.

    At the grid point \(t_{k}\), we calculate the value \(E_{N}\,{=}\,\max \{\varPsi _{j}(k)\}_{j=1}^{N}.\)

  4. 4.

    We select the step size \(h_{k}\) for which \( h_{k}\,{=}\,\tau \left( \frac{\delta }{E_{N}}\right) ^{1/N}\,{\le }\, h_{\max }\) and \( t_{k+1}\,{=}\,t_{k}+h_{k},\) where \(\tau \) is a safety factor and \(h_{\max }\) is the maximum allowed step size.

4 Stability analysis of fractional system

As we know from stability analysis theory, the system will be stable if the roots of its characteristic polynomial are negative or have negative real parts if they are complex conjugate. But in fractional sense the concept of stability differs from the integer sense. In this section, necessary theorems with their related results will be utilized dealing with commensurate and incommensurate systems of fractional order.

Table 1 Equilibrium points of system (1)
Full size table

For fractional-order system \(D_{t}^{\alpha }x\,{=}\,f(x)\). Let \(f(p)\,{=}\,0\), then \(x\,{=}\,p\) is said to be an equilibrium point of the system. Furthermore, a saddle point is an equilibrium point at which the equivalent linearized model has at least one eigenvalue in the stable region and one in the unstable region. A saddle point is called a saddle point of index 1 if one of the eigenvalues is unstable and the others are stable. Also is called a saddle point of index 2 if it has one stable eigenvalue and two unstable ones Tavazoei and Haeri (2007). In chaotic systems, it is noted that scrolls are generated only around saddle points of index 2, and the saddle points of index 1 are responsible for connecting scrolls.

Lemma 2

Matignon (1996) The autonomous fractional-order system \(D_{t}^{\alpha }x\,{=}\,Ax\), \(x(0)\,{=}\,x_{0}\), where \(0\,{<}\,\alpha _{i}\,{\le }\, 1\), \(x\,{\in }\, \mathcal {R}^{n}\) and \(A\,{\in }\, \mathcal {R}^{n\times n}\), is called asymptotically stable if and only if \(\left| \text {arg}\left( \sigma _{A}\right) \right| \,{>}\,\frac{\alpha \pi }{2}\) for all eigenvalues of A, and is called stable if and only if \(\left| \text {arg}\left( \sigma _{A}\right) \right| \,{\ge }\, \frac{\alpha \pi }{2}\) and those critical eigenvalues that satisfy \(\left| \text {arg}\left( \sigma _{A}\right) \right| \,{=}\,\frac{\alpha \pi }{2}\) have geometric multiplicity one, whereas \(\sigma _{A}\) represents the spectrum of A.

Lemma 3

Deng et al. (2007) Consider the following incommensurate n-dimensional linear fractional-order system

$$\begin{aligned} {c} D_{t}^{\alpha _{1}}x_{1}= & {} a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n},\nonumber \\ D_{t}^{\alpha _{2}}x_{2}= & {} a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n},\nonumber \\&\vdots \\ D_{t}^{\alpha _{n}}x_{n}= & {} a_{n1}x_{1}+a_{12}x_{n}+\cdots +a_{nn}x_{n},\nonumber \end{aligned}$$
(11)

where \(0\,{<}\,\alpha _{i}\,{\le }\, 1\) such that \(\alpha _{i}\,{=}\,\frac{v_{i}}{u_{i}}\), \( \left( v_{i},u_{i}\right) =1,\) \(v_{i},u_{i}\,{\in }\, \mathcal {Z}^{+}\), \( i\,{=}\,1,2,\ldots ,n\). Let M be the lowest common multiple of the denominators \( u_{i}\)’s of \(\alpha _{i}\)’s. Then, system (11) is asymptotically stable if \(\left| \text {arg}\left( \lambda \right) \right| \,{>}\,\frac{ \pi }{2M}\) for all the roots \(\lambda \)’s of equation \(det\left( diag\left( \left[ \lambda ^{M\alpha _{1}},\lambda ^{M\alpha _{2}},\ldots , \lambda ^{M\alpha _{N}}\right] \right) -(a_{ij})_{n\times n}\right) \,{=}\,0.\)

Consequently, the equilibrium point is asymptotically stable if the condition \(\frac{\pi }{2M}-\underset{i}{\min }\left| \text {arg}\left( \lambda _{i}\right) \right| \,{<}\,0\) is satisfied. Indeed, the condition \( \frac{\pi }{2M}-\underset{i}{\min }\left| \text {arg}\left( \lambda _{i}\right) \right| \) is called the instability measure for equilibrium points of fractional order systems (IMFOS). Thus, if \(IMFOS\,{<}\,0\), then the fractional system is asymptotically stable, whereas in fact \(IMFOS\,{\ge }\, 0\) is a necessary condition for the system to be have chaotically. It has been proved numerically that the last condition is necessary but not sufficient to exhibit chaos Tavazoei and Haeri (2008).

For the nonlinear fractional-order system \(D_{t}^{\alpha _{i}}x\,{=}\,f(x)\), \( 0\,{<}\,\alpha _{i}\,{\le }\, 1\) \((i\,{=}\,1,2,\ldots ,n)\), \(\lambda \)’s are considered to be the eigenvalues of the Jacobian matrix \(J\,{=}\,\left. \frac{\partial f}{\partial x }\right| _{x=p}\). Hence, the equilibrium point is asymptotically stable for p if the condition \(\left| \text {arg}\left( \sigma _{J}\right) \right| \,{=}\,\left| \text {arg}\left( \lambda _{i}\right) \right| \,{>}\,\frac{\pi }{2p}\) is satisfied; for more details, we refer to Petras (2010), Zhen et al. (2011), Gafiychuk et al. (2008), Gafiychuk and Datsko (2010).

Fig. 1
figure 1

Chaotic attractors and phase diagram of Rabinovich–Fabricant system. a Phase plane diagram of x(t) and y(t), b phase plane diagram of y(t) and z(t), c phase plane diagram of x(t) and z(t) and d 3dim chaotic attractor

Full size image

5 Application and simulation

5.1 Integer-order Rabinovich–Fabricant model

Consider the Rabinovich–Fabricant system (1) in which the parameters \(a\,{=}\,0.87\ \text {and}\ b\,{=}\,1.1\). This system is chaotic at the initial conditions \((-1,0,0.5)\). Now, by solving the following system

$$\begin{aligned} y(z+x^{2}-1)+ax= & {} 0, \nonumber \\ x(3z-x^{2}+1)+ay= & {} 0, \\ -2z(b+xy)= & {} 0,\nonumber \end{aligned}$$
(12)

we obtain five equilibrium points as

$$\begin{aligned} {\small E}_{1}= & {} {\small (0,0,0),} \\ {\small E}_{2}= & {} {\small (1.4797,-0.743396,0.542195),} \\ {\small E}_{3}= & {} {\small (-1.4797,0.743396,0.542195),} \\ {\small E}_{4}= & {} {\small (0.518267,-2.12246,0.943838)}, \\ {\small E}_{5}= & {} {\small (-0.518267,2.12246,0.943838)}. \end{aligned}$$

The Jacobian matrix of system (1) that evaluated at the equilibrium point \( E\,{=}\,(x,y,z)\) is given by

$$\begin{aligned} J(x,y,z)=\left[ \begin{array}{c} 2xy+a \\ 3z-3x^{2}+1 \\ -2yz \end{array}\quad \begin{array}{c} z+x^{2}-1 \\ a \\ -2xz \end{array}\quad \begin{array}{c} y \\ 3x \\ -2xy-2b \end{array} \right] \end{aligned}$$

and its characteristic polynomial is given by

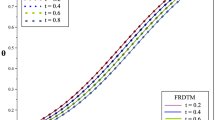
$$\begin{aligned} p(\lambda )= & {} 3.86518-8.8x^{2}+6.6x^{4}+7.3418xy\\&-\,8x^{3}y+6x^{5}y+3.48x^{2}y^{2}+4.4z\\&-\,5.22x^{2}z-12x^{3}yz-1.74y^{2}z\\&-\,6.6z^{2}+6xyz^{2}+(-2.0711-4x^{2}\\&+\,3x^{4}-6.14xy-4x^{2}y^{2}\\&+\,2z+6x^{2}z+2y^{2}z-3z^{2})\lambda +0.46\lambda ^{2}+\lambda ^{3}. \end{aligned}$$

Table 1 shows the equilibrium points of system (1), corresponding eigenvalues and their nature. Anyhow, chaotic attractors and phase plane diagram of Rabinovich–Fabricant system with the initial data \( (x(0),y(0),z(0))\,{=}\,(-1,0,0.5),\) parameters \((a,b)\,{=}\,(0.87,1.1)\) and the time step \(h\,{=}\,0.005\) are presented graphically by applying the multistep technique to system (1) as shown in Fig. 1.

5.2 Fractional-order Rabinovich–Fabricant model

Consider the model of fractional-order Rabinovich–Fabricant system has the following form:

$$\begin{aligned} D_{t_{0}}^{\alpha _{1}}x(t)= & {} y(z+x^{2}-1)+ax, \nonumber \\ D_{t_{0}}^{\alpha _{2}}y(t)= & {} x(3z-x^{2}+1)+ay,\\ D_{t_{0}}^{\alpha _{3}}z(t)= & {} -2z(b+xy), \nonumber \end{aligned}$$
(13)

where \(0\,{<}\,\alpha _{i}\,{<}\,1,i\,{=}\,1,2,3\), a and b are nonnegative constants, and \( D_{t_{0}}^{\alpha _{1}}\) denotes the Caputo fractional derivative of order \( \alpha _{i}\). Indeed, if \(\alpha _{i}\,{=}\,1,\forall i\), then system (13) reduce to classical Rabinovich–Fabricant system (1).

By using the GDTM to system (13), we have the following recurrence relations formula

$$\begin{aligned} \left. \begin{array}{l} {\small X(k+1)=}\frac{\varGamma (k\alpha _{1}+1)}{\varGamma ((k+1)\alpha _{1}+1)} \left( \begin{array}{l} {\mathop {\displaystyle \sum }\limits _{i=0}^{k}}{\small Y(i)Z(k-i)-Y(k)} \\ \quad +\,{\mathop {\displaystyle \sum }\limits _{i=0}^{k}}{\mathop {\displaystyle \sum }\limits _{j=0}^{i}}{\small Y(j)X(i-j)X(k-i)+aX(k)} \end{array} \right) , \\ Y{\small (k+1)=}\frac{\varGamma (k\alpha _{2}+1)}{\varGamma ((k+1)\alpha _{2}+1)} \left( \begin{array}{l} {\mathop {\displaystyle \sum }\limits _{i=0}^{k}}3X{\small (i)Z(k-i)}+X{\small (k)} \\ \quad -\,{\mathop {\displaystyle \sum }\limits _{i=0}^{k}}{\mathop {\displaystyle \sum }\limits _{j=0}^{i}}X{\small (j)X(i-j)X(k-i)+aY(k)} \end{array} \right) , \\ Z{\small (k+1)=}\frac{-\varGamma (k\alpha _{3}+1)}{\varGamma ((k+1)\alpha _{3}+1)} \left( 2b{\small Z(k)+}{\mathop {\displaystyle \sum }\limits _{i=0}^{k}}{\mathop {\displaystyle \sum }\limits _{j=0}^{i}}X{\small (j)Y(i-j)Z(k-i)} \right) , \end{array} \right\} \end{aligned}$$
(14)

where X(k), Y(k) and Z(k) are transformed functions of x(t),  y(t) and z(t), respectively. With GDTM of the initial conditions in the form \(X(0)\,{=}\,c_{1},\) \(Y(0)\,{=}\,c_{2},\) \(Z(0)\,{=}\,c_{3}\). The process generates a sequence of approximate solutions such that

$$\begin{aligned} x_{i}(t)= & {} \sum \limits _{k\text { }=1}^{N}X_{i}(k)(t-t_{i-1})^{k\alpha _{1}}, \nonumber \\ y_{i}(t)= & {} \sum \limits _{k\text { }=\ 1}^{N}Y_{i}(k)(t-t_{i-1})^{k\alpha _{2}}, \\ z_{i}(t)= & {} \sum \limits _{k\text { }=\ 1}^{N}Z_{i}(k)(t-t_{i-1})^{k\alpha _{3}},\nonumber \end{aligned}$$
(15)

Therefore, the multistep approximate series solutions of system (15) can be given by

$$\begin{aligned} x(t)= & {} \left\{ \begin{array}{l} \displaystyle \sum \limits _{k=0}^{K}X_{1}(k)t^{k\alpha _{1}},\quad t\in [0,t_{1}], \\ \displaystyle \sum \limits _{k=0}^{K}X_{2}(k)(t-t_{1})^{k\alpha _{1}},\quad t\in [t_{1},t_{2}], \\ \vdots \\ \displaystyle \sum \limits _{k=0}^{K}X_{M}(k)(t-t_{M-1})^{k\alpha _{1}},\quad t\in [t_{M-1},t_{M}], \end{array} \right. \\ y(t)= & {} \left\{ \begin{array}{l} \displaystyle \sum \limits _{k=0}^{K}Y_{1}(k)t^{k\alpha _{2}},\quad t\in [0,t_{1}], \\ \displaystyle \sum \limits _{k=0}^{K}Y_{2}(k)(t-t_{1})^{k\alpha _{2}},\quad t\in [t_{1},t_{2}], \\ \vdots \\ \displaystyle \sum \limits _{k=0}^{K}Y_{M}(k)(t-t_{M-1})^{k\alpha _{2}},\quad t\in [t_{M-1},t_{M}], \end{array} \right. \\ z(t)= & {} \left\{ \begin{array}{l} \displaystyle \sum \limits _{k=0}^{K}Z_{1}(k)t^{k\alpha _{3}},\quad t\in [0,t_{1}],\\ \displaystyle \sum \limits _{k=0}^{K}Z_{2}(k)(t-t_{1})^{k\alpha _{3}},\quad t\in [t_{1},t_{2}], \\ \vdots \\ \displaystyle \sum \limits _{k=0}^{K}Z_{M}(k)(t-t_{M-1})^{k\alpha _{3}},\quad t\in [t_{M-1},t_{M}], \end{array} \right. \end{aligned}$$

where \(t\,{\in }\, \left[ t_{i-1},t_{i}\right] ,\) \(X_{i}(k),\) \(Y_{i}(k)\) and \( Z_{i}(k) \) for \(i\,{=}\,1,2,\ldots ,n\) satisfy the following recurrence relations

$$\begin{aligned}&{\small X}_{i}{\small (k+1)=}\frac{\varGamma (k\alpha _{1}+1)}{\varGamma ((k+1)\alpha _{1}+1)}\\&\qquad \times \,\left( \begin{array}{l} {\mathop {\displaystyle \sum }\limits _{j=0}^{k}}{\small Y}_{i}{\small (j)Z}_{i}{\small (k-j)-Y}_{i}{\small (k) } \\ \quad +\,{\mathop {\displaystyle \sum }\limits _{l=0}^{k}}{\mathop {\displaystyle \sum }\limits _{m=0}^{l}}{\small Y}_{i}{\small (m)X}_{i}{\small (l-m)X} _{i}{\small (k-l)+aX}_{i}{\small (k)} \end{array} \right) ,\\&Y_{i}{\small (k+1)=}\frac{\varGamma (k\alpha _{2}+1)}{\varGamma ((k+1)\alpha _{2}+1)}\\&\qquad \times \, \left( \begin{array}{l} {\mathop {\displaystyle \sum }\limits _{j=0}^{k}}{\small 3X}_{i}{\small (j)Z}_{i}{\small (k-j)+X}_{i}{\small (k)} \\ \quad -\,{\mathop {\displaystyle \sum }\limits _{l=0}^{k}}{\mathop {\displaystyle \sum }\limits _{m=0}^{l}}{\small X}_{i}{\small (m)X}_{i}{\small (l-m)X} _{i}{\small (k-l)+aY}_{i}{\small (k)} \end{array} \right) ,\\&Z_{i}{\small (k+1)=}\frac{-\varGamma (k\alpha _{3}+1)}{\varGamma ((k+1)\alpha _{3}+1)}\\&\qquad \times \, \left( 2b{\small Z}_{i}{\small (k)+}{\mathop {\displaystyle \sum }\limits _{l=0}^{k}}{\mathop {\displaystyle \sum }\limits _{m=0}^{l}} {\small X}_{i}{\small (m)Y}_{i}{\small (l-m)Z}_{i}{\small (k-l)}\right) , \end{aligned}$$

with intial conditions \(X_{i}(0)\,{=}\,x_{i}(t_{i-1})\,{=}\,x_{i-1}(t_{i-1}),\) \(Y_{i}(0){=} y_{i}(t_{i-1})\,{=}\,y_{i-1}(t_{i-1}) \) and \( Z_{i}(0)\,{=}\,z_{i}(t_{i-1})\,{=}\,z_{i-1}(t_{i-1}) \) starting with \( X_{0}(0)\,{=}\,c_{1},\) \(Y_{0}(0)\,{=}\,c_{2} \), and \(Z_{0}(0)\,{=}\,c_{3}\).

Our next goal is to illustrate some numerical results of the MsGDTM solutions of the fractional Rabinovich–Fabrikant system in numeric values. In fact, results from numerical analysis are an approximation, in general, which can be made as accurate as desired. Because a computer has a finite word length, only a fixed number of digits are stored and used during computations. The agreement between the IRKM and the multistep numerical solutions is investigated for fractional Rabinovich–Fabrikant model at various T by computing absolute errors and relative errors of numerically approximating as shown in Tables 2, 3, 4, respectively. Anyhow, it is clear from these tables that the numerical solutions are in close agreement with each others, while the accuracy is in advance by using multistep technique. Indeed, we can conclude that higher accuracy can be achieved by computing further MsGDT iterations.

Table 2 The absolute errors for x(t) of system (13) at \(\alpha \,{=}\,1\)
Full size table
Table 3 The absolute errors for y(t) of system (13) at \(\alpha \,{=}\,1\)
Full size table
Table 4 The absolute errors for z(t) of system (13) at \(\alpha \,{=}\,1\)
Full size table

For numerical simulation, we start with initial data \( (x(0),y(0),z(0))\,{=}\,(-1,0,0.5) \) and time step \(h\,{=}\,0.005\). On the other hand and according to Lemma 4.1, the eqilibrium points of system (13) will be as follows: The equilibrium point \(E_{1}\,{=}\,(0,0,0)\) is stable for \(\alpha _{i}\,{<}\,0.544 \); the equilibrium points

$$\begin{aligned}&E_{2}=(1.4797,-0.743396,0.542195) \quad \text {and } \\&E_{3}=(-1.4797,0.743396,0.542195) \end{aligned}$$

are stable for \(\alpha _{i}<0.991\); the equilibrium points

$$\begin{aligned}&E_{4}=(0.518267,-2.12246,0.943838)\quad \text {and } \\&E_{5}=(-0.518267,2.12246,0.943838) \end{aligned}$$

are unstable for \(0\,{<}\,\alpha _{i}\,{<}\,1,\) \(i\,{=}\,1,2,3\). Figure 2 shows the time trajectories of system (13) with \(\alpha _{i}\,{=}\,0.9\), \(i\,{=}\,1,2,3\), \( 0\le t\le 20\).

Fig. 2
figure 2

Time trajectories of fractional Rabinovich–Fabricant system with \( \alpha _{1}\,{=}\,\alpha _{2}\,{=}\,\alpha _{3}\,{=}\,0.9,\) \(t\,{\in }\, \left[ 0,20\right] \)

Full size image

Figure 3 shows the chaotic behavior with phase diagram of system (13) with \( \alpha _{i}\,{=}\,0.9\), \(i\,{=}\,1,2,3 \). Also, Fig. 4 shows the time trajectories of system (13) with \(\alpha _{i}\,{=}\,0.54,\) \(i\,{=}\,1,2,3,\) \( 0\,{\le }\, t\,{\le }\, 20 \). While Figs. 5 and  6 show the stability behavior of system (13) for \(\alpha _{i}<0.544.\)

Fig. 3
figure 3

Chaotic attractors and phase diagram of fractional Rabinovich–Fabricant system at \(\alpha _{i}\,{=}\,0.9,\) \(i\,{=}\,1,2,3\). a Phase plane diagram of x(t) and y(t), b phase plane diagram of y(t) and z(t), c phase plane diagram of x(t) and z(t) and d 3dim chaotic attractor

Full size image
Fig. 4
figure 4

Time trajectories of fractional Rabinovich–Fabricant system with \( \alpha _{1}\,{=}\,\alpha _{2}\,{=}\,\alpha _{3}\,{=}\,0.54,\) \(t\in \left[ 0,20\right] \)

Full size image
Fig. 5
figure 5

Phase diagram of fractional Rabinovich–Fabricant system with \( \alpha _{1}\,{=}\,\alpha _{2}\,{=}\,\alpha _{3}\,{=}\,0.54\)

Full size image
Fig. 6
figure 6

Chaotic attractors of fractional Rabinovich–Fabricant system with \( \alpha _{1}\,{=}\,\alpha _{2}\,{=}\,\alpha _{3}\,{=}\,0.54\)

Full size image

6 Conclusions

Constructing a mathematical model for nonlinear real-world systems, as well as developing numeric-analytic solution for such model, is very important issue in mathematics, physics and engineering. In the present study, we proposed and applied analytical–numerical technique, so-called MsGDTM, to handle nonlinear time-fractional Rabinovich–Fabrikant model in Caputo sense. Also, the stability analysis of this model is discussed quantitatively and guarantee that the chaos control occurs if the necessary conditions are satisfied. Our graphical representations explicitly reveal the complete reliability and efficiency of the presented method with a great potential in scientific applications. It may be concluded that the suggested method is very powerful, straightforward and promising algorithm in finding analytic approximate form solution for wide classes of fractional DEs. Computations of this paper have been carried out by using the computer package of MATHEMATICA.