An improved ant colony algorithm for robot path planning

Abstract

To solve the problems of convergence speed in the ant colony algorithm, an improved ant colony optimization algorithm is proposed for path planning of mobile robots in the environment that is expressed using the grid method. The pheromone diffusion and geometric local optimization are combined in the process of searching for the globally optimal path. The current path pheromone diffuses in the direction of the potential field force during the ant searching process, so ants tend to search for a higher fitness subspace, and the search space of the test pattern becomes smaller. The path that is first optimized using the ant colony algorithm is optimized using the geometric algorithm. The pheromones of the first optimal path and the second optimal path are simultaneously updated. The simulation results show that the improved ant colony optimization algorithm is notably effective.

1 Introduction

Creating collision-free trajectories for mobile robots, which is known as the path-planning problem, is considered one of combination optimal problems. Many approaches have been suggested in the literatures (Gu et al. 2015; Ma et al. 2015; Wen et al. 2015; Zhao et al. 2015; Xie and Wang 2014; Geng et al. 2012; Peng et al. 2015) to solve different optimization problems in a wide variety of application domains including engineering, biology, economics, industry and many more other complex real world problems. In general, the path-planning problem is considered one of the basic problems in robotics and it addresses the creation of a continuous motion that connects a starting point and a goal point in the configuration area of a robot while avoiding collisions with present obstacles (Cheng et al. 2010; Botzheim et al. 2012).

At present, the methods proposed to solve the path-planning problem are divided into two categories: the traditional method based on a mathematical model [such as the grid method (Borenstein and Koren 1991) and artificial potential field method (Khatib 1986; Brooks 1986)] and a bionic optimization algorithm that is suitable for a complex environment [such as the artificial fish algorithm (Xu and Zhu 2012), genetic algorithm (Castillo et al. 2007), particle swarm algorithm (Wu et al. 2009), and ant colony algorithm (Mavrovouniotis and Yang 2011)]. The grid method is a method of global path planning in a large-scale environment. It has some disadvantages, such as large storage space, and low calculation efficiency. The artificial potential field method is a mature robot local path-planning method and is suitable for real-time control, but it is easy to fall into the local optimum and deadlock phenomena. The disadvantages of bionic optimization methods are a large searching space, complicated algorithm, and low searching efficiency. The method easily falls into a local optimal path, and it can-not find a feasible path in some cases (Cheng et al. 2010). Therefore, the search for an effective path-planning method for a mobile robot in a complicated environment has become a subject of significant interest and a currently active research field (Savsani et al. 2014).

In optimization, bionic optimization is probably best known for ant colony optimization (ACO) (Wang 2015). It is a global optimization algorithm. A central concern in this algorithm is the balance between exploration of the search space, and exploitation of the knowledge that can be considered representing the collective knowledge of the group (Parpinelli and Lopes 2015). The main problem of this method is how to improve the global search ability and convergence speed of the algorithm. To quickly find the global optimal path, the ant colony algorithm must make the search space as large as possible and take advantage of prior knowledge. The essence is to solve contradictions between the algorithm’s randomness and the pheromone update intensity. This problem causes many researchers to perform in-depth research on this topic from two directions: search strategy and pheromone update strategy, such as bidirectional different search strategies and taboo table optimization strategy (Kang et al. 2014), turn-back search strategy (Wang et al. 2008) and Max–Min ant system (Sttzle and Hoos 1997). Additionally, in the past few years, many hybrid intelligent optimization algorithms were proposed as solutions to the path-planning problem. A fusion algorithm of ant colony and particle swarm (Shuang et al. 2011) was introduced to navigate a mobile robot in an environment filled with obstacles. In addition, (Liu et al. 2010) proposed a combination of an ant colony algorithm with an immune algorithm to solve the TSP problem.

The main characteristics of our proposed algorithm are that the artificial potential field and geometric local optimization are combined in the process of searching for the global optimal path. It can effectively generate good solutions quickly, and lowers the risks of trapping in a local optimum. First, the path pheromone diffuses in the direction of the potential field force during in the ant searching process; thus, the ants tend to search for a higher fitness subspace, and the algorithm changes the “blind” search into a “bias” search. It reduces the cross paths to a certain extent, and the first path is obtained. The modified ACO is named as ACO-PD. Second, using the geometrical optimization method, the searched paths are optimized, and the cross paths, circular paths and saw tooth paths are completely eliminated. The pheromones of both paths are simultaneously updated. The modified ACO is named as ACO-PDG. The difference between the method in this paper and the literature (Luo and Wu 2010) is the way in which pheromone diffusion modes and the pheromone updating strategy. The farmer pheromone has higher smoothness and its pheromone updating speed is faster than that of the latter algorithm; thus, the collaborative capability of ant is enhanced greatly.

The rest of the paper is structured as follows. In Sect. 2, the problems that affect the convergence speed in ACO algorithm are mentioned. All the theoretical background for the proposed algorithm is presented in Sect. 3. The proposed algorithm, which was derived from a combination of the ACO, based on the diffusion of local pheromones, and the geometric method, is presented in Sects. 3.2 and 3.3. The implementation of the method is described in full details in Sect. 3.4. The effects of the proposed method on the pheromone distribution are illustrated in Sect. 4. The corresponding simulation results are presented in Sect. 5. Finally, the conclusions are provided in Sect. 6.

2 The standard ACO

The ant colony optimization is a pheromone-mediated communication between individual activities. The ants randomly walk and find the path to the destination while laying down chemical trails that are called pheromones. The pheromone trail transmits a message to other members of the colony. The other ants are likely to follow the trail instead of randomly traveling. If they eventually find the path to the destination, they reinforce the trail by depositing more pheromone (Lim et al. 2008). Simultaneously, the pheromone trail starts to evaporate and reduce its attraction. Obviously, the longer paths have a higher magnitude of evaporation than the shorter paths. Thus, by comparison, the intensity of lain pheromone on the shortest path, gradually increases to the level that balances with the evaporation rate, which causes the quantity of pheromone on the shorter path to grow faster than the corresponding longer one. Through pheromone accumulation, which is called the autocatalytic process (positive feedback), the probability that any single ant chooses the path to follow is quickly biased towards the shorter one (Erin et al. 2010; Shi et al. 2014).

The ACO has the following defects. First, the ACO is a heuristic bionic optimization method. To find the global optimal path, the searching space must be sufficiently large. Second, the ants avoid obstacles and navigate themselves to the goal by reducing the pheromone concentration near the obstacles after several encounters with the obstacle. Third, the ACO is a random search algorithm; particularly in the initial stage, the random search makes it inevitably produce a large number of local cross paths, circular paths and saw-tooth paths. Many ants lose their bearings and cannot find the full paths. All aforementioned defects are characterized by high computational costs, premature convergence and low search efficiency.

3 Proposed methods

3.1 Environment model

This article uses the two-dimensional grid method to represent the robot environment, and the grid squares are divided into two types: free grid square, which is represented by zero, and obstacle grid square, which is represented by one. The robot can only move in the free grid. The goal of robot path planning is to look for a grid set that contains the starting grid, ending grid and an orderly grid subset and to avoid the obstacle grids when encountering them

3.2 Local pheromone diffusion model

The robot motion can be interpreted as the motion of a particle in a gradient vector field, which is generated by positively and negatively charged electric particles. In this analogy, the robot is a positive charge, and the goal is a negative particle that generates attractive forces to attract the robot to the goal. The obstacles act as positive charges that generate repulsive forces that force the robot away from the obstacles. The combination of an attractive force and repulsive forces drives the robot in a safe path to the goal (Wei et al. 2013). The resultant force is closely related to the layout of the obstacles and target in the environment. In this paper, considering the overall layout of the obstacles and target in the environment, a diffusible pheromone of the current path point is used to improve the pheromone concentration along the direction of the artificial potential field force. The potential function $U_\mathrm{{total}}(p)$ given by (1) comprises two parts, the attractive potential function $U_\mathrm{{att}}(p)$ given by (2), and the repulsive potential function $U_\mathrm{{rep}}(p)$ given by (3). The mobile robot is driven by the total force f(p) given by (4) to the goal along the safe path.

$$\begin{aligned} U_\mathrm{{total}}(p)=U_\mathrm{{att}}(p)+U_\mathrm{{rep}}(p) \end{aligned}$$

(1)

$$\begin{aligned} U_\mathrm{{att}}(p)=\frac{1}{2}K_a(p-p_e)^2 \end{aligned}$$

(2)

$$\begin{aligned} U_\mathrm{{rep}}(p)=\left\{ \begin{array}{ll} \frac{1}{2}K_r(\frac{1}{\rho }-\frac{1}{\rho }_o)^2, &{}\quad \hbox {if}\quad \rho \le \rho _o; \\ 0, &{}\quad \hbox {if}\quad \rho <\rho _o \end{array} \right. \end{aligned}$$

(3)

$$\begin{aligned} f(p)=-\nabla U_\mathrm{{total}}(p)= \sum \limits _{i=1}^{m} f_{\mathrm{re}(i)}+f_{\mathrm{at}} \end{aligned}$$

(4)

where p and $p_e$ present the positions of the mobile robot and the goal of the system, $K_a$ and $K_r$ are scalar variables that represent the attractive and repulsive proportional gains of the functions, $\rho _o$ is the limit distance of influence of the potential field, and $\rho$ is the shortest distance to the obstacle, $f_{\mathrm{re}(i)}$ (i $=$ 1, 2, $\ldots$, m) is the repulsive forces, and $f_\mathrm{{at}}$ is the attractive force. The repulsive forces $f_{\mathrm{re}1}$, $f_{\mathrm{re}2}$, $f_{\mathrm{re}3}$ and the attractive force $f_\mathrm{{at}}$ are shown in Fig. 1. The resultant force is $f(\theta )$, and its direction is determined by $\theta$. Because of the potential field repulsive force, the pheromone concentration of the areas near the obstacles is low, and the ants have a decreased risk of visiting these areas (such as area one). The ants tend to explore the path along trajectory one.

Fig. 1

Resultant force direction

There are eight grids around the ant, and the grid numbers run from one to eight as shown in Fig. 2. Their angle range is $\theta _j \subset [(j-1) \times \frac{\pi }{4}- \frac{\pi }{8}, (j-1) \times \frac{\pi }{4} + \frac{\pi }{8} ]$, ($j= 1, 2, \ldots , 8)$. When the angle $\theta$ of the combination force is within a given angle range $\theta _j$, the grid number j to visit is described by (5).

$$\begin{aligned} \theta _j = (j-1) \times \frac{\pi }{4}- \frac{\pi }{8} \end{aligned}$$

$$\begin{aligned} j=\mathrm{round}\left( \frac{8 \theta + \pi }{2 \pi }+1\right) \end{aligned}$$

(5)

Fig. 2

Pheromone diffusion direction

Assume that the diffusion of pheromone in any direction obeys an approximately Gaussian distribution. The simplified model is shown in Fig. 3. The amount of diffusion pheromone at a given position is described by (6).

Fig. 3

Pheromone diffusion model

$$\begin{aligned} \frac{ \tau ^{''}_{ij}}{ \varphi (i)}= \frac{ga}{eo}= \frac{ab}{ob}= \frac{r- \xi }{r} \end{aligned}$$

$$\begin{aligned} \tau ^{''}_{ij}= \gamma \varphi (i) \frac{r- \xi }{r} \end{aligned}$$

(6)

where $\gamma$ is the diffusion coefficient, $\varphi (i)$ is the amount of pheromone diffusion source, r is the pheromone diffusion radius, $\xi$ is the distance between two grids, and $\tau ^{''}_{ij}$ is the amount of diffused pheromone from grid i to j. Assume that the edge length of the grid is one. When pheromone $\varphi (i)$ of the current grid spreads to the diagonal grid, the amount of diffused pheromone at a given grid n is described by (7).

$$\begin{aligned} r= ob = \sqrt{2}+\frac{\sqrt{2}}{2} \end{aligned}$$

$$\begin{aligned} \xi = oa= \sqrt{2} \end{aligned}$$

$$\begin{aligned} \tau ^{''}_{in}=\left\{ \begin{array}{ll} \gamma \varphi (i) \frac{3 \sqrt{2}/2- \sqrt{2}}{3 \sqrt{2}/2}=0.33 \gamma \varphi (i), &{}\quad { n \in B} \\ 0, &{}\quad {n \notin B} \end{array} \right. \end{aligned}$$

(7)

where B is the set of free grids.

When the pheromone $\varphi (i)$ of the current grid spreads to the vertical or horizontal grid, the amount of diffused pheromone at a given position (i, k) is described by (8).

$$\begin{aligned} \tau ^{''}_{ik}=\left\{ \begin{array}{ll} \gamma \varphi (i) \frac{3 \sqrt{2}/2- 1}{3 \sqrt{2}/2}=0.53 \gamma \varphi (i), &{}\quad { k \in B} \\ 0, &{}\quad {n \notin B} \end{array} \right. \end{aligned}$$

(8)

3.3 Geometry optimization path method

The aforementioned method for robot path planning can optimize the local path to some extent and can improve the searching efficiency of the path. The remaining local paths that require optimization are optimized using the geometric method. According to the characteristics of the local path, different measures are used.The relationships between two straight lines given by equation sets (9) and (10) are two situations in a two-dimensional coordinate system: parallel and intersecting. The end coordinates of the segments are A($x_1,y_1$), B($x_2,y_2$), C($x_3,y_3$) and D($x_4,y_4$), as shown in Fig. 4.

Fig. 4

Analysis of the intersection of two line segments

Line AB:

$$\begin{aligned} \left\{ \begin{array}{l} x=x_1+k_{AB}(x_2-x_1)\\ y=y_1+k_{AB}(y_2-y_1) \end{array} \right. \end{aligned}$$

(9)

Line CD:

$$\begin{aligned} \left\{ \begin{array}{l} x=x_3+k_{CD}(x_4-x_3)\\ y=y_3+k_{CD}(y_4-y_3) \end{array} \right. \end{aligned}$$

(10)

If the lines AB and CD intersect at E, the equation set (11) satisfies formula (12) and has a unique solution, which is described by (13) and (14).

$$\begin{aligned} \left\{ \begin{array}{l}k_{AB}(x_2-x_1)+k_{CD}(x_4-x_3)=x_3-x_1\\ k_{AB}(y_2-y_1)+k_{CD}(y_4-y_3)=y_3-y_1\\ \end{array} \right. \end{aligned}$$

(11)

$$\begin{aligned} \Delta = \left| \begin{array}{ll} x_2-x_1 &{} x_3-x_4 \\ y_2-y_1 &{} y_3-y_4 \\ \end{array} \right| \ne 0 \end{aligned}$$

(12)

$$\begin{aligned} k_{AB}= \frac{1}{\Delta }= \left| \begin{array}{ll} x_2-x_1 &{} x_3-x_4 \\ y_2-y_1 &{} y_3-y_4 \\ \end{array} \right| \end{aligned}$$

(13)

$$\begin{aligned} k_{CD}= \frac{1}{\Delta }= \left| \begin{array}{ll} x_2-x_1 &{} x_3-x_1 \\ y_2-y_1 &{} y_3-y_1 \\ \end{array} \right| \end{aligned}$$

(14)

If the line segments AB and CD intersect at E, the solution of the equation set satisfies formula (15).

$$\begin{aligned} \left\{ \begin{array}{l} 0 \le k_{AB} \le 1 \\ 0 \le k_{CD} \le 1 \\ \end{array} \right. \end{aligned}$$

(15)

Intersection E satisfies formula (16).

$$\begin{aligned} \left\{ \begin{array}{l} \text {Max}(x_1,x_4) \le x \le \text {Min}(x_2,x_3) \\ \text {Max}(y_1,y_3) \le y \le \text { Min}(y_2,y_4) \end{array} \right. \end{aligned}$$

(16)

If the end coordinates of path segments AB and CD satisfy formulas (12), (13), (14) and (15), the path ABCD is optimized to path AD. The angle between two adjacent path segments satisfies formula (17), as shown in Fig. 5.

Fig. 5

Analysis of saw tooth

$$\begin{aligned} \Lambda = \left| \begin{array}{l} \mathrm{arctan}( \frac{y_i-y_{i-1}}{x_i-x_{i-1}})-\mathrm{arctan}( \frac{x_i-x_{i+1}}{y_i-y_{i+1}})\\ \end{array} \right| \end{aligned}$$

(17)

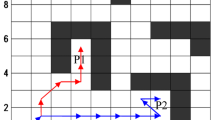
If angle $\Lambda$ equals 45$^\circ$, path DABCE is optimized to path DACE. In Fig. 6, the solid line trajectory P ( $\rightarrow$ $\rightarrow$ ⑥ $\rightarrow$ ② $\rightarrow$ ③ $\rightarrow$ ④ $\rightarrow$ ⑧ $\rightarrow$ $\rightarrow$ $\rightarrow$ ) is a part of the global path, and the circular path L( $\rightarrow$ ⑥ $\rightarrow$ ② $\rightarrow$ ③ $\rightarrow$ ④ $\rightarrow$ ⑧ $\rightarrow$ $\rightarrow$ ) can be removed. Then the path P can be optimized to path P1( $\rightarrow$ $\rightarrow$ $\rightarrow$ ).

Fig. 6

Analysis of circular path

Fig. 7

Pheromone distribution of the ACO at 6, 8 10 times

Optimization steps:

Step 1: Obtain the numbers of the current grid and its adjacent grids, i.e., , and the grid subset $\Gamma$(⑤ ⑥ ⑦ ⑨ ).

Step 2: Remove grid in the taboo list and obstacle grid ⑤ from subset $\Gamma$. Obtain the free grids $\Gamma 1$(⑥ ⑦ ⑨ ).

Step 3: In turn, look for the position of grid that belong to $\Gamma 1$ in the grid set P. Take grid that is adjacent to current grid , whose place is at the end of the position list, as the next grid.

Step 4: Connect the current grid to grid . Path P is optimized to path P1( $\rightarrow$ $\rightarrow$ $\rightarrow$ ).

Step 5: Repeat the above steps for all remaining paths.

Fig. 8

Pheromone distribution of the ACO-PD at 6, 8 10 times

3.4 Description of the algorithm

The ACO-PD has the following operating steps:

Step 1: Extract the environment land feature and build an environment map, which is represented by grids.

Step 2: The ACO and potential field method are initialized with the required arguments.

Step 3: According to the general formulas (6), (7) and (8), the local pheromone of the current grid spreads to the adjacent grids along the direction of the combination force.

$$\begin{aligned} \tau _{ij(t)}=\tau _{ij(t)}+\tau _{ij}^{''}(t) \end{aligned}$$

where $\tau _{ij}$ is the amount of pheromone at the given grid j. Step 4: The ant k moves from grid i to grid j with the following probability:

$$\begin{aligned} p_{ij}^k =\frac{\tau _{ij}^ \alpha (t) \eta _{ij}^ \beta (t)}{\sum \nolimits _{s \subset \mathrm{allowed}}^{}\tau _{is}^ \alpha (t) \eta _{is}^ \beta (t)} \end{aligned}$$

Where $\alpha$ and $\beta$ are positive real parameters whose values determine the relative importance of pheromone versus heuristic information. Furthermore, $\tau _{ij}^ \alpha$ and $\eta _{ij}^ \beta (t)$ are the pheromone value and heuristic value that are associated with an available solution route, respectively.

Step 5: Add grid j to the taboo list $B_j$.

Step 6: Carry out step three if the ant k does not arrive the goal grid.

Step 7: Save the path $T_k^{'}$ that the ant k searched and its length $L_{k}^{'}$.

Step 8: The pheromone is updated according to the equation

$$\begin{aligned} \Delta \tau _{ij}^{'}(t,t+1)= \sum \limits _{k=1}^{m} \Delta \tau _{ij}^{'k}(t,t+1) \end{aligned}$$

$$\begin{aligned} \tau _{ij}(t+1)=(1- \rho ) \tau _{ij}(t)+ \Delta \tau _{ij}^{'}(t,t+1) \end{aligned}$$

(18)

where $\rho$ is the rate of pheromone evaporation, $\Delta \tau _{ij}^{'}$ is the amount of deposited pheromone, and $\Delta \tau _{ij}^{'k}$ is the amount of pheromone deposited by ant k, which is typically given by:

$$\begin{aligned} \Delta \tau _{ij}^{'k}=\left\{ \begin{array}{ll} \frac{Q}{L_{k}^{'}}, &{}\quad \hbox {if\, ant}\, k \ \hbox {traveles\, on \,edge}\, (i,j) \\ 0, &{}\quad \hbox {otherwise} \end{array} \right. \end{aligned}$$

Step 9: Optimize path $T_k^{'}$ to $T_k$ according to the general formulas (12), (13), (14), (15) and (17). Then, save path $T_k$ and its length $L_k$.

Step 10: The amount of pheromone is updated again according to the following equation:

$$\begin{aligned} \Delta \tau _{ij}^{k}=\left\{ \begin{array}{ll} \frac{Q}{L_{k}}, &{}\quad \hbox {if\, edge}\, (i,j)\, \hbox {is\, a\, part\, of\, path}\, T_k \\ 0, &{}\quad \hbox {otherwise} \end{array} \right. \end{aligned}$$

$$\begin{aligned} \Delta \tau _{ij}(t,t+1)= \sum \limits _{k=1}^{m} \Delta \tau _{ij}^{k}(t,t+1) \end{aligned}$$

$$\begin{aligned} \tau _{ij}(t+1)=(1- \rho ) \tau _{ij}(t)+ \Delta \tau _{ij}(t,t+1) \end{aligned}$$

(19)

Step 11: Select the optimal path in this cycle and save it.

Fig. 9

Comparison of the numbers of lost ants

Fig. 10

Comparison of the iterations

Fig. 11

Comparison of the global optimal paths

Fig. 12

Pheromone distribution of the ACO-PDG at 6, 8, 10 times

4 Pheromone distribution

The artificial potential field is a common local path-planning method for the mobile robot. The superposition of locally diffused pheromone based on artificial potential force and global pheromone increases the pheromone concentration of a high fitness solution space and, consequently, enhances the probability of searching such subspace. It strengthens the search process guidance (Wang et al. 2008) and updates the global pheromone intensity, as shown in Figs. 7 and 8.

Fig. 13

Local path optimization

The impacts of local diffusion pheromone on the number of lost ants, iterative times and path length are shown in the bottom part of Figs. 9, 10 and 11. (Without getting into too much detail because of the space constraints). These figures show only the relationships in these cases, and the pheromone volatilization coefficient $\rho$ is 0.5. The graph shows that, in comparison to the standard ACO solution, the algorithm ACO-PD reduces the number of lost ants number, iterative times and improves the searching efficiency. Thus, the algorithm ACO-PD diffusion can strongly improve the quality of the standard ACO.

When an ant finishes building a path using the first method, the path is optimized to another better path using the geometric method. In each iteration, each ant generates two candidate solutions; meanwhile, the amount of pheromone on the two paths is updated by (18) and (19) which further increases the intensity of the pheromone of the global path. These results are shown in Fig. 12.

Fig. 14

Simulation diagram of path planning

Fig. 15

Feature parameters

Table 1 Comparison of the iteration times, path length for the three methods

5 Experimental results and analysis

In this paper, the simulation process is based on the Ant-Cycle model.The simulation environment is shown in Fig. 13. The first grid is the starting point, and the 400th grid is the target point. The optimal path length is 30.3848. The parameters are: heuristic factor $\alpha =1.1$, expected heuristic factor $\beta =12$, pheromone evaporation coefficient $\rho =0.5$, ant number $m=10$, diffusion coefficient $\gamma =0.01$, and cycle number $K=200$.

Fig. 16

a Standard ACO convergence curves. b ACO-PD convergence curves. c ACO-PDG convergence curves

The blue solid line is the path that the ant searched using the ACO-PD method, which is near the global optimal path (as shown in Fig. 13), and its length is 51.1127. The red heavy line is the local optimal path (A and B are crossed paths; C, F, G and H are saw-tooth paths; D and E are circular paths.). The red line is the optimal path using ACO-PDG method. Its length is 41.4558, as shown in Fig. 14.

It can be seen from the figures that the ACO-PD algorithm strengthens the search process guidance and reduces the number of lost ants with incomplete paths. The path from this algorithm is near the global optimal path. It is optimized further using the geometry method to avoid crossed paths, circular path and saw tooth path. Each ant generates two candidate solutions and its search efficiency is improved.

Table 2 Comparison of the iteration times, path length for the three methods

Three feature points, A($x_1,l_1$), B($x_2,l_1$) and C($x_3,l_2$) on the simulation diagram, are used to compare the performances of the three algorithms (standard ACO, ACO-PD and ACO-PDG) in the paper in detail, as shown in Fig. 15. Parameter $x_1$ is the iteration time to first find the global optimal path, and $l_1$ is the length of the path. Parameter $x_2$ is the minimum iteration time to continuously find the global optimal path. Parameter $x_3$ is the iteration time of the convergence path, and $l_2$ is the length of the convergence path.

To verify the feasibility of the proposed approach, a number of simulation experiments were performed. For each algorithm, ten simulation trials were performed, and the average result was taken. The results are compared in Table 1.

In Table 1, every algorithm can search for the global optimal path at 30.3848. The standard ACO takes 11 iterations on average to find the global optimal path. Seven simulation trials converge to a local optimum at 33.7990, and the standard ACO converges to the global optimum only three times. The difference between the $x_1$ and $x_2$ group data from the experiment is large, which significantly affects the convergence rate. The ACO-PD averages 7.9 iterations to find the global optimum, and it converges to the global optimum six times. As the difference between the $x_1$ and $x_2$ group data decreases, the convergence rate is enhanced. The second, fourth, fifth ,seventh eighth and tenth convergent curves are better. Compared with the standard ACO solution, the ACO-PD provides better performance and lowers the risks of trapping in a local optimum. After 2.6 iterations, on average, the ACO-PDG reaches its best solution at 30.3848. Each ant can search two candidate solutions (the red and the blue trajectories shown in Fig. 13) per loop iteration and, consequently, enhance the update intensity of pheromone. $x_1$, $x_2$ and $x_3$ are equal, and the convergence rate is significantly enhanced. Otherwise, the ACO-PDG can lower the risks of trapping in a local optimum, and every simulation trial can converge to a global optimum at 30.3848. The convergent curves of the three algorithms in the same environment are shown in Fig. 16. The third convergent curve is better than the others.

To verify the feasibility of the proposed approach, some simulation experiments were performed in the environment of the literature (Luo and Wu 2010). The results are compared in Table 2, and the simulation diagram is shown in Fig. 17. The convergent curves of the three algorithms in the same environment are shown in Fig. 18.

Fig. 17

Simulation diagram of path planning

Fig. 18

a Standard ACO convergence curves. b ACO-PD convergence curves. c ACO-PDG convergence curves

Table 3 Comparison of the performance for the two methods

In Table 2, the standard ACO find the global optimal path at 35.0711 only five times, and eight simulation trials converge to a local optimum. The difference between the $x_1$ and $x_2$ group data from the experiment is large. The ACO-PD find the global optimal path eight times, and it converges to local optimum five times. As the difference between the $x_1$ and $x_2$ group data decreases, the convergence rate is enhanced. Compared with the standard ACO solution, the ACO-PD provides better performance and lowers the risks of trapping in a local optimum. After 1.2 iterations, on average, the ACO-PDG reaches its best solution at 35.0771. The conclusion is that the ACO-PDG performs better than the two other algorithms.

In Table 3, simulation experiments were performed ten times to compare this approach with another previously developed approach ACO-PF (Luo and Wu 2010) in the same environment. $n_c$ is the number of simulations that search for the global optimum; $\overline{l}$ is the average length of the convergence path; $\overline{n}$ is the average number of searches for the global optimum. The experimental results show that both algorithms can search the global optimum, but the proposed approach in this article reduces the iteration from 11 and 12 to 2 and 2.2, respectively, and obviously accelerates the rate of iteration convergence.

6 Conclusion

This article has shown that the proposed technique is an interesting new approach to solving the path planning problem. The approach is a combination of the artificial intelligence algorithm and the geometry optimization method, i.e., an ACO based on the diffusion of local pheromone and a local path optimum based on geometry. The local diffusion pheromone is applied to the ACO for problems that are represented in a large search space. The method ACO-PD strengthens the search process guidance and reduces the number of ants with incomplete paths. The path from the first algorithm is optimized using the geometry method to avoid crossed paths; thus, in each iteration, each ant generates two candidate solutions. The method ACO-PDG enhances the update intensity of pheromones by updating the pheromones twice per iteration loop. To test the effectiveness of the approach, a number of simulation experiments were performed to compare this approach with other previously developed approaches. The experimental results show that the proposed approach can effectively generate good solutions quickly, and lowers the risks of trapping in a local optimum.