Construction of Tree Network with Limited Delivery Latency in Homogeneous Wireless Sensor Networks

Abstract

In this paper we propose an approximation algorithm, which is called ADCMCST (algorithm with the minimum number of child nodes when the depth is restricted), to construct a tree network for homogeneous wireless sensor network, so as to reduce and balance the payload of each node, and consequently prolong the network lifetime. When the monitoring node obtains the neighbor graph, ADCMCST tries to find a tree topology with a minimum number of child nodes, and then broadcast the topology to every node, and finally a tree network is constructed. Simulation results show that ADCMCST could greatly reduce the topology formation time, and achieve good approximation results; when the compression ratio is less than 70 %, the network lifetime of ADCMCST will be larger than that of energy driven tree construction.

1 Introduction

As wireless communication technology and micro electromechanical sensing technology are developing rapidly, wireless sensor network has emerged. It is deployed in the monitoring area by a large number of nodes, through wireless communication to form a multi-hop ad hoc network system [1]. The typical application models include two categories: one is the sensor nodes continuously monitor surrounding states or events, and the results are passed to the monitoring node [2]; and the other is the monitoring node issues command to the sensor nodes, and the sensor nodes perform the corresponding command. In both of them, the tree topology is a preferable choice [3].

According to the similarities and differences of function between nodes, wireless sensor networks can be divided into two types: the homogeneous and the heterogeneous. In the homogeneous wireless sensor network [4], all nodes except the monitoring node, which is called sensor nodes, have the same function and status, which are responsible for data collection, processing and forwarding to monitoring node. However, in the heterogeneous wireless sensor network [5], nodes are classified into monitoring node, relay nodes and sensor nodes. Sensor nodes are responsible for data collection, and relay nodes are only responsible for data forwarding but not responsible for data collection.

Since sensor nodes in wireless sensor network are mainly powered by battery, their energy is limited. We should try to balance their energy consumption to extend the network lifetime [6]. Although we can achieve above goal by scheduling of data transmission [7], network topology also plays an important role. Thus during the course of constructing a tree network, we must take the energy consumption into consideration. When the number of nodes is small, we can manually configure them to form a tree network and to achieve above objectives; but when the number of nodes becomes larger, manual configuration will be unrealistic. Therefore, researching on the automatic construction of tree network is very important.

In this paper, we propose an algorithm, which is called as ADCMCST (algorithm with the minimum number of child nodes when the depth is restricted), to automatically construct a tree network based on the homogeneous wireless sensor network, by searching a tree topology with the minimum number of child nodes when the depth of the tree is constrained, according to the neighborship between all the nodes. Because it is a NP-Hard problem, we propose an approximation algorithm to resolve it. The innovations of this paper are two fold: first, the network depth is limited, so the maximum forwarding delay, which is evaluated by hops, of data packet could be guaranteed; second, the number of child nodes is minimized, which helps to reduce and balance the payload of each node and consequently prolong the network lifetime.

The rest of this paper is organized as follows: Section 2 is the related methods to construct tree networks; Sect. 3 describes the model of the homogeneous wireless sensor network; Sect. 4 provides an algorithm to construct the tree topology; the performance analysis and comparison are in Sect. 5; and this paper is concluded in Sect. 6.

2 Related Methods

In this section, we present some typical tree topology construction methods which are proposed for different purposes, and the pros and cons are also discussed.

Ding [8] proposed a distributed heuristic algorithm based on effective energy of nodes to form an aggregation tree. The algorithm lets every node select the node with the maximum residual energy and the minimum hop to the monitoring node as its parent node. However, this method may lead to unbalanced payload and serious packet collision because it does not limit the degree. And what’s more, the priority of maximum residual energy and the minimum hop is not discussed, which might lead to the energy of some node be used up rapid when the node is nearest to the monitor node.

In order to prolong network lifetime, Wu [9] proposed a centralized construction algorithm. It translates the residual energy of a node into its degree, and the lower the residual energy is, the larger the degree is. So the method is formulated to search a tree with the minimum degree. Although it could maximize the network lifetime, it does not take the network depth into consideration, so it may lead to large transmission hops.

Singhal [10] divided all nodes into a lot of clusters, utilized the minimum spanning tree algorithm to construct a tree for every cluster, and combined these trees to form a tree-like network. Just like the method in [9], this method is also used to maximize network lifetime. However, different from our method, its lifetime is effected not by the number of child nodes but by the transmission distance between two nodes.

Andreou [11] proposed an energy driven tree construction (ETC) algorithm, which puts all nodes into different layers. Each node could only communicate with the nodes in the adjacently higher layer, and node selects the upper one with the minimum number of child nodes as its parent node. This method could not only ensure the timely packet relay but also balance the payload, and consequently prolongs the network lifetime. And the method is compared by ours.

In order to construct a balanced tree to minimize the packet collision, Georigios [12] proposed a distributed algorithm to minimize the number of child nodes based on an a-priori established unbalanced tree. However, it does not discuss how to construct the initial tree and the depth constraint is not taken into account, and consequently the resultant tree could not ensure timely packet delay.

In Zigbee network, the maximum number of child nodes and relay nodes and depth are predetermined, which may lead to the existence of orphan nodes. In order to reduce the number of orphan nodes, Pan [13] proposed an algorithm to construct tree network which contains nodes as much as possible and how to reduce the orphan nodes is its purpose. However, how to determine the depth and degree are not discussed. Although the depths are both limited in Pan’s and ours, the degree is constrained in Pan’s but not in our method. Our method is trying to reduce the degree of the final tree, which may be still bigger than the pre-selected degree of Pan’s. And what’s more, the method in [13] is based on heterogeneous network, but our method is based on homogeneous network.

In order to provide users with satisfied throughput and delay for multimedia contents over the Internet, Su [14] constructs a tree network by defining a layered degree, i.e. out-degree and in-degree, according to the capacity of node and the streaming rate. Although this tree network could achieve better performance, it does not take the network lifetime and delay into consideration, so it is not suitable for wireless sensor networks.

3 Network Model

The model of the homogeneous wireless sensor network is shown in Fig. 1. The model is denoted as a directed graph $\vec {G}=(V,E)$, where $V$ is the set of all the nodes and ${\vert }V{\vert }$ is the number of nodes, and $E$ is the set of all the directed edges. For any edge $e_{i,j} \in E$, it means node $j$ could reliably receive the data packet from node $i$. In this model, there is a monitoring node, i.e. node 1, and the rests are sensor nodes. Sensor nodes collect the information of surrounding environment, and transmit them to the monitoring node in multi-hop manner.

Fig. 1

Model of the homogeneous wireless sensor network

We assume that every node has a global unique physical address to identify itself and the same transmission power, and the communication links are symmetric. In order to ensure the stable neighborship, only two nodes whose received power from each other is bigger than some preset value could be neighbors. Node could communicate point-to-point with its neighboring nodes.

In homogeneous wireless sensor network, all sensor nodes have the same function and collect the same environment information. We assume that any sensor node could amalgamate its own data with other data from the received packets, and compress them for forwarding to other node in order to reduce the power consumption [15, 16]. We also assume that every data packet has the same size and each node has its own data to be transmitted, so the compression ratio $C$ of each node is defined as follows:

$$\begin{aligned} C=\frac{N_s -1}{N_r } \end{aligned}$$

(1)

where $N_{s}$ denotes the number of packets to be sent, $N_{r}$ denotes the number of received packets from its child nodes. The maximum value of $N_{s}$ is $N_{r} + 1$, which means that $C$ equals to 1 and there is no compression. The minimum value of $N_{s}$ is 1, which means that $C$ equals to 0. $C$ equaling to 0 mainly depends on the concrete application. For example, when the network is used to monitor environmental information such as electronic device temperature, electronic device working time, and coal gas density and so on, to obtain the maximum or minimum value, each sensor node only needs to compare the received data from child nodes with its own data, and select one to forward.

When the monitoring node obtains the neighbor graph, it generates a tree topology $T_{e}$ with the minimum number of child nodes when the depth is constrained. And then, it floods the tree topology to all nodes, such that every node knows its parent node and child nodes. Next we give proposition 1.

Proposition 1

given a directed graph $\vec {G}=(V,E)$ and the depth upper bound $L_{s}$, searching a tree with the minimum number of child nodes when the depth is restricted (DCMCST) is a NP-Hard problem.

Proof

we know that finding a tree with the minimum number of child nodes from an undirected graph is a NP-Hard problem [19], and because the undirected graph is a special one from the directed graph, so above problem could be reduced to finding a tree with the minimum number of child nodes from a directed graph (MDST); When $L_{s} \rightarrow \infty$ DCMCST is equivalent to MDST, which means that MDST is a special case of DCMCST. So MDST could be further reduced to DCMDST. So we conclude that DCMDST is also a NP-Hard problem.

4 Tree Network Construction

In this section, we first give the depth lower bound that the tree topology could be; then we propose an approximation algorithm ADCMCST to construct a tree topology when the depth upper bound is given; finally, we demonstrate the implementation procedure of the tree network.

4.1 Depth Lower Bound

Obviously, we must know the minimum depth $L_{l}$ that the tree topology could be according to the neighbor graph $\vec {G}=(V,E)$, which helps users to select a preferable depth $L_{s}$ for the final tree network. If $L_{s} < L_{l}$, we could not achieve a tree network that contains all the nodes. So, the first thing is to determine the minimum value of $L_{l}$.

Proposition 2

Given a directed graph $\vec {G}=(V,E)$, for any node $v \in V$, if we let $v$ be the root node, and traverse the graph using breadth first search algorithm (BFS), we will get a BFS tree $T_{bfs}$. The depth of the BFS tree is the minimum of all the spanning trees from $\vec {G}$.

Proof

for any node $v \in V$, we denote the depth of $T_{bfs}$ rooted at $v$ as $d_{bfs}$. We assume that there is a Non-BFS tree $T_{n-bfs}$ rooted at $v$ whose detph $d_{n-bfs}$ is less than $d_{bfs}$.We let $d_{bfs}(x)$ represent the depth of node $x$ in the tree $T_{bfs}$ and let $d_{n-bfs}(x)$ represent the depth of node $x$ in the tree $T_{n-bfs}$. Because of $d_{n-bfs} < d_{bfs}$, there must be a node denoted as $n$ satisfying $d_{n-bfs}(n) < d_{bfs}(n)$. However, according to the property of the breadth first search algorithm, the depth of any node in the tree $T_{bfs}$ could be reduced. It is in contradiction with the assumption. So we could conclude that the depth of any spanning tree will not be less than that of the BFS tree rooted at the same node. $\square$

According to the proposition 2, we could easily get the depth lower bound $L_{l}$: let the monitoring node be the root, traverse the graph $\vec {G}$ using BFS algorithm and obtain a BFS tree. The depth of the BFS tree is the minimum depth $L_{l}$.

4.2 Approximation Algorithm

After getting $L_{l}$, the user selects a preferable depth $L_{s}$ which satisfies $L_{s} \ge L_{l}$, and then the monitoring node searches a tree topology to minimize the number of child nodes of the tree when the depth $L_{s}$ is given. The number of child nodes of a tree is defined as the number of child nodes of a node which has the maximum number of child nodes in the tree. Because it is a NP-Hard problem demonstrated by proposition 1, in the next, we propose an approximation algorithm, which is called as ADCMCST, to resolve it. ADCMCST includes two aspects: main body which is shown in Table 1 and local optimization procedure which is shown in Table 2.

Table 1 Main body

Table 2 Local optimization procedure

In the main body of the approximation algorithm, we try to reduce the number of child nodes of every node, which depends on the local optimization procedure. Radha [20] has proposed a local optimization procedure to minimize the number of child nodes; however, he does not take the depth constraint into consideration. So in the next, we give an improved local optimization procedure.

If the local optimal procedure is successful, the number of child nodes of node $n$ will reduce one, and there must be another node $n$’ whose child nodes is increased one. However, the step S2_2 ensures the number of child nodes of node $n$ is still larger than that of node $n$’.

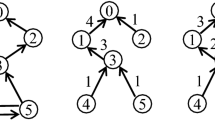
Next, we give an example of constructing an inner tree with depth not more than 3 (the depth of monitoring node is 0) to demonstrate the procedure of our approximation algorithm based on Fig. 1. Firstly, the monitoring node sets itself as the root, traverses the graph using BFS algorithm and gets an initial tree shown in Fig. 2a; because the number of child nodes of node 1 is maximal, so we locally optimize the node 1; we could see that the number of child nodes of node 1 is 4 and its child nodes are from node 2 to node 5. If the number of edges pointing to any of the child nodes of node 1 is over 3 in graph ${\mathop {G}\limits ^{\rightharpoonup }}$, we delete these inner edges from ${\mathop {G}\limits ^{\rightharpoonup }}$, and the result is shown in Fig. 2b; combining Fig. 2a with Fig. 2b, we get a temporal directed graph ${\mathop {G}\limits ^{\rightharpoonup }}$, which is shown in Fig. 2c; selecting node 3 and deleting the directed edge from node 3 to node 1, Fig. 2c becomes Fig. 2d; we let node 3 be the root and find a path to the monitoring node 1 using BFS algorithm, and we get the path node 3-$>$node 2-$>$node 1; we optimize the temporal tree according to the new path and obtain an optimized tree shown in Fig. 2e; now check whether the depth of the new temporal tree is satisfied with the preset value, and the local optimization procedure is finished if satisfied, otherwise we recover above procedures and reselect a new node to be optimized. Continue above procedures and we will get the final tree shown in Fig. 2f.

Fig. 2

Example of constructing an inner tree with depth not more than 3

4.3 Implementation

The procedure of forming a tree network is as follows: firstly, monitoring node obtains the neighbor graph ${\mathop {G}\limits ^{\rightharpoonup }}=(V,E)$ by broadcasting [9], which contains finding stage and forming stage, and the details are shown in next paragraph; secondly, the monitoring node obtains the minimum depth $L_{l}$ which is stated in Sect. 4.1 and returns the result to user, and user subsequently selects an upper bound $L_{s}$; thirdly, the monitoring node searches a tree topology $T_{e}$ using the ADCMCST algorithm; and finally the monitoring node floods $T_{e}$ to every senor node. Thus a tree network is formed. Although this implementation is a centralized manner, it can be easily extended to the distributed manner [17, 18]. The CSMA/CA could be used by the nodes to access the wireless channel.

The finding stage is initiated by the monitoring node, and the details are as follows: firstly, monitoring node broadcasts a “Hello” packet which contains $<$ ID, deep $>$ , where ID denotes the physical address of and deep is set to 0; secondly, any node except the monitoring node receives the “Hello” packet, it labels the node sending the “Hello” packet as its neighbor; thirdly, if the node is the first time to receive the “Hello” packet, it sets its deep equal to the deep in the packet plus one and then generates a new “Hello” packet to broadcast; otherwise it compares the deep in the received packet with previous received packet, and if the former is less than the later, the node regenerates a “Hello” packet to broadcasts. In the new “Hello” packet, ID denotes its physical address and deep equals to that in the received packet plus one; and finally, when all nodes could not receive any “Hello” packet, the finding stage is finished.

When the finding stage is finished, each node knows its neighbors. Next we give the procedures of the forming stage, which is initiated by the leaf nodes who do not receive the “Hello” packet where the value of deep is larger than that of itself. Firstly, node broadcasts a “Neighbor” packet which contains $<$ Neighbor, deep $>$ . Neighbor denotes the neighbor graph that the node learns, and deep denotes the depth of the node; Secondly, if any node is the first time to receives the “Neighbor” packet, or the value of deep in the received packet is bigger than its own “Neighbor” packet which has been broadcast, it combine the Neighbor in the received packet with is own neighbor graph to form a new neighbor graph, generate a new “Neighbor” packet to broadcast; and finally, when above procedures are finished, monitoring node obtains all the half-baked neighbor graphs. After combining all these graphs, the monitoring node will form a full neighbor graph.

5 Analysis and Simulations

In this section, we will evaluate ADCMCST algorithm in terms of time complexity and approximation ratio from analysis and simulations, and evaluate the payload, delay and lifetime of the network which is formed by our algorithm.

5.1 Analysis

ADCMCST algorithm includes two aspects: main body and local optimization procedure. In the main body, we need to order all nodes to form a queue and thereafter to insert the two nodes the number of whose child nodes have been changed into the queue, so the time complexity of the ordering is $O(n)$. Meanwhile, the local optimization procedure will be invoked by $n^{3}$ times [19], so the time complexity of the main body is $O(n^{3} + n)$, equivalent to $O(n^{3})$. In the local optimization procedure, the complexity of BFS is $O(n + e)$, so the complexity of local optimizing one node is $O(n(n + e))$. Thus we conclude that the time complexity of the approximation algorithm is $O(n^{4}(n + e))$, which is quasi-polynomial. Although the complexity is somewhat high, the real run time is not such long which will be shown in simulations.

Proposition 3

Suppose OPT($I)$ denotes the number of child nodes of the optimal tree, and $A(I)$ denotes the maximal number of child nodes in the tree constructed by our ADCMCST algorithm. Then the following inequality is satisfied:

$$\begin{aligned} A(I)\le b\times OPT(I)+\left\lceil {\log _b n} \right\rceil \end{aligned}$$

(2)

Where $b$ is a positive integer larger than 1 and $n$ is the total number of nodes.

Proof

As to the tree $T_{e}$ constructed by our approximation algorithm, it has the following feature: from the initial tree which is formed by the BFS algorithm based on the neighbor graph $G$, through a variety of temporary tree $T_{t}$ to the final tree $T_{e}$, the depth of all of these trees does not exceed $L_{s}$. For the final tree $T_{e}$, no matter whether it is an optimal tree, we use $S_{k}$ denotes the collection of all the nodes the number of whose child nodes are not less than $k$, and then there are least ($k - 1){\vert }\hbox {S}_{k}{\vert } + 1$ nodes among the child nodes of $S_{k}$, which satisfy that any of them is not descendant of others [20].

Obviously, if we take any of these ($k - 1){\vert }\hbox {S}_{k}{\vert } + 1$ nodes as a root and search a new path to the monitoring node, the path must traverse some node in $S_{k-1}^{{\prime }}$ where $S_{k-1}^{{\prime }}$ is a subset of $S_{k-1}$. It must be noted that there may exist some nodes in $S_{k-1}$, which will cause the depth of tree exceed $L_{s}$, and the collection of these nodes is $S_{k-1} \backslash S_{k-1}^{\prime }$. If there is a path which does not go through any of the nodes in $S_{k-1}$ such that the depth of the new tree does not exceed $L_{s}, T_{e}$ will not be the final tree because we could reduce the number of nodes in $S_{k}$ by one using the local optimization procedure. So we can conclude that for any final tree $T_{e}$ constructed by our approximation algorithm, there must be at least ($k - 1){\vert }\hbox {S}_{k}{\vert } + 1$ nodes in $S_{k}$ satisfying that any of them which have a path to monitoring node must go through some node in $S_{k-1}^{{\prime }}$. Thus we get the following inequality [20]:

$$\begin{aligned} \begin{array}{l} OPT(I)\ge \frac{(k-1)|S_k |+1}{|S_{k-1}^{\prime } |} \\ \quad \ge \frac{(k-1)|S_k |}{|S_{k-1} |} \\ \end{array} \end{aligned}$$

(3)

And then for any positive integer $b$ which is bigger than 1, there must be an integer $i$ which satisfies [19]:

$$\begin{aligned} i\ge A(I)-\left\lceil {\log _b n} \right\rceil +1 \end{aligned}$$

(4)

such that ${\vert }\hbox {S}_{i-1}{\vert } \le b{\vert } S_{i}{\vert }$. If we let $k$ equal to $i$ we can get:

$$\begin{aligned} OPT(I)\ge \frac{(i-1)|S_i |}{b|S_i |} \end{aligned}$$

(5)

i.e. $i \le b \times OPT(I) + 1$. Combining with (3), we obtain the relationship between $OPT(I)$ and $A(I)$:

$$\begin{aligned} A(I)\le b\times OPT(I)+\left\lceil {\log _b n} \right\rceil \end{aligned}$$

(6)

Thus, proposition 3 is proved. $\square$

The result shows that our algorithm could achieve the same effect with that in [20] which is used to construct a tree without depth constraint.

5.2 Simulations

The simulation runs on a notebook PC whose CPU is Duo8400 and memory capacity is 2G. The simulation software is Matlab 7.0.

In order to evaluate the running time of our approximation algorithm, we compare it with the enumeration algorithm. It needs egregious time for the enumeration algorithm when the number of nodes is large, so we only take a small number of nodes into consideration. We first setup three completely connected networks, in which the numbers of nodes are 4, 5 and 6 respectively and one of them is the monitoring node. The running time of the two algorithms are shown in Fig. 3. It could be seen that the running time of the enumeration algorithm rapidly increases when the number of nodes is from 4 to 6; however, the time of our ADCMCST approximation algorithm increases slowly. For example, when the number of nodes increases from 4 to 6, the running time of the enumeration algorithm increases about 80 times, but the running time of our algorithm only increases about 6 times.

Fig. 3

Running time under different test scenario

In order to find out the running time of the approximation algorithm further, we do a second simulation. We assume that the region is a square with 50 m $\times$ 50 m and the communication distance is 20 m. We generate 50 scenarios randomly, and obtain the average running time under different number of nodes and depths. The results are shown in Fig. 4. We could see that the running time is reduced when the depth increases. For example the time is reduced by about 45 % when the depth increased by 4. And the running time increases slowly when the number of nodes increases. The results show that in order to construct a tree network fast, we could increase the depth somewhat. However, increasing the depth will improve the relay time of packets from leaf nodes to monitoring node.

Fig. 4

Running time under different number of nodes

In order to evaluate the approximation ratio of our algorithm, we build six completely connected networks, in which the numbers of nodes are 20, 60, 80, 120, 160 and 200 respectively. For each of them, we generate 10 different tree networks with the depth varied from 1 to 10, and totally we get 60 cases. Only in the completely connected networks could we compute the optimal results manually. The approximation results are shown in Table 3 and the value in the bracket denotes the difference between our ADCMCST algorithm and the optimal result. The number of case where the approximation value equaling to the optimal value is 35, accounting for 58.3 %. The worst case is that the approximation value is 3 greater than the optimal value, and however, the number of them is 2, only accounting for 3.3 %.

Table 3 Approximation ratio under different depth and number of nodes

In order to evaluate the network performance of our ADCMCST algorithm, we compare it with the ETC algorithm [11]. We assume that the region is a square with 50 m $\times$ 50 m and the transmission radius of each node is 20 m. Sending a packet needs 1 energy unit and receiving a packet needs 0.5 energy units [21]. The total energy of each node is 1,000 unit. Each sensor node periodically collects the data every 1 s and sends it to its parent node after receiving all the data from its child nodes.

First we compare the maximum and the variance of payload of the two algorithms. In this paper, the maximum of payload which has impact on the network lifetime is the maximal number of child nodes of a node, and the variance of payload represents the payload balance of a tree.

Figure 5 shows the maximum of payload when the number of nodes changes from 20 to 40. Obviously, the maximal number of child nodes of our algorithm is in inversely proportional to the depth of the tree. We could see that when $L_{s} = L_{l}$, our algorithm is far superior to that of ETC, and the reasons are twofold: on the one hand, as for the ETC, only when the number of child nodes of a node is above some threshold, the node will try to decrease its child nodes, and our algorithm has no the threshold; on the other hand, our algorithm will reduce the child nodes of a node in the tree by changing the depth of one of the child nodes, which will not happen in ETC.

Fig. 5

Maximum payload under different number of nodes

Figure 6 shows the variance of payload when the number of nodes changes from 20 to 40. When the depth increases, the termination possibility of our algorithm due to the depth constraint reduces, and consequently the payload of the final tree tends to be more balanced, which results in lower variance. When $L_{s} = L_{l}$, the variance of our algorithm is far superior to that of ETC, which demonstrates that our algorithm tries the best to find the balanced tree, and of course the payload is more balanced than that of ETC.

Fig. 6

Variance of payload under different number of nodes

We then compare the average and the variance of the delay of the two algorithms. In this paper, the average of the delay is the average hop counts that a packet transmitted from a sensor node to the monitoring node, and it has impact on the network lifetime.

Figure 7 shows the average of delay when the number of nodes changes from 20 to 40. Obviously, the average of delay increases when $L_{s}$ increases. From this figure, we could see that when $L_{s} = L_{l}$, the average of our algorithm is a little bigger than that of ETC. This is because our algorithm will change the depth of some node in order to decrease the maximal number of child nodes of a node, which results in the increment of the delay and ETC never increases the depth of the node.

Fig. 7

Average delay under different number of nodes

Figure 8 shows the variance of delay when the number of nodes changes from 20 to 40. From this figure, we can see that the variance of our algorithm is in proportion to the depth. It is easy to understand that when depth increases, the difference of the delay of different final trees becomes larger, and consequently results in larger variance. When $L_{s} = L_{l}$, the variance of our algorithm is a little smaller than that of ETC. This is because ETC does not change the depth of node, and result in the delay is more influent to the nodes distribution. In contrast, our algorithm reduces this influence by regulating the depths of some nodes.

Fig. 8

Variance of delay under different number of nodes

Finally, we compare the lifetime of the tree networks constructed by the two algorithms. We does not take the energy consumption for constructing the tree network into consideration, and the network lifetime is defined as from the time that the network begins to normally running to the time that one node uses up its energy.

Figure 9 shows the lifetime of the tree networks under different number of nodes when the compress ratio changes from 0 to 1 and $L_{s} = L_{l}$. Figure 10 shows the network lifetime under different depth when the compress ratio changes from 0 to 1 and the number of nodes is 30. From these two figures, we could see that the performance of our algorithm is superior to that of ETC when the compression ratio is 0; and the difference decreases when the compression ratio increases. The lifetimes of the two algorithms are almost the same when the compression ratio is about 0.7, and the performance of our algorithm will be a little inferior to that of ETC when the compression ratio continues to increase. We know that when the compression ratio approaches to zero, the received packets coming from all the child nodes are compressed to one packet. More child nodes will result in more power consumption. But if a node changes its depth, it will only increase the power consumption of its direct parent node, but have no influence on other indirect parent node. So the depth of the tree has a little influence on the lifetime, but the maximal number of child nodes of the tree will impact the lifetime. From Fig. 5, we see that the maximal number of child nodes of our tree is less than ETC, so the lifetime of our algorithm will be longer than ETC. However, when the compression ratio approaches to one, it means that there has no compression for packets. If node changes its depth, it will not only increase the power consumption of its direct parent node, but also increase the power consumption of its indirect parent, and the latter has more influence on the lifetime of network. From Fig. 7, we see that the average hop of our tree is a little bigger than ETC, so the lifetime of ETC will be a little longer than our algorithm These results show that our approximation is suitable for the applications when the compression ratio is somewhat small.

Fig. 9

Network Lifetime under different number of nodes

Fig. 10

Network lifetime under different depth

6 Conclusions

For the typical application of wireless sensor networks, tree topology is the preferable choice. In this paper, we propose an approximation algorithm for constructing a tree network. When the monitoring node obtains the neighbor graph, it uses the approximation algorithm to construct a tree topology with minimum number of child nodes when the depth is constrained, and after then, the monitoring node distributes the topology to every node to form a tree network. Simulation results show that our approximation algorithm could greatly reduce the constructing time, and the approximation ratio is very perfect. Compared with the ETC algorithm, we find that when the compression ratio is less than 70 %, the network lifetime of our approximation algorithm is larger than that of ETC.