Efficiently mining uncertain high-utility itemsets

Abstract

Data mining consists of deriving implicit, potentially meaningful and useful knowledge from databases such as information about the most profitable items. High-utility itemset mining (HUIM) has thus emerged as an important research topic in data mining. But most HUIM algorithms can only handle precise data, although big data collected in real-life applications using experimental measurements or noisy sensors is often uncertain. In this paper, an efficient algorithm, named Mining Uncertain High-Utility Itemsets (MUHUI), is proposed to efficiently discover potential high-utility itemsets (PHUIs) in uncertain data. Based on the probability-utility-list (PU-list) structure, the MUHUI algorithm directly mines PHUIs without generating candidates, and can avoid constructing PU-lists for numerous unpromising itemsets by applying several efficient pruning strategies, which greatly improve its performance. Extensive experiments conducted on both real-life and synthetic datasets show that the proposed algorithm significantly outperforms the state-of-the-art PHUI-List algorithm in terms of efficiency and scalability, and that the proposed MUHUI algorithm scales well when mining PHUIs in large-scale uncertain datasets.

1 Introduction

In the context of the rapid growth of wireless and information technologies, “big data” has become a very popular issue in recent years as it can provide useful insights for business services and sales strategies. The main issues of interest in research on “big data” are how to handle databases with high volume, velocity, variety, value and veracity. Knowledge Discovery in Database (KDD) aims at finding meaningful and useful information in massive amounts of data (Agrawal et al. 1993a, b; Agrawal and Srikant 1994a; Chen et al. 1996; Han et al. 2004). Two fundamental issues in KDD, having numerous applications in various domains, are frequent itemset mining (FIM) and association rule mining (ARM) (Agrawal et al. 1993b; Agrawal and Srikant 1994a).

In contrast with traditional FIM and ARM, high-utility itemset mining (HUIM) (Chan et al. 2003; Liu et al. 2005; Yao et al. 2004; Yao and Hamilton 2006) considers both quantities and unit profits of items to measure how “useful” or interesting an item or itemset is. An itemset is said to be a high-utility itemset (HUI) if its utility in a database is no less than a user-specified minimum utility count. In general, the “utility” of an item/set can be interpreted as how interesting an item/set is to users in real-life applications, in terms of factors such as weight, cost, risk, and profit. Chan et al. first proposed the concept of HUIM (Chan et al. 2003). Yao et al. then defined a unified framework for mining high-utility itemsets (HUIs) (Yao et al. 2004). The goal of HUIM is to identify items or itemsets in customer transactions that may be rare, but yield a high profit. HUIM plays a critical role in data analysis and has been widely utilized to discover knowledge and mine valuable information in databases. Many algorithms have been developed for HUIM such as Two-Phase (Liu et al. 2005), IHUP (Ahmed et al. 2009), HUP-growth (Lin et al. 2011), UP-growth (Tseng et al. 2010), UP-growth+ (Tseng et al. 2013), HUI-Miner (Liu and Qu 2012), and FHM (Fournier-Viger et al. 2014).

In real-life applications, a massive amount of incomplete data is collected from uncertain data sources such as wireless sensor network, RFID, GPS, and WiFi systems (Aggarwal and Yu 2009; Aggarwal 2010), and the size of the collected uncertain data may be very large. However, traditional data mining technologies for handling precise data cannot be directly applied to incomplete, uncertain, or inaccurate data for discovering information required by businesses. In recent years, numerous algorithms have been developed to discover useful knowledge in uncertain data such as UApriori (Chui et al. 2007), UFP-growth (Leung et al. 2008), UH-mine (Aggarwal et al. 2009), CUFP-growth (Lin and Hong 2012), and MBP (Wang et al. 2010). Mining frequent itemsets in uncertain data is currently a very active research area (Aggarwal and Yu 2009; Liu et al. 2013; Tong et al. 2012; Wang et al. 2012).

In real-life applications, utility and probability are two different measures for assessing the interestingness of an object (e.g., how useful a pattern is). The utility is a subjective semantic measure (the “utility” represents the interest that the user has in a pattern based on his a priori knowledge and goals), while probability is an objective measure (the probability of a pattern represents how likely it is to exist) (Geng and Hamilton 2006). In real-life situations, an item/set may not only be present or absent from a transactional database but it can also be associated with an existential probability. This is especially the case when data are collected using experimental measurements or wireless equipment. In market basket analysis, each transaction recorded by wireless equipment contains several items, annotated with their purchase quantities and existence probabilities. In risk prediction, the risk that events may occur is also indicated by occurrence probabilities. For example, the event $<(A$, 1); (D, 5); (E, 3); 90 %$>$ indicates that this event consisting of three sub-events {A, D, E} with occurrence frequencies {1, 5, 3} has a 90 % probability of occurring. Since the “utility” of a pattern measures the importance of the pattern to the user (i.e., risk, weight, cost, and profit), HUIM can be used as an efficient method to discover interesting patterns in uncertain data, for many real-life applications. But up to now, most HUIM algorithms have been developed to handle precise data, and hence are not suitable for mining patterns in uncertain data. If a traditional HUIM algorithm is applied on uncertain data, it may discover several useless or misleading patterns since the discovered HUIs may have low existential probabilities. To the best of our knowledge, PHUIM (Lin et al. 2015c) is the first algorithm to address the issue of mining HUIs in uncertain data. However, the task of mining high-utility itemsets in uncertain data, especially large-scale uncertain databases, remains very costly in terms of execution time. Therefore, it is a non-trivial task and an important challenge to design more efficient algorithms to solve the limitations of previous work (Lin et al. 2015c).

In this paper, an efficient mining algorithm named Mining Uncertain High-Utility Itemsets (MUHUI) in uncertain data is proposed to effectively discover the high Potential and High-Utility Itemsets (PHUIs). The major contributions of this paper are summarized as follows:

• 1. Few studies on HUIM have addressed the problem of mining HUIs in uncertain data by considering both the semantic utility measure and the objective probability measure. In this paper, an algorithm named MUHUI is designed to successfully and directly mine HUIs in uncertain databases, without generating candidates.

• 2. Based on the utility and probability measures, several strategies are developed to prune the search space early and thus efficiently reduce the number of unpromising itemsets. These strategies can greatly reduce the search space for mining HUIs and considerably improve the mining performance.

• 3. Extensive experiments show that the results obtained by mining HUIs in uncertain data and precise data are quite different, and that the proposed algorithm is more efficient than the state-of-the-art PHUI-List algorithm for mining uncertain HUIs in terms of runtime, effectiveness of its pruning strategies and scalability. In particular, the MUHUI algorithm shows better scalability than the PHUI-List algorithm for very large uncertain databases.

2 Related work

Mining frequent itemsets in uncertain data (UFIM) has been extensively studied and has emerged as an important issue in recent years (Aggarwal and Yu 2009; Chui et al. 2007; Leung et al. 2008; Liu et al. 2013; Tong et al. 2012; Wang et al. 2012). Approaches for UFIM can be generally viewed as based on either the expected support-based model (Aggarwal et al. 2009; Chui et al. 2007; Leung et al. 2008) or the probabilistic frequency model (Bernecker et al. 2009; Sun et al. 2010). Most algorithms for UFIM, such as UApriori (Chui et al. 2007), UFP-growth (Leung et al. 2008), UH-mine (Aggarwal et al. 2009), and CUFP-Miner (Lin and Hong 2012), belong to the expected support-based model. Recently, Tong et al. proposed a novel representation for mining frequent itemsets in uncertain data using uniform measures (Tong et al. 2012), which combines the two above models. Novel algorithms for mining uncertain frequent itemsets are frequently proposed. However, none of them considers the utility measure. High-utility itemset mining (HUIM) is different from FIM and ARM, as it considers both the local transaction utilities (occurrence quantities) and external utilities (unit profits) of items to discover profitable itemsets in quantitative databases.

The concept of HUIM was first proposed by Chan et al. (2003). Yao et al. then defined a strict unified framework for HUIM (Yao et al. 2004). Since the downward closure property of ARM no longer holds in HUIM, Liu et al. proposed the TWU model (Liu et al. 2005). This latter is used by a pruning property called the transaction-weighted downward closure (TWDC), to greatly reduce the number of unpromising candidates when mining HUIs using a level-wise approach. Several tree-based approaches for mining HUIs have also been proposed such as IHUP (Ahmed et al. 2009), HUP-growth (Lin et al. 2011), UP-growth (Tseng et al. 2010), and UP-growth+ (Tseng et al. 2013). Despite that these pattern-growth approaches outperform previous approaches, they still suffer from the problem of generating a huge number of candidates and storing them in memory, to obtain the actual HUIs. To address this issue of traditional HUIM, the HUI-Miner algorithm was proposed. It directly mines HUIs without performing multiple database scans and without generating candidates, thanks to a novel utility-list structure (Liu and Qu 2012). The FHM algorithm was further proposed to enhance the performance of HUI-Miner by considering the occurrence frequencies of pairs of items (Fournier-Viger et al. 2014). FHM can greatly reduce the number of operations to be performed to discover HUIs using only a little bit more memory for keeping track of the occurrences frequencies of pairs of items.

Besides traditional HUIM, several variations of the problem of HUIM have been studied. Lin et al. proposed a series of approaches for mining HUIs in dynamic databases by considering record insertion (Lin et al. 2015f), record deletion (Lin et al. 2015a), and record modification (Lin et al. 2015d). The UDHUP algorithm was proposed to mine up-to-date HUIs, which can be applied in real-world situations for discovering up-to-date information about profitable itemsets (Lin et al. 2015e). Lan et al. proposed several algorithms for mining on-shelf HUIs (Lan et al. 2011, 2014), by considering time periods where products are sold. An improved FOSHU algorithm (Fournier-Viger and Zida 2015) was also designed to efficiently mine on-shelf HUIs. Another recently studied issue in HUIM is to discover the top–k HUIs. The TKU algorithm was proposed to mine the top-k HUIs in transaction databases (Wu et al. 2012), and the T-HUDS algorithm was proposed to mine top-k HUIs in data streams (Zihayat and An 2014). Mining high-utility itemsets with multiple minimum utility thresholds is also an interesting topic, where multiple thresholds are used instead of a single minimum utility threshold (Lin et al. 2015b). The development of other algorithms for HUIM is in progress. However, most HUIM algorithms are designed to handle precise data. To the best of our knowledge, PHUIM (Lin et al. 2015c) is the first algorithm for mining high-utility itemsets in uncertain data.

3 Preliminaries and problem statement

The probabilistic frequent itemset (PFI) model (Bernecker et al. 2009; Sun et al. 2010) aims at finding itemsets that have a high probability of being frequent. In real-life applications, the derived high-utility itemsets are, however, usually rare. Hence, the probabilistic frequent itemsets model is not suitable for discovering high-utility itemsets in uncertain databases. In contrast, the expected support model considers that an itemset is an expected frequent itemset if its expected support (the sum of its existential probabilities) in an uncertain database exceeds a user-specified minSup  threshold (Aggarwal et al. 2009; Chui et al. 2007; Leung et al. 2008), which is similar to the potential probability model used in the MUHUI algorithm, proposed in this paper. In addition, it is possible to distinguish between the “tuple uncertainty” and “attribute uncertainty” models. The former (Nilesh and Dan 2007) considers that each tuple is associated with an existential probability, while the latter associates an existential probability to each attribute. The derived patterns using these models have a high probability of being HUIs in an uncertain database. Hence, in this paper, the tuple uncertainty model (Nilesh and Dan 2007) and the uncertainty calculated model which are somewhat similar to the expected support-based model (Aggarwal et al. 2009; Chui et al. 2007; Leung et al. 2008) are adopted to design the proposed MUHUI algorithm.

3.1 Preliminaries

Assume that an uncertain quantitative database $D =$ {$T_{1}$, $T_{2}$,..., $T_{n}$} contains n transactions, where each transaction has a unique identifier, TID. Let $I =$ {$i_{1}$, $i_{2}$,..., $i_{m}$} be a finite set of m distinct items in D, such that each transaction $T_{q}\in D$ is a subset of I. Moreover, assume that each item $i_{j}$ occurring in a transaction is associated with a purchase quantity $q(i_{j}$, $T_{q}$). As in the tuple uncertainty model (Nilesh and Dan 2007), each transaction $T_{q}\in D$ has a unique probability of existence $p(T_{q}$), which indicates that $T_{q}$ exists in D with a probability $p(T_{q}$). Assume that the unit profit of each item is given in a profit table, ptable $=$ {pr $_{1}$, pr $_{2}$,..., pr $_{m}$}, where pr $_{j}$ is the unit profit of item $i_{j}$. A $k-$itemset X, denoted as $X^{k}$, is a set of k distinct items {$i_{1}$, $i_{2}$,..., $i_{k}$}. Furthermore, let there be two user-specified thresholds called the minimum utility threshold ($\varepsilon$) and the minimum potential probability threshold ($\mu$).

Table 1 shows an example of a tuple uncertainty quantitative database. The corresponding predefined profit table is shown in Table 2. In this example, assume that the two thresholds are, respectively, set to $\varepsilon$ ($=$15 %) and $\mu$($=$18 %) by the user.

Table 1 A tuple uncertain database

Table 2 The profit table

Definition 1

The utility of an item $i_{j}$ in a transaction $T_{q}$ is denoted as $u(i_{j}, T_{q}$) and defined as:

$$\begin{aligned} u( {i_j,T_q })=q( {i_j,T_q })\times pr( {i_j }). \end{aligned}$$

For example, the utility of item {A} in $T_{1}$ is u(A, $T_{1})=q(A$, $T_{1}) \quad \times$ pr(A) ($= 1\times 6$) ($=6$).

Definition 2

The probability that an item/itemset X occurs in a transaction $T_{q}$ is denoted as $p(X, T_{q}$), and defined as $p(X, T_{q}) = p(T_{q}$), where $p(T_{q}$) is the existential probability of $T_{q}.$

For example, consider an item (A) and an itemset (AD) in $T_{1}$; p(A, $T_{1}) = p(T_{1}$) ($= 0.95$), and p(AD, $T_{1})=p(T_{1})(=0.95$).

Definition 3

The utility of an itemset X in a transaction $T_{q}$ is denoted as $u(X, T_{q}$), and defined as:

$$\begin{aligned} u( {X,T_q })=\sum \limits _{i_j \in X\wedge X\subseteq T_q } {u(i_j ,T_q ).} \end{aligned}$$

For example, the utility of itemset (AD) in $T_{1}$ is calculated as u(AD, $T_{1})=u(A, T_{1})+u(D$, $T_{1})=q(A, T_{1}) \times$ pr $(A)+q(D, T_{1}$) $\times$ pr(D) ($= 1$ $\times$ $6 + 4$ $\times$ 1) ($= 10$).

Definition 4

The utility of an itemset X in a database D is denoted as u(X), and defined as:

$$\begin{aligned} u( X)=\sum \limits _{X\subseteq T_q \wedge T_q \in D} {u(X,T_q )}. \end{aligned}$$

For example, $u(A)=u(A$, $T_{1})+u(A$, $T_{3})+u(A$, $T_{6})+u(A$, $T_{7}$) ($= 6 + 12 + 6 + 18$) ($= 42$), and u(AD) $=$ u(AD, $T_{1})+u$(AD, $T_{6})+u$(AD, $T_{7}$) ($= 10 + 7 + 21$) ($=38$).

In the expected support-based model used in uncertain data mining, the expected support of an itemset X in a database D is defined as the sum of the support of X for each possible world $W_{j}$ (the probability of $W_{j}$ being the true world) (Chui et al. 2007; Tong et al. 2012):

$$\begin{aligned} expSup(X)=\sum \limits _{i=1}^{\vert D\vert } {\left( \prod \limits _{x_i \in X} {p(x_i,T_q )} \right) }. \end{aligned}$$

The probability measure of a pattern in an uncertain database, for the problem addressed in this paper, is defined as follows.

Definition 5

The potential probability of an itemset X in a database D is denoted as Pro(X), and is defined as:

$$\begin{aligned} Pro( X)=\sum \limits _{X\subseteq T_q \wedge T_q \in D} {p(X,T_q )}. \end{aligned}$$

For example, in Table 1, Pro($A) = p(A$, $T_{1})+p(A$, $T_{3})+p(A$, $T_{6}$) $+$ p(A, $T_{7}$) ($= 0.95 + 0.50 + 1.00 + 0.80$) ($=3.25$), and Pro(AD) $=$ p(AD, $T_{1}$) $+$ p(AD, $T_{6})+p$(AD, $T_{7}$) ($= 0.95 + 1.00 + 0.80$) ($=2.75$).

Definition 6

The transaction utility of a transaction $T_{q}$ is denoted as tu($T_{q}$), and is defined as:

$$\begin{aligned} tu( {T_q })=\sum \limits _{j=1}^m {u(i_j,T_q ),} \end{aligned}$$

where m is the number of items in $T_{q}$.

For example, the transaction utility of $T_{1 }$ is calculated as tu($T_{1})=u(A$, $T_{1})+u(C$, $T_{1})+u(D$, $T_{1}$) ($= 6 + 30 + 4$) ($=40$). The transaction utilities of transactions $T_{1}$ to $T_{10}$ of Table 1 are shown in Table 3.

Table 3 The transaction utility of each transaction

Definition 7

The total utility in a database D is denoted as TU, and defined as:

$$\begin{aligned} TU=\sum \limits _{T_q \in D} {tu(T_q )}. \end{aligned}$$

For example, the total utility in the running example is calculated as: TU ($= 40 + 15 + 33 + 30 + 15 + 27 + 51 + 48 + 14 + 15$) ($=288$).

Definition 8

An itemset X in a database D is said to be a high-utility itemset (HUI) if $u(X) \ge \varepsilon \times$ TU. Otherwise, it is called a low-utility itemset.

In the running example, the itemset (AD) is not an HUI since u(AD) ($=38$), which is smaller than (15 % $\times$ 288) ($=43.2$). The itemset (ACD) is an HUI in D since u(ACD) ($=98$) $>$ 43.2. If the minimum utility threshold is set to 15 %, there are twelve HUIs, as shown in Table 4.

Table 4 The derived HUIs for the running example

Definition 9

An itemset X in a database D is said to be a potential high-utility itemset (PHUI) if it satisfies the following two conditions: (1) X is an HUI, i.e., $u(X) \ge$ $\varepsilon \times$ TU, and (2) Pro $(X) \ge \mu$ $\times \vert D\vert$. A PHUI is thus an itemset having both a high potential probability and a high utility.

3.2 Problem statement

Let there be an uncertain database D having a total utility TU, and the user-specified minimum utility threshold $\varepsilon$ and minimum potential probability threshold $\mu$. The problem of mining an uncertain database to discover high-utility itemsets (MUHUI) is to find all potential high-utility itemsets (PHUIs), i.e., all itemsets having a utility no less than ($\varepsilon \times$ TU), and a probability no less than ($\mu$ $\times \quad \vert D\vert$).

Hence, the goal of MUHUI is to mine all highly profitable patterns having a high probability, by taking into account both the semantic utility measure and the objective probability measure. Consider the database of the running example shown in Tables 1 and 2, and that the minimum utility threshold and minimum potential probability threshold are, respectively, set to 15 and 18 %. The set of PHUIs is shown in Table 5.

Table 5 The derived PHUIs for the running example

4 The proposed MUHUI Algorithm

Recently, the PHUI-List algorithm was proposed to efficiently mine HUIs in uncertain databases. The experimental evaluation of PHUI-List indicates that it outperforms the upper bound-based PHUI-UP algorithm (Lin et al. 2015c). However, PHUI-List explores the search space of itemsets by generating itemsets, and a costly join operation has to be recursively performed to construct the probability-utility-list (PU-list) structure of each itemset, to evaluate its probability and utility information. In this section, a novel algorithm named MUHUI is proposed to more efficiently mine PHUIs. The PU-list structure is adopted in the proposed MUHUI algorithm. The PU-list structure is introduced thereafter.

4.1 The PU-list structure

The PU-list structure is an efficient vertical data structure. For a given itemset, it stores information about the TIDs of transactions where the itemset appears, and information about its probability, utility, and remaining utility in these transactions. Let there be two item/sets X and Y. A total order $\prec$ is defined such that $X \prec Y$(i.e., X precedes Y) if the PU-list of X is constructed before the PU-List of Y. Furthermore, an itemset {$X\cup i$} is said to be an extension of X if i is a 1-itemset, and $X \prec$ {$X\cup i$}. The PU-list structure is formally defined as follows.

Definition 10

Given an itemset X and a transaction (or itemset) T such that $X\subseteq T$, the set of all items in T that are not in X is denoted as $T \backslash X$, and the set of all items appearing after X in T is denoted as T / X. Thus, $T/X \subseteq$ $T \backslash X$.

For example, consider $X =$ (CD) and the transaction $T_{7}$ in Table 1, $T_{7}\backslash X =$ (AE), and $T_{7}/X= (E$).

Definition 11

(Probability-Utility-list, PU-list). The PU-list of an itemset X in a database D is denoted as X.PUL. It consists of a set of entries (elements), such that there is an element for each transaction $T_{q}$ where X appears ($X \subseteq T_{q }\in D$). An element representing a transaction $T_{q}$ contains four fields storing: (1) the TID of the transaction $T_{q}$ (denoted as $\underline{{{\varvec{tid}}}}$), (2) the probabilities of X in $T_{q}$ (denoted as $\underline{{{\varvec{prob}}}}$), (3) the utility of X in $T_{q}$ (denoted as $\underline{{{\varvec{iu}}}}$), and (4) the remaining utility of X in $T_{q}$ (denoted as $\underline{{{\varvec{ru}}}}$). For an element representing a transaction $T_{q}$, the field $\underline{{{\varvec{iu}}}}$ is calculated as:

$$\begin{aligned} X.iu=\sum \limits _{i_{j}\in X\wedge X\subseteq T_q } {u(i_{j},T_q )}, \end{aligned}$$

and the field $\underline{{{\varvec{ru}}}}$ is calculated as:

$$\begin{aligned} X.ru=\sum \limits _{i_j \in (T_q /X)} {u(i_j,T_q )}. \end{aligned}$$

The PU-list structure is designed to store and compress all the information from an uncertain database that is relevant for exploring the search space starting from a given itemset X. An important property of the PU-list structure is that the probability and utility information of any k-itemset can be obtained from its PU-list. Moreover, the PU-list of a k-itemset can be obtained by joining the PU-list of its parent node with the PU-list of one of its uncle node, i.e., the PU-lists of two ($k-1$)-itemsets. The join operation is very efficient since it does not require scanning the database. Moreover, the size of the PU-list of a k-itemset is never greater than the one of its parent node, i.e., ($k-1$)-itemset. By the above properties, the construction of the PU-list of any itemset in the search space can be done whenever necessary. The PU-list construction procedure is shown in Algorithm 1.

Note that the TWU ascending order of items is adopted as the processing order in the proposed MUHUI algorithm. Initially, only the PU-lists of items that are members of the set of high transaction-weighted probabilistic and utilization itemsets (HTWPUIs) are constructed, since only those items may appear in PHUIs, and thus other items do not need to be considered by the recursive search process (additional explanations about the concept of HTWPUI (Lin et al. 2015c) will be given in the next subsection). Consider the running example. The set of HTWPUIs of length 1 is denoted as HTWPUI$^{1}$ and contains the following itemsets {TWU(A) $=$ 151, Pro(A) $=$ 3.25; TWU(B) $=$ 125, Pro(B) $=$ 3.36; TWU(C) $=$ 211, Pro(C) $=$ 5.26; TWU(D) $=$ 177, Pro(D) $=$ 5.75; TWU(E) $=$ 192, Pro(E) $=$ 4.61}. The processing order of items by ascending order of TWU is ($B \prec A \prec D \prec E \prec C$). Thus, the constructed PU-lists of items in HTWPUI$^{1 }$are shown in Fig. 1.

Fig. 1

The constructed PU-lists of items in HTWPUI$^{1}$

The PU-list of an itemset can be used to calculate the following important information.

Definition 12

Let the sum of the utilities of an itemset X in D be denoted as X.IU, and defined as:

$$\begin{aligned} X.IU=\sum \limits _{X\subseteq T_q \wedge T_q \in D} {(X.iu)}. \end{aligned}$$

Definition 13

Let the sum of the remaining utilities of an itemset X in D be denoted as X.RU, and defined as:

$$\begin{aligned} X.RU=\sum \limits _{X\subseteq T_q \wedge T_q \in D} {(X.ru)}. \end{aligned}$$

Definition 14

For an itemset X, Pro(X) is the sum of the probabilities of X in D. Pro(X) can be easily calculated using the PU-list of X as:

$$\begin{aligned} {Pro}(X)=\sum \limits _{X\subseteq T_q \wedge T_q \in D} {(X.{prob})}. \end{aligned}$$

For example, consider the database shown in Fig. 1. The itemset (B) appears in five transactions having the TIDs {2, 3, 5, 8, 9}. B.IU is calculated as ($3 + 6 + 3 + 3 + 9$)$= 24$, and B.RU is calculated as ($12 + 27 + 12 + 45 + 15$) $=$ 111. The itemset (BC) appears in two transactions having the TIDs $=$ {2, 8}. BC.IU $=$ ($3 + 10$) $+$ ($3 + 40$) $=$ 56, and BC.RU $=$ ($12 + 0$) $+$ ($45 + 0$) $= 57$.

4.2 Search space and properties used by the MUHUI Algorithm

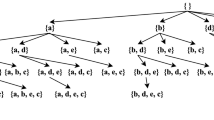
Based on previous studies, the complete search space of a pattern-based mining algorithm can be represented as a set-enumeration tree (Rymon 1992). Therefore, the search space of the proposed MUHUI algorithm can also be represented as a set-enumeration tree where the ascending order of TWU values of HTWPUI$^{1}$ is used as processing order. Each node in the set-enumeration tree represents an itemset, which is an extension of its parent node (except for the root node, which represents the empty set and has no parent). In the running example, the TWU ascending order of items is ($B \prec A \prec D \prec E \prec C$). The corresponding set-enumeration tree is as shown in Fig. 2.

Fig. 2

The set-enumeration tree

The PU-list structure keeps all the information from an uncertain database that is necessary for discovering PHUIs, in terms of TID, probability, utility, and remaining utility. Two important properties related to probability and utility are used in the proposed MUHUI algorithm to reduce the search space, and are described by the following lemmas.

Lemma 1

The sum of all the probabilities of any node in the set-enumeration tree is equal or greater than the sum of the probabilities of any of its child nodes (extensions).

Proof

Let there be a ($k-1$)-itemset $X^{k-1}$ ($k \ge$ 2) corresponding to a node in the set-enumeration tree. Furthermore, let $X^{k}$ be any child node of $X^{k-1}$. Since $p(X^{k}$, $T_{q})=p(T_{q}$) for any transaction $T_{q}$ in D, it can be found that:

$$\begin{aligned} \frac{p(X^k,T_q )}{p(X^{k-1},T_q )}=\frac{p(T_q )}{p(T_q )}={1.} \end{aligned}$$

Since $X^{k-1}$ is a subset of $X^{k}$, the TIDs of $X^{k}$ are a subset of the TIDs of $X^{k-1}$. Hence,

$$\begin{aligned} {Pro}(X^k)= & {} \sum \limits _{X^k\subseteq T_q \wedge T_q \in D}{p(X^k,T_q )} \\\le & {} \sum \limits _{X^{k-1}\subseteq T_q \wedge T_q \in D} {p(X^{k-1},T_q )} = {Pro}(X^{k-1}) \\\Rightarrow & {} {Pro}(X^k)\le {Pro}(X^{k-1}). \\ \end{aligned}$$

Therefore, this lemma holds. $\square$

Lemma 2

For any node X in the set-enumeration tree, the sum of X.IU and X.RU is greater than or equal to the sum of the utilities of any of its child nodes (extensions).

Proof

From Liu and Qu (2012), this lemma holds. $\square$

4.3 Proposed pruning strategies

Based on the PU-list structure and the above properties related to the probabilities and utilities of itemsets, five efficient pruning strategies are designed in the MUHUI algorithm to prune unpromising itemsets early. Using these strategies, a smaller part of the search space is explored for discovering PHUIs, which speeds up the discovery of PHUIs. As in the PHUI-UP algorithm (Lin et al. 2015c), MUHI efficiently eliminates some unpromising candidates using the transaction-weighted probabilistic and utilization downward closure (TWPUDC) property. The TWPUDC property is also adopted in the MUHUI algorithm. It is applied before the construction of a series of PU-lists for extensions of an itemset. As previously explained, the well-known downward closure property of ARM (Agrawal et al. 1993b; Agrawal and Srikant 1994a) cannot be directly applied in HUIM to mine HUIs. To address this issue, the transaction-weighted utilization downward closure (TWDC) property with TWU upper bound (Liu et al. 2005) was proposed to reduce the search space in HUIM. The TWDC property has been extended in the PHUI-UP algorithm (Lin et al. 2015c) for mining PHUIs in uncertain data. Details of this property are provided thereafter.

Definition 15

The transaction-weighted utility (TWU) of an itemset X in a database D is the sum of the transaction utilitiestu ($T_{q}$) of each transaction $T_{q}$ containing X, and is defined as:

$$\begin{aligned} \textit{TWU}( X)=\sum \limits _{X\subseteq T_q \wedge T_q \in D} {tu(T_q )}. \end{aligned}$$

Definition 16

An itemset X in a database D is said to be a high transaction-weighted utilization itemset (HTWUI) if $TWU(X) \quad \ge TU \times \varepsilon$.

For example, in Table 1, the TWU of item (A) is calculated as TWU(A) ($=$ tu($T_{1}$) + tu($T_{3}$) $+$ tu($T_{6}$) $+$ tu($T_{7})$) ($= 40 + 33 + 27 + 51$) ($=151$). Since TWU(A) ($=151$) $>$ (288 $\times$ 15 % $=$ 43.2), item (A) is an HTWUI. Based on Liu et al. (2005), the set of high-utility itemsets is a subset of the set of HTWUIs, that is, HUIs $\subseteq$ HTWUIs.

Definition 17

An itemset X in a database D is called a high transaction-weighted probabilistic and utilization itemset (HTWPUI) if (1) $TWU(X) \ge \varepsilon \times$ TU, and (2) $Pro(X) \ge \mu \times \vert D\vert$.

For example, in Tables 1 and 2, since $\mu$ is set to 18 %, the minimum potential probability is calculated as (18 % $\times$ 10) (= 1.8). For example, consider item (A). Since TWU(A) (= 151) ($>$ 43.2), Pro($A)=p(A$, $T_{1}$) + p(A, $T_{3})+p(A$, $T_{6})+p(A$, $T_{7}$) (= 0.9 + 0.85 + 0.75 + 0.45) (= 3.91) ($>$ 1.5), item (A) is an HTWPUI.

Theorem 1

(Downward closure property of HTWPUI). Let X $^{k-1}$ be a (k–1)-itemset. Furthermore, let X $^{k}$ be a k-itemset that is a superset of X $^{k-1}$ (i.e., $X^{k-1} \quad \subseteq X^{k}$), and assume that both $X^{k}$ and X$^{k-1}$ are HTWPUIs in the uncertain database. The downward closure property of HTWPUIs indicates that TWU($X^{k-1}$) $\ge$ TWU($X^{k}$) and Pro ($X^{k-1}$) $\ge$ Pro($X^{k}$) (Lin et al. 2015c).

Proof

Since $X^{k-1} \subseteq X^{k}$, the TIDs of $X^{k}$ is a subset of the TIDs of $X^{k-1}$. Thus,

• $\begin{array}{l} 1.\quad \textit{TWU}(X^k)=\sum \nolimits _{X^k\subseteq T_q \wedge T_q \in D} {tu(T_q )}\\ \qquad \qquad \le \sum \nolimits _{X^{k-1}\subseteq T_q \wedge T_q \in D} {tu(T_q )} = \textit{TWU}(X^{k-1})\\ \qquad \qquad \Rightarrow \textit{TWU}(X^k)\le TWU(X^{k-1}). \\ \end{array}$

• $\begin{array}{l} 2.\quad {Pro}(X^k)=\sum \nolimits _{X^k\subseteq T_q \wedge T_q \in D} {p(X^k,T_q )}\\ \qquad \;\; \le \sum \nolimits _{X^{k-1}\subseteq T_q \wedge T_q \in D} {p(X^{k-1},T_q )} = {Pro}(X^{k-1})\\ \qquad \quad \!\!\Rightarrow {Pro}(X^k)\le {Pro}(X^{k-1}). \\ \end{array}$

Therefore, if $X^{k}$ is an HTWPUI, any of its subset $X^{k-1}$ is also an HTWPUI. $\square$

Theorem 2

(PHUIs $\subseteq$ HTWPUIs). The transaction-weighted probabilistic and utilization downward closure (TWPUDC) property ensures that PHUIs $\subseteq$ HTWPUIs. Hence, if an itemset is not an HTWPUI, then none of its supersets are PHUIs (Lin et al. 2015c).

Proof

According to Lin et al. (2015c), this theorem holds.

By utilizing the TWPUDC property, we only need to construct the PU-lists of promising itemsets, i.e., the HTWPUIs. If an itemset is an HTWPUI, all its subsets are HTWPUIs, and if an itemset is not an HTWPUI, all its supsersets are not HTWPUIs. Hence, only the PU-lists of 1-items that are HTWPUIs need to be built and considered by the proposed MUHUI algorithm, for discovering all PHUIs. $\square$

Pruning strategy 1

During the first database scan, we can obtain the TWU and probability value of each item appearing in the database. If the TWU of an item i (TWU(i)) and the sum of all the probabilities of i (Pro(i)) do not satisfy the two conditions: 1) TWU(i) $\ge \varepsilon \times$ TU, and 2) Pro(i) $\ge \mu \ \times \vert$D$\vert$, this item can be directly pruned, because none of its supersets is a PHUI.

Rationale

According to Theorems 1 and 2, this pruning strategy holds.

Pruning strategy 2

When traversing the set-enumeration tree using a depth-first search, if the sum of all the probabilities of a tree node in its constructed PU-list is less than the minimum potential probability, then none of its children is a PHUI.

Rationale

Lemma 1 shows that if the sum of the probabilities of an itemset is less than the minimum potential probability ($\mu$ $\times \vert D\vert$), this itemset cannot be a PHUI, as well as its child nodes (extensions). Hence, by calculating the sum of all the probabilities of each itemset, many unpromising itemsets and their extensions can be identified as irrelevant and be directly pruned.

Pruning strategy 3

When traversing the set-enumeration tree using a depth-first search strategy, if the sum of X.IU and X.RU in the constructed PU-list is less than the minimum utility count, none of the children (extensions) of node X is a PHUI.

Rationale

Lemma 2 shows that if the sum X.IU + X.RU of a tree node is less than the minimum utility count ($\varepsilon$ $\times$ TU), any of its child nodes (extensions) is an unpromising itemset (is not a PHUI). Thus, by calculating the sum of the utilities and remaining utilities for each node, child nodes of unpromising itemsets can be identified as irrelevant and be pruned directly.

Furthermore, the efficient Estimated Utility Co-occurrence Pruning (EUCP) strategy (Fournier-Viger et al. 2014) is also extended in the proposed MUHUI algorithm to speed up the discovery of PHUIs. The EUCP is defined as follows.

Lemma 3

(Estimated utility co-occurrence pruning strategy, EUCP) If the TWU of a 2-itemset is less than the minimum utility count, any superset of this 2-itemset is not an HTWUI nor an HUI.

Proof

Let X be a 2-itemset, and $X^{k}$ be a k-itemset (k $\ge$ 3) that is a superset of X. Since TWU($X^{k}) \le$ TWU($X^{k-1}$) and HUIs $\subseteq$ HTWUIs, if a 2-itemset X has TWU($X) \le$ TU $\times$ $\varepsilon$, X is not a HTWUI, and any superset of X of length k $\ge$ 3 is neither an HTWUI nor an HUI.

The concept of PHUI is defined using two constraints. Thus, if an itemset is not an HUI, it is also not a PHUI. The EUCP strategy is applied in the proposed algorithm to prune additional unpromising itemsets. Based on the EUCP strategy, a huge number of unpromising k-itemsets (k $\ge$ 3) can be efficiently pruned. To effectively apply the EUCP strategy, a structure named Estimated Utility Co-occurrence Structure (EUCS) (Fournier-Viger et al. 2014) is built. It is a matrix that stores the TWU values of all 2-itemsets. Note that the EUCS is built during the second database scan after discovering the set HTWPUI$^{1}$. The EUCS built for the database of the running example is shown in Table 6. Since the TWU value of (AC) is calculated as TWU(AC) =tu($T_{1}$) + tu($T_{6}$) +tu($T_{7}) (=40 + 27 + 51) (=118)$, the value of (AC) in Table 6 is set to 118. $\square$

Table 6 The EUCS built for the running example

Pruning strategy 4

Let X be an itemset (node) encountered during the depth-first search of the set-enumeration tree. If the TWU of a 2-itemset Y $\subseteq$ X according to the constructed EUCS is less than the minimum utility threshold, X is not an HTWPUI and it is also not a PHUI. Hence, none of its child nodes is a PHUI, and the construction of the PU-lists of X and its children does not need to be performed.

Rationale

According to definition 17, Lemmas 1 and 3, this pruning strategy is correct. Since PHUIs $\subseteq$ HTWPUIs, if TWU($X) \le$ TU $_{ }\times$ $\varepsilon$ for a 2-itemset X, X is not an HTWPUI. Moreover, X and all its supersets are not PHUIs (note that all extensions of X in the set-enumeration tree are supersets of X). Based on the EUCP strategy, a huge number of unpromising $k-$itemset (k $\ge$ 2) can be pruned.

Since the information about the probability of an itemset X (Pro(X)) can be easily obtained from its PU-list, Pro(X) can also be used to reduce the search space. The key idea is that after constructing the PU-list of an itemset X, if X.PUL is empty or if Pro($X) < \vert D\vert \times \mu$, the PU-list X.PUL can be directly skipped, and does need to be added to the set of extensions of X’s parent node. Thus, X.PUL will not be used to generate any other itemsets.

Pruning strategy 5

Let X be an itemset (node) encountered during the depth-first search of the set-enumeration tree. After constructing the PU-list of the itemset X, if X.PUL is empty or Pro(X) is less than the minimum probability threshold, X is not a PHUI, and none of its child nodes is a PHUI. Hence, PU-lists of the child nodes of X do not need to be constructed.

Rationale

According to Lemma 1, this pruning strategy is correct.

Based on the five designed pruning strategies, a great number of unpromising itemsets can be efficiently pruned and the construction of the PU-lists of their extensions can be avoided, which effectively reduces the number of join operations and the search space in the set-enumeration tree. The proposed MUHUI algorithm is described thereafter.

The main procedure of MUHUI (Algorithm 2) takes four parameters as input: an uncertain quantitative database D, the corresponding profit tableptable, the minimum utility threshold $\varepsilon$, and the minimum potential probability threshold $\mu$. The algorithm first scans the uncertain database to calculate TWU(i) and Pro(i) for each item $i\in I$(Line 1), and finds the set HTWPUI $^{1}$, which is denoted as $I^{*}$(Line 2, pruning strategy 1). After sorting $I^{*}$ according to the TWU ascending order (Line 3), the MUHUI algorithm scans D again to construct the PU-list of each item in HTWPUI $^{1}$, that is each item $i\in I^{*}$, and build the EUCS (Line 4). After that, the procedure PHUI-Search (Line 5) is recursively called to discover all PHUIs using a depth-first search. The PHUI-Search procedure is presented below.

The PHUI-Search procedure (Algorithm 3) takes five parameters as input: X, extendOfX, $\varepsilon$, $\mu$, and the EUCS. The procedure first checks if each itemset $X_{a}$ in extendOfX is a PHUI (Lines 2 to 5). Strategies 2 and 3 are then applied to determine whether extensions of $X_{a}$ satisfy the two required conditions for pursuing the depth-first search (Line 6). If these conditions are met, a for loop is performed to combine $X_{a }$ with each itemset $X_{b}$ in extendOfX such that b  is after a according to the TWU ascending order, to obtain an itemset $X_{ab}$. However, before constructing the PU-list of an itemset $X_{ab }$ (Evfimievski et al. 2002), the MUHUI algorithm applies the EUCP strategy to check if it is necessary to build the PU-list of $X_{ab}$ (Line 9, pruning strategy 4). If the PU-list should be built, the construction procedure Construct(X, X $_{\varvec{a}}$, X $_{{\mathcal {b}}}$) is called (Line 11). After the for loop has ended, all the PU-lists of promising extensions of $X_{a}$ have been constructed (Lines 8 to 16). Note that for each itemset $X_{ab}$ that is a promising 1-extension of itemset $X_{a}$(Line 10), if the PU-list of $X_{ab}$ is such that $X_{ab}.PUL$ $\ne$ Ø $\ne$ Pro($X_{ab}) \ge \vert D \vert \times \mu$ (pruning strategy 5), $X_{ab}$ is put into the set extendOfX $_{a}$ so that extensions of $X_{ab}$ will be considered by the recursive depth-first search. Otherwise, $X_{ab}$ is directly pruned (Lines 12–14). The designed PHUI-Search procedure is recursively applied to mine PHUIs (Line 17). Based on the PU-list structure and the five proposed pruning strategies, the MUHUI algorithm can directly mine PHUIs in uncertain databases without candidate generation and by performing only two database scans, and the MUHUI algorithm is correct and complete for discovering the complete set of PHUIs.

4.4 An illustrated example

In this section, a simple example is given to illustrate how the proposed MUHUI algorithm is applied step-by-step to discover PHUIs. Consider the database of the running example shown in Tables 1 and 2 that the minimum utility threshold $\varepsilon$ is set to 15 %, and that the minimum potential probability threshold ($\mu$) is set to 18 %.

The MUHUI algorithm first scans the uncertain database to calculate the TWU(i) and Pro(i) values of each item $i\in I$. Each item i that satisfies TWU $(i) \ge$ $\varepsilon \times$ TU and Pro($i) \ge \mu \times \vert D\vert$ is added to the set HTWPUI$^{1}$. In this example, it is found that the set HTWPUI$^{1}$ is equal to {A: 151, 3.25; B: 125, 3.36; C: 211, 5.26; D: 177, 5.75; E: 192, 4.61}. After that, items in HTWPUI$^{1}$ are sorted by TWU ascending order, that is ($B \prec A \prec D \prec E \prec C$). The MUHUI algorithm then scans the uncertain database again to extract the necessary information for performing the depth-first search (i.e., $\underline{{{\varvec{tid}}}}$, $\underline{{{\varvec{prob}}}}$, $\underline{{{\varvec{iu}}}}$ and $\underline{{{\varvec{ru}}}}$) for each item in each transaction. The PU-list structures are then constructed for all items in HTWPUI$^{1}$. After that, MUHUI recursively applies the depth-first search procedure PHUI-Search to mine PHUIs. The item (B) is first processed. Since (B) does not satisfy the PHUI conditions, as $B.{IU} = 24 <$ (228 $\times 25{\,\%}~=~43.2$) and Pro($B) = 3.36 >$ (10 $\times 18{\,\%} = 1.8$), the item (B) is not a PHUI. But since ($B.{IU }+ B$.RU) $=$ (24 + 111) $(=135)$ is no less than the minimum utility count$(=43.2)$, and Pro($B) = 3.36 >$ 1.8, its children nodes may be PHUIs, and extensions of this item will be considered by the depth-first search.

For each 2-itemset having itemset (B) as prefix, the MUHUI algorithm applies the EUCP strategy to check whether it is necessary to build its PU-list. The first child node (BA) is first considered. Since TWU(BA) ($= 33 <$ 43.2), as shown in Table 6, node (BA) and all its children are not PHUIs and can be pruned. The construction of the PU-list of itemset (BA) and the depth-first search starting from node (BA) are thus terminated. The next child node (BD) is then processed in the same way, as well as other nodes. Based on the PU-lists of itemsets in HTWPUI$^{1}$, the built PU-lists of promising 2-itemsets having itemset (B) as prefix are shown in Fig. 3.

Fig. 3

The built PU-lists of itemsets in HTWPUI$^{2}$ having (B) as prefix

After that, the node (BD) is considered by the depth-first search. Based on its PU-list, the sum of the utilities and probabilities of (BD) can be calculated as BD.IU ($= 24 <$ 43.2) and Pro(BD) ($= 2.1 >$ 1.8). The node (BD) and all its children are not PHUIs and can be directly pruned. The next child node (BE) is then processed in the same way, as well as the other nodes. After traversing the set-enumeration tree, the complete set of PHUIs has been discovered by the MUHUI algorithm, by performing only two database scans. The final result is shown in Table 5.

5 Experimental evaluation

In this section, substantial experiments were conducted to evaluate the performance of the proposed MUHUI algorithm. The performance of the proposed MUHUI algorithm is compared with the PHUI-UP and PHUI-List algorithms (Lin et al. 2015c) for mining PHUIs, in terms of runtime, pattern analysis, memory usage, effect of pruning strategies, and scalability. The PHUI-UP and PHUI-List algorithms are the first proposed algorithms for mining HUIs in uncertain data. PHUI-List is the state-of-the-art algorithm for mining PHUIs, as it was shown to considerably outperform the PHUI-UP algorithm. Note that the performance of the proposed MUHUI algorithm is not compared with traditional HUIM algorithms such as Two-Phase (Liu et al. 2005), IHUP (Ahmed et al. 2009), HUP-growth (Lin et al. 2011), UP-growth (Tseng et al. 2010), UP-growth+ (Tseng et al. 2013), HUI-Miner (Liu and Qu 2012), and FHM (Fournier-Viger et al. 2014), because those are not designed for mining patterns in uncertain data. Besides, in this experiment, two versions of MUHUI are used. The first one, denoted as MUHUI2, adopts all the designed pruning strategies, while the second one, denoted as MUHUI1, does not use pruning strategy 5. Experiments have been conducted by varying the minimum utility threshold (abbreviated as MU) while other parameters where fixed, and by varying the minimum potential probability threshold (abbreviated as MP) while other parameters where fixed.

Fig. 4

Runtime for various MUs and a fixed MP

5.1 Experimental setup and datasets description

All algorithms in the experiments were implemented in Java and were run on a personal computer equipped with an Intel Core i5-3460 dual-core processor and 4 GB of RAM, running the 32-bit Microsoft Windows 7 operating system. Both real-life and synthetic datasets were used in the experiments. Three real-life datasets (foodmart Microsoft 2016, accident FIMDR 2012, and retail FIMDR 2012) and one synthetic dataset (T10I4D100K Agrawal and Srikant 1994b) were used. The foodmart dataset contains customer transactions from a chain store. It contains unit profit information and purchase quantities for all items. The retail dataset contains 88,162 transactions from a retail store. It contains 16,470 distinct items, the average transaction length is 10.3 items, and the largest transaction has 76 items. The accident dataset contains anonymous traffic accident data for a public road in Belgium. It has 340,183 distinct items, 468 transactions, and the average transaction length is 33.8 items. The synthetic dataset T10I4D100K was generated using the IBM Quest Synthetic Dataset Generator (Agrawal and Srikant 1994b). It contains 100,000 distinct items, 870 transactions, the average transaction length is 10.1 items, and the largest transaction has 29 items. The foodmart dataset is very sparse, while accidents is a very dense dataset.

Both purchase quantities (internal) and unit profits (external) were assigned to the items in the accident, retail, and T10I4D100K datasets using a simulation method proposed in previous studies  (Liu and Qu 2012; Liu et al. 2005; Tseng et al. 2010), except for the foodmart dataset. In addition, due to the tuple uncertainty property, a unique probability value in the range of (0.5, 1.0] was assigned to each transaction in these datasets.

5.2 Runtime

The runtime of the compared algorithms for various MUs and a fixed MP, and various MPs and a fixed MU, are respectively compared and shown in Figs. 4 and 5.

Fig. 5

Runtime for various MPs and a fixed MU

From Fig.  4, it can be observed that the runtimes of all the algorithms decrease when MU is increased. In particular, the proposed MUHUI algorithm can be up to one or two orders of magnitude faster than the PHUI-UP algorithm, and that it outperforms the state-of-the-art PHUI-List algorithm on all datasets. This is reasonable since an upper bound-based generate-and-test approach performs less well than a vertical PU-list-based approach. Besides, the MUHUI algorithm uses five pruning strategies to prune unpromising itemsets early and reduce the search space. Thus, it can avoid performing costly join operations for constructing a huge number of PU-lists for mining PHUIs, compared to the PHUI-List algorithm. When the MU is set quite low, longer HTWPUIs are discovered by the PHUI-UP algorithm, and thus it takes more time to process these patterns using a generate-and-test mechanism, especially for dense datasets. Because the PHUI-List, MUHUI1 and MUHUI2 algorithms directly identify PHUIs in the set-enumeration tree without generating candidates and using a depth-first search rather than a level-wise search, they can effectively avoid performing multiple time-consuming database scans. Moreover, the MUHUI algorithm applies five pruning strategies to prune unpromising items early, which greatly speed up the discovery of PHUIs, compared to the PHUI-List algorithm.

As shown in Fig. 5, it can be observed that (1) the MUHUI algorithm outperforms the PHUI-List algorithm for various MPs and a fixed MU on the four datasets. (2) The runtime of PHUI-UP sharply decreases when the MP is increased, while the runtimes of PU-list-based algorithms steadily decrease. (3) The runtime of the MUHUI algorithm with different pruning strategies is always less than the runtime of the PHUI-List algorithm. (4) MUHUI2 has the best performance, and is always faster than MUHUI1. These results are reasonable for the previously mentioned reasons. Although the PHUI-UP algorithm uses the TWPUDC property to reduce the search space, it still performs a level-wise search to explore the search space, and generates and tests a huge amount of candidates for mining PHUIs. Among these candidates few of them are PHUIs. Therefore, when the MP is set high, many redundant unpromising candidates are pruned early, and thus the search space and runtime of the PHUI-UP algorithm sharply decreases while those of the PHUI-List and MUHUI algorithms steadily decrease. Overall, the MUHUI algorithm is about one to two orders of magnitude faster than PHUI-UP, and always more efficient than PHUI-List, especially on large datasets. Furthermore, the performance gap becomes wider when the MU or MP parameters are decreased.

5.3 Patterns analysis

To analyze the relationships between MUHUI and traditional HUIM, and evaluate whether the proposed MUHUI framework is acceptable, the number of patterns in terms of PHUIs and HUIs was also compared. Note that HUIs were generated using a traditional HUIM algorithm named HUI-Miner, and the PHUIs were generated by the proposed MUHUI algorithm. Besides, the useable ratio of the derived high-utility itemsets (abbreviated as useRatio) and redundant ratio of PHUIs (abbreviated as redRatio) are studied. The two ratios are defined as follows:

$$\begin{aligned} useRatio= & {} \frac{\vert \mathrm{PHUIs}\vert }{\vert \mathrm{HUIs}\vert }\times 100\,\% ; \quad \mathrm{{and}}\\ redRatio= & {} \frac{\vert \mathrm{HUIs-PHUIs}\vert }{\vert \mathrm{HUIs}\vert }\times 100\,\% \text{ or } 100\,\% -useRatio. \end{aligned}$$

The results of pattern analysis for HUIs and PHUIs under various MUs and a fixed MP, and for various MPs and a fixed MU are, respectively, shown in Tables 7 and 8.

Table 7 Analysis of useRatio and redRatio for various MUs and a fixed MP

Table 8 Analysis of useRatio and redRatio for various MPs and a fixed MU

In Table 7, it can be observed that the number of PHUIs is always smaller than the number of HUIs for various MUs on both sparse and dense datasets, which demonstrates the usefulness of incorporating an objective probability measure with the subjective individual preference utility measure, for mining PHUIs. Data uncertainty influences the discovered results since numerous HUIs are discovered but few of them are PHUIs when considering the probability value of each transaction in an uncertain dataset. This situation happens when the MU is set to small values, as the redRatio increases when the MU is decreased, while the useRatio decreases. In real-world applications, high-utility itemset mining aims at discovering itemsets with high utility that have a high existential probability for helping a manager or retailer to take efficient business decisions. When the MU is increased, fewer HUIs and PHUIs are produced by HUI-Miner and the designed approach, but the useRatio increases. This is reasonable since the proposed algorithm is used to discover PHUIs by considering both the utility and the probability constraints, while HUI-Miner discovers HUIs by only considering the utility constraint. When the MU is increased and the MP is fixed, the number of unpromising itemsets pruned by the utility constraint increases, and the number of redundant HUIs having a low existential probability is greater, and are filtered, and thus the useRatio decreases.

In Table 8, it can be observed that (1) fewer PHUIs are discovered by the MUHUI algorithm compared to the number of HUIs discovered by HUI-Miner for various MPs and a fixed MU, for the four uncertain datasets. (2) The number of discovered HUIs remains steady as the MP is increased, whereas the number of PHUIs decreases. (3) The useRatio decreases as the MP is increased, whereas the redRatio increases for a fixed MU on all datasets. These results are reasonable and explained as follows. The proposed MUHUI algorithm applies two constraints for mining PHUIs, while HUI-Miner only considers the utility constraint for discovering HUIs. Thus, the number of PHUIs is always no greater than the number of HUIs, while the number of HUIs does not change when the MP is increased. Moreover, the number of PHUIs dramatically decreases when the MP is increased; more derived HUIs are considered as redundant patterns w.r.t. non-PHUIs since their existential probabilities are less than the MP. Thus, the higher the MP is, the lower the useRatio is. In particular, the discovered PHUIs can be considered as valuable patterns compared to patterns discovered using traditional HUI mining algorithms since the data uncertainty factor often occurs in real-life situations. It can be concluded that numerous discovered HUIs may not be patterns of interest that can help a manager or retailer to take efficient business decisions, since the probability factor is not considered, and thus the proposed MUHUI framework is suitable for mining high-probability and high-utility patterns in uncertain data.

5.4 Effect of the different pruning strategies

To evaluate the effect of the different pruning strategies, the number of visited nodes in the search space is compared. Since the comparison of runtime and memory usage has already been presented, only the number of visited nodes in the set-enumeration tree is discussed in this subsection. In the following, the number of nodes visited by the PHUI-List, MUHUI1 and MUHUI2 algorithms is denoted as $N_{1}$, $N_{2}$,and $N_{3}$, respectively. Experimental results for various MUs and MPs are, respectively, shown in Figs. 6 and 7.

Fig. 6

Number of visited nodes using different pruning strategies for various MUs and a fixed MP

Fig. 7

Number of visited nodes using different pruning strategies for various MPs and a fixed MU

In Figs. 6 and 7, it is obvious that $N_{1} \ge N_{2}\ge N_{3}$ for all datasets and all tested parameter values, and that the number nodes in the search space (set-enumeration tree) visited by the proposed MUHUI algorithm changes when different pruning strategies are applied. MUHUI prunes a greater number of unpromising itemsets compared to the PHUI-List algorithm. An interesting observation is that the gap between $N_{1}$ and $N_{2}$, and the gap between $N_{2}$ and $N_{3}$ grow wider when the MU or MP is decreased. This indicates that the various pruning strategies can greatly influence the number of visited nodes in the search space. This observation is due to the fact that the PHUI-List algorithm performs an exhaustive search in the set-enumeration tree, and builds the PU-lists of unpromising k-itemsets ($k \ge$ 2, which are not HTWPUIs), which is very time consuming especially when the thresholds are set quite low. On the other hand, MUHUI uses the EUCP strategy to check the TWU value of each itemset and determine if a processed node and its child nodes are promising, early. When the number of distinct items in a dataset is large, the search space is huge (a property of the set-enumeration tree). Pruning strategies 4 and 5 considerably reduce the search space by pruning subtrees. When a processed node is pruned, a greater number of subtrees is pruned, and thus the search space becomes smaller.

In addition, these results also show that pruning strategy 5, using the probability value, can prune many unpromising itemsets and thus avoid constructing a series of PU-lists for them and their child nodes. Although the number $N_{3}$ is slightly less than $N_{2}$ on the retail dataset, as shown in Figs. 6b and 7b, it can still be observed that $N_{3}$ is quite smaller than $N_{2}$ for the foodmart and accidents datasets. It can be concluded that the proposed pruning strategy 5 is reasonable and acceptable.

5.5 Memory usage

In this section, the memory usage of the compared algorithms is compared. All memory measurements were done using the standard Java API. The performance of the algorithms was evaluated for various MUs and a fixed MP, and for various MPs and a fixed MU. Results are, respectively, shown in Figs. 8 and 9.

Fig. 8

Memory usage for various MUs and a fixed MP

Fig. 9

Memory usage for various MPs and a fixed MU

In Figs. 8 and 9, it can be clearly seen that the proposed MUHUI algorithm consumes less memory than the PHUI-UP algorithm, but consumes more memory than the state-of-the-art PHUI-List algorithm except for the retail dataset. In particular, the memory usages of the two PU-list-based algorithms, PHUI-List and MUHUI, gradually change when the parameters are varied, for the four datasets. The reasons for this behavior are similar to the reasons given in the runtime analysis. This result is reasonable since both PHUI-List and MUHUI are PU-list-based algorithms, and they can easily prune unpromising itemsets using the actual utilities and remaining utilities. The reason why PHUI-List always consumes a little bit more memory than MUHUI is that it has to spend extra memory for storing the additional EUCS data structure. Thanks to the advantage of the designed vertical PU-list data structure, the proposed PU-list-based MUHUI algorithm discovers PHUIs by considering the utility and probability constraints, and more efficient pruning strategies are proposed in MUHUI to improve its performance. Hence, the memory usage of the MUHUI algorithm is somehow similar to that of the PHUI-List algorithm.

In addition, the memory usage for the PHUI-UP algorithm sharply decreases when the MU or MP is increased. For the PHUI-List and MUHUI algorithms, the main memory cost is to initialize its PU-list structures. In particular, as the MU or MP is increased, MUHUI1 and MUHUI2 require less memory to build the EUCS for storing the co-occurrence relationships of 2-itemsets. Therefore, the memory usage of the proposed MUHUI algorithm is reduced and acceptable.

5.6 Scalability and efficiency

In Fig. 10, the scalability of the four algorithms is compared on the synthetic dataset T10I4N4KD$\vert X\vert$K, where the number of transaction is varied. In this experiment, the MP is set to 0.05 %, the MU is set to 0.1 %, and the number of transactions $\vert X \vert$ is varied from 100 to 500 (thousand transactions).

Fig. 10

Scalability results

In Fig. 10a, it can be observed that the runtimes of all compared algorithms linearly increase as the dataset size $\vert X \vert$ is increased. The performance of MUHUI1 and MUHUI2 is relatively stable when $\vert X \vert$ is varied. As the size of the dataset increases, the runtime of MUHUI1 is close to that of MUHUI2, but MUHUI1 is considerably faster than PHUI-List. In particular, the runtime gap between the runtimes of these two algorithms grows wider when the dataset size increases. This is reasonable since all the items in T10I4N4KD$\vert X\vert$K have similar distributions. As the dataset size increases, runtimes of the algorithms linearly increase. It can be observed that the proposed MUHUI algorithm scales well for large datasets. Figure 10b compares memory usage of the four algorithms. These results indicate that memory usage also linearly grows with respect to database size. In addition, we observe that the memory usages of the four PU-list-based algorithms increase less rapidly than the memory usage of the PHUI-UP algorithm.

In Fig. 10c, it can be observed that few HUIs found by traditional HUIM algorithms are actually PHUIs. MUHUI1 and MUHUI2 both visit less nodes than the PHUI-List algorithm when the dataset size is varied, as it can be observed in Fig. 10d. From these results of the scalability test, it can be concluded that the proposed MUHUI algorithm has better scalability than the state-of-the-art PHUI-List algorithm.

6 Conclusions and future work

Many approaches were previously proposed for mining high-utility itemsets in precise data. But few studies have addressed the problem of mining high-utility itemsets in uncertain data. In this paper, an efficient algorithm called Mining of Uncertain data for High-Utility Itemsets (MUHUI) is proposed to discover itemsets having both a high utility and a high existential probability in an uncertain database. The previous state-of-the-art algorithm, named PHUI-List, suffers from the problem of performing multiple join operations to construct PU-lists, which is time consuming, and may face the problem of a very large search space when thresholds are set to small values. The MUHUI algorithm integrates several efficient pruning strategies to discover PHUIs more efficiently than the PHUI-List algorithm. The proposed PU-list structure stores information about both the probabilities and utilities of itemsets. Several efficient pruning strategies have also been designed to speed up the discovery of PHUIs, and avoid constructing the PU-lists of a large number of unpromising itemsets. Substantial experiments both on real-life and synthetic datasets show that the proposed MUHUI algorithm consumes slightly more memory than the PHUI-List algorithm, but is generally much faster, visits less nodes in the set-enumeration tree, and has better scalability. In particular, the MUHUI algorithm has better scalability than the PHUI-List algorithm on large-scale uncertain datasets.

For future work, many interesting issues can be studied related to the problem of mining high-utility itemsets in uncertain data, such as incremental mining of PHUIs, mining PHUIs in streams, and up-to-date PHUI mining. In addition, how to design more efficient algorithms for mining PHUIs can also be considered for future work.