Marginal patch alignment for dimensionality reduction

Abstract

Patch alignment (PA) framework provides us a useful way to obtain the explicit mapping for dimensionality reduction. Under the PA framework, we propose the marginal patch alignment (MPA) for dimensionality reduction. MPA performs the optimization from the part to the whole. In the phase of the patch optimization, the marginal between-class and within-class local neighborhoods of each training sample are selected to build the local marginal patches. By performing the patch optimization, on the one hand, the contributions of each sample for optimal subspace selection are distinguished. On the other hand, the marginal structure information is exploited to extract discriminative features such that the marginal distance between the two different categories is enlarged in the low transformed subspace. In the phase of the whole alignment, a trick is performed to unify all of the local patches into a globally linear system and make MPA obtain the whole optimization. The experimental results on the Yale face database, the UCI Wine dataset, the Yale-B face database, and the AR face database, show the effectiveness and efficiency of MPA.

1 Introduction

Dimensionality reduction (DR) is an effective method of avoiding the “curse of dimensionality”. It has achieved remarkable success in the fields of computer vision and pattern recognition. Linear discriminant analysis (LDA; Belhumeur et al. 1997) is one of the most famous DR techniques. It is also called the parametric discriminant analysis (PDA) in (Fukunaga 1990) since it uses the parametric form of the scatter matrix. LDA aims to preserve information between the data of different classes. To achieve this goal, LDA maximizes the between-class scatter meanwhile minimizing the within-class scatter. However, the excellent performance of LDA is based on the assumption that the samples in each class satisfy the Gaussian distribution. In real world, this assumption is hard to realize. Thus, they suffer performance degradation in cases of non-Gaussian distribution. Besides this, the available features of LDA are limited because the rank of the between-class matrix is at most $c-1$, where c is the number of classes. It is often insufficient to separate the classes well with only $c-1$ features, especially in high-dimensional spaces. In addition, LDA only uses the centers of classes to compute the between-class scatter matrix, and thus fails to capture the marginal structure of classes effectively, which has been proven to be essential in classification.

Even with the above limitations, LDA still performs well and is one of representative linear dimensionality reduction methods. However, LDA, as a global method, exploits the linear global Euclidean structure and fails to use the nonlinear local information. Liu et al. (2004) and Mtiller et al. (2001) applied the kernel trick to handle the nonlinearities of data structure. These kernel methods map data points from the original feature space into another higher dimensional one such that the data structure becomes linear.

The well-known nonlinear dimensionality reduction (NLDR) methods, e.g., locally linear embedding (LLE; Roweis and Saul 2000), Isomap (Tenenbaum et al. 2000), and Laplacian eigenmap (Belkin and Niyogi 2003), are proposed based on the hypothesis that data in a complex high-dimensional data space may reside more specifically on or nearly on a low-dimensional manifold embedded within the high-dimensional space (Yang et al. 2011). All these NLDR methods are implemented restrictedly on training data and cannot provide us with explicit maps on new test data. Bengio et al. (2003) presented a kernel solution to solve this problem, in which LE, Isomap, and Laplacian Eigenmaps are integrated into the same eigen-decomposition framework, and then they were considered as learning eigenfunctions of a kernel. Their methods achieve the satisfactory results. After that, He et al. proposed locality preserving projections (LPP; He et al. 2005; He and Niyogi 2003) and neighborhood preserving embedding (NEP; He et al. 2005) to obtain the linear projections and achieved good classification performance.

Recently, Zhang et al. (2009) proposed the locality-based patch alignment (PA) framework. Many dimensionality reduction methods can be unified into the PA framework, even that they are based on different embedding criteria, such as PCA, LDA, LLE, NPE, ISOMAP, LE, LPP, and local tangent space alignment (LTSA; Zhang and Zha 2004). The PA framework helps us to better understand the common properties and intrinsic difference in different algorithms. The PA framework consists of two stages: part optimization and whole alignment. In the phase of part optimization, the local patches are built by each sample and the related ones and aim to capture the local geometry (locality) of data. In the second phase, all part optimizations are integrated to form the final global coordinate for all independent patches based on the alignment trick (Zhang et al. 2009). Different algorithms were shown to construct whole alignment matrices in an almost identical way, but vary with patch optimization. Under the PA framework, Zhang et al. (2009) proposed discriminative locality alignment (DLA) to overcome the mentioned limitations of LDA. In DLA, a local nearest patch is built by one sample associated with its related nearest samples. In the phase of patch optimization, the within-class compactness is represented as the sum of distances between each point and its K1-nearest neighbors of the same class; while the separability of different classes is characterized as the sum of distances between each sample and its K2-nearest neighbors of the different classes. By performing the patch optimization, the samples with the same class-label should cluster better than before, but it does not guarantee that the marginal distance can be enlarged larger than before.

The marginal structure information has been proved to be essential in classification and has attracted more and more attention. Many margin maximization-based algorithms have been developed, e.g., (MMC; Li et al. 2006), (MFA; Yan et al. 2007), and (MMDA; Yang et al. 2009). These methods all exploit the marginal samples, which contain much discriminative information than other samples, to extract the discriminative features such that the extracted features are more suitable for classification. This also motivates us to exploit the local marginal discriminative information to develop a novel nonparametric DR technique, called marginal patch alignment (MPA). In MPA, we select the between-class and within-class local marginal samples of each training sample to build the marginal patches. It is obvious that the marginal patches can contain most discriminative information than other patches. Based on these local marginal patches, the within-class compactness is represented as the sum of distances between each sample and its K1 within-class marginal samples associated with the nearest between-class samples; while the separability of different classes is characterized as the sum of distances between the two local marginal means. By performing marginal patch optimization, the marginal structure can be found and the discriminative information is exploited. As a result, the marginal distances between the two different categories can be enlarged in a direct way.

Unlike DLA, MPA focuses on marginal samples rather than the nearest samples. MPA selects the marginal samples to build patches, and then performs the patch optimization to push them away, such that the marginal distances become larger than before. The way taken by MPA is more direct than that of DLA in enlarging the marginal distance. More concretely, MPA first finds the K2 nearest between-class neighbors in each other’s class, and then turns back to find the K1 within-class marginal samples. By such a way, the selected within-class samples near the margin of different classes are maybe not the nearest samples of the given sample. While this does not affect us to make the samples with the same class-labels clustered better than before.

The remainder of this paper is organized as follows: Section 2 outlines the PA framework. Section 3 describes the proposed MPA algorithm. Section 4 presents the advantages of MPA. Section 5 verifies the effectiveness of MPA through experiments on the Wine dataset from UCI, the Yale face database, the Yale-B face database, and the AR face database. Finally, our conclusions are drawn in Sect. 6.

2 Patch alignment (PA) framework

In the PA framework (Zhang et al. 2009), if considering a dataset with N measurements, we can build N patches for each training sample. Each patch consists of a training sample and its associated ones, which depend on both characteristics of the dataset and the objective of an algorithm. With these built patches, optimization can be imposed on them based on an objective function, and then the alignment trick (Zhang et al. 2009) can be utilized to unify all the patches into a global coordinate. The specific procedure of the PA framework is listed as follows:

2.1 Part optimization

Considering an arbitrary training sample $\vec {x}_i$ and its K associated samples (e.g., nearest neighbors) $\vec {x}_{i1} ,\ldots \vec {x} _{iK}$, we build the patch $\vec {X} _i =[ \vec {x}_i ,\vec {x} _{i1} ,\ldots ,\vec {{x}} _{iK}]$. For $\vec {{X}}_i$, we have a part mapping $f_i :\vec {{X}} _i \mapsto \vec {{Y}} _i$, by which we can obtain $\vec {{Y}} _i = [\vec {{y}} _i ,\vec {{y}} _{i_1 } ,\ldots ,\vec {{y}} _{i_K } ]$, the low-dimensional representation of $\vec {{X}} _i$. Let us perform the part optimization on $\vec {{Y}} _i$ as follows:

$$\begin{aligned} \arg \mathop {\min }\limits _{\vec {{Y}} _i }\,tr\left( \vec {{Y}} _i \vec {{L}} _i \vec {{Y}} _i^T \right) , \end{aligned}$$

(1)

where $tr(\cdot )$ is the trace operator; $\vec {{L}} _i \in R^{(K+1)\times (K+1)}$ is the patch optimization matrix and varies with the different algorithms.

Fig. 1

Illumination of the optimized result

2.2 Whole alignment

For each patch $\vec {{X}} _i$, its low-dimensional representation $\vec {{Y}} _i$can be put into a global coordinate as follows:

$$\begin{aligned} \vec {{Y}} _i =\vec {{Y}} \vec {{S}} _i , \end{aligned}$$

(2)

where $\vec {{Y}} =[\vec {{y}} _1 ,\ldots ,\vec {{y}} _N ]$ is the global coordinate, $\vec {{y}} _i$ can be obtained by $f_i {:}\vec {{x}} _i \mapsto \vec {{y}} _i$ for $i=1,\ldots ,N$, and $\vec {{S}} _i$ is a selection matrix. The entry of $\vec {{S}} _i$ is defined as below:

$$\begin{aligned} (\vec {{S}} _i )_{pq} =\left\{ {{\begin{array}{*{20}l} {1 \quad \mathrm{if}\; p=F_i \left\{ q \right\} } \\ {0 \quad \mathrm{otherwise}} \\ \end{array} }} \right. \end{aligned}$$

(3)

where $F_i =\{i,i_1 ,\ldots ,i_K \}$ denotes the index set of the $i^{th}$ patch, which is built by the training sample $\vec {{x}} _i$ and its K associated ones. Then, Eq. (1) can be rewritten as follows:

$$\begin{aligned} \arg \mathop {\min }\limits _{\vec {{Y}}} tr\Big (\vec {{Y}} \vec {{S}} _i \vec {{L}} _i \vec {{S}}_i^T \vec {{Y}}^T \Big ). \end{aligned}$$

(4)

Now, we can perform the whole alignment. Let $i=1,\ldots ,N$ and sum over all the part optimizations described as Eq. (4) as follows:

$$\begin{aligned} \arg \mathop {\min }\limits _{\vec {{Y}}} \sum \limits _{i=1}^N {tr\Big (\vec {{Y}} \vec {{S}} _i \vec {{L}} _i \vec {{S}} _i^T \vec {{Y}}^T \Big )} . \end{aligned}$$

(5)

Impose $U^{T} U=I_d$ in Eq. (5). The optimal projection matrix U is obtained by solving the following objective function:

$$\begin{aligned} \begin{array}{l} \arg \mathop {\min }\limits _{U} \displaystyle \sum \limits _{i=1}^N {tr\Big (U^{T} \vec {{X}} \vec {{S}} _i \vec {{L}} _i \vec {{S}} _i^T \vec {{X}}^{T} U \Big )} \\ \mathrm{s.t.} \; U^{T} U=I_d \\ \end{array} \end{aligned}$$

(6)

3 Marginal patch alignment (MPA)

3.1 Motivations

Let us first consider a two-class problem. $X=[x_1,x_2,\ldots ,x_N ]$ is the training sample set, where N is the total training number. Assumed that $x_i$ is the sample from Class 1. Now, we find its K2-nearest samples in Class 2. Collect these K2-nearest neighbors in $X_i^2 =[x_{i_1 } ,\ldots ,x_{ik2}]$ and calculate their local mean vector $m_i^2$. Now, we turn back to find the K1-nearest neighbors of $m_i^2$ in Class 1 and collect them in ${X_i}^{1} =[x_{i}^{1} ,\ldots ,x_{i^K1}]$. The mean of these K1 samples is denoted by $m_i^1$. Collect the two parts of neighbors of $x_i$ together and build the $i^{th}$ marginal patch as $X_i =[x_i ,x_{i1} ,\ldots ,x_{iK1} ,x_{i1 } ,\ldots ,x_{iK2} ]$.

Now, we define the between-class marginal distance of $x_i$ as follows:

$$\begin{aligned} d_b (x_i )=\left\| {m_i}^{2} -{m_i}^1 \right\| ^2 . \end{aligned}$$

(7)

The within-class marginal distance of $x_i$ is defined as follows:

$$\begin{aligned} d_w (x_i )=\sum \limits _{j=1}^{K1} \left\| {x_i} -{x}_{i^j} \right\| ^{2} ({w}_{i})_j \end{aligned}$$

(8)

where $(w_i )_j =\exp (-\left\| {x_i -x_{ij} } \right\| ^2/\partial )$, $\partial$ is a parameter. Usually, we can choose the parameter $\partial$ as the square of the average Euclidean distance between $x_i$ and all its within-class marginal data points. More details above the selection of the parameter can refer (Belkin and Niyogi 2001).

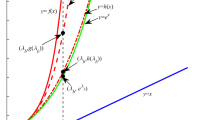
Our goal is to find a linear transform matrix P, such that the transformed marginal distance between the two difference classes can be enlarged, i.e., the transformed samples with different class-labels are push away. Meanwhile, the within-class samples are pulled closer. Figure 1 shows the optimized result.

3.2 Marginal patch optimization

In the transformed space, the within-class marginal distances $d_w (y_i )$ generally characterizes the compactness of the marginal patch $Y_i =[y_i ,y_{i^1} ,\ldots ,y_{i^{K1}} ,y_{i_1 } ,\ldots ,y_{i_{K2} } ]$. By performing algebraic operation, $d_w (y_i )$ can be deduced as follows:

$$\begin{aligned} d_w (y_i )= & {} \sum \limits _{j=1}^{K1} {\left\| {y_i -y_{i^j} } \right\| } (w_i)_j \nonumber \\= & {} tr\left\{ {\left( {{\begin{array}{*{20}c} {y_i -y_{i^1} } \\ \vdots \\ {y_i -y_{i^{K1}}} \\ \end{array} }}\right) \mathrm{diag}\left( w_i^t \right) \big [y_i -y_{i^1} ,\ldots ,y_i -y_{i^{K1}}\big ]} \right\} \nonumber \\= & {} tr \Big (Y_i L_{w(i)} Y_i^T \Big ) \end{aligned}$$

(9)

where $L_{w(i)} ={\left( {{\begin{array}{*{20}c} I_{K1+1} \\ 0 \\ \end{array} }} \right) \left( {{\begin{array}{*{20}c} -e^T_{K1} \\ I_k1 \\ \end{array} }} \right) } \mathrm{diag}(w_i )[-e_{K1} ,I_{K1}]L_{w(i)} = {\left( {{\begin{array}{*{20}c} I_{K1+1} \\ 0 \\ \end{array} }} \right) }^T,e_{K1} =[1,\ldots ,1]^T\in R^{K1\times 1}$, and $I_{K1} = \mathrm{diag}(1,\ldots ,1)\in R^{K1\times K1}$

Similarly, the between-class marginal distance $d_b(y_i )$ in the transformed space characterizes the separability of the marginal samples with different class-labels. $d_b(y_i )$ can be deduced as follows:

$$\begin{aligned} d_b (y_i )= & {} \left\| {\hat{m}_i^1 -\hat{m}_i^2 } \right\| ^2 \nonumber \\= & {} \left\| {\frac{1}{K1}\sum \limits _{j=1}^{K1} {y_{i^j} -\frac{1}{K2}\sum \limits _{s=1}^{K2} {y_{i_s } } } } \right\| ^2 \nonumber \\= & {} tr\left( Y_i \Omega _i \Omega _i^T Y_i^T\right) \nonumber \\= & {} tr\left( Y_i L_{b(i)} Y_i^T \right) \end{aligned}$$

(10)

where $_{ }L_{(b)i} =\Omega _i \Omega _i^T$ and $\Omega _i ={\left[ {{\begin{array}{c@{\quad }c} 0 &{} 0 \\ 0 &{} {I_{K1+K2} } \\ \end{array} }} \right] }[0,\underbrace{\frac{1}{K1},\ldots ,\frac{1}{K1}}_{K1},\underbrace{-\frac{1}{K2},\ldots ,-\frac{1}{K2}}_{K2}]^T$.

3.3 Whole alignment

For better classification, the marginal distance between the two categories in the low-dimensional transformed space should be as large as possible. To achieve this goal, for each marginal patch, the distance from each sample to its corresponding within-class marginal points should be as small as possible, i.e., maximizing $d_w (y_i )$ . At the same time, the distance between the two means of marginal patches with different class-labels should be as large as possible, i.e, maximizing $d_b (y_i )$. Unifying both two distance functions, we have

$$\begin{aligned}&\arg \mathop {\max }\limits _{y_i} (d_b (y_i)-\beta d_w (y_i )) \nonumber \\&\quad =\arg \mathop {\max }\limits _{y_i} \left( \left\| {\frac{1}{K1}\sum \limits _{j=1}^{K1} {y_{i^j} -\frac{1}{K2}\sum \limits _{s=1}^{K2} {y_{i_s }}}} \right\| ^2\right. \nonumber \\&\left. \qquad \qquad \quad \;-\beta \sum \limits _{j=1}^{K1} {\left\| {y_i-y_{i^j} } \right\| ^2} (w_i)_j\right) \nonumber \\&\quad =\arg \mathop {\max }\limits _{yi} tr\Big (Y_i L_{b(i)} Y_i^T \Big )-\beta tr\Big (Y_i L_{w(i)} Y_i^T\Big ) \end{aligned}$$

(11)

where the parameter $\beta$ is a scale factor to adjust the tradeoff between the two measurements of the within-class distance and the between-class distance (i.e., the compactness and separability) (Zhang et al. 2009). The main factor that can cause the imbalance is the unequal numbers K1 and K2, of the same-class and different-class marginal neighbors. In our paper, we simply set $\beta =1$ to place the same weight on two distances. In addition, we can set $\beta$in the range of [0, 1]. If $\beta =0$, obviously, the within-class marginal distances will be neglected and the between-class marginal distances become very crucial. The marginal discriminative information can only be captured by exploring the between-class marginal structure. In such a case, an appropriate K2 becomes very important. When $K 2= T$, where T is the number of training sample per class, the between-class local marginal mean is the class-mean. The class-mean contains less class marginal information. So K2 should not be set too large. On the contrary, if we set K2 too small, such as 1, that means only a very small amount of training samples are utilized in the learning the discriminative structure information, which may lead to suboptimal performance. Zhang et al. (2008) provides us a more simple way to choose parameters K1 and K2. We can follow it to find the optimal parameters K1 and K2. Based on the optimal parameters K1 and K2, the sensitivity of objective function caused by $\beta$ can be reduced to some extent.

Having finished the marginal patch optimization, we now perform the whole alignment. The low-dimensional representation of the $i^{th}$ patch $Yi=[y_i ,y_{i1} ,\ldots ,y_{iK1} ,y_{i1},\ldots y_{iK2} ]$ can be integrated into a global coordinate$Y=[y_1^ ,y_2 ,\ldots ,y_N^ ]$ by a selection matrix $S_i$, i.e,

$$\begin{aligned} Y_i =YS_i, \end{aligned}$$

(12)

where $Y=P^T X$ and

$$\begin{aligned} {(S_i)}_{pq}=\left\{ {_{0 \quad \mathrm{otherwise}}^{1 \quad \mathrm{if}\; p\;\in \;\Gamma _i \{q\}} } \right. \end{aligned}$$

(13)

and $\Gamma _i =\{i,i^1,\ldots ,i^{K1},i_1 ,\ldots ,i_{K2} \}.$

Let $i=1,\ldots ,N$ and we have N sub-optimizations of Eq. (11). Sum up all of them and then perform the whole alignment as follows:

$$\begin{aligned} \begin{aligned}&\arg \mathop {\max }\limits _Y \sum \limits _{i=1}^N {\Big (tr\Big (YS_i L_{b(i)} S_i^T Y^T\Big )-\beta tr\Big (YS_i L_{w(i)} S_i^T Y^T\Big )\Big )} \\&\quad =\arg \mathop {\max }\limits _Y tr\Big (Y\sum \limits _{i=1}^N {\Big (S_i L_{b(i)} S_i^T -\beta S_i L_{w(i)} S_i^T \Big )Y^T\Big )}\\&\quad =\arg \mathop {\max }\limits _Y tr(YLY^T) \\ \end{aligned} \end{aligned}$$

(14)

where L is the alignment matrix and

$$\begin{aligned} L=\sum \limits _{i=1}^N {\Big (S_i L_{b(i)} S_i^T -\beta } S_i L_{w(i)} S_i^T \Big ). \end{aligned}$$

(15)

The optimal transformed matrix $P_\mathrm{MPA} =\left[ {p_1 ,\ldots ,p_d } \right]$ is constructed by the eigenvectors of

$$\begin{aligned} \mathrm{XLX}^TP=\lambda P \end{aligned}$$

(16)

associating with d maximal eigenvalues $\lambda$.

3.4 Algorithm of MPA

In summary of the description above, the marginal patch alignment (MPA) algorithm is given below:

• Step 1: Project all the training samples into a PCA-transformed subspace with the projective matrix of $P_\mathrm{PCA}$.

• Step 2: For each sample $x_i$, find its K2 between-class marginal samples $X_i^2 =[x_{i_1 } ,\ldots ,x_{i_{k2} } ]$ and K1 within-class marginal neighbors $X_i^1 =[x_{i^1} ,\ldots ,x_{i^{K1}}]$. And then build the $i^{th}$ marginal patch $X_i =[x_i ,x_{i^1} ,\ldots ,x_{i^{K1}} ,x_{i_1 } ,\ldots ,x_{iK2} ]$.

• Step 3: Calculate the alignment matrix L by Eq. (15).

• Step 4: Solve the standard eigenequation of $\mathrm{XLX}^TP=\lambda P$ and obtain the transformed matrix $P_\mathrm{MPA}.$

• Step 5: Output the final linear transformed matrix $P^*=P_\mathrm{PCA} P_\mathrm{MPA}$.

Once $P^*$ is obtained, we can project all the samples into the optimal transformed space with the projective matrix of $P^*$, and then select the minimum distance classifier (MDC; Gonzalez and Woods 1997) for classification.

3.5 Extension to multi-class case

Let us consider the multi-class cases in the observation space. Suppose there are c pattern classes. Let $X=\{X_i ^{li}\}$ be the training sample set, where $i=1,\ldots ,N$, and $l_i \,\in \{1,\ldots ,c\}$ is the class-label of $x_i$. Now, we need to adjust some steps of the MPA algorithm in two-class case. More concretely, in step 2, we turn to find the K2 between-class marginal neighbors in Class s (where $s=1,\ldots ,c$ and $s\ne l_i )$, and collect them in $(\chi _b )_i^s$. Calculate the mean of these between-class marginal neighbors $(m_b)_i^s$ and find K1 nearest neighbors of $(m_b)_i^s$ in Class $l_i$. The K1 nearest neighbors is called the within-class marginal samples of $x_i$ with respect to Class s. Collect them in $(\chi _w )_i^s =\{x_{i^j} ^s\}$ for $j=1,\ldots ,K1$.

Now, we calculate the within-class marginal distance and between-class marginal distance of $y_i$ in the transformed space, respectively, as follows:

$$\begin{aligned}&{D_w}(y_i )=\mathop \sum \limits _{l=1,l\ne l_i }^c \mathop \sum \limits _{j=1}^{K1} \left\| {yi-y^l_{i^j} } \right\| \left( w^l_i\right) _{j,}\end{aligned}$$

(17)

$$\begin{aligned}&D_b (y_i )=\sum \limits _{l=1,l\ne l_i }^c {\left\| {\frac{1}{K1}\sum \limits _{j=1}^{K1} {y_{ij}^l -\frac{1}{K2}\sum \limits _{t=1}^{K2} {y_{it}^l } } } \right\| }^2. \end{aligned}$$

(18)

Perform the marginal patch optimization as follows:

$$\begin{aligned} {\mathrm{arg}}\mathop {\mathrm{max}}\limits _{y_i } (D_b (y_i )-\beta \,D_w (y_i )). \end{aligned}$$

(19)

The remaining steps are the same as the ones in two-class case.

4 Advantages of MPA

The proposed MPA has the following advantages:

• The contributions of each sample for optimal subspace selection are distinguished in the phase of marginal patch optimization.

• The number of the available features is more than $c-$1, where c is the number of classes. In the high-dimensional space, it usually needs more features to separate the classes well.

• The marginal samples contain more discriminative information than those in other patches. MPA takes the marginal samples into account, and thus can well preserve marginal discriminability of classes.

• Without prior information on data distributions, “marginal patch optimization” can characterize the separability of different classes well and the “whole alignment” can help us to obtain the global optimization.

• Like the nonlinear dimensionality reduction method, MPA can find the nonlinear boundary structural information for different classes hidden in the high-dimensional data, even the data with non-Gaussian distribution. This can be explained by examining the vectors. As illustrated in Fig. 2, MPA has the advantage of utilizing the boundary information. More concretely, the MPA’s between-class scatter matrix spans a space involving the subspace spanned by the vectors ${\{}{v}_{2}, \ldots , {v}_{8}{\}}$ where boundary structure is embedded. Therefore, the boundary information can be fully utilized. We compare MPA with LDA, and find LDA computes the between-class scatter matrix only using the vector v$_{1}$, which is merely the difference between the centers of the two classes. It is obvious that v$_{1}$ fails to capture the boundary.

Fig. 2

MPA’s between-class scatter and LDA’s between-class scatter. v$_{1}$: difference vector of the centers of two classes; ${\{}{v}_{2}, \ldots , {v}_{8}{\}}$: difference vectors from the local means located in the classification boundary

Fig. 3

Samples of a person from the Yale database

5 Experiments

In this section, the proposed MPA method is evaluated using the Yale face database, the UCI Wine dataset, the Yale-B face database, and the AR face database and compared with PCA, FLDA, LPP, maximum margin criterion (MMC; Li et al. 2006), and DLA. For LPP, we select the Gaussian kernel $t=\infty$. Note that, in our experiment, LPP and MPA use the K-nearest neighbor algorithm to select the neighbors. The neighbor parameters are set by the global searching strategy. For distinction, the neighbor parameter is denoted by K in LPP, the within-class and the between-class neighbor parameters in MPA are denoted as K1 and K2, respectively. After extracting features, MDC is employed for classification. The experiments are executed on a computer system of Intel(R) Core(TM) i5-4440 CPU @ 3.10GHz 3.10GHz and 8.00 GB with Matlab R2010a.

5.1 Experiments on the Yale face database

The Yale face database is constructed at the Yale Center for Computational Vision and Control. It contains 165 grayscale images of 15 individuals. The images demonstrate the variations in lighting condition, facial expression, and with/without glasses. The size of each cropped image is 100 $\times$ 80. Figure 3 shows some sample images of one individual. These images vary as follows: center-light, with glasses, happy, left-light, without glasses, normal, right-light, sad, sleep, surprised, and winking.

In the following section, we continue our experiments with random training samples. T(=3, 4, 5, and 6) images are randomly selected from the image gallery of each individual to form the training sample set. The remaining 11-T images are used for test. The selection of neighbor parameters of LPP and MPA is similar to that in UCI Wine database. For FLDA, LPP, MMC, and MPA, we first project the data set into a 44-dimensional PCA subspace. We independently run the system 20 times. Table 1 shows the average recognition rates and their corresponding 95 % intervals of each method. The maximal average recognition rates of six methods versus the variation of the size of training set are illustrated in Fig. 4. From Table 1 and Fig. 4, we can see that:

• 1. MPA significantly outperforms PCA, FLDA, LPP, MMC, and DLA, no matter with the variation of the size of training samples in each class.

• 2. By comparing with the column of Table 2 with respect to FLDA, we find its recognition rate has degraded a lot when the number of training sample increases to 4. The possible reason is that FLDA is sensitive to outliers. Compared with the “center-light” image, the “left-light” and the “right-light” images of each class can be treated as outliers. The outlier images may affect the class-mean and cause error in estimate of scatters. This will finally lead to the projection of FLDA inaccurate (Xu et al. 2014). In contrast, MPA builds the adjacency relationship of data points using K2 between-class nearest marginal neighbors and the K1 within-class marginal neighbors. Most outlier images of different persons lie on the margin of class manifold. MPA focuses on the classification margin. Thus, most outliers may be treated as the marginal points and used to calculate the between-class scatter (i.e., the between-class marginal distance). At the same time, the outliers may be treated as the within-class marginal samples. By minimizing the within-class marginal distance, the same-class samples cluster better than before, and the marginal distance between the different classes also become larger. From this point of view, MPA seems to be more robust to outliers than FLDA.

Table 1 The maximal average recognition rates (%) and t and the corresponding 95 % intervals of six methods on the Yale face database

Fig. 4

The maximal average recognition rates of six methods versus the variation of the size of training set in the Yale face database

5.2 Experiments on the Wine dataset from UCI

Wine dataset is a real-life dataset from the UCI machine learning repository (http://archive.ics.uci.edu/ml). Wine has 13 features, 3 classes and 178 instances. 48 instances of each class are selected and used in the experiments.

In our experiments, T (=10, 15, 20, 25, and 30) samples per class are randomly selected for training and the remainders for testing. The experiment is repeated for 30 times. PCA, FLDA, LPP, MMC, DLA, and the proposed MPA algorithm are, respectively, used for feature extraction based on the original 13-dimensional features. We set the range of neighbor parameter K of LPP from 2 to$_{ }3T-1$ with an interval of 1. Similarly, the range of between-class parameter K2 of MPA is set from 1 to T with an interval of 1, and the within-class parameter K1 of MPA is set from 1 to $T-1$ with an interval of 1. And then, we choose the neighbor parameter associated with the top recognition rate as the optimal one. Table 2 lists the maximal average recognition rates and the 95 % interval of each method on the UCI Wine database across 30 runs. The maximal average recognition rates of six comparative methods versus the variation of the size of training set are illustrated in Fig. 5 . Observing Table 2 and Fig. 5, we find MPA is the best one among six feature extraction methods, irrespective of the variation in the size of training samples in each class.

Table 2 The maximal average recognition rates (%) and the corresponding 95 % intervals of six methods on the UCI Wine database

5.3 Experiments on the extended Yale-B face database

The extended Yale B face database (Lee et al. 2005) contains 38 human subjects under 9 poses and 64 illumination conditions. The 64 images of a subject in a particular pose are acquired at camera frame rate of 30 frames/ second, so there is only small change in head pose and facial expression for those 64 images. All frontal-face images marked with P00 are used, and each image is resized to 42$\times$48 pixels in our experiment. Some sample images of one person are shown in Fig. 6.

Fig. 5

The maximal average recognition rates of PCA, FLDA, LPP, MMC, DLA, and MPA versus the variation of the size of training set in UCI Wine dataset

Fig. 6

Samples of a person under pose 00 and different illuminations, which are cropped images in the extended Yale-B face database

Table 3 The maximal average recognition rates (%) and the corresponding 95 % intervals of six methods on the Yale-B face database

Fig. 7

The maximal average recognition rates of PCA, FLDA, LPP, MMC, DLA, and MPA versus the variation of the size of training set in the Yale-B face database

In our experiments,T (=10, 15, 20, and 25) images are randomly selected from the image gallery of each individual to form the training sample set. The remaining images are used for testing. PCA, FLDA, LPP, MMC, DLA, and MPA are, respectively, used for feature extraction. Note that, FLDA, LPP, MMC, DLA, and MPA are performed on the 150-dimensional PCA subspace. Similarly, the neighbor parameters of MPA are set as that used in the UCI Wine dataset. In addition, considering the case of large training samples, we take the strategy of searching from global to local. Let neighbor parameter of LPP vary from 2 to 38$T-1$ with an interval of 5, and select the parameter associated with the best recognition rate. After that, we reset the range to a smaller one which surrounds the parameter associated with the best recognition rate. The optimal neighbor parameter is the one associated the top recognition rate. For each T, we run the system 20 times and record the top average recognition rate and the corresponding 95 % interval of each method in Table 3. Figure 7 shows us the histogram of experimental results. By comparing the experimental results in Table 3 and Fig. 7, we find that the top recognition rate of MPA is also higher than other methods. It is well known that the illumination variation problem is one of the well-known problems in face recognition in uncontrolled environment. The experimental results in Yale-B face database verify the validity of the proposed method in dealing the changing illumination on images.

Fig. 8

Sample images of one person in the AR face database

Table 4 The maximal average recognition rates (%) and the corresponding 95 % intervals of six methods on the AR database across 10 runs

5.4 Experiments on the AR face database

The AR face database (Martinez and Benavente 1998, 2006) contains over 4000 color face images of 126 people, including frontal views of faces with different facial expressions, lighting conditions and occlusions. The images of 120 persons including 65 males and 55 females are selected and used in our experiments. The pictures of each person are taken in two sessions (separated by two weeks) and each section contains seven color images without occlusions. The face portion of each image is manually cropped and then normalized to 50$14 \times T$40 pixels. The sample images of one person are shown in Fig. 8.

We randomly choose T (= 2, 4, and 6) images from the images gallery of each individual to form the training sample set. The remaining $14-T$ images are used for testing. The proposed algorithm is compared with PCA, FLDA, LPP, DLA, and MMC. For fair comparisons, 220 principal components are kept for FLDA, LPP, MMC, DLA, and MPA methods in the PCA step. For each given T, we average the results over 10 random splits and report the means in Table 4. The maximal average recognition rates of six methods versus the variation of the size of training set are illustrated in Fig.9. Observing Table 4 and Fig. 9, we find that MPA can achieve higher recognition rates than PCA, FLDA, MMC, and DLA no matter with the variation of the size of training samples in each class. But MPA and LPP achieve the comparative results.

Fig. 9

The maximal average recognition rates of PCA, FLDA, LPP, MMC, DLA, and MPA versus the variation of the size of training set in the AR face database

6 Conclusions

Under the PA framework, we developed a dimensionality reduction technique, termed MPA. In MPA, the marginal points associated with each training sample are selected to build the local patches. By performing patch optimization, we distinguish the contributions of each sample for optimal subspace selection by exploiting the marginal structure information of each sample to extract the useful discriminative features. As a result, the marginal distances between the two different categories are accordingly enlarged in the low-dimensional transformed subspace. The following whole alignment unifies all of local patches into a globally linear system and makes the algorithm obtain the whole optimization. The proposed MPA method is evaluated using the Yale face database, the UCI Wine dataset, the Yale-B face database, and the AR face database. The experimental results demonstrate that MPA outperforms other comparative methods.