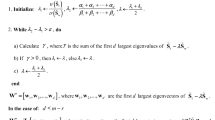Schatten-p Norm Based Linear Regression Discriminant Analysis for Face Recognition

Abstract

Locality-regularized linear regression classification (LLRC) shows good performance on face recognition. However, it sorely performs on the original space, which results in degraded classification efficiency. To solve this problem, we propose a dimensionality reduction algorithm named schatten-p norm based linear regression discriminant analysis (SPLRDA) for image feature extraction. First, it defines intra-class and inter-class scatters based on schatten-p norm, which improves the capability to deal with illumination changes. Then the objective function which incorporates discriminant analysis is derived from the minimization of intra-class compactness and the maximization of inter-class separability. Experiments carried on some typical databases validate the effectiveness and robustness of our method.

1 Introduction

Dimensionality reduction has played a key role in many fields such as machine learning, face recognition and data mining. It devotes to excavate the low dimensional features from high dimensional data while preserving the intrinsic information existed in data.

During the past few decades, a lot of dimensionality reduction algorithms using for feature extraction has been proposed. Principal component analysis (PCA) [1] and linear discriminant analysis (LDA) [2] are two typical methods. As an unsupervised approach, PCA projects high dimensional data onto a variance preserving subspace. In contrast, LDA, as a supervised method, aims to minimize within-class scatter and maximize between-class scatter to extract more discriminative features using labeled class information. However, it often suffers from small sample size (sss) [4] problem resulting from the singularity of within-class scatter. However, the above linear algorithms do not have the capabilities to capture the nonlinear structure embedded in image matrix. A lot of nonlinear feature extraction algorithms have been proposed to excavate the manifold structure of data, such as isometric mapping (ISOMAP) [5], Laplacian eigenmaps (LE) [6] and locally linear embedding (LLE) [7]. ISOMAP extends multidimensional scaling by incorporating the geodesic distances imposed by a weighted graph. LE finds the low-dimensional manifold structure by building a graph, whose node and connectivity are data points and proximity of neighboring points. LLE determines the low-dimensional representations of data by focusing on how to preserves the locally linear structure and minimizes the linear reconstruction error. However, the so called out-of-sample problem often occurs in those nonlinear algorithms. To solve the out-of-sample problem, locality preserving projection (LPP) [8] was proposed. LPP minimizes the local reconstruction error to preserve local structure and obtain the optimal projection matrix.

After feature extraction, data classification is another step for face recognition. Many classification methods have been proposed, such as nearest neighbor classifier (NNC) [9] and linear regression classification (LRC) [10]. More recently, Brown et al. proposed a locality-regularized linear regression classification (LLRC) [11] method using a specific class as the neighbor of a training sample to classify and improve the accuracy of classification.

Although the above feature extraction and classification methods obtain great performances, each of them are designed independently. Therefore, they may be not fit each other perfectly. Using the rule of LRC, Chen et al. proposed reconstructive discriminant analysis (RDA) [12]. In 2018, Locality-regularized linear regression discriminant analysis (LLRDA) [13] deriving from LLRC was proposed to extract features. LLRDA ameliorates the LLRC by performing intra-class and inter-class scatter in the feature subspace, which brings more appropriate features for LLRC. However, in the feature subspace, LLRDA measures the reconstruction error utilizing L2 norm, which causes the strong sensitiveness to illumination changes and outliers. To alleviate the deficiency of L2 norm based methods, many algorithms basing on schatten-p norm have been developed. To improve the robustness to illumination changes and outliers, two-dimensional principal component analysis based on schatten-p norm (2DPCA-SP) [14] was presented using shatten-p norm to measure the reconstruction error. Incorporating the discriminant analysis and schatten-p norm to extract discriminative and robust features, two-dimensional discriminant analysis based on schatten-p norm (2DDA-SP) [15] was proposed. In 2018, Shi et al. proposed robust principal component analysis via optimal mean by joint 2, 1 and schatten p-norms minimization (RPOM) [16] imposing an schatten-p norm based regularized term to suppress the singular values of reconstructed data. Motivated by the above methods, we propose an LLRC based feature extraction method named schatten-p Norm based linear regression discriminant analysis (SPLRDA) utilizing schatten-p norm to improve the robustness to illumination changes. The main advantages of out algorithm are listed below: (1) Features are directly extracted from matrix rather than vectors reshaped from original image; (2) A specific class is assumed to be the neighborhood of a training sample instead of selecting from all samples when calculating the reconstruction vector β; (3) Discriminant analysis is incorporated to obtain discriminative features; (4) In the feature subspace, we measure the similarity distances by schatten-p norm whose parameter p is adjustable, which is more robust to illumination changes and outliers.

The rest parts of this paper are organized as follows. Sect. 2 briefly reviews the background knowledge of LRC and LLRC. The presented SPLRDA method is introduced in Sect. 3. The experimental results and analysis are arranged in Sect. 4. Finally, Sect. 5 concludes this paper.

2 Related Work

Suppose $X = \left[ {x_{1} ,\,x_{2} , \ldots ,\,x_{n} } \right]$ be a set of n training images of $C$ classes. Given the number of images in $i$th class is $n_{i}$, therefore, we have $\sum\nolimits_{i = 1}^{C} {n_{i} } = n$. $x_{i}$ denotes the $i$th reshaped image whose dimension $N$ is the product of the row and column numbers of original $i$th image. In this section, LRC and LLRC are reviewed briefly.

2.1 LRC

LRC [10] is based on the assumption that a sample can be represented as a linear combination of samples from same class. The task of LRC is finding which class the testing sample $y$ belongs to. Let $y$ be a test sample from the $i$th class, then it can be reconstructed approximately by:

$$ y = X_{i} \beta_{i} $$

(1)

where $\beta_{i} \, \in \,R^{{n_{i} \times 1}}$ is the reconstruction coefficient vector with respect to training image set of class $i$. $\beta_{i}$ is calculated by least square estimation (LSE) method as:

$$ \beta_{i} = \left( {X_{i}^{T} X_{i} } \right)^{ - 1} X_{i}^{T} y $$

(2)

Utilizing the estimated $\beta_{i}$, $y$ can be reconstructed as:

$$ \hat{y}_{i} = X_{i} \left( {X_{i}^{T} X_{i} } \right)^{ - 1} X_{i}^{T} y $$

(3)

Since $\hat{y}_{i}$ should approximate to $y$, the reconstruction error based on Euclidean norm is defined as:

$$ \begin{aligned} l\left( y \right) & = \mathop {\hbox{min} }\limits_{i} \left\| {y - \hat{y}_{i} } \right\|^{2} \\ & { = }\mathop {\hbox{min} }\limits_{i} \left\| {y - X_{i} \left( {X_{i}^{T} X_{i} } \right)^{ - 1} X_{i}^{T} y} \right\|^{2} \\ \end{aligned} $$

(4)

where $l\left( y \right)$ represents the class label of $y$.

2.2 LLRC

Different from LRC, LLRC [11] pays more attention to the local linearity of each sample and considers it to be more important than global linearity. Therefore, images from a specific class instead of all samples are supposed to be the neighborhood of a image sample based on this principle, Brown et al. presented an constraint of locality regularization on LRC by sorely involving $k$ closest images to the query image based on Euclidean distance measure.

The $k$ nearest neighbors set of testing sample $y$ in class $i$ is denoted by $\tilde{X}_{i} = \left[ {x_{i1} ,\,x_{i2} , \ldots ,\,x_{ik} } \right]\, \in \,R^{N \times k}$. Similar to the LRC, the label of $y$ is computed by minimizing the reconstruction error as below:

$$ l\left( y \right) = \mathop {\hbox{min} }\limits_{i} \left\| {y - \tilde{X}_{i} \left( {\tilde{X}_{i}^{T} \tilde{X}_{i} } \right)^{ - 1} \tilde{X}_{i}^{T} y} \right\|^{2} $$

(5)

3 Our Method

3.1 Problem Formulation

Suppose $x_{i}^{j} \, \in \,R^{a \times b}$ be the $j$th training sample of $i$th class, then its intra-class and inter-class reconstruction error are defined respectively as:

$$ \sum\limits_{i,j} {e_{i}^{j} } = \sum\limits_{i,j} {\left\| {x_{i}^{j} - \tilde{X}_{i}^{j} \tilde{\beta }_{i}^{j} } \right\|}_{sp}^{p} $$

(6)

$$ \sum\limits_{i,j,m} {e_{im}^{j} } = \sum\limits_{i,j,m} {\left\| {x_{i}^{j} - \tilde{X}_{im}^{j} \tilde{\beta }_{im}^{j} } \right\|}_{sp}^{p} $$

(7)

where $\tilde{X}_{i}^{j}$ and $\tilde{X}_{im}^{j}$ denote the k nearest neighbors set of $x_{i}^{j}$ in class $i$ and class m respectively. Class $m$ is one of the K nearest heterogeneous subspaces of $x_{i}^{j}$. The intra-class scatter characterizes the compactness of each training samples class, while the inter-class scatter describes the separability between different classes. $\left\| \bullet \right\|_{sp}$ denotes the schatten-p norm. Since we know that the singular value decomposition of x is defined as:

(8)

The schatten-p norm can be represented by [15]:

$$ \left\| x \right\|_{sp} \,=\, \left( {\sum\limits_{i = 1}^{\hbox{min} (m,n)} {\sigma_{i}^{p} } } \right)^{{\frac{1}{p}}} = \left[ {Tr\left( {xx^{T} } \right)^{{\frac{p}{2}}} } \right]^{{\frac{1}{p}}} $$

(9)

where $\sigma_{i}$ is the $i$th singular value of $x$. If the parameter $p$ was set to be 1, the schatten-p norm becomes the nuclear norm, which is famous for its capability for solving illumination changes. In the experiments, we can adjust $p$ to the value that attains best performance for face recognition. Suppose the optimal projection matrix be denoted by $A\, \in \,R^{b \times s} \left( {s\, < \,b} \right)$. In the feature subspace, the corresponding data can be replaced by:

$$ y_{i}^{j} = x_{i}^{j} A $$

(10a)

$$ Y_{i}^{j} = \left[ {\tilde{X}_{i}^{j\left( 1 \right)} A,\,\tilde{X}_{i}^{j\left( 2 \right)} A, \ldots ,\,\tilde{X}_{i}^{j\left( k \right)} A} \right] $$

(10b)

$$ Y_{im}^{j} = \left[ {\tilde{X}_{im}^{j\left( 1 \right)} A,\,\tilde{X}_{im}^{j\left( 2 \right)} A, \ldots ,\,\tilde{X}_{im}^{j\left( k \right)} A} \right] $$

(10c)

where $y_{i}^{j} \, \in \,R^{a \times s}$, $Y_{i}^{j} \, \in \,R^{a \times ks}$ and $Y_{im}^{j} \, \in \,R^{a \times ks}$. Therefore, to find an optimal projection matrix which projects the original data into feature subspace, the function performed in the feature subspace should be maximized:

$$ f\left( A \right) = \left[ {\sum\limits_{i,j,m} {\left\| {y_{i}^{j} - Y_{im}^{j} \tilde{\beta }_{im}^{j} } \right\|_{sp}^{p} } \, - \,\sum\limits_{i,j} {\left\| {y_{i}^{j} - Y_{i}^{j} \tilde{\beta }_{i}^{j} } \right\|_{sp}^{p} } } \right]\quad {\text{s}} . {\text{t}} .\;A^{T} A = I_{s} $$

(11)

3.2 Problem Solving

As analyzed in the last subsection, the optimization problem can be formulated and simplified as:

$$ \begin{aligned} \mathop {\arg \hbox{max} }\limits_{A} f\left( A \right) & = \mathop {\arg \hbox{max} }\limits_{A} \left[ {\sum\limits_{i,j,m} {\left\| {y_{i}^{j} - Y_{im}^{j} \tilde{\beta }_{im}^{j} } \right\|_{sp}^{p} } - \sum\limits_{i,j} {\left\| {y_{i}^{j} - Y_{i}^{j} \tilde{\beta }_{i}^{j} } \right\|_{sp}^{p} } } \right] \\ & = \mathop {\arg \hbox{max} }\limits_{A} \left[ {\sum\limits_{i,j,m} {\left\| {x_{i}^{j} A - \tilde{X}_{im}^{j} \tilde{\beta }_{im}^{j} A} \right\|} - \sum\limits_{i,j} {\left\| {x_{i}^{j} A - \tilde{X}_{i}^{j} \tilde{\beta }_{i}^{j} A} \right\|_{sp}^{p} } } \right] \\ & = \mathop {\arg \hbox{max} }\limits_{A} \left\{ {\sum\limits_{i,j,m} {Tr\left[ {B_{ij}^{m} AA^{T} \left( {B_{ij}^{m} } \right)^{T} } \right]^{{\frac{p}{2}}} } - \sum\limits_{i,j} {Tr\left[ {W_{ij} AA^{T} \left( {W_{ij} } \right)^{T} } \right]^{{\frac{p}{2}}} } } \right\} \\ & \, \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad s.t. \, A^{T} A = I_{s} \\ \end{aligned} $$

(12)

where $B_{ij}^{m} = x_{i}^{j} - \tilde{X}_{im}^{j} \tilde{\beta }_{im}^{j}$ and $W_{ij} = x_{i}^{j} - \tilde{X}_{i}^{j} \tilde{\beta }_{i}^{j}$. Based on the objective function, the Lagrangian function can be built as:

$$ L\left( {A,\,\Lambda } \right) = \sum\limits_{i,j,m} {Tr\left[ {B_{ij}^{m} AA^{T} \left( {B_{ij}^{m} } \right)^{T} } \right]^{{\frac{p}{2}}} } - \sum\limits_{i,j} {Tr\left[ {W_{ij} AA^{T} \left( {W_{ij} } \right)^{T} } \right]^{{\frac{p}{2}}} } - Tr\left[ {\Lambda \left( {A^{T} A - I_{s} } \right)} \right] $$

(13)

Taking the derivative of $L$ with respect to $A$, we have:

$$ \frac{\partial L}{\partial A} = 2\sum\limits_{i,j,m} {\left( {B_{ij}^{m} } \right)^{T} D_{ij}^{m} } B_{ij}^{m} A - 2\sum\limits_{i,j} {\left( {W_{ij} } \right)^{T} H_{ij} } W_{ij} A - 2\Lambda A $$

(14)

where $D_{ij}^{m} = \frac{p}{2}\left[ {B_{ij}^{m} AA^{T} \left( {B_{ij}^{m} } \right)^{T} } \right]^{{\frac{p - 2}{2}}}$ and $H_{ij} = \frac{p}{2}\left[ {W_{ij} AA^{T} \left( {W_{ij} } \right)^{T} } \right]^{{\frac{p - 2}{2}}}$. $\Lambda \, \in \,R^{s \times s}$ is the symmetric Lagrangian multiplier matrix. To look for the maximum point of objective function, (14) is set to be zero, then the Eq. (14) is changed to:

$$ \left( {S_{b} - S_{w} } \right)A = A\Lambda $$

(15)

where $S_{b} = \sum\nolimits_{i,j,m} {\left( {B_{ij}^{m} } \right)}^{T} D_{ij}^{m} B_{ij}^{m}$ and $S_{w} = \sum\nolimits_{i,j} {\left( {W_{ij} } \right)}^{T} H_{ij} W_{ij}$. Both $S_{b}$ and $S_{w}$ rely on $A$. If $\left( {S_{b} - S_{w} } \right)$ is a known constant matrix and considering the orthogonal constraint $A^{T} A = I_{s}$, the optimal projection matrix $A$ can be calculated by solving the eigen value decomposition problem as below:

$$ A^{T} \left( {S_{b} - S_{w} } \right)A =\Lambda $$

(16)

According to (15), since $\left( {S_{b} - S_{w} } \right)$ is symmetric and each element in the diagonal of $\Lambda$ is an eigen value of $\left( {S_{b} - S_{w} } \right)$, $A$ is formed by the $s$ eigen vectors corresponding to $s$ largest eigen values of $\left( {S_{b} - S_{w} } \right)$. Since the objective function is bounded by $A^{T} A = I_{s}$ and it increases after each iteration, the convergence of this algorithm can be realized. Based on these analyses, we propose an iterative algorithm to obtain the optimal projection matrix. The algorithm is concluded in Algorithm 1.

4 Experiments

In this section, extensive experiments are conducted on ORL [17] and CMU PIE [18] databases to testify the effectiveness of our method in the condition that p = 1/4, 1/2, 3/4 respectively. Meanwhile, we compare SPLRDA with other state-of-art feature extraction methods such as PCA [1], LDA [2], LPP [8] and RDA [12]. Different classifiers are adopted to measure the performance of each method. All the algorithms have been run for five times independently to obtain average recognition rates. We only exhibit the highest results for comparison and analysis.

4.1 Experiments on ORL Database

The ORL face database includes 400 face images belonging to 40 individuals. Each person has 10 images distinct from view direction, facial expression (mouth opened or closed, laughing or calm), facial details (with or without glasses) and illumination. Each image has been normalized to the size of 112 × 92 with 256 gray levels.

Ten samples of one individual are displayed in Fig. 1. In our experiments, we cropped each image manually and resized it to 32 × 32 pixels. l (l = 4, 5) images per person are randomly selected for training while the remainders for testing. Note that k ranges from 1 to l − 1 and K ranges from 1 to C − 1. To observe the effect of k, K is fixed to $\left\lfloor {C/2} \right\rfloor + 1$ and k is varied from 1 to l − 1.

Fig. 1.

Ten samples of one individual in ORL database

Figure 2 shows the recognition rates of SPLRDA plus LLRC with varied k. The results indicate that out method achieves best performances when k = 2 and k = 3 associating with l = 5 and l = 4, which demonstrates the effectiveness of exploiting neighborhood structure. Therefore, to detect the effect of K, we fixed k to 3 and 2 corresponding to l = 4 and l = 5 respectively, and varied K from 3 to C − 1 in increments of 4. Figure 3 displays the recognition rates of SPLRDA plus LLRC with varied K. From Fig. 3, it can be seen that parameter K does affect the performance of our method and they all gain best recognition rates when K achieves highest value. Average recognition rates of all methods are displayed in Table 1. In the experiments, we tested these feature extraction methods under three different classifiers. Experimental results verify that classifier matters the performance of face recognition and our method fits LLRC better than other related methods. From Table 1, we can see that when l = 4 and l = 5, SPLRDA achieves best recognition rates in the condition that p = 1/4, which demonstrates the effectiveness of our method.

Fig. 2.

Recognition rates of SPLRDA plus LLRC with varied k

Fig. 3.

Recognition rates of SPLRDA plus LLRC with varied K

Table 1. Recognition accuracy of each method in ORL database

4.2 Experiments on CMU PIE Database

The CMU PIE face database contains 68 different individuals with more than 40,000 face images. Each image of an individual differs from others in poses, illumination and expression. This database is stipulated that 4 different expressions, 43 different illumination changes and 13 different poses should be satisfied for images of an individual. This database includes five near-frontal poses (C05, C07, C09, C27 and C29). We choose C05 subset for our experiments. The subset contains 1632 images of 68 individuals. In the experiments, all the images were cropped and resized to 64 × 64 pixels. Figure 4 shows ten samples of one individual in CMU PIE database.

Fig. 4.

Ten samples of one individual in CMU PIE database

In the experiments, we randomly choose l (6, 7, 8) images per person for training and the remainders for testing. Table 2 reports the recognition rates with different classifiers. From Table 2, some observations are concluded as follow: (1) unsupervised methods (PCA and LPP) perform worse than other supervised methods because labeled information are not be exploited; (2) Although RDA plus LRC gains high recognition rate, it performs worse than SPLRDA plus LLRC since neighborhood structure of data is not utilized; (3) SPLRDA achieves better performance than other methods, which verifies that our method is better than other related methods.

Table 2. Recognition accuracy of each method in CMU PIE database

5 Conclusion

In this paper, a novel feature extraction method named schatten-p norm based linear regression discriminant analysis (SPLRDA) has been proposed. It not only incorporates schatten-p norm reducing the interference of illumination changes but also exploits neighborhood structure, which fits LLRC well. Experiments has demonstrated the reliability and effectiveness of our method. It performs better than other related methods.