1 Introduction

Ball screw-based linear motion systems are widely used in precision motion tool applications [1]. The performance of the servo controller used in linear motion systems depends on its response to the machine dynamics. The PID control algorithm is employed in most industrial controllers due to its simple, efficient and easy implementation. It can use proportional action to correct errors, integral action to eliminate steady state offsets, and derivative action to anticipate the future [2]. The PID-based servo controller used in linear motion systems should be optimally tuned to respond to the positional errors due to feed screw pitch and torsion errors [3], temperature induced errors [4, 5], and encoder measurement errors [6]. The traditional PID tuning algorithms [7, 8] use complex equations which require domain expertise to design an optimal controller for motion control applications. Also, since these algorithms focus on specific operating characteristics of the system, they will not respond appropriately when those values change. Hence, the tuning of PID controllers using meta-heuristic optimization algorithms has been proposed by researchers in recent decades [9]. The optimization algorithms used in PID controllers search for optimal tuning parameters. The objective function is defined in the optimization algorithms to meet the specific performance criterion [10].

Kitsios and Pimenides designed a PID controller for a servo motor using genetic algorithm (GA) techniques. Since the integral squared error (ISE) function weights errors equally independent of time which results in a long settling time, the integral time squared error (ITSE) is used as performance criteria to improve the step response of a controller [11]. Mirzal et al. compared the results of objective functions of integral time absolute error (ITAE), integral absolute error (IAE), mean squared error (MSE), ITSE, and ISE, in tuning GA based PID controllers [12]. Mohd Sazli et al. implemented a PID controller using GA and a Differential Evolution (DE) algorithm by assigning MSE and IAE as their objective functions [13]. Renato A. Krohling and Joost P. Rey designed a GA based optimal PID algorithm which uses ITSE as its performance index [14]. A GA based optimized shaped permanent magnet model is used for improving the performance parameters of the permanent magnet Vernier machine [15, 16]. Anil kumar and Giriraj kumar used MSE, IAE, ITAE, and ISE as their error minimizing performance indices for tuning a PID controller using the whale optimization algorithm [17]. WaelNaji et al. proposed GA based optimization of a PID controller for a multi variable process in which ITAE is chosen as a main performance criterion due to its shorter settling time and overshoot [18].

Since the classical error minimizing functions such as ITAE, ISE, IAE, and MSE are insufficient for enhancing optimal tuning of PID parameters, the time domain parameters such as settling time (Ts), rise time (Tr), steady state error (Ess) and percentage of overshoot (M) are included in the objective function. The weights are selected for the above criteria based on the performance requirements of the user [19]. Latha et al. proposed a PSO based multi-objective algorithm for tuning the PID controller of stable and unstable systems. The multi-objective function is formulated using a weighted sum of ISE and time domain constants such as overshoot Mp and settling time ts. The weights for the above three constraints are selected as w1 = w2 = 1 and w3 = 0.5 [20]. Arturo Y et al. proposed a GA based multi-objective function which uses a weighted sum of ISE, MSE, and peak overshoot value for tuning servo systems. The weights for the above constraints are selected as w1 = w2 = 0.3and w3 = 0.4 [21]. Andrey et al. proposed a GA based multi objective optimization technique which uses two objective functions independently to provide better reference tracking and disturbance rejection [22]. A GA-based optimized model is used for improving the performance parameters of axial flux permanent magnet machine (AFPM) [23, 24]. Oguzhan Karahan proposed a multi-objective cost function that includes four performance parameters such as steady state error, overshoot, settling time, and rise time for optimal tuning of PID parameters using the cuckoo search algorithm [25]. M. H. A. Hassan used a modified ITAE function for tuning the PID parameters of a brushed dc motor [26]. Ayman A.aly proposed a multi-objective function based on ITAE, peak overshoot, and steady state error, in which the weights for the objective function are selected randomly by a user [27].

According to the research papers, researchers choose the error minimizing functions ISE, IAE, MSE, ITSE, and ITAE for tuning the PID controller depending on the nature of the applications. Few scholars use a weighted sum function that combines any one or more of the error minimization functions with performance criteria functions (Tr, Ts, Mp) to achieve optimal performance results. But, the weights for these functions are selected based on user requirements or through an error and trial approach.

In this paper, a new multi-objective function that includes ITAE and time domain parameters such as overshoot, rise time, and settling time is used for optimal tuning of servo controller parameters. The weights for the above performance criteria functions are obtained from MOGA pareto optimal solutions. The novel multi-objective function is evaluated with the model of a servo based linear motion system using PSO, WOA, BAT, and AO algorithms. The obtained results using the proposed objective function show superior results to those obtained using conventional error minimizing functions such as ITAE and typical PID and FOPID controller algorithms.

2 Mathematical Modeling of Linear Motion System

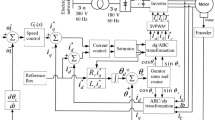
Figure 1 shows the schematic diagram of a linear motion system that consists of a DC servo motor and ball screw assembly. The rotary motion provided by the DC servo motor is converted into a linear motion using the ball screw assembly. Ball screws are often stated in terms of lead, which is the linear movement the nut makes per one screw revolution.

Fig. 1
figure 1

Schematic diagram of linear motion system

Full size image

The transfer function for the linear motion system is derived using the equations of the DC servo motor and ball screw assembly [28]. The electrical circuit of the DC servo motor is given in Fig. 2. The transfer function of a DC servo motor [29] is given in Eq. (1).

$$\frac{\theta \left( s \right)}{{V_{a} \left( s \right)}} = \frac{{k_{1} }}{{\left[ {J_{m} s^{2} + B_{m} s} \right]\left[ {L_{a} s + R_{a} } \right] + k_{t} k_{b} s}}$$
(1)

where θ(s) is angular position, Jm, Bm are mechanical constants, Ra, La are armature resistance and Inductance, k1, kb is Torque and emf constants

Fig. 2
figure 2

Electrical equivalent circuit of DC servo motor

Full size image

The mechanical constants Jm and Bm must be specified to analyze the DC servo motor coupled to the ball screw assembly. The mechanical constants Jm and Bm is calculated using the gear box relationship, N1and N2, the inertia JL and damping BL of the load, as given in Eq. (2)

$$J_{m} = J_{a} + J_{L} \left( {\frac{{{\text{N}}_{1} }}{{{\text{N}}_{2} }}} \right)^{2} ; \quad B_{m} = B_{a} + B_{L} \left( {\frac{{{\text{N}}_{1} }}{{{\text{N}}_{2} }}} \right)^{2}$$
(2)

The transfer function of linear motion system is given by

$$G\left( s \right) = \frac{{k_{1} }}{{\left[ {P[J_{m} s^{2} + B_{m} s} \right]\left[ {L_{a} s + R_{a} } \right] + k_{1} k_{b} s]}}$$
(3)

where P = 2π/L, L represents the lead of the screw.

The specifications of the linear motion control system [30] consisting of a DC servo motor and ball screw assembly are given in Table1. Substituting the parameter values of the linear motion system into Eq. 3, gives the transfer function as

$$G\left( s \right) = \frac{232600}{{s^{3} + 18.44s^{2} + 30.37s}}$$
(4)
Table 1 Parameters of linear motion control system
Full size table

3 MOGA Based Objective Function

The objective functions used for tuning PID controllers can be classified into integral and performance-index based functions. The integral functions that are used to tune PID controllers are as follows:

$$IAE = \int\limits_{0}^{t} {\left| {e\left( t \right)} \right|{\text{d}}t~}$$
(5)
$$ITAE = \int\limits_{0}^{t} {t\left| {e\left( t \right)} \right|{\text{d}}t}$$
(6)
$$ISE = \int\limits_{0}^{t} {e^{2} \left( t \right){\text{d}}t}$$
(7)
$$MSE = \frac{1}{t}\int\limits_{0}^{t} {\left( {e\left( t \right)} \right)^{2} {\text{d}}t}$$
(8)

where e (t) is the system error, which is the difference between the set point and actual value.

The maximum overshoot, steady state error, rise time and settling time are the performance based indices functions used to tune the PID controller.

$${\text{Minimize }}\left( {{\text{F1}},{\text{ F2}},{\text{ F3}},{\text{ F4}}} \right)$$
(9)
$${\text{Minimize }}\left( {{\text{ITAE}},{\text{ T}}_{{\text{r}}} ,{\text{T}}_{{\text{s}}} ,{\text{ M}}_{{\text{p}}} } \right)$$
(10)

Equation (9) refers four objective functions of MOGA ie. F1, F2, F3, F4, where function F1 represents the integral based error minimizing function (ITAE) and the function F2, F3, F4 are rise time, settling time and peak overshoot respectively.

The MOGA algorithm generates a set of pareto optimal solutions denoted by Po = \(\left\{ {\overrightarrow {{k_{po1} ,}} \overrightarrow {{k_{po2} ,}} \ldots .,\overrightarrow {{k_{pon} ,}} } \right\}\) based on the above objective functions for optimal tuning of the PID controller. Given the objective function \(\overrightarrow { f\left( k \right)} = \left[ {f_{1 } (\overrightarrow {k)} ,f_{2 } (\overrightarrow {k)} , \ldots ,f_{m} (\overrightarrow {k)} } \right]\), pareto front generated by MOGA is given by:

$$P_{f} = \left\{ {\begin{array}{*{20}c} {f_{1 } \left( {\overrightarrow {{k_{po1} }} } \right)} & {f_{2 } \left( {\overrightarrow {{k_{po1} }} } \right)} & \cdots & {f_{m } \left( {\overrightarrow {{k_{po1} }} } \right)} \\ {f_{1 } \left( {\overrightarrow {{k_{po2} }} } \right)} & {f_{2 } \left( {\overrightarrow {{k_{po2} }} } \right)} & \cdots & {f_{m } \left( {\overrightarrow {{k_{po2} }} } \right)} \\ {f_{1 } \left( {\overrightarrow {{k_{pon} }} } \right)} & {f_{2 } \left( {\overrightarrow {{k_{pon} }} } \right)} & \cdots & {f_{m} \left( {\overrightarrow {{k_{pon} }} } \right)} \\ \end{array} } \right\}$$
(11)

The pareto front generated by a MOGA is converted into a single weighted sum of objective functions given by:

$$J\left( {\vec{k}} \right) = \mathop \sum \limits_{i = 1}^{m} w_{i} f_{i} \left( {\vec{k}} \right)$$
(12)

where wi are the weights of the objective functions that give the relative importance of the individual objective functions on the overall multi-objective function. The weights of the individual objective functions are calculated using the following relation:

$$w_{i} = \frac{1}{{\mu_{i } \times \mathop \sum \nolimits_{j = 1}^{l} \frac{1}{{\mu_{j} }}}}$$
(13)

where µi and µj are the mean values of the pareto solutions obtained using individual objective functions.

Figure 3 is the block diagram of proposed MOGA based PID tuning of linear motion system. The proposed objective function is formulated by the weighted sum of the objective function given by:

$$J\left( X \right) = w_{IT} J_{IT} + w_{r} J_{r} + w_{s} J_{s} + w_{po} J_{po}$$
(14)

where wIT, wr, ws, wpo are the weights for ITAE, rise time, settling time, and peak overshoot calculated using pareto optimal values obtained using the MOGA algorithm.

Fig. 3
figure 3

Block diagram of MOGA based PID Tuning

Full size image

4 Servo PID Tuning Algorithms

4.1 PSO Servo-PID Tuning

Particle Swarm Optimization (PSO) is a popular stochastic optimization approach that is based on social behavior. In PSO, the particle adjusts its movement in order to achieve its individual best position as well as the global best position achieved by any member of its neighborhood [31]. The pseudo code for PSO algorithm is given below.

figure c

In each iteration, the particle position and velocity are updated using the following equations:

$$V_{i}^{k + 1} = wV_{i}^{k + 1} + C_{1} r_{i1}^{k} \left( {P_{i}^{k} - X_{i}^{k} } \right) + C_{2} r_{i2}^{k} \left( {P_{g}^{k} - X_{i}^{k} } \right)$$
(15)
$$X_{i}^{k + 1} = X_{i}^{k} + V_{i}^{k + 1}$$
(16)

where i is the swarm size, w is the inertia weight, ri1 and ri2 are random numbers uniformly distributed within the range of 0 to 1, and c1 and c2 are the cognitive and social parameters, respectively. Figure 4 is the pseudo code for the PSO algorithm. At each iteration, the PSO algorithm updates the position and velocity of each particle based on the given objective function.

Fig. 4
figure 4

PID tuning of a linear motion system using a Matlab PID auto-tuner b FOPID Controller

Full size image

4.2 WOA Based Servo PID Tuning

In the WOA optimization technique, the behavior of humpback whales attacking prey using a method of prey encircling, bubble-net strategy and search for prey is mathematically modelled. The humpback whales travel in a shrinking circle around the prey while also swimming along a spiral-shaped path [32]. The behavior of encircling the prey is modelled by the equation:

$$\vec{D} = \left| {\vec{C}.\vec{X}*\left( t \right) - \vec{X}\left( t \right)} \right|$$
(17)
$$\vec{X}\left( {t + 1} \right) = \vec{X}*\left( t \right) - \vec{A}.\vec{D}$$
(18)

where X* is the updated best position vector, \(\overrightarrow {X }\) is the current position vector and \(\vec{A},\vec{C}\) are coefficient vectors calculated as follows:

$$\vec{A} = 2\vec{a}.\vec{r} - \vec{a}$$
$$\vec{c} = 2.\vec{r}$$

where \(\vec{r}\) is a random vector in [0,1], \(\vec{a}\) is decreased linearly from 2 to 0 during the process of iterations.

The behavior of bubble net attacking method is modelled as:

$$\vec{X}\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {\vec{X}*\left( t \right) - \overrightarrow {{A~}} .\vec{D}~} \hfill & {if\;~p < 0.5} \hfill \\ {\overrightarrow {{D'}} ~.e^{{bl}} .\cos \left( {2\pi l} \right) + \vec{X}*\left( t \right)} \hfill & {~if~\;p \ge 0.5} \hfill \\ \end{array} } \right.$$
(19)

where p is a random number in [0,1], b is a constant representing the shape of the logarithmic spiral, l is a random number in [− 1,1].

The behavior of random prey search is modelled as follows:

$$\vec{D} = \left| {\vec{C}.\overrightarrow {{X_{rand} }} - \vec{X}} \right|$$
(20)
$$\vec{X}\left( {t + 1} \right) = \overrightarrow {{X_{rand} }} - \vec{A}.\vec{D}$$
(21)

The pseudo code for WOA algorithm is given below:

figure d

4.3 Bat Based Servo PID Tuning

The Bat algorithm uses echolocation characteristics of micro bats to find prey. Bats fly at a random velocity vi at point xi with a fixed frequency fi, varying its wavelength l, and loudness A0 in search of prey. They may automatically adjust the wavelength (or frequency) of their generated pulses as well as the rate of pulse emission r in the range [0, 1] depending on the proximity of their target [33]. Each bat's frequency, velocity, and position are updated as follows:

$$f_{i} = f_{\min } + \left( {f_{\max } - f_{\min } } \right)\beta$$
(22)
$$v_{i} \left( t \right) = v_{i} \left( {t - 1} \right) + \left( {x_{i} \left( t \right) - x*} \right)$$
(23)
$$x_{i} \left( t \right) = x_{i} \left( {t - 1} \right) + v_{i} \left( t \right)$$
(24)

where β is a random number in [0, 1], x* is the current global best position obtained by comparing the fitness values of all the n bats. The pseudo code for the BAT algorithm is given below:

figure e

4.4 Aquila Based Servo PID Tuning

The Aquila optimizer is a newly designed algorithm based on the Aquila's prey-catching behavior. The Aquila catches its prey using the four methods listed below. 1) By completing a high soar with a vertical stoop, it recognizes the prey area and chooses the optimum hunting area (Enlarged exploration) 2) When a high soar locates a prey spot, the Aquila circles over it, prepares the land, and then attacks, a maneuver known as Contour flight with short glide attack(Narrowed exploration) 3) Once the prey location has been precisely detected, the Aquila descends vertically with a preliminary attack to detect the prey reaction, a method known as "low flying with slow descent attack” (Enlarged exploitation) 4) When the Aquila gets close enough to the target, it uses stochastic motions dubbed "walking and grabbing" to attack the prey on the ground [34]. These four methods can be mathematically modelled as given below:

The enlarged exploration is given by the equation:

$$X_{1} \left( {t + 1} \right) = X_{best} \left( t \right) \times \left( {1 - \frac{t}{T}} \right) + \left( {X_{M} \left( t \right) - X_{best} \left( t \right)*rand} \right)$$
(25)

where Xbest (t) is the best position obtained until the tth iteration, the term (1 − t/T) is used to control the expanded exploration, and XM(t) is the mean position value of the current solutions at the tth iteration.

The narrowed exploration is given by the equation:

$$X_{2} \left( {t + 1} \right) = X_{best} \left( t \right) \times Levy\left( D \right) + X_{R} \left( t \right) + \left( {y - x} \right)*rand$$
(26)

where X2 (t + 1) is the position of the next iteration of t, D is the dimension space, XR(t) is the random position taken in the range of [1N] at the ith iteration and Levy(D) is the levy flight distribution function which is given by:

$${\text{Levy}}\left( {\text{D}} \right) = s \times \frac{\mu \times \sigma }{{\left| v \right|^{{\frac{1}{\beta }}} }}$$
(27)

where s is a constant value assigned as 0.01, u and v are random numbers between 0 and 1 and σ is calculated using the equation:

$$\sigma = \left( {\frac{{\left( {1 + \beta } \right) \times \sin e\left( {\frac{\pi \beta }{2}} \right)}}{{\left( {\frac{1 + \beta }{2}} \right) \times \beta \times 2^{{\left( {\frac{\beta - 1}{2}} \right)}} }}} \right)$$
(28)

where β is a fixed constant value of 1.8.

In Eq. (26), y and x are used to configure the spiral shape in the search, which are calculated using the equation:

$$y = r \times \cos \left( \theta \right)$$
(29)
$$x = r \times \sin \left( \theta \right)$$
(30)

where,

$$r = r_{1} + U \times D_{1}$$
(31)
$$\theta = - w \times D_{1} + \theta_{1}$$
(32)
$$\theta_{1} = \frac{3 \times \pi }{2}$$
(33)

The enlarged exploitation is modelled using the equation:

$$X_{3} \left( {t + 1} \right) = \left( {X_{best} \left( t \right) - X_{M} \left( t \right)} \right) \times \alpha - rand + \left( {\left( {UB - LB} \right) \times rand + LB} \right) \times \delta$$
(34)

where X3 (t + 1) is the position obtained using the third search method for the next iteration of t, Xbest (t) is the best obtained position until ith iteration, XM (t) is the mean value of the current position at tth iteration, rand refers to a random value in [0,1], α and δ are the exploitation adjustment parameters kept at small values.LB and UB are the lower and upper bounds of the PID tuning parameters.

The narrowed exploitation is given by the equation:

$${\text{X}}_{4} \left( {{\text{t}} + 1} \right) = {\text{QF}} \times {\text{X}}_{{{\text{best}}}} \left( {\text{t}} \right) - \left( {{\text{G}}_{1} \times {\text{X}}\left( {\text{t}} \right) \times {\text{rand}}} \right) - {\text{G}}_{2} \times {\text{Levy}}\left( {\text{D}} \right) + {\text{rand}} \times {\text{G}}_{1}$$
(35)

where X4(t + 1) is the position obtained using the fourth search method for the next iteration of t, QF refers to the quality function at tth iteration given by the equation:

$$QF\left( t \right) = t^{{\frac{2 \times rand() - 1}{{\left( {\left( {1 - T} \right)^{2} } \right)}}}}$$
(36)

G1 is the different motions used by Aquila to track the prey given by the equation:

$${\text{G}}_{1} = 2 \times {\text{rand}}() - 1$$
(37)

G2 refers to the flight slope of Aquila having values decreasing from 2 to 0, which is given by the equation:

$$G_{2} = 2 \times \left( {1 - \frac{t}{T}} \right)$$
(38)

The pseudo code for AO algorithm is given below.

figure f

5 Results and Discussion

The linear motion system model given in Eq. (3) is initially tuned using the PID auto tuner function available in matlab. The PID auto-tuner function which includes the required robustness in the model provides high peak overshoot and settling time as shown in Fig. 4a and Table 2. The model is then tuned using the FOPID controller using the ninteger tool box in matlab. The five parameters are tuned to enhance the performance against uncertainties in system model, high frequency noise and load disturbances. The five parameters are tuned as follows: kp = 0.00048, Ki = 0.00017, KD = 0.00021, λ = − 0.5, µ = 0.05. The FOPID algorithm gives better performance parameters than the classical PID algorithm as shown in Fig. 8b and Table 2. The closed loop stability of the proposed model is verified using the bode plot for PID and FOPID controllers as shown in Fig. 5a and b.

Table 2 Tuning and performance parameters of PID and FOPID controller
Full size table
Fig. 5
figure 5

Bode plot of a linear motion system tuned using a PID controller b FOPID controller

Full size image

This transfer function given in Eq. (3) is used for optimal tuning of the Servo PID controller used in linear motion systems using a heuristic approach. In this work, a new objective function is presented based on the ITAE, rise time, settling time, and maximum overshoot. The weights for this proposed objective function are calculated using pareto optimal sets of the MOGA algorithm. The parameters used for tuning a linear motion system using the MOGA algorithm are given in Table 3. The MOGA algorithm generates forty-eight data sets of pareto optimal solutions of the PID parameters and their corresponding pareto front sets. The mean, contribution percentage, and weights of the pareto front sets are calculated as given in Table 4. The multi-objective function (J(X)) is formulated by combining four objective functions (ITAE, tr, ts, Mp) using the weighted sum function. The novel multi-objective function used for optimal servo PID tuning of the linear motion control system is given in Eq. (39).

$$J\left( X \right) = 0.8713*ITAE + 0.1162*t_{r} + 0.0054*t_{s} + 0.0071*M_{p}$$
(39)
Table 3 MO-GA Algorithm parameters for tuning linear motion control system
Full size table
Table 4 Objective function weight calculation using pareto front sets
Full size table

The new multi-objective function is tested using the PSO algorithm and its performance parameters are compared with conventional PID error minimizing objective functions. Figure 6. shows the convergence curves of various objective functions. The proposed function shows better convergence compared to the other conventional objective functions. The new cost function outperforms the error minimizing functions such as IAE, ISE, ITAE, and MSE in terms of peak overshoot, settling time, and steady state error, as shown in Table 5 and Fig. 7.The proposed multi-objective function is also tested using the most popular recently developed heuristic algorithms such as WOA, BAT, and AO. The heuristic algorithm parameters initialized for tuning the linear motion control system are shown in Table 6. The PID factors of the linear motion control system are tuned by the WOA technique using the most popular single objective function ITAE, and a proposed multi-objective function (J(X)). Table 7 shows the performance parameters for the WOA based servo PID tuning using two objective functions. The multi-objective function shows a large reduction in peak overshoot and steady state error with rise and settling time close to the single objective function as shown in Fig. 8.

Fig. 6
figure 6

PSO convergence curve for various objective functions

Full size image
Table 5 PSO based servo PID tuning of linear motion control system
Full size table
Fig. 7
figure 7

PSO step output of linear motion control system for various objective functions

Full size image
Table 6 Heuristic Algorithm parameters for tuning linear motion control system
Full size table
Table 7 WOA based servo PID tuning of linear motion control system
Full size table
Fig. 8
figure 8

WOA based step output of linear motion control system for objective functions ITAE and J(X)

Full size image

The BAT algorithm is used to tune the PID values of a linear motion system using a single objective function, ITAE and the proposed objective function, J(X). This algorithm shows a large improvement in peak overshoot and steady state error with respect to multi-objective function as shown in Table 8 and Fig. 9.

Table 8 BAT based servo PID tuning of linear motion control system
Full size table
Fig. 9
figure 9

BAT algorithm based step output of linear motion control system for objective functions ITAE and J(X)

Full size image

Finally, the proposed objective function (J(X)) is tested using the recently developed Aquila optimizer algorithm for a linear motion system, and the results are compared with the function ITAE. The function J(X) improves on the ITAE in peak overshoot, settling time and steady state error, and has a rise time similar to the ITAE as shown in Table 9 and Fig. 10.

Table 9 AO based servo PID tuning of linear motion control system
Full size table
Fig. 10
figure 10

AO based step output of linear motion control system for objective functions ITAE and J(X)

Full size image

Figure 11 and Table 10 shows the comparison results of step output of a linear motion system tuned by the optimization algorithm using error minimizing objective function ITAE. The PSO and AO algorithm provides better result in terms of peak overshoot percentage, while WOA and BAT shows improvement in terms of settling time.

Fig. 11
figure 11

Performance of optimization algorithm for objective function ITAE

Full size image
Table 10 Performance of optimization algorithm for servo PID tuning of linear motion control system using ITAE
Full size table

Figure 12 and Table 11 shows the comparison results of step output of a linear motion system tuned by the optimization algorithm using proposed multi-objective function J(X). The comparison of Table 10 and 11 reveal that the new function gives good optimal performance than single objective function and classical PID and FOPID controllers. The hardware validation of the proposed methodology can be done using the hardware set up shown in Fig. 13. It consists of a real time compact RIO (cRIO) FPGA controller, a NI-9502 servo drive module, a kollmorgen servo motor, and a Bosch Rexroth linear motion system. This hardware setup can be programmed in a LabVIEW environment using the LabVIEW soft motion module 18.0.

Fig. 12
figure 12

Effectiveness of optimization algorithm for multi-objective function, J(X)

Full size image
Table 11 Performance of optimization algorithm for servo PID tuning of linear motion control system using multi-objective function J(X)
Full size table
Fig. 13
figure 13

Hardware setup for validating propose methodology

Full size image

The PID interactive tuning panel of the servo position control program is tuned using the parameters predicted using the conventional PID controller and the novel cost function based soft tuning algorithms, and the validated results of the performance parameters are shown in Table 12. The unit step plot obtained for various tuning algorithms is shown in the Fig. 14a–f. From Fig. 14 and Table 12, it is concluded that the proposed PID tuning parameters using multi-objective based optimization algorithms provide better performance results for linear motion systems than the conventional PID control tuning algorithms. Table 13 shows the error comparison results of the simulation and the validation done for the linear motion system using the matlab and the LabVIEW tools.

Table 12 Comparison of the performance parameters with validation results
Full size table
Fig. 14
figure 14

Validation plots of the linear motion system for a Auto tuned PID controller b FOPID controller c PSO tuned PID d WOA tuned PID e BAT tuned PID f AO tuned PID

Full size image
Table 13 Error analysis results of simulation in matlab and validation in labview tool
Full size table

A small variation in validation results is observed compared to the simulation results due to the precision of the pid tuning parameters. Since the matlab model accepts the tuning parameters with more precision than the LabVIEW, the results obtained in simulation are more accurate than the validation. The error difference between simulation and validation for the PID auto tuner is found to be less, and steady state error is found to be better in validation.

The error difference in the FOPID controller is also found to be less in all performance parameters. The PSO algorithm provides higher peak overshoot and settling time than simulation and provides better rise time and steady state error in validation. The WOA algorithm provides better results, except for a small increase in peak overshoot. The performance results of the BAT algorithm are superior in all parameters. The error difference is less in the AO algorithm for peak overshoot and rise time and better in validation for settling time and steady state error. The validation results show that the proposed heuristic algorithm based tuning provides better results than conventional PID tuning.

6 Conclusion

The optimal servo PID control tuning is necessary in order to maintain the positional accuracy in linear motion control systems. The error minimizing functions such as IAE, ITAE, ITSE, ISE, and MSE used by the heuristic algorithms do not satisfy all the performance needs of a linear motion system. A new multi-objective function is presented based on the optimal choice of weights obtained using MOGA techniques for four conflicting objective functions (ITAE, rise time, settling time, maximum overshoot). The proposed function is tested for linear motion control systems using familiar heuristic algorithms such as PSO, WAO, BAT, and the recently developed Aquila optimizer, and the results are compared with the commonly used objective function ITAE. The simulation results show that the proposed objective function shows better performance results in terms of peak overshoot and steady state error compared to the ITAE and also produces results similar to the ITAE in terms of rise and settling time. The proposed algorithm validated in the LabVIEW environment also shows that the heuristic algorithms provide better performance results than the conventional PID controllers.