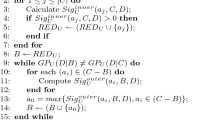Minimal attribute reduction with rough set based on compactness discernibility information tree

Abstract

Minimal attribute reduction plays an important role in rough set. Heuristic algorithms are proposed in literature reviews to get a minimal reduction and yet an unresolved issue is that many redundancy non-empty elements involving duplicates and supersets exist in discernibility matrix. To be able to eliminate the related redundancy and pointless elements, in this paper, we propose a compactness discernibility information tree (CDI-tree). The CDI-tree has the ability to map non-empty elements into one path and allow numerous non-empty elements share the same prefix, which is recognized as a compact structure to store non-empty elements in discernibility matrix. A complete algorithm is presented to address Pawlak reduction based on CDI-tree. The experiment results reveal that the proposed algorithm is more efficient than the benchmark algorithms to find out a minimal attribute reduction.

1 Introduction

Rough set theory, proposed by Pawlak in the 1980s, is a theory for the study of intelligent systems characterized by inexact, uncertain or vague information. It has found successful applications in such fields of artificial intelligence as machine learning, knowledge discovery, decision analysis, process control and pattern recognition (Slowinski 1992). It has become one of the flash points in the research area of information science.

Attribute reduction is one of the most important parts in rough set, which is defined as a process of deleting redundant attributes from larger set of condition attributes. As a consequence in Thangavel and Pethalakshmi (2009), up to now, many strategies for finding reducts have been investigated, such as discernibility matrix strategy (Chen et al. 2012; Zhou et al. 2014), positive region strategy (Qian et al. 2010; Jiang et al. 2011) and other strategies [information entropy (Zheng and Yan 2012; Jiang et al. 2015), Wasp Swarm Optimization (Huilian and Yuanchang 2012; Lustiana et al. 2013), hybrid genetic (Yuan 2014), Ant Colony Optimization (Majdi and Derar 2013; Lustiana et al. 2013)].

Discernibility matrix is a beautiful theoretical result for finding reducts in rough set, which was introduced in Skowron and Rauszer (1992). Both the rows and columns of the matrix correspond to the objects. An element $m_{i,j}$ of the matrix is the set of all attributes on which the corresponding two objects $x_{i}$ and $x_{j}$ have distinct values. Now, many researchers study attribute reduction based on discernibility matrix (or discernibility function) (Jiang et al. 2008; Yao and Zhao 2009; Chen et al. 2012; Zhou et al. 2014). Moreover, vast heuristic algorithms were proposed based on discernibility matrix. In Jiang et al. (2008), an elegant algorithm for finding a reduct based on the discernibility matrix and an order of attributes was introduced. In Yao and Zhao (2009), Yao and his colleagues introduced a method for constructing a minimal discernibility matrix whose elements were either the empty set or singleton set. The union of all elements in the minimal discernibility matrix produces a reduct. In Zhou et al. (2014), a quick attribute reduction algorithm based on the improved discernbility matrix was introduced as well. During the process of finding reducts using the discernibility matrix, these algorithms have high cost of storage and heavy computing load. Since numerous redundancy non-empty elements involving duplicates and supersets exist in discernibility matrix. To eliminate the related redundancy elements, some elegant methods were proposed. In Jiang et al. (2008), a new discernibility matrix was introduced, which regards a decision-making class as a decision-making rule. It reduces the non-empty elements in the discernibility matrix. In addition, a novel condensing tree structure C-Tree and improving C-Tree were introduced in Yang and Yang (2008, 2011), respectively, which are order-tree based on the difference ordering strategy of condition attributes. Although they resolve the problem about the duplicates in the discernibility matrix and have lower space complexity as compared to the discernibility matrix, they never consider how to resolve the superset problem. Therefore, it is necessary to design a new method to store non-empty elements in discernibility matrix.

Generally speaking, researchers want to find not the set of all reducts, but a minimal reduct of a given decision table. Since a minimal reduct is a minimal subset of attributes that provides the same descriptive ability as the entire set of attributes (Yao and Zhao 2009). Thus, many heuristic methods for finding minimal reducts have been investigated (Vinterbo and Øhrn 2000; Jiang 2012; Ding et al. 2012; Dongyi and Zhaojiong 2014).

For example, in Vinterbo and Øhrn (2000), Vinterbo and Øhrn introduced a genetic algorithm for computing minimal hitting sets. In Jiang (2012), an algorithm for finding a minimal reduct based on attribute enumeration tree was also proposed. In Ding et al. (2012), Co-PSAR was introduced based on particle swarm optimization to find a minimal reduct. At the same time, an algorithm based on rough set and Wasp Swarm Optimization was also proposed in Huilian and Yuanchang (2012), which searches through the attribute space for finding a minimal reduct based on attribute significance. Moreover, in Dongyi and Zhaojiong (2014), an algorithm based on discrete artificial bee colony to find a minimal reduct was proposed as well.

In these methods, though heuristic algorithms for finding minimal reducts are effective, many of them can not always find a minimal reduct when decision tables are given and even the result is just a superset of a reduct sometimes.

With the above analysis, in this paper, a new data structure to store non-empty elements in the discernibility matrix, called compactness discernibility information tree (CDI-tree in short), is proposed. It is an extended order-tree based on the given order of condition attributes. The CDI-tree has the ability to eliminate duplicates and allow numerous non-empty elements share one path or the same prefix. It is recognized as a compact structure to store non-empty elements in discernibility matrix. To further eliminate supersets in discernibility matrix, CDI-tree incorporates some pruning strategies, such as core attribute pruning strategy, un-extension path strategy and truncation path (or deleting subtree) pruning strategy. Moreover, the time complexity of constructing a CDI-tree is $O$($\vert C \vert *\vert U\vert ^{2})$. In particular, the space complexity of the CDI-tree is far less than $O(\vert C\vert *\vert U\vert ^{2})$ in most cases. To demonstrate the usefulness and flexibility of the CDI-tree, one heuristic algorithm for finding a minimal reduct is suggested. The approximately strategy of it is to involve deleting unimportant attributes in each iteration. The experiment results reveal that the proposed algorithm is more efficient than the benchmark algorithms to find out a minimal reduct. And the time complexity of this algorithm is $O$($\vert C\vert ^{2}*\vert U\vert ^{2})$. At last, we prove in theory that the reduction found by this algorithm is a Pawlak reduction (by Pawlak, a reduction $R$ is a Pawlak reduction, if and only if POS$_{R}(D)=\mathrm{POS}_{C}(D)$, and $\forall a \quad \in R, \mathrm{POS}_{R-\{a\}}(D)\ne$POS$_{C}(D)$, Here, POS is the positive region).

The rest of this paper is structured as follows: in Sect. 2, we give basic concepts and attribute reduction related to rough set. In Sect. 3, we introduce the building process of CDI-tree. In Sect. 4, based on CDI-tree method, a heuristic algorithm is proposed to get a minimal reduct. At the same time, we prove in theory that the reduction found by this algorithm is a Pawlak reduction. In Sect. 5, we perform some experiments to show the usefulness of CDI-tree. Finally, we conclude the paper in Sect. 6.

2 Basic concepts of rough set theory

For the convenient description, we introduce some basic notions of information systems at first (Wong and Ziarko 1985; Pawlak 1991; Zhang et al. 2001).

Definition 1

A decision table (information table or information system) is an ordered quadruple $S=(U,C \cup D,V,f)$, where $U$ is a non-empty finite set of objects, $C\cup D$ is a non-empty finite set of attributes, $C$ denotes the set of condition attributes and $D$ denotes the set of decision attributes. $C\cap D=$ Ø. $V$ is the union of attribute domains. $f:U\times (C\cup D)\rightarrow V$ is an information function which associates a unique value of each attribute with every object belonging to $U$. Let ‘$a$’ is an attribute in $C$, $x_{i}$ is an object in $U$, then $f(x_{i},a)$ denotes the value of object $x_{i}$ in attribute ‘$a$’. Table 1 lists a decision table, where $U =\{ u_{1},{\ldots },u_{6}\},C=\{a,b,c,d,e\}$ and $D=\{f\}.$

Table 1 An example of decision table

Given $\vert U\vert = n$, discernibility matrix of the decision table is a matrix which contains $n \times n$ elements. Each element of the discernibility matrix is defined as follows:

$$\begin{aligned} a^*(x_i ,x_j )= & {} \{a\in C\vert j>i\wedge f(x_i ,a)\\\ne & {} f(x_j ,a)\wedge w(x,y)=1) \end{aligned}$$

Here, $\forall x$, $y\in U$, $w(x, y)$ is defined as

$$\begin{aligned} w(x,y)\left\{ {{\begin{array}{ll} 1 &{}\quad {x\in \mathrm{POS}_C (D)\wedge y\notin \mathrm{POS}_C (D)} \\ 1 &{}\quad {x\notin \mathrm{POS}_C (D)\wedge y\in \mathrm{POS}_C (D)} \\ 1 &{}\quad {x,y\in \mathrm{POS}_C (D)\wedge (x,y)\notin \mathrm{ind}(D)} \\ 0 &{}\quad \mathrm{otherwise} \\ \end{array} }} \right. \end{aligned}$$

where ind(D) is an indiscernibility relation on $U$, and POS$_{C}(D)$ is the positive region of $D$ with respect to $C$.

Definition 2

Discernibility information, DI for short, is the non-empty element in discernibility matrix.

Definition 3

Discernibility set, Ds for short, is a set including all non-empty elements in discernibility matrix.

Definition 4

By DM, if $a\in C \wedge \{a\}\in {{\mathbf {DM}}}$, ‘$a$’ is called necessary attribute or core attribute. A set including all necessary attributes is called core and marked as Core(C).

According to above definitions, based on Table 2,   Ds = {{a,b,c,d,e},{a,b,c,d,e},{$b$},{$a,b,c$},{$a,b,c,d$}, {$d$},{$a,c,d$},{$a,b,c,d$}}, Core(C) = {$b,d$}.

Definition 5

A discernibility function $f_{A }$ for a decision table $A$ is a Boolean function of $m$ Boolean variables $a_{1}',{\ldots },a_{m}'$ (corresponding to the attributes $a_{1}$,...,$a_{m})$ defined as follows:

$$\begin{aligned} f_A ({a}'_1 ,\ldots ,{a}'_m )= & {} \wedge \{\vee a^*(x_i ,x_j )\vert 1\\\le & {} j\le i \le n,a^*(x_i ,x_j )\ne \varnothing \} \end{aligned}$$

The set of all prime implicants of $f_{A}$ determines the set of all reducts of $A$.

Example 1

The discernibility function for Table 1 is as follows:

$$\begin{aligned} f_A (a,b,c,d,e,f)= & {} (a\vee b\vee c\vee d\vee e)\\&\times \wedge (a\vee b\vee c\vee d\vee e)\wedge b\\&\times \wedge (a\vee b\vee c)\wedge (a\vee b\vee c\vee d)\\&\times \wedge d\!\wedge \! (a\!\vee \! c\!\vee \! d)\wedge (a\vee b\vee c\vee d). \end{aligned}$$

So Table 1 has one reduction: {$b,d$}.

3 Compactness discernibility information tree: design and construction

Discernibility matrix is a beautiful theoretical result for finding out reducts in rough set. However, there are many redundancy non-empty elements involving duplicates and supersets in discernibility matrix, and all non-empty elements in discernibility matrix are employed to find out reducts, which leads to heavy computing load. Thus, this fact motivates our idea to develop a novel structure to eliminate the related redundancy elements.

In this section, with the help of some concept in Han et al. (2000), Yang and Yang (2008) and Chen et al. (2012), we introduce a compact data structure called compactness discernibility information tree to store non-empty elements in a discernibility matrix efficiently.

Table 2 Discernibility matrix corresponding to Table 1

3.1 Compactness discernibility information tree

A compactness discernibility information tree (or CDI-tree in short) is a tree structure defined as follows:

• 1. It consists of one root labeled as “null”, a set of condition-attribute-prefix subtree as the children of the root, and a condition-attribute-header table.

• 2. Each node in the condition-attribute-prefix subtree consists of five fields: attribute-name, count, parent, children and node-link, where attribute-name registers which condition attribute this node represents, count registers the number of discernibility information represented by the portion of path reaching this node, parent points to its parent node, children points to its all children, and node-link links to the next node in the CDI-tree carrying the same attribute-name, or null if there is none.

• 3. Each entry in the condition-attribute-header table consists of two fields: (1) attribute-name and (2) head of node-link (a pointer pointing to the first node in the CDI-tree carrying the attribute-name).

Based on this definition, we have the following CDI-tree construction algorithm.

Example 2

With the above algorithm, a CDI-tree can be constructed based on Table 1 as follows:

First of all, let od be the given order of condition attributes in Table 1: $\langle a$, $b$, $c$, $d$, $e\rangle$. This order is important since each path of the CDI-tree will follow this order. For each object pair in Table 1, compute its discernibility information using formula (1). Select the attributes in the discernibility information and sort them according to order od.

Second, the first discernibility information {a, b, c, d, e} leads to the construction of the first path or branch of the CDI-tree: $\langle a$:1, $b$:1, $c$:1, $d$:1, $e$:1$\rangle$ ($\langle a$, $b$, $c$, $d$, $e\rangle$ for short), in which each node is represented using the format “attribute-name: count”. For the second discernibility information {a, b, c, d, e}, since its attribute list $\langle a$, $b$, $c$, $d$, $e\rangle$ is identical to the first one, the path is shared with the count of each node along the path incremented by 1. The third discernibility information {$b$} leads to the construction of a new path of the CDI-tree:$\langle b$:1$\rangle$. For the fourth discernibility information {$a,b,c$}, since its attribute list $\langle a$, $b$, $c\rangle$ completely is contained in the existing path $\langle a$, $b$, $c$, $d$, $e\rangle$, thus all nodes behind node ($c)$ must be deleted from path $\langle a$, $b$, $c$, $d$, $e\rangle$, the count of corresponding node along the path is incremented by 1. That is, the original path $\langle a$:2, $b$:2, $c$:2, $d$:2, $e$:2$\rangle$ is modified to $\langle a$:3, $b$:3, $c$:3$\rangle$. For the fifth discernibility information {$a,b,c,d$}, since its attribute list $\langle a,b,c,d\rangle$ completely contains the existing path $\langle a$, $b$, $c\rangle$, thus discernibility information {$a,b,c,d$} is mapped to the existing path $\langle a$, $b$, $c\rangle$, the count of corresponding node along the path is incremented by 1. The sixth discernibility information {$d$} leads to the construction of a new path of the CDI-tree:$\langle d$:1$\rangle$. For the seventh discernibility information {$a,c,d$}, because its attribute list $\langle a$, $c$, $d\rangle$ shares only the prefix $\langle a\rangle$ with the $a$-prefix subtree, $a$’s count is incremented by 1, and one new node ($c$:1) is created and linked as a child of node ($a$:5). At the same time, another new node ($d$:1) is created and linked as a child of node ($c$:1). Repeat above procedure until the last discernibility information {$a$, $b$, $c$, $d$} is inserted into the CDI-tree.

From Fig. 1, we can see that the CDI-tree has the ability to map non-empty elements into one path and allow a lot of non-empty elements share the same prefix. It is recognized as a compact structure to store non-empty elements in discernibility matrix.

Fig. 1

The CDI-tree based on Algorithm 1 and Table 1

It is well known that core is the most important subset of condition attribute set $C$. Since none of its elements can be removed without affecting the classification power of attributes. If core is used to avoid mapping non-empty elements including core attributes into CDI-tree, there are better chances that more paths cannot be constructed if the core of the decision table is not empty, so that the efficiency of constructing CDI-tree can be improved.

With the above observations, we can improve Algorithm 1 based on core attributes, as shown in Algorithm 2.

According to Algorithm 2, a CDI-tree corresponding to Table 1 shows in Fig. 2.

Obviously, from Fig. 2, it shows that the cost of storage can be efficiently reduced as compared to Fig. 1. Moreover, some experimental results are designed in Sect. 5.

For any given decision table, if DIS is a set consisting of all paths in the CDI-tree, then DIS $\varvec{\subseteq }$ DM and $\forall$ DI $\in$ DM–DIS, $\exists$ DI’ $\in$ DIS $\wedge$ DI’ $\varvec{\subseteq }$ DI, that is, the CDI-tree contains all discernibility information to find out reducts and eliminates the duplicates and supersets exiting in the discernibility matrix. Therefore, we can naturally deduce that the existing discernibility matrix-base methods can be used under CDI-tree structure. To efficiently utilize the CDI-tree structure for attribute reduction, one CDI-tree-based rough set attribute reduction algorithm is developed in Sect. 4.

There are several important properties of the CDI-tree that can be derived from the CDI-tree construction process.

Definition 6

(Core node) For a given CDI-tree, if a path contains only one node, then this node is the core node.

Property 1. For a given CDI-tree, the attribute represented by core node is a core attribute.

Rational. If a path contains only one node in CDI-tree, then there must be an element in discernibility matrix containing only one condition attribute that is mapped to this path. According to the definition about core based on the discernibility matrix, the condition attribute represented by the attribute-name of core node is the core attribute.

Property 2. For a given CDI-tree, if $R$ is the attribute set, which consists of all attributes represented by all of the root node’s children, then $\forall A\in$ DM $, R\cap A\ne \varnothing$ (or POS$_{R}(D)$ = POS$_{C}(D))$ holds.

Fig. 2

The CDI-tree based on Algorithm 2 and Table 1

3.2 Complexity analysis of compactness discernibility information tree

For a given decision table with $\vert U \vert$ objects and $\vert C \vert$ condition attributes, the number of non-empty elements in a discernibility matrix is $\vert U \vert ^{2}$ at most. Let the number of different non-empty elements in a discernibility matrix be $N$. In the worst case, $N$ is equal to $\vert U\vert ^{2}$. By the CDI-tree construction process, we know that the number of all paths in the CDI-tree is $N$ at most, and the number of nodes in a path is $\vert C\vert$ at most. So, the space complexity of the CDI-tree is $O(\vert C\vert * \vert U\vert ^{2})$ in the worst case. Moreover, in most cases, the nodes in the CDI-tree are far less than $\vert C\vert *\vert U\vert ^{2}$, because numerous non-empty elements in the discernibility matrix share the same path or the same prefix.

During the CDI-tree construction process, the iteration times of it are $\vert U\vert ^{2}$ at most, and the number of nodes inserting into CDI-tree and the number of nodes deleting from the CDI-tree are $\vert C\vert$ and $N_{i}$ at most in each iteration, respectively. As analyzed above, the time complexity of building an CDI-tree is denoted as follows:

$$\begin{aligned}&\left| C \right| *\left| U \right| ^2+( {N_1 +\cdots +N_{\left| C \right| *\vert U\vert } ^2})=\left| C \right| *\vert U\vert ^2\\&\quad +\,( {N_1 +\cdots +N_{\left| C \right| *\vert U\vert } ^2}). \end{aligned}$$

In addition, the number of nodes in the CDI-tree is $\vert C\vert *\vert U\vert ^{2}$ at most. $N_{1}+\cdots + N_{\vert C\vert *\vert U\vert }^{2}$ is equal to $\vert C \vert *\vert U\vert ^{2}$ in the worst case. So, $\vert C\vert *\vert U\vert ^{2}+(N_{1}+\cdots + N_{\vert C\vert *\vert U\vert }^{2})$ $=2*\vert C\vert *\vert U \vert ^{2}$. The time complexity for building a CDI-tree is $O(\vert C\vert * \vert U\vert ^{2})$.

4 Attribute reduction algorithm based on compactness discernibility information tree

In this section, to efficiently utilize CDI-tree structure for attribute reduction, one CDI-tree-based attribute reduction algorithm is developed. This algorithm is to involve deleting unimportant attributes in each iteration.

4.1 Attribute significance

Attribute significance denotes the significance of attribute in decision table, which offers the powerful reference to the decision. The bigger the significance of attribute, the higher its position in the decision table, otherwise, the lower its position.

Definition 7

The attribute significance is defined as the number of each condition attribute symbol appearing in the CDI-tree, and denoted as Sig(a).

According to Definition 7 and Fig. 1 $Sig(a)=6, Sig(b)=6, Sig(c)=6, Sig(d)=2, Sig(e)=0$.

4.2 Minimal reduction algorithmic descriptions and pseudocode

In this subsection, we propose an algorithm for finding a minimal reduct based on CDI-tree. The approximately strategy of it is to delete a most unimportant attribute in each iteration, which guarantees that this algorithm can keep important attributes. At the same time, this algorithm deletes all paths including core node in every iteration as well.

According to the above description, the pseudocode for finding a minimal reduct based on CDI-tree is shown as follows:

The function mergeSub-tree(currentNode, parentNode) (parentNode is the parent of currentNode) is performed as follows:

• (1) If currentNode is a leaf node, then delete the subtree of parentNode from CDI-tree and return.

• (2) The entire subtree of currentNode is merged with the subtree of parentNode, delete currentNode from CDI-tree, and return.

4.3 Completeness of algorithm

By the viewpoint of discernibility matrix, a reduction is a Pawlak reduction, if ①. $\forall A\in$ Ds, $A\cap R\ne \varnothing$, ②. $\forall a\in R$, $\exists A\in$ Ds, $A\cap (R$–{$a$}) $=$ $\varnothing$. (Jue and Ju 2001).

Theorem 1

If $R$ is a reduction found out by Algorithm 3, then $R$ is a Pawlak reduction.

Proof

According to Algorithm 3, a loop is constructed from step (4) to step (10) in this algorithm. ${\varvec{R}}\cap P=\varnothing$ and $({\varvec{R}}\cup P) \varvec{\subseteq } C$. Suppose the number of the loop is $i$. Here, $i$ is an integer ($\vert C\vert \ge i\ge 0$). DIS is a set, which consists of all paths in the CDI-tree. Let DIS $^{0}$,..., DIS $^{k}$,..., DIS $^{i-1}$, DIS $^{i}$ be a change list of the DIS. Similarly, Let ${\varvec{R}}^{0}$,..., ${\varvec{R}}^{k}$,..., ${\varvec{R}}^{i-1},$ ${\varvec{R}}^{i}$ be a change list of the ${\varvec{R}}.$ Let P $^{0}$,..., P $^{k}$,..., P $^{i-1}$, P $^{i}$ be a change list of the P. Here, ${\varvec{R}}^{0}=\varnothing$, ${\varvec{R}}^{i}={{\mathbf {R}}}$, P $^{0}=\varnothing$, DIS $^{0} \varvec{\subseteq }$ Ds and $\forall$ DI $\in$ Ds–DIS $^{0}$, $\exists$ DI’ $\in$ DIS $^{0} \wedge$ DI’ $\varvec{\subseteq }$ DI. If $m\ge n$, then ${\varvec{R}}^{n}$ $\varvec{\subseteq }$ ${\varvec{R}}^{m}$ and P $^{n}$ $\varvec{\subseteq }$ P $^{m}$ hold. And (1) $\forall A\in$ DIS $^{k}$, $\exists A$’ $\in$ DIS $^{k-1}$, $A\subseteq A$’ holds. (2) $\forall A\in$ DIS $^{k-1}$, if $\not \exists A$’ $\in$ DIS $^{k}$, $A\subseteq A$’ holds, then $\vert A\vert$=1 and $A\subseteq$ ${\varvec{R}}^{k-1}$ hold, that is, $A\cap$ ${\varvec{R}}^{k-1}$ $\varvec{\ne }$ $\varnothing$ holds. (3) $\forall \quad A\in$ DIS $^{k}$, $A$’$\in$ DIS $^{k-1}$, if $A\subseteq A$’, then $A=A$’ or $\vert A\vert$+1=$\vert A$’$\vert$ holds. Moreover, if $A\subseteq A$’ and $\vert A\vert +1=\vert A$’$\vert$, then ($A$’$-A)\subseteq$ P $^{k-1 }$and ($A$’$-A)\,\cap$ ${\varvec{R}}^{k-1}=\varnothing$ hold. In a word, $\forall A\in$ Ds, $A\cap R$ $\varvec{\ne }$  $\varnothing$, and $\forall a\in R$, $\exists A\in$ Ds, $A\cap (R-${$a$}) $=\varnothing$ hold. Therefore, the reduction found out by Algorithm 3 is a Pawlak reduction. $\square$

4.4 Time complexity analysis

According to the analysis in Sect. 3.2, we can observe that the number of nodes in CDI-tree is $\vert C\vert *\vert U\vert ^{2}$ and the time complexity of building a CDI-tree is $O(\vert C\vert * \vert U\vert ^{2})$ in the worst case.

By Algorithm 3, its iteration times is $\vert C\vert$ at most, and the time complexity of computing attribute significance is $O(\vert C\vert *\vert U\vert ^{2})$, and the time complexity of mergeSub-tree (currentNode, parentNode) is $O(\vert C\vert * \vert U\vert ^{2})$ in the worst case. Thus, the time complexity of Algorithm 3 is as follows: $O(\vert C\vert * \vert U\vert ^{2})$ $+ \vert C\vert *$ $O ( \vert C\vert *\vert U \vert ^{2}+\vert C\vert * O(\vert C\vert * \vert U\vert ^{2}) +(\varvec{N}_{1}{+\cdots +N}_{\vert C\vert })$.

Since, N $_{1}$+$\cdots$+N $_{\vert C\vert }$ is equal to $\vert C\vert *\vert U\vert ^{2}$ at most. Therefore, the time complexity of Algorithm 3 is $O(\vert C\vert ^{2}*\vert U \vert ^{2})$.

5 Experimental results and analysis

In this section, to demonstrate the usefulness and compactness of the CDI-tree method, we show some experimental comparisons. First of all, we perform an experiment to verify core attribute pruning strategy that plays an essential role in the CDI-tree construction process when the core of a given decision table is not empty. Second, we perform an experiment to compare the CDI-tree proposed in this paper with C-Tree proposed in Yang and Yang (2008) based on the same discernibility matrix and attribute order. At last, we perform another experiment to demonstrate the reduction results for finding out a minimal reduct between MARACDI-tree, MinARA, JohnsonReducer and SAVGeneticReducer. Here, they are MARACDI-tree in this paper, MinARA in Jiang (2012), JohnsonReducer in Johnson (1974) and SAVGeneticReducer in Vinterbo and Øhrn (2000).

We choose some data sets from UCI database (http://www.ics.uci.edu/~mlearn/Machine-Learning.html) for the comparison. The detailed information shows in Table 3.

Here, $\vert U\vert$ is the number of objects of a decision table, $\vert C\vert$ is the number of the condition attribute, $\vert D\vert$ is the number of decision attribute, and $\vert$ Core(C)$\vert$ is the number of core attribute of a decision table.

Table 3 The Detailed information of the data sets used in the comparison

In addition, the experiments in Sects. 5.1 and 5.2 are conducted on a 3.2-Ghz Pentium® dual-core with 2 GB of memory running Microsoft Windows 7. However, the experiments in Sect. 5.3 are conducted on a 1.73-Mhz Pentium III with 768 MB of memory running Microsoft Windows XP, because JohnsonReducer and SAVGeneticReducer are implemented in ROSETTA and ROSETTA runs Microsoft Windows XP. All codes were compiled using Microsoft Visual Studio 2005.

5.1 Comparisons of constructing CDI-tree with and without core attribute pruning

It is well known that core is the most important subset of condition attribute $C$. None of its elements can be removed without affecting the classification power of attributes. In this part, we perform an experiment to verify core attribute pruning strategy playing an essential role in the CDI-tree construction process when the core of a given decision table is not empty.

During the CDI-tree construction process, core attribute pruning guarantees that the CDI-tree construction algorithm with core attribute pruning. So CDI-tree based on Algorithm 2 (with core attribute pruning) requires the less computational cost and less storage cost than CDI-tree based on Algorithm 1 (without core attribute pruning) as shown in Figs. 3 and 4. Clearly, the CDI-tree based on Algorithm 1 is equal to the CDI-tree based on Algorithm 2 if the core of a given decision table is empty.

The experimental result in Fig. 3 shows that CDI-tree with core attribute pruning needs the less computational cost than CDI-tree without core attribute pruning. Since core attribute pruning guarantees that the CDI-tree construction algorithm does not construct all the paths including any core attribute. For instance, using letter, voting and connect4, the number of nodes in CDI-tree based on Algorithm 1 is approximately 4 times, 12 times and 12 times of the number of nodes in CDI-tree based on Algorithm 2, respectively.

Fig. 3

The number of nodes in CDI-tree on some datasets

In Fig. 4, we can see that CDI-tree with core attribute pruning is obviously faster than CDI-tree without core attribute pruning. For example, using poker hand, letter and shuttle, the running time of CDI-tree with core attribute pruning (or CDI-tree without core attribute pruning) is 118.872 (241.769), 168.885 (307.133) and 739.363 (980.352) respectively.

Fig. 4

The running time on some datasets

In summary, we can conclude that CDI-tree with core attribute pruning needs the less computational cost and less storage cost than CDI-tree without core attribute pruning.

5.2 Comparison of CDI-tree and C-Tree

In this part, we experimentally demonstrate the running time and the storage cost in CDI-tree and C-Tree based on the same discernibility matrix and attribute order. As pointed in Yang and Yang (2008), the C-Tree is a compact tree structure, which may guarantee that less storage cost is required than the discernibility matrix. As compared with CDI-tree, C-Tree can restore all information coming from a discernibility matrix, that is, any non-empty element of a discernibility matrix can have a path in C-Tree. CDI-tree contains all information to find out reducts and integrates many pruning strategies, which can eliminate lots of redundancy elements and achieve compactness storage of the elements in the discernibility matrix. For instance, the non-empty elements, such as {$a$, $b$}, {$a$, $b$, $c$}, {$a$, $b$, $c$}, {$a$, $b$, $c$}, {$a$, $b$, $d$} and {$a$, $b$, $c$, $d$}, share the same path $\langle a$, $b\rangle$ in the CDI-tree. Therefore, we naturally come to the conclusion that CDI-tree needs the less computational cost and less storage cost than C-Tree.

The experimental result in Table 4 shows that CDI-tree is a compact data structure, which also guarantees that the less computational cost and less storage cost are required than C-Tree based on same discernibility matrix and attribute order. For example, using C-Tree structure, chess, connect4, letter, voting and tic-tac-toe contain over 2.6 $\times$ 10$^{6}$, 4.1 $\times$ 10$^{5}$, 3.2 $\times$ 10$^{4}$, 1.6 $\times$ 10$^{4}$ and 5.1 $\times$ 10$^{2}$ nodes, respectively, while they only generate 51, 21, 545, 50 and 45 nodes by employing the CDI-tree, respectively. Furthermore, from Table 3, we can also observe that the running time of C-Tree is approximately 6 times, 3 times and 3 times of CDI-tree in chess, letter and poker hand, respectively. Therefore, it is obvious that the CDI-tree is more compactness than the C-tree, which can also guarantee that less computational cost is required.

Table 4 The experimental result based on C-Tree and CDI-tree

5.3 Comparison of algorithms to find a minimal Reduct

In this part, we compare the method proposed in this paper (MARACDI-tree) with three common reduction methods for finding minimal reducts. They are MinARA algorithm based on attribute enumeration tree (Jiang 2012), JohnsonReducer algorithm and SAVGeneticReducer algorithm. JohnsonReducer invokes a variation of a simple greedy algorithm to compute a minimal reduct, as described by Johnson in Johnson (1974). The algorithm has a natural bias towards finding a single prime implicant of minimal length. SAVGeneticReducer is a genetic algorithm for computing minimal hitting sets, as described by Vinterbo and Øhrn (2000). JohnsonReducer and SAVGeneticReducer are implemented in ROSETTA that is a rough set toolkit for analysis of data. You can check out the ROSETTA homepage at http://www.idi.ntnu.no/~aleks/rosetta/ for information.

We experimentally compare these methods and summarize the results in Table 5. From Table 5, we can observe that MARACDI-tree, MinARA, JohnsonReducer and SAVGeneticReducer often find out a minimal reduct. Table 5 shows that MARACDI-tree, JohnsonReducer and SAVGeneticReducer can find out a minimal reduct on “hayes roth”, whereas MinARA does not. Similarly, MARACDI-tree can find out a minimal reduct on “SPECT”, “tic-tac-toe”, and “poker hand”, whereas MinARA, JohnsonReducer and SAVGeneticReducer cannot. In addition, from Table 5, we can also see that MinARA, JohnsonReducer and SAVGeneticReducer do not suit for large data sets since their workloads are so heavy that they will be stopped because of out of memory in experimental software and hardware environments. In summary, it has been proven that finding a minimal reduct is NP-hard problem. Although we cannot prove in theory that our algorithm can find out a minimal reduct in any cases, from this section we draw a conclusion that MARACDI-tree is the best one to find out a minimal reduct based on UCI datasets.

Table 5 The reduction results to find a minimal reduct.

6 Conclusions

Attribute reduction is the key research point of rough set theory that has been widely studied. An effective way for attribute reduction is to obtain the discernibility matrix. Unfortunately, a large number of redundant elements exist in discernibility matrix such as the same elements and the supersets. In this paper, we propose a CDI-tree recognized as a compact structure to store non-empty elements of a discernibility matrix, which can eliminate the related redundancies and pointless elements. The experimental results demonstrate that CDI-tree has the less computational cost and less storage cost than C-Tree has. A heuristic algorithm is proposed for minimal attribute reduction based on CDI-tree. The experimental performance using UCI datasets shows that the proposed algorithm could find the expected minimal attribute reduction. We plan to have tasks in the future work. First is to explore the methods to get the minimal number of nodes containing in CDI-tree, and the second is to prove in theory that the proposed minimal attribute reduction algorithm could find the minimal reduct for any decision tables.