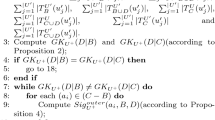An incremental attribute reduction approach based on knowledge granularity for incomplete decision systems

Abstract

Attribute reduction is a core issue in rough set theory. In recent years, with the fast development of data processing tools, information systems may increase quickly in objects over time. How to update attribute reducts efficiently becomes more and more important. Although some approaches have been proposed, they are used for complete decision systems. There are relatively few studies on incremental attribute reduction for incomplete decision systems. We introduce knowledge granularity, that can be obtained by the tolerance classes, to measure the uncertainty in incomplete decision systems. Furthermore, we propose incremental attribute reduction algorithms for incomplete decision systems when adding multiple objects and when deleting multiple objects, respectively. Finally, experimental results show that the proposed incremental approach is effective and efficient to update attribute reducts with the variation of objects in incomplete decision systems.

1 Introduction

Rough set theory, proposed by Pawlak (1982), is a powerful mathematical tool to deal with uncertainty, granularity, and incompleteness of knowledge in information systems. It has been applied successfully in many fields including machine learning, intelligent data analysis, decision making, knowledge engineering, disease diagnosis, and so on (Chen and Tanuwijaya 2011; Derrac et al. 2012; Chen and Chang 2011; Lin et al. 2011; Formica 2012; Wafo Soh et al. 2018; Min et al. 2011; Li et al. 2012, 2016; Wang et al. 2019a; Chen et al. 2013; Liu et al. 2018; D’Eer et al. 2016; Liao et al. 2018; Jothi and Hannah 2016; Zhan et al. 2017; Koley et al. 2016; Afridi et al. 2018; Xu et al. 2017). Since rough set theory can achieve a subset of all attributes which preserves the discernible ability of original features, using the data only with no additional information, it has been widely applied in attribute reduction (also called attribute selection or feature selection) (Dai et al. 2017a; Raza and Qamar 2016; Pacheco et al. 2017; Wang et al. 2016, 2018, 2019b; Cheng et al. 2016; Min and Xu 2016; Raza and Qamar 2017; Li et al. 2017; Das et al. 2017; Tiwari et al. 2018; Lin et al. 2018; Yao and Zhang 2017; Dai et al. 2018.

As we know, attribute reduction plays an important role in data mining and knowledge discovery. Attribute reduction methods can be classified into non-incremental methods and incremental methods according to whether the computation of attribute reduction is from scratch or not when the data vary dynamically. Non-incremental attribute reduction, also called classic attribute reduction or static attribute reduction, has been fully studied and has yielded many important results (Pawlak 1991; Qian and Liang 2008; Xu and Yu 2017; Dai and Tian 2013; Dai and Xu 2013; Liang et al. 2014; Raza and Qamar 2017; Yao and Zhang 2017). In practice, real data may change dynamically nowadays. Non-incremental methods are often infeasible, since they need to compute repeatedly and consume a large amount of computational time. Incremental methods are considered as effective approaches to deal with dynamic data, because they can directly update the results using the previous results from the original decision system. In dynamic data environments, data changes take on three basic forms and the attribute reduction problem has three issues correspondingly: variation of object sets, variation of attribute sets, and variation of attribute values (Xie and Qin 2018). Some achievements have been made to solve these problems. For example, Jing et al. (2016) considered the situation of variation of the attribute sets in complete decision systems, and introduced incremental mechanisms to calculate the new knowledge granularity and presented the corresponding incremental algorithms for attribute reduction based on the calculated knowledge granularity when multiple attributes are added to the decision system. Chen et al. (2016) presented an incremental algorithm for attribute reduction with variable precision rough sets for the same purpose, by introducing two Boolean row vectors to characterize the discernibility matrix and reduct and employing an incremental manner to update minimal elements in the discernibility matrix at the arrival of an incremental sample. Xie and Qin (2018) considered the situation of variation of the attribute values, introduced the concept of an inconsistency degree in an incomplete decision system, and proposed a framework of the incremental attribute reduction algorithm based on three update strategies of inconsistency degree for dynamic incomplete decision systems. Wei et al. (2018) proposed a discernibility matrix based incremental attribute reduction algorithm to incrementally acquire all reducts of dynamic data and another incremental attribute reduction algorithm of more efficiency.

The above methods are suitable only for complete information systems or complete decision systems and cannot be applied to incomplete situations. Thus, further studies on uncertainty measures for incomplete decision systems have been developed. Dai et al. (2013) proposed a new form of conditional entropy and obtained some important properties, which can be used as a reasonable uncertainty measure for incomplete decision systems. Dai et al. (2017b) investigated the uncertainty measures in incomplete interval-valued information systems based on an $\alpha$-weak similarity relation and defined accuracy, roughness, and approximation accuracy to evaluate the uncertainty based on a rough set model constructed. Liu et al. (2016) provided a novel three-way decision model and corresponding algorithm based on incomplete information system by defining a new relation to describe the similarity degree of incomplete information and utilizing interval number to acquire the loss function. Du and Hu (2016) investigated an approach on the basis of the discernibility matrix and the discernibility function to compute all the reducts in incomplete ordered information systems by introducing the characteristic-based dominance relation, and designed a heuristic algorithm with polynomial time complexity for finding a unique reduct using the inner and outer significance measures of each criterion candidate.

Based on the aforementioned survey, we can see that the methods mentioned above have not investigated the incremental attribute reduction mechanism for information decision systems of character as incomplete and dynamic simultaneously. To our best knowledge, there are only a few work on the incremental attribute reduction mechanism for incomplete information decision systems. Shu and Shen (2013) introduced a simpler way of computing tolerance classes than the classical method and presented an incremental attribute reduction algorithm to compute an attribute reduct for a dynamically increasing incomplete decision system. Yang et al. (2017) presented an efficient incremental algorithm including active sample selection process and incremental attribute reduction process from dynamic data sets with increasing samples. Shu and Shen (2014b) proposed an positive region-based attribute reduction algorithm to solve the attribute reduction problem efficiently in incomplete decision systems with dynamically varying attribute sets. Shu and Shen (2014a) employed an incremental manner to compute the new positive region and developed two efficient incremental feature selection algorithms, respectively, for single object and multiple objects with varying feature values. From above, it appears that some of them mainly focused on the variation of attribute sets or attribute values, and others only considered the case of increasing objects dynamically. Thus, being inspired by Dai and Tian (2013), we introduce the tolerance class to measure knowledge granularity for the proposed incremental mechanism and develop two incremental attribute reduction algorithms for incomplete information decision systems in the cases of increasing and decreasing objects respectively.

The remainder of this paper is organized as follows. Section 2 reviews some basic concepts in rough set theory and introduces a tolerance class based presentation of the knowledge granularity. Incremental mechanisms to calculate knowledge granularity, relative knowledge granularity, and significance measurements of attributes for incomplete decision systems when objects vary dynamically and their corresponding attribute reduction algorithms are investigated in Sect. 3. In Sect. 4, experiments and comparisons are conducted. Section 5 concludes the whole paper.

2 Preliminary knowledge

In this section, we first review some basic concepts in rough set theory, which can also be referred to Pawlak (1991), Kryszkiewicz (1998), and Pawlak and Skowron (2007). Furthermore, we recall the concepts of incomplete information systems and decision systems. At last, the tolerance relation is reviewed.

2.1 Basic concepts in rough set theory

An information system is a quadruple $IIS = \left\langle {U,A,V,f} \right\rangle$, where U denotes a non-empty finite set of objects, which is called the universe; A denotes a non-empty finite set of conditional attributes; Vis the union of attribute domains, $V=\bigcup _{a\in A}V_a$, where $V_a$ is the value set of attribute a, called the domain of a; $f:U\times A\rightarrow V$ is an information function which assigns particular values from domains of attribute to objects such as $a\in A, x\in U, f(a,x)\in V_a$, where f(a, x) denotes the value of attribute a for object x. Each attribute subset $B \subseteq A$ determines a binary indiscernible relation as follows:

$$\begin{aligned} {\text {IND}}(B) = \left\{ {\left( {{u_i},{u_j}} \right) \in {U^2}|\forall a \in B,a\left( {{u_i}} \right) = a\left( {{u_j}} \right) } \right\} . \end{aligned}$$

(1)

By the relation ${\text {IND}}(B)$, we obtain the partition of U denoted by $U/{\text {IND}}(B)$ or U / B. For $B \subseteq A$ and $X \subseteq U$, the lower approximation and the upper approximation of X can be defined as follows:

$$\begin{aligned} \underline{B} X&= \left\{ {{u_i} \in U|\left[ {{u_i}} \right] \subseteq X} \right\} \\ \overline{B} X&= \left\{ {{u_i} \in U|\left[ {{u_i}} \right] \cap X \ne \emptyset } \right\} , \end{aligned}$$

where $\underline{B} X$ is a set of objects that belong to X with certainty, while $\overline{B} X$ is a set of objects that possibly belong to X. If $\underline{B} X = \overline{B} X$, X is named B-definable. Otherwise, X is named B-rough. Based on $\underline{B} X$ and $\overline{B} X$, the B-positive region, B-negative region, and B-borderline region of X are defined, respectively, as follows:

$$\begin{aligned} & PO{S_B}(X)= \underline{B} X\\ &NE{G_B}(X)= U - \overline{B} X\\ &B{N_B}= \overline{B} X - \underline{B} X. \end{aligned}$$

2.2 Incomplete decision systems and tolerance relation

An information system is a quadruple $IS = \left\langle {U,A,V,f}\right\rangle$. If there exists $x \in U$ and $a \in A$, such that f(a, x) is equal to a missing value(a null or unknown value, denoted as “*”), i.e., $*\in V_a$, then the information system is called an incomplete information system (IIS). Thus, the IIS can be denoted as: $IIS =\left\langle {U,A,V,f}\right\rangle$, where $* \in V_A$.

A decision system is a quadruple ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$, where D is the decision attribute set, C is the conditional attribute set, and $C \cap D= \emptyset$; V is the union of attribute domain, i.e., $V=V_C\cup V_D$. In general, we assume that $D=\{d\}$. If there exists an $a \in A,x \in U$, such that $f\left( {a,x} \right)$ is equal to a missing value, then the decision system is called an incomplete decision system (IDS). Thus, the IDS can be denoted as: ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$, where $* \in V_C, *\notin V_D$.

Definition 1

Given an incomplete decision system ${\text {IDS}}$ = $\left\langle {U,C \cup D,V,f} \right\rangle$, for any subset of attributes $B \subseteq C$, let T(B) denote the binary tolerance relation between objects that are possibly indiscernible in terms of values of attributes in B. T(B) is defined as

$$\begin{aligned} T(B) &= \{(x,y)|\forall a \in B,f(a,x) = f(a,y)\}\\ &\quad \vee f(a,x) = * \vee f(a,y) = *\}, \end{aligned}$$

(2)

where T(B) is reflexive and symmetric, but not necessarily transitive.

Definition 2

Given an incomplete decision system ${\text {IDS}}$ = $\left\langle {U,C \cup D,V,f} \right\rangle$, $x \in U {\text { and }} B \subseteq C$, the tolerance class of the object x with respect to attribute set B is defined by

$$\begin{aligned} T_B(x) = \left\{ {y|\left( {x,y} \right) \in T(B)} \right\} \end{aligned}$$

(3)

2.3 Knowledge granulation in incomplete decision systems

Definition 3

(Dai and Tian 2013) Given an incomplete decision system ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$, $T_C(x)$ is the tolerance class of object x with respect to attribute set C. Based on the tolerance class, the knowledge granularity of C on U is defined as follows:

$$\begin{aligned} GK_U(C)=\displaystyle {\frac{1}{|U|^2} \sum _{i=1}^{|U|}} {|T_C(u_i)|}, \end{aligned}$$

(4)

where |U| stands for the number of objects in U.

Table 1 Incomplete decision system 1

Example 1

Example for computing of the knowledge granularity.

Table 1 shows an incomplete decision system ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$, where $U=\{ {u_1},{u_2},{u_3},{u_4},{u_5},{u_6},{u_7},{u_8},{u_9} \}$, $C = \{ {a_1},{a_2},{a_3},{a_4},{a_5}\}$ and $D=\{0,1\}$. According to Definition 2, we have $T_C(u_1)=\{u_1,u_6\}$, $T_C(u_2)=\{u_2,u_4,u_8\}$, $T_C(u_3)=\{u_3,u_5\}$, $T_C(u_4)=\{u_2,u_4,u_8\}$, $T_C(u_5)=\{u_3,u_5\}$, $T_C(u_6)=\{u_1,u_6,u_7\}$, $T_C(u_7)=\{u_6,u_7\}$, $T_C(u_8)=\{u_2,u_4,u_8,u_9\}$, and $T_C(u_9)=\{u_8,u_9\}$. According to Definition 3, we have

$$GK_U(C)=\frac{1}{9^2}(2+3+2+3+2+3+2+4+2)=\frac{23}{81}.$$

Similarly, we can get $GK_U(C\cup D)=\frac{19}{81}$.

Proposition 1

Given an incomplete decision system ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$, $P,Q\subseteq C$. IF $P \subseteq Q$, then $GK_U(P)\ge GK_U(Q)$.

Proof

According to Definition 2, we have $\forall u_i\in U$, $T_P(u_i) \supseteq T_Q(u_i)$. Then, we get $|T_P(u_i)|\ge |T_Q(u_i)|$.

Since $GK_U(P)={\frac{1}{|U|^2} \sum _{i=1}^{|U|}} {|T_P(u_i)|}$ and $GK_U(Q)={\frac{1}{|U|^2} \sum \nolimits _{i=1}^{|U|}} {|T_Q(u_i)|}$, we have ${\frac{1}{|U|^2} \sum \nolimits _{i=1}^{|U|}} {|T_P(u_i)|} \ge {\frac{1}{|U|^2} \sum \nolimits _{i=1}^{|U|}} {|T_Q(u_i)|}$.

It is obvious that $GK_U(P)\ge GK_U(Q)$. $\square$

Let ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$ be an incomplete system, $P,Q\subseteq C$. If $P\subseteq Q$, we can see that $GK_U(P)\ge GK_U(Q)$. In other word, the knowledge granularity of attribute set declines with the increase of number of attributes. Thus, the measure of knowledge granularity has the monotonicity with respect to attributes and is reasonable to be used as a uncertainty measure in rough set theory.

Definition 4

Given an incomplete decision system ${\text {IDS}}$ = $\left\langle {U,C \cup D,V,f} \right\rangle$, T(C) and $T(C\cup D)$ are the tolerance relation for attribute set C and $C\cup D$, respectively. The knowledge granularity of C relative to D on U is defined as follows:

$$\begin{aligned} GK_U(D|C)&=GK_U(C)-GK_U(C\cup D)\nonumber \\&= \displaystyle {\frac{1}{|U|^2} \sum _{i=1}^{|U|}} {(|T_C(u_i)|-|T_{C\cup D}(u_i)|)}. \end{aligned}$$

(5)

Definition 5

Given an incomplete decision system ${\text {IDS}}$ = $\left\langle {U,C \cup D,V,f} \right\rangle$, $T_C$, $T_{C-\{a\}}$, $T_{C\cup D}$, and $T_{{(C-\{a\})}\cup D}$ are the tolerance relation for C, $C-\{a\}$, $C\cup D$, and $(C-\{a\})\cup D$, respectively. The significance measure (inner significance) of a in C on U is defined as follows:

$$\begin{aligned}{\text {Sig}}^{\text {inner}}_U(a,C,D)&= \displaystyle {\frac{1}{|U|^2} \sum _{i=1}^{|U|}} {[(|T_{C-\{a\}}(u_i)|}\nonumber \\&\quad -|T_{{(C-\{a\})}\cup D}(u_i)|) - {(|T_C(u_i)|-|T_{C\cup D}(u_i)|)]}, \end{aligned}$$

(6)

where a denotes any one attribute in C and the following are the same.

Definition 6

Given an incomplete decision system ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$, the core of ${\text {IDS}}$ is defined as follows:

$$\begin{aligned} {Core}_C= \{a\in C|{{\text {Sig}}}^{\text {inner}}_U(a,C,D)>0\}. \end{aligned}$$

(7)

If $\forall a\in C, {{\text {Sig}}}^{\text {inner}}_U(a,C,D)=0$, then ${Core}_C= \emptyset$.

Example 2

(Continued from Example 1) According to Definitions 3, 4, and 5, we have

$$\begin{aligned} {\text {Sig}}^{\text {inner}}_U(a_1,C,D)= & {} \frac{1}{81}[(23-19)-(23-19)]=0\\ {\text {Sig}}^{\text {inner}}_U(a_2,C,D)= & {} \frac{1}{81}[(27-19)-(23-19)]=\frac{4}{81}\\ {\text {Sig}}^{\text {inner}}_U(a_3,C,D)= & {} \frac{1}{81}[(29-21)-(23-19)]=\frac{4}{81}\\ {\text {Sig}}^{\text {inner}}_U(a_4,C,D)= & {} \frac{1}{81}[(23-19)-(23-19)]=0\\ {\text {Sig}}^{\text {inner}}_U(a_5,C,D)= & {} \frac{1}{81}[(25-19)-(23-19)]=\frac{2}{81} \end{aligned}$$

Then, we have ${Core}_C=\{a_2,a_3,a_5\}.$

Definition 7

Given an incomplete decision system ${\text {IDS}}$ = $\left\langle {U,C \cup D,V,f} \right\rangle$ and $B\subseteq C$, $T_B$, $T_{B\cup D}$, $T_{B\cup \{a\}}$ and $T_{{(B\cup \{a\})}\cup D}$ are the tolerance relation for B, $B\cup D$, $B\cup \{a\}$ and ${(B\cup \{a\})}\cup D$, respectively. Then, $\forall a \in (C - B )$, the significance measure (outer significance) of a in B on U is defined as follows:

$$\begin{aligned}{\text {Sig}}^{\text {outer}}_U(a,B,D)&= \displaystyle {\frac{1}{|U|^2} \sum _{i=1}^{|U|}} {[(|T_B}(u_i)|-|T_{B\cup D}(u_i)|)\nonumber \\&\quad -{(|T_{B\cup \{a\}}(u_i)|-|T_{(B\cup \{a\})\cup D}(u_i)|)]}. \end{aligned}$$

(8)

Definition 8

Given an incomplete decision system ${\text {IDS}}$ = $\left\langle {U,C \cup D,V,f} \right\rangle$ and $B\subseteq C$, then B is a relative reduct based on the knowledge granularity of ${\text {IDS}}$ if

• (1) $GK_U(D|B)= GK_U(D|C)$.

• (2) $\forall a\in B, GK_U(D|(B-\{a\})) \ne GK_U(D|B)$.

3 Incremental attribute reduction algorithms for incomplete decision systems when objects vary dynamically

After having investigated an incremental mechanism to compute knowledge granularity for incomplete decision systems to which multiple objects are added one by one, this section introduces an incremental attribute reduction algorithm for the addition of multiple objects based on knowledge granularity.

3.1 An incremental mechanism to calculate knowledge granularity for IDS when adding an object

This section investigates changes of tolerance class, relative knowledge granularity, inner significance, and outer significance, and then introduces the incremental mechanism for calculating knowledge granularity when an object is added to an incomplete decision system.

Proposition 2

Given an incomplete decision system ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$, where $U=\{u_1,u_2,\ldots ,u_n\}$denotes a non-empty finite set containing n objects. $u_{(n+1)}$is the incremental object that will be added to IDS, and $T'_C$is the tolerance relation on $U^+=(U\cup \{u_{(n+1)}\})$. The knowledge granularity of C on $U^+$is

$$\begin{aligned} GK_{U^+}(C)=\frac{1}{(n+1)^2}(n^2GK_{U}(C)+2|T'_C(u_{(n+1)})|-1), \end{aligned}$$

(9)

where $\begin{aligned} T'_C(u_{(n+1)}) = \left\{ {u_j|\left( {u_{(n+1)},u_j} \right) \in T'_C, 1\le j\le n+1} \right\} . \end{aligned}$

Proof

After $u_{(n+1)}$ is adding to U, the tolerance class of $u_i$ is

$$\begin{aligned} T'_C(u_i) = \left\{ \begin{array}{l} T_C(u_i)\bigcup \{u_{(n+1)}\},\;(u_i,u_{(n+1)})\in T'_C\;\\ T_C(u_i),\;(u_i,u_{(n+1)})\notin T'_C\; \end{array} \right. ,\quad 1\le i\le n \end{aligned}$$

Suppose

$$\begin{aligned} \varDelta |T_C(u_i)| = \left\{ \begin{array}{l} 1,\;(u_i,u_{(n+1)})\in T'_C\;\\ 0,\;(u_i,u_{(n+1)})\notin T'_C\; \end{array} \right. ,\quad 1\le i\le n \end{aligned}$$

then

$$\begin{aligned} |T'_C(u_i)| = |T_C(u_i)|+\varDelta |T_C(u_i)|,1\le i\le n. \end{aligned}$$

Because tolerance relation is symmetric, if $(u_i,u_{(n+1)})\in T'_C$, then $(u_{(n+1)},u_i)\in T'_C,1\le i\le n$. In other words, if $u_i\in T'_C(u_{(n+1)})$, then $u_{(n+1)}\in T'_C(u_i),1\le i\le n$. Obviously, the number of objects that has tolerance relation with $u_{(n+1)}$ is equal to those whose tolerance class contains $u_{(n+1)}$ except $u_{(n+1)}$ itself after $u_{(n+1)}$ is added to IDS. Then, we can get

$$\begin{aligned} \displaystyle {\sum _{i=1}^{|U|}} {\varDelta |T_C(u_i)|=|T'_C(u_{(n+1)})|-1}. \end{aligned}$$

According to Definition 3, the knowledge granularity of C on $U^+$ is described as follows:

$$\begin{aligned} &GK_{U^+}(C)\\ &\quad =\displaystyle {\frac{1}{|U^+|^2} \sum _{i=1}^{|U^+|}} {|T'_C(u_i)|}\\ &\quad =\displaystyle {\frac{1}{(n+1)^2}\left( \sum _{i=1}^{|U|} |T'_C(u_i)|+|T'_C(u_{(n+1)})|\right) }\\ &\quad =\displaystyle {\frac{1}{(n+1)^2}\left( \sum _{i=1}^{|U|} |T_C(u_i)|+\sum _{i=1}^{|U|} \varDelta |T_C(u_i)|+|T'_C(u_{(n+1)})|\right) }\\ &\quad =\frac{1}{(n+1)^2}(n^2GK_{U}(C)+2|T'_C(u_{(n+1)})|-1). \end{aligned}$$

$\square$

Proposition 3

Given an incomplete decision system ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$. $u_{(n+1)}$is the incremental object. $T'_C(u_{(n+1)})$and $T'_{C\cup D}(u_{(n+1)})$are the tolerance classes of $u_{(n+1)}$with respect to attribute set C and $C\cup D$on $U^+$, respectively. The knowledge granularity of C relative to D on $U^+$is

$$\begin{aligned} GK_{U^+}(D|C)&=\frac{1}{{(n+1)}^2}(n^2GK_U(D|C)+2(|T'_C(u_{(n+1)})|\nonumber \\&\quad -|T'_{C\cup D}(u_{(n+1)})|)), \end{aligned}$$

(10)

where |.| denotes the cardinality of a set.

Proof

According to Definition 4 and Proposition 2, we have

$$\begin{aligned} &GK_{U^+}(D|C)\\ &\quad =GK_{U^+}(C)-GK_{U^+}(C\cup D)\\ &{}\quad =\frac{1}{(n+1)^2}(n^2GK_{U}(C)+2|T'_C(u_{(n+1)})|-1)\\ &\qquad -\frac{1}{(n+1)^2}(n^2GK_{U}(C\cup D)+2|T'_{C\cup D}(u_{(n+1)})|-1)\\ &\quad =\frac{1}{(n+1)^2}(n^2(GK_{U}(C)-GK_{U}(C\cup D))\\ &\qquad +2|T'_C(u_{(n+1)})|-2|T'_{C\cup D}(u_{(n+1)})|) \\ &\quad =\frac{1}{{(n+1)}^2} (n^2GK_U(D|C)+2(|T'_C(u_{(n+1)})|-|T'_{C\cup D}(u_{(n+1)})|)). \end{aligned}$$

$\square$

Proposition 4

Given an incomplete decision system ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$, $u_{(n+1)}$is the incremental object. $T'_{C-\{a\}}(u_{(n+1)})$, $T'_{(C-\{a\})\cup D}(u_{(n+1)})$, $T'_C(u_{(n+1)})$and $T'_{C\cup D}(u_{(n+1)})$are the tolerance classes of $u_{(n+1)}$with respect to attribute set $C-\{a\}$, $(C-\{a\})\cup D$, C and $C\cup D$on $U^+$, respectively. Then $\forall a\in C$, the inner significance of a in C on $U^+$is

$$\begin{aligned}{\text {Sig}}^{\text {inner}}_{U^+}(a,C,D)&=\frac{1}{{(n+1)}^2} (n^2{\text {Sig}}^{\text {inner}}_U(a,C,D)\nonumber \\&\quad +2(|T'_{C-\{a\}}(u_{(n+1)})|- |T'_C(u_{(n+1)})|\nonumber \\&\quad +|T'_{C\cup D}(u_{(n+1)})|- |T'_{(C-\{a\})\cup D}(u_{(n+1)})|)) \end{aligned}$$

(11)

Proof

According to Definition 5 and Proposition 3, we can get

$$\begin{aligned}&{\text {Sig}}^{\text {inner}}_{U^+}(a,C,D)\\&\quad = GK_{U^+}(D|C-\{a\})-GK_{U^+}(D|C)\\&\quad =\frac{1}{{(n+1)}^2} (n^2GK_U(D|C-\{a\})+2(|T'_{C-\{a\}}(u_{(n+1)})|\\&\qquad -|T'_{(C-\{a\})\cup D}(u_{(n+1)})|))-\frac{1}{{(n+1)}^2} (n^2GK_U(D|C)\\&\qquad +2(|T'_C(u_{(n+1)})|-|T'_{C\cup D}(u_{(n+1)})|))\\&\quad =\frac{1}{{(n+1)}^2}(n^2(GK_U(D|C-\{a\})-GK_U(D|C))\\&\qquad +2(|T'_{C-\{a\}}(u_{(n+1)})|-|T'_C(u_{(n+1)})|\\&\qquad +|T'_{C\cup D}(u_{(n+1)})|-|T'_{(C-\{a\})\cup D}(u_{(n+1)})|))\\&\quad =\frac{1}{{(n+1)}^2}(n^2{\text {Sig}}^{\text {inner}}_U(a,C,D)+2(|T'_{C-\{a\}}(u_{(n+1)})|\\&\qquad -|T'_C(u_{(n+1)})|+|T'_{C\cup D}(u_{(n+1)})|-|T'_{(C-\{a\})\cup D}(u_{(n+1)})|)) \end{aligned}$$

$\square$

Proposition 5

Given an incomplete decision system ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$, $u_{(n+1)}$is the incremental object. $|T'_B(u_{(n+1)})$, $T'_{B\cup D}(u_{(n+1)})$, $T'_{B\cup \{a\}}(u_{(n+1)})$and $T'_{B\cup \{a\}\cup D}(u_{(n+1)})$are the tolerance classes of $u_{(n+1)}$with respect to attribute set B, $B\cup D$, $B\cup \{a\}$and $B\cup \{a\}\cup D$on $U^+$, respectively. Then $\forall a\in (C-B)$, the outer significance of a in B on $U^+$is

$$\begin{aligned}{\text {Sig}}_{U^+}^{\text {outer}}(a,B,D)&= \frac{1}{{(n+1)}^2} (n^2{\text {Sig}}^{\text {outer}}_U(a,B,D)\nonumber \\&\quad +2(|T'_B(u_{(n+1)})|-|T'_{B\cup D}(u_{(n+1)})|\nonumber \\&\quad -|T'_{B\cup \{a\}}(u_{(n+1)})|+|T'_{B\cup \{a\}\cup D}(u_{(n+1)})|)) \end{aligned}$$

(12)

Proof

According to Definition 7 and Proposition 3, we can get

$$\begin{aligned}&{\text {Sig}}^{\text {outer}}_{U^+}(a,B,D)\\&\quad =GK_{U^+}(D|B) - GK_{U^+}(D|(B\cup \{a\}))\\&\quad =\frac{1}{{(n+1)}^2} (n^2GK_U(D|B)+2(|T'_B(u_{(n+1)})|\\&\qquad -|T'_{B\cup D}(u_{(n+1)})|))-\frac{1}{{(n+1)}^2} (n^2GK_U(D|B\cup \{a\})\\&\qquad +2(|T'_{B\cup \{a\}}(u_{(n+1)})|-|T'_{B\cup \{a\}\cup D}(u_{(n+1)})|))\\&\quad =\frac{1}{{(n+1)}^2} (n^2(GK_U(D|B)-GK_U(D|B\cup \{a\}))\\&\qquad +2(|T'_B(u_{(n+1)})|-|T'_{B\cup D}(u_{(n+1)})|\\&\qquad -|T'_{B\cup \{a\}}(u_{(n+1)})|+|T'_{B\cup \{a\}\cup D}(u_{(n+1)})|))\\&\quad =\frac{1}{{(n+1)}^2} (n^2{\text {Sig}}^{\text {outer}}_U(a,B,D)+2(|T'_B(u_{(n+1)})|\\&\qquad -|T'_{B\cup D}(u_{(n+1)})|-|T'_{B\cup \{a\}}(u_{(n+1)})|\\&\qquad +|T'_{B\cup \{a\}\cup D}(u_{(n+1)})|)) \end{aligned}$$

$\square$

3.2 An incremental reduction algorithm for IDS when adding one object

First, a traditional heuristic attribute reduction algorithm for decision systems is introduced in Algorithm 1 (Pawlak 1991; Wang et al. 2013; Liang et al. 2014). Based on the incremental mechanism of knowledge granularity above, this subsection introduces an incremental attribute reduction algorithm (see Algorithm 2) under knowledge granularity when adding an object to the decision system. At last, a brief comparison of time complexity between incremental reduction algorithm and traditional heuristic reduction algorithm is given.

The detailed execution process of Algorithm 1 is as follows. In Step 1, an empty set is assigned to $RED_U$. Steps 2–7 are actually used to get the core of the incomplete decision system according to Definition 6, which constitute a loop with |C| times. |C| denotes the number of all conditional attributes in the incomplete decision system. According to Definition 5, the inner significance of an certain $a_j\in C$, that is ${\text {Sig}}^{\text {inner}}_{U}(a_j,C,D)$, is calculated in Step 3. In Step 4, ${\text {Sig}}^{\text {inner}}_{U}(a_j,C,D)$ is compared with zero if ${\text {Sig}}^{\text {inner}}_{U}(a_j,C,D)>0$, then $a_j$ is added to $RED_U$, which denotes $a_j$ is indispensable and should be added to the core of the incomplete decision system. In Step 8, $RED_U$ is assigned to B. Steps 9–15 are actually used to find an attribute set that satisfies the first condition in Definition 8 and a loop stoping until $GP_U(D|B)$ is equal to $GP_U(D|C)$. Steps 10–12 constitute a loop used to calculate the outer significance of an certain $(a_i) \in (C-B)$, that is ${\text {Sig}}^{\text {outer}}_U(a_i,B,D)$ according to Definition 7. In Step 13, $a_0$ is used to store the attribute that has the maximum value of outer significance. In Step 14, $a_0$ is added to B. Steps 16–20 are actually used to delete attributes that satisfy the second condition in Definition 8 and a loop with |B| times. In Step 17, $GP_U(D|(B-\{a\}))$ is compared with $GP_U(D|C)$ if they are equal, then $a_i$ is deleted from B, which indicates that $a_i$ is redundant and cannot be in the reduct of the incomplete decision system. In Step 21, B is assigned to $RED_U$. In Step 22, $RED_U$ is returned as the result of Algorithm 1.

The time complexity of Algorithm 1 is $O(|U|^2|C|^2)$. According to Definition 2, we first compute $T_C(u_i),1\le i \le n$ with a time complexity being O(|U||C|). Then, we can get $GK_U(C)$ with a time complexity being $O(|U|^2|C|)$. Thus, according to Definition 5, the time of calculating ${\text {Sig}}^{\text {inner}}_{U}(a_j,C,D)$ is $O(4|U|^2|C|)\approx O(|U|^2|C|)$. Therefore, the time complexity of Steps 2–7 is $O(|U|^2|C|^2)$. Similarly, the time complexity of Steps 9–15 is $O(|U|^2|C|^2)$, and the time complexity of Steps 16–20 is also $O(|U|^2|C|^2)$. Hence, the time complexity of Algorithm 1 is $O(|U|^2|C|^2)$ based on the foregoing analysis.

In Algorithm 2, $U^+$ denotes the new decision system after adding the incremental object $u_{(n+1)}$ to the original decision system U. The detailed execution process of Algorithm 2 is as follows. In Step 1, the reduct $RED_U$ on U is assigned to B. In Step 2, four tolerance classes of the incremental object $u_{(n+1)}$ in $U^+$, which are $T'_C(u_{(n+1)})$, $T'_{C\cup D}(u_{(n+1)})$, $T'_B(u_{(n+1)})$ and $T'_{B\cup D}(u_{(n+1)})$, are calculated respectively according to Definition 2. In Step 3, the knowledge granularity of B relative to D on $U^+$($GK_{U^+}(D|B)$) and the knowledge granularity of C relative to D on $U^+$($GK_{U^+}(D|C)$) are calculated, respectively, according to Proposition 3. In Step 4, $GK_{U^+}(D|B)$ is compared with $GK_{U^+}(D|C)$ if they are equal, then algorithm flow skips to step 19, which indicates that the reducts of $U^+$ and U are identical. Otherwise, the loop consisting of Steps 7–13 executes. Steps 8-10 constitute a loop used to calculate the outer significance of an certain $(a_i) \in (C-B)$, that is, ${\text {Sig}}^{\text {outer}}_{U^+}(a_i,B,D)$, according to Proposition 5. In Step 11, $a_0$ is used to store the attribute that has the maximum value of outer significance. In Step 12, $a_0$ is added to B. Steps 14–18 are actually used to delete attributes that satisfy the second condition in Definition 8 and a loop with |B| times. In Step 15, $GK_{U^+}(D|(B-\{a\}))$ is compared with $GK_{U^+}(D|C)$ if they are equal, then $a_i$ is deleted from B, which indicates that $a_i$ is redundant and cannot be in the reduct of $U^+$. In Step 19, B is assigned to $RED_{U^+}$. In Step 20, $RED_{U^+}$ is returned as the result of Algorithm 2.

The time complexity of Algorithm 2 is $O(|U||C|^2)$. According to Definition 2, the time complexity of computing $T'_C(u_{(n+1)})$ is O(|U||C|). Then, according to Proposition 3, the time complexity of Steps 2–3 is $O(|U||C|+|U|(|C|+1)+|U||B|+|U|(|B|+1))\approx O(|U||C|).$ According to Proposition 4, the time complexity of Steps 7–13 is $O(|U||C|^2)$. Similarly, the time complexity of Steps 14–18 is $O(|U||C|^2)$. Hence, the time complexity of Algorithm 2 is $O(|U||C|+|U||C|^2)+|U||C|^2)\approx O(|U||C|^2)$ based on the foregoing analysis.

Since the number of objects is $|U|+1$, the time complexity of THA is actually $O(|C|^2(|U|+1)^2)$ when adding the object $u_{n+1}$ to the object set U. Because $|U||C|^2\le (|U|+1)^2|C|^2$, $O(|U||C|^2)$ is much lower than $O((|U|+1)^2|C|^2)$. Hence, KGIRA spends much less time than THA.

3.3 An incremental mechanism to calculate knowledge granularity for IDS when deleting one object

For the sake of convenience, given an incomplete decision system ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$. $U=\{u_1,u_2,\ldots ,u_n\}$ denotes the original object set and $u_n$ denotes the object to be deleted from U. For simplicity, $U^-=U-\{u_n\}=\{u_1,u_2,\ldots ,u_{n-1}\}$ is written as $U^-$ in the following.

Proposition 6

Given an incomplete decision system ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$, where $U=\{u_1,u_2,\ldots ,u_n\}$denotes a non-empty finite set containing n objects. $u_n$is the object that will be deleted from IDS, and $T_C$is the tolerance relation on U. The knowledge granularity of C on $U^-$is

$$\begin{aligned} GK_{U^-}(C)=\frac{1}{{(n-1)}^2}[n^2GK_U(C)-(2|T_C(u_n)|-1)] \end{aligned}$$

(13)

Proof

After $u_n$ is deleting to U, the tolerance class of $u_i$ is

$$\begin{aligned} T''_C(u_i) = \left\{ \begin{array}{l} T_C(u_i)- \{u_n\},\;(u_i,u_n)\in T_C\;\\ T_C(u_i),\;(u_i,u_n)\notin T_C\; \end{array} \right. \;1\le i\le n-1. \end{aligned}$$

Suppose

$$\begin{aligned} \varDelta |T_C(u_i)| = \left\{ \begin{array}{l} 1,\;(u_i,u_n)\in T_C\;\\ 0,\;(u_i,u_n)\notin T_C\; \end{array} \right. \;1\le i\le n-1, \end{aligned}$$

then $|T''_C(u_i)| = |T_C(u_i)|-\varDelta |T_C(u_i)| ,1\le i\le n-1$. Because tolerance relation is symmetric, if $(u_i,u_n)\in T_C$, then $(u_n,u_i)\in T_C,1\le i\le n-1$. In other words, if $u_i\in T_C(u_n)$, then $u_n\in T_C(u_i),1\le i\le n-1$. Obviously, the number of objects that has tolerance relation with $u_n$ is equal to those whose tolerance class contains $u_n$ except $u_n$ itself on U. Then, we can get

$$\begin{aligned} \displaystyle {\sum _{i=1}^{n-1}} {\varDelta |T_C(u_i)|=|T_C(u_n)|-1}. \end{aligned}$$

According to Definition 3, the knowledge granularity of C on $U^-$ is described as follows:

$$\begin{aligned}&GK_{U^-}(C)\\&\quad = \displaystyle {\frac{1}{|U^-|^2} \sum _{i=1}^{|U^-|}} {|T''_C(u_i)|}\\&\quad = \displaystyle {\frac{1}{(n-1)^2}\left( \sum _{i=1}^{n} {|T_C(u_i)|-\sum _{i=1}^{n-1}} \varDelta |T_C(u_i)| -|T_C(u_n)|\right) }\\&\quad = \displaystyle {\frac{1}{(n-1)^2}\left[ \sum _{i=1}^{n} |T_C(u_i)|-(|T_C(u_n)|-1) -|T_C(u_n)|\right] }\\&\quad = \frac{1}{{(n-1)}^2}[n^2GK_U(C)-(2|T_C(u_n)|-1)]. \end{aligned}$$

$\square$

Proposition 7

Given an incomplete decision system ${\text {IDS}} = \left\langle {U,C \cup D,V,f} \right\rangle$, $u_n$is the deleting object. $T_C(u_n)$and $T_{C\cup D}(u_n)$are the tolerance classes of $u_n$with respect to attribute set C and $C\cup D$on U, respectively. The knowledge granularity of C relative to D on $U^-$is

$$\begin{aligned} GK_{U^-}(D|C)&= \frac{1}{{(n-1)}^2}[n^2GK_U(D|C)\nonumber \\&\quad -2(|T_C(u_n)|-|T_{C\cup D}(u_n)|)]. \end{aligned}$$

(14)

Proof

According to Definition 4 and Proposition 6, we have

$$\begin{aligned}&GK_{U^-}(D|C)\\&\quad = GK_{U^-}(C)-GK_{U^-}(C\cup D)\\&\quad = \frac{1}{{(n-1)}^2}[n^2GK_U(C)-(2|T_C(u_n)|-1)]\\&\qquad -\frac{1}{{(n-1)}^2}[n^2GK_U(C\cup D)-(2|T_{C\cup D}(u_n)|-1)]\\&\quad = \frac{1}{{(n-1)}^2}[n^2(GK_U(C)-GK_U(C\cup D))-2(|T_C(u_n)|\\&\qquad -|T_{C\cup D}(u_n)|)]\\&\quad = \frac{1}{{(n-1)}^2}[n^2GK_U(D|C)-2(|T_C(u_n)|-|T_{C\cup D}(u_n)|)] \end{aligned}$$

$\square$

3.4 An incremental reduction algorithm for IDS when deleting an object

Based on the incremental mechanism of knowledge granularity above, this subsection introduces an incremental attribute reduction algorithm (see Algorithm 3) when deleting multiple objects from the decision system.

In Algorithm 3, $U^-$ denotes the new decision system after deleting an object from the original decision system U. The detailed execution process of Algorithm 3 is as follows. In Step 1, the reduct $RED_U$ on U is assigned to B. In Step 2, the knowledge granularity of C relative to D on $U^{-}(GP_{U^-}(D|C))$ is calculated according to Proposition 7. Steps 3–7 are actually used to delete attributes that satisfies the second condition in Definition 8 and a loop with |B| times. In Step 4, $GP_{U^-}(D|(B-\{a_i\}))$ is compared with $GP_{U^-}(D|C)$ if they are equal, then $a_i$ is deleted from B, which indicates that $a_i$ is redundant and cannot be in the reduct of $U^-$. In Step 8, B is assigned to $RED_{U^-}$. In Step 9, $RED_{U^-}$ is returned as the result of Algorithm 3.

The time complexity of Algorithm 3 is $O(|C|^2(n-1))$. According to Definition 2 and Proposition 7, the time complexity of Step 2 is $O((|C|+1)(|U|-1))$. Then, similarly, the time complexity of Steps 3–9 is $O(|C|^2(|U|-1))$. Hence, the time complexity of Algorithm 3 is $O((|C|+1)(|U|-1)+|C|^2(|U|-1))\approx O(|C|^2(|U|-1))$ based on the foregoing analysis.

Since the number of objects is $|U|-1$, the time complexity of THA is actually $O(|C|^2(|U|-1)^2)$ when deleting the object $u_n$ from the object set U. Because $|C|^2(|U|-1)\le |C|^2(|U|-1)^2$, $O(|C|^2(|U|-1))$ is lower than $O(|C|^2(|U|-1)^2)$. Hence, KGIRD spends much less time than THA.

4 Empirical experiments

4.1 A description of data sets and experimental environment

In this section, the proposed incremental attribute reduction approach is tested on several real-life data sets available from the University of California Irvine (UCI) Repository of Machine Learning Database (Dua and Taniskidou 2017). The characteristics of the data sets are summarized in Table 2. For a complete data set, $5\%$ of the attribute values randomly selected from the data set are converted into missing values, which makes them into incomplete decision systems. The proposed algorithms are coded in Eclipse IDE for Java Developers with Neon.3 Release (4.6.3) version using JDK $1.8.0\_111$ version and they have been carried out on a personal computer with the following specification: Intel Core i5-3570 3.4 GHz CPU, 4.0 GB of memory, and 64-bit Win7.

Table 2 Description of data sets

4.2 Performance comparison between algorithm KGIRA and algorithm THA

In the experiments, each original data set is divided into ten parts averagely according to the number of objects. $20\%$ of each data set is used for basic data set and $80\%$ remaining objects is used for incremental data set added one by one in subsequent steps. Objects in incremental data set are added to basic data set one by one. Once the number of objects added reaches $10\%$ of the original data set, the time spent is recorded, until all objects in incremental data set are added to basic data set. In each subfigure of Fig.1, the x-axis is the percent of objects that exist in basic data set and the y-axis is the value of computational time. Circle marked lines are computational time of algorithm THA and asterisk marked lines are computational time of algorithm KGIRA.

From Fig.1, for each data set, the computational time of algorithm KGIRA and algorithm THA increase when the number of objects added to decision system increases. The computational time of algorithm KGIRA is much smaller than that of the algorithm THA. Moreover, the computational time of algorithm KGIRA on the last two data sets, SP and MF, is 174.954 s and 57.221 s, respectively. The computational time of algorithm THA on the same two data sets are both more than 8 h. Therefore, the comparison of the computational time of algorithm KGIRA and algorithm THA on data sets SP and MF is not shown in the graph.

Fig. 1

Results of execution for KGIRA and THA on data sets from UCI

In Table 3, we can find that some reducts obtained by algorithm KGIRA are not the same as those obtained by algorithm THA. Moreover, the number of selected attibutes in reduct, also called the length of reduct (LR), which obtained by algorithm KGIRA is a little more than that obtained by algorithm THA on most of data sets. It is because that algorithm KGIRA gets the reduct based on the previous result.

In Table 4, the precision of classification is calculated on selecting the reducts obtained by the algorithms THA and KGIRA. The classification accuracy is calculated by Naive Bayes Classifier (NB) and Decision Tree algorithm (REPTree) with fivefold cross validation. From Table 4, it is clear that the average classification accuracy of the reducts found by incremental algorithm KGIRA is better than those by algorithm THA. The experimental results show that the incremental algorithm KGIRA can discover a better attribute reduct compared with algorithm THA from the viewpoint of average classification performance. Moreover, incremental algorithm KGIRA can discover a feasible attribute reduct within a rather shorter calculation time.

Table 3 Comparison of reducts between algorithm THA and algorithm KGIRA

Table 4 Comparison of THA and KGIRA on classification accuracy

4.3 Performance comparison between algorithm KGIRD and algorithm THA

In the experiment, each original data set is used for basic data set and divided into ten parts averagely according to the number of objects. Objects are deleted from the basic data set one by one until $20\%$ of the original data set remains. Once the number of objects deleted reaches $10\%$ of the original data set, the time spent is recorded. In each subfigure of Fig. 1, the x-axis is the size of basic data set and the y-axis is the value of computational time. Circle marked lines are computational time of algorithm THA and asterisk marked lines are computational time of algorithm KGIRD.

From Fig. 2, for each data set, the computational time of algorithm KGIRD and algorithm THA increase when the number of objects deleted to decision system increases. The computational time of algorithm KGIRD is much smaller than that of the algorithm THA. Moreover, the computational time of algorithm KGIRD on the last two data sets, SP and MF, is 1777.764 s and 217.447 s, respectively. The computational time of algorithm THA on the same two data sets is both more than eight hours. Therefore, the comparison of the computational time of algorithm KGIRD and algorithm THA on data sets SP and MF is not shown in the graph.

Fig. 2

Results of execution for algorithm KGIRD and algorithm THA on data sets from UCI

In Table 5, we can find that nearly, half of reducts obtained by algorithm KGIRD are not the same as those obtained by algorithm THA. It is because algorithm KGIRD gets the reduct based on the previous result and algorithm THA computes the result from the beginning. Furthermore, reducts obtained by algorithm KGIRD from Table 5 are included in that obtained by algorithm THA from Table 3 on most data sets. This is because the original reducts are obtained by algorithm THA on the original data sets, and then, algorithm KGIRD gets the reducts based on the previous result.

In Table 6, the classification performance is calculated on the reducts obtained by algorithms THA and KGIRD. The results of classification accuracy are calculated by Naive Bayes Classifier (NB) and Decision Tree algorithm(REPTree) with fivefold cross validation. From Table 6, it is clear that the average classification accuracy of the reducts found by incremental algorithm KGIRD are little lower than those by algorithm THA, due to the bad performance on the first data set LC. The experimental results show that the incremental algorithm KGIRD can discover a satisfactory attribute reduct from the viewpoint of classification performance. Moreover, incremental algorithm KGIRD can discover a feasible attribute reduct within a rather shorter calculation time.

Table 5 Comparison of reducts between algorithm THA and algorithm KGIRD

Table 6 Comparison of THA and KGIRD on classification accuracy

5 Conclusion

In this paper, we use knowledge granularity to measure the uncertainty and the importance of attributes in incomplete decision systems. Based on this measure, incremental reduction algorithms for incomplete decision systems are constructed when adding multiple objects and deleting multiple objects one by one, respectively. To test the effectiveness of the constructed attribute selection approaches based on knowledge granularity, experiments on several real-life data from UCI data sets are conducted. Results show that the proposed approaches are effective to reduce the numbers of attributes obviously and incremental approaches are more efficient to update attribute reducts when the objects vary in incomplete decision systems than the non-incremental approach. Compared with existing methods (Jing et al. 2016; Yang et al. 2017), our approaches can deal with incomplete decision systems, which are more complicated. We plan to study knowledge granularity-based incremental attribute reduction solutions for incomplete decision systems under the situation of adding or deleting multiple objects at a time. Furthermore, it is worth of future research to use knowledge granularity to deal with the attribute reduction problem in fuzzy rough sets.