A new approach to similarity and inclusion measures between general type-2 fuzzy sets

Abstract

Interval type-2 fuzzy similarity and inclusion measures have been widely studied. In this paper, the axiomatic definitions of general type-2 fuzzy similarity and inclusion measures are given on the basis of interval type-2 fuzzy similarity and inclusion measures. To improve the shortcomings of the existing general type-2 fuzzy similarity and inclusion measures, we define two new general type-2 fuzzy similarity measures and two new general type-2 fuzzy inclusion measures based on $\alpha$-plane representation theory, respectively, and discuss their related properties. Unlike some existing measures, one of the proposed similarity and inclusion measures are expressed as type-1 fuzzy sets, and therefore these definitions are consistent with the highly uncertain nature of general type-2 fuzzy sets. The theoretical proof is also given to illustrate that the proposed measures are natural extensions of the most popular type-1 fuzzy measures. In the end, the performances of the proposed similarity and inclusion measures are examined.

1 Introduction

Type-1 fuzzy sets (Zadeh 1965) extend the classical notion of set and express the vagueness of real life. After decades of development, type-1 fuzzy sets have been successfully applied in the fields of automatic control, system identification, fault diagnosis, etc. To enhance the ability of systems for dealing with uncertainties and experience more freedom in design than type-1 fuzzy sets, Zadeh (1975) proposed type-2 fuzzy sets. The membership grades of type-2 fuzzy sets are type-1 fuzzy sets on [0, 1]. In highly uncertain situations, the performances of type-2 fuzzy sets are obviously beyond the type-1 fuzzy sets (Karnik et al. 1999). From the time Zadeh presented type-2 fuzzy set theory, its applications were limited due to the computational complexity. On the contrary, interval type-2 fuzzy set, as a simplified version of type-2 fuzzy set, has been made great development. The secondary membership grade of interval type-2 fuzzy set is 1, which makes it relatively simple. Thus, most of researchers were interested in the interval type-2 fuzzy systems (Liang and Mendel 2000). The general type-2 fuzzy sets can handle complex and changing systems, and therefore must be better than the interval type-2 fuzzy sets to deal with uncertainties (John and Coupland 2007).

So far, the investigations about general type-2 fuzzy sets are relatively less due to the computational complexity. In order to simplify the calculation for general type-2 fuzzy sets, researchers proposed various methods. The representation of general type-2 fuzzy sets is one of these methods. There are five kinds of popular representation for general type-2 fuzzy sets: vertical-slice representation, wave-slice representation, geometric representation, $\alpha$-plane representation, and z-slice representation. Vertical-slice representation of type-2 fuzzy set was firstly recognized by researchers, and so type-2 fuzzy systems were studied on the basis of Vertical-slice theory at the beginning (Mendel 2001). Subsequently, Mendel et al. (2006) proposed Wave-slice notation, and claimed that the set operations of type-2 fuzzy sets can be defined under the premise of not using the extension principle. Next, Coupland and John (2004a, b, 2007) proposed computational geometry representation for type-2 fuzzy sets, which is essentially approximate calculation method based on some discretizations to a certain extent, but also can reduce the calculation complexity. Recently, Liu (2008) proposed the $\alpha$-plane representation of type-2 fuzzy sets where centroid computation of type-2 fuzzy sets by using the $\alpha$-plane representation was studied, and it was claimed that the $\alpha$-plane representation can greatly reduce the computational workload. Almost at the same time, the theory of z-slice method has also been proposed in (Wagner and Hagras 2008, 2009, 2010), but Mendel et al. (2009) proved that z-slice method and $\alpha$-plane method are essentially same. The $\alpha$-plane method has been extensively studied (Mendel 2010; Zhai and Mendel 2011), because it can take advantages of the interval type-2 fuzzy sets theory to study the general type-2 fuzzy sets.

Similarity and inclusion measures between general type-2 fuzzy sets are important from applications point of view. In contrast to the investigations discussing similarity and inclusion measures between interval type-2 fuzzy sets (Wu and Mendel 2007; Zeng and Li 2006; Zeng and Guo 2008; Zhang et al. 2009; Wu and Mendel 2008, 2009; Liu and Xiong 2002), the research about similarity and inclusion measures between general type-2 fuzzy sets is relatively scarce (Mitchell 2005; Yang and Lin 2009; Hwang et al. 2011; Rickard et al. 2009). Mitchell (2005) defined a similarity measure for general type-2 fuzzy sets, but it has the following drawbacks: (1) it does not satisfy reflexivity, i.e., the similarity measure between $A$ and $A$ does not equal to 1; (2) the symmetry can not be satisfied; (3) the similarity measure may change from experiment to experiment. In addition, similarity and inclusion measures for general type-2 fuzzy sets based on the vertical slice theory have also been defined in (Yang and Lin 2009; Hwang et al. 2011), but the primary membership of type-2 fuzzy sets in each primary variable must be same. That is to say, the footprint of uncertainty must be same, which limits application scopes of these results. Rickard et al. (2009) used Zadeh’s extension principle to extend Kosko’s definition of the type-1 fuzzy inclusion measure, and defined type-2 fuzzy inclusion measure. However, their inclusion measure does not satisfy reflexivity (Mendel and Wu 2010), i.e., the inclusion measure between $A$ and $A$ does not equal to 1.

In order to expand the theoretical researches of similarity and include measures for general type-2 fuzzy sets, and also to improve the shortcomings of the existing measures, in this paper, we define two new general type-2 fuzzy similarity measures and two new general type-2 fuzzy inclusion measures based on $\alpha$-plane representation theory, respectively. Different from some existing general type-2 fuzzy similarity and inclusion measures, we put forward a new definition for general type-2 fuzzy similarity and inclusion measures, i.e., one of the proposed general type-2 fuzzy similarity and inclusion measures are expressed as type-1 fuzzy sets. The above definition method is consistent with the highly uncertain nature of general type-2 fuzzy set. However, it is not intuitive when the general type-2 fuzzy similarity and inclusion measures are expressed as type-1 fuzzy sets. Thus, another general type-2 fuzzy similarity and inclusion measures are defined as certain value in [0, 1]. The theoretical proof is also given to illustrate that the proposed measures are natural extensions of the most popular type-1 fuzzy measures. The rest of our work is organized as follows. In Sect. 2, the definitions and basic terminologies on general type-2 fuzzy sets will be reviewed briefly, and the axiomatic definitions of general type-2 fuzzy similarity and inclusion measures will also be given. In Sect. 3, the new general type-2 fuzzy similarity and inclusion measures will be defined, and their related properties will also be derived. Furthermore, in Sect. 4 we use numerical examples to examine the performances of the proposed similarity and inclusion measures. The last section concludes this paper.

2 Background

In this section, we review the definitions and basic terminologies on general type-2 fuzzy sets, and give the axiomatic definitions of general type-2 fuzzy similarity and inclusion measures.

2.1 $\alpha$-Plane representation theory for general type-2 fuzzy sets

Definition 2.1

(Mendel 2001) A type-2 fuzzy set, denoted $\tilde{A}$, is expressed as:

$$\begin{aligned} \tilde{A}=\int \limits _{x\in X} {u_{\tilde{A}} (x)/x} =\int \limits _{x\in X} \left[ \int \limits _{u_0 \in J_x^{\tilde{A}} } f_x (u_0 )/u_0\right] \bigg /x \quad J_x^{\tilde{A}} \subseteq [0,1]. \end{aligned}$$

where $J_x^{\tilde{A}}$ is the primary membership of $x;\,f_x (u_0)$ is a secondary membership grade.

In the following sections, the class of all general type-2 fuzzy sets of the universe $x$ is denoted as $F_2 (X)$.

Definition 2.2

(Mendel 2001) The footprint of uncertainty $(FOU)$ of a type-2 fuzzy set, $\tilde{A}$, is the union of all primary memberships, i.e.,

$$\begin{aligned} \textit{FOU}(\tilde{A})=\mathop \cup \limits _{x\in X} J_x^{\tilde{A}}. \end{aligned}$$

Definition 2.3

(Mendel 2001) The upper membership function is associated with the upper bound of $FOU(\tilde{A})$, and is denoted by $\bar{u}_{\tilde{A}} (x)$. The lower membership function is associated with the lower bound of $\textit{FOU}(A)$, and is denoted by $\underline{u}_{\tilde{A}} (x)$.

Definition 2.4

(Mendel et al. 2009) An $\alpha$-plane for general type-2 fuzzy set $\tilde{A}$, which is denoted by $\tilde{A}_\alpha$, is defined as follow:

$$\begin{aligned} \tilde{A}_\alpha&= \int \limits _{x\in X} \int \limits _{u_0 \in J_x^{\tilde{A}} } {\{(x,u_0 )\vert f_x (u_0 )\ge \alpha \}}\\&= \int \limits _{x\in X} {\left[ \int \limits _{u_0 \in [S_L^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{A}} (x\vert \alpha )]} {u_0 }\right] \Bigg /x}\quad \alpha \in [0,1]. \end{aligned}$$

where $[S_L^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{A}} (x\vert \alpha )]$ denote an $\alpha$-cut of the secondary membership function $u_{\tilde{A}} (x)$.

From the Definitions 2.2 and 2.4, we have $FOU(\tilde{A})=\tilde{A}_0$. That is to say, the FOU of a type-2 fuzzy set is the $\alpha =0$ plane. Furthermore, $\alpha /\tilde{A}_\alpha$ can be regarded as a special interval type-2 fuzzy set whose secondary membership grade is equal to $\alpha$.

Definition 2.5

(Mendel et al. 2009) The $\alpha$-plane representation (theorem) for type-2 fuzzy set $\tilde{A}$ is

$$\begin{aligned} \tilde{A}=\mathop \cup \limits _{\alpha \in [0,1]} \alpha /\tilde{A}_\alpha . \end{aligned}$$

From the above definition, we can find that a general type-2 fuzzy set can be decomposed into some special interval type-2 fuzzy sets. As a result, the advantages of interval type-2 fuzzy sets can be used to study general type-2 fuzzy sets, and many complex definitions and representations can also be simplified by using $\alpha$-plane approach. For example, the set-theoretic operations based $\alpha$-plane representation are more intuitionistic than those based on extension principle.

Theorem 2.1

(Mendel et al. 2009) Let $(\tilde{A}\cup \tilde{B})_\alpha$ and $(\tilde{A}\cap \tilde{B})_\alpha$ be $\alpha$ -plane of $\tilde{A}\cup \tilde{B}$ and $\tilde{A}\cap \tilde{B}$, respectively, we have

$$\begin{aligned} \tilde{A}\cup \tilde{B}\!&= \!\!\!\!\mathop \cup \limits _{\alpha \in [0,1]} \alpha /(\tilde{A}_\alpha \cup \tilde{B}_\alpha );\\ \tilde{A}\cap \tilde{B}&= \mathop \cup \limits _{\alpha \in [0,1]} \alpha /(\tilde{A}_\alpha \cap \tilde{B}_\alpha ). \end{aligned}$$

where

$$\begin{aligned} \tilde{A}_\alpha \cup \tilde{B}_\alpha&\!= \int \limits _{x\in X} {\left[ \int \limits _{u_0 \in [S_L^{\tilde{A}} (x\vert \alpha )\vee S_L^{\tilde{B}} (x\vert \alpha ),S_R^{\tilde{A}} (x\vert \alpha )\vee S_R^{\tilde{B}} (x\vert \alpha )]} {u_0 } \right] \Bigg /x} ;\\ \tilde{A}_\alpha \cap \tilde{B}_\alpha&= \int \limits _{x\in X} {\left[ \int \limits _{u_0 \in [S_L^{\tilde{A}} (x\vert \alpha )\wedge S_L^{\tilde{B}} (x\vert \alpha ),S_R^{\tilde{A}} (x\vert \alpha )\wedge S_R^{\tilde{B}} (x\vert \alpha )]} {u_0 } \right] \Bigg /x} \end{aligned}$$

Obviously,  $S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )\!=\!S_L^{\tilde{A}} (x\vert \alpha )\vee S_L^{\tilde{B}} (x\vert \alpha ),\,S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )=S_R^{\tilde{A}} (x\vert \alpha )\vee S_R^{\tilde{B}} (x\vert \alpha ),\,S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )=S_L^{\tilde{A}} (x\vert \alpha )\wedge S_L^{\tilde{B}} (x\vert \alpha )$ and $S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )=S_R^{\tilde{A}} (x\vert \alpha )\wedge S_R^{\tilde{B}} (x\vert \alpha )$ hold.

Definition 2.6

(Hamrawi and Coupland 2010) Let $\tilde{A},\tilde{B}\in F_2 (X)$, define $\tilde{A}\subseteq \tilde{B}$ if $S_L^{\tilde{A}} (x\vert \alpha )\le S_L^{\tilde{B}} (x\vert \alpha )$ and $S_R^{\tilde{A}} (x\vert \alpha )\le S_R^{\tilde{B}} (x\vert \alpha )$ hold for any $\alpha \in [0,1]$ and $x\in X$.

It can be seen that the above containment concept of general type-2 fuzzy sets satisfies the following properties: (1) if $\tilde{A}\subseteq \tilde{B}$ and $\tilde{B}\subseteq \tilde{A}$, then $\tilde{A}=\tilde{B}$; (2) if $\tilde{A}\subseteq \tilde{B}$ and $\tilde{B}\subseteq \tilde{C}$, then $\tilde{A}\subseteq \tilde{C}$; (3) $\tilde{A}\subseteq \tilde{B}\Leftrightarrow \tilde{A}\cap \tilde{B}=\tilde{A}$ and $\tilde{A}\cup \tilde{B}=\tilde{B}$. Thus, the above containment definition of general type-2 fuzzy sets is intuitive and justified. Certainly, the containment concept of type-2 fuzzy sets is still to be properly defined by using other approaches.

In Zhai and Mendel (2011), five uncertainty measures of general type-2 fuzzy sets were studied by using $\alpha$-plane representation theory. Similar to the literature (Zhai and Mendel 2011), in this paper we also make some assumptions on the secondary membership functions. For any $\tilde{A}=\int _{x\in X} {[\int _{u_0 \in J_x^{\tilde{A}} } {f_x (u_0 )/u_0 ]/x} }$, it must satisfy:

$$\begin{aligned}&f_{x} (u_{0})\nonumber \\&\quad = \left\{ \begin{array}{ll} {g_x (u_0 )} &{}\quad {u_0 \in [S_L^{\tilde{A}} (x\vert 0),S_L^{\tilde{A}} (x\vert 1)]}\\ 1 &{}\quad {u_0 \in [S_L^{\tilde{A}} (x\vert 1),S_R^{\tilde{A}} (x\vert 1)]}\\ {h_x (u_0 )} &{}\quad {u_0 \in [S_R^{\tilde{A}} (x\vert 1),S_R^{\tilde{A}} (x\vert 0)]} \\ 0 &{}\quad {u_0 \in (-\infty ,S_L^{\tilde{A}} (x\vert 0))\cup (S_R^{\tilde{A}} (x\vert 0),\infty )}\\ \end{array} \right. , \end{aligned}$$

where $g_x (u_0 )\in [0,1]$ is monotonically non-decreasing, and $h_x (u_0 )\in [0,1]$ is monotonically non-increasing. That is to say, each secondary membership function of $\tilde{A}$ must be a normal and convex type-1 fuzzy set.

2.2 Axiomatic definitions of general type-2 fuzzy similarity and inclusion measures

Similarity and inclusion measures have important applications in the fields of clustering analysis, word computing, fault diagnosis, etc. In contrast to type-1 fuzzy similarity and inclusion measures, there are two explanations about general type-2 fuzzy similarity and inclusion measures. First, general type-2 fuzzy similarity and inclusion measures are type-1 fuzzy sets on [0, 1]. Second, general type-2 fuzzy similarity and inclusion measures are certain value in [0, 1]. In Zhai and Mendel (2011), five uncertainty measures of general type-2 fuzzy sets were studied, and the ultimate manifestation of these measures are type-1 fuzzy sets. In fact, type-2 fuzzy sets are mainly used to describe highly uncertain phenomenon, so it is coincident with the nature of law when the uncertainty measures of type-2 fuzzy sets are expressed as type-1 fuzzy sets. Similarly, the general type-2 fuzzy similarity and inclusion measures should be represented as type-1 fuzzy sets. However, if the general type-2 fuzzy similarity and inclusion measures are expressed as uncertain amounts, then they may be subject to certain restrictions in practical applications because that they are not intuitive. One solution is that these type-1 fuzzy sets are defuzzified, so that one can get some certain values. Another solution is that we directly define these type-2 fuzzy similarity and inclusion measures as certain value in [0, 1]. In summary, if the type-2 fuzzy similarity and inclusion measures are expressed as uncertain amount, they are more in line with the nature of type-2 fuzzy sets. If type-2 fuzzy similarity and inclusion measures are expressed as certain values, they are more intuitive and play an important role in practical applications. In the following, the two situations will be discussed.

Similar to the axiomatic definitions of interval type-2 fuzzy similarity and inclusion measures (Mendel and Wu 2010), we give the axiomatic definitions of general type-2 fuzzy similarity and inclusion measures in next part. Here we define type-2 fuzzy empty set $\tilde{\emptyset }=\int _{x\in X} {[\int _{u_0 \in [0,0]} {1/u_0 ]/x}}$. Obviously, $S_L^{\tilde{\emptyset }} (x\vert \alpha )=S_R^{\tilde{\emptyset }} (x\vert \alpha )=0$ holds for any $x\in X$ and $\alpha \in [0,1]$.

Definition 2.7

A real function $I:F_2 (X)\times F_2 (X)\rightarrow [0,1]$ is called an inclusion measure of general type-2 fuzzy sets, if $I$ satisfies the following axioms:

• (I1) $\forall \tilde{A}\in F_2 (X),I(\tilde{A},\tilde{\emptyset })=0;$

• (I2) $\forall \tilde{A},\tilde{B}\in F_2 (X),\tilde{A}\subseteq \tilde{B}\Leftrightarrow I(\tilde{A},\tilde{B})=1;$

• (I3) $\forall \tilde{A},\tilde{B},\tilde{C}\in F_2 (X),\tilde{A}\subseteq \tilde{B}\subseteq \tilde{C}\Rightarrow I(\tilde{C},\tilde{A})\le I(\tilde{B},\tilde{A}),I(\tilde{C},\tilde{A})\le I(\tilde{C},\tilde{B}).$

Remark 1

If $I(\bullet ,\bullet )$ is a type-1 fuzzy set, then “0” in (I1) is expressed as “1/0”, “1” in (I2) is expressed as “1/1”, and “$\le$” in (I3) represents inclusion relation of type-1 fuzzy sets.

Definition 2.8

A real function $S:F_2 (X)\times F_2 (X)\rightarrow [0,1]$ is called a similarity measure of general type-2 fuzzy sets, if $S$ satisfies the following axioms:

• (S1) $\forall \tilde{A},\tilde{B}\in F_2 (X),S(\tilde{A},\tilde{B})=S(\tilde{B},\tilde{A});$

• (S2) $\forall \tilde{A}\in F_2 (X),S(\tilde{A},\tilde{A})=1;$

• (S3) $\forall \tilde{A},\tilde{B},\tilde{C}\in F_2 (X),\tilde{A}\subseteq \tilde{B}\subseteq \tilde{C}\Rightarrow S(\tilde{A},\tilde{C})\le S(\tilde{A},\tilde{B}),S(\tilde{A},\tilde{C})\le S(\tilde{B},\tilde{C}).$

Remark 2

If $S(\bullet ,\bullet )$ is a type-1 fuzzy set, then “1” in (S2) is expressed as “1/1”, and “$\le$” in (S3) represents inclusion relation of type-1 fuzzy sets.

3 General type-2 fuzzy similarity and inclusion measures

3.1 Definitions of general type-2 fuzzy inclusion measures

The most popular inclusion measure for type-1 fuzzy sets was proposed by Kosko (1990), which is

$$\begin{aligned} I_K (A,B)=\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx}}{\int _{x\in X} {u_A (x)dx} }. \end{aligned}$$

where $A$ and $B$ are type-1 fuzzy sets on $X$. The notation $\int$ is an integral, for discrete universes of discourse X, $\int$ is replaced by the summation $\sum$.

In the following, based on the Definition 2.7 and the foregoing analysis, we define new general type-2 fuzzy inclusion measures. Furthermore, the theoretical proof will also be given to illustrate that the proposed inclusion measures are natural extensions of the type-1 fuzzy inclusion measure $I_K (\bullet ,\bullet )$. The new general type-2 fuzzy inclusion measure is defined as:

$$\begin{aligned} I_1 (\tilde{A},\tilde{B})=\mathop \cup \limits _{\alpha \in [0,1]} \{\alpha /[I_L (\tilde{A},\tilde{B},a),I_R (\tilde{A},\tilde{B},a)]\}. \end{aligned}$$

where

$$\begin{aligned}&I_L (\tilde{A},\tilde{B},a)\!=\!\min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx}}{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx}},\right. \\&\qquad \qquad \qquad \qquad \qquad \quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx}}{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx}}\right\} ;\\&I_R (\tilde{A},\tilde{B},a)\!=\!\max \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} },\right. \\&\qquad \qquad \qquad \qquad \qquad \quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ), S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx}}\right\} . \end{aligned}$$

Theorem 3.1

$I_1 (\bullet , \bullet )$ is an inclusion measure on $F_2 (X)$.

Proof

(I1) $\forall \tilde{A}\in F_2 (X),\,\alpha \in [0,1]$ and $x\in X$, we have $S_L^{\tilde{A}} (x\vert \alpha )\wedge S_L^{\tilde{\emptyset }} (x\vert \alpha )=0$ and $S_R^{\tilde{A}} (x\vert \alpha )\wedge S_R^{\tilde{\emptyset }} (x\vert \alpha )=0$. That is to say, for any $\alpha \in [0,1]$, we have $I_L (\tilde{A},\tilde{B},a)=I_R (\tilde{A},\tilde{B},a)=0$. Thus, $I_1 (\tilde{A},\tilde{\emptyset })=1/0$.

(I2) if $\tilde{A}\subseteq \tilde{B}$, then $S_L^{\tilde{A}} (x\vert \alpha )\le S_L^{\tilde{B}} (x\vert \alpha )$ and $S_R^{\tilde{A}} (x\vert \alpha )\le S_R^{\tilde{B}} (x\vert \alpha )$ hold for any $\alpha \in [0,1]$ and $x\in X$. Thus, $I_L (\tilde{A},\tilde{B},a)=1$ and $I_R (\tilde{A},\tilde{B},a)=1$ hold for any $\alpha \in [0,1]$. We obtain $I_1 (\tilde{A},\tilde{B})=1/1$. On the other hand, if $I_1 (\tilde{A},\tilde{B})=1/1$, then $I_L (\tilde{A},\tilde{B},a)=1$ and $I_R (\tilde{A},\tilde{B},a)=1$ hold for any $\alpha \in [0,1]$. Thus, for any $\alpha \in [0,1]$, we have

$$\begin{aligned} \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} }\!=\!\frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} }=1. \end{aligned}$$

Thus,$\int \nolimits _{x\in X} {[S_L^{\tilde{A}} (x\vert \alpha )-\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))]dx} =\int \nolimits _{x\in X} {[S_R^{\tilde{A}} (x\vert \alpha )-\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))]dx} =0.$

Since $S_L^{\tilde{A}} (x\vert \alpha )-\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))\ge 0$ and $S_R^{\tilde{A}} (x\vert \alpha )-\min (S_R^{\tilde{A}} (x\vert \alpha ), S_R^{\tilde{B}} (x\vert \alpha ))\ge 0$ hold for any $\alpha \in [0,1]$ and $x\in X$, we have $S_L^{\tilde{A}} (x\vert \alpha )=\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))$ and $S_R^{\tilde{A}} (x\vert \alpha )=\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))$. That is to say, $S_L^{\tilde{A}} (x\vert \alpha )\le S_L^{\tilde{B}} (x\vert \alpha )$ and $S_R^{\tilde{A}} (x\vert \alpha )\le S_R^{\tilde{B}} (x\vert \alpha )$ hold for any $\alpha \in [0,1]$ and $x\in X$. Therefore, $\tilde{A}\subseteq \tilde{B}$.

(I3) if $\tilde{A}\subseteq \tilde{B}\subseteq \tilde{C}$, then $S_L^{\tilde{A}} (x\vert \alpha )\le S_L^{\tilde{B}} (x\vert \alpha )\le S_L^{\tilde{C}} (x\vert \alpha )$ and $S_R^{\tilde{A}} (x\vert \alpha )\le S_R^{\tilde{B}} (x\vert \alpha )\le S_R^{\tilde{C}} (x\vert \alpha )$ hold for any $\alpha \in [0,1]$ and $x\in X$. We have $I_L (\tilde{C},\tilde{A},a)\le I_L (\tilde{B},\tilde{A},a)$ and $I_R (\tilde{C},\tilde{A},a)\le I_R (\tilde{B},\tilde{A},a)$ for any $\alpha \in [0,1]$. Thus, $I_1 (\tilde{C},\tilde{A})\le I_1 (\tilde{B},\tilde{A})$. Similarly,$I_1 (\tilde{C},\tilde{A})\le I_1 (\tilde{C},\tilde{B})$. The whole proof is completed. $\square$

Theorem 3.2

If $\tilde{A}$ and $\tilde{B}$ are degenerated to the type-1 fuzzy sets on $X$, then the general type-2 fuzzy inclusion measure $I_1 (\bullet , \bullet )$ becomes the type-1 fuzzy inclusion measure $I_K (\bullet , \bullet )$.

Proof

Since $\tilde{A}$ and $\tilde{B}$ are degenerated to the type-1 fuzzy set on $X$, we have

$$\begin{aligned} \tilde{A}=\int \limits _{x\in U} {u_{\tilde{A}} (x)/x}&= \int \limits _{x\in X} \left[ \int \limits _{u_0 \in J_x^{\tilde{A}} } 1/u_0\right] \bigg /x ,\quad J_x^{\tilde{A}} \in [0,1],\\ \tilde{B}=\int \limits _{x\in U} {u_{\tilde{B}} (x)/x}&= \int \limits _{x\in X} \left[ \int \limits _{u_0 \in J_x^{\tilde{B}} } 1/u_0 \right] \bigg /x ,\quad J_x^{\tilde{B}} \in [0,1]. \end{aligned}$$

That is to say, the primary memberships $J_x^{\tilde{A}}$ and $J_x^{\tilde{B}}$ of $x$ only can take a sole value. Thus, we obtain $S_L^{\tilde{A}} (x\vert \alpha )=S_R^{\tilde{A}} (x\vert \alpha )=S_L^{\tilde{A}} (x\vert 1)$ and $S_L^{\tilde{B}} (x\vert \alpha )=S_R^{\tilde{B}} (x\vert \alpha )=S_L^{\tilde{B}} (x\vert 1)$ for any $x\in X$ and $\alpha \in [0,1]$. If we set $S_L^{\tilde{A}} (x\vert 1)=u_A (x)$ and $S_L^{\tilde{B}} (x\vert 1)=u_B (x)$, then $u_A (x)\in [0,1]$ and $u_B (x)\in [0,1]$ are functions related to $x\in X$. Thus,

$$\begin{aligned}&\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} }\\&\quad =\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx} }{\int _{x\in X} {u_A (x)dx} },\\&\frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} }\\&\quad =\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx} }{\int _{x\in X} {u_A (x)dx} }. \end{aligned}$$

That is to say, for any $\alpha \in [0,1]$, we have

$$\begin{aligned} I_L (\tilde{A},\tilde{B},a)=I_R (\tilde{A},\tilde{B},a)=\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx} }{\int _{x\in X} {u_A (x)dx} }. \end{aligned}$$

Hence, $I_1 (\tilde{A},\tilde{B})=\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx} }{\int _{x\in X} {u_A (x)dx} }$. The whole proof is completed. $\square$

The general steps for computing the general type-2 fuzzy inclusion measure $I_1 (\tilde{A},\tilde{B})$ can be summarized as:

Step1: decide on the numbers of $\alpha$-planes. Call that number $\Delta +1$. Regardless of $\Delta +1$, $\alpha =0$ and $\alpha =1$ must always be used.

Step2: for each $\alpha$, compute $\alpha /[I_L (\tilde{A},\tilde{B},a),I_R (\tilde{A},\tilde{B},a)]$.

Step3: compute $I_1 (\tilde{A},\tilde{B})$.

Noted that the inclusion measure $I_1 (\bullet ,\bullet )$ is a type-1 fuzzy set, so we can obtain the centroid $Centroid(I_1 (\bullet ,\bullet ))$ of $I_1 (\bullet ,\bullet )$ by using centroid defuzzification method. Based on $Centroid(I_1 (\bullet ,\bullet ))$, we can be very intuitive to see the degree to which a type-2 fuzzy set is included in another type-2 fuzzy set. As the foregoing analysis, another program is that we directly define general type-2 fuzzy inclusion measure as certain value in [0, 1]. If the $\alpha$ is broken into $\Delta +1$ values, the general type-2 fuzzy inclusion measure $I_2 (\bullet ,\bullet )$ as a certain value, is defined as follow:

$$\begin{aligned}&I_2 (\tilde{A},\tilde{B})=\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\cdots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} } }}. \end{aligned}$$

Theorem 3.3

$I_2 (\bullet ,\bullet )$ is an inclusion measure on $F_2 (X)$.

Proof

(I1) $\forall \tilde{A}\in F_2 (X),\,\alpha \in [0,1]$ and $x\in X$, we have $S_L^{\tilde{A}} (x\vert \alpha )\wedge S_L^{\tilde{\emptyset }} (x\vert \alpha )=0$ and $S_R^{\tilde{A}} (x\vert \alpha )\wedge S_R^{\tilde{\emptyset }} (x\vert \alpha )=0$. That is to say, for any $\alpha \in [0,1]$, we have

$$\begin{aligned} \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{\emptyset }} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{\emptyset }} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} } }=0. \end{aligned}$$

Thus, $I_2 (\tilde{A},\tilde{\emptyset })=0$.

(I2) if $\tilde{A}\subseteq \tilde{B}$, then $S_L^{\tilde{A}} (x\vert \alpha )\le S_L^{\tilde{B}} (x\vert \alpha )$ and $S_R^{\tilde{A}} (x\vert \alpha )\le S_R^{\tilde{B}} (x\vert \alpha )$ hold for any $\alpha \in [0,1]$ and $x\in X$. Thus, for any $\alpha \in [0,1]$, we have

$$\begin{aligned}&\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} } }\\&\quad =\frac{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} } }=1. \end{aligned}$$

We obtain $I_2 (\tilde{A},\tilde{B})=1$.

On the other hand, if $I_2 (\tilde{A},\tilde{B})=1$, then

$$\begin{aligned}&\Delta +1 =\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx}}}}. \end{aligned}$$

Since $\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} } }\le 1$, we have$\int \nolimits _{x\in X} {[S_L^{\tilde{A}} (x\vert \alpha )-\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))]dx}+\int \nolimits _{x\in X} {[S_R^{\tilde{A}} (x\vert \alpha )-\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))]dx} =0.$

Furthermore, $S_L^{\tilde{A}} (x\vert \alpha )-\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))\ge 0$ and $S_R^{\tilde{A}} (x\vert \alpha )-\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))\ge 0$ hold for any $\alpha \in [0,1]$ and $x\in X$. Thus, $S_L^{\tilde{A}} (x\vert \alpha )\le S_L^{\tilde{B}} (x\vert \alpha )$ and $S_R^{\tilde{A}} (x\vert \alpha )\le S_R^{\tilde{B}} (x\vert \alpha )$ hold for any $\alpha \in [0,1]$ and $x\in X$. That is to say, $\tilde{A}\subseteq \tilde{B}$.

(I3) if $\tilde{A}\subseteq \tilde{B}\subseteq \tilde{C}$, then $S_L^{\tilde{A}} (x\vert \alpha )\le S_L^{\tilde{B}} (x\vert \alpha )\le S_L^{\tilde{C}} (x\vert \alpha )$ and $S_R^{\tilde{A}} (x\vert \alpha )\le S_R^{\tilde{B}} (x\vert \alpha )\le S_R^{\tilde{C}} (x\vert \alpha )$ hold for any $\alpha \in [0,1]$ and $x\in X$. That is to say, for any$\alpha \in [0,1]$, we have

$$\begin{aligned}&I_2 (\tilde{C},\tilde{A})=\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{C}} (x\vert \alpha ),S_L^{\tilde{A}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{C}} (x\vert \alpha ),S_R^{\tilde{A}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{C}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{C}} (x\vert \alpha )dx} } }}\\&\quad =\frac{1}{\Delta +1}\sum _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1} {\frac{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{C}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{C}} (x\vert \alpha )dx} } }}\\&\quad \le \frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1} {\frac{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{B}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{B}} (x\vert \alpha )dx} } }}\\&\quad =\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{B}} (x\vert \alpha ),S_L^{\tilde{A}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{B}} (x\vert \alpha ),S_R^{\tilde{A}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{B}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{B}} (x\vert \alpha )dx} } }}\\&\quad =I_2 (\tilde{B},\tilde{A}). \end{aligned}$$

Similarly, $I_2 (\tilde{C},\tilde{A})\le I_2 (\tilde{C},\tilde{B})$. The whole proof is completed. $\square$

Theorem 3.4

If $\tilde{A}$ and $\tilde{B}$ are degenerated to the type-1 fuzzy sets on $X$, then the general type-2 fuzzy inclusion measure $I_2 (\bullet ,\bullet )$ becomes the type-1 fuzzy inclusion measure $I_K (\bullet ,\bullet )$.

Proof

If $\tilde{A}$ and $\tilde{B}$ are degenerated to the type-1 fuzzy set on $X$, from the discussion of Theorem 3.2, we have $S_L^{\tilde{A}} (x\vert 1)=u_A (x)$ and $S_L^{\tilde{B}} (x\vert 1)=u_B (x)$, where $u_A (x)\in [0,1]$ and $u_B (x)\in [0,1]$ are functions related to $x\in X$. Thus, for any $\alpha \in [0,1]$, we have

$$\begin{aligned}&\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx}}{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} } }\\&=\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx} +\int _{x\in X}{\min (u_A (x),u_B (x))dx} }{\int _{x\in X} {u_A(x)dx+\int _{x\in X} {u_A (x)dx} } }\\&=\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx} }{\int _{x\in X} {u_A (x)dx} }. \end{aligned}$$

That is to say, $I_2 (\tilde{A},\tilde{B})=\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx} }{\int _{x\in X} {u_A (x)dx} }$. The whole proof is completed. $\square$

Remark 3

Rickard et al. (2009) used Zadeh’s extension principle to define a general type-2 fuzzy inclusion measure. It should be noted that the measure defined there is also represented as type-1 fuzzy set. Rickard’s inclusion measure has important application values. However, it does not satisfy reflexivity. From Theorem 3.1, we find that the proposed measure $I_1 (\bullet ,\bullet )$ can satisfy reflexivity. Furthermore, it will also be seen that the proposed inclusion measures $I_1 (\bullet ,\bullet )$ and $I_2 (\bullet ,\bullet )$ would obtain more desirable properties than Rickard’s inclusion measure from Sect. 3.3. The inclusion measures of general type-2 fuzzy sets based on the vertical slice theory have also been defined in (Yang and Lin 2009; Hwang et al. 2011), but it is required that the FOU of two general type-2 fuzzy sets must be same. From the definitions of $I_1 (\bullet ,\bullet )$ and $I_2 (\bullet ,\bullet )$, one can know that the proposed measures have not such limitations.

3.2 Definitions of general type-2 fuzzy similarity measures

The most popular similarity measure for type-1 fuzzy sets was proposed by Jaccard (Wu and Mendel 2009), which is

$$\begin{aligned} S_J (A,B)=\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx}}{\int _{x\in X} {\max (u_A (x),u_B (x))dx}}. \end{aligned}$$

where $A$ and $B$ are type-1 fuzzy sets on $X$. The notation $\smallint$ is an integral, for discrete universes of discourse $X$, $\smallint$ is replaced by the summation $\sum$.

In the following, based on the Definition 2.8 and the foregoing analysis, we define new general type-2 fuzzy similarity measures. Furthermore, the theoretical proof will also be given to illustrate that the proposed similarity measures are natural extensions of the type-1 fuzzy similarity measure $S_J (\bullet ,\bullet )$. The new general type-2 fuzzy similarity measure is defined as:

$$\begin{aligned} S_1 (\tilde{A},\tilde{B})=\mathop \cup \limits _{\alpha \in [0,1]} \{\alpha /[S_L (\tilde{A},\tilde{B},a),S_R (\tilde{A},\tilde{B},a)]\} \end{aligned}$$

where

$$\begin{aligned} S_L (\tilde{A},\tilde{B},a)=\min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx}},\right. \\ \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx}}\right\} ;\\ S_R (\tilde{A},\tilde{B},a)=\max \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx}},\right. \\ \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx}}\right\} . \end{aligned}$$

Theorem 3.5

$S_1 (\bullet ,\bullet )$ is a similarity measure on $F_2 (X)$.

Proof

(S1) and (S2) are trivial.

(S3) if $\tilde{A}\subseteq \tilde{B}\subseteq \tilde{C}$, then $S_L^{\tilde{A}} (x\vert \alpha )\le S_L^{\tilde{B}} (x\vert \alpha )\le S_L^{\tilde{C}} (x\vert \alpha )$ and $S_R^{\tilde{A}} (x\vert \alpha )\le S_R^{\tilde{B}} (x\vert \alpha )\le S_R^{\tilde{C}} (x\vert \alpha )$ hold for any $\alpha \in [0,1]$ and $x\in X$. Thus, for any $\alpha \in [0,1]$, we have

$$\begin{aligned} S_L (\tilde{A},\tilde{C},a)&= \min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{C}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{C}} (x\vert \alpha ))dx} },\right. \\&\quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{C}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{C}} (x\vert \alpha ))dx}}\right\} \\&= \min \left\{ \frac{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{C}} (x\vert \alpha )dx} },\frac{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} }{\int _{x\in X} {S_R^{\tilde{C}} (x\vert \alpha )dx}}\right\} \\&\le \min \left\{ \frac{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{B}} (x\vert \alpha )dx} },\frac{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx}}{\int _{x\in X} {S_R^{\tilde{B}} (x\vert \alpha )dx}}\right\} \\&= \min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx}},\right. \\&\quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx}}\right\} . \end{aligned}$$

That is to say, $S_L (\tilde{A},\tilde{C},a)\le S_L (\tilde{A},\tilde{B},a)$. Similarly, we obtain $S_R (\tilde{A},\tilde{C},a)\le S_R (\tilde{A},\tilde{B},a)$.

Therefore, $S_1 (\tilde{A},\tilde{C})\le S_1 (\tilde{A},\tilde{B})$. Similarly, $S_1 (\tilde{A},\tilde{C})\le S_1 (\tilde{B},\tilde{C})$. The whole proof is completed. $\square$

Theorem 3.6

If $\tilde{A}$ and $\tilde{B}$ are degenerated to the type-1 fuzzy sets on $X$, then the general type-2 fuzzy similarity measure $S_1 (\bullet ,\bullet )$ becomes the type-1 fuzzy similarity measure $S_J (\bullet ,\bullet )$.

Proof

If $\tilde{A}$ and $\tilde{B}$ are degenerated to the type-1 fuzzy set on $X$, from the discussion of Theorem 3.2, we have $S_L^{\tilde{A}} (x\vert 1)=u_A (x)$ and $S_L^{\tilde{B}} (x\vert 1)=u_B (x)$, where $u_A (x)\in [0,1]$ and $u_B (x)\in [0,1]$ are functions related to $x\in X$. Thus, for any $\alpha \in [0,1]$, we have

$$\begin{aligned} S_L (\tilde{A},\tilde{B},a)=S_R (\tilde{A},\tilde{B},a)=\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx} }{\int _{x\in X} {\max (u_A (x),u_B (x))dx} }. \end{aligned}$$

That is to say, $S_1 (\tilde{A},\tilde{B})=\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx} }{\int _{x\in X} {\max (u_A (x),u_B (x))dx} }$. The whole proof is completed. $\square$

Noted that the similarity measure $S_1 (\bullet ,\bullet )$ is a type-1 fuzzy set, so we can obtain the centroid $Centroid(S_1 (\bullet ,\bullet ))$ of $S_1 (\bullet ,\bullet )$ by using centroid defuzzification method. If the $\alpha$ is broken into $\Delta +1$ values, the general type-2 fuzzy similarity measure $S_2 (\bullet ,\bullet )$ as a certain value, is defined as follow:

$$\begin{aligned}&S_2 (\tilde{A},\tilde{B})=\frac{1}{\Delta +1}\sum \limits _{\alpha = 0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }}. \end{aligned}$$

Theorem 3.7

$S_2 (\bullet ,\bullet )$ is a similarity measure on $F_2 (X)$.

Proof

(S1) and (S2) are trivial.

(S3) if $\tilde{A}\subseteq \tilde{B}\subseteq \tilde{C}$, then $S_L^{\tilde{A}} (x\vert \alpha )\le S_L^{\tilde{B}} (x\vert \alpha )\le S_L^{\tilde{C}} (x\vert \alpha )$ and $S_R^{\tilde{A}} (x\vert \alpha )\le S_R^{\tilde{B}} (x\vert \alpha )\le S_R^{\tilde{C}} (x\vert \alpha )$ hold for any $\alpha \in [0,1]$ and $x\in X$. Thus, for any $\alpha \in [0,1]$, we have

$$\begin{aligned}&S_2 (\tilde{A},\tilde{C})=\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{C}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{C}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{C}} (x\vert \alpha ))dx} +\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{C}} (x\vert \alpha ))dx} }}\\&\quad \quad =\frac{1}{\Delta +1}\sum _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1} {\frac{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{C}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{C}} (x\vert \alpha )dx} }}\\&\quad \quad \le \frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1} {\frac{\int \limits _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{B}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{B}} (x\vert \alpha )dx} }}\\&\quad \quad =\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad \quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }}\\&\quad \quad =S_2 (\tilde{A},\tilde{B}). \end{aligned}$$

Similarly, $S_2 (\tilde{A},\tilde{C})\le S_2 (\tilde{B},\tilde{C})$. The whole proof is completed. $\square$

Theorem 3.8

If $\tilde{A}$ and $\tilde{B}$ are degenerated to the type-1 fuzzy sets on $X$, then the general type-2 fuzzy similarity measure $S_2 (\bullet ,\bullet )$ becomes the type-1 fuzzy similarity measure $S_J (\bullet ,\bullet )$.

Proof

If $\tilde{A}$ and $\tilde{B}$ are degenerated to the type-1 fuzzy set on $X$, from the discussion of Theorem 3.2, we have $S_L^{\tilde{A}} (x\vert 1)=u_A (x)$ and $S_L^{\tilde{B}} (x\vert 1)=u_B (x)$, where $u_A (x)\in [0,1]$ and $u_B (x)\in [0,1]$ are functions related to $x\in X$. Thus, for any $\alpha \in [0,1]$, we have

$$\begin{aligned}&S_2 (\tilde{A},\tilde{B})=\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }}\\&\quad =\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx} +\int _{x\in X} {\min (u_A (x),u_B (x))dx} }{\int _{x\in X} {\max (u_A (x),u_B (x))dx} +\int _{x\in X} {\max (u_A (x),u_B (x))dx} }}\\&\quad =\frac{\int _{x\in X} {\min (u_A (x),u_B (x))dx} }{\int _{x\in X} {\max (u_A (x),u_B (x))dx} }. \end{aligned}$$

The whole proof is completed. $\square$

Remark 4

Observe that if $\tilde{A}$ and $\tilde{B}$ become interval type-2 fuzzy sets, then $S_2 (\bullet ,\bullet )$ reduces to the interval type-2 fuzzy similarity measure defined in Wu and Mendel (2009).

Remark 5

Mitchell (2005) defined a general type-2 fuzzy similarity measure sets by using wave-slice representation theory, but Mitchell’s similarity measure does not satisfy reflexivity and symmetry. However, from Theorem 3.5 and Theorem 3.7, it is clear that the proposed similarity measures $S_1 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ have improved the shortcomings. Furthermore, the proposed measures have also no limitations to the FOU of two general type-2 fuzzy sets.

3.3 Properties of general type-2 fuzzy similarity and inclusion measures

In this subsection, some properties of general type-2 fuzzy similarity and inclusion measures will be derived.

Theorem 3.9

For any $\tilde{A},\tilde{B},\tilde{C}\in F_2 (X),$ if $\tilde{B}\subseteq \tilde{C}$, then the following statements hold:

• (1) $I_1 (\tilde{A},\tilde{B})\le I_1 (\tilde{A},\tilde{C})$;

• (2) $I_2 (\tilde{A},\tilde{B})\le I_2 (\tilde{A},\tilde{C})$.

Proof

(1) Since $\tilde{B}\subseteq \tilde{C}$, we have $S_L^{\tilde{B}} (x\vert \alpha )\le S_L^{\tilde{C}} (x\vert \alpha )$ and $S_R^{\tilde{B}} (x\vert \alpha )\le S_R^{\tilde{C}} (x\vert \alpha )$ for any $\alpha \in [0,1]$ and $x\in X$. Thus, for any $\alpha \in [0,1]$, we can obtain

$$\begin{aligned} I_L (\tilde{A},\tilde{B},a)&= \min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} },\right. \\&\quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx}} \right\} \\&\le \min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{C}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} },\right. \\&\left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{C}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx}}\right\} \\&= I_L (\tilde{A},\tilde{C},a).\\ I_R (\tilde{A},\tilde{B},a)&= \max \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} },\right. \\&\quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx}} \right\} \\&\le \max \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{C}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} },\right. \\&\quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{C}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx}}\right\} \\&= I_R (\tilde{A},\tilde{C},a). \end{aligned}$$

Therefore, $I_1 (\tilde{A},\tilde{B})\le I_1 (\tilde{A},\tilde{C})$.

(2) From $\tilde{B}\subseteq \tilde{C}$, we have

$$\begin{aligned}&I_2 (\tilde{A},\tilde{B})=\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} } }}\\&\quad \le \frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{C}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{C}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} } }}\\&\quad =I_2 (\tilde{A},\tilde{C}). \end{aligned}$$

The whole proof is completed. $\square$

Theorem 3.10

For any $\tilde{A},\tilde{B}\in F_2 (X)$, the following statements hold:

• (1) $S_1 (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B})=S_1 (\tilde{A},\tilde{B})$;

• (2) $S_2 (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B})=S_2 (\tilde{A},\tilde{B})$.

Proof

(1) For any $\alpha \in [0,1]$, we have

$$\begin{aligned} S_L (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B},a)&= \min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} },\right. \\&\quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} }\right\} \\&= \min \left\{ \frac{\int _{x\in X} {S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )dx} },\right. \\&\quad \left. \frac{\int _{x\in X} {S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} }{\int _{x\in X} {S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )dx}}\right\} \\&= \min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} },\right. \\&\quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx}} \right\} \\&= S_L (\tilde{A},\tilde{B},a). \end{aligned}$$

Similarly, $S_R (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B},a)=S_R (\tilde{A},\tilde{B},a)$. Thus, $S_1 (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B})=S_1 (\tilde{A},\tilde{B})$.

(2) $S_2 (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B})$

$$\begin{aligned}&=\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} }{\int {x\in X} {\max (S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\max (S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} }}\\&\quad =\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )dx} }}\\&\quad =\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }}\\&\quad =S_2 (\tilde{A},\tilde{B}). \end{aligned}$$

The whole proof is completed. $\square$

Theorem 3.11

For any $\tilde{A},\tilde{B}\in F_2 (X)$, the following statements hold:

• (1) $I_1 (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B})=S_1 (\tilde{A},\tilde{B})$;

• (2) $I_2 (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B})=S_2 (\tilde{A},\tilde{B})$;

• (3) $S_1 (\tilde{A},\tilde{A}\cap \tilde{B})=I_1 (\tilde{A},\tilde{B})$;

• (4) $S_2 (\tilde{A},\tilde{A}\cap \tilde{B})=I_2 (\tilde{A},\tilde{B})$.

Proof

(1) For any $\alpha \in [0,1]$, we have

$$\begin{aligned}&I_L (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B},a)\\&\quad =\min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )dx} },\right. \\&\quad \quad \quad \quad \quad \quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )dx} }\right\} \\&\quad =\min \left\{ \frac{\int _{x\in X} {S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )dx} },\frac{\int _{x\in X} {S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} }{\int _{x\in X} {S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )dx}}\right\} \\&\quad =\min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} },\right. \\&\quad \quad \quad \quad \quad \quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx}} \right\} \\&\quad =S_L (\tilde{A},\tilde{B},a). \end{aligned}$$

Similarly, $I_R (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B},a)=S_R (\tilde{A},\tilde{B},a)$. Thus, $I_1 (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B})=S_1 (\tilde{A},\tilde{B})$.

(2) $I_2 (\tilde{A}\cup \tilde{B},\tilde{A}\cap \tilde{B})$

$$\begin{aligned}&=\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} \!+\!\int _{x\in X} {\min (S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha ),S_R^{\tilde{A}\!\cap \! \tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}\!\cup \! \tilde{B}} (x\vert \alpha )dx\!+\!\int _{x\in X} {S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )dx} } }}\\&\quad =\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{A}\cup \tilde{B}} (x\vert \alpha )dx} } }}\\&=\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }}\\&\quad =S_2 (\tilde{A},\tilde{B}). \end{aligned}$$

(3) For any $\alpha \in [0,1]$, we have

$$\begin{aligned}&S_L (\tilde{A},\tilde{A}\cap \tilde{B},a)\\&\quad =\min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} },\right. \\&\quad \quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx}}\right\} \\&\quad =\min \left\{ \frac{\int _{x\in X} {S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} },\right. \\&\quad \quad \left. \frac{\int _{x\in X} {S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} }{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx}} \right\} \\&\quad =\min \left\{ \frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} },\right. \\&\quad \quad \left. \frac{\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx}}\right\} \\&\quad =I_L (\tilde{A},\tilde{B},a). \end{aligned}$$

Similarly, we have $S_R (\tilde{A},\tilde{A}\cap \tilde{B},a)=I_R (\tilde{A},\tilde{B},a)$. Thus, $S_1 (\tilde{A},\tilde{A}\cap \tilde{B})=I_1 (\tilde{A},\tilde{B})$.

(4) $S_2 (\tilde{A},\tilde{A}\cap \tilde{B})$

$$\begin{aligned}&\quad =\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad \quad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} \!+\!\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {\max (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} \!+\!\int _{x\in X} {\max (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha ))dx} }}\\&\quad =\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\quad {\frac{\int _{x\in X} {S_L^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{A}\cap \tilde{B}} (x\vert \alpha )dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx} +\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} }}\\&\quad =\frac{1}{\Delta +1}\sum \limits _{\alpha =0,\frac{1}{\Delta },\frac{2}{\Delta },\ldots ,\frac{\Delta -1}{\Delta },1}\\&\qquad {\frac{\int _{x\in X} {\min (S_L^{\tilde{A}} (x\vert \alpha ),S_L^{\tilde{B}} (x\vert \alpha ))dx} +\int _{x\in X} {\min (S_R^{\tilde{A}} (x\vert \alpha ),S_R^{\tilde{B}} (x\vert \alpha ))dx} }{\int _{x\in X} {S_L^{\tilde{A}} (x\vert \alpha )dx+\int _{x\in X} {S_R^{\tilde{A}} (x\vert \alpha )dx} } }}\\&\quad =I_2 (\tilde{A},\tilde{B}). \end{aligned}$$

The whole proof is completed. $\square$

Remark 6

From the Theorems 3.1 to 3.11, it can be seen that the proposed measures improve the shortcomings of the existing measures since that the proposed measures satisfy more desirable properties. Furthermore, the proposed measures are natural extensions of the most popular type-1 fuzzy measures. As a result, the proposed measures keep the characteristics of the most popular type-1 fuzzy measures. Unlike some existing measures, the similarity measure $S_1 (\bullet ,\bullet )$ and inclusion measure $I_1 (\bullet ,\bullet )$ are expressed as type-1 fuzzy sets, and therefore the definitions are consistent with the highly uncertain nature of general type-2 fuzzy sets.

4 Examples

In this section, we by several examples examine the performances of the proposed general type-2 fuzzy similarity and inclusion measures. By doing so, we hope to solve the following issues:

(1) If $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ are type-1 fuzzy sets, do the shapes of these type-1 fuzzy sets have inevitable link with the shapes of secondary membership functions of the general type-2 fuzzy sets?

Remark 7

As is well known, the secondary membership functions of general type-2 fuzzy sets are type-1 fuzzy sets. Furthermore, it is noted that the proposed measures $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ are also expressed as type-1 fuzzy sets. Hence, one needs to investigate whether the shapes of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ have inevitable link with the shapes of secondary membership functions of the general type-2 fuzzy sets. These may be guidance for the further applications of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$, for example, perceptual computing and clustering.

(2) Do $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ converge to real values as $\Delta$ increases?

Remark 8

Since $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ are expressed as type-1 fuzzy sets, they may be subject to certain restrictions in practical applications since that they are not intuitive. Hence, we can obtain the centroid $Centroid(I_1 (\bullet ,\bullet ))$ of $I_1 (\bullet ,\bullet )$ by using centroid defuzzification method. Based on $Centroid(I_1 (\bullet ,\bullet ))$, one can be very intuitive to see the degree to which a general type-2 fuzzy set is included in another general type-2 fuzzy set. However, it should be noted that $Centroid(I_1 (\bullet ,\bullet ))$ is relative to the numbers of $\alpha$-planes, i.e., $\Delta$. In real applications, we should decide on how many $\alpha$-planes will be used. Thus, it is necessary to judge the convergence of $Centroid(I_1 (\bullet ,\bullet ))$.

(3) Do $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ converge to real values as $\Delta$ increases?

Remark 9

Since $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ are also relative to the numbers of $\alpha$-planes, i.e., $\Delta$. Of course, it is desirable to consider the convergences of $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$.

(4) The performance comparisons about $I_1 (\bullet ,\bullet )$ and $I_2 (\bullet ,\bullet )$, $S_1 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$.

Remark 10

By comparisons, we hope to see the differences about $I_1 (\bullet ,\bullet )$ and $I_2 (\bullet ,\bullet )$, and $S_1 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$, so that we can get some guidance in real applications.

Because Gaussian membership function, triangular membership function and trapezoid membership function are the normal situation in practical applications of type-2 fuzzy systems, various cases should be tested based on different choices made for these membership functions. In this section, we present nine cases.

Case 1: Gaussian function with randomly generated triangular vertical slice.

Let $\tilde{A},\tilde{B}$ be two general type-2 fuzzy sets on $X=[0,10]$. Their upper membership functions and lower membership functions are Gaussian functions:

$$\begin{aligned}&\bar{u}_{\tilde{A}} (x)=e^{-\frac{(x-6)^2}{8}};\,\underline{u}_{\tilde{A}} (x)=e^{-\frac{(x-6)^2}{2}};\bar{u}_{\tilde{B}} (x)=e^{-\frac{(x-4)^2}{18}};\\&\quad \underline{u}_{\tilde{B}} (x)=e^{-\frac{(x-4)^2}{2}}. \end{aligned}$$

where FOU of $\tilde{A}$ are shown in Fig. 1a, and FOU of $\tilde{B}$ are shown in Fig. 1b. For any $x$, the secondary membership function $u_{\tilde{A}} (x)$ is triangular membership function, whose apex is determined by the following formula:

$$\begin{aligned} \hbox {Apex}=\underline{u}_{\tilde{A}} (x)+rand*(\bar{u}_{\tilde{A}} (x)-{u}_{\tilde{A}} (x)). \end{aligned}$$

where $rand\in [0,1]$ is randomly generated value. For any $x$, the secondary membership function $u_{\tilde{B}} (x)$ is also triangular membership function, whose apex computation formula is same with the $\tilde{A}$.

Fig. 1

a The FOU of $\tilde{A}$ for case 1, case 2 and case 3. b The FOU of $\tilde{B}$ for case 1, case 2 and case 3

The membership functions of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for $\Delta =$10,000 is depicted in Fig. 4a. $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 5a. $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 6a.

Case 2: Gaussian function with randomly generated trapezoid vertical slice.

Let $\tilde{A},\tilde{B}$ be two general type-2 fuzzy sets on $X=[0,10]$. Their FOU are same with Case 1, shown in Fig. 1a, b. For any $x$, the secondary membership function $u_{\tilde{A}} (x)$ is trapezoid membership function, whose top left and right endpoint are determined by the following formulas:

$$\begin{aligned} \hbox {Lapex}&= \underline{u}_{\tilde{A}} (x)+0.8*rand*(\bar{u}_{\tilde{A}} (x)-\underline{u}_{\tilde{A}} (x));\\ \hbox {Rapex}&= \underline{u}_{\tilde{A}} (x)+rand*(\bar{u}_{\tilde{A}} (x)-\underline{u}_{\tilde{A}} (x)). \end{aligned}$$

where $rand\in [0,1]$ is randomly generated value. For any $x$, the secondary membership function $u_{\tilde{B}} (x)$ is also trapezoid membership function, whose top endpoint computation formulas are same with the $\tilde{A}$.

The membership functions of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for $\Delta =$10,000 is depicted in Fig. 4b. $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 5b. $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 6b.

Case 3: Gaussian function with randomly generated Gaussian vertical slice.

Let $\tilde{A},\tilde{B}$ be two general type-2 fuzzy sets on $X=[0,10]$. Their FOU are same with Case 1, shown in Fig. 1a, b. For any $x$, the secondary membership function $u_{\tilde{A}} (x)$ is Gaussian membership function, whose mean is determined by $\mu =(\bar{u}_{\tilde{A}} (x)+\underline{u}_{\tilde{A}} (x))/2$ and standard deviation $\sigma$ is determined by the following formula:

$$\begin{aligned} \sigma =10*rand. \end{aligned}$$

where $rand\in [0,1]$ is randomly generated value. For any $x$, the secondary membership function $u_{\tilde{B}} (x)$ is also Gaussian membership function, whose mean and standard deviation computation formulas are same with the $\tilde{A}$.

The membership functions of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for $\Delta =$10,000 is depicted in Fig. 4c. $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 5c. $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 6c.

Case 4: Triangular function with randomly generated triangular vertical slice.

Let $\tilde{A},\tilde{B}$ be two general type-2 fuzzy sets on $X=[0,10]$. Their upper membership functions and lower membership functions are triangular functions: $\bar{u}_{\tilde{A}} (x)=\hbox {trimf}(x,[-2,2, 20]);\,\underline{u}_{\tilde{A}} (x) =0.8\,*\, \hbox {trimf}(x [-1,3,15]);\,\bar{u}_{\tilde{B}}(x)=trimf(x, [-20,5,50]);\,{u}_{\tilde{B}} (x)=0.8\,*\, trimf(x,[-10,8,35])$. Where $\hbox {trimf}$ denotes triangular function, the first parameter and third parameter of $[]$ denote bottom left and right endpoint, respectively, and the second parameter of $[]$ denote apex. Where FOU of $\tilde{A}$ are shown in Fig. 2a, and FOU of $\tilde{B}$ are shown in Fig. 2b. For any $x$, the secondary membership functions $u_{\tilde{A}} (x)$ and $u_{\tilde{B}} (x)$ are triangular membership functions, whose apex computation formulas are same with Case 1.

Fig. 2

a The FOU of $\tilde{A}$ for case 4, case 5 and case 6. b The FOU of $\tilde{B}$ for case 4, case 5 and case 6

The membership functions of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for $\Delta =$10,000 is depicted in Fig. 4d. $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 5d. $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 6d.

Case 5: Triangular function with randomly generated trapezoid vertical slice.

Let $\tilde{A},\tilde{B}$ be two general type-2 fuzzy sets on $X=[0,10]$. Their FOU are same with Case 4, shown in Fig. 2a, b. For any $x$, the secondary membership functions $u_{\tilde{A}} (x)$ and $u_{\tilde{B}} (x)$ are trapezoid membership functions, whose top endpoint computation formulas are same with Case 2.

The membership functions of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for $\Delta =$10,000 is depicted in Fig. 4e. $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 5e. $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 6e.

Case 6: Triangular function with randomly generated Gaussian vertical slice.

Let $\tilde{A},\tilde{B}$ be two general type-2 fuzzy sets on $X=[0,10]$. Their FOU are same with Case 4, shown in Fig. 2a, b. For any $x$, the secondary membership functions $u_{\tilde{A}} (x)$ and $u_{\tilde{B}} (x)$ are Gaussian membership functions, whose mean and standard deviation computation formulas are same with Case 3.

The membership functions of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for $\Delta =$10,000 is depicted in Fig. 4f. $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 5f. $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 6f.

Case 7: Trapezoid function with randomly generated triangular vertical slice.

Let $\tilde{A},\tilde{B}$ be two general type-2 fuzzy sets on $X=[0,10]$. Their upper membership functions and lower membership functions are trapezoid functions: $\bar{u}_{\tilde{A}} (x)=\hbox {trapmf}(x, [-8,2,5,20])$;

${u}_{\tilde{A}} (x)=0.7*\hbox {trapmf}(x ,[-5,3,8,15]);$ $\bar{u}_{\tilde{B}} (x)=\hbox {trapmf}(x,[-18,3,6,25]); \quad {u}_{\tilde{B}} (x)=0.6*\hbox {trapmf}(x,[-5, 6,7,19]).$ Where $\hbox {trapmf}$ denotes trapezoid function, the first parameter and four parameter of $[]$ denote bottom left and right endpoint, respectively, and the second parameter and third parameter of $[]$ denote top left and right endpoint, respectively. Where FOU of $\tilde{A}$ are shown in Fig. 3a, and FOU of $\tilde{B}$ are shown in Fig. 3b. For any $x$, the secondary membership functions $u_{\tilde{A}} (x)$ and $u_{\tilde{B}} (x)$ are triangular membership functions, whose apex computation formulas are same with Case 1.

Fig. 3

a The FOU of $\tilde{A}$ for case 7, case 8 and case 9. b The FOU of $\tilde{B}$ for case 7, case 8 and case 9

The membership functions of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for $\Delta =$10,000 is depicted in Fig. 4g. $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 5g. $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 6g.

Fig. 4

a $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for Case 1. b $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for Case 2. c $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for Case 3. d $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for Case 4. (e) $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for Case 5. f $I_1 (\bullet ,\bullet )$ and $S_1(\bullet ,\bullet )$ for Case 6. g $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for Case 7. h $I_1 (\bullet ,\bullet )$ and $S_1(\bullet ,\bullet )$ for Case 8. i $I_1 (\bullet ,\bullet )$ and $S_1(\bullet ,\bullet )$ for Case 9

Fig. 5

a $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for Case 1. b $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for Case 2. c $Centroid(I_1 (\bullet ,\bullet ))$  and  $Centroid(S_1 (\bullet ,\bullet ))$  for Case 3. d $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for Case 4. e $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$  for Case 5. f $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for Case 6. g $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for Case 7. h $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for Case 8. i       $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for Case 9

Fig. 6

a $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for Case 1. b $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for Case 2. c $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for Case 3. d $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for Case 4. e $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for Case 5. f $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for Case 6. g $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for Case 7. h $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for Case 8. i $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for Case 9

Case 8: Trapezoid function with randomly generated trapezoid vertical slice.

Let $\tilde{A},\tilde{B}$ be two general type-2 fuzzy sets on $X=[0,10]$. Their FOU are same with Case 7, shown in Fig. 3a, b. For any $x$, the secondary membership functions $u_{\tilde{A}} (x)$ and $u_{\tilde{B}} (x)$ are trapezoid membership functions, whose top endpoint computation formulas are same with Case 2.

The membership functions of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for $\Delta =$10,000 is depicted in Fig. 4h. $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 5h. $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 6h.

Case 9: Trapezoid function with randomly generated Gaussian vertical slice.

Let $\tilde{A},\tilde{B}$ be two general type-2 fuzzy sets on $X=[0,10]$. Their FOU are same with Case 7, shown in Fig. 3a, b. For any $x$, the secondary membership functions $u_{\tilde{A}} (x)$ and $u_{\tilde{B}} (x)$ are Gaussian membership functions, whose mean and standard deviation computation formulas are same with Case 3.

The membership functions of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ for $\Delta =$10,000 is depicted in Fig. 4i. $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 5i. $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ for $\Delta$ ranging from 1 to 5,000 are shown in Fig. 6i.

Observe from Fig. 4a–i that, regardless of the natures of the secondary membership functions of $\tilde{A}$ and $\tilde{B}$, the shapes of membership functions of $S_1 (\bullet ,\bullet )$ and $I_1 (\bullet ,\bullet )$ are always similar to the trapezoid when $\Delta =$10,000. But noted that we only describe the membership functions of $S_1 (\bullet ,\bullet )$ and $I_1 (\bullet ,\bullet )$ when $\Delta =$10,000. This is because that $\Delta$ is greater, $S_1 (\bullet ,\bullet )$ and $I_1 (\bullet ,\bullet )$ are more close to the true values. In fact, this can be derived from the definitions of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$. It is noted that we only discuss the cases that the secondary membership functions of general type-2 fuzzy sets are Gaussian membership function, triangular membership function or trapezoid membership function. Since Gaussian membership function, triangular membership function and trapezoid membership function are normal and convex, we have $[I_L (\tilde{A},\tilde{B},1),I_R (\tilde{A},\tilde{B},1)]\ne \emptyset$ from the definition of $I_1 (\bullet ,\bullet )$. That is to say, the 1-cut set of $I_1 (\bullet ,\bullet )$ is a closed interval. Furthermore, from the convexity of secondary membership functions, we can see that $I_1 (\bullet ,\bullet )$ is convex. Hence, the shape of $I_1 (\bullet ,\bullet )$ is the trapezoid. It is similar to the analysis of $S_1 (\bullet ,\bullet )$.

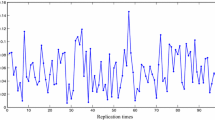
From Fig. 5a–i, we find that $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ are always volatile. Even if $\Delta$ is increased to 5,000, most of the situations for $Centroid (I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ are still not stabilized. Especially, for the cases three, seven, eight and nine, we almost do not see a trend of convergence. In fact, $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid(S_1 (\bullet ,\bullet ))$ are obtained by using centroid defuzzification method to $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$. It is noted that the shapes of $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ are easily influenced by the value of $\Delta$. Thus, $Centroid(I_1 (\bullet ,\bullet ))$ and $Centroid (S_1 (\bullet ,\bullet ))$ are always volatile as the value of $\Delta$.

From Fig. 6a–i, we can obtain that $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ as $\Delta$ increases, will soon stabilize and converge to a certain value. The above conclusions show that $I_2 (\bullet ,\bullet )$ and $S_2 (\bullet ,\bullet )$ have more practical values. However, $I_1 (\bullet ,\bullet )$ and $S_1 (\bullet ,\bullet )$ are coincident with the nature of and the semantic interpretation of general type-2 fuzzy sets, and therefore may have more further research topics.

5 Conclusions

In this paper, the new general type-2 fuzzy similarity and inclusion measures have been defined by using $\alpha$-plane theory. The proposed measures improve the shortcomings of the existing measures. Furthermore, the proposed measures are natural extensions of the most popular type-1 fuzzy measures. As a result, the proposed measures keep the characteristics of the most popular type-1 fuzzy measures. Since the proposed measures are relative to the numbers of $\alpha$-planes, we should decide on how many $\alpha$-planes will be used in real applications. However, it is difficult to decide on the numbers of $\alpha$-planes in theory. Of course, the larger the numbers of $\alpha$-planes are, the more stable proposed measures are, whereas if the numbers of $\alpha$-planes are too large, the computing time would increase. Hence, it is of high interest to find efficient algorithm to handle the problem, and further research will focus on this issue.