New stability conditions for GRNs with neutral delay

Abstract

In this paper, the asymptotic stability problem of genetic regulatory networks with time-varying/constant neutral delay is considered. By introducing a new Lyapunov–Krasovskii functional and applying the free weighting matrix technique, sufficient delay-dependent stability conditions are developed and presented in terms of strict linear matrix inequality, which can be easily verified by using the LMI toolbox. Finally, two numerical examples are provided to demonstrate the effectiveness and reduced conservativeness of the proposed algorithm.

1 Introduction

Over the past decades, genetic regulatory networks have received increasing attention in the biological, engineering and other research fields. In order to study gene regulation processes in living organisms, several mathematical models are constructed based on large amounts of experimental data (see Lestas et al. 2008; Smolen et al. 2000; Gebert et al. 2007; Kauffman 1969; Jong 2002 and the references therein).

It is well known that time delay will inevitably occur due to the slow process of transportation and translation of protein. The existence of time delays may lead to instability, which motivates many people to study the stability of delayed genetic regulatory networks (GRNs). Various results concerning GRNs with time delay have been reported (see, for example, Ren and Cao 2010; Li et al. 2006, 2007; Wang et al. 2008, 2009, 2010; Banks and Mahaffy 1978; Chen and Aihara 2002; Cao and Ren 2008; Zhou et al. 2009). However, the existing gene networks models in many cases cannot characterize the properties of the GRNs precisely due to their complicated dynamic properties in the real world. It is natural and important that GRNs may contain some information about the derivative of the past state, which motivates us to study the stability of GRNs of neutral type. Although there are various stability conditions available for neutral neural networks (Liu and Zong 2009; Zhang et al. 2005; Feng et al. 2009; Park et al. 2008; Ren and Cao 2006; Li and Yang 2010; Lou et al. 2010; Balasubramaniam et al. 2010; Lakshmanan et al. 2011; Rakkiyappan et al. 2011), little work has been done on the stability of GRNs with neutral delay (Jung et al. 2010). It is noted that in Jung et al. (2010) it is required that the time-varying delays be differentiable and the discrete delay be equal to the neutral delay. However, these conditions may not be satisfied in some practical circumstances.

Motivated by the above discussions, we shall further study the problem of the delay-dependent asymptotic stability of GRNs with neutral delay. Different from (Jung et al. 2010), the discrete delay may be non-differentiable, and it is unnecessarily equal to the neutral delay. We shall introduce a new Lyapunov–Krasovskii functional to arrive at sufficient delay-dependent stability conditions by means of the free weighting matrix technique. Since these conditions are expressed by strict linear matrix inequality (LMI), it is easy to apply the MATLAB LMI toolbox to deal with them. We shall further illustrate the usefulness of the theoretical findings through two numerical examples. Moreover, some comparisons are also made between the results in Jung et al. (2010) and this paper to show the reduced conservativeness achieved by our results.

Notations. In this paper, the n-dimensional Euclidean space is denoted by $\mathbf{R}^{n}. \mathbf{R}^{n\times m}$ is the set of all n × m real matrices. I denotes the identity matrix with appropriate dimensions. $0<P\in\mathbf{R}^{n\times n}$ implies that P is a real symmetric positive definite matrix. In a matrix, the term of symmetry is represented by the asterisk $\ast.$

2 Problem formulation

By Li et al. (2006), GRNs with time-varying delays can be described by the following differential equations:

$$ \begin{aligned} \dot{m_i}(t) &= -a_im_i(t)+G_i(p_1(t-\sigma(t)),\quad p_2(t-\sigma(t)), \ldots,p_n(t-\sigma(t))),\\ \dot{p_i}(t) &= -c_ip_i(t)+d_im_i(t-\tau(t)), \quad(i=1,2,\ldots,n), \end{aligned} $$

(1)

where m _i (t) and p _i (t) denote the concentration of mRNA and protein of the ith node, respectively, a _i and c _i are the degradation rates of the mRNA and the protein, d _i is the translation rate, and the function G _i is the feedback regulation of the protein on the transcription of the ith gene which usually takes the Hill form. Throughout this paper, the sum logic is used to describe the regulatory function, i.e.,

$$ G_i(p_1(t),p_2(t),\ldots,p_n(t))=\sum\limits_{j=1}^ng_{ij}(p_j(t)), $$

where $g_{ij}(\cdot)$ is usually a monotonically increasing function. If transcription factor j is an activator of gene i, then

$$ g_{ij}(p_j(t))=\beta_{ij}\frac{p_j(t)^{H_j}}{\rho_j^{H_j} +p_j(t)^{H_j}}; $$

if transcription factor j is a repressor of gene i, then

$$ g_{ij}(p_j(t))=\beta_{ij}\frac{\rho_j^{H_j}} {\rho_j^{H_j}+p_j(t)^{H_j}}, $$

where H _j is the Hill coefficient, ρ _j is a positive constant, and β _ij is a constant that describes the transcriptional rate of transcriptional factor j to gene i. Let b _ij  = β _ij if transcription factor j is an activator of gene i; b _ij  =  −β _ij if transcription factor j is a repressor of gene i; b _ij  = 0 if there is no link between genes i and j. Then, the GRNs (1) can be described as:

$$ \begin{aligned} \dot{m_i}(t) &= -a_im_i(t)+\sum_{j=1}^nb_{ij}g_{j}(p_j(t-\sigma(t)))+k_i,\\ \dot{p_i}(t) &= -c_ip_i(t)+d_im_i(t-\tau(t)), \end{aligned} $$

(2)

where $g_{j}=\frac{\rho_j^{H_j}}{\rho_j^{H_j}+p_j(t)^{H_j}},\quad k_i=\sum\nolimits_{j\in K_i}\beta_{ij}, K_i$ is the set of repressors of gene i. Rewrite system (2) in the following compact matrix form:

$$ \begin{aligned} \dot{m}(t) =-Am(t)+B g(p(t-\sigma(t)))+M,\\ \dot{p}(t) =-Cp(t)+D m(t-\tau(t)), \end{aligned} $$

(3)

where

$$ \begin{aligned} A = diag[a_1,a_2,\ldots,a_n],\ \ \ \ C=diag[c_1,c_2,\ldots,c_n],\\ D = diag[d_1,d_2,\ldots,d_n],\ \ \ \ M =[k_1,k_2,\ldots,k_n]^T. \end{aligned} $$

Let $m^*$ and $p^*$ be an equilibrium point of the system (3), that is,

$$ \begin{aligned} \dot{m}^* &=-Am^*+B g(p^*)+M, \\ \dot{p}^* &=-Cp^*+D m^*. \end{aligned} $$

Now, let $x(t)=m(t)-m^*, y(t)=p(t)-p^*$. Then we have:

$$ \begin{aligned} \dot{x}(t) &=-Ax(t)+B f(y(t-\sigma(t))),\\ \dot{y}(t) &=-Cy(t)+Dx(t-\tau(t)), \end{aligned} $$

(4)

where

$$ f(y(t-\sigma(t)))=[f_1(y_1(t-\sigma(t))),f_2(y_2(t-\sigma(t))), \ldots,f_n(y_n(t-\sigma(t)))]^T, $$

and

$$ f_i(y_i(t-\sigma(t)))=g_i(p_i(t-\sigma(t)))-g_i(p_i^*). $$

We need the following assumption in this paper:

Assumption 1

For $i=1,2,\ldots,n,$ there exist constants k ⁻ _i , k ⁺ _i such that the regulatory function $g_i(\cdot)$ satisfies

$$ k_i^-\leq\frac{g_i(u)-g_i(v)}{u-v}\leq k_i^+,\quad \forall u\neq v\in {\mathbf{R}}. $$

(5)

It is clearly seen that f _i (y) satisfies the sector condition

$$ k_i^-\leq\frac{f_i(y)}{y}\leq k_i^+, \quad \forall y\neq0\in{\mathbf{R}}, $$

(6)

which is equivalent to:

$$ (f_i(y)-k_i^-y)(f_i(y)-k_i^+y)\leq0. $$

For convenience, let

$$ K =diag\left[\frac{k_1^++k_1^-}{2},\ldots,\frac{k_n^++k_n^-}{2}\right], \ \ L =diag[k_1^+k_1^-,\ldots,k_n^+k_n^-]. $$

Remark 1

Assumption 1 in this paper is the same as that in Lou et al. (2010), and it is a much milder condition than the monotonically increasing condition since the constants k ⁻ _i , k ⁺ _i are allowed to be positive, negative, or zero. Therefore, Assumption 1 is weaker than those in Li et al. (2006, 2007); Wang et al. (2008, 2010); Banks and Mahaffy (1978); Chen and Aihara (2002); Wang et al. (2009).

In this paper, we shall study the GRNs model with time-varying neutral delay given by:

$$ \begin{aligned} \dot{x} (t) &=-Ax(t)+B f(y(t-\sigma(t))),\\ \dot{y}(t) &=-Cy(t)+D_1x(t-\tau_1(t))+D_2\dot{x}(t-\tau_2(t)), \end{aligned} $$

(7)

where the time-varying delays σ(t), τ₁(t) and τ₂(t) are assumed to satisfy

$$ 0\leq\sigma(t)\leq\sigma,\quad 0\leq\tau_1(t)\leq\tau_1, \quad 0\leq\tau_2(t)\leq\tau_2,\quad \dot{\tau}_2(t)\leq\tau. $$

Remark 2

The GRNs model is a highly useful tool for discovering higher order structure of an organism and gaining deep insights into both static and dynamic behaviors. Well-characterized GRNs can help understand genetic mechanisms responsible for evolutionary changes and design approaches for cell/tissue engineering.

To get the main results, the following lemmas are needed in this paper:

Lemma 1

(Ren and Cao 2006) Let $P\in \mathbf{R}^{n\times n}$ be a positive definite matrix. Then, for $y(t)\in \mathbf{R}^n$ and scalar α > 0,

$$ \left(\int\limits_{t-\alpha}^ty(s)\hbox{d}s\right)^TP\left(\int\limits_{t-\alpha} ^ty(s)\hbox{d}s\right)\leq\alpha\int\limits_{t-\alpha}^ty(s)^TPy(s)\hbox{d}s. $$

Lemma 2

(Liu and Zong 2009) Suppose that $x(t)\in\mathbf{R^{n}}$ be continuously differentiable with first order derivative. Then for any matrix $P\in\mathbf{R^{n\times n}}>0 ,$ any $Y=[M_1, M_2]\in\mathbf{R^{n\times 2n}}, h>0,$ we have

$$ - \int\limits_{{t - h}}^{t} {\dot{x}\left( s \right)^{T} P\dot{x}\left( s \right)} \hbox{d}s\hfill \\ \le \left[ {\begin{array}{llll} {x\left( t \right)} \\ {x\left( {t - h} \right)} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} M_{1} + M_{1}^{T} & - M_{1}^{T} + M_{2} \\ *\, & - M_{2} - M_{T}^{2} \\ \end{array} } \right]\left[ {\begin{array}{llll} {x\left( t \right)} \\ {x\left( {t - h} \right)} \\ \end{array} } \right] \hfill \\ \quad + \left[ {\begin{array}{llll} {x\left( t \right)} \\ {x\left( {t - h} \right)} \\ \end{array} } \right]^{T} Y^{T} P^{{ - 1}} Y\left[ {\begin{array}{llll} {x\left( t \right)} \\ {x\left( {t - h} \right)} \\ \end{array} } \right] \hfill \\ $$

Lemma 3

(Li and Yang 2010) Let 0 < τ ₁ ≤ τ(t) ≤ τ₂, Q _i , (i = 1, 2, 3) be some constant matrices with appropriate dimensions. Then

$$ Q_1+(\tau_2-\tau(t))Q_2+(\tau(t)-\tau_1)Q_3 < 0 $$

if the following inequalities hold

$$ \begin{aligned} &Q_1+(\tau_2-\tau_1)Q_2 < 0 \\ &Q_1+(\tau_2-\tau_1)Q_3 < 0 \end{aligned} $$

3 Main results

In this section, we present the delay-dependent conditions that ensure the asymptotic stability of the equilibrium point for the GRNs (7).

Theorem 1

System (7) with time-varying neutral delay is asymptotically stable if there exist matrices $P= \left[ \begin{array}{lllll} P_{11} &\ P_{12} &\ P_{13} &\ P_{14} &\ P_{15} \\ \ast &\ P_{22} &\ P_{23}&\ P_{24} &\ P_{25} \\ \ast &\ \ast &\ P_{33} &\ P_{34} &\ P_{35} \\ \ast &\ \ast &\ \ast &\ P_{44} &\ P_{45} \\ \ast &\ \ast &\ \ast &\ \ast &\ P_{55} \\ \end{array}\right] > 0, Q= \left[\begin{array}{*{20}l} Q_{11}&Q_{12}\\ * &Q_{22}\end{array}\right]>0, Q_i>0, (i=1,2,\ldots,6), R_k>0 , S_k>0, (k=1,2,3), \Uplambda_1=diag[\lambda_{11},\ldots,\lambda_{1n}]>0, \Uplambda_2=diag[\lambda_{21},\ldots,\lambda_{2n}]>0, \Uplambda_3=diag[\lambda_{31},\ldots,\lambda_{3n}]>0$ and the free matrices $M_l (l=1,2,\ldots,12), N_j (j=1,2,\ldots,7)$ with appropriate dimensions such that the following LMIs hold:

$$ \left[\begin{array}{llll} \Upphi & F_1 & F_3 & F_5 \\ \ast & -\frac{1}{\tau_1} R_1& 0 & 0 \\ \ast & \ast & -\frac{1}{\tau_2} R_3 & 0\\ \ast & \ast & \ast & -\frac{1}{\sigma} R_2 \\ \end{array}\right]< 0,\\ \left[\begin{array}{llll} \Upphi & F_1 & F_3 & F_6 \\ \ast & -\frac{1}{\tau_1} R_1& 0 & 0 \\ \ast & \ast & -\frac{1}{\tau_2} R_3 & 0\\ \ast & \ast & \ast & -\frac{1}{\sigma} R_2 \\ \end{array} \right] <0, $$

(8)

$$ \left[\begin{array}{llll} \Upphi & F_1 & F_4 & F_5 \\ \ast & -\frac{1}{\tau_1} R_1& 0 & 0 \\ \ast & \ast & -\frac{1}{\tau_2} R_3 & 0\\ \ast & \ast & \ast & -\frac{1}{\sigma} R_2 \\ \end{array} \right]< 0,\\ \left[\begin{array}{llll} \Upphi & F_1 & F_4 & F_6 \\ \ast & -\frac{1}{\tau_1} R_1& 0 & 0 \\ \ast & \ast & -\frac{1}{\tau_2} R_3 & 0\\ \ast & \ast & \ast & -\frac{1}{\sigma} R_2 \\ \end{array} \right] <0 ,\\ $$

(9)

$$ \left[ \begin{array}{llll} \Upphi & F_2 & F_3 & F_5 \\ \ast & -\frac{1}{\tau_1} R_1& 0 & 0 \\ \ast & \ast & -\frac{1}{\tau_2} R_3 & 0\\ \ast & \ast & \ast & -\frac{1}{\sigma} R_2 \\ \end{array} \right]<0,\\ \left[ \begin{array}{llll} \Upphi & F_2 & F_3 & F_6 \\ \ast & -\frac{1}{\tau_1} R_1& 0 & 0 \\ \ast & \ast & -\frac{1}{\tau_2} R_3 & 0\\ \ast & \ast & \ast & -\frac{1}{\sigma} R_2 \\ \end{array} \right] <0,\\ $$

(10)

$$ \left[ \begin{array}{llll} \Upphi & F_2 & F_4 & F_5 \\ \ast & -\frac{1}{\tau_1} R_1& 0 & 0 \\ \ast & \ast & -\frac{1}{\tau_2} R_3 & 0\\ \ast & \ast & \ast & -\frac{1}{\sigma} R_2 \\ \end{array} \right] < 0,\\ \left[ \begin{array}{llll} \Upphi & F_2 & F_4 & F_6 \\ \ast & -\frac{1}{\tau_1} R_1& 0 & 0 \\ \ast & \ast & -\frac{1}{\tau_2} R_3 & 0\\ \ast & \ast & \ast & -\frac{1}{\sigma} R_2 \\ \end{array} \right] < 0 , $$

(11)

with

$$ \begin{aligned} \Upphi &= \Upphi ^{T} = \left( {\Upphi _{{ij}} } \right)_{{18 \times 18}} , \\ F_{1} &= \left[ {0,M_{2} ,0, \ldots ,0,M_{{1_{{ \downarrow _{9} }} }} ,0, \ldots ,0} \right]_{{18 \times 1}}^{T} , \\ F_{2} &= \left[ {M_{3} ,0, \ldots ,0,M_{{4_{{ \downarrow _{9} }} }} ,0, \ldots ,0} \right]_{{18 \times 1}}^{T} , \\ F_{3} &= \left[ {0,0,M_{6} ,0, \ldots ,0,M_{{5_{{ \downarrow _{{10}} }} }} ,0, \ldots ,0} \right]_{{18 \times 1}}^{T} , \\ F_{4} &= \left[ {M_{7} ,0, \ldots ,0,M_{{8_{{ \downarrow _{{10}} }} }} ,0, \ldots ,0} \right]_{{18 \times 1}}^{T} , \\ F_{5} &= \left[ {0, \ldots ,0,M_{{10_{{ \downarrow _{{13}} }} }}^{T} ,0,M_{9}^{T} } \right]_{{18 \times 1}}^{T} , \\ F_{6} &= \left[ {0, \ldots ,0,M_{{11_{{ \downarrow _{{12}} }} }}^{T} ,0, \ldots ,0,M_{{12}}^{T} } \right]_{{18 \times 1}}^{T} , \\ \Upphi _{{11}} &= Q_{1} + Q_{2} + \tau _{1} S_{1} + \tau _{2} S_{3} + M_{3} + M_{3} T + M_{7} + M_{7}^{T} \\ &\quad + P_{{14}} + P_{{14}}^{T} + P_{{15}} + P_{{15}}^{T} - N_{1} A - AN_{1}^{T} , \\ \Upphi _{{12}} &= - P_{{14}} + P_{{24}}^{T} + P_{{25}}^{T} ,\Upphi _{{13}} = - P_{{15}} + P_{{34}}^{T} + P_{{35}}^{T} , \\ \Upphi _{{14}} &= P_{{44}}^{T} + P_{{45}}^{T} ,\Upphi _{{15}} = P_{{45}} + P_{{55}} ,\Upphi _{{16}} = P_{{11}} - N_{1} - AN_{2}^{T} , \\ \Upphi _{{17}} &= P_{{12}} ,\Upphi _{{18}} = P_{{13}} ,\Upphi _{{19}} = - M_{3}^{T} + M_{4} ,\Upphi _{{1,10}} = - M_{7}^{T} + M_{8} , \\ \Upphi _{{1,17}} & = N_{1} B - AN_{3}^{T} , \\ \Upphi _{{1,11}} &= \Upphi _{{1,12}} = \Upphi _{{1,13}} = \Upphi _{{1,14}} = \Upphi _{{1,15}} = \Upphi _{{1,16}} = \Upphi _{{1,18}} = 0 \\ \Upphi _{{22}} &= - Q_{1} - M_{2} - M_{2}^{T} - P_{{24}} - P_{{24}}^{T} ,\Upphi _{{23}} = - P_{{25}} - P_{{34}}^{T} , \\ \Upphi _{{24}} &= - P_{{44}} ,\Upphi _{{25}} = - P_{{45}} ,\Upphi _{{26}} = P_{{12}}^{T} ,\Upphi _{{27}} = P_{{22}} , \\ \Upphi _{{28}} &= P_{{23}} ,\Upphi _{{29}} = - M_{1} + M_{2}^{T} , \\ \Upphi _{{2,10}} &= \Upphi _{{2,11}} = \Upphi _{{2,12}} = \Upphi _{{2,13}} = \Upphi _{{2,14}} = \Upphi _{{2,15}} = \Upphi _{{2,16}} = \Upphi _{{2,17}} = \Upphi _{{2,18}} = 0, \\ \Upphi _{{33}} &= - Q_{2} - M_{6} - M_{6}^{T} - P_{{35}} - P_{{35}}^{T} ,\Upphi _{{34}} = - P_{{45}}^{T} ,\Upphi _{{35}} = - P_{{55}} \\ \Upphi _{{36}} &= P_{{13}}^{T} ,\Upphi _{{37}} = P_{{23}}^{T} ,\Upphi _{{38}} = P_{{33}} ,\Upphi _{{3,10}} = - M_{5} + M_{6}^{T} , \\ \Upphi _{{39}} &= \Upphi _{{3,11}} = \Upphi _{{3,12}} = \Upphi _{{3,13}} = \Upphi _{{3,14}} = \Upphi _{{3,15}} = \Upphi _{{3,16}} = \Upphi _{{3,17}} = \Upphi _{{3,18}} = 0, \\ \Upphi _{{44}} &= - \frac{1}{{\tau _{1} }}S_{1} ,\Upphi _{{45}} = 0,\Upphi _{{46}} = P_{{14}}^{T} ,\Upphi _{{47}} = P_{{24}}^{T} ,\Upphi _{{48}} = P_{{34}}^{T} , \\ \Upphi _{{49}} &= \Upphi _{{4,10}} = \Upphi _{{4,11}} = \Upphi _{{4,12}} = \Upphi _{{4,13}} = \Upphi _{{4,14}} = \Upphi _{{4,15}} = \Upphi _{{4,16}} = \Upphi _{{4,17}} = \Upphi _{{4,18}} = 0, \\ \Upphi_{{55}} &= - \frac{1}{{\tau _{2} }}S_{3} ,\Upphi _{{56}} = P_{{15}}^{T} ,\Upphi _{{57}} = P_{{25}}^{T} ,\Upphi _{{58}} = P_{{35}}^{T} , \\ \Upphi _{{59}} &= \Upphi _{{5,10}} = \Upphi _{{5,11}} = \Upphi _{{5,12}} = \Upphi _{{5,13}} = \Upphi _{{5,14}} = \Upphi _{{5,15}} = \Upphi _{{5,16}} = \Upphi _{{5,17}} = \Upphi _{{5,18}} = 0, \\ \Upphi _{{66}} &= Q_{3} + Q_{4} + Q_{6} + \tau _{1} R_{1} + \tau _{2} R_{2} + \tau _{2} R_{3} - N_{2} - N_{2}^{T} , \\ \Upphi _{{67}} &= \Upphi _{{68}} = \Upphi _{{69}} = \Upphi _{{6,10}} = \Upphi _{{6,11}} = \Upphi _{{6,12}} = \Upphi _{{6,13}} = \Upphi _{{6,14}} = \Upphi _{{6,15}} = \Upphi _{{6,16}} = \Upphi _{{6,18}} = 0, \\ \Upphi _{{77}} &= - Q_{3} ,\Upphi _{{88}} = - Q_{4} ,\Upphi _{{6,17}} = N_{2} B - N_{3}^{T} , \\ \Upphi _{{78}} &= \Upphi _{{79}} = \Upphi _{{7,10}} = \Upphi _{{7,11}} = \Upphi _{{7,12}} = \Upphi _{{7,13}} = \Upphi _{{7,14}} = \Upphi _{{7,15}} =\Upphi _{{7,16}} = \Upphi _{{7,17}} = \Upphi _{{7,18}} = 0, \\ \Upphi _{{89}} &= \Upphi _{{8,10}} = \Upphi _{{8,11}} = \Upphi _{{8,12}} =\Upphi _{{8,13}} = \Upphi _{{8,14}} = \Upphi _{{8,15}} = \Upphi _{{8,16}} = \Upphi _{{8,17}} = \Upphi _{{8,18}} = 0, \\ \Upphi _{{99}} &= M_{1} + M_{1}^{T} - M_{4} - M_{4}^{T} + N_{4} D_{1} + D_{1} N_{4}^{T} , \\ \Upphi _{{9,11}} &= N_{4} D_{2} + D_{1} N_{5}^{T} ,\Upphi _{{9,12}} = - N_{4} C + D_{1} N_{6}^{T} , \\ \Upphi _{{9,15}} &= - N_{4} + D_{1} N_{7}^{T} , \\ \Upphi _{{9,10}} &= \Upphi _{{9,13}} = \Upphi _{{9,14}} = \Upphi _{{9,16}} = \Upphi _{{9,17}} = \Upphi _{{9,18}} = 0, \\ \Upphi _{{10,10}} &= M_{5} + M_{5}^{T} - M_{8} - M_{8}^{T} , \\ \Upphi _{{10,11}} &= \Upphi _{{10,12}} = \Upphi _{{10,13}} = \Upphi _{{10,14}} = \Upphi _{{10,15}} = \Upphi _{{10,16}} = \Upphi _{{10,17}} = \Upphi _{{10,18}} = 0, \\ \Upphi _{{11,11}} &= N_{5} D_{2} + D_{2} N_{5}^{T} - \left( {1 - \tau } \right)Q_{6} ,\Upphi _{{11,12}} = - N_{5} C + D_{2} N_{6}^{T} , \\ \Upphi _{{11,15}} &= - N_{5} + D_{2} N_{7}^{T} ,\Upphi _{{11,13}} = \Upphi _{{11,14}} = \Upphi _{{11,16}} = \Upphi _{{11,17}} = \Upphi _{{11,18}} = 0, \\ \Upphi _{{12,12}} &= Q_{5} + Q_{{12}} + Q_{{12}}^{T} + \sigma S_{2} + M_{{11}} + M_{{11}}^{T} - N_{6} C - CN_{6}^{T} - \Uplambda _{2} L, \\ \Upphi _{{12,13}} &= - Q_{{12}} ,\Upphi _{{12,14}} = Q_{{22}} ,\Upphi _{{12,15}} = Q_{{11}} - N_{6} - CN_{7}^{T} , \\ \Upphi _{{12,16}} &= \Uplambda _{2} K,\Upphi _{{12,17}} = 0,\Upphi _{{12,18}} = - M_{{11}}^{T} + M_{{12}} , \\ \Upphi _{{13,13}} &= - Q_{5} - M_{{10}} - M_{{10}}^{T} ,\Upphi _{{13,14}} = - Q_{{22}} , \\ \Upphi _{{13,15}} &= \Upphi _{{13,16}} = \Upphi _{{13,17}} = 0, \\ \Upphi _{{13,18}} &= - M_{9} + M_{{10}}^{T} ,\Upphi _{{14,14}} = - \frac{1}{\sigma }S_{2} ,\Upphi _{{14,15}} = Q_{{12}}^{T} , \\ \Upphi _{{14,16}} &= \Upphi _{{14,17}} = \Upphi _{{14,18}} = 0, \\ \Upphi _{{15,15}} &= \sigma R_{2} - N_{7} - N_{7}^{T} ,\Upphi _{{15,16}} = \Uplambda _{1} ,\Upphi _{{15,17}} = \Upphi _{{15,18}} = 0, \\ \Upphi _{{16,16}} &= - \Uplambda _{2} ,\Upphi _{{16,17}} = \Upphi _{{16,18}} = 0,\Upphi _{{17,17}} = - \Uplambda _{3} + N_{3} B + B^{T} N_{3}^{T} , \\ \Upphi _{{17,18}} &= \Uplambda _{3} K,\Upphi _{{18,18}} = M_{9} + M_{9}^{T} - M_{{12}} - M_{{12}}^{T} - \Uplambda _{3} L \end{aligned} $$

Proof

Consider the following Lyapunov–Krasovskii functional:

$$ V(t)=V_1(t)+V_2(t)+V_3(t)+V_4(t), $$

where

$$ \begin{aligned} V_{1} \left( t \right) &= \left[ \begin{array}{*{20}c} x\left( t \right) \\ x\left( {t - \tau _{1} } \right) \hfill \\ x\left( {t - \tau _{2} } \right) \hfill \\ \int\limits_{{t - \tau _{1} }}^{t} {x\left( s \right)\hbox{d}s} \hfill \\ \int\limits_{{t - \tau _{2} }}^{t} {x\left( s \right)\hbox{d}s} \hfill \\ \end{array} \right]^{T} P\left[ \begin{array}{*{20}c} x\left( t \right) \hfill \\ x\left( {t - \tau _{1} } \right) \hfill \\ x\left( {t - \tau _{2} } \right) \hfill \\ \int\limits_{{t - \tau _{1} }}^{t} {x\left( s \right)\hbox{d}s} \hfill \\ \int\limits_{{t - \tau _{2} }}^{t} {x\left( s \right)\hbox{d}s} \hfill \\ \end{array} \right]\\ & \quad + \left[ \begin{array}{*{20}c} y\left( t \right) \hfill \\ \int\limits_{{t - \sigma }}^{t} {y\left( s \right)\hbox{d}s} \hfill \\ \end{array} \right]^{T} Q\left[ \begin{array}{*{20}c} y\left( t \right) \hfill \\ \int\limits_{{t - \sigma }}^{t} {y\left( s \right)\hbox{d}s} \hfill \\ \end{array} \right], \end{aligned} $$

$$\begin{aligned} V_{2} \left( t \right)& = \int\limits_{{t - \tau _{1} }}^{t} \left[ {x^{T} \left( s \right)Q_{1} x\left( s \right) + \dot{x}^{T} \left( s \right)Q_{3} \dot{x}\left( s \right)} \right]\hbox{d}s \\ & \quad + \int\limits_{{t - \tau _{2} }}^{t} \left[ {x^{T} \left( s \right)Q_{2} x\left( s \right) + \dot{x}^{T} \left( s \right)Q_{4} \dot{x}\left( s \right)} \right]\hbox{d}s \\ & \quad + \int\limits_{{t - \sigma }}^{t} {y^{T} \left( s \right)Q_{5} y\left( s \right)\hbox{d}s} + \int\limits_{{t - \tau _{2} \left( t \right)}}^{t} {\dot{x}^{T} \left( s \right)Q_{6} \dot{x}\left( s \right)\hbox{d}s} , \end{aligned}$$

$$ \begin{aligned} V_{3} \left( t \right) &= 2\sum\limits_{{i = 1}}^{n} {\lambda _{{1i}} } \int\limits_{0}^{{y_{i} \left( t \right)}} {f_{i} \left( s \right)\hbox{d}s} ,\\ V_{4} \left( t \right) &= \int\limits_{{ - \tau_{1}}}^{0} \int\limits_{{t + s}}^{t} {\left[ {x^{T} \left( \theta \right)S_{1} x\left( \theta \right) + \dot{x}^{T} \left( \theta \right)R_{1} \dot{x}\left( \theta \right)} \right]\hbox{d}\theta \hbox{d}s }\\ & \quad + \int\limits_{{ - \sigma }}^{0} \int\limits_{{t + s}}^{t} {\left[ {y^{T} \left( \theta \right)S_{2} y\left( \theta \right) + \dot{y}^{T} \left( \theta \right)R_{2} \dot{y}\left( \theta \right)} \right]\hbox{d}\theta \hbox{d}s} \\ &\quad + \int\limits_{{ - \tau_{2}}}^{0} {\int\limits_{{t + s}}^{t} {\left[ {x^{T} \left( \theta \right)S_{3} x\left( \theta \right) + \dot{x}^{T} \left( \theta \right)R_{3} \dot{x}\left( \theta \right)} \right]} \,\hbox{d}\theta \hbox{d}s.} \end{aligned} $$

Calculating the time derivative of V(t) along the solution of the system (7), we have:

$$ \dot{V}(t) = \dot{V}_1(t)+\dot{V}_2(t)+\dot{V}_3(t)+\dot{V}_4(t), $$

(12)

where

$$ \begin{aligned} \dot{V}_{1} \left( t \right) &= 2\left[ \begin{array}{*{20}c} x\left( t \right) \hfill \\ x\left( {t - \tau _{1} } \right) \hfill \\ x\left( {t - \tau _{2} } \right) \hfill \\ \int\limits_{{t - \tau _{1} }}^{t} {x\left( s \right)\hbox{d}s} \hfill \\ \int\limits_{{t - \tau _{2} }}^{t} {x\left( s \right)\hbox{d}s} \hfill \\ \end{array} \right]^{T} P\left[ \begin{array}{*{20}c} \dot{x}\left( t \right) \hfill \\ \dot{x}\left( {t - \tau _{1} } \right) \hfill \\ \dot{x}\left( {t - \tau _{2} } \right) \hfill \\ x\left( t \right) - x\left( {t - \tau _{1} } \right) \hfill \\ x\left( t \right) - x\left( {t - \tau _{2} } \right) \hfill \\ \end{array} \right] \\ &\quad+ 2\left[ \begin{array}{*{20}c} y\left( t \right) \hfill \\ \int\limits_{{t - \sigma }}^{t} {y\left( s \right)\hbox{d}s} \hfill \\ \end{array} \right]^{T} Q\left[ \begin{array}{*{20}c} \dot{y}\left( t \right) \hfill \\ y\left( t \right) - y\left( {t - \sigma } \right) \hfill \\ \end{array} \right], \end{aligned}$$

(13)

$$\begin{aligned} \dot{V}_{2} \left( t \right) &\le x^{T} \left( t \right)\left[ {Q_{1} + Q_{2} + Q_{6} } \right]x\left( t \right) + \dot{x}^{T} \left( t \right)\left[ {Q_{3} ,Q_{4} } \right]\dot{x}\left( t \right)\\ & \quad - x^{T} \left( {t - \tau _{1} } \right)Q_{1} x\left( {t - \tau _{1} } \right) - x^{T} \left( {t - \tau _{2} } \right)Q_{2} x\left( {t - \tau _{2} } \right)\\ & \quad - \dot{x}^{T} \left( {t - \tau _{1} } \right)Q_{3} \dot{x}\left( {t - \tau _{1} } \right) \\ &\quad - \dot{x}^{T} \left( {t - \tau _{2} } \right)Q_{4} \dot{x}\left( {t - \tau _{2} } \right)\\ & \quad - \left( {1 - \tau } \right)\dot{x}^{T} \left( {t - \tau _{2} \left( t \right)} \right)Q_{6} \dot{x}\left( {t - \tau _{2} \left( t \right)} \right) \\ &\quad+ y^{T} \left( t \right)Q_{5} y\left( t \right) - y^{T} \left( {t - \sigma } \right)Q_{5} y\left( {t - \sigma } \right), \end{aligned}$$

(14)

$$ \dot{V}_{3} \left( t \right) = 2f^{T} \left( {y\left( t \right)} \right)\Uplambda _{1} \dot{y}\left( t \right), $$

(15)

$$ \begin{aligned}\dot{V}_{4} \left( t \right)& = \dot{x}^{T} \left( t \right)\left[ {\tau _{1} R_{1} + \tau _{2} R_{3} } \right]\dot{x}\left( t \right) + x^{T} \left( t \right)\left[ {\tau _{1} S_{{1}} + \tau _{2} S_{3} } \right]x\left( t \right)\\ &\quad+ \dot{y}^{T} \left( t \right)\left[ {\sigma R_{2} } \right]\dot{y}\left( t \right) + y^{T} \left( t \right)\left[ {\sigma S_{2} } \right]y\left( t \right)\\ & \quad - \int\limits_{{t - \tau _{1} }}^{t} {\left[ {x^{T} \left( \theta \right)S_{1} x\left( \theta \right) + \dot{x}^{T} \left( \theta \right)R_{1} \dot{x}\left( \theta \right)} \right]\hbox{d}\theta \hbox{d}s}\\ & \quad - \int\limits_{{t - \sigma }}^{t} {\left[ {y^{T} \left( \theta \right)S_{2} y\left( \theta \right) + \dot{y}^{T} \left( \theta \right)R_{2} \dot{y}\left( \theta \right)} \right]\hbox{d}\theta \hbox{d}s}\\ & \quad - \int\limits_{{t - \tau _{2} }}^{t} {\left[ {x^{T} \left( \theta \right)S_{3} x\left( \theta \right) + \dot{x}^{T} \left( \theta \right)R_{3} \dot{x}\left( \theta \right)} \right]\hbox{d}\theta \hbox{d}s} . \end{aligned} $$

(16)

By Lemma 1, we obtain:

$$ - \int\limits_{{t - \tau _{1} }}^{t} {x^{T} \left( s \right)S_{1} x\left( s \right)\hbox{d}s \le - \frac{1}{{\tau _{1} }}\left( {\int\limits_{{t - \tau _{1} }}^{t} {x\left( s \right)\hbox{d}s} } \right)^{T} S_{1} \left( {\int\limits_{{t - \tau _{1} }}^{t} {x\left( s \right)\hbox{d}s} } \right),} $$

(17)

$$ - \int\limits_{{t - \tau _{2} }}^{t} {x^{T} \left( s \right)S_{3} x\left( s \right)\hbox{d}s \le - \frac{1}{{\tau _{2} }}\left( {\int\limits_{{t - \tau _{2} }}^{t} {x\left( s \right)\hbox{d}s} } \right)^{T} S_{3} \left( {\int\limits_{{t - \tau _{2} }}^{t} {x\left( s \right)\hbox{d}s} } \right),} $$

(18)

$$ - \int\limits_{{t - \sigma }}^{t} {y^{T} \left( s \right)S_{2} y\left( s \right)\hbox{d}s \le - \frac{1}{\sigma }\left( {\int\limits_{{t - \sigma }}^{t} {y\left( s \right)\hbox{d}s} } \right)^{T} S_{2} \left( {\int\limits_{{t - \sigma }}^{t} {y\left( s \right)\hbox{d}s} } \right).} $$

(19)

It follows from Lemma 2 that

$$ \begin{aligned} \,&- \int\limits_{{t - \tau _{1} }}^{t} {\dot{x}^{T} \left( \theta \right)R_{1} \dot{x}\left( \theta \right)} \hbox{d} \theta \hfill \\ &= - \int\limits_{{t - \tau _{1} }}^{{t - \tau _{1} \left( t \right)}} {\dot{x}^{T} \left( \theta \right)R_{1} \dot{x}\left( \theta \right)\hbox{d}\theta } - \int\limits_{{t - \tau _{1} \left( t \right)}}^{t} {\dot{x}^{T} \left( \theta \right)R_{1} \dot{x}\left( \theta \right)\hbox{d}\theta } \hfill \\ &\le \left[ \begin{array}{*{20}c} x\left( {t - \tau _{1} \left( t \right)} \right) \hfill \\ x\left( {t - \tau _{1} } \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} M_{1} + M_{1}^{T} & - M_{1}^{T} + M_{2} \hfill \\ * & - M_{2} - M_{2}^{T} \hfill \\ \end{array} \right]\,\left[ \begin{array}{*{20}c} x\left( {t - \tau _{1} \left( t \right)} \right) \hfill \\ x\left( {t - \tau _{1} } \right) \hfill \\ \end{array} \right] \hfill \\ & + \left[ {\tau _{1} - \tau _{1} \left( t \right)} \right]\left[ \begin{array}{*{20}c} x\left( {t - \tau _{1} \left( t \right)} \right) \hfill \\ x\left( {t - \tau _{1} } \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{aligned} M_{1}^{T} \hfill \\ M_{2}^{T} \hfill \\ \end{aligned} \right]R_{1}^{{ - 1}} \left[ {M_{1} \,M_{2} } \right]\left[ \begin{array}{*{20}c} x\left( {t - \tau _{1} \left( t \right)} \right) \hfill \\ x\left( {t - \tau _{1} } \right) \hfill \\ \end{array} \right] \hfill \\ &+ \left[ \begin{array}{*{20}c} x\left( t \right) \hfill \\ x\left( {t - \tau _{1} \left( t \right)} \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} M_{3} + M_{3}^{T} & - M_{3}^{T} + M_{4} \hfill \\ * & - M_{4} - M_{4}^{T} \hfill \\ \end{array} \right]\left[ \begin{array}{*{20}c} x\left( t \right) \hfill \\ x\left( {t - \tau _{1} \left( t \right)} \right) \hfill \\ \end{array} \right] \hfill \\ & + \tau _{1} \left( t \right)\left[ \begin{array}{*{20}c} x\left( t \right) \hfill \\ x\left( {t - \tau _{1} \left( t \right)} \right) \hfill \\ \end{array} \right]\left[ \begin{array}{*{20}c} M_{3}^{T} \hfill \\ M_{4}^{T} \hfill \\ \end{array} \right]R_{1}^{{ - 1}} \left[ {M_{3} \,M_{4} } \right]\left[ \begin{array}{*{20}c} x\left( t \right) \hfill \\ x\left( {t - \tau _{1} \left( t \right)} \right) \hfill \\ \end{array} \right], \hfill \\ \end{aligned} $$

(20)

$$ \begin{aligned} \,& - \int\limits_{{t - \tau _{2} }}^{t} {\dot{x}^{T} \left( \theta \right)R_{3} \dot{x}\left( \theta \right)\hbox{d}\theta } \hfill \\ & = - \int\limits_{{t - \tau _{2} }}^{{t - \tau _{2} \left( t \right)}} {\dot{x}^{T} \left( \theta \right)R_{3} \dot{x}\left( \theta \right)\hbox{d}\theta } - \int\limits_{{t - \tau _{2} \left( t \right)}}^{t} {\dot{x}^{T} \left( \theta \right)R_{3} \dot{x}\left( \theta \right)\hbox{d}\theta } \hfill \\ & \le \left[ \begin{array}{*{20}c} x\left( {t - \tau _{2} \left( t \right)} \right) \hfill \\ x\left( {t - \tau _{2} } \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} M_{5} + M_{5}^{T} &- M_{5}^{T} + M_{6} \hfill \\ *& \, - M_{6} - M_{6}^{T} \hfill \\ \end{array} \right]\,\left[ \begin{array}{*{20}c} x\left( {t - \tau _{2} \left( t \right)} \right) \hfill \\ x\left( {t - \tau _{2} } \right) \hfill \\ \end{array} \right] \hfill \\ & + \left[ {\tau _{2} - \tau _{2} \left( t \right)} \right]\left[ \begin{array}{*{20}c} x\left( {t - \tau _{2} \left( t \right)} \right) \hfill \\ x\left( {t - \tau _{2} } \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} M_{5}^{T} \hfill \\ M_{6}^{T} \hfill \\ \end{array} \right]R_{3}^{{ - 1}} \left[ {M_{5} \,M_{6} } \right]\left[ \begin{array}{*{20}c} x\left( {t - \tau _{2} \left( t \right)} \right) \hfill \\ x\left( {t - \tau _{2} } \right) \hfill \\ \end{array} \right] \hfill \\ & + \left[ \begin{array}{*{20}c} x\left( t \right) \hfill \\ x\left( {t - \tau _{2} \left( t \right)} \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} M_{7} + M_{7}^{T} &- M_{7}^{T} + M_{8} \hfill \\ *& \, - M_{8} - M_{8}^{T} \hfill \\ \end{array} \right]\left[ \begin{array}{*{20}c} x\left( t \right) \hfill \\ x\left( {t - \tau _{2} \left( t \right)} \right) \hfill \\ \end{array} \right] \hfill \\ & + \tau _{2} \left( t \right)\left[ \begin{array}{*{20}c} x\left( t \right) \hfill \\ x\left( {t - \tau _{2} \left( t \right)} \right) \hfill \\ \end{array} \right]\left[ \begin{array}{*{20}c} M_{7}^{T} \hfill \\ M_{8}^{T} \hfill \\ \end{array} \right]R_{3}^{{ - 1}} \left[ {M_{7} \,M_{8} } \right]\left[ \begin{array}{*{20}c} x\left( t \right) \hfill \\ x\left( {t - \tau _{2} \left( t \right)} \right) \hfill \\ \end{array} \right], \hfill \\ \end{aligned} $$

(21)

$$ \begin{aligned} \, & - \int\limits_{{t - \sigma }}^{t} {\dot{y}^{T} \left( \theta \right)R_{2} \dot{y}\left( \theta \right)\hbox{d}\theta } \hfill \\ & = - \int\limits_{{t - \sigma }}^{{t - \sigma }} {\dot{y}^{T} \left( \theta \right)R_{2} \dot{y}\left( \theta \right)\hbox{d}\theta } - \int\limits_{{t - \sigma \left( t \right)}}^{t} {\dot{y}^{T} \left( \theta \right)R_{2} \dot{y}\left( \theta \right)\hbox{d}\theta } \hfill \\ &\le \left[ \begin{array}{*{20}c} y\left( {t - \sigma \left( t \right)} \right) \hfill \\ y\left( {t - \sigma } \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} M_{9} + M_{9}^{T} & - M_{9}^{T} + M_{1} 0 \hfill \\ * & - M_{{10}} - M_{{10}}^{T} \hfill \\ \end{array} \right]\,\left[ \begin{array}{*{20}c} y\left( {t - \sigma \left( t \right)} \right) \hfill \\ y\left( {t - \sigma } \right) \hfill \\ \end{array} \right] \hfill \\ & \quad + \left[ {\sigma - \sigma \left( t \right)} \right]\left[ \begin{array}{*{20}c} y\left( {t - \sigma \left( t \right)} \right) \hfill \\ y\left( {t - \sigma } \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} M_{9}^{T} \hfill \\ M_{{10}}^{T} \hfill \\ \end{array} \right]R_{2}^{{ - 1}} \left[ {M_{9} \,M_{{10}} } \right]\left[ \begin{array}{*{20}c} y\left( {t - \sigma \left( t \right)} \right) \hfill \\ y\left( {t - \sigma } \right) \hfill \\ \end{array} \right] \hfill \\ & \quad+ \left[ \begin{array}{*{20}c} y\left( t \right) \hfill \\ y\left( {t - \sigma \left( t \right)} \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} M_{{11}} + M_{{11}}^{T} &- M_{{11}}^{T} + M_{{12}} \hfill \\ * & - M_{{12}} - M_{{12}}^{T} \hfill \\ \end{array} \right]\left[ \begin{array}{*{20}c} y\left( t \right) \hfill \\ y\left( {t - \sigma \left( t \right)} \right) \hfill \\ \end{array} \right] \hfill \\ & \quad + \sigma \left( t \right)\left[ \begin{array}{*{20}c} y\left( t \right) \hfill \\ y\left( {t - \sigma \left( t \right)} \right) \hfill \\ \end{array} \right]\left[ \begin{array}{*{20}c} M_{{11}}^{T} \hfill \\ M_{{12}}^{T} \hfill \\ \end{array} \right]R_{2}^{{ - 1}} \left[ {M_{{11}} \,M_{{12}} } \right]\left[ \begin{array}{*{20}c} y\left( t \right) \hfill \\ y\left( {t - \sigma \left( t \right)} \right) \hfill \\ \end{array} \right]. \hfill \\ \end{aligned} $$

(22)

On the other hand, from system (7) and for any matrices $N_j (j=1,2,\ldots,7)$ with appropriate dimensions, there hold

$$ 0 = 2\left[ \begin{array}{*{20}c} x\left( t \right) \hfill \\ \dot{x}\left( t \right) \hfill \\ f\left( {y\left( {t - \sigma \left( t \right)} \right)} \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} N_{1} \hfill \\ N_{2} \hfill \\ N_{3} \hfill \\ \end{array} \right] \times \left[ { - Ax\left( t \right) - \dot{x}\left( t \right)Bf\left( {y\left( {t - \sigma \left( t \right)} \right)} \right)} \right., $$

(23)

$$ 0 = 2\left[ \begin{array}{*{20}c} y\left( t \right) \hfill \\ \dot{y}\left( t \right) \hfill \\ x\left( {t - \tau _{1} \left( t \right)} \right) \hfill \\ \dot{x}\left( {t - \tau _{2} \left( t \right)} \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} N_{4} \hfill \\ N_{5} \hfill \\ N_{6} \hfill \\ N_{7} \hfill \\ \end{array} \right] \times \left[ {D_{1} x\left( {t - \tau _{1} \left( t \right)} \right) + D_{{20}} \dot{x}\left( {t - \tau _{2} \left( t \right)} \right) - C_{y} \left( t \right)\dot{y}\left( t \right)} \right]. $$

(24)

Noticing the sector condition (6), for any $\lambda_{2i}>0, \lambda_{3i}>0(i=1,2,\ldots,n),$ we have:

$$ - \lambda _{{2i}} \left( {f_{i} y_{i} \left( t \right)} \right) - k_{i}^{ + } \left( {y_{i} \left( t \right)} \right)\left( {f_{i} \left( {y_{i} \left( t \right)} \right) - k_{i}^{ - } \left( {y_{i} \left( t \right)} \right)} \right) \ge 0, \\ -\lambda_{{3i}}\left(f_i(y_i(t-\sigma(t)))-k_{i}^{+}(y_i(t-\sigma(t)))\right)\\ \times \left( {f_{i} \left( {y_{i} \left( {t - \sigma \left( t \right)} \right)} \right) - k_{i}^{ - } \left( {y_{i} \left( {t - \sigma \left( t \right)} \right)} \right)} \right) \ge 0, $$

which can be further rewritten into the following compact matrix forms:

$$ \begin{aligned} -& \sum\limits_{{i = 1}}^{n} {\lambda_{2i}} \left[ \begin{array}{*{20}c} f\left( {y\left( t \right)} \right) \hfill \\ y\left( t \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} e_{i} e_{i}^{T} & - \frac{{k_{i}^{ + } + k_{i}^{ - } }}{2}e_{i} e_{i}^{T} \hfill \\ - \frac{{k_{i}^{ + } + k_{i}^{ - } }}{2}e_{i} e_{i}^{T} &k_{i}^{ + } k_{i}^{ - } e_{i} e_{i}^{T} \hfill \\ \end{array} \right]\left[ \begin{array}{*{20}c} f\left( {y\left( t \right)} \right) \hfill \\ y\left( t \right) \hfill \\ \end{array} \right] \\ &= \left[ \begin{array}{*{20}c} f\left( {y\left( t \right)} \right) \hfill \\ y\left( t \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} - \Uplambda _{2} &\Uplambda _{2} K \hfill \\ \Uplambda _{2} K & - \Uplambda _{2} L \hfill \\ \end{array} \right]\left[ \begin{array}{*{20}c} f\left( {y\left( t \right)} \right) \hfill \\ y\left( t \right) \hfill \\ \end{array} \right] \ge 0,\, \end{aligned}$$

(25)

$$\begin{aligned} -& \sum\limits_{{i = 1}}^{n} {\lambda_{3i}} \left[ \begin{array}{*{20}c} f\left( {y\left( {t - \sigma \left( t \right)} \right)} \right) \hfill \\ y\left( {t - \sigma \left( t \right)} \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} e_{i} e_{i}^{T} & - \frac{{k_{i}^{ + } + k_{i}^{ - } }}{2}e_{i} e_{i}^{T} \hfill \\ - \frac{{k_{i}^{ + } + k_{i}^{ - } }}{2}e_{i} e_{i}^{T} &k_{i}^{ + } k_{i}^{ - } e_{i} e_{i}^{T} \hfill \\ \end{array} \right] \\ &\times \left[ \begin{array}{*{20}c} f\left( {y\left( {t - \sigma \left( t \right)} \right)} \right) \hfill \\ y\left( {t - \sigma \left( t \right)} \right) \hfill \\ \end{array} \right]\\ &= \left[ \begin{array}{*{20}c} f\left( {y\left( {t - \sigma \left( t \right)} \right)} \right) \hfill \\ y\left( {t - \sigma \left( t \right)} \right) \hfill \\ \end{array} \right]^{T} \left[ \begin{array}{*{20}c} - \Uplambda _{3} &\Uplambda _{3} K \hfill \\ \Uplambda _{3} K &- \Uplambda _{3} L \hfill \\ \end{array} \right]\left[ \begin{array}{*{20}c} f\left( {y\left( {t - \sigma \left( t \right)} \right)} \right) \hfill \\ y\left( {t - \sigma \left( t \right)} \right) \hfill \\ \end{array} \right] \ge 0,\, \end{aligned}$$

(26)

where $\Uplambda_2=diag[\lambda_{21},\ldots,\lambda_{2n}]>0,$ $\Uplambda_3=diag[\lambda_{31},\ldots,\lambda_{3n}]>0.$

Taking (12)–(26) into account, we get

$$ \begin{aligned}\dot{V}\left( t \right) &\le \eta ^{{T\left( t \right)}} \left\{ \Upphi + \left( {\tau _{1} - \tau _{1} \left( t \right)} \right)F_{1} R_{1}^{{ - 1}} F_{1}^{T} + \tau _{1} \left( t \right)F_{2} R_{1}^{{ - 1}} F_{2}^{T}\right.\\& \quad + \left( {\tau _{2} - \tau _{2} \left( t \right)} \right)F_{3} R_{3}^{{ - 1}} F_{3}^{T} + \tau _{2} \left( t \right)F_{4} R_{3}^{{ - 1}} F_{4}^{T}\\ & \quad \left. + \left( {\sigma - \sigma \left( t \right)} \right)F_{5} R_{2}^{{ - 1}} F_{5}^{T} + \sigma \left( t \right)F_{6} R_{2}^{{ - 1}} F_{6}^{T} \right\}\eta \left( t \right), \end{aligned}$$

(27)

where $\eta(t)=[x^T(t)\ x^T(t-\tau_1)\ x^T(t-\tau_2) \int\nolimits_{t-\tau_1}^tx(s)\hbox{d}s \int\nolimits_{t-\tau_2}^tx^T(s)\hbox{d}s\ \dot{x}^T(t) \\ \dot{x}^T(t-\tau_1)\ \dot{x}^T(t-\tau_2)\ x^T(t-\tau_1(t)) x^T(t-\tau_2(t))\ \dot{x}^T(t-\tau_2(t))\ y^T(t) \\ y^T(t-\sigma) \int\nolimits_{t-\sigma}^ty^T(s)\hbox{d}s \dot{y}^T(t)\ f^T(y(t)) f^T(y(t-\sigma(t))) y^T(t-\sigma(t))]^{T}.$

Next, we shall prove

$$\begin{aligned} && \Upphi+(\tau_1-\tau_1(t))F_1R_1^{-1}F_1^T+\tau_1(t)F_2R_1^{-1}F_2^T+ (\tau_2-\tau_2(t))F_3R_3^{-1}F_3^T \\&&+\tau_2(t)F_4R_3^{-1}F_4^T +(\sigma-\sigma(t))F_5R_2^{-1}F_5^T+\sigma(t)F_6R_2^{-1}F_6^T<0,\end{aligned} $$

(28)

where $\Upphi$ is defined in (8)–(11).

By Lemma 3, it easily follows that (28) holds if the following inequalities hold:

$$ \Upphi+\tau_1F_1R_1^{-1}F_1^T +\tau_2F_3R_3^{-1}F_3^T+\sigma F_5R_2^{-1}F_5^T< 0, $$

(29)

$$ \Upphi+\tau_1F_1R_1^{-1}F_1^T +\tau_2F_3R_3^{-1}F_3^T+\sigma F_6R_2^{-1}F_6^T < 0, $$

(30)

$$ \Upphi+\tau_1F_1R_1^{-1}F_1^T +\tau_2F_4R_3^{-1}F_3^T+\sigma F_5R_2^{-1}F_5^T < 0, $$

(31)

$$ \Upphi+\tau_1F_1R_1^{-1}F_1^T +\tau_2F_4R_3^{-1}F_4^T+\sigma F_6R_2^{-1}F_6^T < 0, $$

(32)

$$ \Upphi+\tau_1F_2R_1^{-1}F_2^T +\tau_2F_3R_3^{-1}F_3^T+\sigma F_5R_2^{-1}F_5^T < 0, $$

(33)

$$ \Upphi+\tau_1F_2R_1^{-1}F_2^T +\tau_2F_3R_3^{-1}F_3^T+\sigma F_6R_2^{-1}F_6^T < 0, $$

(34)

$$ \Upphi+\tau_1F_2R_1^{-1}F_2^T +\tau_2F_4R_4^{-1}F_3^T+\sigma F_5R_2^{-1}F_5^T < 0, $$

(35)

$$ \Upphi+\tau_1F_2R_1^{-1}F_2^T +\tau_2F_4R_3^{-1}F_4^T+\sigma F_6R_2^{-1}F_6^T < 0. $$

(36)

By the Schur complement formula and after some manipulations, we can conclude that (29)–(36) are true if (8)–(11) hold, which further implies that $\dot{V}(t)<0.$ Therefore, the GRNs (7) are asymptotically stable according to the Lyapunov stability theory. The proof is complete.$\square$

Remark 3

Theorem 1 provides a delay-dependent stability condition which guarantees the asymptotic stability of the neutral GRNs (7). Different from Theorem 1 in Jung et al. (2010), here the discrete delays are unnecessarily differentiable. Moreover, the discrete delay and the neutral delay are not required to be equal to each other. Therefore, compared with Theorem 1 in Jung et al. (2010), Theorem 1 in this paper can be regarded as an extension of Jung et al. (2010).

When the discrete delays and the neutral delay are constant, i.e., σ(t) = σ, τ₁(t) = τ₁, τ₂(t) = τ₂, the GRNs (7) turn into

$$ \begin{aligned} \dot{x} (t) &=-Ax(t)+B f(y(t-\sigma)),\\ \dot{y}(t) &=-Cy(t)+D_1x(t-\tau_1)+D_2\dot{x}(t-\tau_2). \end{aligned} $$

(37)

We have the following theorem for the GRNs (37):

Theorem 2

The GRNs (37) with constant neutral delay are asymptotically stable if there exist matrices $P=\left[\begin{array}{lllll} P_{11} & P_{12} & P_{13} & P_{14} \\ \ast & P_{22} & P_{23}& P_{24} \\ \ast & \ast & P_{33} & P_{34} \\ \ast & \ast & \ast & P_{44} \\ \end{array}\right] >0, Q=\left[\begin{array}{llllll} Q_{11} & Q_{12} \\ \ast & Q_{22}\\ \end{array} \right]>0, Q_i>0 (i=1,2,3,4,5), R_k>0, S_k>0 (k=1,2,3), \Uplambda_1=diag[\lambda_{11},\ldots,\lambda_{1n}]>0, \Uplambda_2=diag[\lambda_{21},\ldots,\lambda_{2n}]>0,$ and the free matrices M _l (l = 1, 2, 3, 4, 5, 6), N _j (j = 1, 2, 3, 4, 5, 6, 7) with appropriate dimensions such that the following LMI holds:

$$ \left[ \begin{array}{llll} \Uppsi & F_1 & F_2 & F_3 \\ \ast & -\frac{1}{\tau_1}T_1 & 0 & 0 \\ \ast & \ast & -\frac{1}{\tau_2}T_2 & 0 \\ \ast & \ast & \ast & -\frac{1}{\sigma}T_3 \\ \end{array} \right] < 0 $$

(38)

where

$$ \begin{aligned} \Uppsi &= \Uppsi^T=(\Uppsi_{ij})_{13\times13}, \\ F_1&=[M_1,0,M_2,0,\ldots,0]_{13\times1}^T,\\ F_2&=[M_3,M_4,0,\ldots,0]_{13\times1}^T,\\ F_3&=[0,\ldots,0,M_{5_{\downarrow_{8}}},M_6,0, \ldots,0]_{13\times1}^T,\\ \Uppsi_{11} &=Q_1+Q_2+M_1+M_1^T +M_3+M_3^T +P_{13}+P_{13}^T\\ &+P_{14}+P_{14}^T+\tau_1R_1+\tau_2R_2-N_1A-AN_1^T.\\ \Uppsi_{12} &=-P_{14}+P_{23}^T+P_{24}^T-M_3^T+M_4,\Uppsi_{13}= -P_{13}-M_1^T+M_2,\\ \Uppsi_{14}&=P_{33}+P_{34}^T, \Uppsi_{15}=P_{34}+P_{44},\Uppsi_{16} =P_{11}-N_1-AN_2^T,\\ \Uppsi_{17}&=P_{12},\Uppsi_{18}=\Uppsi_{19}=\Uppsi_{1,10}=\Uppsi_{1,11} =\Uppsi_{1,12}=0,\\ \Uppsi_{1,13}&=N_1B-AN_3^T,\Uppsi_{22}=-P_{24}-P_{24}^T-Q_2-M_4-M_4^T,\\ \Uppsi_{23}&=-P_{23},\Uppsi_{24}=-P_{34}^T,\Uppsi_{25}=-P_{44}^T, \Uppsi_{26}=P_{12}^T,\\ \Uppsi_{27}&=P_{22},\Uppsi_{28}=\Uppsi_{29}=\Uppsi_{2,10}=\Uppsi_{2,11}= \Uppsi_{2,12}=\Uppsi_{2,13}=0,\\ \Uppsi_{33}&=-Q_1-M_2-M_2^T+N_4D_1+D_1N_4^T,\Uppsi_{34}=-P_{33},\\ \Uppsi_{35}&=-P_{34},\Uppsi_{36}=0,\Uppsi_{37}=N_4D_2+D_1N_5^T,\\ \Uppsi_{38}&=-N_4C+D_1N_6^T,\Uppsi_{3,11}=-N_4+D_1N_7^T,\\ \Uppsi_{39}&=\Uppsi_{3,10}=\Uppsi_{3,12}=\Uppsi_{3,13}=0, \Uppsi_{44}=-\frac{1}{\tau_1}R_1,\\ \Uppsi_{46}&=P_{13}^T,\Uppsi_{47}=P_{23}^T,\\ \Uppsi_{45}&=\Uppsi_{48}=\Uppsi_{49}=\Uppsi_{4,10}=\Uppsi_{4,11}= \Uppsi_{4,12}=\Uppsi_{4,13}=0,\\ \Uppsi_{55}&=-\frac{1}{\tau_2}R_2,\Uppsi_{56}=P_{14}^T, \Uppsi_{57}=P_{24}^T,\\ \Uppsi_{58}&=\Uppsi_{59}=\Uppsi_{5,10}=\Uppsi_{5,11}=\Uppsi_{5,12}= \Uppsi_{5,13}=0,\\ \Uppsi_{66}&=Q_4+\tau_1T_1+\tau_2T_2-N_2-N_2^T,\\ \Uppsi_{67}&=\Uppsi_{68}=\Uppsi_{69}=\Uppsi_{6,10}=\Uppsi_{6,11}= \Uppsi_{6,12}=0,\\ \Uppsi_{6,13}&=N_2B-N_3^T,\Uppsi_{77}=-Q_4+N_5D_2+D_2N_5^T,\\ \Uppsi_{78}&=-N_5C+D_2N_5^T,\Uppsi_{7,11}=-N_5+D_2N_7^T,\\ \Uppsi_{79}&=\Uppsi_{7,10}=\Uppsi_{7,12}=\Uppsi_{7,13}=0,\\ \Uppsi_{88}&=Q_{12}+Q_{12}^T+Q_3+\sigma R_3+M_5+M_5^T-N_6C-CN_6^T-\Uplambda_1L,\\ \Uppsi_{89}&=-Q_{12}-M_5^T+M_6, \Uppsi_{8,10}=Q_{22},\Uppsi_{8,11}=Q_{11}-N_6-CN_7^T,\\ \Uppsi_{8,12}&=\Uplambda_1K,\Uppsi_{8,13}=0,\Uppsi_{99}=-Q_3-M_6-M_6^T -\Uplambda_2L,\\ \Uppsi_{9,10}&=-Q_{22},\Uppsi_{9,11}=\Uppsi_{9,12}=0,\\ \Uppsi_{9,13}&=\Uplambda_2K, \Uppsi_{10,10}=-\frac{1}{\sigma}R_3,\Uppsi_{10,11}=Q_{12}^T, \Uppsi_{10,12}=\Uppsi_{10,13}=0,\\ \Uppsi_{11,11}&=\sigma T_3-N_7-N_7^T,\Uppsi_{11,12}=\Uppsi_{11,13}=0,\Uppsi_{12,12}= Q_5-\Uplambda_1,\\ \Uppsi_{12,13}&=0, \Uppsi_{13,13}=-Q_5-\Uplambda_2+N_3B+B^TN_3^T, \end{aligned} $$

Proof

Consider the following Lyapunov–Krasovskii functional:

$$ V(t)=V_1(t)+V_2(t)+V_3(t)+V_4(t)+V_5(t), $$

where

$$ \begin{aligned} V_1(t)&=\left[\begin{array}{l} x(t)\\ x(t-\tau_2) \\ \int\limits_{t-\tau_1}^t x(s)\hbox{d}s \\ \int\limits_{t-\tau_2}^t x(s)\hbox{d}s\\ \end{array} \right]^T P\left[\begin{array}{l} x(t) \\ x(t-\tau_2) \\ \int\limits_{t-\tau_1}^t x(s)\hbox{d}s \\ \int\limits_{t-\tau_2}^t x(s)\hbox{d}s\\ \end{array} \right]\\ +\left[\begin{array}{l} y(t) \\ \int\limits_{t-\sigma}^t y(s)\hbox{d}s \\ \end{array} \right]^T Q \left[\begin{array}{l} y(t) \\ \int\limits_{t-\sigma}^t y(s)\hbox{d}s \\ \end{array} \right], \\ V_2(t)&= \int\limits_{t-\tau_1}^tx^T(s)Q_1x(s)\hbox{d}s+\int\limits_{t-\tau_2}^tx^T(s)Q_2x(s)\hbox{d}s+ \int\limits_{t-\sigma}^ty^T(s)Q_3y(s)\hbox{d}s, \\ V_3(t)&= \int\limits_{t-\tau_2}^t\dot{x}^T(s)Q_4\dot{x}(s)\hbox{d}s+ \int\limits_{t-\sigma}^{t}f^T(y(s))Q_5f(y(s))\hbox{d}s,\\ V_4(t)&=\int\limits_{-\tau_1}^0\int\limits_{t+s}^tx^T(\theta)R_1x(\theta)\hbox{d}\theta \hbox{d}s+ \int\limits_{-\tau_2}^0\int\limits_{t+s}^tx^T(\theta)R_2x(\theta)\hbox{d}\theta \hbox{d}s\\ && +\int\limits_{-\sigma}^0\int\limits_{t+s}^ty^T(\theta)R_3y(\theta)\hbox{d}\theta \hbox{d}s,\\ V_5(t)&=\int\limits_{-\tau_1}^0\int\limits_{t+s}^t\dot{x}^T(\theta)T_1\dot{x} (\theta)\hbox{d}\theta \hbox{d}s+ \int\limits_{-\tau_2}^0\int\limits_{t+s}^t\dot{x}^T(\theta)T_2\dot{x}(\theta) \hbox{d}\theta \hbox{d}s\\ && +\int\limits_{-\sigma}^0\int\limits_{t+s}^t\dot{y}^T(\theta)T_3\dot{y} (\theta)\hbox{d}\theta \hbox{d}s. \end{aligned} $$

The remaining process of the proof is similar to that of Theorem 1, thus it is omitted here for brevity.$\square$

Remark 4

As it is well known, there are no unique, exact mathematical descriptions for modeling genetic networks. Therefore, the robust stability problem and robust control problem [as considered in Jin and Meng (2011, 2009)] should also be studied for GRNs with neutral time delay, which will be interesting topics for future research.

4 Numerical examples

Now, we provide two numerical examples to show the effectiveness of the theoretical results developed in this paper.

Example 1

In Elowitz and Stanislas (2000), the dynamics of repressilator is theoretically predicted and experimentally investigated. That system is a cyclic negative-feedback loop consisting of three repressor genes (lacl, tetR and cl) and their promoters. It is described as follows:

$$ \begin{aligned} \dot{m}_i &=-\gamma_i m_i+\frac{\beta_i}{1+p^{n}_j} \\ \dot{p}_i &=-\delta_i(p_i-m_i) \end{aligned} $$

where i = lacl, tetR, cl; j = cl, lacl, tetR, and n is a Hill coefficient, m _i and p _i are the concentrations of the three mRNA and repressor-protein, and δ _i  > 0 denotes the ratio of the protein decay rate to the mRNA decay rate. This system is investigated in Li et al. (2006). Taking the neutral time delay and the transcriptional time delay into account, the above equations are rewritten in the vector form as follows (Jung et al. 2010):

$$ \begin{aligned} \dot{x} (t)&=-Ax(t)+B f(y(t-\sigma(t))),\\ \dot{y}(t) &=-Cy(t)+D_1x(t-\tau_1(t))+D_2\dot{x}(t-\tau_2(t)), \end{aligned} $$

(39)

where

$$ A = diag[3,3], \quad B=\left[ \begin{array}{ll} 0.8 & 0 \\ 0.8 & 0.8 \\ \end{array} \right],\quad C=diag[2.5 , 2.5], \\ D_1=\left[ \begin{array}{ll} 0.5& 0\\ 0 & 0.5 \\ \end{array}\right] \quad D_2=\left[\begin{array}{ll} 0.6 & 0\\ 0 & 0.6 \\ \end{array}\right],\quad f(y)=\frac{y^2}{1+y^2}. $$

Then we have

$$ k_i^{+}=0.65,k_i^-=0, K=diag[0.325 , 0.325], L=0. $$

Assuming that the time delays are

$$ \tau_1(t)=|\sin(t)|, \tau_2(t)=0.5+0.5\sin(t), \sigma(t)=|\sin(t)|. $$

It is easily verified that Theorem 1 in Jung et al. (2010) is not applicable because the discrete delays τ₁(t) and σ(t) are not differentiable. Hence, it fails to conclude whether these GRNs are globally asymptotically stable or not. However, by using the MATLAB LMI Toolbox, it can be seen that the LMIs in (8)–(11) are feasible and

$$ \begin{aligned} P_{11} &= \left[\begin{array}{ll} 86.0161 & -21.0499\\ -21.0499 & 45.0905 \end{array}\right] , \quad P_{12} =\left[\begin{array}{ll} -0.0029 & 0.0001\\ -0.0084 & -0.0005 \end{array} \right] ,\\ P_{13} &= \left[\begin{array}{ll} 0.0140 & 0.0000\\ -0.0026 & 0.0035 \end{array} \right] , \quad P_{14} = \left[\begin{array}{ll} 0.2340 & 0.0393\\ -0.0136 & 0.1187 \end{array}\right] ,\\ P_{15}&= \left[\begin{array}{ll} 0.1590 & 0.0137\\ -0.0150 & 0.0748 \end{array}\right] , \quad P_{22}= \left[\begin{array}{ll} 1.4201 & -0.3282\\ -0.3282 & 0.9248 \end{array}\right],\\ P_{23}&= \left[\begin{array}{ll} -0.0003 & 0.0000\\ 0.0003 & -0.0027 \end{array}\right], \quad P_{24}=\left[\begin{array}{ll} 0.0773 & -0.0576\\ -0.0402 & 0.0447 \end{array}\right],\\ P_{25} &= \left[\begin{array}{ll} -0.0459 & -0.0056\\ -0.0050 & -0.0528 \end{array}\right], \quad P_{33}=\left[\begin{array}{ll} 1.4285 & -0.3295\\ -0.3295 & 0.9290 \end{array}\right],\\ P_{34}&=\left[\begin{array}{ll} -0.0178 & 0.0074\\ 0.0021 & -0.0275 \end{array}\right], \quad P_{35}=\left[\begin{array}{ll} 0.0767 &-0.0411\\ -0.0275 & 0.0574 \end{array}\right],\\ P_{44}&=\left[\begin{array}{ll} 1.6775 & 0.0545\\ 0.0545 & 1.7015 \end{array}\right], \quad P_{45}=\left[\begin{array}{ll} -0.3933 & -0.0019\\ -0.0014 & -0.3912 \end{array}\right],\\ P_{55}&=\left[\begin{array}{ll} 1.6614 & 0.0373\\ 0.0373 & 1.6715 \end{array}\right], \quad Q_{11}=\left[\begin{array}{ll} 25.3269 & -3.0633\\ -3.0633 & 14.3504 \end{array}\right],\\ Q_{12}&=\left[\begin{array}{ll} -0.0150 & -0.0286\\ -0.0364 & -0.0766 \end{array}\right], \quad Q_{22}=\left[\begin{array}{ll} 1.4721 & -0.0767\\ -0.0767 & 1.2941 \end{array}\right]. \end{aligned} $$

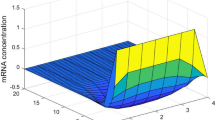
Therefore, by Theorem 1, we conclude that the GRNs (7) with the above parameters are asymptotically stable, which shows that for this example the asymptomatic stability condition in this paper is less conservative than that in Jung et al. (2010). The convergence dynamics of the system in Example 1 is shown in Fig. 1.

Fig. 1

Transient response of x _i (t) and y _i (t), i = 1, 2

Example 2

Consider the GRNs (37) with the following parameters:

$$ \begin{aligned} A &=\left[\begin{array}{ll} 0.3 & 0 \\ 0 & 0.3 \\ \end{array} \right],\ B=\left[\begin{array}{ll} 0 & 3.5 \\ 3.5 & 0 \\ \end{array} \right],\ C=\left[\begin{array}{ll} 2.5 & 0 \\ 0 & 2.5 \\ \end{array} \right],\\ D_1 &=\left[\begin{array}{ll} 0.2 & 0\\ 0 & 0.2 \\ \end{array} \right],\ D_2=\left[\begin{array}{ll} 8 & 0 \\ 0 & 0.8 \\ \end{array}\right],\ f(y)=\frac{y^2}{1+y^2}. \end{aligned} $$

Then we have

$$ k_i^{+}=0.65,k_i^-=0, K=diag[0.325 , 0.325], L=0. $$

Assume that the time delays satisfy

$$ \sigma=0.1, \tau_1=0.995, \tau_2=1. $$

As τ₁ ≠ τ₂, Theorems 1 in Jung et al. (2010) fails to check whether these GRNs are globally asymptotically stable or not. However, by resorting to Theorem 2 in this paper and the Matlab LMI Toolbox, we obtain:

$$ \begin{aligned} P_{11} &= \left[\begin{array}{ll} 37.6874 & 0\\ 0 & 37.6874 \end{array}\right] ,\quad P_{12} = \left[\begin{array}{ll} -9.4112 & 0\\ 0 & -9.4112 \end{array}\right] ,\\ P_{13} &=\left[\begin{array}{ll} -0.3848 & 0\\ 0 & -0.3848 \end{array}\right] ,\quad P_{14} = \left[\begin{array}{ll} -3.7548 & 0\\ 0 & -3.7548 \end{array}\right] ,\\ P_{22} &= \left[\begin{array}{ll} 6.7550 & 0\\ 0 & 6.7550 \end{array}\right],\quad P_{23}=\left[\begin{array}{ll} -1.1085 & 0\\ 0 & -1.1085 \end{array}\right],\\ P_{24}&=\left[\begin{array}{ll} 0.4419 & 0\\ 0 & 0.4419 \end{array}\right],\quad P_{33}=\left[\begin{array}{ll} 4.0319 & 0\\ 0 & 4.0319 \end{array}\right],\\ P_{34}&=\left[\begin{array}{ll} -0.0576 & 0\\ 0 & -0.0576 \end{array}\right],\quad P_{44}=\left[\begin{array}{ll} 4.6757 & 0\\ 0 & 4.6757 \end{array}\right],\\ Q_{11}&=\left[\begin{array}{ll} 77.0255 & 0\\ 0 & 77.0255 \end{array}\right],\quad Q_{12}=\left[\begin{array}{ll} 7.3880 & 0\\ 0 & 7.3880 \end{array}\right],\\ Q_{22}&=\left[\begin{array}{ll} 22.4188 & 0\\ 0 & 22.4188 \end{array}\right]. \end{aligned} $$

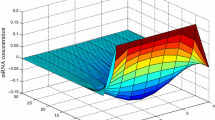
Therefore, the given GRNs are globally asymptotically stable by Theorem 2. The trajectories of x(t) and y(t) are illustrated in Fig. 2, which also indicate that the GRNs with the above parameters are globally asymptotically stable.

Fig. 2

Transient response of x _i (t) and y _i (t), i = 1, 2

5 Conclusions

In this paper, we have investigated the problem of the asymptotic stability problem of genetic regulatory networks with time-varying/constant neutral delays. With the introduction of a new Lyapunov–Krasovskii functional and the use of the free weighting matrix technique, we have derived the sufficient delay-dependent stability conditions for GRNs. These conditions can be easily verified with the MATLAB LMI toolbox since they appear in the form of strict LMIs. It has been shown that the proposed stability conditions are applicable no matter whether the discrete delay is equal to the neutral delay or not. Finally, two numerical examples have been presented, which clearly show the effectiveness of the new stability conditions (including the reduced conservativeness).