Introduction

Development of genome sequencing and gene recognition has been accumulating a wealth of experimental data. This creates a new challenge to biology of understanding how genes and proteins work collectively, i.e. the analysis of these data. This challenge leads to a significant increase of computer applications for modeling and data interpretation methods. The aim is to develop computer simulations that mimic biological phenomena, data or patterns, such as complex biochemical reactions and genetic networks in cellular media (Turner et al. 2004). Real genetic systems are composed of a large number of reactions and reacting species. There are too many items to include them all in models. It is rather difficult to find an effective method to construct a complete model and analyze such a complex model. So we only consider the concentrations of mRNAs and proteins. Recently, there have been many efforts for modeling genetic regulatory networks using different classes of mathematical models (Hasty et al. 2001; De Jong 2002). Basically, there are two types of genetic network models. i.e. the Boolean models and the differential equation model (Smolen et al. 2000; Kobayashi et al. 2002; Bolouri and Davidson 2002; Wang et al. 2004; Benuskova and Kasabov 2008). Boolean network model interprets gene interactions as connections between genes. The state of gene expression is simplified as being either completely ON or completely OFF. The Boolean expression state converges to a terminal state via a series of state transitions that is determined by the designed Boolean rules. In the differential equation models, the variables describe the concentrations of gene products, such as mRNAs and proteins, as continuous values of the gene regulation systems.

Recently, the genetic regulatory networks in the form of differential equations have been well studied. Becskei and Serrano (2000) designed and constructed simple gene circuits consisting of a regulator and transcriptional repressor modules in Escherichia coli and they showed the gain of stability produced by negative feedback. In Chen and Aihara (2002), a model for genetic regulatory networks with time delays was proposed and nonlinear properties of the model in terms of local stability and bifurcation was analyzed. In Li et al. (2006a), a nonlinear model for genetic regulatory networks with SUM regulatory functions was presented. Genetic networks with delays and stochastic perturbations were studied and sufficient conditions of stability were derived in terms of linear matrix inequalities (LMI). Li et al. (2006b) provided a theoretical method for analyzing the synchronization of coupled nonidentical genetic oscillators. Sufficient conditions for the synchronization as well as the estimation of the bound of the synchronization error were also obtained. Authors Ren and Cao (2008) studied the robust stability of the genetic regulatory networks with time-delays, and present some sufficient conditions using Lyapunov functional theory and LMI technique. In Cao and Ren (2008), discrete-time versions of the continuous-time genetic regulatory networks with SUM regulatory functions are formulated and studied, and obtained sufficient conditions for exponential stability of the discrete-time genetic regulatory networks with delays.

In fact, for most genetic regulatory system, there are two types of reactions (De Jong 2002): fast reaction and slow reaction. Fast reaction, such as dimerization, binding reactions and other medical modification reaction, we can assume this reaction is immediately and time delay is reduced to zero. While transcription and translation involve a number of multi-stage reactions, there is a time lag in the peaks between mRNA molecules and proteins of gene. On the other side, mRNA and proteins may be synthesized at different locations (i.e. nucleus and cytoplasm, respectively), thus transportation or diffusion of mRNA and proteins between these two locations results in sizeable delays. That is, time delays exist in genetic regulatory networks, and possible effects of time delays have attracted some attentions (Chen and Aihara 2002; Li et al. 2006a; Ren and Cao 2008; He and Cao 2008).

Stochasticity is ubiquitous in biology. Noise in the form of random fluctuations arises in genetic regulatory network in one of two ways. Intrinsic noise is inherent in the biochemical reactions. Its magnitude is proportional to the inverse of the system size, and its origin is often thermal. On the other hand, external noise originates environment fluctuation (Hasty et al. 2000).

In the applications and designs of genetic networks, there are often some unavoidable uncertainties such as model errors, external perturbations, and parameter fluctuations, which can cause the networks to be unstable (Ren and Cao 2008). There are some papers have studied stability of neural networks with stochastic perturbations or parameter uncertainties (Huang and Feng 2007; Liao et al. 2001; Wang et al. 2006, 2007; Zhang et al. 2007), that give us some suggests for studying genetic regulatory networks. In this paper, we aim to analyze the stability of genetic networks in the forms of differential equations. We consider the delayed genetic regulatory networks not only with stochastic perturbations but also with parameter uncertainties. To our best knowledge, there are few paper to investigate it. By using Lyapunov functional theory and LMI technique, Novel criteria are derived to guarantee the asymptotic and robust stability of such genetic networks.

The rest of this paper is organized as follows. In section “Model and analysis”, problem formulation and preliminaries are given. In section “Stochastic stability condition of uncertain genetic networks with time-varying delays”, several sufficient criteria are derived for checking globally robust stability of the genetic regulatory networks with stochastic perturbations and time-varying delays. In section “Illustrative examples”, two examples are given to show the effectiveness of the proposed results. Finally, conclusions are given in section “Conclusions”.

Notation

For convenience, some notations are introduced. For a real square matrix X, the notation X > 0(X < 0) means that X is symmetric and positive definite (negative definite). I is the identity matrix with appropriate dimension. The superscript ‘‘T’’ represents the transpose. For τ > 0, ℘([−τ, 0]; R n) denotes the family of continuous functions φ from [−τ, 0] to R n with the norm ||φ|| = sup–τ ≤ ϑ ≤ 0|φ(ϑ)|. Let (Ω, F, {F t } t ≻ 0, P) be a complete probability space with a filtration {F t } t ≥ 0 satisfying the usual conditions (i.e. it is right continuous and F 0 contains all P-pull sets); \( L_{{F_{0} }}^{p} ([ - h,0];R^{n} ) \)the family of all F 0-measurable ℘([−τ, 0]; R n)-valued random variables ξ = {ξ(θ): −τ ≤ θ ≤ 0} such that sup–τ ≤ θ ≤ 0 E|ξ(θ)|p < ∞ where E stands for the mathematical expectation operator with respect to the given probability measure P; ℘2,1(R n × R +; R +) the family of all nonnegative functions V(x, t) on R n × R + which are continuously twice differentiable in x and differentiable in t.

Model and analysis

Authors considered a genetic regulatory network model (Li et al. 2006a):

$$\left\{\begin{array}{l}\dot{m}_{i} (t) = - a_{i} m_{i} (t) +b_{i} (p_{1} (t),p_{2} (t), \ldots ,p_{n} (t)),\\ \dot{p}_{i} (t)= - c_{i} p_{i} (t) + d_{i} m_{i} (t),\quad i = 1,2, \ldots ,n. \\\end{array}\right.$$
(1)

where \( m_{i} (t),p_{i} (t) \in R \) are the concentrations of mRNA and protein of the ith node. a i and c i are the rates of degradation of mRNA and protein, respectively; d i is the translation rate, and b i is the regulatory function of the ith gene, which is generally a nonlinear function of the variables (p 1(t), p 2(t), …, p n (t)), and nonlinear function is monotonic with each variable.

In this paper, we considered the genetic regulatory networks with time delay described by the following differential equation:

$$\left\{ \begin{array}{*{20}c} {\dot{m}_{i} (t) = - a_{i} m_{i} (t) + B_{i} (p_{1} (t - \tau_{1} (t)),p_{2} (t - \tau_{1} (t)), \ldots ,p_{n} (t - \tau_{1} (t))),} \\ {\dot{p}_{i} (t) = - c_{i} p_{i} (t) + d_{i} m_{i} (t - \tau_{2} (t)),\quad i = 1,2, \ldots ,n.} \\ \end{array}\right. $$
(2)

where τ 1(t), τ 2(t) are transcriptional delays, for any single gene in the network, there are one output p i (t − τ 1(t)) to other genes and multiple inputs p j (t − τ 1(t)) (j = 1, 2, …, n) from other genes. The structure and regulation mechanism of the genetic work can be seen in Chen and Aihara (2002). As a monotonic increasing or decreasing regulatory function, B i is usually the Michaelis–Menten or Hill form. In this paper we take B i (p 1(t), p 2(t), …, p n (t)) = ∑ j B ij (p j (t)), which is called SUM logic (Li et al. 2006a). That is each transcription factor acts additively to regulate the ith gene. The function B ij (p j (t)) is a monotonic function of the Hill form.

$$ B_{ij} (p_{j} (t)) = \left\{ {\begin{array}{*{20}c} {\alpha_{ij} \tfrac{{(p_{j} (t)/\beta )^{H} }}{{1 + (p_{j} (t)/\beta )^{H} }},} & {\frac{{{\text{if}}\,{\text{transcription}}\,{\text{factor}}\,j}}{{{\text{is}}\,{\text{an}}\,{\text{activator}}\,{\text{of}}\,{\text{gene}}\,i}}} \\ {\alpha_{ij} \tfrac{1}{{1 + (p_{j} (t)/\beta )^{H} }},} & {\frac{{{\text{if}}\,{\text{transcription}}\,{\text{factor}}\,j}}{{{\text{is}}\,{\text{a}}\,{\text{repressor}}\,{\text{of}}\,{\text{gene}}\,i}}} \\ \end{array} } \right. $$
(3)

where H is the Hill coefficient, β is a positive constant, and α ij is the dimensionless transcriptional rate of transcriptional factor j to gene i, which is a bounded constant. Note that

$$ \tfrac{1}{{1 + (p_{j} (t)/\beta )^{H} }} = 1 - \tfrac{{(p_{j} (t)/\beta )^{H} }}{{1 + (p_{j} (t)/\beta )^{H} }} $$

Hence, we can rewrite (2) as:

$$ \left\{ \begin{array}{*{20}c} {\dot{m}_{i} (t) = - a_{i} m_{i} (t) + \sum\limits_{j = 1}^{n} {B_{ij} g(p_{j} (t)) + I_{i} } ,} \\ {\dot{p}_{i} (t) = - c_{i} p_{i} (t) + d_{i} m_{i} (t - \tau_{2} (t)),\quad i = 1,2, \ldots ,n} \\ \end{array}\right. $$
(4)

where g(x) = (x/β)H/[1 + (x/β)H] is a monotonically increasing function, I i is defined as basal rate \( I_{i} = \sum\nolimits_{{j \in L_{i} }} {\alpha_{ij} } , \) and L i is the set of repressors of gene i. \( B = (B_{ij} ) \in R^{n \times n} \) is defined as:

$$ B_{ij} = \left\{ {\begin{array}{*{20}c} {\alpha_{ij} } \hfill & {{\text{if}}\,{\text{transcription}}\,{\text{factor}}\,j\,{\text{is}}\,{\text{an}}\,{\text{activator}}\,{\text{of}}\,{\text{gene}}\,i,} \hfill \\ 0 \hfill & {{\text{if}}\,{\text{there}}\,{\text{is}}\,{\text{no}}\,{\text{link}}\,{\text{from}}\,{\text{gene}}\,j\,{\text{to}}\,i ,} \hfill \\ { - \alpha_{ij} } \hfill & {{\text{if}}\,{\text{transcription}}\,{\text{factor}}\,j\,{\text{is}}\,{\text{a}}\,{\text{repressor}}\,{\text{of}}\,{\text{gene}}\,{\text{i}} .} \hfill \\ \end{array} } \right. $$
(5)

In compact matrix form, (4) can be rewritten as

$$\left\{\begin{array}{l} {\dot{m}(t) = - Am(t) + Bg(p_{j} (t -\tau_{1} (t))) + I,} \\ {\dot{p}(t) = - Cp(t) + Dm(t - \tau_{2}(t)).} \\ \end{array}\right. $$
(6)

where m(t) = [m 1(t), m 2(t), …, m n (t)]T, p(t) = [p 1(t), p 2(t), …, p n (t)]T, \( g(p(t - \tau_{1} (t)) = [g_{1} (p_{1} (t - \tau_{1} (t)),g_{2} (p_{2} (t - \tau_{1} (t)), \ldots ,g_{n} (p_{n} (t - \tau_{1} (t))], \) \( [m(t - \tau_{2} (t)) = [m_{1} (t_{1} - \tau_{2} (t)),m_{2} (t_{2} - \tau_{2} (t)), \ldots ,m_{n} (t_{n} - \tau_{2} (t))]^{T} , \) I = [I 1, I 2, …, I n ]T, A = diag{a 1, a 2, …, a n }, C = diag{c 1, c 2, …, c n }, D = diag{d 1, d 2, …, d n }. Let (m*, p*)T be an equilibrium point of (6), which satisfies the following relationship:

$$ \left\{ \begin{array}{*{20}c} { - Am^{\ast} + Bg(p^{\ast}) + I = 0} \hfill \\ { - Cp^{\ast} + Dm^{\ast} = 0} \hfill \\ \end{array}\right. $$
(7)

For convenience, we will shift an intended equilibrium point (m*, p*) of the system (6) to the origin. Using x(t) = m(t) − m*, y(t) = p(t) − p*, we have

$$ \begin{gathered} \dot{x}(t) = - Ax(t) + Bf(y(t - \tau_{1} (t))), \hfill \\ \dot{y}(t) = - Cy(t) + Dx(t - \tau_{2} (t)). \hfill \\ \end{gathered} $$
(8)

where x(t) = [x 1(t), x 2(t), …, x n (t)]T, y(t) = [y 1(t), y 2(t), …, y n (t)]T, f(y(t)) = [f 1(y 1(t)), f 2(y 2(t)), …, f n (y n (t))]T, f i (y i (t)) = g i (y i (t) + p i *) − g i (p i *), since g i (·) is a monotonically increasing function with saturation, and if there exists matrix G = diag{g 1, g 2, …}, then it satisfies that

$$ 0 \le \tfrac{{g_{i} (x) - g_{i} (y)}}{x - y} \le g_{i} . $$

for all \( x,y \in R \) with x ≠ y. From the relationship of f(·) and g(·), f(·) satisfied that

$$ 0 \le \tfrac{{f_{s} (x)}}{x} \le g_{i} . $$
(9)

which is equivalent to the following one:

$$ f_{i} (x)(f_{i} (x) - g_{i} x) \le 0. $$
(10)

In the following, we consider stability of delayed genetic regulatory networks with parameter uncertainties and stochastic perturbations:

$$ \left\{ \begin{array}{l} {{\text{d}}x(t) = \{ - (A + \Updelta A)x(t) + (B + \Updelta B)f(y(t - \tau_{1} (t))\} {\text{d}}t +[(H_{0} + \Updelta H_{0} )y(t) + (H_{1} + \Updelta H_{1} )y(t -\tau_{1} (t)]{\text{d}}\omega (t),} \hfill \\ {{\text{d}}y(t) = \{- (C + \Updelta C)y(t) + (D + \Updelta D)x(t - \tau_{2} (t))\}{\text{d}}t.} \hfill \\ \end{array}\right. $$
(11)

where ΔA, ΔB, ΔC, ΔD, ΔH 0 and ΔH 1 are parameter uncertainties, τ 1(t), τ 2(t) are unknown time-varying delays satisfying 0 ≤ τ 1(t) ≤ h 1, 0 ≤ τ 2(t) ≤ h 2 and \( \dot{\tau }_{1} (t) \le d_{1} < 1,\dot{\tau }_{2} (t) \le d_{2} < 1, \) where h 1, h 2, d 1 and d 2 are known constants. \( \omega (t) = [\omega_{ 1} (t),\omega_{ 2} (t), \ldots ,\omega_{m} (t)]^{T} \in R^{m} \) is a m-dimensional Brownian motion defined on a complete probability space (Ω, F, {F t } t ≥ 0, P), and ΔA, ΔB, ΔC, ΔD, ΔH 0 and ΔH 1 are defined as:

$$ \begin{array}{*{20}c} {\Updelta A = M_{1} F(t)E_{1} ,} & {\Updelta B = M_{2} F(t)E_{2} ,} & {\Updelta C = M_{3} F(t)E_{3} ,} \\ {\Updelta D = M_{4} F(t)E_{4} ,} & {\Updelta H_{0} = M_{5} F(t)E_{5} ,} & {\Updelta H_{1} = M_{6} F(t)E_{6} .} \\ \end{array} $$
(12)

where M 1, M 2, M 3, M 4, M 5, M 6, E 1, E 2, E 3, E 4, E 5 and E 6 are known constant real matrices with appropriate dimensions. F(t) is unknown time-varying matrix satisfying

$$ F^{T} (t)F(t) \le I $$
(13)

Remark 1

It should be noted that, if let H 0 = H 1 = 0, the model (11) becomes the same form as Ren and Cao (2008). If we let ΔA = ΔB = ΔC = ΔD = 0, the model (11) is equivalent to the one investigated in Li et al. (2006a).

Remark 2

The parameter uncertainty structure described in (12) and (13) has been widely exploited in robust control and robust filtering of uncertain systems. Many practical systems possess parameter uncertainties which can be either exactly modeled or over bounded by (13). The stochastic term, [(H 0 + ΔH 0)y(t) + (H 1 + ΔH 1)y(t − τ 1(t)]dω(t), can be viewed as stochastic perturbations related to the gene current states and delayed states.

Remark 3

Time delay is an important factor in considering the stability of real genetic system. It is known that the time delay is different at different reaction stages and at different time due to complexity and sensitiveness of biochemical reaction (De Jong 2002), so constant delays cannot reflect the real regulate process, accordingly, we use time-varying delays in this paper.

Next, we give the definition of global robust asymptotic stability for the uncertain stochastic genetic regulatory networks:

Definitions 1

For the genetic regulatory network (11) and \( \xi \in L_{{F_{0} }}^{2} ([ - h,0];R^{n} ), \) the trivial solution (equilibrium point) is robustly, globally, asymptotically stable in the mean square if, for all admissible uncertainties satisfying (12), the following holds:

$$ \mathop {\lim }\limits_{t \to \infty } E|x(t;\,\xi )|^{2} = 0 $$
(14)

We recall the following useful lemmas:

Lemma 1

(Boyd et al. 1994). The following LMI

$$ \left[ {\begin{array}{*{20}c} {Q(x)} & {S(x)} \\ {S^{T} (x)} & {R(x)} \\ \end{array} } \right] > 0, $$

where Q(x) = Q T(x), R(x) = R T(x),  and S(x) depend affinely on x, is equivalent to

$$ R(x) > 0,\quad \quad \,Q(x) - S(x)R^{ - 1} (x)S^{T} (x) > 0. $$

Lemma 2

(Gu 2000). For any constant matrix \( M \in R^{n \times n} \), M = M T > 0, scalar γ > 0, vector function ω:[0, γ] → R n such that the integrations are well defined, the following inequality holds:

$$ \left[ {\int\limits_{0}^{\gamma } {\omega (s){\text{d}}s} } \right]^{T} \,M\left[ {\int\limits_{0}^{\gamma } {\omega (s){\text{d}}s} } \right] \le \gamma \int\limits_{0}^{\gamma } {\omega^{T} (s)M\omega (s){\text{d}}s.} $$

Lemma 3

(Liao et al. 2002) Given any real matrices Σ1, Σ2, Σ3 of appropriate dimensions and a scalar ɛ > 0 such that \( 0 < \Upsigma_{3} = \Upsigma_{3}^{T} . \) Then, the following inequality holds:

$$ \sum_{1}^{T} \sum_{2} + \sum_{2}^{T} \sum_{1} \le \varepsilon\sum_{1}^{T} \sum_{3} \sum_{1} + \varepsilon^{ - 1} \sum_{2}^{T}\sum_{3}^{ - 1} \sum_{2} . $$

Stochastic stability condition of uncertain genetic networks with time-varying delays

We first consider stochastic genetic regulatory networks without parameter uncertainties:

$$ \left\{ \begin{aligned} \hbox{d}x(t) = & \{ - Ax(t) + Bf(y(t -\tau _{1} (t)))\} \hbox{d}t + \{ H_{0} y(t) + H_{1} y(t - \tau_{1} (t))\} \hbox{d}\omega (t), \\ \hbox{d}y(t) &= \{ - Cy(t) +Dx(t - \tau _{2} (t)) \} \hbox{d}t. \\\end{aligned} \right. $$
(15)

We have the following result:

Theorem 1

System (15) is globally asymptotically stable in the mean square, if there exist symmetric positive definite matrices P 1, P 2, Q 1, Q 2, S 1, S 2 and positive scalar λ, such that the following LMIs holds:

$$ \Upomega_{1} = \left[ {\begin{array}{*{20}c} {\Uppi_{1} } & 0 & 0 \\ 0 & {D^{T} D - (1 - d_{2} )Q_{2} } & 0 \\ 0 & 0 & { - h_{2}^{ - 1} S_{2} } \\ \end{array} } \right] < 0,\quad \quad \Upomega_{2} = \left[ {\begin{array}{*{20}c} {\Uppi_{2} } & 0 & 0 & 0 & {H_{0}^{T} P_{1} } \\ 0 & { - (1 - d_{1} )Q_{1} + \lambda G^{T} G} & 0 & 0 & {H_{1}^{T} P_{1} } \\ 0 & 0 & { - \lambda I + B^{T} B} & 0 & 0 \\ 0 & 0 & 0 & { - h_{1}^{ - 1} S_{1} } & 0 \\ {P_{1}^{T} H_{0} } & {P_{1}^{T} H_{1} } & 0 & 0 & { - P_{1} } \\ \end{array} } \right] < 0, $$
(16)

where

$$ \begin{aligned} \Uppi_{1} = & - P_{1} A - A^{T} P_{1} + Q_{2} + P_{1}^{2} + h_{2} S_{2} , \\ \Uppi_{2} = & - P_{2} C - C^{T} P_{2} + Q_{1} + h_{1} S_{1} + P_{2}^{2} . \\ \end{aligned} $$

Proof

Using schur complement, Ω2 < 0 implies that

$$ \begin{gathered} \Upomega_{2} = \left[ {\begin{array}{*{20}c} {\Uppi_{2} } & 0 & 0 & 0 \\ 0 & { - (1 - d_{1} )Q_{1} + \lambda G^{T} G} & 0 & 0 \\ 0 & 0 & { - \lambda I + B^{T} B} & 0 \\ 0 & 0 & 0 & { - h_{1}^{ - 1} S_{1} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {H_{0}^{T} } \\ {H_{1}^{T} } \\ 0 \\ 0 \\ \end{array} } \right]P_{1} [\begin{array}{*{20}c} {H_{0} } & {H_{1} } & 0 & 0 \\ \end{array} ] < 0. \hfill \\ \hfill \\ \end{gathered} $$

Constructing a positive definite Lyapunov–Krasovskii functional as follows:

$$ \begin{array}{*{20}c} {V(x(t),y(t),t) = y^{T} (t)P_{2} y(t) +x^{T} (t)P_{1} x(t)} \\ { + \int\limits_{t - \tau_{1} (t)}^{t}{y^{T} (s)Q_{1} y(s)} {\text{d}}s + \int\limits_{t - \tau_{2}(t)}^{t} {x^{T} (s)Q_{2} } x(s){\text{d}}s} \\ + \int\limits_{ -h_{1} }^{0} {\int\limits_{t + s}^{t} {y^{T} (\eta )S_{1} y(\eta){\text{d}}\eta {\text{d}}s} } + \int\limits_{ - h_{2} }^{0}{\int\limits_{t + s}^{t} {x^{T} (\eta )S_{2} } x(\eta){\text{d}}\eta {\text{d}}s.} \\ \end{array} $$

By Itô’s differential formula (Oksendal 2003), the stochastic derivative of V(x(t), y(t), t) along the trajectory of system (15)

$$ \begin{array}{*{20}c} {{\text{d}}V(x(t),y(t),t) \le \{ 2x^{T} (t)P_{1} [ - Ax(t) + Bf(y(t - \tau_{1} (t))]} \\ { +\,[H_{0} (t)y(t) + H_{1} (t)y(t - \tau_{1} (t)]^{T} P_{1} [H_{0} (t)y(t)} \\ { + H_{1} (t)y(t - \tau_{1} (t)] + 2y^{T} (t)P_{2} [ - Cy(t) + Dx(t - \tau_{2} (t))]} \\ { + y^{T} (t)Q_{1} y(t) - (1 - d_{1} )y^{T} (t - \tau_{1} (t))Q_{1} y(t - \tau_{1} (t))} \\ { + x^{T} (t)Q_{2} x(t) - (1 - d_{2} )x^{T} (t - \tau_{2} (t))Q_{2} x(t - \tau_{2} (t))} \\ { + h_{1} y^{T} (t)S_{1} y(t) - \int\limits_{{t - \tau_{1} (t)}}^{t} {y^{T} (s)} S_{1} y(s){\text{d}}s + h_{2} x^{T} (t)S_{2} x(t)} \\ { - \int\limits_{{t - \tau_{2} (t)}}^{t} {x^{T} (s)S_{2} x(s){\text{d}}s\} {\text{d}}t + 2x^{T} (t)P_{1} } [H_{0} (t)y(t)} \\ { + H_{1} (t)y(t - \tau_{1} (t)]dw(t).} \\ \end{array} $$

From Lemma 3, the following inequalities hold:

$$ 2x^{T} (t)P_{1} Bf(y(t - \tau_{1} (t))) \le x^{T} (t)P_{1}^{2} x(t) + f^{T} (y(t - \tau_{1} (t)))B^{T} Bf(y(t - \tau_{1} (t))). $$
(17)
$$ 2y^{T} (t)P_{2} Dx(t - \tau_{2} (t)) \le y^{T} (t)P_{2}^{2} y(t) + x^{T} (t - \tau_{2} (t))D^{T} Dx(t - \tau_{2} (t)). $$
(18)

From (9), we obtain the follow inequality easily,

$$ f^{T} (y(t - \tau_{1} (t))f(y(t - \tau_{1} (t)) - y^{T} (t - \tau_{1} (t)G^{T} Gy(t - \tau_{1} (t) \le 0. $$
(19)

Noticing that, for a scalar λ > 0, we have

$$ - \lambda [f^{T} (y(t - \tau_{1} (t))f(y(t - \tau_{1} (t)) - y^{T} (t - \tau_{1} (t)G^{T} Gy(t - \tau_{1} (t)] \ge 0. $$
(20)

Substituting (17), (18) and (20) into dV(x(t), y(t), t) and by use of Lemma 2, we have

$$\begin{aligned}{\text{d}}V(t) \le \left\{\vphantom{\left(\int\limits_{{t -\tau_{2} (t)}}^{t} {x(s){\text{d}}s} \right)^{T}} x^{T} (t)( -P_{1} A - A^{T} P_{1} +Q_{2} + h_{2} S_{2} + P_{1}^{2} )x(t)\right.\\{ + x^{T} (t -\tau_{2} (t))(D^{T} D - (1 - d_{2} )Q_{2} )x(t -\tau_{2} (t))} \\{ - h_{2}^{ - 1} \left(\int\limits_{{t - \tau_{2} (t)}}^{t}{x(s){\text{d}}s} \right)^{T} S_{2} \left(\int\limits_{{t -\tau_{2} (t)}}^{t} {x(s){\text{d}}s} \right) + y^{T} (t)( -P_{{^{2} }} C - C^{T} P_{2} } \\ { + Q_{1} + h_{1} S_{1} +P_{2}^{2} )y(t) + y^{T} (t - \tau_{1} (t))( - (1 - d_{1} )Q_{1}}\\{ + \lambda G^{T} G)y(t - \tau_{1} (t)) + f^{T} (y(t - \tau_{1}(t))( - \lambda I + B^{T} B)} \\\left.\vphantom{\left(\int\limits_{{t - \tau_{2} (t)}}^{t}{x(s){\text{d}}s} \right)^{T}} \times f(y(t - \tau_{1} (t)) -h_{1}^{ - 1} \left(\int\limits_{{t - \tau_{1} (t)}}^{t}{y(s){\text{d}}s} )^{T} S_{1} (\int\limits_{{t - \tau_{1}(t)}}^{t} {y(s){\text{d}}s} \right)\right\} {\text{d}}t \\ { + \{2x^{T} (t)P_{1} [H_{0}(t)y(t) + H_{1} (t)y(t - \tau_{1} (t))]\} {\text{d}}\omega (t)} \\{ = \{ \xi_{1}^{T} (t)\Upomega_{1} \xi_{1} (t) + \xi_{2}^{T}(t)\Upomega_{2} \xi_{2} (t)\} {\text{d}}t} \\ { + \{ 2x^{T}(t)P_{1} [H_{0} (t)y(t) + H_{1} (t)y(t - \tau_{1} (t))]\}{\text{d}}\omega (t).} \\ \end{aligned} $$
(21)

where

$$ \xi_{1}^{T} (t) = [x^{T} (t),x^{T} (t - \tau_{2} (t)),\left( {\int\limits_{{t - \tau_{2} (t)}}^{t} {x(s){\text{d}}s} } \right)^{T} ,\xi_{2}^{T} (t) = \left[ {y^{T} (t),y^{T} (t - \tau_{1} (t)),f^{T} (y - \tau_{1} (t)),\left( {\int\limits_{{t - \tau_{1} (t)}}^{t} {y(s){\text{d}}s} } \right)^{T} } \right]. $$

Since the expectation of \( \{ 2x^{T} (t)P_{1} [H_{0} (t)y(t) + H_{1} (t)y(t - \tau_{1} (t))]\} {\text{d}}\omega (t) \) is equal to zero, when Ω1 < 0 and Ω2 < 0. Taking the mathematical expectation of both sides of (21), we have

$$ E[{\text{d}}V(x(t),y(t),t)] \le E\left[ {(\xi_{1}^{T} (t)\Upomega_{1} \xi_{1} (t) + \xi_{2}^{T} (t)\Upomega_{2} \xi_{2} (t)){\text{d}}t} \right] < 0 $$
(22)

where E is the mathematical expectation operator. It indicates that the genetic regulatory network (15) is asymptotically stable in mean square. This completes the proof.

Remark 4

We introduce a new Lyapunov–Krasovskii functional. The Lyapunov–krasovskii functional not only dealt with the time-varying delays but also consider the upper bounds of time delays. That is, both time-varying delay and the upper bound of time delays have been brought into the final robust stability condition, and the effect factor of time delays is considered in genetic regulatory networks, the LMIs condition can reflect more characters of genetic regulatory networks.

Remark 5

In spite of considerable variations and random perturbations of biochemical parameters, the genetic regulatory networks can keep homeostasis in metabolism and developmental programs of living cells (Yuh et al. 1998). i.e. despite the stochastic function of regulatory within cells, most cellular events are ordered and precisely regulated. That is, genetic networks system can reach stability by auto regulation. In fact, genetic regulatory network is an essentially continuous and complicated dynamical system. So the research of stability of genetic regulatory networks is necessary. The LMIs conditions provide one sufficient criteria of estimating the stability of genetic regulatory networks.

Theorem 2

The genetic regulatory network (11) is asymptotically robustly stable if there exist positive matrices P i , Q i , S i (i = 1, 2) and scalars λ > 0 and l i  > 0 (i = 1, 2, …, 6) such that the following LMIs hold:

$$ \Upomega_{1}^{*} = \left[ {\begin{array}{*{20}c} {\gamma_{1} } & 0 & 0 & { - P_{1} M_{1} } & 0 \\ * & {\gamma_{2} } & 0 & 0 & {D^{T} M_{4} } \\ * & * & { - h_{2}^{ - 1} S_{2} } & 0 & 0 \\ * & * & * & { - l_{1} I} & 0 \\ * & * & * & * & {M_{4}^{T} M_{4} - l_{2} I} \\ \end{array} } \right] < 0,\quad \quad \Upomega_{2}^{*} = \left[ {\begin{array}{*{20}c} {\kappa_{1} } & {H_{0}^{T} PH_{1} } & 0 & 0 & { - P_{2} M_{3} } & 0 & {H_{0}^{T} P_{1} M_{5} } & {H_{0}^{T} P_{1} M_{6} } \\ * & {\kappa_{2} } & 0 & 0 & 0 & 0 & {H_{1}^{T} P_{1} M_{5} } & {H_{1}^{T} P_{1} M_{6} } \\ * & * & {\kappa_{3} } & 0 & 0 & {B^{T} M_{2} } & 0 & 0 \\ * & * & * & { - h_{1}^{ - 1} S_{1} } & 0 & 0 & 0 & 0 \\ * & * & * & * & { - l_{3} I} & 0 & 0 & 0 \\ * & * & * & * & * & { - l_{4} I + M_{2}^{T} M_{2} } & {M_{5}^{T} P_{1} M_{6} } & 0 \\ * & * & * & * & * & * & {\kappa_{4} } & 0 \\ * & * & * & * & * & * & * & {\kappa_{5} } \\ \end{array} } \right] < 0 $$
(23)

where

$$ \begin{array}{*{20}c} {\gamma_{1} = - P_{1} A - A^{T} P_{1} + Q_{2} + P_{2}^{2} + h_{2} S_{2} + l_{1} E_{1}^{T} E_{1} ,} \\ {\gamma_{2} = - (1 - d_{2} )Q_{2} + DD^{T} + l_{2} E_{4}^{T} E_{4} ,} \\ {\kappa_{1} = - P_{2} C - C^{T} P_{2} + Q_{1} + h_{1} S_{1} + P_{2}^{2} + l_{3} E_{3}^{T} E_{3} } \\ { + H_{0}^{T} P_{1} H_{0} + l_{5} E_{5}^{T} E_{5} ,} \\ {\kappa_{2} = - (1 - d_{1} )Q_{1} + \lambda G^{T} G + H_{1}^{T} P_{1} H_{1} + l_{6} E_{6}^{T} E_{6} ,} \\ {\kappa_{3} = - \lambda I + B^{T} B + l_{4} E_{2}^{T} E_{2} ,} \\ {\kappa_{4} = - l_{5} I + M_{5}^{T} P_{1} M_{5} ,} \\ {\kappa_{5} = - l_{6} I + M_{6}^{T} P_{1} M_{6} .} \\ \end{array} $$

and * denotes the symmetric term in a symmetric matrix.

Proof

Taking the same Lyapunov–Krasovskii functional as that in the proof of Theorem 2, and replacing A, B, C, D, H 0 and H 1 by A + M 1 F(t)E 1, B + M 2 F(t)E 2, C + M 3 F(t)E 3, D + M 4 F(t)E 4, H 0 + M 5 F(t)E 5, H 1 + M 6 F(t)E 6, respectively.

From (13), we can get following inequalities.

$$ \begin{array}{*{20}c} {l_{1} x^{T} (t)E_{1}^{T} E_{1} x(t) - l_{1} (F(t)E_{1} x(t))^{T} (F(t)E_{1} x(t)) \ge 0,} \hfill \\ {l_{2} x^{T} (t - \tau_{2} (t))E_{4}^{T} E_{4} x(t - \tau_{2} (t)) - l_{2} (F(t)E_{4} x(t - \tau_{2} (t)))^{T} (F(t)E_{4} x(t - \tau_{2} (t))) \ge 0,} \hfill \\ {l_{3} y(t)E_{3}^{T} E_{3} y(t) - l_{3} (F(t)E_{3} y(t))^{T} (F(t)E_{3} y(t)) \ge 0,} \hfill \\ {l_{4} f^{T} (y(t - \tau_{1} (t)))E_{2}^{T} E_{2} f(y(t - \tau_{1} (t))) - l_{4} (F(t)E_{2} \times f(y(t - \tau_{1} (t))))^{T} (F(t)E_{2} f(y(t - \tau_{1} (t)))) \ge 0,} \hfill \\ {l_{5} y(t)E_{5}^{T} E_{5} y(t) - l_{5} (F(t)E_{5} y(t))^{T} (F(t)E_{5} y(t)) \ge 0,} \hfill \\ {l_{6} y^{T} (t - \tau_{1} (t))E_{6}^{T} E_{6} y(t - \tau_{1} (t)) - l_{6} (F(t)E_{6} y(t - \tau_{1} (t)))^{T} (F(t)E_{6} y(t - \tau_{1} (t))) \ge 0} \hfill \\ \end{array} $$
(24)

Using the above inequalities, then

$$ {\text{d}}V(x(t),y(t),t) \le \{ \zeta_{{_{1} }}^{T} (t)\Upomega_{1}^{*} \zeta_{1} (t) + \zeta_{2}^{T} (t)\Upomega_{2}^{*} \zeta_{2} (t)\} {\text{d}}t + \{ 2x^{T} (t)P_{1} [H_{0} (t)y(t) + H_{1} (t)y(t - \tau_{1} (t))]\} {\text{d}}\omega (t). $$
(25)

where

$$ \begin{gathered} \zeta_{1} (t) = \left[ {x^{T} (t),x^{T} (t - \tau_{2} (t)),\left( {\int_{{t - \tau_{2} (t)}}^{t} {x(s){\text{d}}s} } \right)^{T} ,(F(t)E_{1} x(t))^{T} ,(F(t)E_{4} x(t - \tau_{2} (t)))^{T} } \right]^{T} , \hfill \\ \zeta_{2} (t) = \left[ \begin{gathered} y^{T} (t),y^{T} (t - \tau_{1} (t)),f^{T} (y(t - \tau_{1} (t))),\left( {\int_{{t - \tau_{1} (t)}}^{t} {y(s){\text{d}}s} } \right)^{T} ,(F(t)E_{3} y(t))^{T} , \hfill \\ (f(t)E_{2} f(y(t - \tau_{1} (t))))^{T} ,(F(t)E_{5} y(t))^{T} ,(F(t)E_{6} y(t - \tau_{1} (t)))^{T} \hfill \\ \end{gathered} \right]^{T} . \hfill \\ \end{gathered} $$

Since \( \Upomega_{1}^{*} < 0,\ \Upomega_{2}^{*} < 0, \) we have

$$ E[{\text{d}}V(x(t),y(t),t)] = E\left[ {(\zeta_{{_{1} }}^{T} (t)\Upomega_{1}^{*} \zeta_{1} (t) + \zeta_{2}^{T} (t)\Upomega_{2}^{*} \zeta_{2} (t)){\text{d}}t} \right] < 0. $$
(26)

For all x(t), y(t) except for x(t) = y(t) = 0. Therefore, the genetic regulatory network (11) is asymptotically stable in mean square. This completes the proof.

Remark 6

Noise always exist and need processing in process of data measurement. The gene expression data obtained from experiments is especially noisy. Robustness is a accuracy measurement of extracting the weight matrix of genetic regulatory network with the existence of noise

Remark 7

In Li et al. (2006a), the authors studied stochastic stability of genetic networks with time-varying delays, however, the parameter uncertainty was not considered in the models, and The stochastic disturbance term in this paper we give is the form of \( [(H_{0} + \Updelta H_{0} )y(t) + (H_{1} + \Updelta H_{1} )y(t - \tau_{1} (t)]{\text{d}}\omega (t). \) Therefore, our results and those established in [11] are complementary each other.

Remark 8

Gene regulation process is an inherent noisy process, the determinate model cannot commendably reflect the real gene regulation process, the stochastic model considering noise disturbances and parameter uncertainties in this paper is in close proximity to the real gene regulation process than determinate model. Ren and Cao studied the uncertain genetic networks with time-varying delays, and several LMI-based conditions were proposed to guarantee the stability of the equilibrium point of genetic networks. However, the stochastic term was not taken into account in the models. Therefore, our developed results in this paper are more general than those reported in Ren and Cao (2008).

Remark 9

A cycle of most eukaryotes is composed of four stages (Chen and Wang 2004): G1(Gap) phase in which size of the cell is increased by constantly producing RNA and synthesizing protein. S phase in which the cell continuous to produce new proteins and grows in size. And M(mitosis) phase in which chromosomes segregate and cell division takes place. While regulation of gene expression at different stages of protein synthesis (De Jong 2002). Transcription and translation are important process, from the description of introduction, we known that there exist time-varying delays in process of transcription and translation, that is, the time-varying delays can also affect the cell cycle, which need much more further research.

Illustrative examples

In this section, we present two examples to show the effectiveness and correctness of our theoretical results.

Example 1

In Elowitz and Leibler (2000), the dynamics of repressilator has been theoretically predicted and experimentally investigated in Escherichia coli. The repressilator is a cyclic negative-feedback loop comprising three repressor genes (lacl, tetR and cl) and their promoters. The kinetics of system are described as follows:

$$ \dot{m}_{i} = - m_{i} + \tfrac{\alpha }{{1 + p_{j}^{n} }},\quad \quad \dot{p}_{i} = - \beta (p_{i} - m_{i} ). $$

where i = lacl, tetR, cl; j = cl, lacl, tetR, m i and p i are the concentrations of the three mRNA and repressor-proteins, and β > 0 denotes the ratio of the protein decay rate to mRNA decay rate.

We consider a three-node genetic regulatory networks (15) with stochastic disturbance and transcriptional time delay, where

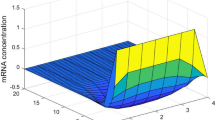
$$ \begin{array}{*{20}c} {A = {\text{diag(3}}. 5, 4, 2 ),} \hfill & {C = {\text{diag(2}}. 5, 2. 5, 2. 5 ),} \hfill \\ {D = {\text{diag(}}0. 6,0. 7, 1 ),} \hfill & {H_{ 0} {\text{ = diag(0}} . 2 , 0 . 2 , 0 . 2 ) ,} \hfill \\ {H_{ 1} = {\text{diag(}}0. 3,0. 3,0. 3 ),} \hfill & {B = \left[ {\begin{array}{*{20}c} 0 \hfill & 1 \hfill & { - 1} \hfill \\ { - 1} \hfill & 0 \hfill & 1 \hfill \\ { - 1} \hfill & { - 1} \hfill & 0 \hfill \\ \end{array} } \right]} \hfill \\ \end{array} $$

and f(x) = x 2/(1 + x 2), i.e. the Hill coefficient is 2. It is easy to know that the maximal value of the derivative of f(x) is less than g i  = 0.65, Assume time delay τ 1(t) = 1 + 0.5 sin (t), τ 1(t) = 0.5 + 0.5 cos (t) and τ 1 = 1.25, τ 2 = 0.75, d 1 = d 2 = 0.25. According to Theorem 1, if the LMI (16) hold, then the genetic network is globally asymptotic stable in mean square. The simulation of trajectories and phase graph of m(t) and p(t) are show in Fig. 1. By using the MATLAB LMI Toolbox (Gahinet et al. 1995), we solve the LMI (16) and obtain

$$ \begin{gathered} P_{1} = \left[ {\begin{array}{*{20}c} {36.2053} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {31.3224} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {62.3129} \hfill \\ \end{array} } \right],\quad \quad P_{2} = \left[ {\begin{array}{*{20}c} {79.5411} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {79.5411} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {79.5411} \hfill \\ \end{array} } \right], \hfill \\ Q_{1} = \left[ {\begin{array}{*{20}c} {118.6103} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {118.6103} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {118.6103} \hfill \\ \end{array} } \right],\quad \quad Q_{2} = \left[ {\begin{array}{*{20}c} {87.9061} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {88.9510} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {74.1024} \hfill \\ \end{array} } \right], \hfill \\ S_{1} = \left[ {\begin{array}{*{20}c} {51.7302} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {52.1224} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {45.1345} \hfill \\ \end{array} } \right],\quad \quad S_{2} = \left[ {\begin{array}{*{20}c} {46.4566} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {46.4566} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {46.4566} \hfill \\ \end{array} } \right]. \hfill \\ \end{gathered} $$

λ = 63.9422.

Fig. 1
figure 1

Trajectories and phase graph of m(t) and p(t) for Example 1

Full size image

Therefore, the genetic regulatory network (15) with stochastic disturbance and time-varying delays is asymptotically stable.

Example 2

Now, let us consider a five-node delayed stochastic genetic regulatory network (11) with norm bounded uncertainties. The network coefficients are given as follows:

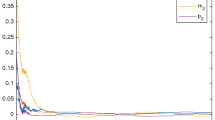
$$ \begin{array}{*{20}c} {A = {\text{diag}}(3,4,5,4,4),} \\ {C = {\text{diag}}(5,4,5,4.5,4),} \\ {D = {\text{diag}}(0.3,0.2,0.4,0.2,0.2),} \\ {H_{0} = {\text{diag}}(0.3,0.3,0.3,0.3,0.3),} \\ {H_{1} = {\text{diag}}(0.2,0.2,0.2,0.2,0.2),} \\ {M_{1} = M_{2} = M_{3} = M_{4} = M_{5} = M_{6} } \\ { = {\text{diag}}(0.3,0.3,0.3,0.3,0.3),} \\ {E_{1} = E_{2} = E_{3} = E_{4} = E_{5} = E_{6} = {\text{diag}}(0.2,0.2,0.2,0.2,0.2);} \\ \end{array} $$
$$ B = \left[ {\begin{array}{*{20}c} 0 \hfill & { - 1} \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ { - 1} \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 1 \hfill & { - 1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ \end{array} } \right]. $$

The simulation of trajectories and phase graph of m(t) and p(t) with \( F(t) = {\text{diag}}\{ \sin (t),\cos (2t),\cos (t),\cos^{2} (t), - \sin (t)\} \) are show in Fig. 2. Again, by solving the LMI (23) for the same parameters, we have

Fig. 2
figure 2

Trajectories and phase graph of m(t) and p(t) for Example 2

Full size image

  • P 1 = diag(100.0412, 81.0543, 59.9681, 77.5957, 81.0543),

  • P 2 = diag(75.4597, 99.5427, 75.0213, 85.6906, 99.5427),

  • Q 1 = diag(294.2091, 291.9178, 294.2575, 293.3227, 291.9178),

  • Q 2 = diag(208.6455, 208.6287, 208.8624, 208.6488, 208.6287),

  • S 1 = diag(120.3644, 120.3778, 120.3997, 120.3833, 120.3778),

  • S 2 = diag(111.6799, 110.7737, 111.6990, 111.3293, 110.7737),

  • λ = 157.0317, l 1 = 150.5257, l 2 = 150.6112, l 3 = 150.4322,

  • l 4 = 150.5630, l 5  = 151.2316, l 6 = 151.2004

which indicates from Theorem 2 that the delayed uncertain stochastic genetic regulatory network (11) is robustly, globally, asymptotically stable in the mean square.

Conclusions

In this paper, we have dealt with the problem of global asymptotic and robust stability analysis for stochastic delayed genetic regulatory networks, which involve stochastic perturbations, parameter uncertainties and time-varying delays. There are exist time-varying delays in process of transcription and translation of gene expression, while process of transcription and translation occupy a majority of cell cycle. So the time-varying delays can also affect the cell cycle. Effect on gene regulate process of cell cycle may result in other dynamical behaviors, such as switch, oscillation and bifurcation, which need much more further research.