Kriging with external drift for functional data for air quality monitoring

Abstract

Functional data featured by a spatial dependence structure occur in many environmental sciences when curves are observed, for example, along time or along depth. Recently, some methods allowing for the prediction of a curve at an unmonitored site have been developed. However, the existing methods do not allow to include in a model exogenous variables that, for example, bring meteorology information in modeling air pollutant concentrations. In order to introduce exogenous variables, potentially observed as curves as well, we propose to extend the so-called kriging with external drift—or regression kriging—to the case of functional data by means of a three-step procedure involving functional modeling for the trend and spatial interpolation of functional residuals. A cross-validation analysis allows to choose smoothing parameters and a preferable kriging predictor for the functional residuals. Our case study considers daily PM₁₀ concentrations measured from October 2005 to March 2006 by the monitoring network of Piemonte region (Italy), with the trend defined by meteorological time-varying covariates and orographical constant-in-time variables. The performance of the proposed methodology is evaluated by predicting PM₁₀ concentration curves on 10 validation sites, even with simulated realistic datasets on a larger number of spatial sites. In this application the proposed methodology represents an alternative to spatio-temporal modeling but it can be applied more generally to spatially dependent functional data whose domain is not a time interval.

1 Introduction

In recent years there has been an increasing interest in modeling functional data that, in environmental studies, often arise when dense sets of measurements are recorded over a period of time or over some domain (depth or height for instance). Statistical methods for analyzing this type of data are enclosed in a new branch of statistics called Functional Data Analysis (FDA; Ramsay and Silverman 2002, 2005; Ferraty and Vieu 2006). Over the last few years the analysis of functional data has been the focal attention of the statistical community. Functional data models provide a suitable framework for the statistical analysis of several environmental phenomena involving continuous time evolution and/or spatial variation. The functional autoregressive model in Salmerón and Ruiz-Medina (2009) extends the classical autoregressive model to the infinite-dimensional space context. In Ruiz-Medina and Salmerón (2010) the problem of functional filtering of an autoregressive Hilbertian (ARH) process, affected by additive Hilbertian noise, is addressed when the functional parameters defining the ARH(p) equation are unknown. Pseudodifferential evolution models have been widely used in the description of biological, geophysical and environmental systems. As an interesting case, Ruiz-Medina and Fernández-Pascual (2010) consider the case where functional sample information is available from such systems. Despite these references, the scarce amount of contributions in the FDA inferential area has stood out. In particular, more recently, attention has been directed to spatially dependent functional data so that the term Spatial Functional Statistics has been introduced; Delicado et al. (2010), Ruiz-Medina (2012), Horváth and Kokoszka (2012, Chap. 17-8), and Kokoszka (2012) give a review of recent contributions and open challenges in this field. Specifically, for geostatistical data, the problem to predict a curve at a specified location using the curves at available locations has been addressed in Giraldo et al. (2009, 2010, 2011), Nerini et al. (2010) by generalizing univariate and multivariate geostatistical techniques to the functional context and giving rise to the so-called functional kriging. Nevertheless, these recently developed geostatistical techniques for functional data consider ordinary kriging models such that the mean function of the process is supposed to be constant. In many applicative contexts this assumption is not realistic, hence there is need for methodologies suitable for non-stationary functional data. In this context, Caballero et al. (2013) provide a solution to the problem of the spatial prediction of functional data in the absence of stationarity when the spatial trend is modeled as a function of the coordinates only. Actually Gromenko and Kokoszka (2013) develop a methodology to estimate a mean function that is a linear combination of known covariate functions, but this mean function does not depend on space since it is defined to represent the mean temporal evolution of spatially distributed curves. Instead Temiyasathit et al. (2009) propose a procedure to obtain spatial prediction of ozone concentration profiles using meteorological variables. They use multiple linear regression to model the wavelet coefficients of the ozone profile as a function of the wavelet coefficients of the profiles of meteorological variables. In a later stage, kriging is used to interpolate the regression coefficients at unsampled locations.

In classical geostatistics, spatial prediction for nonstationary processes is performed by taking into account a spatial trend (also called “drift”) that is modeled as a function of the coordinates only—in the Universal kriging—or defined “externally” through some auxiliary/exogenous variables—in the kriging with external drift (KED) model. Being mathematically equivalent, also the term Regression Kriging is used to specify that the drift and residuals are fitted separately and then summed up afterwards (Hengl et al. 2007). In this paper, we propose to extend the KED model to the case of functional data by means of a three-step procedure allowing for the introduction of exogenous variables, both scalar and functional, in a functional drift. We focus on the air quality monitoring, and in particular on particulate matter that is the most problematic pollutant for health and has only decreased slightly over the last decade in Europe ¹, despite primary PM emissions from transport have been reduced (but emissions of primary PM from commercial, institutional and households fuel combustion have increased) (EEA 2012). In the Po Valley the limit values fixed by the European and national directives (EU Council Directive 1999/30/EC) are usually not met, especially in urban areas and during the winter season. In this context, particulate matter concentration spatial prediction is useful for assessing air quality and health risk also where no monitoring stations are displaced, and an effective prediction can be reached only by taking into account meteorological and orographical covariates. Since air quality pollutants and meteorological variables are gathered along time, with a certain frequency, we consider their underlying functional form and treat the observed time series as functional data. Then, by including meteorological and orographical information in the external drift, we carry out the proposed functional kriging with external drift (FKED) to predict curves of particulate matter concentration. The dataset of our case study has already been considered by Cameletti et al. (2011, 2012). In Cameletti et al. (2011) six hierarchical models are compared: they share a common large-scale component whereas the residual detrended process is modeled by specifying certain spatio-temporal covariance functions with increasing complexity. The authors conclude that the model named “A1”, whose residual process has a purely spatial covariance function, is preferable because of good performance at a reasonable computational cost (models are fitted by MCMC); while the model called “C” has a slightly better prediction capability but a larger computational cost [since a spatial process evolving in time according to an AR(1) equation is involved]. Such computational cost can be reduced by implementing a stochastic partial differential equations (SPDE) approach with the INLA algorithm, as done in Cameletti et al. (2012) where predictions at the same validation sites are obtained with slightly worst performance but quite smaller computational time.

Here, with the same dataset, we adopt a functional data approach such that the temporal component is hidden in the data domain. Since the issue of which approach—between functional and space–time geostatistics—should be used is still open, we aim to compare the spatial prediction capability of our proposal at the same validation sites by means of some performance indexes (also used in Cameletti et al. 2011). However, when many observations per functional data are collected and there is interest in prediction of a whole function—and not a single value—at an unvisited site, geostatistics for functional data should be the natural approach. Even more if the functional data domain is not temporal.

The paper is organized as follows. In Sect. 2 we propose a methodology to carry out kriging with external drift for functional data and suggest a criterion to choose the smoothing parameters and find a preferable kriging predictor among three different alternatives. Then we apply Functional KED to predict curves of particulate matter concentration in Sect. 3, where results of a cross-validation analysis are presented and an application on a validation dataset allows to assess its spatial prediction capability. In Sect. 4, we use the real dataset as a basis to simulate curves spatially correlated and explore the large sample behavior of the proposed procedure. A discussion with insights on further developments follows in Sect. 5.

2 Kriging with external drift for functional data

2.1 Notations and assumptions

Let $\Upupsilon_s = \left\{Y_{s}(t); t \in T \right\}$ be a functional random variable (f.r.v.) observed at location ${s \in D \subseteq \mathbb{R}^d, }$ whose realization is a function of $t \in T$—that is a functional data—where T is a compact subset of ${\mathbb{R}}$ (Ferraty and Vieu 2006). Assume that we observe a sample of curves $\Upupsilon_{s_i},$ for $s_i \in D, i=1, \ldots, n,$ that take values in a separable Hilbert space of square integrable functions. The set $\left\{\Upupsilon_{s}, s \in D \right\}$ constitutes a functional random field or a spatial functional process as defined in (Delicado et al. 2010), that can be non-stationary and whose elements are supposed to follow the model

$$ \Upupsilon_s = \mu_s + \epsilon_s. $$

(1)

The term μ _s is interpreted as a drift describing a spatial trend while $\epsilon_s$ represents a residual random field that is zero-mean, second-order stationary and isotropic, so that

• (i) ${\mathbb{E}(\Upupsilon_s)= \mu_s, \quad s \in D; }$

• (ii) ${\mathbb{E}(\epsilon_s)= 0, \quad s \in D; }$

• (iii) $Cov(\epsilon_{s_i}, \epsilon_{s_j}) = C(h), \quad \forall s_i, s_j \in D\; \text{with}\quad h = \left\|s_i- s_j\right\|.$

At the generic site $s_i, i=1, \ldots, n,$ and at point t model (1) can be rewritten as a functional concurrent linear model (Ramsay and Silverman 2005)

$$ Y_{s_i}(t)= \mu_{s_i}(t) + \epsilon_{s_i}(t), $$

(2)

with the drift

$$ \mu_{s_i}(t)= \alpha(t) + \sum_p \gamma_p(t) C_{p,i} + \sum_q \beta_{q}(t)X_{q,i}(t), $$

(3)

where α(t) is a functional intercept, C _p,i is the pth scalar covariate and X _q,i (t) is the qth functional covariate at site s _i , γ _p (t) and β _q (t) are the covariate coefficients. In the drift (3) both scalar and functional covariates are included, and the coefficients γ _p (t) and β _q (t) are also of a functional nature, allowing to estimate nonlinear effects of a covariate.

2.2 Functional kriging

In order to predict a curve at an unmonitored site s ₀, taking into account exogenous variables in the drift, we propose a three-step procedure. At the first step the functional regression model (2) with functional response and scalar and functional covariates is fitted by generalized cross-validation (GCV) as specified in Sect. 2.4, in order to estimate the drift coefficients and obtain the functional residuals

$$ e_{s_i}(t) = Y_{s_i}(t) - \hat{\mu}_{s_i}(t) = Y_{s_i}(t) - \left[ \hat{\alpha}(t) + \sum_p \hat{\gamma}_p(t) C_{p,i} + \sum_q \hat{\beta}_{q}(t) X_{q,i}(t)\right] . $$

At the second step the residual curve prediction at the unmonitored site s ₀ can be obtained by ordinary kriging for functional data (OKFD) (Giraldo et al. 2011), according to which

$$ \hat{e}_{s_0}(t)= \sum_{i=1}^n \lambda_i e_{s_i}(t), $$

where the kriging coefficients ${\lambda_i \in \mathbb{R}}$ are constant, so that the predicted curve is a linear combination of data residual curves. The weights λ _i are determined as the solution of a linear system written to solve the optimization problem

$$ \min_{\lambda_1, \ldots, \lambda_n} \int_T Var\left( \hat{e}_{s_0}(t) - e_{s_0}(t) \right) dt, \quad \hbox {s.t.} \; \sum_{i=1}^n \lambda_i =1, $$

where, similarly to classical geostatistics, some semivariogram values need to be known. In particular, the kriging coefficients λ _i depend on the so-called trace-semivariogram defined for a zero-mean weakly-stationary process as $\upsilon(h)= \int_T \upsilon_h(t) dt$ where $\upsilon_h(t) = \frac{1}{2} Var\left(e_{s_i}(t) - e_{s_j}(t) \right)$ with the Euclidean distance $h = \left\|s_i- s_j\right\|.$ This is estimated by (for further details see Giraldo et al. 2011)

$$ \hat{\upsilon}(h)= \frac{1}{2 \left| N(h)\right|} \sum_{i,j \in N(h)} \int_T \left(e_{s_i}(t) - e_{s_j}(t) \right)^2 dt, $$

where $N(h) = \{(s_i, s_j) : \left\|s_i- s_j\right\| = h\}$ and |N(h)| is the number of distinct elements in N(h). Once the trace-semivariogram is estimated for a sequence of G values h _g , a classical parametric model (exponential or Matérn for example) can be fitted to the points $(h_g, \hat{\upsilon}(h_g)), g=1,\ldots, G,$ as in classical geostatistics.

As an alternative to the ordinary kriging, we can consider “continuous time-varying kriging” for functional data (CTKFD; Giraldo et al. 2010), providing

$$ \hat{e}_{s_0}(t)= \sum_{i=1}^n \lambda_i(t) e_{s_i}(t), $$

where the kriging coefficients depend on t. This predictor is a hybrid between ordinary kriging and the functional linear concurrent (point-wise) model such as shown in (Ramsay and Silverman 2005). The estimation of the functional parameters $\lambda_i(t), i=1,\ldots,n,$ is carried out by using an approach based on the use of Nb basis functions. The curves and the functional parameters are represented in terms of basis functions, that is

$$ e_{s_i}(t)= \sum_{l=1}^{Nb} a_{il} B_l(t) \quad \hbox{and} \quad \lambda_i(t) = \sum_{l=1}^{Nb} b_{il} B_l(t). $$

(4)

The coefficients a _il are assumed to form a multivariable random field $\left\{ \alpha_l \right\}_{l=1}^{Nb}$ with $\alpha_l= (a_{1l}, \ldots, a_{nl})$ and multivariate geostatistics, such as a linear model of coregionalization (LMC) (Wackernagel 1995), is applied to estimate cross-covariances. Then an optimization problem is solved to have a BLUP so that b _il are estimated (for further details see Giraldo et al. 2010).

Another option is considering the so-called “functional kriging total model” (FKTM; Giraldo et al. 2009; Nerini et al. 2010) where the kriging coefficients are defined on T × T and the prediction at t is obtained integrating over T, that is

$$ \hat{e}_{s_0}(t)= \sum_{i=1}^n \int_T \lambda_i(\tau,t) e_{s_i}(\tau) d\tau. $$

Again the curves and the functional parameters $\lambda_i(\tau,t) i=1,\ldots,n$ are expanded in terms of Nb basis functions, as

$$ e_{s_i}(t)= \sum_{l=1}^{Nb} a_{il} B_l(t) \quad \hbox{and} \quad \lambda_i(\tau,t) = \sum_{j=1}^{Nb} \sum_{l=1}^{Nb} c^i_{jl} B_j(\tau) B_l(t), $$

and again a LMC is fitted in order to give a solution to the problem of estimating the functional parameters λ _i (τ, t) through the estimation of c ⁱ _jl .

Finally, at the third stepwe get the prediction at the unmonitored site s ₀ by adding—as in the classical regression kriging—the two terms, that is

$$ \hat{Y}_{s_0}(t) = \hat{\mu}_{s_0}(t) +\hat{e}_{s_0}(t), $$

where $\hat{\mu}_{s_0}(t) = \hat{\alpha}(t) + \sum_p \hat{\gamma}_p(t) C_{p,0} + \sum_q \hat{\beta}_{q}(t) X_{q,0}(t)$ depends on the covariate values C _p,0 and $X_{q,0}(\cdot)$ at the site s ₀.

2.3 Choosing the smoothing parameters and evaluating kriging predictors

Despite the functional framework, data are usually gathered as a finite discrete set of pairs $(t_j, y_{ij}), t_j \in T, j=1, \ldots, M, i=1, \ldots, n,$ and (unless there is no observational noise)

$$ y_{ij}= Y_{s_i}(t_j) + \delta_{ij}, $$

where δ _ij represents a measurement error and $Y_{s_i}(\cdot)$ is a continuous function that corresponds to a realization of the functional random field $\left\{\Upupsilon_{s}, s \in D \right\}$ at the site s _i . The set of points $\left\{ t_j \right\}_{j=1}^M \subset T$ can be considered the same for all functions in a functional dataset, and often these points are evenly spaced in T. We make here these assumptions but in general the set of points where a curve is observed could vary from site to site. In the latter case, more attention needs to be paid when converting discrete data to functional data (by using for example free knots for the splines smoothing introduced below).

The conversion from discrete data to curves involves smoothing, and linear combinations of B-spline functions B _l (t) (spline functions are constructed by joining polynomials of degree d together at points called “knots”) are used since they are flexible and appropriate for use in general environmental variables, while Fourier basis functions are appropriate when in presence of periodic data (Ramsay and Silverman 2005).

Then, for all t the curve ${Y}_{s_{i}}(t)$ is estimated by

$$ \tilde{Y}_{s_{i}}(t)=\sum_{l=1}^{K+d+1} \hat{c}^i_l B_l(t), $$

(5)

where d is the spline degree (in the following d = 3 so that we have cubic splines) and K the number of interior knots in the domain T = (a, b) of the function Y _{s_i} . Note that the number of basis functions in (5) is now Nb = K + d + 1 and smoothed data $\tilde{Y}_{s_i}(t_j)$ will be used to fit Model (2) in the case study presented in Sect. 3, since we assume to have observational noise.

Spline coefficients ${\bf c}^i= (c_1^{i}, \ldots, c_{K+d+1}^i)$ are estimated, for each i, by adopting a penalized least squares criterion

$$ PENSSE({\bf c}^i) = \sum_j (y_{ij} - Y_{s_i}(t_j))^2 + \eta \int_T [D^2 Y_{s_i}(t)]^2 dt, $$

(6)

where Y _{s_i} (t) = ∑ ^K+d+1 _l=1 c ⁱ _l B _l (t), η is the penalty parameter, D ² denotes the second derivative and the penalty term is chosen as the integrated square of the second derivative that quantifies the total curvature of the function (and hence its roughness). The parameter η controls the trade-off between the fit to the observed data and the smoothness of the fitted curve, so that when η is large the fitted curve is smoother but the data fits worse. In order to estimate spline coefficients by minimizing PENSSE we need to fix a value for η and, in addition, we need to choose a sequence of K interior knots $\xi =(\xi_1, \xi_2, \ldots, \xi_K).$ By taking equally spaced knots in T = (a, b) we need only to fix the number of knots K, besides η, while d = 3 is fixed.

Since the aim here is to predict a whole function Y _{s_0}(t) at an unmonitored site s ₀, we adopt a choice criterion based on leave-one-out cross-validation (as introduced in Giraldo et al. 2010, 2011). Data gathered at each site s _i is temporarily removed from the dataset and a smoothed function is predicted at this location using a functional kriging predictor based on the remaining smoothed functions, for $K \in [K_{min}, K_{max}]$ and $\eta \in [\eta_{min}, \eta_{max}].$ Then the optimal values (K ^*, η ^*) are those minimizing the function

$$ FCVr(K, \eta) = \sum_{i=1}^n SSE(i)= \sum_{i=1}^n \sum_{j=1}^{M} \left(y_{ij} - \hat{Y}_{s_i}(t_j)^{(i)}\right){^2}, $$

(7)

where $\hat{Y}_{s_i}(t_j)^{(i)}$ is the prediction at s _i evaluated at t _j , by leaving s _i data out of the sample. In (Giraldo et al. 2010, 2011) a similar procedure has been called functional cross-validation and the objective function FCV contains squared differences between smoothed data and predictions. Here we call the function FCVr—where r stands for raw—to stress the fact that raw data y _ij are compared to the predicted values $\hat{Y}_{s_i}(t_j)^{(i)}$ when evaluating SSE at each site. This is motivated by the fact that using smoothed data $\tilde{Y}_{s_i}(t_j)$ instead of raw data y _ij in (7) would provide a minimum value when K is small and η large (we have observed this in our case study); in that case the smoothed functions $\tilde{Y}_{s_i}(t)$ would be close to the overall mean function and the predictions would be easier to obtain—with SSE smaller—but they would be too smooth in the air quality context, where we want to predict concentration peaks that people breaths (removing only the observational noise).

Besides the choice of the smoothing parameters, the function FCVr allows to compare the three alternatives OKFD, CTKFD and FKTM at the second step of the procedure proposed in this paper [also by looking in detail SSE(i) values]. Moreover, in order to compare our proposal to competitors, such as Bayesian hierarchical models in (Cameletti et al. 2011) (for which cross-validation is computationally unfeasible), we use 10 validation sites and some prediction capability indexes in Sect. 3.3.

2.4 Implementation details

To implement our proposal all computations are coded in R (R Development Core 2012). First of all, the conversion to functional data is realized by using the fda package (Ramsay et al. 2012) that also contains the function fRegress for fitting a concurrent functional linear model, as shown in (Ramsay et al. 2009, Chap. 10). However, only univariate independent variables are currently allowed and indeed the case of a functional response prediction in practice remains largely unexplored. Then to implement the first step of our procedure we need to figure out how to estimate the covariate coefficients in the drift (3) in an alternative way. In classical geostatistics, μ _s is seen as a deterministic large scale component and when it is supposed to depend on exogenuous variables the related coefficients are estimated by least squares criteria. In the functional framework, where the covariate coefficients are also functional, we follow Ivanescu et al. (2012) who propose a general framework for smooth regression of a functional response on one or multiple functional predictors by re-writing a functional linear model as a standard additive model. In particular in our model the functional coefficients in (3) are assumed to be expandable as

$$ \alpha(t) = \sum_{l=1}^{k_0} A_{0,l}(t) c_{0,l}, \quad \gamma_p(t) = \sum_{l=1}^{k_p} a_{p,l}(t) c_{p,l} \quad \hbox{and} \quad \beta_{q}(t) = \sum_{l=1}^{k_q} a_{q,l}(t) c_{q,l}, $$

where A _0,l (t), a _p,l (t) and a _q,l (t) are known basis functions, while c _0,l , c _p,l and c _q,l are the related coefficients (to be estimated). Then we can write

$$ \gamma_{p}(t)C_{p,i} = \sum_{l=1}^{k_p} a_{p,l}(t)C_{p,i} c_{p,l} = \sum_{l=1}^{k_p}A_{p,l,i}(t)c_{p,l}, $$

and

$$ \beta_{q}(t)X_{q,i}(t) = \sum_{l=1}^{k_q} a_{q,l}(t)X_{q,i}(t) c_{q,l} = \sum_{l=1}^{k_q}A_{q,l,i}(t)c_{q,l}, $$

so that the functional linear model (2) can be re-written as a standard additive model

$$ Y_{s_i}(t) = \sum_{l=1}^{k_0} A_{0,l}(t) c_{0,l} + \sum_{p}\sum_{l=1}^{k_p}A_{p,l,i}(t)c_{p,l} + \sum_{q}\sum_{l=1}^{k_q}A_{q,l,i}(t)c_{q,l} + \epsilon_{s_i}(t), $$

where A _p,l,i (t) = a _p,l (t)C _p,i and A _q,l,i (t) = a _q,l (t)X _q,i (t) are known because C _p,i and X _q,i (t) are “observed” without noise. This representation makes it possible to fit a concurrent functional linear model by means of the robust mgcv package (Wood 2012a), where the underlying representation and estimation of the models is based on a penalized regression spline approach, with automatic smoothness selection by using the generalized cross validation (GCV) criterion (see Wood 2004, 2011). This entails that k ₀, k _p and k _q are chosen as very large inside the GCV procedure and penalties are designed to suppress excessive roughness of the functional parameters.

Then, at the second step, we apply kriging for functional data in three alternative ways to the functional residuals in order to get predictions at the temporarily out of sample site in cross-validation or at the 10 validation sites. The first method OKFD is implemented by means of the geofd package (Giraldo et al. 2012) that includes the automatic choice of a model (in a list) for a trace-variogram, by minimizing the SSE between the theoretical variogram and the empirical one. Instead CTKFD and FKTM are carried out by our own R code (available upon request) that takes advantage of the package gstat (Pebesma 2004) when fitting a linear coregionalization model. By adding predicted drifts and residuals, at the third step, we obtain predicted curves of the response variable that are compared with the observed time series later.

3 Spatial prediction of PM₁₀ curves

3.1 Data

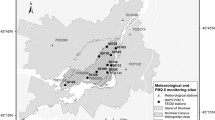
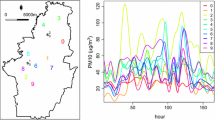
Our case study considers daily PM₁₀ concentrations (in μg/m³) measured from October 2005 to March 2006 (so that M = 182) by the monitoring network of Piemonte region (Italy) in 24 sites (red triangles in Fig. 1). For model performance assessing we have 10 extra validation stations (blue dots in Fig. 1) as in (Cameletti et al. 2011, 2012), where the same dataset is considered. We carry out a cross-validation analysis in the following section, but the set of validation sites allows us to compare our results with those in (Cameletti et al. 2011). The exogenous variables in the trend term are: (i) coordinates (UTMX and UTMY, in km) and altitude (A, in m), that are scalar; (ii) daily maximum mixing height (HMIX, in m), daily total precipitation (PREC, in mm), daily mean wind speed (WS, m/s), daily mean temperature (TEMP, in °K) and daily emission rates of primary aerosols (EMI, in g/s), that are functional. Note that the time-varying variables are obtained from a nested system of deterministic computer-based models implemented by the environmental agency ARPA Piemonte (Finardi et al. 2008). For a complete description and preliminary analysis of the data we refer to (Cameletti et al. 2011). In order to stabilize the within-station variances and making the marginal distribution of PM₁₀ data approximately normal, we also choose to transform data by the logarithm; Fig. 2 shows the curves of log(PM ₁₀), obtained by using cubic splines, at the 24 monitoring sites. Moreover, since the ranges of the covariates are quite different, a standardization procedure is applied subtracting the mean and dividing by the standard error computed considering the 24 monitoring stations (note that functional covariates are standardized after the smoothing step).

Fig. 1

Locations of the 24 PM₁₀ monitoring sites—red triangles—and 10 validation stations—blue dots. (Color figure online)

Fig. 2

Smoothed time series of log(PM ₁₀) at the 24 monitoring sites (color changes with sites)

3.2 Cross-validation

The leave-one-out cross-validation procedure described in Sect. 2.3, is applied to find the optimal smoothing parameters (K ^* and η ^*) and to compare the three alternatives for kriging functional residuals. For the number of interior knots K we fix the set of possible values 25, 51, 77, 90, 103, 116, 129, 142, 155, such that there are from 1 to 6 knots per week (in the dataset we have 26 weeks). Note that K + 4 = Nb is the number of spline coefficients to be estimated—see Delicado et al. (2010)—that is also equal to the number of considered basis functions. Instead for the penalty parameter η we take—since it is usual to explore η values for a few log units (Ramsay et al. 2009)—the set of possible values 0, 10, 10², 10³, 10⁴, defined as a power of 10 and visualized on a logarithmic scale. Clearly, when η = 0 the criterion (6) is not penalized and the fitted curve could be very close to data, as much as possible with the selected basis functions (cubic splines here). When OKFD is applied, an automated algorithm chooses the exponential model for the trace-variogram almost always (sometime a spherical one is chosen during the cross-validation). For CTKFD and FKTM, based on a preliminary exploration of the dataset, an exponential model was used for all direct variograms and cross-variograms for the LMC.

Figure 3 (left) shows the contour plot of the function FCVr(K, η) in case of OKFD at the second step, using a logarithmic scale for η. The FCVr surfaces for the alternatives CTKFD and FKTM—not reported here—are very similar although their values are generally slightly larger, while for a few values of (K, η)—as for example (155, 0) in the CTKFD case—FCVr becomes very large or impossible to evaluate for singularity problems; i.e. for some sites SSE is missing or too large (and so FCVr is not plotted in the profiles in Fig. 3, right). This fact occurs when the number of interior knots K is large, making large the number Nb of “variables” in the LMC to fit in CTKFD and FKTM procedures and small the functional residuals to krige. ² Anyway, in all the three cases, FCVr is smaller when η = 0. Hence, to compare the cases of minimum FCVr, the profiles FCVr(K, 0) are shown in Fig. 3 (right). It is evident that FCVr decreases sharply until K = 77, then the rate of decrease is smaller but in the OKFD case we can observe a small increasing for the largest K. It is also clear that, among the three methods, OKFD is preferable in terms of FCVr and Table 1 shows values of the 24 SSE(i) for the three cases (OKFD, CTKFD and FKTM) when K = 116 and η = 0. Overall, SSE(i) values are very close in the CTKFD and FKTM cases. In a few cases (see numbers in italic font) OKFD has slightly larger values but there is only one case that worths to be noted, that is site 14 CN—Piazza II Regg. Alpini, where SSE is quite larger for OKFD. However this site is outside the spatial domain when it is left out in cross-validation, and the same happens to site 24 Verbania where the worst performance occurs.

Fig. 3

FCVr surface for OKFD (left) and FCVr(K, 0) profiles in the three kriging cases (right)

Table 1 SSE(i) over 24 fitting sites (red triangles in Fig. 1) for FKED with the three alternative second steps: OKFD_116_0, CTKFD_116_0 and FKTM_116_0 corresponds to OKFD, CTKFD and FKTM respectively with K = 116 and η = 0

Moreover OKFD is preferable because CTKFD and FKTM could be numerically instable and involve the fitting of a linear coregionalization model that is highly computational time demanding (while OKFD is fast). To apply OKFD in our case study, we observe in Fig. 3 (right) that the values minimizing FCVr are K ^* = 142 and η ^* = 0, although (116, 0) and (129, 0) give very close results. In fact Fig. 4 shows very similar predicted curves at the 24 sites (when left out one at a time) obtained by OKFD at the second step and the couple (K, η) equal to (116, 0) and (142, 0).

Fig. 4

Cross-validation results: 24 predicted curves when K = 116 (left) and K = 142 (right), η = 0, with OKFD at the second step

3.3 Prediction at the validation sites

Following the results of the cross-validation, we apply our proposal with OKFD at the second step and (K, η) = (142, 0). Let us note that the number of interior knots K, related to the number of basis functions Nb = K + 4, has to be fixed at the beginning of the application (for the smoothing step and for fitting a FLM to the smoothed data) so that the first step results change if K changes.

The functional intercept in (3) is decomposed as α(t) = α ₁ + α ₂(t), since in fitting an additive model the smooth terms are subject to sum-to-zero identifiability constraints (Wood 2004). The estimated scalar intercept is $\hat{\alpha}_1= 3.93$ on the log scale, that corresponds to an average pollution level of about 50.9 μg/m³ while $\hat{\alpha}_2(t)$ is shown in Fig. 5, where we can observe that it changes in time mostly at the beginning and end of the considered winter semester. The estimated functional coefficients $\hat{\gamma}_p(t)$ of the scalar covariates UTMX, UTMY and A, and $\hat{\beta}_{q}(t)$ of the functional covariates HMIX, PREC, WS, TEMP and EMI are also shown in Fig. 5. All covariates are significant (p values for the smooth terms are obtained as discussed in Wood 2012b) as they were in (Cameletti et al. 2011), but now we can observe how they vary with time. In fact, for all the six models considered in (Cameletti et al. 2011) the estimated covariate coefficients—that are scalar—are negative except the one for the emissions (EMI). Instead our results show estimated functional coefficients varying with time with different behaviours, although they are negative in most of the t domain except for HMIX and TEMP—that change sign in time—and EMI that has a positive relationship with PM₁₀, as expected. Hence the importance of meteorological variables on air quality is confirmed, as well as the significant effect of altitude (A) in reducing PM₁₀ concentration.

Fig. 5

Estimated functional coefficients. First row $\hat{\alpha}_2(t), \hat{\gamma}_{UTMX}(t), \hat{\gamma}_{UTMY}(t).$ Second row $\hat{\gamma}_{A}(t), \hat{\beta}_{HMIX}(t), \hat{\beta}_{PREC}(t).$ Third row $\hat{\beta}_{WS}(t), \hat{\beta}_{TEMP}(t), \hat{\beta}_{EMI}(t).$

By applying the second and third step of the proposed FKED, we get predictions in the 10 validation sites (blue dots in Fig. 1). To have a detailed example, Fig. 6 shows raw data y _ij , smoothed data $\tilde{Y}_{s_i}(t),$ the predicted drift $\hat{\mu}_{s_i}(t)$ and the predicted curve $\hat{Y}_{s_i}(t)$ at the sites 25 Biella—Largo Lamarmora and 30 Saliceto. The contribution of kriging residuals is clear at site 25, where the predicted curve has a local (in time) variability that the predicted drift does not reach. Instead at site 30, where we have the worst results, the predicted drift is—for the most part of time—not close to the observed data and the contribute of kriging does not compensate enough because this site is the farthest from the 24 sites used to fit the model.

Fig. 6

Prediction at 25 Biella—Largo Lamarmora (top) and 30 Saliceto (bottom). Black raw data y _ij , blue smoothed data $\tilde{Y}_{s_i}(t)$, green predicted drift $\hat{\mu}_{s_i}(t)$ and red predicted curve $\hat{Y}_{s_i}(t)$. (Color figure online)

In order to assess the spatial prediction capability of FKED, we compare observed and predicted data at the 10 validation sites, by evaluating performance indexes as in Cameletti et al. (2011) (a simple residual analysis is also performed in Cameletti et al. 2012). Since we evaluate different predictors, we take as observed data the raw data y _ij , despite their observational noise, also because smoothed data change with (K, η). We consider four indicators based on the differences between predicted and observed data: the usual root mean square error (RMSE) and the correlation coefficient ρ, together with the normalized mean bias factor (NMBF) (Yu et al. 2006) and the weighted normalized mean square error of the normalized ratios (Poli and Cirillo 1993). For a fixed location s _i , let z _j and $\hat z_j$ be the observed and predicted time series (in our case y _ij and $\widehat{Y}_{s_i}(t_j)$) respectively, with $j=1,\ldots, M$ and let $\bar{z}$ and $\bar{\hat z}$ be the corresponding mean values. The normalized mean bias factor is defined on ${\mathbb{R}}$ by

$$ \hbox {NMBF} = \left\{\begin{array}{ll} \frac{\sum_j \hat z_j}{\sum_j z_j} - 1& \quad \hbox {if} \; \bar{\hat z} \ge \bar{z}\\ 1 - \frac{\sum_j z_j}{\sum_j \hat z_j} & \quad \hbox {if} \; \bar{\hat z} < \bar{z}\\ \end{array}\right., $$

and has the advantage of both avoiding inflation due to low values of observations and overcoming the asymmetry problem between overestimation and underestimation, as discussed in (Yu et al. 2006). The weighted normalized mean square error of the normalized ratios is defined by

$$ \hbox {WNNR}= \frac{\sum_j s_j^2 (1-k_j)^2}{\sum_j s_j k_j}, $$

where $s_j = z_j/ \bar{z}$ is the weight and $k_j= \exp\left(-|\ln(\hat z_j/z_j)|\right)$ is the normalized ratio. WNNR is positive and has the advantage of taking properly into account the peaks of observed data (see the discussion in Poli and Cirillo 1993).

Table 2 shows values of the four indexes in the case of FKED with OKFD at the second step and (K, η) = (142, 0), called “OKFD_142_0” in the following (and in Fig. 7). Predictions are generally good, with a slight underestimation in 7 out of 10 sites (see NMBF). Correlations between predicted and observed data is above 0.75, except for the site 30-Saliceto where we get the worst results in terms of prediction performance for all the four indexes, as expected by looking at Fig. 6 (bottom). That figure also shows one of the sites where FKED performs better, that are 25 and 33: for both of them the kriging predictor takes advantage of information given by very close neighbours.

Table 2 Performance indexes over 10 validation sites (blue dots in Fig. 1) of FKED with OKFD at the second step and (K, η) = (142, 0), called “OKFD_142_0”

Fig. 7

Boxplots of the performance measure distributions computed for each model over the 10 validation stations (blue dots in Fig. 1). Models are FKED with the three alternative second steps (OKFD, CTKFD and FKTM), K = 116, 129, 142 and η = 0, and Model A1 in (Cameletti et al. 2011). OKFD_116_0 corresponds to OKFD with (K, η) = (116, 0) and so on

A summary of Table 2 can be seen in Fig. 7 by looking at the indexes distribution boxplots for OKFD_142_0. Figure 7 also shows boxplots synthesizing the four indexes at the 10 validation sites for OKFD with (K, η) = (116, 0) and (K, η) = (129, 0), as well as for CTKFD and FKTM with K = 116, 129, 142 and η = 0 (called by “name_K_η”). We apply the proposed FKED to obtain predictions at the 10 validation sites also with CTKFD and FKTM and some values of K in order to confirm the cross-validation results in comparing the three alternatives. Indeed, leave-one-out cross-validation is sometimes criticized in spatial modeling because the estimated spatial structure could change every time that a site is left out and, in addition, we experienced numerical problems during cross-validation with CTKFD and FKTM. By considering the whole dataset and predicting at the 10 validation sites, we obtain performance index values that allow us to compare OKFD, CTKFD and FKTM.

Moreover, a table similar to Table 2 for Model A1 in Cameletti et al. (2011) is summarized through the last boxplots, where Model A1 is a spatio-temporal hierarchical model with a purely spatial covariance function (the residual spatio-temporal process is serially independent) fitted by MCMC on the same dataset. Note that cross-validation requires re-fitting the model for each left-out datum and becomes practically unfeasible when a model is fitted by MCMC; this is why here we compare FKED models and Model A1 on the 10 validation sites.

Boxplots in Fig. 7 confirm that results with a number of knots equal to 116, 129 and 142 (and so 120, 133 and 146 basis functions) are very similar for OKFD, with a light better performance when K = 142 as known from the cross-validation results in Sect. 3.2 Note that RMSE is just a transformation of FCVr, so that they are equivalent preference criteria. Also in the case of CTKFD the number K = 142 seems to be preferable, whereas it does not for FKTM (see e.g. Pearson boxplots). In comparing the three second step alternatives, this analysis with 10 validation sites confirms that OKFD is generally preferable, as seen by means of FCVr in Sect. 3.2 Only NMBF seems to say that it is overall worst but the only difference is at site 30 with NMBF ≅ −0.13 not highlighted as outlier, whereas NMBF ≅ −0.16 for CTKFD and FKTM.

With the same data, and hence the same 10 validation sites, six different hierarchical models are compared in Cameletti et al. (2011): Model A1 is suggested as preferable for its good performance at a reasonable cost because Model C has a better prediction performance but requires additional computational costs, since it includes an autoregressive component (as already said in Sect. 1) By looking at boxplots in Fig. 7 we can compare FKED models with Model A1 and see that performances are not so different. In fact, if we exclude the “critical” site 30 Saliceto model OKFD_142_0 has RMSE ranging from 0.196 to 0.481 while for Model A1 RMSE’s range is (0.215,0.527). Analogously, without site 30 Pearson correlation ranges are (0.762, 0.943) and (0.779, 0.958) for OKFD_142_0 and A1, respectively; as well as WNNR ranges are (0.002, 0.018) and (0.003, 0.013). Moreover, for both models NMFB > 0.05 in 3 out of 10 sites. Hence overall OKFD_142_0 performance is comparable to A1’s one except that for site 30 and for its ability to predict observed peaks. However a worst WNNR was expected since observed raw data are smoothed when converted to functional data, so that a part of observed peaks is smoothed away as observational noise.

To give another bit of comparison, let us note that with the same dataset (Cameletti et al. 2012) consider a spatio-temporal model with an autoregressive component (very similar to Model C in Cameletti et al. 2011), approximated by a Gaussian Markov Random Field and fitted by adopting the INLA algorithm, and obtain a global RMSE equal to 0.5328 and the correlation coefficient equal to 0.7015 when the 10 validation sites are taken altogether.

4 Large sample behaviour

The asymptotic theory for spatial prediction has been object of study during the last decades. Prediction based on kriging has been scrutinized in a number of papers. In the mid eighties, Molnar (1985) shows some mathematical properties of the classical and universal Kriging method investigating certain conditions for the convergence of these methods as the number of observation points tends to infinite. Lahiri et al. (2002) consider the least-squares approach for estimating parameters of a spatial variogram and establish consistency and asymptotic normality of these estimators under general conditions. Large-sample distributions are also established under a spatial regression model where the sampling design possibly has an infill sampling component. Crujeiras and Van Keilegom (2010) study the asymptotic and finite sample properties of an estimator of a nonlinear regression function when errors are spatially correlated, and when the spatial dependence structure is unknown. Vazquez and Bect (2010) and Sakata et al. (2010) deal with several issues related to the pointwise consistency of the kriging predictor when the mean and the covariance functions are known. These questions are of general importance in the context of computer experiments. The analysis is based on the properties of approximations in reproducing kernel Hilbert spaces.

When we look at the more complete picture of the spatio-temporal context, we can hardly find information on kriging asymptotics. For example, Zhang and Zheng (2012) study the asymptotic properties of maximum likelihood estimates under a general asymptotic framework for spatial-temporal linear models. Finally, we should add that the mixed field of functional and spatio-temporal prediction is completely open to asymptotic properties. At the best of our knowledge nothing can be found in this line. This would be object of a completely new paper focused on this topic. Thus we have preferred to show some light in this regard based on simulations.

Hence, in order to explore the large sample behavior of the proposed three-steps predictor, we carry out a simulation study where the real dataset—described in Sect. 3—is used as a basis for generating realistic simulated data. First of all, we consider Piemonte region as the spatial domain where we randomly select spatial sites whose coordinates belong to a regular grid with resolution 4 × 4 km that covers Piemonte, neighbor Italian regions and parts of foreign countries (4,032 grid points). Such a regular grid defines the spatial support of the output of a numerical model implemented by the environmental agency ARPA Piemonte (as already said in Sect. 3.1) that provides us with time-varying, meteorological and emission, covariates. The grid points on Piemonte region are 1,587 and among them we randomly select 200 sites, in total, and we then consider different sample sizes: 25, 50, 100 and 200. Figure 8 (left column) shows the selected sites, increasing from 25 to 200, and the 10 validation sites from the real dataset in the previous section.

Fig. 8

Left locations of n randomly selected sites—red triangles—and 10 real validation stations—blue dots. Right simulated functional dataset at n sites. Sample size n = 25, 50, 100, 200 from top to bottom. (Color figure online)

To obtain realistic data from a non-stationary spatial functional process, following the model (1), we simulate separately a drift and a stationary residual process. The drift functions are created by means of Eq. (3) with functional coefficients equal to those estimated from the real dataset and shown in Fig. 5, whereas the scalar and functional covariates are known. Instead, to obtain realizations of a functional random field we apply Eq. (4)-left, with the spline coefficients simulated as realizations of a multivariable random field. This last one is simulated by means of predict.gstat in gstat package (Pebesma 2004) and its variograms and cross-variograms are those estimated for the real dataset, when a LMC is fitted to apply CTKFD or FKTM, with K = 142. The four (nested) functional dataset are shown in Fig. 8 (right column).

Therefore we apply our proposal with OKFD at the second step (since in Sect. 3 we have seen that it has a better performance at a lower computational cost) and we obtain predictions at the 10 validation sites (blue points in Figs. 1, 8). When comparing predicted functions with the observed raw data at these 10 sites, we get values of the four performance indexes described in Sect. 3.3 that are summarized by boxplots in Fig. 9 for all the considered sample sizes. It is evident that the larger the sample size, the lower the variability of the four measures reflected in the green boxplots (for n = 200), except for the Pearson case that is not that clear. Indeed, the median values of RMSE and WNNR obtained with n = 200 are lower than those obtained from other sample sizes, while the Pearson median for n = 200 is the highest one.

Fig. 9

Boxplots of the performance measure distributions computed for each sample size over the 10 validation stations (blue dots in Figs. 1, 8). Predictions are obtained with OKFD at the second step and (K, η) = (142, 0)

5 Discussion

We can obtain in practice realizations of a multivariate functional random field ${\{\mathbf{Y}_s(t), s\in D\subset \mathbb{R}^d, t\in T\}. }$ Given $s_i \in D, i=1,\ldots,n,$ and p functional variables, we have the realization

$$ \begin{aligned} {\mathbf{Y}}_s(t)&=[(Y_{s_1,1}(t),\ldots,Y_{s_n,1}(t)),\ldots,(Y_{s_1,p}(t),\ldots,Y_{s_n,p}(t))]^T\\ &=[{\mathbf{Y}}_{s_i,1}(t),\ldots,{\mathbf{Y}}_{s_i,p}(t)]^T. \end{aligned} $$

In this case we could be interested in predicting simultaneously the vector of random functions $\mathbf{Y}_{s_0}(t)=(Y_{s_0,1}(t),\ldots,Y_{s_0,p}(t)),$ based on all the information of $\mathbf{Y}_s(t)$ available. For example suppose that we have several pollutants curves at each sampling site $s_i, i=1,\ldots,n$ and we want to predict them at unmonitored sites. This scenario is the natural extension of multivariate geostatistics (Ver Hoef and Cressie 1993) to the multivariate functional geostatistics. In addition, if we consider scalar and functional covariates we would have the multivariate functional kriging with external drift. By extending (2) to the multivariate functional context, we have the model

$$ {\mathbf{Y}}_{s_i}(t)=\mu_{s_i}(t)+{\mathbf{\varepsilon}}_{s_i}(t), $$

with $\mu_{s_i}(t)=(\mu_{s_i,1}(t),\ldots,\mu_{s_i,p}(t))^T,$ and ${\varepsilon}_{s_i}(t)=(\varepsilon_{s_i,1}(t),\ldots,\varepsilon_{s_i,p}(t))^T, i=1,\ldots,n.$ Following the same idea proposed in this work, if we want to predict simultaneously a random vector of functional variables at the unmonitored site s ₀, we need to estimate initially the vector of functional residuals $\mathbf{e}_{s}(t)=\mathbf{Y}_s(t)-\mu_{s}(t)$ and then, in a second step, carry out prediction of a vector of functional residuals $\mathbf{\hat e}_{s_0}(t)=(\hat e_{s_0,1}(t),\ldots,\hat e_{s_0,p}(t)).$ Two problems must be solved to fulfill these tasks. First a multivariate functional regression model must be estimated and posteriorly a multivariate functional kriging predictor used for predicting the vector of functional residuals. At the best of our knowledge these topics have not been studied and are open research problems.We think that a possible solution could be obtained by using basis functions for smoothing the set of curves $\mathbf{Y}_{s_i}(t).$ Thus, we can propose a classical multivariate regression model with the responses corresponding to the coefficients estimated from the smoothing process. In this case we would obtain a matrix of residuals which could be predicted by using multivariate geostatistics. This approach looks reasonable from a technical point of view. However the estimation of the covariance structure by means of a LMC (or any other method) is restrictive in practice even with a small number of responses and basis functions. This alternative deserves special attention.

In this work, we propose kriging with external drift for functional data that are curves along time. Thus, we have an alternative to spatio-temporal modeling capable to predict a whole curve and providing covariate nonlinear effects’ estimates straightforwardly. Moreover covariates—and response too—can be observed with different time frequency, so that treating time series data as functional data can be advantageous because a possible time misalignment problem can be avoided.

Our proposal is not necessarily an alternative to spatio-temporal modeling and indeed it can be applied to functional data that do not vary in time, as for example PM vertical profiles measured along height by an instrument deployed on a tethered balloon or climate variables measured by means of high technology radiosondes launched in the atmosphere. It is relevant to mention that in these cases a multivariate kriging approach could be also considered for predicting e _{s_0}(t). With this approach the vector $(e_{s_i}(t_1), \ldots, e_{s_i}(t_M)),$ with $t_1, \ldots, t_M$ corresponding to discrete values of the domain T, is the observation of a M dimensional random variable at site $s_i, i=1, \ldots ,n.$ Then a cokriging predictor (Ver Hoef and Cressie 1993) could be applied to predict the random vector $(\hat e_{s_0}(t_1), \ldots, \hat e_{s_0}(t_M))$ at the unmonitored site s ₀. Then a parametric or nonparametric model could be fitted to these values for reconstructing a whole function $\hat e_{s_0}(t).$ This approach is restrictive when M is large (the common situation in functional data analysis) and the methods based on OKFD, CTKFD, and FKTM, which involve the use of basis functions for smoothing the data, are a better option from a practical point of view.

For estimating the functional spatial trend we propose a functional regression model but other alternatives such as functional nonparametric models (Ferraty et al. 2011) could be considered. On the other hand, we take advantage of additive models theory to carry out variable selection (if the need arises, in our case study covariates were previously selected Cameletti et al. 2011). Gromenko and Kokoszka (2013) derive a test to determine the significance of the regression coefficients when the mean function is a linear combination of known covariate functions and depends only on time. Further research to develop inference for drift model selection for spatially correlated functional data is necessary.

For kriging functional residuals we use and compare three alternatives, namely OKFD, CTKFD and FKTM. In our case study, both cross-validation results and good predictions on the validation sites suggest to choose the simplest version where kriging coefficient are constant. Nevertheless, the desirable application of these methods to other datasets could reveal different performances.

Finally, it would be convenient to provide confidence bands for the predicted curves and, to this goal, a resampling procedure to evaluate the prediction uncertainty is part of our ongoing research.