Risk assessment of agricultural irrigation water under interval functions

Abstract

In recent years, water shortages and unreliable water supplies have been considered as major barriers to agricultural irrigation water management in China, which are threatening human health, impairing prospects for agriculture and jeopardizing survival of ecosystems. Therefore, effective and efficient risk assessment of agricultural irrigation water management is desired. In this study, an inexact full-infinite two-stage stochastic programming (IFTSP) method is developed. It incorporates the concepts of interval-parameter programming and full-infinite programming within a two-stage stochastic programming framework. IFTSP can explicitly address uncertainties presented as crisp intervals, probability distributions and functional intervals. The developed model is then applied to Zhangweinan river basin for demonstrating its applicability. Results from the case study indicate that compromise solutions have been obtained. They provide the desired agricultural irrigation water-supply schemes, which are related to a variety of tradeoffs between conflicting economic benefits and associated penalties attributed to the violation of predefined policies. The solutions can be used for generating decision alternatives and thus help decision makers to identify desired agricultural irrigation targets with maximized system benefit and minimized system-failure risk. Decision makers can adjust the existing agricultural irrigation patterns, and coordinate the conflict interactions among economic benefit, system efficiency, and agricultural irrigation under uncertainty.

1 Introduction

Over the past decades, risk assessment of water resource management has raised increasing concerns due to deteriorated ecosystems, decreased vegetation cover, varied runoff pattern, and changed climate condition (Guo and Huang 2009; Li et al. 2010a, 2011). In addition, growing population, varying natural conditions, and shrinking water availabilities have exacerbated the difficulty to assess risk in water resource management. In recent years, water shortages and unreliable water supplies have been considered as major barriers to sustainable water resource management, which are threatening human health, impairing prospects for agriculture and jeopardizing survival of ecosystems (CDDC 2004). Thus, risk assessment is desired for reduction of such conflicts and losses. Previously, a large number of systems analysis methods were developed in water resource management (Smith 1973; Abrishamchi et al. 1991; Javaid and David 1992; Manocchi and Mecarelli 1994; Mainuddin et al. 1997; Amir and Fisher 1999; Singh et al. 2001; Liu and Tong 2011; Li et al. 2010b; Lv et al. 2010; Su et al. 2011).

However, variety of complexities and uncertainties exist among multifarious activities in water resource systems and their socio-economic and environmental implications. For instance, spatial and temporal variations exist in system components, such as available amount of water, irrigation targets and irrigation quota; moreover, fluctuations would be associated with crop production prices that are functions of many stochastic factors. For past decades, a large number of stochastic mathematical programming (SMP) and interval-parameter programming (IPP) technologies were developed to cope with these challenges (Loucks et al. 1981; Eiger and Shamir 1991; Maqsood et al. 2005; Chang 2005; Mujumdar and Nirmala 2007; Li et al. 2009a, b, c, 2010b; Guo et al. 2010; Fan and Huang 2012).

Among these approaches, two-stage stochastic programming (TSP) is effective for problems where a risk analysis of policy scenarios is desired and the related data are random in nature (Li and Huang 2008). TSP is advantageous because it deals with recourse, which chooses corrective actions after a random event has taken place. In TSP, a decision is firstly made before values of random variables are known and then, after the random events have taken place and their values are known, a second decision can be made in order to minimize “penalties” that may appear due to any infeasibility. TSP methods were widely applied to assess risk existing in water resources management over the past decades (Kovacs et al. 1986; Ferrero et al. 1998; Huang and Loucks 2000; Kibzun and Nikulin 2001; Seifi and Hipel 2001; Maqsood et al. 2005; Guo et al. 2010; Li et al. 2010b). For example, Ferrero et al. (1998) assessed risks of multi-reservoir systems using a two-stage dynamic programming approach. Seifi and Hipel (2001) presented a improved linear programming method for long-term reservoir operation planning with stochastic inflows. Maqsood et al. (2005) formulated a two-stage stochastic program technique for assessing the system risk of water resources management under uncertainty. Li et al. (2010b) developed and mixed two-stage stochastic programming model for capacity planning of flood diversion under uncertainty. Francesco (2011) proposed an innovative application, using a two stage method hybrid with conditional robust nonparametric frontier and multivariate adaptive regression curve in evaluating water sector in Italy. However, in practical problems, information quality which can be obtained from many parameters is not satisfactory enough to be expressed as probability density functions. Besides, even if these distributions are available, their representations in large-scale TSP models could be extremely challenging.

Interval-parameter programming (IPP) technology is efficient for handling uncertainties expressed as interval numbers without known probability distributions and membership functions, which can exist in model’s objective function and constraints. IPP allows uncertainties to be directly communicated into optimization process and resulting solutions; it also does not lead to more complicated intermediate models, and thus has a relatively low computational requirement (Huang 1996; Huang and Cao 2011). However, conventional IPP can only solve the problems containing crisp interval coefficients [a, b], whose lower and upper bounds (i.e., a and b) are both deterministic and definitely known. This is based on the assumption that these interval coefficients are unchanged even if they could be affected by associated impact factors. In real-world problems, some parameters have been depicted as functional intervals [f(a), g(a)], where f(a) and g(a) are functions of a. Thus, conventional methods have difficulties in tackling functional intervals. Full-infinite programming (FIP) technique can tackle the uncertainties expressed as crisp intervals and functional intervals with infinite objectives and infinite constraints (Weber 1985; Zhu et al. 2011).

Therefore, this study aims to develop an inexact full-infinite two-stage stochastic programming (IFTSP) model for helping assessment risk of agricultural water management in Zhangweinan river basin, China. IFTSP will integrate approaches of interval-parameter programming (IPP) and full-infinite programming (FIM) within a two-stage stochastic programming (TSP) framework, such that uncertainties expressed as crisp intervals, probability distributions, and functional intervals can be addressed. Moreover, it can reflect tradeoffs between conflicting economic benefits and the associated penalties attributed to the violation of irrigation targets. Obtained results can help decision makers to adjust or justify the existing agriculture irrigation plans, identify desired water-allocation policies for agricultural irrigation under uncertainty, and assist in gaining insight into the tradeoffs between system risk and benefit.

2 Case study

2.1 Overview of the study system

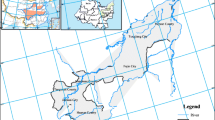
Zhangweinan river basin (latitude 112°−118°E, longitude 35°–39°N) is located in the east of Taiyue mountain, in the south of Fuyanghe river and in the north of Yellow river (Fig. 1). Zhangweinan river flows through Shanxi, Henan, Hebei, Shandong provinces, and flows into Bohai Sea in Tianjin at the end. Drainage area of Zhangweinan river basin is 37,700 km², accounting for 11.9 % of the total area of Haihe river basin (EBCZR 2003; HRCC 2003). Zhangweinan river basin is located in the temperate semi-arid, semi-humid monsoon climate zone. In this basin, mean annual temperature is around 14 °C and mean annual precipitation is 608.4 mm. It deserves to mention that Yuecheng reservoir is the largest reservoir in Zhangweinan river basin, with average inflow of 0.76 × 10⁹ m³ (statistics from 1962 to 2007). Furthermore, Zhangweinan river basin is one of the main food and cotton producing regions in North China, which covers a population of about 30 million and the cultivated area reaches to 293 × 10³ ha. In irrigation regions of this basin, wheat, maize and cotton are the main crops and consume the majority of water from Yuecheng reservoir. Water for agricultural using is delivered through Zhangnan channel to irrigation districts in Anyang and through Minyou channel to irrigation districts in Handan (DRIZRA 2008).

Fig. 1

Location of the Zhangweinan river basin

However, Zhangweinan river basin is a typical severe water resource shortage area in the north of China. Farm production of Zhangweinan river basin faces a series of serious problems for water using. First of all, the precipitation of Zhangweinan river basin has uneven distribution of time. For example, the precipitation in winter accounts for only 2 % of annual precipitation. In comparison, the precipitation accounts for more than half of annual precipitation in summer (especially in July and August) (EBCZR 2003; HRCC 2003). Thus, the average amount of per capita water in Zhangweinan river basin is 212 m³ is far below average level in China (equivalent to 7.42 % of national average). In addition, there are some issues in development and utilization of water resource in Yuecheng reservoir resulting in water shortage: (1) due to reduced precipitation, underlying surface changes and the increasing of reservoirs and diversion channels in upper basin, the water followed into Yuecheng reservoir is decreasing; (2) as unreasonable pumped well layout and groundwater over-exploitation in irrigation area, ground water level has declined and cannot be rebound; (3) since available water reduction and demand and supply changes, existing water distribution program cannot satisfy the need of social and economic development in current. To sum up, with these variability precipitations, frequent water shortage and drought in agricultural irrigation area often occurs in Zhangweinan river basin and brings more and more serious economic problems (HRCC 2003; GEF 2007). As the decrease of water supply from Yuecheng reservoir, how to make adjustments for irrigation areas in order to reduce the losses caused by water shortage and maximize the cultivate benefits is an important issue faced by government planners. Therefore, effective water resources management in for agricultural irrigation in Zhangweinan river basin is significant for both agricultural production and economic development.

However, it is obvious that a plenty of complexities exist in agricultural irrigation system, presented as uncertainties in economic and technical data, randomness in water availability, policy analysis in water supply, economic activities and benefit, as well as limited resources (Huang and Loucks 2000; Maqsood et al. 2005; Li et al. 2010b). Figure 2 presents interrelationships among various system components in water resource management. Spatial and temporal variations exist in such system components as stream flows and agricultural irrigation targets. These complexities could become further compounded by not only interactions among many uncertain system components but also their economic implications. Moreover, water availability fluctuates dynamically due to the varying river-flow of reservoir. Thus, worse water shortage may arise from insufficiency water supply schemes under disadvantageous river-flow conditions. Therefore, under such complexities, effective optimization approach is needed for allocating and managing agricultural irrigation in more efficient and effective ways for obtaining a desired trade-off between environmental objectives and maximized system benefits.

Fig. 2

Interrelationships among various system components

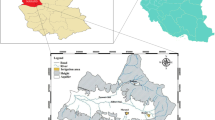
In this study, agricultural irrigation districts supplied by Yuecheng reservoir are chosen as the study areas in order to discuss water resources optimal allocation. Thus, optimal agricultural irrigation schemes for each distribution can be achieved, which can give theoretical bases to water resource allocation under uncertainties in this basin. Figure 3 indicates that there are fifteen study areas in this region, including fifteen subareas, including Quzhou county, Feixiang county, Guangping county, Chengan county, Wei county, Ci county, Linzhang county, Daming county, Wenfeng district, Beiguan district, Yindu district, Longan district, Anyang county, Neihuang county and Kaifaqu district.

Fig. 3

Schematic diagram of study area

3 Modeling formulation

In this study, the problem under consideration is how to allocate agricultural irrigation area in fifteen irrigation subareas to maximize expected system benefit under different water flows from Yuecheng reservoir. An extended consideration is for more uncertainties in other parameters. Then, interval parameters can be introduced into TSP framework to communicate uncertainties into optimization process. What’s more, traditional intervals always expressed as crisp interval coefficients [a, b], whose lower and upper bounds (i.e., a and b) are both deterministic and clearly known, which is always based on assumption that these interval coefficients are unchanged. In real-world problems, this viewpoint is vague when interval bounds are related to external impact factors, which may lead to functional intervals. Therefore, interval-parameter programming (IPP) and full-infinite programming (FIP) technique are a potential approach for accounting for above complexities, which can be introduced into TSP model. Thus, an inexact full-infinite two-stage stochastic programming (IFTSP) model can be written as follows (Zhu et al. 2012):

$$ \begin{aligned} Maxmize \, f^{ \pm } = & \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\left[ {\left( {DC_{ij}^{ \pm } - DZ_{ij}^{ \pm } } \right)/DA_{ij}^{ \pm } } \right] \times GZ_{ij}^{ \pm } \times DJ_{ij}^{ \pm } \left( \delta \right) \times TL_{ij}^{ \pm } } } \\ & - \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{l} {p_{k} \times CH_{ij}^{ \pm } \left( \delta \right) \times PD_{ijk}^{ \pm } } } } \\ \end{aligned} $$

(1a)

subject to:

(1) Process constraints

$$ \Updelta TL_{ij} = TL_{ij}^{ + } - TL_{ij}^{ - } \;{\text{and}}\;y_{ij} \in \left[ {0,1} \right],\quad i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(1b)

(1) Availability constraints

$$ PD_{ijk}^{ \pm } \le TL_{ij}^{ \pm } \quad i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(1c)

(2) Capital punishment constraints

$$ \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{l} {p_{k} \times CH_{ij}^{ \pm } \left( \delta \right) \times PD_{ijk}^{ \pm } } } } \le UD_{j}^{ \pm } \left( \mu \right)\quad for\;all \, \delta \in \left[ {\delta l,\delta u} \right],\;i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(1d)

(3) Flow quantity constraints

$$ \sum\limits_{i = 1}^{15} {\sum\limits_{j}^{3} {W_{j}^{ \pm } (TL_{ij}^{ \pm } - PD_{ijk}^{ \pm } )} } \le SW_{k}^{ \pm } ,\;k = 1,2, \ldots ,l $$

(1e)

(4) Nonnegative constraints

$$ TL_{{ij{ \max }}}^{ \pm } \ge TL_{ij}^{ \pm } \ge PD_{ijk}^{ \pm } \ge 0,\quad i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(1f)

where $DJ_{ij}^{ \pm } \left( \delta \right),\;CH_{ij}^{ \pm } \left( \delta \right)$ and $UD_{j}^{ \pm } \left( \mu \right)$ are functional interval parameters. Thus, an optimized set of $TL_{ij}^{ \pm }$ values can be identified by having $y_{i}$ as decision variables; this optimized set may correspond to a maximized system benefit under uncertain generation targets $TL_{ij}^{ \pm }$ (Li et al. 2006). In detail, let $TL_{ij}^{ \pm } = TL_{ij}^{ - } + y_{i} \times \Updelta TL_{ij}^{ \pm }$, where $\Updelta TL_{ij} = TL_{ij}^{ + } - TL_{ij}^{ - }$,and $0 \le y_{i} \le 1$. When $TL_{ij}^{ \pm }$ approach their lower bounds (i.e. when $y_{i} = 0$), a relatively high benefit would be obtained; however, a higher penalty may have to be paid when demand is not satisfied. Conversely, when $TL_{ij}^{ \pm }$ reach their upper bounds (i.e. when $y_{i} = 1$), a lower benefit would be obtained but, at the same time, a lower risk of violating promised targets (and thus lower penalty). Then, model (2) can be transformed into two deterministic submodels. Because of the objective is to minimize system cost, the submodel corresponding to $f^{ + }$can be formulated firstly as follows:

Submodel 1:

$$ \begin{aligned} Maxmize \, f^{ + } = & \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\left[ {\left( {DC_{ij}^{ + } - DZ_{ij}^{ + } } \right)/DA_{ij}^{ + } } \right] \times GZ_{ij}^{ + } \times DJ_{ij}^{ + } \left( \delta \right) \times \left( {TL_{ij}^{ - } + y_{ij} \times \Updelta TL_{ij}^{ \pm } } \right)} } \\ & - \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{l} {p_{k} \times CH_{ij}^{ - } \left( \delta \right) \times PD_{ijk}^{ - } } } } \\ \end{aligned} $$

(2a)

subject to:

(1) Process constraints

$$ \Updelta TL_{ij} = TL_{ij}^{ + } - TL_{ij}^{ - } \;{\text{and}}\;y_{ij} \in \left[ {0,1} \right],\quad i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(2b)

(1) Availability constraints

$$ PD_{ijk}^{ - } \le (TL_{ij}^{ - } + y_{i} \times \Updelta TL_{ij}^{ \pm } )\quad i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(2c)

(2) Capital punishment constraints

$$ \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{l} {CH_{ij}^{ - } \left( \delta \right) \times PD_{ijk}^{ - } } } }\, \le\, UD_{j}^{ + } \left( \mu \right)\quad \text{for \; all} \, \delta \in \left[ {\delta l,\delta u} \right],\;i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(2d)

(3) Flow quantity constraints

$$ \sum\limits_{i = 1}^{15} {\sum\limits_{j}^{3} {W_{j}^{ + } (TL_{ij}^{ - } + y_{i} \times \Updelta TL_{ij}^{ \pm } - PD_{ijk}^{ - } )} } \le SW_{k}^{ + } ,\quad k = 1,2, \ldots ,l $$

(2e)

(4) Nonnegative constraints

$$ TL_{{ij{ \max }}}^{ + } \ge TL_{ij}^{ + } \ge PD_{ijk}^{ - } \ge 0,\quad i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(2f)

where $PD_{ijk}^{ - }$ and$y_{i}$ are decision variables. Let $y_{i \, opt} ,\;D_{ijk \, opt}^{ - }$ be the solutions of submodel (2). Optimized first-stage variable is $TL_{ij \, opt}^{ \pm } = TL_{ij}^{ - } + y_{iopt} \Updelta TL_{ij}^{ \pm }$, which may correspond to the optimized upper-bound objective-function value. Then, submodel corresponding to $f_{{}}^{ - }$ can be formulated as follows:

Submodel 2:

$$ \begin{aligned} Maxmize \, f^{ - } = & \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\left[ {\left( {DC_{ij}^{ - } - DZ_{ij}^{ - } } \right)/DA_{ij}^{ - } } \right] \times GZ_{ij}^{ - } \times DJ_{ij}^{ - } \left( \delta \right) \times } } \left( {TL_{ij}^{ - } + y_{i \, opt} \times \Updelta TL_{ij}^{ \pm } } \right) \\ \, - \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{l} {p_{k} \times CH_{ij}^{ + } \left( \delta \right) \times PD_{ijk}^{ + } } } } \\ \end{aligned} $$

(3a)

subject to:

(1) Process constraints

$$ \Updelta TL_{ij} = TL_{ij}^{ + } - TL_{ij}^{ - } \quad i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(3b)

(1) Availability constraints

$$ PD_{ijk}^{ + }\, \le\, \left( {TL_{ij}^{ - } + y_{i \, opt} \times \Updelta TL_{ij}^{ \pm } } \right)\quad i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(3c)

(2) Capital punishment constraints

$$ \sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{l} {p_{k} \times CH_{ij}^{ + } \left( \delta \right) \times PD_{ijk}^{ + } } } }\, \le\, UD_{j}^{ - } \left( \mu \right)\quad \text{for \; all} \, \delta \in \left[ {\delta l,\delta u} \right],\;i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(3d)

(3) Flow quantity constraints

$$ \sum\limits_{i = 1}^{15} {\sum\limits_{j}^{3} {W_{j}^{ - } (TL_{ij}^{ - } + y_{i \, opt} \times \Updelta TL_{ij}^{ \pm } - PD_{ijk}^{ + } )} } \,\le\, SW_{k}^{ - } ,\quad k = 1,2, \ldots ,l $$

(3e)

(4) Nonnegative constraints

$$ TL_{{ij{ \max }}}^{ - } \ge TL_{ij}^{ - } \ge PD_{ijk}^{ + } \ge 0,\quad i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,l $$

(3f)

Detailed nomenclatures for variables and parameters are provided in Appendix. In model (1), the objective is to maximize expected net system benefit through allocating the agricultural irrigation area. Constraints can help define interrelationships among decision variables and agricultural irrigation management conditions. In this study, interest rate is defined as the independent variable. Its range is from 3.29 to 4.02. Since there are parameters’ limitations in data collection, just net crop benefit ($DJ_{ij}^{ \pm }$), reduction of net benefit (i.e. penalty$CH_{ij}^{ \pm }$) and investment expense for penalty [$UD_{j}^{ - } \left( \mu \right)$] are defined functional interval numbers, while others are considered to be deterministic or crisp interval numbers.

Moreover, according to the agricultural statistic data generated from Handan and Anyang from 2004 to 2007, reduction of net benefit for various crops (wheat, maize and cotton) in study subareas were estimated from market tendency in past two years, described in Table 1. Moreover, Table 2 presents pre-regulated target values for agriculture irrigation targets (surface water) in study subareas. Irrigation targets have been promised to each crop in each subarea. If water demand is satisfied, benefits to farmers will happen. On the other hand, when the promised amount of surface water is not delivered, farmers are forced to use more ground water for irrigation, which results in more production costs and environmental problems; otherwise, a reduction of crop production would be occurred due to water shortage. These would then result in penalties (i.e. reduction of benefits) on local economy. Figure 4 declares available water resources for irrigation under different reservoir inflow levels. Since the inflow of Yuecheng Reservoir is stochastic and varies significantly, it is divided into seven discrete intervals with probability distributions (cumulative probability distribution) to approximate the stochastic inflow value. Thus, seven reservoir inflows are given, which are named as very-low, low, low-medium, medium, medium-high, high and very-high, respectively. For each inflow, an interval number representing the available amount of water resources for irrigation could be achieved.

Table 1 Reduction of net benefit for various crops in each subarea

Table 2 Pre-regulated target values for agriculture irrigation targets in each subarea

Fig. 4

Available water resources for irrigation under different reservoir inflow levels

4 Result analysis

Objective of the IFTSP model is to maximize the expected value of the system benefit under different inflow levels of Yuecheng Reservoir over planning horizon. Solutions provide an effective linkage between predefined irrigation policies and associated economic implications (e.g., losses and penalties caused by improper policies). Obtained solutions contain a combination of deterministic, crisp intervals, probability distributions, and functional intervals, which can facilitate the reflection of uncertainties. Interval solutions can help managers obtain multiple decision alternatives, as well as provide bases for further analyses of tradeoffs between system benefit and irrigation schemes.

Results have been obtained through solving IFTSP model. Solutions for objective-function value and most of the non-zero decision variables were interval numbers. Results of optimized agricultural irrigation targets for three crops could be obtained through $TL_{ij \, opt}^{ \pm } = TL_{ij}^{ - } + \Updelta TL_{ij}^{ - }\, \times\, y_{i \, opt} .$ For example, results of $y_{1 \, opt}^{{}} = y_{{ 2 { }opt}}^{{}} = 1$ indicate that optimized agricultural irrigation area targets would respond to their upper-bound target values. This means that manager is optimistic for water supply to existing policies. Each optimized agricultural irrigation area would vary between fixed demand and probabilistic shortage under a given stream condition and with an associated probability (i.e. optimal irrigation areas = $TL_{ij \, opt}^{ - } + \Updelta TL_{ij}^{ \pm } \times y_{i \, opt} - PD_{ijk \, opt}^{ \pm }$). Figure 5 provides solutions of optimal irrigation targets under various reservoir inflow levels. In general, a higher objective-violation level can lead to an increased system benefit; however, this increase also corresponds to a raised risk level (i.e. lower system reliability and lower satisfaction degree. Results demonstrate that multifarious policies in pre-regulating the promised irrigation area targets would lead to different economic values and target-violation risk. In case of insufficient water, the allotment to farmers should be first decreased but guaranteeing the minimum promised target. Agricultural irrigation patterns vary among crops with uncertain characteristics under different flow levels. According to the figure, there is a steadily increasing tendency of optimal agricultural irrigation area from very-low water flow level to very-high level. Each agricultural irrigation area is difference between the promised target and probabilistic shortage. For example, the optimized irrigation area targets would be [268.85, 373.98] × 10³ ha under very-low water flow level, [273.91, 391.11] × 10³ ha under low water flow level, [284.36, 408.66] × 10³ ha under low water flow level, [301.25, 415.03] × 10³ ha under medium water flow level, [307.37, 424.19] × 10³ ha under medium-high water flow level, [320.02, 424.19] × 10³ ha under high water flow level, and [340.08, 424.19] × 10³ ha under very-high water flow level.

Fig. 5

Optimal irrigation targets for wheat under different reservoir inflow levels

For fifteen study areas, excessed areas would be various under different water flows from Yuecheng reservoir. Deficits would occur if water resources available from the reservoir do not meet crops’ demands. This is because long-standing water shortage in Yuecheng reservoir and agricultural irrigation allocations would generate increased allowances and thus reduce excess flows. Table 3 shows excess area for agriculture irrigation under different water flow levels (including very-low, low, low-medium, medium, medium-high, high and very-high). Results indicate that each violation level would result in varied agricultural irrigation area patterns. Tendency of the amount of excess area for wheat would uniformly downward. For example, under very-low water flow level, there would be excess areas of [4169, 14771] ha when p = 0.17; under low water flow level, there would be excess areas of [2482, 14166] ha when p = 0.09; under low-medium water flow level, there would be excess areas of [728, 13121] ha when p = 0.14. Similarly, the amount of excessed area for maize and cotton perform the same trend in planning horizon. For maize, the excess area would change from 0 ha to 530 ha when water flow levels are from very-low to very-high. For cotton, excess area would also have a crosscurrent as water flow levels changing from very-low to very-high level. What’ more, there would be no excessed areas under medium-high, high and very-high flow levels for maize.

Table 3 Excess area for agriculture irrigation under different reservoir inflow levels

Solution of $f_{opt}^{ \pm }$ = RMB¥ [33612.31, 82495.03] × 10⁶ provides two extremes of expected system benefit under optimal agricultural irrigation pattern. As actual value of each variable or parameter varies within its two bounds, the system benefit may change correspondingly between $f_{opt}^{ - }$ and $f_{opt}^{ + }$ with varied reliability levels. Planning for lower-bound of objective function value will lead to a lower system benefit with a lower risk of violating the agricultural irrigation target. Conversely, planning with a higher system benefit will correspond to a higher possibility of violating agricultural irrigation target when approaching upper-bound of the objective-function value. Therefore, there is a tradeoff between agricultural irrigation benefit and system-failure risk. Figure 6 illustrates agricultural irrigation benefit for growing different crops. Based on local water resource management policy, the amount of benefit would be RMB¥ [13401.15, 25325.76] × 10⁶ for wheat, RMB¥ [15130.55, 28373.82] × 10⁶ for maize, as well as RMB¥ [4133.33, 7757.33] × 10⁶ for cotton. Table 4 declared the detail information of benefit for fifteen study areas. For example, Anyang county would obtain the highest benefit for wheat and maize (RMB¥ [2309.40, 4358.33] × 10⁶ and RMB¥ [3069.823, 5766.74] × 10⁶, respectively), while Chengan county receives the highest benefit for cotton (RMB¥ [1162.10, 2183.57] × 10⁶). Besides, Kaifaqu district has no cotton growing plan, so there are no benefit solutions for this area.

Fig. 6

Agricultural irrigation benefit for different crops

Table 4 Agricultural irrigation benefit for different crop in study area

Solutions of $PD_{ijk}^{ \pm }$ reflect variations of potential system condition caused by uncertain inputs. Table 5 shows penalty expense for violating the promised targets for each crop in all the study subareas. It is indicated that the lower-bound of $PD_{ijk}^{ \pm }$ (i.e. $PD_{ijk}^{ - }$) corresponds to a higher system benefit; in comparison, the upper-bound of $PD_{ijk}^{ \pm }$ (i.e. $PD_{ijk}^{ + }$) leads to a lower system benefit. For wheat in Quzhou county, the solution of $PD_{11}^{ \pm }$ = RMB¥ [1193, 1351] × 10⁶ means that, there would be RMB¥ 1193 × 10⁶ shortage under advantageous conditions, and there would be a shortage of RMB¥ 1351 × 10⁶ under demanding conditions. Penalty obtained by irrigation for wheat would turn up in study areas. For maize and cotton, in Quzhou County, there would be no shortage under advantageous and disadvantageous conditions. In comparison, for maize, penalty only occurs with an amount of RMB¥ [219, 574] × 10⁶ in Longan district. For cotton, the amount of penalty would be RMB¥ [0, 25] × 10⁶ for Daming county, RMB¥ [21, 46] × 10⁶ for Wenfeng district, RMB¥ [48, 79] × 10⁶ for Longan district, RMB¥ [109, 238] × 10⁶ for Anyang county, respectively.

Table 5 Penalty for violating the promised targets for various crops in each subarea

Solutions can provide stable intervals for objective function values and decision variables under different levels of stream flow. They can be easily interpreted for generating multiple decision alternatives. Solutions from IFTSP model provides desired agricultural irrigation patterns, which balance various interruptible water supply goals while appropriately hedging against the effects of water shortage. Moreover, in the modeling formulation, economic penalties as corrective measures (or recourses) against any infeasibilities arising due to a particular realization of uncertainty are taken into account. Complexities associated with agricultural irrigation area allocation amounts arise mainly from limited supply and increasing demand. An optimistic policy corresponding to the upper bound system benefits may be subject to a high risk of system failure; a policy which is too conservative may lead to a waste of resources. Thus, IFTSP model has an advantage in providing an effective linkage between pre-regulated water-management policies and associated economic implications. Moreover, solutions under multifarious policies for agricultural irrigation area allocation can represent a variety of options for tackling the trade-off between system cost and system-failure risk.

5 Conclusions

In this study, an inexact full-infinite two-stage stochastic programming (IFTSP) model has been developed. IFTSP model is derived from incorporation of interval-parameter programming (IPP) and full-infinite programming (FIP) within a two-stage stochastic programming (TSP) framework. By allowing uncertainties expressed as crisp intervals, probability distributions, and functional intervals to be incorporated within the optimization framework. Moreover, it can provide an effective linkage between predefined policies and associated penalties attributed to the failure to comply with the pre-regulated targets. IFTSP model has advantages over the system in reflecting uncertainties, assessing risks and tackling tradeoffs among system reliability and objectivity: continuous variable solutions are related to decisions of water supply, and interval solutions can help decision makers obtain multiple decision alternatives. Moreover, it can support analyses for a variety of policy scenarios associated with multiple levels of economic penalties.

Developed IFTSP model has been applied to a case study for helping assess risk of agriculture irrigation water in Zhangweinan river basin, China. Based on an interactive algorithm and a derivative algorithm, the model can be transformed into two deterministic submodels which correspond to the upper and lower bounds of desired objective-function value. Besides, a number of resources and economic factors have been integrated into the modeling framework. Interval solutions, which are feasible and stable in given decision space, can then be obtained by solving the two submodels sequentially. IFTSP model can reflect tradeoffs between conflicting economic benefits and the associated penalties attributed to the violation of irrigation targets. Obtained results can help decision makers to identify a desired agricultural irrigation schemes for Zhangweinan river basin under uncertainty. The solutions can be used for generating decision alternatives and thus help water resources managers to identify desired agricultural irrigation targets with maximized system benefit and minimized system-failure risk. So, decision makers can adjust the existing agricultural irrigation patterns, and coordinate the conflict interactions among economic benefit, system efficiency, and agricultural irrigation. However, there is still much space to improve the proposed model. IFTSP can be extended to other engineering and environmental problems, for example, reservoir capacity planning, flood management and risk assessment which is of challenge for mathematicians. Moreover, multiple independent variables can be taken into consideration for dealing with functional intervals.