1 Introduction

The global warming and associated impacts on human society have drawn considerable concerns from academic circles, public, and governments. Keller (2009) reviewed some of the key issues concerning global warming. Climate change impact assessment studies have aroused newer interest in local stochastic weather simulation, as the output of General Circulation Models (GCMs) cannot directly be used in any regional hydrologic model of interest (Wigley et al. 1990; Carter et al. 1994). Statistical downscaling techniques, which relate large-scale climate variables (or predictors) to regional- or local-scale meteorologic/hydrologic variables (or predictands), can serve as a tool to generate synthetic weather data required for climate change impact assessment studies. Several single-site stochastic models are available for simulation of weather series. An important limitation of these single-site models is that they simulate weather separately for single sites. Therefore, the resulting weather series for different sites are independent of each other, whereas strong spatial correlation may exist in real weather data. Few stochastic models have been developed to produce weather series simultaneously at multiple sites, mainly for daily precipitation, such as the space–time model (Bardossy and Plate 1992; Bogardi et al. 1993; Sanso and Guenni 1999), non-homogeneous hidden Markov models (NHMMs) (Hughes et al. 1999; Bellone et al. 2000; Robertson et al. 2004) and nonparametric non-homogeneous hidden Markov model (NNHMM) (Mehrotra and Sharma 2005a). These approaches are comparatively complicated in both calibration and implementation. Further, statistical downscaling models also fail to model the variability of the predictand (Wilby et al. 2004) and, therefore, going by the values of rainfall amount directly obtained from atmospheric variables may not always be realistic. In view of these, the present study proposes to represent the rainfall pattern of all the stations in a river basin, not by using rainfall amounts but by using a rainfall state of the basin. A statistical downscaling technique is developed for prediction of future day rainfall state from GCM-simulated climate variables. The proposed model contains two modules, namely training and forecasting, to be implemented. Multi-site rainfall data is clustered with the help of an unsupervised data classification technique to identify rainfall states present in the rainfall data. A supervised data classification technique-based model is trained to establish relationship between the input data containing current day standardized climate predictors along with previous day(s) rainfall state and the output data containing the current day rainfall state. The trained model is used to forecast present day rainfall state of a river basin with the help of principal components obtained from GCM output and previous day(s) rainfall state. This approach overcomes the limitations of capturing cross correlations of raingage stations and estimates the future rainfall states of the river basin. The generated rainfall states can further be used for predicting rainfall amounts.

The rest of the paper is organized as follows. Section 2 deals with the literature review on statistical downscaling techniques. The model formulation is described in Sect. 3. Salient features of study area and data used in this research are detailed in Sect. 4. Section 5 gives details on the proposed unsupervised data classification technique viz. K-means algorithm to cluster the feature data and cluster validity tests normally performed on the clustered data to identify the optimum number of clusters. The CART model, the steps involved in building CART tree, and the advantages of using CART are detailed in Sect. 6. Derivation of rainfall states from multi-site rainfall data, training and validation of the CART model, forecast of future day rainfall state using GCM output, and interpretation of results are detailed in Sect. 7. Section 8 summarizes the conclusion of this study.

2 Statistical downscaling techniques: a review

Statistical downscaling methods use identified system relationships derived from observed data (Wigley et al. 1990; Hewitson and Crane 1996). In this approach, a statistical model, which relates large-scale climate variables (or predictors) to regional- or local-scale climate/hydrologic variables (or predictands), is developed to derive the regional information about the climate/hydrologic variable. Statistical downscaling techniques can be broadly classified into three categories: transfer function-based methods, weather pattern-based approaches, and stochastic weather generators.

Transfer function-based regression models (e.g. Wigley et al. 1990; Wilby 1998; Wilby et al. 2003, 2004; Buishand et al. 2004; Ghosh and Mujumdar 2008) are conceptually a simple way of representing linear or nonlinear relationship between the predictor and predictand. The methods used in transfer function-based models include multiple regression (Murphy 1999), canonical correlation analysis (von Storch et al. 1993), and sparse Bayesian learning with Relevance Vector Machine (Ghosh and Mujumdar 2008).

Weather typing approaches (e.g. Hay et al. 1991; Bardossy and Plate 1992; Conway and Jones 1998; Schnur and Lettenmaier 1998) involve grouping local, meteorologic variables in relation to different classes of atmospheric circulation. The weather states are achieved by applying methods, such as cluster analysis to atmospheric fields (Corte-Real et al. 1995; Huth 1997; Kidson and Renwick 2002) or using circulation schemes (Bardossy and Caspary 1990; Jones et al. 1995). These methods have limited success in reproducing the persistence characteristics of at-site wet and dry spells (Wilby 1994). Hidden Markov models (HMMs), on the contrary, are used to classify spatial rainfall patterns and then to infer the corresponding weather pattern for prediction of rainfall occurrence. Persistence characteristics of at-site wet and dry spells are well captured by HMMs (Rabiner and Juang 2003). The non-homogeneous hidden Markov models (NHMM) (Hughes and Guttorp 1994; Hughes et al. 1999; Charles et al. 1999, 2004) capture spatial variability in daily precipitation by way of identifying distinct patterns in the multi-station daily precipitation record and approximately capture the temporal variability through persistence in the weather states.

Weather generators (Wilks 1992; Khalili et al. 2009), on the other hand, produce artificial time series of weather data of unlimited length for a location based on the statistical characteristics of observed weather at that location. Stochastic weather generators are generally developed in two steps: the first step focuses on modeling of daily precipitation, while the second step concentrates on modeling other climate/hydrologic variables of interest conditional upon precipitation occurrence. The model proposed by Wilks (1998) uses familiar first-order Markov chain model for rainfall occurrence combined with mixed exponential distributions for non-zero rainfall amounts. This approach is further extended for prediction of multi-station rainfall (Wilks 1998). Mehrotra and Sharma (2007) conceptualized a semi-parametric model comprising a two-state first-order Markov model for multi-station rainfall occurrence and kernel density estimation-based approach for generation of rainfall amounts on the simulated wet days.

Other popular nonparametric approaches offer a different framework for downscaling precipitation. These models are solely based on the observed data, thus avoiding the need to estimate any parameters for the downscaling period. Two commonly used nonparametric stochastic models are kernel density estimation (Sharma et al. 1997; Sharma 2000; Sharma and O’Neill 2002; Harrold et al. 2003a, b) and K-nearest-neighbor (KNN)-based resampling methods (Lall and Sharma 1996; Mehrotra et al. 2004; Mehrotra and Sharma 2005a, b; Rajagopalan and Lall 1999; Harrold et al. 2003a; Yates et al. 2003).

Summarily, parametric models, like HMM and the model proposed by Wilks (1999), require a large number of parameters to maintain the spatial and temporal structures. The NHMM-based models are computationally intensive. The nonparametric alternatives, like the KNN, on the other hand, do not require specific parameters to be estimated. However, models based on KNN-logic resample the rainfall at all locations on a given day with replacement and, therefore, result in responses that cannot be different from what was observed (Mehrotra and Sharma 2005a, b). The weather typing-based approaches involve grouping local, meteorologic variables in relation to different classes of atmospheric circulation. The developed relationship between weather type and local climate variables may not hold good in a future climate scenario.

Considering the complexities involved in modeling the spatial and temporal variabilities, a novel method is proposed in the present study to represent the rainfall pattern of all the stations in a river basin by using a rainfall state of the basin. This approach overcomes the limitations of capturing cross correlations of raingage stations by way of grouping the rainfall data into various clusters.

3 Model formulation

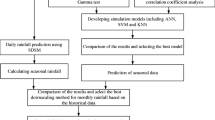
The main objective of this study is to derive the rainfall state of a river basin from large-scale atmospheric variables, which can further be used for generating multi-site rainfall amounts. The proposed statistical downscaling technique couples the K-means clustering technique and a supervised data classification technique, namely Classification And Regression Tree (CART), to achieve the objective. A flow chart depicting the model for estimation of daily rainfall state of a river basin is given in Fig. 1. The various steps involved in the estimation of future daily rainfall state are as follows:

  • Step 1: Adopt a suitable unsupervised data classification technique, such as K-means clustering technique, for clustering the observed multi-site rainfall data of the river basin concerned to identify the rainfall states present in the rainfall data.

  • Step 2: Perform Principal Component Analysis (PCA) to reduce the dimensions of the standardized predictor data, i.e. NCEP/NCAR reanalysis climate data set, pertaining to the study area and preserve the eigen vectors obtained therein. The dimensionally-reduced climate variables represent a large fraction of the variability contained in the original data.

  • Step 3: Train the CART model(s) to establish relationship between the input data containing current day standardized and dimensionally-reduced climate predictors along with previous day(s) rainfall state and the output data containing the current day rainfall state.

  • Step 4: Apply bias correction for the downloaded GCM output data to obtain bias-corrected GCM data.

  • Step 5: Obtain principal components of GCM data by performing PCA of the bias-corrected GCM data with the help of principal directions (eigen vectors) obtained during PCA of NCEP/NCAR reanalysis data.

  • Step 6: Use the trained CART model to derive present day rainfall state of the river basin with the help of principal components obtained from GCM output and rainfall state of the previous day.

Fig. 1
figure 1

Flow chart for estimation of future rainfall state

Full size image

The main advantage of the present statistical downscaling technique is the use of simple and easy-to-use K-means clustering technique for grouping the rainfall data to identify rainfall states and the use of classification and regression tree-based model for prediction of future rainfall state, which is less computationally intensive and requires less number of parameters to model. Also the CART model permits us to have both continuous and discrete or both data type as predictors and a discrete data as predictand. The present downscaling technique also represents the pattern of rainfall in a river basin by using a rainfall state of the basin and, thereby, overcomes the limitations of capturing cross correlations of raingage stations. Conventional statistical downscaling techniques used for prediction of rainfall in a river basin also fail to capture the variability of the predictand. Therefore, it is more realistic to first derive the rainfall states from atmospheric variables (which may not suffer from the above-mentioned limitation) and then generate rainfall amount from the rainfall state.

4 Study area and data

The Mahanadi River is a major peninsular river of India flowing from west to east. It drains an area of 141,589 km2, and has a length of 851 km from its origin. The river originates in a pool at an elevation of about 442 m above MSL from Pharsiya village in Raipur district of Chhattisgarh State. The Mahanadi basin lies north-east of Deccan plateau between latitudes 19°21′N and 23°35′N and longitudes 80°30′E and 87°00′E. Important tributaries of the Mahanadi River are Seonath, Jonk, Hasdeo, Mand, Ib, Tel, and Ong. The location map and basin map of the Mahanadi River is given in Fig. 2. The Mahanadi River splits into at least six major distributaries and numerous smaller channels near the city of Cuttack, before meeting Bay of Bengal. The delta region through which these tributaries flow is a densely-populated (with population of 400–450 people per km2), flat, and extremely fertile region.

Fig. 2
figure 2

a Location of Mahanadi Basin in India. b Mahanadi Basin map (Source: Irrigation Atlas of India)

Full size image

Reanalysis data on (a) mean sea level pressure (MSLP), (b) relative humidity, (c) eastward wind field (UWind), (d) northward wind field (VWind), and (e) surface air temperature, which resemble output of any GCM, downloaded from the official website of National Center for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR) reanalysis project (Kalnay et al. 1996; http://www.cdc.noaa.gov/cdc/reanalysis/reanalysis.shtml) are generally used as predictor data for training and validating any statistical downscaling model. Often, simple linear relationship between the predictor and predictand provides a general idea on the aerial extent of data required for statistical downscaling. Figure 3 shows the contour plots of Pearson correlation coefficient between the predictor variables and the rainfall data for the region between latitudes 5°–40°N and longitudes 60°–120°E. The selection of the aerial domain for downscaling is mainly based on the Indian summer monsoon activity. To account for the physical processes, such as low pressure area over the northern and central Indian subcontinent and the movement of air current from the Indian Ocean through Bay of Bengal towards the low-pressure area during the Indian summer monsoon in the present stochastic model, the climate data for 144 (12 × 12) grid points falling under the region between latitudes 7.5°–35°N and longitudes 70°–97.5°E are extracted from the NCEP/NCAR data.

Fig. 3
figure 3

Contour plot of Pearson correlation coefficient between rainfall and predictor variables

Full size image

The third generation coupled GCM (CGCM3.1) output for experiments, such as 20C3M, SRESA1B, COMMIT, SRESA2, and SRESB1 downloaded from website of Canadian Centre for Climate Modeling and Analysis (CCCMA) (http://www.cccma.ec.gc.ca/data/cgcm3/cgcm3.shtml), forms the ensemble of future climate scenario predictor data for generation of future rainfall state. As the grid spacing of the GCM grid points does not match with the NCEP/NCAR grid points, the GCM data are interpolated to obtain the GCM output at NCEP grid points.

Standardization (Wilby et al. 2004) of GCM predictor data is carried out prior to statistical downscaling to reduce systematic biases in the means and variances of GCM predictors relative to the observations or the NCEP/NCAR data. The standardization of NCEP/NCAR reanalysis data is carried out by subtracting the mean and dividing the standard deviation of the predictor variables of NCEP/NCAR reanalysis data for the predefined baseline period. The baseline period considered in this study is from 1951 to 2000. This duration is sufficient to establish a reliable climatology and is neither too long nor too contemporary to include a strong global change signal. However, standardization of GCM data is corrected with the help of mean and standard deviation of predictor data pertaining to 20C3M experiment for the same duration. The standardized climate predictor for any day contains 720 data attributes represented by MSLP, specific humidity, wind fields (zonal and meridional), and surface temperature at 144 NCEP/NCAR grid points (five climate variables in each gridpoint; i.e. 144 × 5 = 720 attributes in total) of the study region. Statistical modeling with high-dimensional correlated data will be computationally expensive. Therefore, Principal Component Analysis (PCA) is carried out to reduce the dimension of the NCEP/NCAR predictor. It is found that 98% of the variability of the original data set is explained by the first 142 principal components of the dimensionally-reduced data. Hence, the first 142 principal components of the NCEP/NCAR data for the baseline period are used for training and validating the proposed statistical model. It is also very much essential to preserve the eigen vectors obtained during PCA of the NCAP/NCAR data to obtain the principal components of bias-corrected GCM data.

A high-resolution (1° × 1° lat/long) gridded daily rainfall data for the Indian region developed by India Meteorological Department (IMD) is used in this study (Rajeevan et al. 2005). The daily gridded rainfall dataset is based on 1803 stations that have at least 90% data availability for the period 1951–2000. Indian summer monsoon daily rainfall data for the Mahanadi basin represented by 19 grid points are picked up for further analysis. The main objective of this study is to generate rainfall state (predictand) for future climate scenarios with the use of climate predictor variables. Before developing any statistical relationship between the predictor and predictand, it is essential to identify the possible rainfall states in the observed rainfall data for the study region. An unsupervised data classification technique, namely K-means clustering, is used for identification of possible rainfall states in rainfall data.

5 Unsupervised classification

Clustering is an unsupervised data classification technique used to group together feature vectors, which are close to one another in a multi-dimensional feature space, to uncover some inherent structure which the data possess. A simple partitional clustering procedure, namely K-means method, is adopted in this study to identify the rainfall states for the study area.

5.1 K-means clustering

The K-means algorithm (McQueen 1967) is commonly used to identify clusters in a given dataset. Let x i denote the ith feature vector in the n-dimensional attribute space {x i  = [x i1, …, x ij , …x in ] ∈ ℜn}. The K-means algorithm is an iterative procedure in which the feature vectors move from one cluster to another to minimize the objective function, F, defined as:

$$ F = \sum\limits_{k = 1}^{K} {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{{N_{k} }} {d^{2} \left( {x_{ij}^{k} ,x_{.j}^{k} } \right)} } } $$
(1)

where d 2(x k ij , x k.j ) is the squared Euclidian distance between feature vectors, K is the number of clusters, N k is the number of feature vectors in cluster k, x k ij is the value of attribute j in the feature vector i assigned to cluster k, and x k.j is the mean value of attribute j for cluster k, computed as: \( x_{.j}^{k} = {{\sum\nolimits_{i = 1}^{n} {x_{ij}^{k} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {x_{ij}^{k} } } {N_{k} }}} \right. \kern-\nulldelimiterspace} {N_{k} }} \)

By minimizing F in Eq. 1, the distance of each feature vector from the center of the cluster to which it belongs is minimized. The computational steps involved in programming K-means algorithm to obtain clusters for a given value of K are as follows:

  1. (1)

    Set ‘current iteration number’ t = 0 and maximum number of iterations to t max.

  2. (2)

    Initialize K cluster centers to random values in the multi-dimensional feature vector space.

  3. (3)

    Initialize the ‘current feature vector number’ i to 1.

  4. (4)

    Determine Euclidean distance of ith feature vector x i from centers of each of the K clusters, and assign it to the cluster whose center is nearest to it.

  5. (5)

    If i < N, increment i to i + 1 and go to step (4), else continue with step (6).

  6. (6)

    Update the centroid of each cluster by computing the average of the feature vectors assigned to it. Then compute F for the current iteration t using Eq. 1. If t = 0, increase t to t + 1 and go to step (3). If t > 0, compute the difference in the values of F for iterations t and t − 1. Terminate the algorithm if the change in the value of F between two successive iterations is insignificant, else continue with step (7).

  7. (7)

    If t < t max, update t to t + 1 and go to step (3), else terminate the algorithm.

The optimal value attained by F depends on the assumed number of clusters (K) and initialized values of their centers.

5.2 Cluster validation measures

Many clustering algorithms require the number of clusters given as an input parameter. This is a potential problem, as this number is often not known. To overcome this problem, a number of cluster validation indices have been proposed in the literature. A cluster validation index, by definition, is a number that indicates the quality of a given clustering. Hence, if the correct number of clusters is not known, one can execute a clustering algorithm multiple times varying the number of clusters in each run from some minimum to some maximum value. For each clustering obtained under this procedure, the validation indices are computed. Eventually, the clustering that yields the best index value is returned as the final result. Cluster validation measures, such as the Dunn’s index (Dunn 1973), the Davies–Bouldin index (Davies and Bouldin 1979), and the Silhouette index used in this study that reflect compactness, connectedness, and separation of cluster partitions, are detailed below.

5.2.1 Dunn’s index

The Dunn’s index (V D) defines the ratio between the minimal intra-cluster distance to maximal inter-cluster distance, and is computed as follows:

$$ V_{\text{D}} = \mathop {\min }\limits_{1 \le i \le K} \left\{ {\mathop {\min }\limits_{1 \le j \le K,j \ne j} \left[ {{\frac{{\delta \left( {C_{i} ,C_{j} } \right)}}{{\mathop {\max }\limits_{1 \le k \le K} \Updelta \left( {C_{k} } \right)}}}} \right]} \right\} $$
(2)

where

$$ \delta \left( {C_{i} ,C_{j} } \right) = \mathop {\min }\limits_{{x_{i} \in C_{i} ,x_{j} \in C_{j} }} \left[ {d\left( {x_{i} ,x_{j} } \right)} \right] $$

is the distance between clusters C i and C j (inter-cluster distance), and

$$ \Updelta \left( {C_{k} } \right) = \mathop {\max }\limits_{{x_{i} ,x_{j} \in C_{i} }} \left[ {d\left( {x_{i} ,x_{j} } \right)} \right] $$

is the intra-cluster distance of cluster C k . The value of K for V D, which is maximized, is taken as the optimal number of clusters.

5.2.2 Davies–Bouldin index

The Davies–Bouldin index (V DB) is a function of the ratio of the sum of within-cluster scatters to between-cluster separation, and is given by:

$$ V_{\text{DB}} = \frac{1}{k}\sum\limits_{k = 1}^{K} {\mathop {\max }\limits_{k,k \ne l} \left\{ {{\frac{{S_{k,q} + S_{l,q} }}{{d_{kl,\lambda } }}}} \right\}} $$
(3)

The scatter within the kth cluster S k,q and the Minkowski distance of order λ between the centroids that characterize clusters C j and C k are computed as follows:

$$ S_{k,q} = \left( {{\frac{1}{{N_{k} }}}\sum\limits_{{x_{i} \in C_{k} }} {\left\| {x_{i} - z_{k} } \right\|\left| {_{2}^{q} } \right.} } \right)^{{\frac{1}{q}}} $$
(4)
$$ d_{kl,\lambda } = \left\| {z_{k} - z_{l} } \right\|_{\lambda} \,= \left( {\sum\limits_{j = 1}^{n} {\left| {x_{.j}^{k} - x_{.j}^{l} } \right|^{\lambda } } } \right)^{{{\frac{1}{\lambda }}}} $$
(5)

where z k is the centroid of cluster k, and S k,q is the qth root of the qth moment of the Euclidean distance of feature vectors in cluster k with respect to its centroid. First moment (q = 1) and Minkowski distance of order 2 (λ = 2) are used in the present study. A small value for V DB indicates good partition, which corresponds to compact clusters with their centers far apart.

5.2.3 Silhouette index

The silhouette width of the ith vector in the cluster C j is defined as follows:

$$ s_{i}^{j} = {\frac{{b_{i}^{j} - a_{i}^{j} }}{{{ \max }\left\{ {a_{i}^{j} ,b_{i}^{j} } \right\}}}} $$
(6)

The average distance a j i between the ith vector in the cluster C j and the other vectors in the same cluster is given by:

$$ a_{i}^{j} = {\frac{1}{{m_{j} - 1}}}\sum\limits_{k = 1,k \ne j}^{{m_{j} }} {d\left( {X_{i}^{j} ,X_{k}^{j} } \right)} ,\quad i = 1, \ldots ,m_{j} $$
(7)

The minimum average distance b j i between the ith vector in the cluster C j and all the vectors clustered in the clusters C k , k = 1, …, K, k ≠ j is given by:

$$ b_{i}^{j} = \mathop {\min }\limits_{n = 1, \ldots ,K,n \ne j} \left\{ {{\frac{1}{{m_{n} }}}\sum\limits_{k = 1}^{{m_{n} }} {d\left( {X_{i}^{j} ,X_{k}^{n} } \right)} } \right\},\quad i = 1, \ldots ,m_{j} $$
(8)

From Eq. 6, it follows that the values of s j i varies between −1 and +1 (both inclusive).

The silhouette of the cluster C j is defined as

$$ S_{j} = {\frac{1}{{m_{j} }}}\sum\limits_{i = 1}^{{m_{j} }} {s_{i}^{j} } $$
(9)

and the global Silhouette index of the clustering is given by:

$$ S = \frac{1}{K}\sum\limits_{j = 1}^{K} {S_{j} } $$
(10)

Both a cluster’s silhouette and the global silhouette take values between −1 and +1 (both inclusive).

6 Supervised classification

Supervised classification is a machine learning technique for learning a function from training data. The training data consist of pairs of input objects (typically vectors) and desired outputs. The output of the function can be a continuous value or can predict a class label of the input object. The task of the supervised learner is to predict the value of the function for any valid input object after having seen a number of training examples (i.e. pairs of input and target output).

The CART model builds classification and regression trees for predicting continuous dependent variables (regression) and categorical predictor variables (classification). In most general terms, the purpose of the analysis via tree-building algorithms is to determine a set of if-then logical (split) conditions that permit accurate prediction or classification of cases. The tree is built through a process known as binary recursive partitioning algorithm. This is an iterative process of splitting the data into partitions, and then splitting it up further on each of the branches. The steps involved in building CART are as follows:

  1. (1)

    Initially, place all observations in the training set (the pre-classified records that are used to determine the structure of the tree) at the root node. This node is considered impure or heterogeneous, since it contains all observations. The goal is to devise a rule that initially breaks up these observations and creates groups or binary nodes that are internally more homogeneous than the root node.

  2. (2)

    Starting with the first variable, split a variable at all of its possible split points (at all of the values the variable assumes in the sample). At each possible split point of the variable, the sample splits into two binary or child nodes.

  3. (3)

    Apply goodness-of-split criteria to each split point and evaluate the reduction in impurity or heterogeneity due to the split.

  4. (4)

    Select the best split on the variable as that split for which reduction in impurity is the highest.

  5. (5)

    Repeat steps (2)–(4) for each of the remaining variable at the root node and rank all of the ‘best’ splits on each variable according to the reduction in impurity achieved by each split.

  6. (6)

    Select the variable and its best split point that reduces most of the impurity of the root or parent node.

  7. (7)

    Assign classes to these nodes according to a rule that minimizes misclassification cost.

  8. (8)

    Repeatedly apply steps (2)–(7) to each non-terminal child node at each of the successive stages.

  9. (9)

    Continue the splitting process and build a larger tree. The largest tree can be achieved if the splitting process continues until every observation constitutes a terminal node.

  10. (10)

    Prune the results using cross-validation and create a sequence of nested tree, and select the optimal tree based on minimum cross-validation error rate.

The advantages of using the CART model are:

  1. (a)

    It makes no distributional assumption of any kind, either on dependent or on independent variables. No predictor variable in CART is assumed to follow any kind of statistical distribution;

  2. (b)

    The predictor variables in CART can be a mixture of categorical, interval, and continuous;

  3. (c)

    CART is not affected by outliers, colinearities, heteroscedasticity or distributional error structure that affect parametric procedures;

  4. (d)

    CART has the ability to detect and reveal interactions in the dataset;

  5. (e)

    CART is invariant under monotonic transformation of independent variables; and

  6. (f)

    CART effectively deals with higher-dimensional data.

7 Results and discussion

7.1 Derivation of rainfall states

As a first step in building the statistical model for predicting the occurrence of future rainfall states, the K-means algorithm is used to cluster gridded rainfall data of 19 grid points for a period of 50 years from 1951 to 2000 representing the Mahanadi basin. As this is an unsupervised clustering without any target output, validation/testing is not required/possible for K-means algorithm. The clustering algorithm tries to minimize the objective function in Eq. 1. As such, the optimum number of clusters is not known, the K-means algorithm is executed several times varying the number of clusters (K) in each run. The K-means algorithm gives, in each run, classified cluster identification (ID) for each rainfall vector and cluster centroids as the main output, which are preserved for computation of cluster validation indices. The optimum number of clusters is worked out based on the cluster validity indices. The three cluster validation measures mentioned above (i.e. Dunn’s index, Davies–Bouldin index, and Silhouette index) are computed for each cluster obtained under the K-means clustering technique. Figure 4a–c shows plots of various cluster validity indices computed against the number of clusters used for clustering. Table 1 gives the cluster centroids as computed using the K-means clustering technique for clusters varying from 2 to 5. It is observed from Table 1 that the cluster centroid for almost dry condition is found to be well separated from the cluster centroids of other states in all groups of clusters. From hydrologic point of view, it is important to separate out the almost dry conditions and, therefore, number of clusters greater than 2 is considered for identification of the optimum number of clusters in this study. It is also observed that the cluster validity measures show the optimum cluster as 3 for number of clusters greater than 2. Therefore, the clusters obtained by the K-means algorithm for k = 3 clusters are adjudged as the best clusters, and the respective cluster indices are considered as the predictand for training the CART model. The rainfall states are thus named as “almost dry,” “medium,” and “high” on the basis of rainfall amounts present in the cluster centroid. Considering both the rainfall values as well as the number of rainy days in unsupervised classification may provide a more realistic rainfall state estimation and can be considered as a potential research area.

Fig. 4
figure 4

Computed cluster validity measures

Full size image
Table 1 Centroids of clusters computed by K-means clustering technique
Full size table

7.2 Training and validation of the CART model

The standardized and dimensionally-reduced NCEP/NCAR reanalysis data, containing 142 principal components representing five climate variables, viz. MSLP, specific humidity, wind fields (U, V Wind), and air temperature for 144 grid points of the study area, represents the predictor data set. The rainfall states identified by the K-means clustering technique form the predictand to train the CART model. Three possible models considered for training and validation purpose are given below:

$$ {\text{Model\;1: }} { }R(t) = f\left\{ {m(t),m(t - 1),R(t - 1)} \right\} $$
(11)
$$ {\text{Model\,2: }} { }R(t) = f\left\{ {m(t),m(t - 1),R(t - 1),R(t - 2)} \right\} $$
(12)
$$ {\text{Model\,3: }} { }R(t) = f\left\{ {m(t),m(t - 1),R(t - 1),R(t - 2),R(t - 3)} \right\} $$
(13)

where R(t)/m(t) is the state of rainfall/set of atmospheric variables on the tth day, and R(t − i)/m(t − i) is the state of rainfall/set of atmospheric variables on the (t − i)th day. The relationship/function (f) (Eqs. 11–13) used in CART considers both continuous (values of atmospheric/climate variables) and discrete (lag rainfall states) variables as input and only discrete variable as output (present rainfall state).

Standardized and dimensionally-reduced NCEP/NCAR predictor data and concurrent rainfall states for a period of 33 years from 1951 to 1983 are used for training the CART models and the remaining predictor data for a period of 18 years from 1986 to 2003 are used for validating the trained CART models. Therefore, a total of three training and three validation runs are taken for models referred in Eqs. 11–13. The model validation results are used to compute skill measures, such as success rate of model prediction (SRMP), Heidke skill score (HSS) (Wilks 1995) and χ2 goodness-of-fit test statistic to reliably identify the best model for future use.

The success rate of model prediction (SRMP) for a 3 × 3 contingency table, as given in Table 2, can be defined as:

$$ {\text{SRMP}} = {\frac{{\left( {a + e + i} \right)}}{{\left( {a + b + c + d + e + f + g + h + i} \right)}}} \times 100 $$
(14)

The value of SRMP ranges from 0 to 100, with 0 for poor forecasts and 100 for perfect forecasts.

Table 2 Contingency table for state-to-state transition
Full size table

The Heidke score is based on the hit rate as the basic accuracy measure defined as (Wilks 1995):

$$ {\text{HSS}} = {\frac{{\left( {{{\left( {a + e + i} \right)} \mathord{\left/ {\vphantom {{\left( {a + e + i} \right)} n}} \right. \kern-\nulldelimiterspace} n}} \right) - \left[ {\left( {a + b + c} \right)\left( {a + d + g} \right) + \left( {d + e + f} \right)\left( {b + e + h} \right) + \left( {g + h + i} \right)\left( {c + f + i} \right)} \right]/n^{2} }}{{1 - \left[ {\left( {a + b + c} \right)\left( {a + d + g} \right) + \left( {d + e + f} \right)\left( {b + e + h} \right) + \left( {g + h + i} \right)\left( {c + f + i} \right)} \right]/n^{2} }}} $$
(15)

Thus, perfect forecasts receive Heidke scores of one, forecasts equivalent to the reference forecasts receive zero scores, and forecasts worse than reference forecasts receive negative scores. However, HSS > 0.15 indicates a reasonably good forecast (Maity and Nagesh Kumar 2008).

Similarly, the association between the forecasts and the observed rainfall based on the χ2 distribution can be found to decide whether or not the null hypothesis H 0 is plausible; the null hypothesis is defined as: There is no association between the observed and the forecasted rainfall occurrence.

The χ2 statistic is defined as:

$$ \chi^{2} = \sum\limits_{i = 1}^{3} {\sum\limits_{j = 1}^{3} {{\frac{{\left( {f_{ij} - e_{ij} } \right)^{2} }}{{e_{ij} }}}} } $$
(16)

where f ij ’s are the entries in the table of observed frequencies in the contingency table, and \( e_{ij} = \left\{ {{\text{row(}}i ) {\text{total}} \times {\text{column(}}j ) {\text{total}}} \right\}/\left( {\text{grand total}} \right) \)’s are the corresponding expected frequencies under the null hypothesis H 0. Under H 0, the test statistic χ2 has, approximately, a χ2 distribution with (r − 1)(c − 1) degrees of freedom, where r and c are the numbers of rows and columns in the contingency table. As with the χ2 goodness-of-fit test, H 0 is usually rejected only for large values of χ2.

The SRMP (in percentage), HSS, and χ2 goodness-of-fit statistic computed for the results of all the model runs are presented in Table 3. It is observed that the SRMP, HSS, and χ2 goodness-of-fit statistic computed for the results of Model 1 validation run are 63.86%, 0.17, and 126.8, respectively, which are found to be the highest among all the runs. Since the computed HSS for the results of Model 1 run (0.17) is higher than 0.15, one can infer that Model 1 gives a reasonably good forecast (Maity and Nagesh Kumar 2008).

Table 3 CART training and validation results
Full size table

The upper 10 and 5% points for χ 24 are 7.78 and 9.49, respectively. It is observed that the χ2 goodness-of-fit statistic computed for the Model 1 validation results (χ2 = 126.8) is much higher than the upper 10 and 5% point values. Hence, the null hypothesis H 0 would be rejected at both 10 and 5% significance levels. Thus, there is a strong evidence of association between the forecasts and the observed rainfall as far as the χ2 goodness-of-fit statistic is concerned. The SRMP, HSS, and χ2 goodness-of-fit statistic computed for the results of validation runs of the above three models indicate that the performance of Model 1 is better than Model 2 or Model 3. Therefore, Model 1 is selected for forecasting the occurrence of future day rainfall states using GCM output.

7.3 Forecast of future day rainfall states using GCM output

The principal components of third generation coupled GCM (CGCM3.1) outputs for experiments, such as 20C3M, SRESA1B, COMMIT, SRESA2 and SRESB1, are used for driving the trained CART model for estimation of rainfall states for future scenarios of climate change. Tables 4, 5, 6, 7, and 8 give a 25-year wise breakup of number of days forecasted falling under different rainfall states. The percentage-wise occurrences of rainfall states for various scenarios are given in Fig. 5.

Table 4 25-yearwise breakup of number of rainy days forecasted falling under different states: (a) K-means cluster used for training the model; and (b) Model results for CGCM3.1 output with 20C3M experiment
Full size table
Table 5 25-yearwise breakup of number of rainy days forecasted falling under different states for the COMMIT experiment
Full size table
Table 6 25-yearwise breakup of number of rainy days forecasted falling under different states for the SRESA1B experiment
Full size table
Table 7 25-yearwise breakup of number of rainy days forecasted falling under different states for the SRESA2 experiment
Full size table
Table 8 25-yearwise breakup of number of rainy days forecasted falling under different states for the SRESB1 experiment
Full size table
Fig. 5
figure 5

Percentage-wise breakup of occurrence of rainfall states

Full size image

A customary look at Fig. 5a, b shows that model results obtained for CGCM3.1 output with 20C3M experiment almost match with K-means clusters used for training the model. Further, it is observed that the model results obtained for COMMIT experiment are consistent with that of the 20C3M experiment (Fig. 5c), and also there is no significant trend in the occurrence of “almost dry,” “medium,” and “high” rainfall states. The model results obtained for SRESA1B experiment (Fig. 5d) show an increase in “almost dry” states, a decrease in “medium” rainfall states, and an increase in “high” rainfall states.

Figure 5e depicts the model results obtained for SRESA2 experiment. It shows no significant increase in the number of “almost dry” states for the first two periods (2001–2025 and 2026–2050), and an increase in the number of “almost dry” states for the third period (2051–2075). The fourth period (2076–2100) shows a decrease in the number of “almost dry” states. The number of “medium” rainfall states slightly increases for periods 2001–2025 and 2026–2050, and then steadily decreases for the remaining periods. There is a slight decrease in the number of “high” rainfall states for periods 2001–2025 and 2026–2050, a marginal increase in the number of “high” rainfall states for periods 2026–2050 and 2051–2075, and a steep increase in the number of “high” rainfall states for periods 2051–2075 and 2075–2100.

Figure 5f shows no increase in “almost dry” rainfall states for the periods 2001–2025 and 2026–2050, and then a steady increase in almost dry rainfall states for the periods 2026–2050 and 2076–2100. It is also observed that there is a slight increase in “medium” rainfall states for the periods 2001–2025 and 2026–2050, and then a decrease for the periods 2026–2050 and 2076–2100. The “high” rainfall states marginally decrease for periods 2001–2025 and 2026–2050, and then there is no significant trend in “high” rainfall states.

7.4 Transition probability

Tables 9, 10, 11, 12 and 13 give 25-year wise state–state transition probability matrix computed for the results of model runs for the four experiments: COMMIT, SRESA1B, SRESA2, and SRESB1. Figure 6 shows the plots of “almost dry–almost dry,” “medium–medium,” and “high–high” rainfall state transition probabilities obtained for model outputs for all the experiments.

Table 9 Transition probability: (a) results of K-means clustering with three clusters; and (b) model results for CGCM3.1 output with 20C3M experiment
Full size table
Table 10 Transition probability for the COMMIT experiment
Full size table
Table 11 Transition probability for the SRESA1B experiment
Full size table
Table 12 Transition probability for the SRESA2 experiment
Full size table
Table 13 Transition probability for SRESB1 experiment
Full size table
Fig. 6
figure 6

Plot of state–state transition probabilities

Full size image

7.4.1 COMMIT experiment

The state-to-state transition probability plots drawn for COMMIT experiment are shown in Fig. 6a. It is observed that there is no major trend in the almost dry–almost dry, medium–medium, and high–high rainfall states. This shows consistency in predictability of the CART model.

7.4.2 SRESA1B experiment

Figure 6b shows the state–state transition probability plots obtained for the SRESA1B experiment. It is observed that there is no significant trend in almost dry–almost dry state transition probabilities for the periods 2001–2025 and 2026–2050 and also for the periods 2051–2075 and 2076–2100. A marginal increase in almost dry–almost dry transition probabilities is noticed for the periods 2026–2050 and 2051–2075. The medium–medium rainfall state transition probabilities for the periods 2001–2025 and 2026–2050 show a marginal increase in trend, and then steadily decrease for the remaining periods: 2026–2050 and 2075–2100. The high–high rainfall transition probabilities initially show a slight decrease in trend for the periods 2001–2025 and 2026–2050, and then a steep increase in trend for the remaining periods. The increase in the transition probability of high–high rainfall states suggests that there is a possibility of clustering of high rainfall days together, which may result in severe flooding.

7.4.3 SRESA2 experiment

Figure 6c shows the state–state transition probability plots obtained for the SRESA2 experiment. No significant trend in the almost dry–almost dry state transition probabilities is observed for the periods 2001–2025 and 2026–2050 and also for the periods 2051–2075 and 2076–2100. A marginal increase in trend in almost dry–almost dry state transition probabilities is observed for the periods 2026–2050 and 2051–2075. The medium–medium rainfall state transition probabilities show a marginal increase in trend for the period 2001–2025 and 2026–2050, and then show a steady to steep increase in trend for the remaining periods. At the same time, the high–high rainfall transition probabilities show a slight decrease in trend for the periods 2001–2025 and 2026–2050, and then show a steep to very steep increase in trend for the remaining periods.

7.4.4 SRESB1 experiment

Figure 6d shows the state–state probability plots obtained for the SRESB1 experiment. The figure shows no trend in the almost dry–almost dry state transition probabilities for the periods 2001–2025 and 2026–2050, and then a slight steady increase in trend for the remaining periods. The medium–medium rainfall transition probabilities show a marginal increase in trend for the periods 2001–2025 and 2026–2050 and a marginal decrease in trend for 2026–2050 and 2051–2075. No trend in medium–medium rainfall state transition probabilities is observed for the remaining periods: 2051–2075 and 2076–2100. A steady decrease in trend is observed for the high–high rainfall state transition probabilities for the periods 2001–2025 and 2026–2050. A slight to steep increase in trend is observed for the remaining periods.

Although there are differences between the projected results for different scenarios, it is generally observed that there is a possibility of increase in the occurrences for almost dry and high rainfall states. On the other hand, the number of days with medium rainfall state reduces. This denotes an increase in the occurrences of extreme weather events (either almost dry state or high rainfall state) in future. Interesting results are observed in terms of transitional probabilities. The transitional probability of high–high rainfall state is found to be significantly increasing in future. The predictions of increase of almost dry days and decrease of medium rainfall days are similar to the predictions of Ghosh and Mujumdar (2007) and Mujumdar and Ghosh (2008), where the possibilities of reduction of rainfall and streamflow in the Mahanadi River basin are explored. Moreover, some of the earlier models using transfer function-based approaches failed to predict extreme rainfall events correctly (e.g. Ghosh and Mujumdar 2008). Therefore, the changes in high rainfall events as forecasted by those analyses are not reliable. The present study does not have any limitation for capturing the high rainfall states and, hence, shows the possibility of an increase in the number of high rainfall days. This increase is consistent with the recent trend analysis (of Central India Summer Monsoon Rainfall) by Goswami et al. (2006), where an increase in the occurrences of heavy rainfall states is observed. It should be noted that the results presented here are based on single-GCM outputs. There is a possibility of obtaining different results if different GCMs are used. Therefore, analysis with a single GCM may not be reliable (Ghosh and Mujumdar 2007; Mujumdar and Ghosh 2008). Multi-ensemble analysis with multiple GCMs and subsequent uncertainty modeling is required before any water resources decision-making incorporating climate change.

Some recent observations show that the Mahanadi basin is vulnerable to the impact of climate change. For example, analysis of instrumental climate data revealed that the mean surface air temperature over the Mahanadi basin has increased at a rate of 1.1°C per century, which is statistically significant compared to the national average of 0.4°C (Rao 1995). Recent past records of Orissa also show that this is the most affected region of India due to climate change (www.cseindia.org/programme/geg/pdf/orissa.pdf). A small change in the circulation pattern may result in a significant change in rainfall of the case study area. Increase in trend observed in the occurrence of almost dry rainfall state, coupled with a steady decrease in the occurrence of medium rainfall state, may result in less water availability, which, in turn, may increase the frequency of drought in the study area. Secondly, the increase in trend observed in the occurrence of high rainfall state along with the increase in high–high rainfall state transitional probability shows possibilities of continuous heavy downpour for few days in the monsoon. This may lead to severe flooding in the lower Mahanadi basin, where the population density is also high. It is summarized that potential impact of climate change in the Mahanadi basin will likely be huge, with predicted freshwater shortages, sweeping changes in food production conditions, and increases in deaths from floods, storms, heat waves, and droughts.

8 Summary and conclusion

The work reported in this paper contributes towards developing methodologies for predicting the state of rainfall at local or regional scale for a river basin from large-scale GCM output of climatological data. As a first step towards statistical downscaling, an agglomerative clustering technique, namely K-means algorithm, is adopted for clustering the gridded rainfall data pertaining to the Mahanadi River basin in India. The rainfall states arrived with the help of clustering technique form the predictand for the statistical downscaling model developed for prediction of future day rainfall occurrence. Principal Component Analysis (PCA) is performed on NCEP/NCAR reanalysis data pertaining to the study area to reduce the dimensions of predictor attributes and the computed eigen vectors are preserved to derive principal components of other GCM data. The CART models are trained with principal components of NCEP/NCAR reanalysis data for a period of 33 years from 1951 to 1983 as predictor and the concurrent rainfall states derived for the river basin using the K-means clustering algorithm as predictand. The trained CART models are tested with the remaining predictor data for a period of 17 years from 1984 to 2000. The CART model with lag-1 rainfall as the predictor rainfall state is found to be the best model for prediction of future day rainfall occurrence. This model is capable of producing a satisfactory value of goodness-of-fit in terms of success rate of model prediction (SRMP), Heidke skill score (HSS), and χ2 value.

General Circulation Model outputs for five climate scenarios (20C3M, COMMIT, SRESA1B, SRESA2, and SRESB1) are standardized, i.e. bias-corrected and transformed into principal components using the preserved NCEP/NCAR eigen vectors. The trained CART model is then driven with principal components of GCM outputs for the different climate scenarios. Twenty-five-year wise predicted rainfall states falling in various categories of rainfall states namely ‘almost dry,’ ‘medium,’ and ‘high’ are computed. State-to-state transition probabilities are also computed for the results of various experiments.

The results corroborate the possibility of an increase in the occurrences of ‘almost dry’ and ‘high’ rainfall states and a decrease in the occurrences of ‘medium’ rainfall states. It is interesting to note that the transition probability for high–high rainfall is reported to increase in future, which suggests the possibility of clustering of heavy rainfall days together. Therefore, it is concluded that the occurrence of daily rainfall in the Mahanadi basin will be severely affected due to climate change. A pronounced increasing trend in the occurrence of high rainfall states may cause flooding situation in the basin. Also, the increasing trend in the occurrences of almost dry states coupled with decreasing trend in the occurrences of medium rainfall states may cause a critical situation for the Hirakud dam (a major dam across the Mahanadi River) in meeting the future irrigation and power demands. The methodology developed herein can be used to project the occurrence of rainfall also for other GCMs and scenarios. The future day rainfall states thus predicted for the Mahanadi basin will be used for generation of rainfall amounts, which, in turn, will be a valuable input to study the impact of climate change on local hydrology.