1 Introduction

Weather generators are increasingly being used in a variety of water resource studies due to their ability to provide series of weather data for any length of time with similar statistics as observations to which the weather generators have been fitted. Richardson weather generator (WGEN) (Richardson 1981; Richardson and Wright 1984) is the most commonly used weather generator, and uses a first-order two-state Markov chain model to generate precipitation occurrences and distribution function, such as gamma or exponential, to model precipitation amounts. Another basic type of weather generator is the one by Semenov and Barrow (1997), which uses semi-empirical distributions to simulate precipitation processes. There are also non-parametric weather generators (Brandsma and Buishand 1997), which use the resampling of a weather variables vector on a day of interest from the historical data by conditioning on the simulated values of previous days.

These weather generators operate at a single site, and thus fail to reproduce the spatial dependence present in the observed data. In fact, the extension of the weather event over the watershed implies that the weather data at a given weather station is likely to be correlated with those in the surrounding area. Further research has therefore been conducted to develop multi-site weather generators, such as space-time models (Bardossy and Plate 1992; Bogardi et al. 1993), which use the atmospheric circulation patterns with conditional distributions and conditional spatial covariance functions. Non-homogeneous hidden Markov model (Bellone et al. 2000; Hughes and Guttorp 1994a, b; Hughes et al. 1999) uses a discrete weather state to link the large scale atmospheric measures and the small scale spatially discontinuous precipitation field. A multi-site weather generator based on a nearest-neighbor resampling from historical data has been developed by Buishand and Brandsma (2001). Wilks (1998) developed a multi-site version of the Richardson weather generator based on serially independent but spatially correlated random numbers.

The multi-site weather generators presented above are designed using relevant statistic information, but yield difficulties in their implementation, and produce limited results. Wilks (1998) proposes an interesting multi-site framework using the Richardson model, but is unable to do away with certain practical difficulties, such as the computational burden and the correlation matrix positive definiteness constraint. Wilks (1998) proposes also one attempt to alleviate the spatial intermittence problem using a 3-parameter mixed exponential, but further improvements are required in this regard. An algorithm simplifying the execution of Wilks’ approach has been developed by Brissette et al. (2007), with a multi-exponential function to improve the reproduction of seasonal spatial intermittence. Tae-woong et al. (2007) used the Markovian model for occurrence process as in wilks (1998), but the dependence of occurrence is directly considered among stations using space-time Markov model.

Regarding the multi-site generation of temperature and solar radiation data, the main earlier approaches were those developed by Wilks (1999) and Buishand and Brandsma (2001). The first uses an extension of the weakly stationary generating process from 3 to 3 k dimensions, where k is the total number of locations. However, this extension yields correlation matrices that are not easy to handle, particularly for a large station network, and the coefficients of interstation correlations are not necessarily all significant. The second approach uses historical data, which cannot deal with climate change studies.

Multi-site generation approach of daily precipitation data has been developed by Khalili et al. (2007). This approach adopts the Richardson weather generator, and uses the spatial autocorrelation concept to reproduce the spatial dependence seen in georeferenced observations. The core advantage of using spatial autocorrelation lies in its ability to summarize the spatial dependence over a watershed in a single number, which minimizes computation requirements, and highlights the straightforwardness of the approach when used for a large data set. Using a proper weight matrix, which is required for the computation of spatial autocorrelation, the multi-site approach can reproduce observed daily spatial autocorrelations, and implies the reproduction of observed monthly pairwise correlations. The approach by Khalili et al. (2007) allows an accurate simulation of precipitation processes, while maintaining daily spatial autocorrelations and monthly interstation correlations. However, while the simple exponential distribution function used to model precipitation amounts ensures a practically good fit with these precipitation amounts, it fails to fulfill the spatial intermittence property, which means that the precipitation amounts at a given station depend on whether the surrounding stations are wet or dry. It is thus not appropriate to model the precipitation amounts at a given station without considering the occurrence states in the surrounding stations.

This paper focuses firstly on improving the simulation of precipitation amounts in order to obtain an accurate reproduction of daily spatial intermittence using spatial autocorrelation concept. Secondly, it examines the use of spatial autocorrelation for a straightforward multi-site generation of daily temperature and solar radiation data. The next section presents a definition of spatial autocorrelation. Section 3 presents the general theory of stochastic multi-site generation approach of daily precipitation data (Khalili et al. 2007) and the suggested method for improving the spatial intermittence of precipitation amounts. The proposed methodology for multi-site generation of daily temperature and solar radiation data is described in Sect. 4. Section 5 presents and discuses the results of the proposed approaches.

2 Definition of spatial autocorrelation

Spatial autocorrelation is a correlation among the values of a single variable, taking into account their arrangement in geographic space (Griffith 2003). This statistic complies with the first law of geography mentioned by Tobler (1970) “Everything is related to everything else, but near things are more related than distant things”. A more useful spatial autocorrelation statistic is Moran’s I (Moran 1950; Odland 1988; Griffith 2003), presented as:

$$ I = \frac{{{{\sum\nolimits_{i = 1}^{n} {\left( {x_{i} - \bar{x}} \right)\sum\nolimits_{j = 1}^{n} {w_{ij} \left( {x_{j} - \bar{x}} \right)} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {\left( {x_{i} - \bar{x}} \right)\sum\nolimits_{j = 1}^{n} {w_{ij} \left( {x_{j} - \bar{x}} \right)} } } {\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {w_{ij} } } }}} \right. \kern-\nulldelimiterspace} {\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {w_{ij} } } }}}}{{\sum\nolimits_{i = 1}^{n} {\left( {x_{i} - \bar{x}} \right)^{2} /n} }} $$
(1)

where x i denotes the observed value of a single variable X at location i, \( \bar{x} \) is the average of the x i over n locations, and w ij is the spatial weight between two locations i and j. In the matrix form of the right side of Eq. 1, all weights are stored within the spatial weight matrix W(n, n). Usually, this matrix may be in a row-standardized form, which means that all weights in a row will sum up to 1. If the weight matrix is used without row-standardization, this does not change the degree of spatial autocorrelation. In fact, to compensate for the effect of the non-row-standardization form, the term \( \frac{n}{{\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {w_{ij} } } }} \) in Moran’s I expression will not be equal to 1 as it is when each row sums to 1.

It should be noted that Moran’s I computes the dependence among values of a single variable, which are weighted according to their locations respective to each other. It therefore differs from the Pearson product moment correlation coefficient, which measures the relation between two variables without weight parameters. In precipitation context, the single variable X used in Moran’s I (Eq. 1) represents the values of the precipitation processes observed at the set of stations on a given day as:

$$ X = \left[ {x_{1} ,...,\,x_{n} } \right] $$
(2)

According to the precipitation process to be generated, the x i may be either the occurrence state at location i or the precipitation amount. For the occurrence process, the value 0 is assigned to the dry state and 1 to the wet state considered as the state of at least 0.254 mm of precipitation amount.

Moran’s I has an expected value of (−1/(n − 1)) (Moran 1950; Cliff and Ord 1981), and can vary between −1 and 1 (Griffith 2003). When neighbouring values of a sequenced variable tend to be similar, the resulting Moran’s I will be larger than −1/(n − 1)), and the spatial autocorrelation is said to be positive. When neighbouring values tend to be dissimilar, the resulting Moran’s I will be smaller than (−1/(n − 1)), and the spatial autocorrelation is said to be negative. When these values are independent over space, the Moran’s I will be equal to (−1/(n − 1)).

The spatial weight matrix is an important concept in the analysis of spatial autocorrelation. The matrix has zero diagonal elements because w ii  = 0 by convention, and there are no restrictions on the off-diagonal elements. A wide range of suggestions have been proposed in the literature for specifying spatial weights (Odland 1988; Ullah and Giles 1991; Anselin 1980; Murdoch et al. 1993). An appropriate spatial weighting function can be selected which assigns weights to each pair of locations. The value of the spatial autocorrelation depends on the selected weight matrix and on the observed data. The weight matrix may not only be derived from the geographical information, but also from other information describing the relation between locations (Odland 1988). Khalili et al. (2007), in their multi-site generation approach of daily precipitation data, took advantage of this flexibility in defining the spatial weight between each pair of stations to reproduce not only the observed daily spatial autocorrelations over the watershed, but also the monthly interstation correlations.

3 Multi-site generation approach of daily precipitation data

The multi-site generation approach of daily precipitation data (Khalili et al. 2007) uses a spatial moving average process to generate spatially autocorrelated random numbers, whose spatial autocorrelations can reproduce the observed daily spatial autocorrelations in the synthetic time series of precipitation occurrences and amounts. Spatially autocorrelated random numbers are used in the Richardson weather generator to simulate the precipitation occurrences using the first-order Markov chain model.

Another set of spatially autocorrelated random numbers was used to simulate the synthetic precipitation amounts by inverting the simple exponential cumulative distribution function. However, to reproduce adequate spatial intermittence, it appears important to think about the relationship between the precipitation amounts at a given station and the occurrence states over the watershed before setting out to model the precipitation amounts. This obviously highlights the potential of employing spatial autocorrelation to investigate the spatial interaction between the occurrence processes over the watershed.

Data from the Peribonca River Basin watershed is used to carry out investigations to that effect. As anticipated, relationship is found between the Moran values for occurrence processes and the mean of precipitation amounts at each station and month. Consequently, the simple exponential distribution will be used, but with the rate parameter, which represents the inverse of the precipitation mean, derived from these relationships. Regression functions can be used to determine the mean of precipitation amounts according to the spatial autocorrelation of the occurrence processes computed over the watershed. In doing so, the resulting simple exponential distribution will be called a spatial exponential distribution, in order to indicate that the mean of this distribution is defined according to the spatial dependence of the occurrence states at the set of stations.

Furthermore, it may be interesting to suggest another structure of spatial dependence by allowing the Moran’s I to be computed without removing the average as:

$$ {\text{SDI}} = \frac{{{{\sum\nolimits_{i = 1}^{n} {x_{i} \sum\nolimits_{j = 1}^{n} {w_{ij} x_{j} } } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {x_{i} \sum\nolimits_{j = 1}^{n} {w_{ij} x_{j} } } } {\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {w_{ij} } } }}} \right. \kern-\nulldelimiterspace} {\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {w_{ij} } } }}}}{{\sum\nolimits_{i = 1}^{n} {x_{i}^{2} /n} }} $$
(3)

This formula, which provides positive and higher values, appears to offer a more significant correlation between the mean of precipitation amounts and the spatial dependence of occurrence states. This spatial structure can be called a spatial dependence indicator (SDI), in order to differentiate it from the Moran’s I. Of course, this latter is more appropriate for computing the spatial autocorrelation because it is designed with the measure of covariance. While this condition is logically required for the statistical testing, the multi-site generation approach can be carried out regardless of the data form. One could opt for the formula which deals properly with his objective.

Thus, to simulate the synthetic precipitation amounts, the multi-site weather generator will use a set of uniform [0, 1] random numbers v t (k), which are spatially autocorrelated, as presented in Khalili et al. (2007), and the spatial exponential cumulative distribution function. The synthetic precipitation amount is thus generated by inversion, such that:

$$ F\left[ {r_{t} \left( k \right)} \right] = 1 - \exp \;\left( { - \lambda_{t} \left( k \right)\;r_{t} \left( k \right)} \right) $$
(4)

and

$$ r_{t} \left( k \right) = - \ln \left( {1 - v_{t} \left( k \right)} \right)/\lambda_{t} (k) $$
(5)

where F is the spatial exponential cumulative distribution function.

r t (k) is the synthetic precipitation amount at site k on day t.

λ t (k) is the inverse of the precipitation mean at site k on day t defined using the regression function established for the given month, and according to the spatial dependence computed for the occurrence values at the set of stations on day t.

4 Multi-site generation approach of daily temperature and solar radiation data

To simulate daily maximum temperature, minimum temperature and solar radiation data, Richardson (1981) proposed a weakly stationary generating process (Matalas 1967).

$$ \chi_{p,k} (j) = A{{\upchi}}_{p,k - 1} (j) + B\varepsilon_{p,k} (j) $$
(6)

where χ p,k (j) and χ p,k−1(j) are matrices (3,1) of maximum temperature (j = 1), minimum temperature (j = 2) and solar radiation (j = 3) residuals for days k and k − 1 of year p. Note that these residuals are the deviations of temperatures and solar radiation from the appropriate wet or dry mean \( \bar{X}_{k} \left( j \right), \) normalized by the appropriate wet or dry standard deviation σ k (j).

$$ {{\upchi}}_{p,k} \left( j \right) = \frac{{X_{p,k} \left( j \right) - \bar{X}_{k} \left( j \right)}}{{\sigma_{k} \left( j \right)}} $$
(7)

ɛ p,k (j) is matrix (3,1) of independent standard normal random numbers N[0,1] for day k of year p.

A and B are matrices (3,3) whose elements are defined from lag 0 and lag 1 serial and cross-correlation coefficient matrices of observed residuals.

$$ A = M_{1} \;M_{0}^{ - 1} $$
(8)
$$ BB^{T} = M_{0} - M_{1} M_{0}^{ - 1} M_{1}^{T} $$
(9)

where M 0 and M 1 are matrices of lag 0 and lag 1 serial and cross-correlations, respectively such that:

$$ M_{0} = \left[ {\begin{array}{*{20}c} 1 & {\rho_{{x_{T\max ,0} \;x_{T\min ,0} }} } & {\rho_{{x_{T\max ,0} \;x_{{{\text{Sr}},0}} }} } \\ {\rho_{{{{\upchi}}_{T\min ,0\;} {{\upchi}}_{T\max ,0} }} } & 1 & {\rho_{{{{\upchi}}_{T\min ,0\;} {{\upchi}}_{{{\text{Sr}},0}} }} } \\ {\rho_{{x_{{{\text{Sr}},0}} \;x_{T\max ,0} }} } & {\rho_{{x_{{{\text{Sr}},0}} \;x_{T\min ,0} }} } & 1 \\ \end{array} } \right] $$
(10)
$$ M_{1} = \left[ {\begin{array}{*{20}c} {\rho_{{{{\upchi}}_{T\max ,0} \;{{\upchi}}_{T\max , - 1\;} }} } & {\rho_{{{{\upchi}}_{T\max ,0} \;{{\upchi}}_{T\min , - 1\;} }} } & {\rho_{{{{\upchi}}_{T\max ,0} \;{{\upchi}}_{{{\text{Sr}}, - 1\;}} }} } \\ {\rho_{{{{\upchi}}_{T\min ,0\;} {{\upchi}}_{T\max , - 1} }} } & {\rho_{{{{\upchi}}_{T\min ,0\;} {{\upchi}}_{T\min , - 1} }} } & {\rho_{{{{\upchi}}_{T\min ,0\;} {{\upchi}}_{{{\text{Sr}}, - 1}} }} } \\ {\rho_{{{{\upchi}}_{{{\text{Sr}},0\;}} {{\upchi}}_{T\max , - 1} }} } & {\rho_{{{{\upchi}}_{{{\text{Sr}},0\;}} {{\upchi}}_{T\min , - 1} }} } & {\rho_{{{{\upchi}}_{{{\text{Sr}},0\;}} {{\upchi}}_{{{\text{Sr}}, - 1}} }} } \\ \end{array} } \right] $$
(11)

where \( \rho_{{{{\upchi}}_{i,0} \;{{\upchi}}_{j,0\;} }} \) is the lag 0 cross-correlation coefficient between the residuals of variable i and the residuals of variable j.

\( \rho_{{{{\upchi}}_{i,0} \;{{\upchi}}_{j,\, - 1} }} \)is the lag 1 cross-correlation coefficient between the current residuals of variable i and the previous residuals of variable j.

\( \rho_{{{{\upchi}}_{i,0} \;{{\upchi}}_{i, - 1} }} \) is the lag 1 serial correlation of variable i.

The Cholesky factorization technique can be used to obtain the B matrix.

Daily maximum temperature, minimum temperature and solar radiation are then found by multiplying the simulated daily residuals by the appropriate wet or dry standard deviation and adding the appropriate wet or dry mean. This of course means that the computation of daily means and standard deviations is conditional on the wet or dry state of the day, with the state determined by the simulated occurrence process on that day.

The multi-site generation approach of daily temperature and solar radiation data can be carried out using spatially autocorrelated standard normal random numbers in the weakly stationary generating process (Eq. 6). The spatial autocorrelations of these numbers are defined such as to allow the synthetic time series to exhibit the same daily spatial autocorrelations as those observed. Note that the observed daily spatial autocorrelations to be reproduced are the averages of daily spatial autocorrelations observed between the selected weather stations over their shared recording years. As for precipitation data, this approach focuses on the spatial autocorrelation over the watershed, but the interstation correlations of weather data should be automatically reproduced for each pair of stations and month. The Moran’s I will serve to compute the spatial autocorrelation. The next section illustrates how to generate spatially autocorrelated random numbers.

4.1 Spatially autocorrelated random numbers model

The multi-site generation of daily temperature and solar radiation data involves the spatial moving average process (Cliff and Ord 1981; Cressie 1993) for generating spatially autocorrelated random numbers such that:

$$ V_{T{\rm max} } = \gamma_{T{\rm max} } \times W \times u_{T{\rm max} } + u_{T{\rm max} } $$
(12)
$$ V_{T{\rm min} } = \gamma_{T{\rm min} } \times W \times u_{T{\rm min} } + u_{T{\rm min} } $$
(13)
$$ V_{\text{Sr}} = \gamma_{\text{Sr}} \times W \times u_{\text{Sr}} + u_{\text{Sr}} $$
(14)

where V Tmax(n,1), V Tmin(n,1) and V Sr(n,1) are vectors of n spatially autocorrelated random numbers to generate the maximum temperature, the minimum temperature and the solar radiation processes, respectively at the n locations. W(n,n) is a weight matrix.

γ Tmax, γ Tmin and γ Sr are the moving average coefficients to be used for the maximum temperature, the minimum temperature and the solar radiation processes, respectively. The extreme eigenvalues of the weight matrix establish the range of these coefficients, which is \( \left] {\frac{ - 1}{{w_{\max } }};\frac{ - 1}{{w_{\min } }}} \right[, \) where w max is the maximum positive eigenvalue and w min is the largest negative eigenvalue in absolute value.

u Tmax(n,1), u Tmin(n,1) and u Sr(n,1) are vectors of n independent and normally distributed random numbers to be used for the maximum temperature, the minimum temperature and the solar radiation processes, respectively.

The multi-site approach involves the spatial moving average model because it consists of a simple computation that does not require weight matrix operations. Thus, the multi-site approach remains straightforward for a large data set.

4.2 Multi-site temperature and solar radiation model

The multi-site generation approach of daily temperature and solar radiation data aims at using the weakly stationary generating process (Eq. 6) with a vector ɛ p,k (j) containing spatially autocorrelated standard normal random numbers generated by the three earlier spatial moving average processes (Eqs. 12, 13, 14). For example, to generate the daily temperature and solar radiation data at a 3rd station, the 3rd component from V Tmax, the 3rd component from V Tmin and the 3rd component from V Sr will respectively compose the vector ɛ p,k (j) used in the multi-site model such that:

$$ \chi_{p,k} (j) = A\;\chi_{p,k - 1} (j) + B\;\left( {\begin{array}{*{20}c} {V_{T{\rm max }} \left( {3,1} \right)} \\ {V_{T{\rm min} } \left( {3,1} \right)} \\ {V_{\text{Sr}} \left( {3,1} \right)} \\ \end{array} } \right) $$
(15)

Note that the three components V Tmax(3,1), V Tmin(3,1) and V Sr(3,1) are independent, but each is spatially autocorrelated with the remaining n-1 components of the same vector type, V Tmax, V Tmin or V Sr, respectively, which will be used for the remaining stations. Also, these components are normally distributed because u Tmax(3,1), u Tmin(3,1) and u Sr(3,1) are chosen to be normally distributed. However, a mean and variance normalization of V Tmax(3,1), V Tmin(3,1) and V Sr(3,1) is needed to obtain a mean of zero and a variance of unity required for the weakly stationary generating process. This operation does not affect the spatial autocorrelations of these random numbers. Thus, all the conditions sought by the weakly stationary generating process regarding ɛ p,k (j) are satisfied.

As shown by the multi-site model, the weakly stationary generating process is used as in Richardson (1981) model without any further changes. The regionalization of this model is thus conducted only through the spatial autocorrelation of the random numbers. Spatial autocorrelation is therefore the crucial issue at stake here. In fact, for a given weight matrix, and for different values of the moving average coefficients γ Tmax, γ Tmin and γ Sr, the spatial moving average processes can provide spatially autocorrelated random numbers with different degrees of spatial autocorrelation. It is thus worth asking which values of γ Tmax, γ Tmin and γ Sr should be used in the spatial moving average processes to reproduce the observed spatial autocorrelations in the synthetic daily temperature and solar radiation data.

4.3 Moving average coefficients estimation

Obtaining suitable values of γ Tmax, γ Tmin and γ Sr is realized in the same manner as with precipitation data (Khalili et al. 2007). In fact, using different values of these coefficients from their range defined above, one can obtain via the three spatial moving average processes (Eqs. 12, 13, 14) spatially autocorrelated random numbers, which exhibit different spatial autocorrelation values noted I V,Tmax, I V,Tmin and I V,Sr. These notations mean the spatial autocorrelations computed by the Moran’s I (Eq. 1) for V Tmax, V Tmin and V Sr intended for the generation of maximum temperature, minimum temperature and solar radiation, respectively. When these random numbers are integrated into the weakly stationary generating process model, the latter generates synthetic time series that also have different spatial autocorrelations, noted I Tmax, I Tmin and I Sr.

This operation results in three relationships. The first is between the coefficients γ Tmax and the resulting spatial autocorrelations I Tmax for the synthetic maximum temperature data. The second is between the coefficients γ Tmin and the resulting spatial autocorrelations I Tmin for the synthetic minimum temperature data, and the third relationship is assumed to be established between the coefficients γ Sr and the resulting spatial autocorrelations I Sr for the synthetic solar radiation data. These relationships (I Tmax, γ Tmax), (I Tmin, γ Tmin) and (I Sr, γ Sr) can be established monthly and used to extract the γ Tmax, γ Tmin and γ Sr values linked to the observed I Tmax, I Tmin and I Sr, respectively.

The spatial moving average processes will then be reused with the appropriate γ Tmax, γ Tmin and γ Sr values to provide the spatially autocorrelated random numbers that allow the reproduction of the observed I Tmax, I Tmin and I Sr in the synthetic temperature and solar radiation time series.

Figure 1 recapitulates the proposed multi-site generation approach of daily temperature and solar radiation data. The parameter estimation and the generation phases are presented for a given month. Var can be Tmax, Tmin or Sr. m is the total number of γ Tmax, γ Tmin or γ Sr values taken from their range, and l is the total number of days in a given month. However, because solar radiation data are not available for the used watershed, the multi-site model is used only for maximum and minimum temperature. The results presented are for a 50-year simulation period.

Fig. 1
figure 1

Flow chart for the proposed multi-site generation approach, Var can be Tmax, Tmin or Sr

Full size image

5 Results and discussion

5.1 Results of spatial intermittence approach

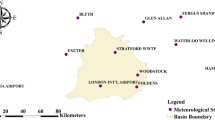
The multi-site generation approach of daily precipitation data (Khalili et al. 2007) was tested with data from the Chute du Diable sub-basin of the Peribonca River Basin (Fig. 2). This region, which is characterized by a wet climate, relatively cool summers and snow precipitations from November to April, is also used in this paper. Seven stations in this watershed are selected: Peribonca, Hemon, Bonnard, Chute-du-Diable, Chute-des-Passes, St-Léon-de-Labrecque and Normandin CDA. The location of these stations is provided in Fig. 2 and in Table 1.

Fig. 2
figure 2

The Chute du diable sub-basin of the Peribonca river basin, showing the location of meteorological stations

Full size image
Table 1 Location and recorded years of the used stations
Full size table

As previously indicated, the precipitation amounts at each station should be simulated, while taking into account the occurrence spatial dependence over the watershed. To realize this method, one-first needs to select a spatial weight matrix, which represents the relation between each pair of stations. In this respect, the inverse square distance method is used to represent the distance relations among the weather stations, but other spatial weighting functions not limited to geographical information may be used. The resulting weight matrix is:

$$ W = \left[ {\begin{array}{*{20}c} 0 & {0.0980} & {0.0053} & {0.4972} & {0.0154} & {0.1963} & {0.1879} \\ {0.1426} & 0 & {0.0087} & {0.0745} & {0.0226} & {0.0511} & {0.7006} \\ {0.0956} & {0.1082} & 0 & {0.0997} & {0.5103} & {0.0946} & {0.0916} \\ {0.2707} & {0.0279} & {0.0030} & 0 & {0.0094} & {0.6494} & {0.0396} \\ {0.1462} & {0.1475} & {0.2677} & {0.1646} & 0 & {0.1523} & {0.1217} \\ {0.1314} & {0.0235} & {0.0035} & {0.7986} & {0.0107} & 0 & {0.0321} \\ {0.2325} & {0.5960} & {0.0063} & {0.0901} & {0.0158} & {0.0594} & 0 \\ \end{array} } \right] $$
(16)

The first row contains the spatial weights between the Peribonca station and the other stations in the order given above. The second row presents the spatial weights between the Hemon station and the remaining stations, and so on. Note that the spatial weight between each station and itself is 0 by convention, and that the matrix is row-standardized.

Using the spatial dependence indicator (SDI) discussed earlier, the spatial dependence of precipitation occurrences was computed using the shared period for all stations, which is 14 years starting from 1963 to 1976. Relationships are then obtained between the mean of precipitation amounts and the SDI values for each station and month. Figure 3 shows an example of such a relationship obtained for the Peribonca station in September. An exponential regression fit is used to evaluate the mean of precipitation amounts according to the spatial dependence of occurrence values because it gives a best fit to the scatter plot.

Fig. 3
figure 3

Relationship between the mean of precipitation amounts (mm) of Peribonca station and the spatial dependence values of occurrences over the watershed in September

Full size image

As was introduced by Wilks (1998), the statistic “continuity ratio” is used to test the accuracy of the spatial intermittence in the synthetic precipitation time series. This statistic is computed for each pair of station (i,j), and is the ratio of the mean of the nonzero precipitation amounts at station i when station j is dry, to the mean of the nonzero precipitation amounts at station i when station j is wet, such that:

$$ {\text{Continuity}}\;{\text{ratio}} = \frac{{E\left[ {r_{t} \left( i \right)|r_{t} \left( i \right) > 0,\;r_{t} \left( j \right) = 0} \right]}}{{E\left[ {r_{t} \left( i \right)|r_{t} \left( i \right) > 0,\;r_{t} \left( j \right) > 0} \right]}} $$
(17)

Figure 4a and b illustrate the spatial intermittence results using the simple exponential function (a) and the spatial exponential functions (b) to fit the precipitation amounts. The use of the spatial exponential functions greatly improves the results, and confirms the dependence of the precipitation means at a given station on the occurrence states at the set of stations. Each point in this graph represents the continuity ratio for each pair of stations and month. 504 points are therefore plotted in this graph. The departure from the 45-degree reference line can be attributed to the scatter plot obtained in certain relationships between the mean of precipitation amounts and the SDI values of the occurrences due to sampling variations related to the small sample size (14 years).

Fig. 4
figure 4

Spatial intermittence using the simple exponential function (a) and the spatial exponential functions (b)

Full size image

5.2 Results of multi-site generation approach of daily temperature data

As was the case for the precipitation processes (Khalili et al. 2007), the multi-site generation approach of daily temperature data was achieved using different weight matrices. In a first step, the results for the row-standardized weight matrix using the inverse square distance method, presented above, are reported.

Using this weight matrix, the variation range of the moving average coefficients γ Tmax and γ Tmin is ]−1;1.3254[, according to the extreme eigenvalues of this matrix. Therefore, taking values from this range, the synthetic temperature data exhibit spatial autocorrelations I Tmax and I Tmin, which are linked to these moving average coefficient values. Figure 5 shows such a relationship for the maximum temperature in July. Similar curves are obtained for the other months as well as for the minimum temperature. Because the third-order polynomial functions produce the best fit to the data set, they may be chosen to describe these relationships. Once the γ Tmax and γ Tmin values linked to all the observed I Tmax and I Tmin are found for each month, the spatial moving average processes are reused as is the multi-site temperature model, to generate synthetic time series with the required values for daily spatial autocorrelations.

Fig. 5
figure 5

Relationship between the moving average coefficients γ Tmax and the spatial autocorrelations I Tmax for maximum temperature data in July

Full size image

Figure 6a and b illustrate the observed and simulated daily spatial autocorrelations of maximum and minimum temperature, respectively. The observed ones are averaged over the shared recorded period between the seven stations, which is 14 years, while the simulated ones are averaged over the 50-year simulation period. While the daily spatial autocorrelations are adequately reproduced, the monthly interstation correlations are underestimated, as shown in Fig. 7a and b. These monthly pairwise correlations are assumed to be reproduced in the synthetic daily temperature data automatically via the reproduction of daily spatial autocorrelations.

Fig. 6
figure 6

Observed and simulated daily spatial autocorrelations of maximum temperature (a) and minimum temperature (b)

Full size image
Fig. 7
figure 7

Observed versus simulated interstation correlations of daily maximum temperature (a) and minimum temperature (b) between each pair of the seven stations and month

Full size image

This problem occurred because the used weight matrix is based on the inverse square distance method. Such a distance criterion can result in spatial weights, which are practically null. Therefore, a loss of correlation will be observed between the corresponding pair of stations, which are actually correlated. It is thus very important to not mechanically use the distance criterion methods to model the weight matrix, but rather, to select an appropriate function that adequately describes the dependence between each pair of stations, particularly for this multi-site approach, which must satisfy the interaction over the watershed.

Khalili et al. (2007) returned to this issue in the multi-site generation approach of daily precipitation data, and they mitigated the problem using monthly weight matrices modeled with monthly interstation correlations of daily precipitation data. This paper pursues the same idea for temperature data, and another analysis is realized using monthly weight matrices expressed through the monthly interstation correlations of daily temperature data.

However, the analyses conducted for this study using the Moran’s I reveal a particular behaviour of this statistic when georeferenced data are practically similar or close to their average. In fact, the Moran’s I measures the spatial autocovariance of neighbouring values composing a single sequenced variable. Thus, if all values are close to their average, the resulting Moran’s I will be equal to its expected value (−1/(n − 1)). This does not of course mean that the values are independent over space, but rather, it is a consequence of the similarity of the values with their average. This behaviour can occur here when the n values t of the daily maximum or minimum temperature observed at the n stations are practically close to their average. Therefore, the Moran’s I of a variable T containing the n daily temperature values such that:

$$ T = [t(1) \ldots t(n)] $$
(18)

will be almost at its expected value.

However, this issue should not be regarded as a problem. On the contrary, because in this case, the values of spatial autocorrelation are approximately equal to the Moran’s I expectation, one does not need to establish the monthly relationships between the moving average coefficients and the spatial autocorrelations of both maximum and minimum temperatures to reproduce the observed daily spatial autocorrelations. One can simply use the spatial moving average processes with γ Tmax and γ Tmin of unity or equal to the mean over their range.

Using the monthly weight matrices, adequate interstation correlations were computed for the synthetic daily temperature data for each pair of stations and month, as shown in Fig. 8a and b. The observed ones are calculated over the shared recorded period between each pair of stations, while the simulated ones are calculated over the 50-year simulation period. Figure 9a and b illustrate the observed versus simulated monthly means of daily maximum and minimum temperature, respectively, for each station. It would appear that the multi-site generation approach adequately reproduces these statistics.

Fig. 8
figure 8

Observed versus simulated interstation correlations of daily maximum temperature (a) and minimum temperature (b) between each pair of the seven stations and month using the monthly weight matrices

Full size image
Fig. 9
figure 9

Observed versus simulated monthly means of daily maximum temperature (a) and minimum temperature (b)

Full size image

Because the seven stations are practically all close to each other, all the interstation correlations of daily temperature data are high. It is thus interesting to check whether the multi-site generation approach can reproduce different magnitudes of monthly pairwise correlations. Two other stations, Nitchequon and Shefferville, located north of the Peribonca watershed, are thus added to this analysis. Because these two stations are located far from the others, they are unlikely to be influenced by the same weather phenomena as the others, and the monthly correlations between them and the remaining stations are not as high. Figure 10a and b illustrate the observed and simulated interstation correlations of daily maximum and minimum temperature between each pair of the nine stations and month. It appears that the multi-site approach adequately reproduces different correlation values.

Fig. 10
figure 10

Observed versus simulated interstation correlations of daily maximum temperature (a) and minimum temperature (b) between each pair of the nine stations and month using the monthly weight matrices

Full size image

The multi-site generation approach is also applied using the SDI instead of Moran’s I. Figure 11a and b show the observed and simulated interstation correlations of daily maximum and minimum temperature between each pair of the nine stations and month. The results are generally satisfactory despite the overestimation of some correlations in the minimum temperature case. SDI values are also efficiently reproduced, as shown in Figure 12a and b.

Fig. 11
figure 11

Observed versus simulated interstation correlations of daily maximum temperature (a) and minimum temperature (b) between each pair of the nine stations and month using the monthly weight matrices and SDI

Full size image
Fig. 12
figure 12

Observed and simulated daily spatial dependence of maximum temperature (a) and minimum temperature (b) using the monthly weight matrices and SDI

Full size image

6 Conclusion

Multi-site generation approach has been proposed using spatial autocorrelation. This concept summarizes the spatial dependence over the entire watershed in a single statistic. The essence of this approach lies in the reproduction, in a single step, of the observed daily spatial autocorrelations and the observed monthly interstation correlations using appropriate spatial weight matrices. The basic idea is to use, in the weather generator, suitable spatially autocorrelated random numbers, which can reproduce these observed statistics.

This paper is an extension of the multi-site generation approach proposed by Khalili et al. (2007). The first issue was the improvement of the synthetic spatial intermittence. The feasible solution presented here involves the approximation of the mean of precipitation amounts used in the simple exponential function by a regression function of the occurrence spatial dependence at the set of weather stations. Such a method was proposed because the mean of precipitation amounts at a given station is not a free parameter, but rather, depends on the occurrence states over the watershed. Therefore, monthly spatial exponential functions were established for each station. This approach greatly improves the reproduction of synthetic spatial intermittence.

A multi-site generation approach of daily maximum temperature, minimum temperature and solar radiation data was also presented in this paper. This approach adopted the weakly stationary generating process used in the Richardson weather generator, with no modifications made to the model, but only random numbers have to be spatially autocorrelated. Spatial moving average processes were used to generate the spatially autocorrelated random numbers that can reproduce the observed daily spatial autocorrelations in the synthetic time series. Because of a lack of solar radiation data, the multi-site weakly stationary generating process was only tested for maximum and minimum temperature data. This approach has been shown to perform well in the generation of these data. Sufficiently accurate daily spatial autocorrelations and monthly interstation correlations were obtained in the synthetic time series.

Finally, results presented in this paper show the efficiency of the developed multi-site weather generator and its ease of implementation. The use of multi-site generated weather data is important to account for weather spatial dependence, which has a significant effect on various meteorology dependent projects, such as hydrological modelling and other environmental research.