Introduction

The World’s temperate mixed-species forests are mainly distributed in northeastern North America, Europe, and eastern Asia. The Asian temperate mixed forests are mostly located in Northeast China, covering Daxing’an, Xiaoxing’an and Changbai Mountains. These regions in China possess over 45 million hectares of forests and nearly 3.2 billion cubic meters of timber. In recent years, the quantity, distribution, and dynamics of forest carbon storage have received increasing attention in the research of global climate change and carbon cycles (Pacala et al. 2001; Malhi et al. 2002; Pan et al. 2011). Forest carbon stock is commonly calculated by multiplying forest biomass by carbon concentration rate. Therefore, accurately estimating tree and stand biomass is essential for investigating the effects of global climate change on forest carbon storage and cycling in ecosystems (Picard et al. 2012; Mu et al. 2013).

Tree-level biomass can be obtained via a destructive method, in which trees are actually felled, cut into sections, and weighed for each of the tree components (e.g., stems, branches, foliage, and roots). Obviously this method is very time consuming and costly. A common practice is to select a representative sample of a given species, and obtain tree biomass and other variables by the destructive method. Regression models are then developed relating tree biomass to tree diameter (D) or other easily measured tree variables. It has been proven that these biomass models of total and tree component biomass can provide accurate and reliable estimation for the biomass of forest ecosystems (Gower et al. 1999; Wang 2006). Although wood-specific gravity, tree crown, and tree age are considered as additional predictors in order to improve the accuracy of biomass equations, they are much more difficult to obtain in practice (Peri et al. 2010; Gargaglione et al. 2010; Cai et al. 2013). In contrast, tree height (H) can be measured relatively easily, and in fact the different tree heights at the same diameter obviously influence tree-level biomass equations (Peri et al. 2010). Studies show that adding tree height into biomass equations can significantly improve model fitting and performance (António et al. 2007; Zhou et al. 2007; Li and Zhao 2013).

To date, three forms of allometric biomass equations are commonly used in the literature, i.e., W = a·D b, W = a·(D 2·H)b, and W = a·D b·H c, where D and H are tree diameter and height, respectively; and a, b, and c are model coefficients (e.g., Carvalho and Parresol 2003; Wang 2006; Menendez-Miguelez et al. 2013). The studies of model comparison indicate that using the equation W = a·(D 2·H)b can improve model fitting and performance for total, aboveground, stem and root biomass, but not for branch, foliage and crown biomass, whereas the equation W = a·D b·H c is more flexible than other functions, and can generally improve model accuracy for total, sub-totals and component biomass (Bi et al. 2004; Battulga et al. 2013; Cai et al. 2013).

It is well known that an allometric equation assumes either an additive error structure (i.e., Y = a·X b + ε) or a multiplicative error structure (i.e., Y = a·X b·ε). If the additive error structure is assumed, nonlinear regression should be used to directly fit the power function to tree biomass data. If the multiplicative error structure is assumed, logarithmic transformation is usually applied to convert the nonlinear power function to a log-linear model. Over the last two decades, however, many modelers determine which error structure is appropriate to a given biomass data set based on their experience rather than a statistical analysis (Lai et al. 2013). To facilitate the objective determination on the model error structures, Bi et al. (2004) proposed to test the error structure of a power function by the ratio of the mean squared error (MSE) of the nonlinear model to that of the log-linear model. Xiao et al. (2011) and Ballantyne (2013) outlined an approach of likelihood analysis to evaluating and comparing model error structures, which was recently used for tree root biomass (Lai et al. 2013). Compared with the MSE ratio approach, the likelihood analysis is considered consistent with the core principles of statistics, and more suitable in determining the model error structures of biomass models (Ballantyne 2013).

When we have more than one tree components in the biomass data, the additivity property of models for estimating tree total, sub-total, and component biomass should be taken into account due to the inherent correlations among the biomass components measured on the same sample trees. Although this additivity property has been posed by several researchers (e.g., Kozak 1970; Cunia and Briggs 1984; Chiyenda and Kozak 1984), it is often ignored in many practices of biomass modeling. To ensure the additivity property, various model specification and parameter estimation methods have been proposed for linear models (e.g., Cunia and Briggs 1984; Chiyenda and Kozak 1984; Parresol 1999) and nonlinear models (e.g., Reed and Green 1985; Greene 1999; Tang et al. 2001; Tang and Wang 2002). Among these methods, seemly unrelated regression (SUR) and nonlinear seemly unrelated regression (NSUR) are more general and flexible (Parresol 2001; Li and Zhao 2013). SUR and NSUR allow that each component model may have its own independent variables and each model can use its own weighting function for heteroscedasticity, which results in a lower variance for the total tree biomass model (Parresol 2001). Thus, SUR and NSUR have become more popular as the parameter estimation methods for linear and nonlinear biomass equations (Bi et al. 2004, 2010; Brandeis et al. 2006; Návar 2009; Russell et al. 2009; Menendez-Miguelez et al. 2013; Li and Zhao 2013).

To date, hundreds of biomass equations have been developed for more than 100 species around the world (Jenkins et al. 2003; Zianis et al. 2005). However, there are few models published for tree root biomass due to the difficulty and costs of extracting tree roots in reality (Chave et al. 2005; Zianis 2008; Woodall et al. 2011; Alvarez et al. 2012; Cai et al. 2013; Li and Zhao 2013). Wang (2006) developed biomass equations for ten hardwood species in Northeast China, but his biomass data were collected from a limited forest region with a relatively small sample size for each species. In general, biomass equations for temperate forests across the forest regions of Northeast China have not been accurately quantified, or have not been established for some valuable species.

In this study, the biomass data included 472 trees that were harvested and measured for stem, root, branch, and foliage biomass from nine hardwood species in Northeast China. The objectives of this study were: (1) to examine the error structures of biomass equations by the likelihood analysis; (2) to construct two additive systems of biomass equations, one based on tree diameter (D) only and one based on both tree diameter (D) and height (H), using three constraints and seemingly unrelated regressions (SUR); (3) to evaluate the accuracy of biomass estimates, and (4) to investigate the sources of prediction errors for total and component biomass equations across the nine tree species.

Data and methods

Data

Study area description

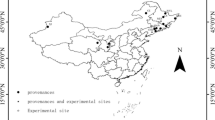
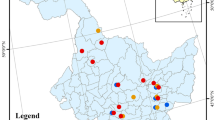
This study was conducted in Northeast China encompassing the Daxing’an Mountains (from 121°12′E to 127°00′E and from 50°10′N to 53°33′N), the Xiaoxing’an Mountains (from 127°42′E to 130°14′E and from 46°28′N to 49°21′N) and the Changbai Mountains (from 127°40′E to 128°16′E and from 41°35′N to 47°57′N), located in Heilongjiang Province and Jilin Province, P.R. China (Fig. 1). The elevation ranges from 300 to 700 m above the sea level in Daxing’an Mountains, from 600 to 1000 m in Xiaoxing’an Mountains, and from 800 to 1500 m in Changbai Mountains. The soils in the three regions are mostly Haplumbrepts or Eutroboralfs (or dark brown forest soil in Chinese Taxonomic System). The climate is continental monsoon climate. In Daxing’an Mountains, the mean annual rainfall ranges from 500 to 750 mm and mean annual temperature is from −1 to −2.8 °C; in Xiaoxing’an Mountains, the mean annual rainfall is from 550 to 670 mm and mean annual temperature is from −2 to 2 °C, and in Changbai Mountains, the mean annual rainfall is from 600 to 900 mm and mean annual temperature is from −7 to 3 °C.

Fig. 1
figure 1

The location of study area and plot distribution in Northeast, People’s Republic of China

Full size image

These temperate forests are dominated by White birch (Betula platyphylla), Amur linden (Tilia amurensis), Maple (Acer mono), Dahurian birch (Betula davuria), Mongolian oak (Quercus mongolica), Dahurian poplar (Populus davidiana), and mixed hardwood forest dominated by Amur linden (Tilia amurensis), Maple (Acer mono), Manchurian ash (Fraxinus manshurica), Manchurian walnut (Juglans mandshurica), Mongolian oak (Quercus mongolica) and Manchurian elm (Ulmus laciniata). The characteristics of these forest types are described in Table 1.

Table 1 Characteristics of forest types from which the sample trees were selected
Full size table

Tree biomass data

The data used in this study were selected from a large data set of tree biomass. The nine hardwood species included White birch (Betula platyphylla), Dahurian poplar (Populus davidiana), Mongolian oak (Quercus mongolica), Amur linden (Tilia amurensis), Dahurian birch (Betula davuria), Manchurian ash (Fraxinus manshurica), Manchurian walnut (Juglans mandshurica), Maple (Acer mono) and Manchurian elm (Ulmus laciniata) in secondary forests. A total of 78 plots were selected, 20 plots from Daxing’an Mountains, 28 from Xiaoxing’an Mountains, and 30 from Changbai Mountains (Fig. 1). Each plot was 30 × 30 m or 20 × 30 m in size. These sample plots were established in August of 2009, 2010, 2011 and 2012. A total of 472 trees for these nine natural hardwood species were sampled. Both White birch and Dahurian poplar trees were collected from all three regions, while the other trees were sampled from Xiaoxing’an Mountains and Changbai Mountains. The destructive sampling procedure was as follows: the stems of the sampled trees were cut at the ground and the total height (H), length of live crown, and diameter at breast height (D) were immediately measured and recorded. Then, the stems were cut into 1-m sections and each section was weighed and recorded. At the end of each stem section, a 2- to 3-cm-thick disc was cut, weighed, and taken to the laboratory for determining moisture content. The live crown (from the first dead branch to the base of the terminal bud) was equally marked into three layers (i.e., top, middle, and bottom). All live branches in each crown layer were cut and weighed, respectively. Then, in each crown layer 3–5 branches were cut and the branch and foliage were separated and weighed, respectively. The branches and foliage were then sampled (about 50–100 g), weighed and taken to the laboratory for moisture content determination. Due to the heavy workload and difficulty in root excavation, harvesting fine roots (<5 mm) was unrealistic (Wang 2006). In this study, the zone of excavating roots was approximately a 3-m radius circle, and the fine roots (<5 mm) were not included. So the results were slightly biased by this constraint. The roots of the sampled trees were divided into large roots (diameter ≥5 cm), medium roots (diameter 2–5 cm), and small roots (diameter <2 cm). Each root class was sampled (about 100–200 g), weighed, and taken to the laboratory for moisture content determination. All stem, branch, foliage, and root samples were oven-dried at 80 °C and weighed. The dry biomass of each component was calculated by multiplying the fresh weight of each component by the dry/fresh ratio of each component. For each sampled tree, the sum of branch dry biomass and foliage dry biomass yielded crown dry biomass. The sum of crown dry biomass and stem dry biomass gave aboveground biomass. The sum of aboveground dry biomass and root dry biomass produced total tree biomass.

In summary, a total of 472 trees for nine natural hardwood species were included in this study. Table 2 lists the descriptive statistics of tree diameter (cm), height (m), and total biomass (kg) for each species.

Table 2 Descriptive statistics of diameter at breast height (D), tree height (H), and total biomass (kg) for the nine species (N is sample size)
Full size table

Model specification

The primary results indicated that W = a·D b·H c significantly improved model fitting and performance from W = a·D b, while W = a·(D 2·H)b only marginally improved model fitting and performance. Therefore, the following allometric biomass equations were used to estimate the total, sub-total and component biomass W (in kg dry weight) of nine hardwood species from tree diameter (D, cm) and height (H, m) based on the literature (Bi et al. 2004; Balboa-Murias et al. 2006; Hosoda and Iehara 2010; Chan et al. 2013):

$$W = a \cdot D^{b}$$
(1)
$$W = a \cdot D^{b} \cdot H^{c} .$$
(2)

In this study, there were four tree components involved (e.g., stems, roots, branches, and foliage). If a biomass equation is fitted to each component separately, the inherent correlations among the biomass of tree components that were measured on the same sample trees are ignored. Consequently, the sum of biomass predictions from the separate models of tree components will not equal the biomass prediction from the total tree model, or aboveground model or crown model, i.e., the additivity property of biomass equations is not held. Therefore, we decided to use both Eqs. (1) and (2) as the basic models to construct the additive systems of biomass equations with three constraints (total = stems + branches + foliage + roots; aboveground = stems + branches + foliage; and crown = branches + foliage).

Further, there are two kinds of error structures (additive and multiplicative) for Eqs. (1) and (2). We used likelihood analysis to compare the appropriateness of the two error structures for each of the nine species, following the method of Xiao et al. (2011). For each species, we fitted the Eqs. (1) and (2) using nonlinear regression on the untransformed data (hereafter, NLR), and then using linear regression on the log-transformed data (hereafter, LR). The model parameters and σ 2 were estimated for each model. To select between two error structures, we calculated the value of the log-likelihood function (logL) for each model so that the Akaike Information Criterion (AICc) was computed as follows (Xiao et al. 2011):

$$AICc = 2k - 2\log L + \frac{{2k\left( {k + 1} \right)}}{N - k - 1}$$
(3)

where k is the number of parameters [k = 3 in Eq. (1) and k = 4 in Eq. (2)], and N is the sample size. The AICc for the NLR model is named AICcNLR and the AICc for the LR model is named AICcLR. If AICcNLR − AICcLR < −2, the assumption of additive error structure is favored and thus we proceeded with the results obtained from NLR. If AICcNLR − AICcLR > +2, the assumption of multiplicative error structure is favored and thus we proceeded with the results obtained from LR. If |AICcNLR − AICcLR| ≤ 2, neither model error structure is favored, then model averaging may be adopted. For most of our biomass equations of the nine tree species, the likelihood analyses of the error structures for Eqs (1) and (2) yielded lower AICc for the LR models compared to the NLR models. The ΔAICc values (i.e., AICcNLR − AICcLR) were much greater than 2 (Appendix Table 5). Thus, at least for our data, LR should be favored over NLR to fit both Eqs (1) and (2).

Let W t , W a , W r , W s , W b , W f , and W c represent the total biomass, aboveground biomass, root biomass, stem biomass, branch biomass, foliage biomass, and crown biomass in kg, respectively. Two additive systems of seven equations with cross-equation constraints on the structural parameters and cross-equation error correlation for four tree biomass components, sub-total (aboveground and crown) biomass, and total biomass are as follows:

(1) The additive system of log-transformed equations with three constraints based on the multiplicative error structure of Eq. (1) (\(W = a \cdot D^{b}\)) is specified as follows:

$$\begin{aligned} \ln W_{r} &= \ln \left( {a_{11} } \right) + b_{12} \cdot \ln D + \varepsilon_{r} = a_{11}^{*} + b_{12}^{*} \cdot \ln D + \varepsilon_{r} \hfill \\ \ln W_{s} &= \ln \left( {a_{21} } \right) + b_{22} \cdot \ln D + \varepsilon_{s} = a_{21}^{*} + b_{22}^{*} \cdot \ln D + \varepsilon_{s} \hfill \\ \ln W_{b} &= \ln \left( {a_{31} } \right) + b_{32} \cdot \ln D + \varepsilon_{b} = a_{31}^{*} + b_{32}^{*} \cdot \ln D + \varepsilon_{b} \hfill \\ \ln W_{f} &= \ln \left( {a_{41} } \right) + b_{42} \cdot \ln D + \varepsilon_{f} = a_{41}^{*} + b_{42}^{*} \cdot \ln D + \varepsilon_{f} \hfill \\ \ln W_{c} &= \ln \left( {W_{b} + W_{f} } \right) + \varepsilon_{c} = \ln \left( {a_{31} \cdot D^{{b_{32} }} + a_{41} \cdot D^{{b_{42} }} } \right) + \varepsilon_{c} \hfill \\ \ln W_{a} &= \ln \left( {W_{s} + W_{b} + W_{f} } \right) + \varepsilon_{a} = \ln \left( {a_{21} \cdot D^{{b_{22} }} + a_{31} \cdot D^{{b_{32} }} + a_{41} \cdot D^{{b_{42} }} } \right) + \varepsilon_{a} \hfill \\ \ln W_{t} &= \ln \left( {W_{r} + W_{s} + W_{b} + W_{f} } \right) + \varepsilon_{t} = \ln \left( {a_{11} \cdot D^{{b_{12} }} + a_{21} \cdot D^{{b_{22} }} + a_{31} \cdot D^{{b_{32} }} + a_{41} \cdot D^{{b_{42} }} } \right) + \varepsilon_{t} , \hfill \\ \end{aligned}$$
(4)

where ln denotes the natural logarithm, a ij and b ij are the regression coefficients, and ε i is the model error term.

(2) Based on the multiplicative error structure of Eq. (2) (\(W = a \cdot D^{b} \cdot H^{c}\)), the following model specification was adopted for the nine species with the additional predictor H:

$$\begin{aligned} \ln W_{r} &= a_{11}^{*} + b_{12}^{*} \cdot \ln D + c_{13}^{*} \cdot \ln H + \varepsilon_{r} \hfill \\ \ln W_{s} &= a_{21}^{*} + b_{22}^{*} \cdot \ln D + c_{23}^{*} \cdot \ln H + \varepsilon_{s} \hfill \\ \ln W_{b} &= a_{31}^{*} + b_{32}^{*} \cdot \ln D + c_{33}^{*} \cdot \ln H + \varepsilon_{b} \hfill \\ \ln W_{f} &= a_{41}^{*} + b_{42}^{*} \cdot \ln D + c_{43}^{*} \cdot \ln H + \varepsilon_{f} \hfill \\ \ln W_{c} &= \ln \left( {a_{31} \cdot D^{{b_{32} }} \cdot H^{{c_{33} }} + a_{41} \cdot D^{{b_{42} }} \cdot H^{{c_{43} }} } \right) + \varepsilon_{c} \hfill \\ \ln W_{a} &= \ln \left( {a_{21} \cdot D^{{b_{22} }} \cdot H^{{c_{23} }} + a_{31} \cdot D^{{b_{32} }} \cdot H^{{c_{33} }} + a_{41} \cdot D^{{b_{42} }} \cdot H^{{c_{43} }} } \right) + \varepsilon_{a} \hfill \\ \ln W_{t} &= \ln \left( {a_{11} \cdot D^{{b_{12} }} \cdot H^{{c_{13} }} + a_{21} \cdot D^{{b_{22} }} \cdot H^{{c_{23} }} + a_{31} \cdot D^{{b_{32} }} \cdot H^{{c_{33} }} + a_{41} \cdot D^{{b_{42} }} \cdot H^{{c_{43} }} } \right) + \varepsilon_{t} . \hfill \\ \end{aligned}$$
(5)

To ensure the additivity or compatibility property among tree component equations, the seemingly unrelated regressions (SUR) in the SAS/ETS Model Procedure (SAS Institute, Inc. 2011) were used to fit the above two systems of biomass equations for each species, in which the coefficients of the tree component biomass models were simultaneously estimated (Bi et al. 2004; Balboa-Murias et al. 2006; Li and Zhao 2013).

Model evaluation

In this study, the additive systems of biomass equations were fitted to the entire data set (sample size N). The model validation was accomplished by a jackknifing technique, in which a biomass model was built using all-but-one observation (sample size N − 1) and then the fitted model was used to predict the value of the dependent variable for the held-out observation (Quint and Dech 2010; Li and Zhao 2013). The model fitting was assessed by three goodness-of-fit statistics [Eqs. (6)–(8)], and the model performance was evaluated by three model validation statistics of jackknifing [Eqs. (9)–(11)] as follows:

$${\text{Coefficient of determination}}{\kern 1pt} \;R^{2} = 1 - \frac{{\sum\limits_{i = 1}^{N} {(\ln W_{i} - \ln \widehat{W}_{i} )^{2} } }}{{\sum\limits_{i = 1}^{N} {(\ln W_{i} - \ln \overline{W} )^{2} } }}$$
(6)
$${\text{Adjusted coefficient of determination}}\;R_{a}^{2} = 1 - \left( {1 - R^{2} } \right)\left( {\frac{N - 1}{N - k}} \right)$$
(7)
$${\text{Root mean squared error}}\;{\text{RMSE}} = \sqrt {\text{MSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^{N} {(\ln W_{i} - \ln \widehat{W}_{i} } )^{2} }}{N - k}}$$
(8)
$${\text{Jackknifing residual}}\;e_{i, - i} = \left( {\ln W_{i} - \ln \widehat{W}_{i, - i} } \right)$$
(9)
$${\text{Mean absolute bias}}\;{\text{MAB}} = \frac{{\sum\limits_{i = 1}^{N} {\left| {e_{i, - i} } \right|} }}{N}$$
(10)
$${\text{Mean absolute percent bias}}\;{\text{MAB}}\% = \frac{{\sum\limits_{i = 1}^{N} {\left( {\frac{{\left| {e_{i, - i} } \right|}}{{\ln W_{i} }}} \right) \times 100} }}{N},$$
(11)

where \(\ln W_{i}\) is the ith observed log-transformed biomass value, \(\ln \widehat{W}_{i}\) is the ith predicted log-transformed biomass value from the model which was fitted using the entire data (sample size N), \(\ln \, \overline{W}\) is the mean of log-transformed biomass value, \(\ln \widehat{W}_{i, - i}\) is the predicted value of the ith observed value by the fitted model which was fitted by (N − 1) observations without the use of the ith observation, and k is the number of model parameters.

Results

Model fitting for two additive systems of biomass equations

For the nine natural hardwood species, two additive systems of log-transformed biomass equations [Eqs. (4), (5)] were fitted to the biomass data by the SUR method. The estimated coefficients of two systems with D only or both D and H as the predictor variables are shown in Table 3. As expected, there were some degrees of variation among the four components of biomass. For Eq. (4), the estimated slope coefficients of stem biomass, b *22 , were most stable, ranging from 2.3450 to 2.7104 with an average of 2.4856. The estimated slope coefficients for branch biomass, b *32 , were most variable, ranging from 2.0328 to 3.5220 with an average of 2.8165. Similarly, the estimated slope coefficients of stem biomass for Eq. (5), b *22 , were also stable, ranging from 1.6698 to 2.1479 with an average of 1.9549, whereas the most variable exponent coefficients were also found for branch biomass. The estimated coefficients, i.e., c *13 , c *23 , c *33 and c *43 , were relatively small and variable.

Table 3 Coefficient estimates of two additive systems of log-transformed biomass equations with three constraints, using the SUR estimation method
Full size table

Table 4 shows the goodness-of-fit statistic (i.e., adjusted coefficient of determination R 2 a ), and root mean squared error (RMSE) for each biomass equation. The results indicated that all equations in Eq. (4) with D only as the predictor variable fitted the biomass data well, with R 2 a >89 % and RMSE<0.4. Most of the total, aboveground, and stem biomass equations produced better model fitting (R 2 a >0.95 and RMSE <0.20), while the root equations had relatively smaller model R 2 a (<0.95) and larger RMSE (>0.20). Among the nine species, the additive system with D only for White birch (Betula platyphylla) had slightly higher R 2 a than those of other species (Table 4).

Table 4 Model fitting statistics of two additive systems of log-transformed biomass equations with three constraints
Full size table

In this study, the tree height (H) was also measured. Thus, both tree D and H were used to develop the second additive system of biomass equations [Eq. (5)]. In comparison with the model fitting of Eq. (4) (D only), the second additive system (D and H) had greater R 2 a and smaller RMSE for total, sub-total and component biomass (Table 4).

Model validation of two additive systems of biomass equations

Further, the model validation statistics [Eqs. (9)–(11)] were computed based on the jackknifing residuals for the two additive systems of biomass equations [Eqs. (4), (5)]. Figure 2 shows MAB and MAB % (representing the magnitude of prediction error) for the two additive systems across the nine species and biomass equations. For total biomass, except Manchurian ash (Fraxinus manshurica), the model prediction errors of the two systems were relatively small (MAB <0.15 and MAB % <5.0 %), and System 2 [Eq. (5)] seemed better than System 1 [Eq. (4)]. Similar results were found for aboveground and stem biomass (MAB <0.20 and MAB % <6 %), and System 2 performed better than System 1 (Fig. 2). On the other hand, the biomass equations for roots, branches, foliage, and crown had less accurate prediction (0.15 < MAB < 0.35 and 10 % < MAB % < 35 %), especially for roots compared to total, aboveground and stem. Adding H into the additive system of biomass equations improved model performance for most biomass equations of the nine hardwood species, especially for Manchurian ash (Fraxinus manshurica). However, this improvement was non-significant for some species [e.g., Mongolian oak (Quercus mongolica), Dahurian poplar (Populus davidiana), and Amur linden (Tilia amurensis)] (Fig. 2).

Fig. 2
figure 2

The mean absolute biases (MAB, left) and mean absolute percent biases (MAB %, right) in total, sub-total and component biomass of the log-transformed biomass equations for nine tree species. QM, Quercus mongolica; PD, Populus davidiana; TA, Tilia amurensis; BP, Betula platyphylla; FM, Fraxinus manshurica; JM, Juglans mandshurica; BD, Betula davuria; UL, Ulmus laciniata; AM, Acer mono

Full size image

Biomass partitioning

The partitioning of tree total biomass into tree components such as stems, branches, foliage and belowground or root biomass is shown in Fig. 3 for the nine natural hardwood species. Because the allocation of tree biomass depends strongly on tree diameters, the comparison of biomass allocation between species is valid and meaningful for trees of similar diameters (Ruiz-Peinado et al. 2012). The biomass partitioning in this study was done using the biomass models fitted for the diameters of 10 and 30 cm.

Fig. 3
figure 3

Biomass partitioning of aboveground and belowground components between nine hardwood species for a a diameter of 10 cm, and b a diameter of 30 cm. QM, Quercus mongolica; PD, Populus davidiana; TA, Tilia amurensis; BP, Betula platyphylla; FM, Fraxinus manshurica; JM, Juglans mandshurica; BD, Betula davuria; UL, Ulmus laciniata; AM, Acer mono

Full size image

For the diameter of 10 cm, the stem (with bark) was the largest biomass component for all nine hardwood species, and the roots were the second most important biomass component. The biomass partitioning was stems 62.0 % [52.8 % (JM)–76.8 % (PD)], branches 11.1 % [5.9 % (PD)–16.2 % (AM)], foliage 3.4 % [1.9 % (PD)–4.7 % (UL)], and roots 23.5 % [15.4 % (PD)–28.1 % (TA)]. The aboveground biomass (i.e., the sum of stems, branches and foliage) was about 76.5 % of the total biomass, while the belowground biomass (i.e., roots) was about 23.5 % of the total biomass (Fig. 3a).

For the diameter of 30 cm, the stem was again the largest biomass component for all nine hardwood species, and both roots and branches were important biomass components. The biomass partitioning was stems 62.8 % [55.9 % (QM)–72.0 % (TA)], branches 15.9 % [9.5 % (TA)–23.1 % (QM)], foliage 2.5 % [1.5 % (TA)–2.9 % (BP and JM)], and roots 18.8 % [14.8 % (PD)–24.1 % (AM)). The aboveground biomass was about 81.2 % of the total biomass, while the belowground biomass was about 18.8 % of the total biomass (Fig. 3b).

Discussion

The relationships between tree biomass and tree variables such as diameter and height are highly correlated exhibiting a power–law relationship. Usually, either W = a·D b or W = a·D b·H c can be used to model these allometric relationships. The power function using D as the only predictor is simple in equation form, easy to fit to biomass data, requires only basic forest inventory data to apply in practice, and usually provides reasonably accurate predictions for many species and regions (Ter-Mikaelian and Korzukhin 1997; Jenkins et al. 2003; Wang 2006; Sierra et al. 2007; Basuki et al. 2009). However, adding tree height or height classes as an additional predictor into biomass equations can significantly improve the model fitting and performance (Bi et al. 2004; Wang et al. 2006; Li and Zhao 2013), especially for some tree component models such as branch and foliage biomass (Wang 2006; Zhou et al. 2007). Our results demonstrated that adding tree height into the system improved most of the biomass equations for the nine hardwood species, which was consistent with the literature (Ketterings et al. 2001; Bi et al. 2004; Cole and Ewel 2006; António et al. 2007; Battulga et al. 2013).

Many modelers used log-transformed linear models (LR) to fit tree biomass data (Smith and Brand 1983; Wang 2006; Zianis and Mencuccini 2003; Zianis et al. 2011). Others fitted the nonlinear power function (NLR) directly to the biomass data of original scale and believed that nonlinear models provided model fitting as good as the log-transformed models (Parresol 2001; Bi et al. 2004; Lambert et al. 2005; Chan et al. 2013). However, Xiao et al. (2011) pointed out that the choice between LR and NLR depends on the distribution of model errors, and provided a likelihood analysis to compare the appropriateness of the two error structures. Although the significance of likelihood analysis is proposed by several authors (Xiao et al. 2011; Ballantyne 2013; Lai et al. 2013), it has not been widely applied in forestry. In this study, we applied likelihood analysis to verify the error structures of tree biomass data, and found that the multiplicative error structure was favored over the additive error structure. Therefore, we constructed two additive systems of log-transformed models [Eqs. (4), (5)], which were validated using the jackknifing technique.

Moreover, many biomass equations published so far are non-additive because they were estimated using least-squares regression (OLS) (Zianis et al. 2011; Cai et al. 2013). The SUR method (Parresol 2001) is a better choice for developing additive biomass equations, which considers contemporaneous correlations among the biomass components and results in more efficient parameter estimation. The benefits of using SUR are not only to ensure the additivity property of biomass equations, but also to reduce the confidence and prediction intervals for biomass estimations (Parresol 2001; Bi et al. 2004; Balboa-Murias et al. 2006).

Because the log-transformed biomass equations predict the logarithmic values of expected biomass, anti-log transformation is necessary in order to obtain the predicted biomass in the original scale. It is well known that this anti-log transformation process leads to a systematic underestimation for the expected biomass. Consequently, a correction factor (CF) of Baskerville (1972), i.e., CF = exp (σ 2/2), is commonly used to correct for the systematic bias introduced by the anti-log transformation. However, Madgwick and Satoo (1975) found that anti-log transformation tended to overestimate biomass if the correction factor is applied, and suggested that the correction factor might be ignored if the bias from anti-log was relatively small compared to the overall variation in the estimate of biomass. In this study, the correction factor values of all biomass equations were less than 1.08, especially for the total, aboveground, and stem biomass equations. The percent biases [Zianis et al. 2011, Eq. (5)] were also rather small ranging from 0.4 to 8.0 % (results not shown). Thus, the correction factor was not necessary for these nine species in this study. The results were also consistent with other previous studies (Beauchamp and Olson 1973; Madgwick and Satoo 1975; Zianis and Mencuccini 2003; Zianis et al. 2011).

Biomass partitioning for the nine hardwood species showed (1) the average proportions of stems remained stable (about 62 %) between small trees (10 cm) and large trees (30 cm); (2) the average proportions of branches increased from 11.1 % for small trees to 15.9 % for large trees; (3) the average proportions of foliage decreased slightly from 3.4 % for small trees to 2.5 % for large trees; and (4) the average proportions of roots decreased from 23.5 % for small trees to 18.8 % for large trees. It is probably because the growth of the root systems of old trees slowed down substantially, while branches became larger and thicker in big trees for some species. For example, the biomass proportions of Mongolian oak (Quercus mongolica): roots decreased from 25.6 % (10 cm) to 18.5 % (30 cm), while braches increased from 8.3 % (10 cm) to 23.1 % (30 cm). Some species such as Dahurian poplar (Populus davidiana) allocated a greater proportion to stems (76.8 %) than to roots (15.4 %) mainly due to its shallow lateral root systems and small crown size in the canopy. The allocation proportion of branches varied across the species, depending on the formation of forks and the thickness of branches. Similarly, the partitioning proportions of roots depended on tree root morphology (e.g., shallow root or deep root), growth process, and soil conditions (Strong and Roi 1983; Canadell et al. 1996; Wang 2006). However, the root excavation was impossible for some individual trees such as Juglans mandshurica and Betula davuria because of their propensity to grow clonally via lateral roots. This phenomenon may introduce errors in estimating the belowground biomass, which in turn influences the partitioning proportions of root biomass. In summary, it is reported in the literature that even though the partitioning of total biomass into tree components varied across tree species and ages, the aboveground biomass is about 75 % and the belowground biomass is about 25 % of the total biomass as the overall average (Niklas and Enquist 2002; Wang et al. 2011). Our results were consistent with the literature.

Wang (2006) developed biomass equations using D as the only predictor for ten hardwood species from the Maoershan Ecosystem Research Station of the Northeast Forestry University in Heilongjiang Province, China, which was part of Changbai Mountains. Seven species (Quercus mongolica, Populus davidiana, Tilia amurensis, Betula platyphylla, Fraxinus manshurica, Juglans mandshurica and Acer mono) were the same as the biomass data in our study. However, the sample size in Wang (2006) was only 10 trees (two dominant, three co-dominant, three intermediate, and two suppressed trees) for each species, and the established biomass equations were not additive for total, sub-totals, and component biomass.

A graphical comparison of total, aboveground, and belowground biomass equations illustrated the differences between our models (System 1) and Wang’s (2006) biomass equations for the seven species (Fig. 4). It was evident that the total and aboveground biomass equations produced similar predictions for most of the seven species, and most of the mean predicted biomass of Wang’s equations fell into the 95 % confidence intervals of mean prediction by our equations, while there were some differences for the belowground biomass equations. For Quercus mongolica, our equations yielded higher predictions for the total, aboveground, and belowground biomass than Wang’s equations, especially for large-sized trees. But our equations produced slightly lower predictions for other species. This may be due to the significant difference of predicting the belowground biomass between the two models. The possible reasons may be (1) data of the two studies came from different study sites; (2) each species of the two studies came from different forest types; and (3) differences in the number of sampled trees and the ranges of tree sizes. These can lead to the differences in terms of tree root morphologic features, soil conditions and growth process (Strong and Roi 1983; Nicoll and Ray 1996).

Fig. 4
figure 4

Total, aboveground and belowground (root) biomass from our biomass equations (solid line) compared to the published equations (dashed line) in Wang (2006) for seven tree species. Quercus mongolica (QM), Populus davidiana (PD), Tilia amurensis (TA), Betula platyphylla (BP), Fraxinus manshurica (FM), Juglans mandshurica (JM), and Acer mono (AM). The dot lines were the lower and upper limits of the 95 % confidence intervals for the mean prediction of biomass

Full size image

Finally, accurately estimating biomass of large trees is critical to stand biomass estimation because large trees usually account for a greater biomass proportion in a stand (Gower et al. 1999). In this study, the largest diameter of the nine species was from 30.4 to 41.1 cm. If these established biomass equations in this study were used to estimate biomass outside of our data range (e.g., diameter >50 cm), the models could produce larger prediction errors. In addition, if our models were used for other regions, caution should be taken because different environmental and growth conditions may yield different allometric relationships between tree biomass and tree variables. Therefore, the biomass equations developed in this study are more suitable to Northeast China.

Conclusion

Two additive systems of biomass equations were developed for nine major hardwood species in Northeast China, including total, aboveground, roots, stem (with bark), branch, foliage, and crown biomass. System 1 used tree diameter D as the only predictor, and System 2 included both tree diameter D and total height H as predictors. We applied likelihood analysis to assess the model error structures of power functions [Eqs. (1), (2)]. The results indicated that the assumption of multiplicative error structure was favored for our biomass data of the nine species. Thus, the log-transformed models were used in the two additive systems.

As expected, the accuracy of the biomass component equations differed for the two additive systems across the nine species. The model R 2 a was >89 % for System 1 (D only) and >91 % for System 2 (both D and H). The model RMSE was relatively small for total, aboveground and stem biomass equations, but larger for root, branch, foliage, and crown biomass. Overall, adding tree height into the system of biomass equations significantly improved model fitting and performance, especially for total, aboveground, and stem biomass.

Moreover, we analyzed the biomass partitioning of aboveground and belowground components for the nine hardwood species. Our results were consistent with the literature such that the stem biomass accounted for the largest proportion of total biomass. The tree biomass data in this study were widely distributed across three forest regions (Daxing’an Mountains, Xiaoxing’an Mountains and Changbai Mountains). Thus, these established biomass equations can be applied to estimate individual tree biomass in Northeast China, and provide basic information for Chinese National Forest Inventory.