1 Introduction

The Finite Element Method (FEM) has in recent decades seen significant development in accurate modeling in Computational Fluid Dynamics (CFD) and Fluid–Structure Interaction (FSI), which are, with the increasing computer power, gaining a growing foothold in engineering design [2]. An FSI problem becomes a Fluid–Object Interaction (FOI) problem when deformations of the structure can be neglected. The solid part of the problem is then approximated by a rigid object, and the equation system for the structural part reduces to the balance of global linear and angular momenta with respect to the center of mass, yielding a system of only three equations in 2D and six equations in 3D. Earlier coupling between CFD and rigid objects was reported in [3] for a cylinder drifting in shear flow and in [4] for vortex-induced vibrations of a cylinder. Other earlier FOI work was reported in conjunction with the Mixed Interface-Tracking/Interface-Capturing Technique (MITICT) in e.g., [5, 6]. Recently FOI methods have been employed in several marine applications in the study of free-surface flows [1, 7,8,9]. In the context of bridge engineering, FOI has been used to study the effect of railings and spoilers on the Hardanger bridge [2] and to simulate the flutter phenomenon for the Great Belt East suspension bridge [10, 11]. However, any direct time-domain validation of free-vibration wind-tunnel experiments are, to the authors’ knowledge, not reported in open literature.

In the present work, the aerodynamics part of the FOI problem is solved using the Arbitrary Lagrangian–Eulerian Variational Multiscale (ALE-VMS) formulation of the Navier–Stokes equations for incompressible flows [2, 12,13,14,15,16] augmented with the weakly-enforced boundary conditions [17,18,19]. This method, which is a moving-mesh method, has proven very effective in a wide range of turbulent flow problems, see e.g., [20,21,22,23], including bridge aerodynamics [24,25,26]. In the category of moving-mesh methods, the Space-Time VMS (ST-VMS) method  [27, 28] has also proven effective in a wide range of problems, including flapping wings [29, 30], heart valve flow [31, 32], disk brake thermo-fluids [33], turbomachinery [34,35,36], and tire aerodynamics with road contact and tire deformation [37].

In engineering design of long-span bridges, aerodynamic performance and stability is one of the major concerns. The aerodynamic stability, which is governed by the self-excited forces, is traditionally studied on small-scale models in the wind tunnel, however, numerous studies [2, 10, 11, 24, 38,39,40,41,42,43] prove CFD and FSI to be a valuable supplement. Most of these studies used the forced-vibration method with a prescribed bridge-deck motion, due to its repeatability, effectiveness and simple identification procedures. For the same reasons, this is also the preferred method in wind-tunnel experiments [44, 45]. However, the free-vibration method, in which the bridge deck is suspended by springs and allowed to vibrate freely, has the advantage of exhibiting the response to wind action directly, rather than filtered through a semi-empirical load theory applied in the forced-vibration method [46]. Therefore, this method is commonly used to validate the forced-vibration results. Another benefit of using the free-vibration technique is that the general aerodynamic performance can be determined directly, rather than from a model that relies on the parameters obtained with the forced-vibration approach.

In this work we use a coupled analysis of the ALE-VMS formulation with weakly-enforced boundary conditions and a modified rigid-object formulation to simulate free-vibration wind tunnel tests of bridge sections. We take the rigid-body dynamics formulation from [1] and augment it with external stiffness and damping to represent the effect of the suspension. Further, we propose a simplified time-integration algorithm that assumes a linear relationship between the time derivative of the Euler angles and rotation vector in the linearization of the rigid-object angular-momentum equations. The formulation is tested on a 1:50 scale model of the Hardanger bridge section at various wind speeds. Several studies have been performed on the same section experimentally [45, 47] and numerically by the same authors using the forced-vibration method [25, 26].

To validate the numerical simulations we have also conducted free-vibration wind tunnel experiments of the same bridge section. The focus in this work has been to evaluate how the formulation is capable of capturing the aerodynamic contribution to the dynamic properties of the coupled system. The aerodynamic damping, which is the driving mechanism of flutter instability, is of particular interest. We consider four wind speeds, including still-wind and the critical wind speed at which flutter occurs.

The paper is organized as follows. The governing equations are presented in the continuous form in Sect. 2 and in the discrete form in Sect. 3. Section 4 introduces the aerodynamic forces with emphasis on flutter analysis. The setup for wind-tunnel experiments and numerical simulations is presented in Sect. 5. The numerical results are presented in Sect. 6 before conclusions are drawn in Sect. 7.

2 Governing equations

In this section we present the governing equations for the aerodynamics rigid-object problems.

2.1 Aerodynamics

The Navier–Stokes equations of incompressible flows in an ALE frame [48] govern the aerodynamics of the problem and are stated as follows. Let \( \hat{\varOmega } \in \mathbb {R}^{n_{sd}} \), \( n_{sd} = 2,3 \), represent the reference fluid mechanics domain with coordinates \( \hat{\mathbf {x}} \) and boundary \( \hat{\varGamma } \), and let \( \varOmega _t \in \mathbb {R}^{n_{sd}} \), \( n_{sd} = 2,3 \), represent the time dependent fluid mechanics domain in the current configuration with coordinates \( \mathbf {x} \) and boundary \( \varGamma _t \). With these definitions, the continuous linear-momentum and mass-balance equations on \( \varOmega _t \) are given, respectively, as

$$\begin{aligned}&\rho \left( \left. \frac{\partial \mathbf {u}}{\partial t}\right| _{\hat{x}} + (\mathbf {u}- \hat{\mathbf {u}}) \cdot \varvec{\triangledown }\mathbf {u}- \mathbf {f}\right) - \varvec{\triangledown }\cdot \varvec{\sigma }= 0, \end{aligned}$$
(1)
$$\begin{aligned}&\varvec{\triangledown }\cdot \mathbf {u}= 0, \end{aligned}$$
(2)

where \( \varvec{\sigma }\) is the Cauchy stress tensor defined as

$$\begin{aligned} \varvec{\sigma }\left( \mathbf {u}, p\right) = -p \mathbf {I}+ 2 \mu \, \varvec{\varepsilon }(\mathbf {u}). \end{aligned}$$
(3)

In the above, \( \mathbf {u}\), p and \( \rho \) are the fluid velocity, pressure and density, respectively. \( \mu \) is the dynamic viscosity and \( \varvec{\varepsilon }(\mathbf {u}) \) is the symmetric gradient of \( \mathbf {u}\). In addition, \( \hat{\mathbf {u}}\) is the velocity of the fluid domain and \( \mathbf {f} \) is the body force per unit mass. The subscript \( |_{\hat{x}} \) on the partial derivative in Eq. (1) denotes that the time derivative is taken with the referential coordinates \( \hat{\mathbf {x}} \) fixed. The spatial derivatives in Eqs. (1)–(3) are taken with respect to \( \mathbf {x}\).

Fig. 1
figure 1

Rigid body, represented by a bridge cross section, in its reference and current configuration

Full size image

2.2 Rigid object

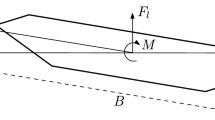
Using the notation in Fig. 1, we let \( \varOmega _0^{b} \) denote the rigid-object reference configuration with coordinates \( \mathbf {X}\) and center of mass \( \mathbf {X}_0 \), and we let \( \varOmega _t^{b} \) denote the rigid-object current configuration with coordinates \( \mathbf {x}\) and center of mass \( \mathbf {x}_0 \). All rigid-object motions can be described by a translation and rotation of its center of mass as

$$\begin{aligned} \mathbf {x}= \mathbf {R}\left( \mathbf {X}- \mathbf {X}_0 \right) +\mathbf {x}_0, \end{aligned}$$
(4)

where \( \mathbf {R} \) is the rotation tensor. From Eq. (4) we obtain the displacement field as

$$\begin{aligned} \mathbf {y} = \mathbf {x}- \mathbf {X}= \left( \mathbf {R} - \mathbf {I}\right) \left( \mathbf {X}-\mathbf {X}_0\right) + \mathbf {d}, \end{aligned}$$
(5)

where \(\mathbf {d}\) is the displacement of the center of mass.

We take the material time derivative in Eq. (5) to obtain the velocity field

$$\begin{aligned} \mathbf {u}= \dot{\mathbf {R}}\left( \mathbf {X}- \mathbf {X}_0\right) + \mathbf {v}, \end{aligned}$$
(6)

where \(\mathbf {v}\) is the velocity of the center of mass. Using Eq. (4), we can express the velocity field in Eq. (6) in terms of the current coordinates as

$$\begin{aligned} \mathbf {u}= \varvec{\varOmega }\left( \mathbf {x}- \mathbf {x}_0\right) + \mathbf {v}, \end{aligned}$$
(7)

where \( \varvec{\varOmega } \) is the skew-symmetric tensor of angular velocities:

$$\begin{aligned} \varvec{\varOmega } = \dot{\mathbf {R}}\mathbf {R}^{-1} = \begin{bmatrix} 0&-\omega _3&\omega _2 \\ \omega _3&0&-\omega _1 \\ -\omega _2&\omega _1&0 \end{bmatrix}. \end{aligned}$$
(8)

Further, we define \( \varvec{\omega } \), the axial vector of \( \varvec{\varOmega } \), as

$$\begin{aligned} \varvec{\omega } = \begin{bmatrix} \omega _1 \\ \omega _2 \\ \omega _3 \end{bmatrix}. \end{aligned}$$
(9)

Eq. (7) can then be written as

$$\begin{aligned} \mathbf {u}= \varvec{\omega }\times \left( \mathbf {x}- \mathbf {x}_0\right) + \mathbf {v}. \end{aligned}$$
(10)

Note that from Eq. (8) it follows that

$$\begin{aligned} \dot{\mathbf {R}} = \varvec{\varOmega }\mathbf {R}, \end{aligned}$$
(11)

which is used as the generating equation for \( \mathbf {R} \).

The rigid-object motion is governed by the balance of global linear and angular momenta, expressed, respectively, as

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}\left( m \mathbf {v} \right) + \mathbf {C}^{lin} \mathbf {v} + \mathbf {K}^{lin}\mathbf {d}= \mathbf {F}, \end{aligned}$$
(12)

and

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}\left( \mathbf {J}_t \varvec{\omega } \right) + \mathbf {C}^{ang} \varvec{\omega } + \mathbf {K}^{ang}\varvec{\theta } = \mathbf {M}. \end{aligned}$$
(13)

In the above equations, \(\mathbf {v}\) and \(\mathbf {d}\) are the center-of-mass velocity and displacement, respectively, \(\varvec{\omega }\) and \(\varvec{\theta }\) are the axial vectors of angular velocities and Euler angles, respectively, and m and \(\mathbf {J}_t\) are the object mass and current-configuration inertia tensor, respectively. The latter quantity may be expressed as

$$\begin{aligned} \mathbf {J}_t = \mathbf {R}\mathbf {J}_0\mathbf {R}^T, \end{aligned}$$
(14)

where the reference-configuration inertia tensor, \( \mathbf {J}_0 \), is given by

$$\begin{aligned} \mathbf {J}_0= & {} \int _{\varOmega _0^{b}} \rho \left( \mathbf {X}- \mathbf {X}_0\right) \cdot \left( \mathbf {X}- \mathbf {X}_0\right) \mathbf {I} \mathrm {d}\varOmega \nonumber \\&- \int _{\varOmega _0^{b}}\rho \left( \mathbf {X}- \mathbf {X}_0\right) \otimes \left( \mathbf {X}- \mathbf {X}_0\right) \mathrm {d}\varOmega . \end{aligned}$$
(15)

In Eq. (12), \( \mathbf {C}^{lin} \) and \( \mathbf {K}^{lin} \) are the linear damping and stiffness matrices, while in Eq. (13) \( \mathbf {C}^{ang} \) and \( \mathbf {K}^{ang} \) are their torsional counterparts. We note that the vector of Euler angles \( \varvec{\theta } \) may be obtained from the rotation matrix \( \mathbf {R} \).

Finally, vectors \( \mathbf {F} \) and \( \mathbf {M} \) represent the external forces and moments acting on the rigid object and are given by

$$\begin{aligned} \mathbf {F} = m \mathbf {g} + \int _{\varGamma _t^{I}}\mathbf {h}~\mathrm {d}\varGamma , \end{aligned}$$
(16)

and

$$\begin{aligned} \mathbf {M} = \int _{\varGamma _t^{I}}\left( \mathbf {x}- \mathbf {x}_0\right) \times \mathbf {h}~\mathrm {d}\varGamma , \end{aligned}$$
(17)

where \( \mathbf {g} \) is the gravitational acceleration vector, and \( \mathbf {h} \) is the aerodynamic traction vector acting on the object surface \( \varGamma _t^I \). Note that gravity does not contribute to Eq. (17) because it creates zero moment around the center of mass.

3 Discrete formulation

The discrete formulation of the coupled FOI problem is presented in what follows. We emphasize the rigid-object formulation, and for a more thorough description of the aerodynamics and mesh motion parts of the problem the reader is referred to [20] and references therein.

3.1 ALE-VMS formulation

At the discrete level, the fluid domain is partitioned into \( n_{el} \) finite element subdomains \( \varOmega _t^e \) and its boundary into \( n_{eb} \) surface elements \( \varGamma _t^b \). We then define finite-dimensional trial functions for the fluid velocity \( \mathbf {u}\) and pressure p, denoted \( \mathcal {S}^h_u \) and \( \mathcal {S}^h_p \), respectively, and their corresponding test functions \( \mathcal {V}^h_u \) and \( \mathcal {V}^h_p \). Superscript h indicate that its attribute is finite-dimensional.

The semi-discrete ALE-VMS formulation is then given as follows. Find \( \mathbf {u}^h \in \mathcal {S}^h_u \) and \( p^h \in \mathcal {S}^h_p \) , such that \( \forall \mathbf {w}^h \in \mathcal {V}^h_u \) and \( q^h \in \mathcal {V}^h_p \):

$$\begin{aligned}&\int _{\varOmega _t}^{} \mathbf {w}^h \cdot \rho \left( \left. \frac{\partial \mathbf {u}^h}{\partial t}\right| _{\hat{x}} + \left( \mathbf {u}^h - \hat{\mathbf {u}}^h\right) \cdot \varvec{\triangledown }\mathbf {u}^h \right) \, \mathrm {d}\varOmega \nonumber \\&\quad + \int _{\varOmega _t} \varvec{\varepsilon }(\mathbf {w}^h):\varvec{\sigma }(\mathbf {u}^h,p^h) \, \mathrm {d}\varOmega + \int _{\varOmega _t} q^h \varvec{\triangledown }\cdot \mathbf {u}^h \, \mathrm {d}\varOmega \nonumber \\&\quad - \int _{\varOmega _t} \mathbf {w}^h \cdot \rho \, \mathbf {f}^h \, \mathrm {d}\varOmega - \int _{(\varGamma _t)_h}\mathbf {w}^h \cdot \mathbf {h}^h \, \mathrm {d}\varGamma \nonumber \\&\quad + \sum _{e=1}^{n_{el}} \int _{\varOmega _t^e} \tau _{\mathrm {SUPS}}\left( \left( \mathbf {u}^h - \hat{\mathbf {u}}^h\right) \cdot \varvec{\triangledown }\mathbf {w}^h + \frac{\varvec{\triangledown }q^h}{\rho } \right) \nonumber \\&\quad \cdot \mathbf {r}_M\left( \mathbf {u}^h,p^h\right) \, \mathrm {d}\varOmega \nonumber \\&\quad + \sum _{e=1}^{n_{el}} \int _{\varOmega _t^e} \rho \nu _{\mathrm {LSIC}}\varvec{\triangledown }\cdot \mathbf {w}^h \mathrm {r}_C(\mathbf {u}^h) \, \mathrm {d}\varOmega \nonumber \\&\quad - \sum _{e=1}^{n_{el}} \int _{\varOmega _t^e} \tau _{\mathrm {SUPS}}\mathbf {w}^h \cdot \left( \mathbf {r}_M\left( \mathbf {u}^h,p^h\right) \cdot \varvec{\triangledown }\mathbf {u}^h \right) \, \mathrm {d}\varOmega \nonumber \\&\quad - \sum _{e=1}^{n_{el}} \int _{\varOmega _t^e} \frac{\varvec{\triangledown }\mathbf {w}^h}{\rho } : \left( \tau _{\mathrm {SUPS}}\mathbf {r}_M\left( \mathbf {u}^h,p^h\right) \right) \nonumber \\&\quad \otimes \left( \tau _{\mathrm {SUPS}}\mathbf {r}_M\left( \mathbf {u}^h,p^h\right) \right) \, \mathrm {d}\varOmega = 0 \end{aligned}$$
(18)

In Eq. (18) \( \mathbf {r}_M \) and \( \mathrm {r}_C \) are residuals of the Navier–Stokes linear-momentum balance and continuity, respectively, given as

$$\begin{aligned} \mathbf {r}_M =&\rho \left( \left. \frac{\partial \mathbf {u}^h}{\partial t}\right| _{\hat{x}} + \left( \mathbf {u}^h - \hat{\mathbf {u}}^h\right) \cdot \varvec{\triangledown }\mathbf {u}^h - \mathbf {f}^h \right) -\varvec{\triangledown }\cdot \varvec{\sigma }\left( \mathbf {u}^h, p^h \right) ,\end{aligned}$$
(19)
$$\begin{aligned} \mathrm {r}_C =&\varvec{\triangledown }\cdot \mathbf {u}^h. \end{aligned}$$
(20)

\(\tau _{\mathrm {SUPS}}\) and \( \nu _{\mathrm {LSIC}}\) are stabilization parameters which are designed to render optimal stability and convergence through extensive studies, see e.g., [49,50,51,52,53,54,55,56,57,58] and references therein, and are adopted from the definitions given in [59].

The surface tractions \( \mathbf {h}^h \) are evaluated on the \( \left( \varGamma _t\right) _h \) part of \( \varGamma _t \). The essential boundary conditions are specified on the \( \left( \varGamma _t\right) _g \) part of \( \varGamma _t \), and are imposed weakly by adding the following terms to the left-hand side of Eq. (18):

$$\begin{aligned}&- \sum _{b=1}^{n_{eb}} \int _{\varGamma _t^b \cap (\varGamma _t)_g} \mathbf {w}^h \cdot \varvec{\sigma }\left( \mathbf {u}^h, p^h \right) \mathbf {n} \, \mathrm {d}\varGamma \nonumber \\&\quad - \sum _{b=1}^{n_{eb}} \int _{\varGamma _t^b \cap (\varGamma _t)_g} \left( 2\mu \varvec{\varepsilon }\left( \mathbf {w}^h\right) \mathbf {n} + q^h \mathbf {n} \right) \cdot \left( \mathbf {u}^h - \mathbf {g}^h \right) \, \mathrm {d}\varGamma \nonumber \\&\quad - \sum _{b=1}^{n_{eb}} \int _{\varGamma _t^b \cap (\varGamma _t)_g^-} \mathbf {w}^h \cdot \rho \left( \left( \mathbf {u}^h - \hat{\mathbf {u}}^h\right) \cdot \mathbf {n}\right) \left( \mathbf {u}^h - \mathbf {g}^h\right) \, \mathrm {d}\varGamma \nonumber \\&\quad + \sum _{b=1}^{n_{eb}} \int _{\varGamma _t^b \cap (\varGamma _t)_g} \tau _{\mathrm {TAN}} \left( \mathbf {w}^h - \left( \mathbf {w}^h \cdot \mathbf {n}\right) \mathbf {n}\right) \nonumber \\&\quad \cdot \left( \left( \mathbf {u}^h - \mathbf {g}^h\right) \left( \left( \mathbf {u}^h - \mathbf {g}^h\right) \cdot \mathbf {n}\right) \mathbf {n}\right) \, \mathrm {d}\varGamma \nonumber \\&\quad + \sum _{b=1}^{n_{eb}} \int _{\varGamma _t^b \cap (\varGamma _t)_g} \tau _{\mathrm {NOR}} \left( \mathbf {w}^h \cdot \mathbf {n} \right) \left( \left( \mathbf {u}^h - \mathbf {g}^h\right) \cdot \mathbf {n}\right) \, \mathrm {d}\varGamma . \end{aligned}$$
(21)

Here \( \mathbf {n} \) is the unit outward normal vector, \( \tau _{\mathrm {TAN}} \) and \( \tau _{\mathrm {NOR}} \) are the boundary penalty parameters in the tangential and normal directions, respectively, as defined in [17], and \( \left( \varGamma _t\right) _{g}^- \) is defined as the inflow part of \( \left( \varGamma _t\right) _g \):

$$\begin{aligned} \left( \varGamma _t\right) _{g}^- = \left\{ \mathbf {x} | \left( \mathbf {u}^h - \hat{\mathbf {u}}^h\right) \cdot \mathbf {n} < 0, \forall \mathbf {x} \subset \left( \varGamma _t\right) _g \right\} . \end{aligned}$$
(22)

3.2 Mesh-moving technique

We make use of an interface-tracking technique [60], where the computed displacement and velocity of the rigid object define the kinematics of the fluid-rigid-object interface and are prescribed as essential boundary conditions in the fluid mesh-moving problem.

We assign the variable \( \hat{\mathbf {y}}(t) \) to the fluid domain displacement, such that \( \frac{\mathrm {d}\hat{\mathbf {y}} }{\mathrm {d}t} = \hat{\mathbf {u}} \) at the fluid-rigid-object interface, and define its trial and test function respectively as \( \mathcal {S}^h_y \) and \( \mathcal {V}^h_y \). The displacements of the fluid domain interior can then be found by solving the linear elastostatics problem in the weak form: Find \( \hat{\mathbf {y}}^h \in \mathcal {S}^h_y \) such that \( \mathbf {w}^h_y \in \mathcal {V}^h_y \):

$$\begin{aligned} \int _{\varOmega _{\tilde{t}}}\varvec{\varepsilon }(\mathbf {w}^h_m) : \mathbf {D}^h \, \varvec{\varepsilon }\left( \hat{\mathbf {y}}^h(t) -\hat{\mathbf {y}}^h(\tilde{t})\right) \, \mathrm {d}\varOmega = 0. \end{aligned}$$
(23)

Here \( \varOmega _{\tilde{t}} \) and \( \hat{\mathbf {y}}^h(\tilde{t}) \) are the fluid mesh nearby configuration and displacement at time \( \tilde{t} < t \), in practice taken at the previous time step. The elastic tensor \( \mathbf {D}^h \) is defined in terms of mesh-dependent Lamé parameters \( \mu ^h \) and \( \lambda ^h \) as given in [1]. With this definition the element Young’s modulus is proportional with the inverse of the Jacobian, making smaller element stiffer and minimize the mesh distortion. This method, introduced in [61,62,63], was named Jacobian-based stiffening in [60].

3.3 Time integration of rigid-object equations

In what follows, we present the time integration algorithm of the rigid-object equations given in Sect. 2.2. Following [64], we employ the midpoint rule in order to preserve the orthonormal properties of the rotation tensor.

Starting with the balance of linear momentum in Eq. (12), the midpoint approximation reads

$$\begin{aligned} \frac{m\left( \mathbf {v}_{n+1} - \mathbf {v}_{n} \right) }{\varDelta t}\,+\, \mathbf {C}^{lin} \frac{\mathbf {v}_{n+1} + \mathbf {v}_n}{2}\,+\,\mathbf {K}^{lin} \frac{\mathbf {d}_{n+1}+\mathbf {d}_n}{2} = \mathbf {F}_{n+1/2}. \end{aligned}$$
(24)

We define the discrete residual vector of linear-momentum equation, \( \mathbf {N}^{lin} \), as

$$\begin{aligned} \mathbf {N}^{lin}\left( \mathbf {v}_{n+1}\right)= & {} \frac{m\left( \mathbf {v}_{n+1} - \mathbf {v}_{n} \right) }{\varDelta t} + \mathbf {C}^{lin} \frac{\mathbf {v}_{n+1} + \mathbf {v}_n}{2} \nonumber \\&+\,\mathbf {K}^{lin} \frac{\mathbf {d}_{n+1}+\mathbf {d}_n}{2} - \mathbf {F}_{n+1/2}. \end{aligned}$$
(25)

The corresponding linearized equation system then reads

$$\begin{aligned} \frac{\partial \mathbf {N}^{lin}}{\partial \mathbf {v}_{n+1}}\varDelta \mathbf {v}_{n+1} = - \mathbf {N}^{lin}\left( \mathbf {v}_{n+1}\right) , \end{aligned}$$
(26)

where the left-hand side matrix becomes

$$\begin{aligned} \frac{\partial \mathbf {N}^{lin}}{\partial \mathbf {v}_{n+1}} = \frac{m}{\varDelta t}\mathbf {I}+ \frac{1}{2}\mathbf {C}^{lin} + \frac{\varDelta t}{4} \mathbf {K}^{lin}. \end{aligned}$$
(27)

In the above equation we used the fact that relationship between \( \mathbf {d}\) and \( \mathbf {v} \) is also approximated using a midpoint rule, which gives

$$\begin{aligned} \frac{\partial \mathbf {d}_{n+1}}{\partial \mathbf {v}_{n+1}} = \frac{\varDelta t}{2} \mathbf {I}, \end{aligned}$$
(28)

and thus explains the factor \(\frac{\varDelta t}{4}\) in front of the \(\mathbf {K}^{lin}\) term in Eq. (27).

We likewise form a discrete residual vector from the angular-momentum Eq. (13) integrated using a midpoint rule:

$$\begin{aligned} \mathbf {N}^{ang}(\varvec{\omega }_{n+1})= & {} \frac{\mathbf {J}_{n+1} \varvec{\omega }_{n+1} - \mathbf {J}_n \varvec{\omega }_n}{\varDelta t} + \mathbf {C}^{ang} \frac{\varvec{\omega }_{n+1}+\varvec{\omega }_{n}}{2}\nonumber \\&+\,\mathbf {K}^{ang}\frac{\varvec{\theta }_{n+1} + \varvec{\theta }_n}{2} - \mathbf {M}_{n+1/2}. \end{aligned}$$
(29)

The corresponding linearized equation system then reads

$$\begin{aligned} \frac{\partial \mathbf {N}^{ang}}{\partial \varvec{\omega }_{n+1}} \varDelta \varvec{\omega }_{n+1} = - \mathbf {N}^{ang}(\varvec{\omega }_{n+1}), \end{aligned}$$
(30)

with the approximate left-hand side matrix given by

$$\begin{aligned} \frac{\partial \mathbf {N}^{ang}}{\partial \varvec{\omega }_{n+1}} \approx \frac{1}{\varDelta t}\mathbf {J}_{n+1} + \frac{1}{2} \mathbf {C}^{ang} + \frac{1}{2} \mathbf {K}^{ang} \frac{\partial \varvec{\theta }_{n+1}}{\partial \varvec{\omega }_{n+1}}, \end{aligned}$$
(31)

where the inertia tensor is assumed to not have a strong dependence on the angular velocity. To obtain an explicit expression for the left-had-side matrix, one needs to calculate the derivative \( \frac{\partial \varvec{\theta }_{n+1}}{\partial \varvec{\omega }_{n+1}} \). In the case of planar motion, it can be shown that

$$\begin{aligned} \varvec{\omega }= \dot{\varvec{\theta }}. \end{aligned}$$
(32)

Assuming midpoint integration of the above equation leads to

$$\begin{aligned} \frac{\partial \varvec{\theta }_{n+1}}{\partial \varvec{\omega }_{n+1}} = \frac{2}{\varDelta t} \mathbf {I}, \end{aligned}$$
(33)

which, in turn, gives

$$\begin{aligned} \frac{\partial \mathbf {N}^{ang}}{\partial \varvec{\omega }_{n+1}} \approx \frac{1}{\varDelta t}\mathbf {J}_{n+1} + \frac{1}{2} \mathbf {C}^{ang} + \frac{\varDelta t}{4} \mathbf {K}^{ang}. \end{aligned}$$
(34)

The matrix-valued discrete residual for the equation governing the evolution of the rotation matrix (see Eq. (11)) may be written as

$$\begin{aligned} \mathbf {N}^{rot}(\mathbf {R}_{n+1}) = \frac{\mathbf {R}_{n+1} - \mathbf {R}_n}{\varDelta t} - \left( \frac{\varvec{\varOmega }_{n+1} + \varvec{\varOmega }_n}{2} \right) \left( \frac{\mathbf {R}_{n+1} + \mathbf {R}_n}{2}\right) . \end{aligned}$$
(35)

The corresponding linearized equation takes on the form

$$\begin{aligned} D \mathbf {N}^{rot} \varDelta \mathbf {R}_{n+1} = - \mathbf {N}^{rot}(\mathbf {R}_{n+1}), \end{aligned}$$
(36)

where the left-hand-side matrix \(D \mathbf {N}^{rot}\) may be directly inferred from Eq. (35) and takes on the form

$$\begin{aligned} D \mathbf {N}^{rot} \approx \frac{1}{\varDelta t} \mathbf {I}- \frac{\varvec{\varOmega }_{n+1} + \varvec{\varOmega }_n}{4}, \end{aligned}$$
(37)

where the spin tensor is assumed to not have a strong dependence on the rotation matrix.

Given all quantities at time level \( t_{n} \); \( \mathbf {d}_n \), \( \mathbf {v}_n \), \( \mathbf {R}_n \), \( \varvec{\omega }_n \) and \( \varvec{\theta }_n \), and the half-step values of the external forces \( \mathbf {F}_{n+1/2} \) and \( \mathbf {M}_{n+1/2} \), we advance the rigid object to the time level \(t_{n+1} \) as follows. The residuals of the rigid-object system, \(\mathbf {N}^{lin}(\mathbf {u}_{n+1})\), \(\mathbf {N}^{ang}(\varvec{\omega }_{n+1})\), and \(\mathbf {N}^{rot}(\mathbf {R}_{n+1})\), are driven to zero by solving Eqs. (26),  (30), and (36) in a sequential fashion, and repeating the sequence until convergence. Increment of the angular velocity is employed to update the spin tensor for the solution of Eq. (37), while increment of the rotation matrix is employed to update the inertia tensor in Eq. (30). Once converged, the rigid-object solution is transferred to the interface mesh and employed as essential boundary conditions for the fluid-mechanics and mesh-motion problems.

Fig. 2
figure 2

Convergence in the \(l_2\)-norm of the rigid-object angular-momentum-balance residual sampled at various rotation angles

Full size image
Fig. 3
figure 3

Object current configurations where convergence of the rigid-body angular-momentum balance is sampled

Full size image

To test the rigid-object algorithm, the convergence of Eq. (30) is studied for a coupled FOI analysis of a coarsely discretized rectangular cylinder. A low natural frequency (\( f_N = 0.1 \) Hz) is chosen such that the dynamic rigid-body forces become stiffness-dominated. Fig. 2, showing the convergence rates of the \(l_2\)-norm of \( \mathbf {N}^{ang} \) for various rotation angles, reveals that the rigid-body formulation exhibits fast convergence. Even for relatively large rotations, the residual is converged to machine precision within a few iterations. The cylinder displaced configuration at the same time levels is shown in Fig. 3.

Remark 1

In the present work, the kinematic constraints employed in all computations result in a planar motion of the bridge deck, and the expression given by Eq. (33) remains valid. In the case of small rotations, approximation of the partial derivative given by Eq. (33) also holds true, and possibly presents a reasonable simplification when deriving the left-hand-side matrix for the general case.

3.4 Time integration of the coupled system

The semi-discrete equations of fluid mechanics (Eq. (18)) and mesh motion (Eq. (23)) are integrated in time using the Generalized-\( \alpha \) technique [59, 65,66,67]. A block-iterative approach is employed, where, within a time step, increments of the fluid mechanics, rigid-object, and mesh motion problems are computed sequentially. This approach is efficient for the present application because the added mass effect is not significant.

4 Simplified flutter analysis

In the following section we give a brief presentation of the aeroelastic forces focusing on the application to flutter analysis. For a more detailed description the reader is referred to [68] and references therein. According to strip theory and the definitions and conventions in Fig. 4, the aerodynamic forces acting on a bridge cross section with height H and width B subjected to wind speed U are decomposed into drag, lift and pitching moment, which are denoted D, L and M, respectively. Their corresponding degrees-of-freedom (DOF) are p, h and \( \theta \), that match the DOFs in the FOI formulation presented in Sect. 2.2.

Flutter analysis deals with the aerodynamic forces that arise from structural motion, namely, the self-excited forces. Disregarding the lateral component, which in our experimental setup is fixed, the self-excited forces are defined in accordance with [46, 69] as

$$\begin{aligned} L^{se}&= \frac{1}{2}\rho U^2 B \bigg ( KH_1^*\frac{\dot{h}}{U} + KH_2^*\frac{B\dot{\theta }}{U} + K^2H_4^*\frac{h}{B} + K^2 H_3^* \theta \bigg ), \end{aligned}$$
(38)
$$\begin{aligned} M^{se}&= \frac{1}{2}\rho U^2 B^2 \bigg ( KA_1^*\frac{\dot{h}}{U} + KA_2^*\frac{B\dot{\theta }}{U} + K^2A_4^*\frac{h}{B} + K^2 A_3^* \theta \bigg ), \end{aligned}$$
(39)

where \( \rho \) is the air density, \( K = B\omega /U \) is the reduced frequency of the structural motion, \( \omega \) being the circular frequency, and \( H^*_i \) and \( A^*_i \), \( i \in \{1,...,4\} \) are the dimensionless flutter derivatives. These are commonly given as functions of the reduced velocity, \( V_{red} = K^{-1} \). Superscript se stands for “self-excited”.

Fig. 4
figure 4

Aeroelastic forces acting on a 1:50 scale model of the Hardanger bridge

Full size image

Using matrix notation, the self-excited forces can expressed as

$$\begin{aligned} \mathbf {q}^{se} = \mathbf {C}_{ae} \dot{\mathbf {r}} + \mathbf {K}_{ae}\mathbf {r}, \end{aligned}$$
(40)

where \( \mathbf {q}^{se} = \left[ L^{se},M^{se}\right] ^T\) and \( \mathbf {r} = \left[ h, \theta \right] ^T\). The matrices \( \mathbf {C}_{ae} \) and \( \mathbf {K}_{ae} \) are commonly recognized as aerodynamic damping and stiffness, respectively, and are given by

$$\begin{aligned} \mathbf {C}^{ae} = \frac{1}{2}\rho U K \begin{bmatrix} H_1^*&BH_2^* \\ BA_1^*&B^2A_2^* \end{bmatrix}, \end{aligned}$$
(41)

and

$$\begin{aligned} \mathbf {K}^{ae} = \frac{1}{2}\rho U^2 K^2 \begin{bmatrix} H_4^*&BH_3^* \\ BA_4^*&B^2A_3^* \end{bmatrix}. \end{aligned}$$
(42)

Given the still-wind mass, damping, and stiffness matrices, \( \mathbf {M}_0 \), \( \mathbf {C}_0 \) and \( \mathbf {K}_0 \), respectively, dynamic equilibrium of the aeroelastic system is then given by

$$\begin{aligned}&\mathbf {M}_0\mathbf {G}_{\ddot{\mathbf {r}}}(\omega ) + \left( \mathbf {C}_0 - \mathbf {C}^{ae}(U,\omega )\right) \mathbf {G}_{\dot{\mathbf {r}}}(\omega ) \nonumber \\&\quad + \left( \mathbf {K}_0 - \mathbf {K}^{ae}(U,\omega )\right) \mathbf {G}_{\mathbf {r}}(\omega ) = \mathbf {G}_{\mathbf {q}}(\omega ). \end{aligned}$$
(43)

Here, \( \mathbf {G}_{\ddot{\mathbf {r}}}(\omega ) \), \( \mathbf {G}_{\dot{\mathbf {r}}}(\omega ) \) and \( \mathbf {G}_{\mathbf {r}}(\omega ) \) are the Fourier transforms (in time) of the acceleration, velocity, and displacement response, respectively. \( \mathbf {G}_{\mathbf {q}}(\omega ) \) is the Fourier transform of the remaining dynamic forces acting on the system, which include buffeting forces as an important contribution.

Fig. 5
figure 5

2D schematic of the free-vibration test rig with the two degrees-of-freedom labeled

Full size image

The stability of the second-order system with \( N = 2 \) still-air vibration modes in Eq. (43) is governed by the eigenvalue problem

$$\begin{aligned}&\left( \lambda _n^2 \mathbf {M}_0 + \right. \lambda _n \left( \mathbf {C}_0 - \mathbf {C}^{ae}(U,\omega )\right) \nonumber \\&\quad + \left. \left( \mathbf {K}_0 - \mathbf {K}^{ae}(U,\omega )\right) \right) \varvec{\varPhi }_n = 0, \quad n = 1,2,... 2N. \end{aligned}$$
(44)

The solution of Eq. (44) gives 2N eigenvalues \( \lambda _n = \mu _n + i\omega _n \) and eigenvectors \( \varvec{\varPhi }_n \), and takes the form

$$\begin{aligned} \mathbf {r}(t) = \sum \limits _{n = 1}^{2N}\varvec{\varPhi }_n \exp \left( (\mu _n + i\omega _n) t \right) . \end{aligned}$$
(45)

To ensure dynamic stability, the real parts \( \mu _n \) of all eigenvalues should be negative, leading to a decaying response. On the other hand, if any complex eigenvalues have a positive real part, Eq. (45) exhibit exponential divergence, which is recognized as flutter. The onset of flutter, or the critical wind speed, \( U_{crit} \), occurs at the lowest wind speed for which the real part of \( \lambda _n \) switches sign. Its corresponding eigenvector then represents the flutter mode.

5 Experimental and computational setup

In what follows, we describe the experimental setup and test strategy for the free-vibration wind tunnel experiments performed in this work, and the analysis setup for the numerical simulations. The considered bridge sectional model is a 1:50 scale model of the Hardanger bridge, which is representative of many modern bridge sections. Its aerodynamic performance has also been studied earlier in [2, 26, 47, 68]. We follow the modus operandi for most such experiments (see [70] and references therein), using coherent scaling of the dimensions and masses of the bridge section and constant ratio between the first heaving and torsional mode.

Although the forced-vibration method is often preferred to assess the aerodynamic performance due its repeatability and simplified parameter identification procedures, the free-vibration method is still commonly used as a verification tool.

5.1 The free-vibration rig

A schematic 2D view of the free-vibration rig is shown in Fig. 5. The sectional model is suspended vertically via rotation arms with a leverage that gives the targeted frequency ratio. In the horizontal direction the rig is pretensioned with lightweight wires, which are sufficiently long to reduce the geometrical stiffness contribution to a minimum. Additional masses to the center bar and rotation arm are introduced to achieve the proper mass scalings. Figure 6 shows the section installed in the wind tunnel.

5.2 Instrumentation

Load cells (AEP Type TS 25 kg) measure the vertical spring forces. From these, we estimate the displacements via relations determined from separate calibration tests of each spring and static measurements of the installed section. From the displacements in each of the springs we easily compute the motions of the sectional model.

To monitor the pretensioning and drag component, load cells are also installed at the upwind horizontal suspension (AEP Type TCA 5 kg). For signal acquisition and analysis we use HBM Quantum X and Catman software.

5.3 Test strategy

In order to study the aerodynamic contributions, we need a precise estimation of the system properties in still-wind. We base the system identification on known masses and eigenfrequencies. Thus we also include the geometrical stiffness from the horizontal pretension. As the inertia cannot be calculated without notable uncertainties, we use a system perturbation technique that involves adding a known amount of inertia to the rotation arm and measuring the change in frequency. Damping is estimated by a logarithmic decrement.

The identified system properties, and the corresponding full scale quantities, are summarized in Table 1. The damping ratios vertically and torsionally are read from single-frequency experiments at amplitudes of \( h = 15 \) mm and \( \theta = 3^{^{\circ }} \), respectively. The full-scale data are taken from [68], and represents the modal quantities of the first symmetrical heaving and torsional modes. The experimental setup renders mass and inertia scaling factors of \( 50.0^2 \) and \( 47.6^4 \), respectively, which plainly satisfy the geometric scaling.

According to Eq. (44), the flutter wind speed is estimated to be \( U_{crit} = \) 8.16 and 7.48 m/s using the numerically and experimentally determined aerodynamic derivatives reported in [26] and [45], respectively.

In this work we consider the still-wind case, as well as wind speeds of approximately 25, 50 100% of \( U_{crit} \).

Fig. 6
figure 6

Sectional model installed for free-vibration experiments. The center bar extends through the circular hole so that most of the apparatus is outside the wind-tunnel walls. Note the horizontal suspension attached to the center bar

Full size image
Table 1 Still-air system properties for the experimental setup
Full size table
Fig. 7
figure 7

Problem mesh. a Full computational domain, b zoom on the leading edge

Full size image

5.4 Analysis setup

The computational domain is taken as a box that represents a 0.25 m-wide slice of the wind tunnel, spanning a distance of 3B upwind and 8B downwind from the bridge-deck centroid. The height is set to 1.815 m, same as the wind-tunnel physical dimension. For the boundary conditions a uniform wind speed U is prescribed on the inflow surface. The walls and transverse boundaries are constrained with no-penetration, and the outflow boundary is traction-free. The bridge deck surface is constrained with weakly-enforced no-slip BC. For the rigid-body, only the vertical-displacement and rotation DOFs are kept active in all simulations.

The air density is set to \( \rho = 1.225 \, \mathrm {kg/m^3}\) and the dynamic viscosity is set to \( \mu = 1.7894 \times 10^{-5} \, \mathrm {kg/ms} \). The time step is set to \( \varDelta t = 0.001 B/U \), which keeps the maximum Courant number at 2.5 or lower.

For discretization we use unstructured linear tetrahedra and triangular prisms, with local refinement near the bridge deck and in its wake region. To guarantee good mesh quality near the bridge deck, we adopt the Solid-Extension Mesh Moving Technique (SEMMT) [71, 72]. In this approach, structured layers of prismatic elements undergo the same rigid-body motion as the bridge deck itself, which preserves the original mesh quality near the bridge deck in the moving-mesh simulations. Moreover, this approach significantly reduces the cost of the mesh-motion problem. Fig. 7 shows an outline of the computational domain and a detailed view of the bridge deck that shows the boundary-layer elements and indicates the general mesh density.

The total number of nodes in the model is 644,000, and the computations are performed in a parallel environment described in [73] using 256 compute cores.

6 Results and discussion

In this section we present the numerical results. Our main goal is to test if FOI formulation is able to capture the effect of the aerodynamic forces on the eigenfrequencies and damping. Especially the latter is of particular interest in the analysis of aerodynamic stability. The damping is represented by the logarithmic decrement, \( \delta \), whose relationship to the damping ratio is given by \( \delta = 2\pi \zeta /\sqrt{1-\zeta ^2}\). A selection of videos and visualizations from the experiments and simulations are available at our Youtube channel ”Structural Dynamics NTNU”.

Fig. 8
figure 8

Displacement of the bridge deck centroid for still-wind simulations with the vertical motion (top) and the torsional motion (bottom) actuated. Wind-tunnel experimental data are aligned at \( t = 0 \)

Full size image
Table 2 A summary of the experimentally and numerically obtained eigenfrequencies and damping ratios for various wind speeds
Full size table

6.1 Still-wind simulations

To test the formulation and assess the still-wind damping and stiffness, free decay simulations are performed for the vertical and torsional degrees-of-freedom. The system properties determined from such experiments are commonly referred to as structural properties, however, as the aerodynamic loads are nonzero, also these have an aerodynamic contribution which can be quantified by the simulations.

The system masses are taken from Table 1. To account for the aerodynamic stiffness contribution (which would slow down the structural motion according to Eq. (44)), the eigenfrequencies are set to \( \omega _h = 5.072 \) and \( \omega _{\theta } = 12.675 \) rad/s. This small adjustment is based on the phase-lag from a one-period test simulation. Similarly, the structural, or external damping ratios are set to \( \zeta _{h} = 5\times 10^{-4} \) and \( \zeta _{\theta } = 7\times 10^{-4} \). For the initial condition the bridge section is ramped up to \( h = 20 \) mm and \( \theta = 3^{^{\circ }}\) from its equilibrium position for the two simulations, respectively. For stability reasons, the inflow velocity is set to small value of \( U = 0.1\,\hbox {m/s}\).

Fig. 8 shows the displacement time histories for the two simulations together with the corresponding wind tunnel experiments. To assess the aerodynamic contribution, the oscillation envelopes of the mechanical damping are shown in the same plot. A summary of the results also follows in Table 2. The almost indistinguishable results prove that with the proper choice of structural stiffnesses and damping the formulation captures the still-wind behavior with excellent accuracy. We also observe that still-wind vertical damping is dominated by the aerodynamic forces.

Fig. 9
figure 9

Logarithmic decrement with respect to the displacement amplitude for the vertical (top) and torsional (bottom) motion in still wind

Full size image
Fig. 10
figure 10

Snapshots of vorticity contours and velocity vectors for the vertical (top) and pitching (bottom) motion in still wind. Here \( t_0 \) represents the time level at a lower peak displacement, and \( T = 2\pi /\omega \) is the period

Full size image
Fig. 11
figure 11

Displacement time series of the bridge deck subjected to a wind speed of \( U = 1.75 \) m/s and actuating the heaving (top) and pitching (bottom) mode. Wind-tunnel experimental data are aligned at \( t = 0 \)

Full size image

Figure 9 shows the logarithmic decrement with respect to the displacement amplitude for the two simulations. First, we notice that the damping is extremely low for the still-wind condition. Further, it appears to vary linearly with the vibration amplitude, a phenomenon which is also reported in [47]. This behavior is very precisely captured in the simulations. The amplitude-dependent damping arises from correlation between the aerodynamic forces and structural velocity. Because vertical motion induces more vorticity, and, consequently, higher energy dissipation than the pitching motion, as can be seen from the snapshots in Fig. 10, it is also subjected to more aerodynamic damping.

6.2 In-wind simulations

Using the same system properties we now perform free-vibration simulations at wind speeds \( U = 1.75\) and 3.85 m/s, where the aeroelastic forces are no longer negligible. The same analysis setup is used as described in Sect. 5.4.

Fig. 12
figure 12

Displacement time series of the bridge deck subjected to a wind speed of \( U = 3.85 \) m/s and actuating the heaving (top) and pitching (bottom) mode. Wind-tunnel experimental data are aligned at \( t = 0 \)

Full size image
Fig. 13
figure 13

Logarithmic decrement with respect to the displacement amplitude for the vertical (top) and torsional (bottom) motion for \( U = 1.75\) m/s

Full size image
Fig. 14
figure 14

Logarithmic decrement with respect to the displacement amplitude for the vertical (top) and torsional (bottom) motion for \( U = 3.85\) m/s

Full size image

Figures 11 and 12 show displacement time histories for \( U = 1.75 \) and \( U = 3.85 \) m/s, respectively, and their corresponding damping ratios are shown in Figs. 13 and 14. Table 2 summarizes the results.

For the vertical displacement DOF, we capture its magnitude very well. Invariance of the aerodynamic damping with respect to the displacement magnitude is also captured with excellent accuracy. Good results are likewise obtained for the torsional DOF, however, the simulation predicts higher aerodynamic damping. This observation corresponds with the overestimation of the \( A^*_1 \) and \( A^*_2 \) aerodynamic derivatives our earlier work [26]. It should be remarked that, already at 25% of the flutter wind speed, the vertical-displacement aerodynamic damping is one order of magnitude higher than the still-wind damping.

The magnitude of the aerodynamic stiffness is slightly overestimated in both DOFs, however, its evolution with the wind speed agrees very well with the experiments.

From the time histories, most prominently for \( U = 3.85 \) m/s, we notice a difference in the mean displacements. This indicates that the simulations produce different absolute values of the aerodynamic lift and pitching moments. However, other sources of errors, e.g. inaccurate alignment of the sectional model, are also present. Since the mean values are removed in the analysis of motion-induced forces and flutter, this issue is not further addressed in this work.

Fig. 15
figure 15

Time histories of the vertical displacement and rotation angle

Full size image

Remark 2

We want to emphasize that although the heaving and pitching time series are hitherto drawn together, they are computed sequentially. The DOF which is not actuated is still active, however, it undergoes vanishingly small excitation due to the narrow-banded nature of the aerodynamic forces which act in the region of the dominating motion.

Remark 3

It should be noted that the reported eigenfrequencies are in fact the damped natural frequencies. The effect of damping on the vibration frequency is, however, vanishingly small compared to the contribution from the aerodynamic stiffness.

6.3 Flutter

Combining the system properties in Table 1 and the aerodynamic derivatives from forced-vibration wind tunnel experiments [45], solution of the eigenvalue problem Eq. (44) gives \(U_{crit} = 7.48\) m/s and a critical vibration frequency of \( \omega _{cr} = 10.11 \) rad/s. From the numerically obtained aerodynamic derivatives reported in [26], the corresponding results are \( U_{crit } = 8.16 \) m/s and \( \omega _{cr} = 8.92 \) rad/s.

Fig. 16
figure 16

Snapshots of vorticity contours and velocity vectors for the flutter simulation. Here \( t_0 \) represents the time level at a lower peak displacement, and \( T = 2\pi /\omega \) is the period

Full size image

From the free-vibration experiments we obtain \( U_{crit} = 8.16 \) m/s and \( \omega _{cr} = 9.80 \) rad/s. Using the same wind velocity in the simulations we obtain a diverging response, which indicates that we are above, but close to \( U_{crit} \). Time histories are shown in Fig. 15, and it is evident that the simulation gives a very accurate representation of the flutter mode in terms of the frequency (\( \omega _{cr} \) = 9.084) and mode shape. A visualization of the flutter mode is given in Fig. 16, from where we see that the bridge deck is undergoing a pitching motion with a center of rotation very close to the leading edge.

The good correspondence between the predicted flutter characteristics obtained numerically by the forced-vibration method in [26] and the experimentally obtained flutter herein provides additional validation of the fluid mechanics part of the computational framework employed in this work.

7 Conclusions

This paper presents an FOI modeling approach with a coupling between the ALE-VMS formulation for fluid dynamics and equations of a rigid object. The rigid-object formulation is augmented with external stiffness and damping, which makes it suitable for many engineering applications, such as vibration analysis of bridge decks.

For the rigid-body formulation we have proposed a modified time-integration algorithm, in which a linear relationship between the Euler-angle time derivative and angular velocity vector is assumed in the expression for the tangent matrix employed in the rigid-object algorithm.

The resulting formulation was employed to simulate the free-vibration wind-tunnel experiments of the 1:50 scale model of the Hardanger bridge section. The latter were also carried out as part of this work. The results show that the FOI formulation reproduces the aeroelastic behavior with excellent accuracy. Tests at different wind speeds reveal the evolution of aerodynamic stiffness and damping, where especially the latter is heavily influenced by the aerodynamic forces. Numerical simulation at the flutter stability limit also show that the FOI formulation captures the critical wind speed and the corresponding vibration mode.

In the context of bridge engineering, free-vibration wind-tunnel experiments often serve to validate their corresponding forced-vibration experiments. Analogously, this work serves as a validation of the forced-vibration computational framework presented by the same authors in [26], which gave flutter characterization that is in very good agreement well with the free-vibration results obtained herein. Besides validation of forced vibrations, the authors believe that the computational framework presented herein can be a valuable tool to quickly assess the more general aeroelastic performance of bridge sections, which is especially important for the front-end engineering design.