Abstract
Computational models based on the phase-field method have become an essential tool in material science and physics in order to investigate materials with complex microstructures. The models typically operate on a mesoscopic length scale resolving structural changes of the material and provide valuable information about the evolution of microstructures and mechanical property relations. For many interesting and important phenomena, such as martensitic phase transformation, mechanical driving forces play an important role in the evolution of microstructures. In order to investigate such physical processes, an accurate calculation of the stresses and the strain energy in the transition region is indispensable. We recall a multiphase-field elasticity model based on the force balance and the Hadamard jump condition at the interface. We show the quantitative characteristics of the model by comparing the stresses, strains and configurational forces with theoretical predictions in two-phase cases and with results from sharp interface calculations in a multiphase case. As an application, we choose the martensitic phase transformation process in multigrain systems and demonstrate the influence of the local homogenization scheme within the transition regions on the resulting microstructures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The microstructure of most materials consists of grains or domains which differ in structure, orientation or chemical composition. Both the evolution of these grains or domains and the resulting heterogeneous microstructure have a decisive influence on the physical and mechanical properties of materials [1, 2]. This is why the understanding of the mechanisms, which are responsible for the evolution of the microstructure, is extremely important in materials science. The movement of interfaces, however, is a complex process, which is influenced by different physical forces. The phase-field method, which has its origin in the fundamental works of van der Waals [3], Ginzburg and Landau [4], Cahn and Hilliard [5] and Halperin et al. [6], offers excellent characteristics, not only for a precise representation of the interface movement, but also for coupling different driving forces, which are responsible for the movement. It has therefore established itself in the modeling of microstructural evolution processes, such as solidification, solid-solid phase transition, growth and coarsening of precipitations, grain growth and martensitic phase transformation [2, 7]. In the phase-field method, we typically map a given sharp interface-free boundary problem onto a diffuse interface one that is constructed of smoothly varying phase-field order parameters. The different physical fields (concentration, stress, strain, etc.) vary continuously across the constructed interface, following the variation of the order parameters. Such a construction is advantageous because it obviates the requirement to track the interface between the phase boundaries during microstructural evolution [1, 8], as morphological evolution is implicitly described through the spatio-temporal evolution of the different order parameters. Concomitant with the evolution of the phase fields, the different physical fields related to the mass, the momentum and the energy are self-consistently described using appropriate conservation equations. Although the process is elegant, appropriate care must be taken in the construction of the evolution equations of the phase-fields and the conservation equations, which generally require a homogenization of the variables exhibiting jumps across the interface in the original sharp interface problem. In the absence of the correct homogenization scheme, artificial jumps in the continuous variables can be introduced into the problem, which then lead to an incorrect mapping of the actual free boundary problem.
When describing solid state transformation processes or predicting microstructure and mechanical property relations, an accurate calculation of the stresses and the mechanical energy at the transition region is indispensable. This requires that the effective material parameters are defined in the diffuse interface regions in non-homogeneous materials, which is usually performed by a local homogenization of the material parameters, using smoothly varying functions of the spatially varying phase-fields. In the phase-field community, there are several homogenization approaches, see [9] for an overview. Khachaturyan’s model [10] is widely established in phase-field applications. In the absence of inelastic strains, the model of Khachaturyan is equal to the Voigt-Taylor (VT) homogenization scheme [11] between locally overlapping phases. The main assumption of the VT approach is that the strains of overlapping phases are the same. For a system with N phases, with an order parameter \(\phi _\alpha \) for the particular phase \(\alpha \), the stress in the isostrain case reads
\(\varvec{\varepsilon }\) is the linearized strain which, in turn, depends on the gradient of the displacement field \({\left( \varvec{\nabla }\varvec{u}\right) }_{ij}=\partial u_i / \partial x_j\) by \(\varvec{\varepsilon }= \big ( \varvec{\nabla }\varvec{u} + \varvec{\nabla }\varvec{u}^T\big )/2\), and \(\sigma _{ij} = {\left( \varvec{\mathcal {C}} [\varvec{\varepsilon } - \tilde{\varvec{\varepsilon }}]\right) }_{ij} = \mathcal {C}_{ijkl}(\varepsilon _{kl} - \tilde{\varepsilon }_{kl})\) is the particular stress component which uses the Einstein summation convention. \(\tilde{\varvec{\varepsilon }}^\alpha \) and \(\varvec{\mathcal {C}}^\alpha \) represent the local inelastic strain and the stiffness tensor of phase \(\alpha \). A complete definition of the interpolation function \(h^\alpha (\varvec{\phi })\) for phase \(\alpha \) and the N-tuple \(\varvec{\phi }\) follows in Sect. 2. This approach is employed in [12,13,14,15,16]. Levitas [17] combines the VT interpolation scheme with an interfacial stress formulation. Assuming equal stresses in the transition region results in the Reuss-Sachs (RS) [18] approximation
where \(\varvec{\mathcal {S}}^\alpha \) is the compliance tensor of phase \(\alpha \). The local homogenization scheme is discussed by Steinbach and Apel [19] and Apel et al. [20]. Ammar et al. [9] propose a Hashin-Shtrikman homogenization between locally existing phases and present an accurate comparison between Khachaturyan’s, the VT, RS and their own approach. Durga et al. [21] and recent works of Schneider et al. [22, 23] investigate the excesses of the stress, strain and the elastic energy for both the VT interpolation and the RS interpolation to estimate the material properties at the interface. As a result of the calculations, it is clear that the RS interpolation delivers an interface free of excess energy, under conditions of uniaxial loading in normal direction, while the conditions of a parallel material circuit with a pure shear loading require a VT interpolation, such that there is no excess contribution from the bulk energy density to the surface energy. With this motivation, Durga et al. [21] propose a model by combining the VT and RS interpolation schemes, wherein a VT interpolation is imposed in order to derive the tangential stress component, and the RS scheme is utilized to determine the normal stress components with respect to the interface. In a recent publication, Mosler et al. [24] present a variational approach for the calculation of stresses and, correspondingly, for the driving force of the phase evolution in the transition region. The model is already formulated for applications with finite deformations and allows the use of arbitrary hyperelastic constitutive equations. A generalization of the model for the usage in polycrystalline systems is discussed by Schneider et al. [25].
In our recent works [22, 23], we investigate the reasons for the additional interfacial excess energy contributions caused by the underlying homogenization assumption and propose a homogenization scheme reflecting the mechanical jump conditions. The resulting stresses are validated by theoretical sharp interface predictions and demonstrate the absence of additional excess energy. One of the main results of our investigations is a potential which contains only continuous variables to calculate the stresses and driving forces. This explicit formulation for the computation of stresses, in combination with the multiphase-field model of Nestler et al. [26], allows the derivation of a model which fulfills the mechanical jump conditions and yields the configurational forces during solid state phase transformations in multiphase systems. This is the topic of the current work, which was comprehensively discussed in the thesis of Schneider [23]. In contrast to the approaches of Mosler et al. [24] and Schneider et al. [25], the presented model provides an explicit formulation of the locally homogenized stresses and the driving forces, which improve the computational efficiency. After the definition of the multiphase-field model used here, we investigate the consequences of the interpolation schemes and demonstrate the reasons for the additional excess energy. Then, we derive the configurational force balance in the phase-field context and demonstrate that the model we derived in our previous work [22] already fulfills this balance. We extend this model for applications to multiphase systems and demonstrate the applicability of the proposed model on martensitic phase transformations in multigrain systems.
2 Multiphase-field model
On the mesoscopic scale, which is situated between the atomistic and the macroscopic length scale, most materials are heterogeneous. The multiphase-field model [26] describes the evolution of the microstructure in multiphase and multicomponent systems on the mesoscopic length scale. Therefore, the parametrization of the simulation region is realized by order parameters, \(\phi _\alpha (\varvec{x}, t)\), \(\alpha = 1, \dots \), N, with N as the number of order parameters. In most materials, the heterogeneity of the material parameters is limited to jumps at the interface between grains or domains. Within the physically separated regions, which are referred to as phases [27], the material parameters are homogeneous. For this reason, each phase can be represented by an order parameter. Each order parameter is part of the N-tuple \(\varvec{\phi }(\varvec{x}, t)\) and represents the respective volume fraction of the individual phases. Within its assigned region, the order parameter becomes \(\phi _\alpha (\varvec{x}, t) = 1\) and outside it assumes the value \(\phi _\alpha (\varvec{x}, t) = 0\). In contrast to models with sharp interfaces, the transition between the phases is diffuse. This means that a volumetric transition region exists, where at least two order parameters coexist. In this diffuse interface region, the value of the order parameters changes continuously in the range of \(0<\phi _\alpha (\varvec{x}, t)<1\), so the phases become continuous fields.
The local condition \(\sum _\alpha \phi _\alpha (\varvec{x}, t) = 1\) must always be satisfied, as the order parameters represent the respective volume fraction of the individual phases. As the interface between the order parameters, and therefore between the phases, stretches over a volumetric region, the grain boundary energy can be reproduced by a volume integral by skillfully choosing the integrand. This leads to a Ginzburg-Landau-type [4] functional. Among others, Nestler et al. [26] have successfully managed to equip the phase-field model with sufficient degrees of freedom, in order to treat the physics at each occurring interface of a system of N phases and the interaction of two adjacent phases individually [28]. This allows the formulation of a Ginzburg-Landau-type integral for multiphase systems and the free energy of the system becomes
with \(\epsilon \) as a parameter for the interface width l. With \(\gamma _{\alpha \beta }\) as the surface energy at an \(\alpha \)–\(\beta \) interface, the contribution of the interfacial energy is represented by the interaction of a gradient energy density, e.g. of the form
and of the potential energy density \(\omega (\varvec{\phi })\) of obstacle- or well-type
as presented in Nestler et al. [26]. The separation of the individual dual contributions of the interfacial energy is made possible by the generalized \(\alpha \)–\(\beta \) gradient \(\varvec{q}_{\alpha \beta }= \phi _\alpha \varvec{\nabla }\phi _\beta - \phi _\beta \varvec{\nabla }\phi _\alpha \) (\(|\varvec{q}_{\alpha \beta }|\) is the vector norm of \(\varvec{q}_{\alpha \beta }\)). According to the application, one can choose between the multi-obstacle potential \(\omega _{\text {ob}}(\varvec{\phi })\) and the multi-well potential \(\omega _{\text {we}}(\varvec{\phi })\). In the case of the multi-obstacle potential, we set \( \omega _{\text {ob}}(\varvec{\phi }) = \infty \) if the N-tuple of the order parameters \(\varvec{\phi } = \phi _1, \ldots , \phi _{N}\) is not in the Gibbs simplex
The additional higher-order contribution \(\propto \phi _\alpha \phi _\beta \phi _{\delta }\) in the potential (5) or \(\propto \phi _\alpha ^2 \phi _\beta ^2 \phi _{\delta }^2\) in the potential (6) respectively prevents the non-physical formation of the so-called third phases [26] in the two-phase region. A comprehensive discussion of this term can be found in Hötzer et al. [29]. In the current work, the multi-obstacle potential \(\omega _{\text {ob}}(\varvec{\phi })\) is used as the energetic potential.
With the interpolation functions \(h^\alpha (\varvec{\phi })\) of the individual phases, the bulk energy density
is assigned to each point in the system. Depending on the application, either the respective order parameter \(\phi _\alpha \) or a variant with a sharper transition can be used for the interpolation function \(h^\alpha (\varvec{\phi })\) [26]. However, it should be ensured that the condition \(\sum _\alpha h^\alpha (\varvec{\phi }) = 1\) is always fulfilled [30]. Based on interpolation functions for two-phase systems, which are exemplified as follows
a normalized interpolation function in polycrystalline systems can be defined as
Such an interpolation function is already used by Schneider et al. [16] for the modeling of crack propagation in multiphase systems.
The variational approach in the presence of the additional constraint \(\sum _\alpha \phi _\alpha = 1\) leads to the following conditions for the equilibrium of the order parameters
as described in [26]. An equilibrium of the total system implies additional balance equations if other field variables, denoted by \((\ldots )\) in Eqs. (3) and (8), are considered. Since the mobilities of the interfaces in this combined system vary considerably, condition (11) is split into dual contributions and an individual mobility \(M_{\alpha \beta }\) is subsequently introduced for each \(\alpha \)–\(\beta \) interface. This leads to Allen-Cahn equations for each single phase in the multiphase system, with different mobilities of the interfaces
Thereby, \(\dot{\phi _\alpha } = \partial \phi _\alpha / \partial t\) is the time derivative of \(\phi _\alpha \) and \(\delta \mathcal {F}/ \delta \phi _\alpha \) is the variational derivative of the total energy, with respect to \(\phi _\alpha \)
where \((\varvec{\nabla }\cdot )\) is the divergence operator. Such an approach was originally proposed by Steinbach and Pezzolla in [31] and was successfully applied by Schneider et al. [16] to describe crack propagation in multiphase systems, with wide-ranging mobilities between solid phases and the crack phase.
3 Consequences of the homogenization methods on the evolution of the order parameters
In our preliminary work [22], we showed that the local homogenization schemes for the calculation of the stresses only yield satisfying results in special one-dimensional cases. The VT approximation provides exact results for the parallel material chain and the RS approximation produces exact results for the serial material chain. General conditions lead to deviations of both schemes, which depend on differences of the respective material parameters \(\varvec{\mathcal {C}}^\alpha \) and the inelastic strains \(\tilde{\varvec{\varepsilon }}^\alpha \). The consequences of the deviations for the evolution equation of the order parameters (12) are discussed in the following.
For the case of infinitesimal deformations, volumetric averaging
of phase-inherent stresses \(\varvec{\sigma }^\alpha \) and strains \(\varvec{\varepsilon }^\alpha \) can be performed with the interpolation function (10), without loss of generality. However, these phase-inherent fields are generally not known and vary depending on the homogenization assumption. With \(W^\alpha (\varvec{\varepsilon }^\alpha )\) as the strain energy density of phase \(\alpha \), the locally averaged Helmholtz strain energy density results in
By considering this total strain energy density and by applying the obstacle potential, the free energy of the system is given by
In order to calculate the interfacial energy, an integral over the gradient energy density \(\epsilon a(\varvec{\phi }, \varvec{\nabla }\varvec{\phi })\) and the free energy potential \(\omega _{\text {ob}}(\varvec{\phi }) / \epsilon \) of the functional (16) can be evaluated in the direction of the interface normal. Independently of the choice of the interface width parameter \(\epsilon \), both potentials are constructed in such a way that this integral exactly equals \(\gamma _{\alpha \beta }\) in the absence of additional driving forces.
For the calculation of the equilibrium profile under the influence of the total strain energy \(\bar{W} (\varvec{\phi }, \bar{\varvec{\varepsilon }})\), a two-phase material chain with a phase transition in the center of the domain is considered. There, the evolution Eq. (12) of the respective order parameters in the two phase region assumes the following form
where x is the spatial coordinate of the material chain. In equilibrium, the local rate of change of the order parameters \(\dot{\phi }_\alpha \) disappears. This yields the following equation for the equilibrium profile
In order to maintain a distortion-free profile of the order parameters, the derivative of the strain energy density, with respect to the order parameters, must vanish in equilibrium. If this is not the case, the profile of the order parameters is distorted by the additional contribution. Since an undistorted profile is required for the calculation of the exact interfacial energy \(\gamma _{\alpha \beta }\), a distortion of the profile causes a deviation from the expected value.
Since the formulation of the total energy by Eq. (16), with a diffuse transition region is supposed to approximate the total energy of the system with sharp interfaces, the excess energy is the difference of the energy within the phases of a system with sharp interfaces and the formulation with a diffuse transition region (16) [5]. Thus, for a one-dimensional system with one transition region, this leads to the following excess energy
where \(W_{\text {SI}}\) is the strain energy density in a sharp interface system [5, 21]. Consequently, any deviation in strain energy, obtained by the diffuse interface approach and the sharp interface method, produces an excess energy within the interface.
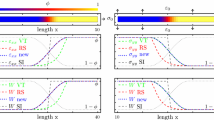
Comparison of the strain energy (left) and the complementary strain energy density (right) for the example of a serial material chain. The simulation setup, using \(\varvec{\mathcal {C}}_\beta = 0.2 \varvec{\mathcal {C}}_\alpha \), \(h^\alpha = \phi _\alpha \) and \(\epsilon = 5\varDelta x\), is shown in the inset of the right figure. The configurational equilibrium conditions \({G^\alpha } = {G^\beta } = {G_\text {SI}}\) and \(\sigma _{xx}^\alpha =\sigma _{xx}^\beta =\sigma _0\) are highlighted with dotted lines. The resulting excess energy of the VT approximation \(E_\text {exc}\) is marked in gray
The VT approximation relies on the fundamental assumption that the total strains \(\varvec{\varepsilon }\) in the transition region are equal. For the calculation of the Cauchy stress \(\bar{\varvec{\sigma }}^{\text {VT}}(\varvec{\phi })\) in the transition region, this assumption results in Eq. (1). Since the total strain \(\varvec{\varepsilon }\) under the VT assumption is phase-independent, it can be used to formulate the strain energy density. According to the model formulations in [12,13,14,15], this leads to the formulation of the strain energy density
On the other hand, the RS approximation assumes that the total stresses \(\varvec{\sigma }\) in the transition region are equal. As the stresses in the transition region are homogeneous, they can be used to formulate the complementary strain energy density \(G(\varvec{\sigma })\). Based on the formulation of the strain energy density with the VT approximation (20), the following relation results for the complementary strain energy density \(\bar{G}^\text {RS}(\varvec{\phi }, \varvec{\sigma })\) by means of a Legendre transformation. With \(\partial {W^\alpha } / \partial \varvec{\varepsilon } = \varvec{\sigma } = \varvec{\mathcal {C}}^\alpha (\varvec{\varepsilon } - \tilde{\varvec{\varepsilon }}^\alpha ) \Rightarrow \varvec{\varepsilon } = \varvec{\mathcal {S}}^\alpha [\varvec{\sigma }] + \tilde{\varvec{\varepsilon }}^\alpha \), the complementary strain energy density of phase \(\alpha \) is given by
Here, \(\varvec{\sigma }\) represents the Cauchy stress, which is given by Eq. (2). This results in the complementary strain energy density in a multiphase system, according to the RS approximation
In order to obtain a distortion-free profile of the order parameters, it is necessary that the derivative \(\partial \bar{W}{(\varvec{\phi }, \bar{\varvec{\varepsilon }})} / \partial \phi _\alpha \) vanishes in the configurational equilibrium condition (18) for a material chain, while holding the locally averaged strain \(\bar{\varvec{\varepsilon }}\) constant. The following refers to a serial material chain setup, as depicted in Fig. 1. Assuming locally averaged strains [see Eq. (14)] one obtains
where the condition \(\partial h^\alpha / \partial \phi _\alpha = - \partial h^\beta / \partial \phi _\alpha \) is used. The requirement for a distortion-free profile results in
for the serial material chain. Imposing \(\tilde{\varepsilon }^\beta =0\) results in the following relation for the configurational equilibrium of a serial material chain
Therein, \(\lambda ^\alpha , \lambda ^\beta \) and \(\mu ^\alpha , \mu ^\beta \) are the respective Lamé constants. In Fig. 1, the strain energy densities of both approximations are shown for the example of the serial material chain and the equilibrium state \({G^\alpha } = {G^\beta } = {G}_\text {SI}\), where \({G}_\text {SI}\) represents the sharp interface complementary strain energy density. Since the potentials \({G^\alpha }(\sigma _{xx})\) and \({G^\beta }(\sigma _{xx})\) depend only on the stress \(\sigma _{xx}\), and since \(\sigma ^\alpha _{xx}=\sigma ^\beta _{xx}=\sigma _0\) applies in the serial material chain, the equilibrium state for the RS approximation is exactly determined, as can be seen on the right side of Fig. 1. It is also clear that the complementary excess energy contribution
vanishes for the case of the RS approximation. Using strain energies, this equilibrium corresponds to an equilibrium line \({W_\text {SI}} = \left( \partial {G}_\text {SI} / \partial \sigma \right) \sigma _0 - {G}_\text {SI} = \varepsilon _{xx} \sigma _0 - {G}_\text {SI}\) between the bulk energies, defined through the reverse Legendre transformation of \({G}_\text {SI}\). The difference between the equilibrium line \(W_\text {SI}\) and \(\bar{W}^\text {VT}\) leads to excess energy, according to Eq. (19), and is highlighted in gray in Fig. 1.
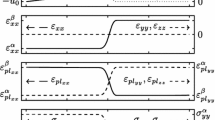
Comparison of the strain energy (left) and the complementary strain energy density (right) for the example of a parallel material chain. The simulation setup, using \(\varvec{\mathcal {C}}_\beta = 0.2 \varvec{\mathcal {C}}_\alpha \), \(h^\alpha = \phi _\alpha \) and \(\epsilon = 5 \varDelta x\), is shown in the inset of the left figure. The configurational equilibrium conditions \({W^\alpha } = {W^\beta } = {W_\text {SI}}\) and \(\varepsilon _{yy}^\alpha =\varepsilon _{yy}^\beta =\varepsilon _0\) are highlighted with dotted lines. The resulting excess energy of the RS approximation \(E^*_\text {exc}\) is marked in gray
For the case of the parallel material chain, which is shown in the inset of Fig. 2, the applied boundary condition and the configurational equilibrium condition (18) directly imply
where \(\tilde{\varepsilon }_{yy}^\beta = 0\) was chosen. The profiles of the strain energy densities for this case are shown in Fig. 2. In this case, the configurational equilibrium condition \({W^\alpha } = {W^\beta } = {W_\text {SI}}\) holds at one point, which is shown on the left side of Fig. 2. For the complementary strain energy, this equilibrium state leads to the equilibrium line \({G_\text {SI}} = \partial {W_\text {SI}} / \partial \varepsilon _{yy} - {W_\text {SI}} = \sigma _{yy}\varepsilon _0 - {W_\text {SI}}\). The deviation of \(\bar{G}^\text {RS}(\bar{\sigma }_{yy}(\varvec{\phi }))\) from the equilibrium line \({G_\text {SI}}\) within the interface region results in an additional complementary excess energy \(E^*_{\text {exc}}\) [see Eq. (26)], which is highlighted in gray in Fig. 2.
In case of the serial material chain, the excess energy of the VT approximation leads to a narrowing transition region, and in case of the parallel material chain, the complementary excess energy of the RS approximation causes the interface to widen. This, in turn, modifies the effective interfacial energy, as discussed in Durga et al. [21] and Schneider et al. [22].
4 Configurational force balance for infinitesimal deformations
The investigation of the driving force on inhomogeneities in continuum mechanics goes back to Eshelby [32, 33]. Displacements, vacancies, voids, cracks, but also inclusions in a medium are examples of such inhomogeneities. In 1975, Eshelby calculated the configurational forces on inhomogeneities [33]. Based on a variational approach, Gurtin derived the balance equations on the singular plane in a two-phase region [34, 35]. This results in the balance of linear momentum on a singular surface
and in an additional energetic condition
\(\varvec{S}\) is the first Piola–Kirchoff stress tensor and \(\varvec{n}^s\) is the normal vector of a singular plane, \(\llbracket . \rrbracket \) denotes the jump of a value through the interface, W is the strain energy density, \(\varvec{F}\) represents the deformation gradient and \((\cdot )\) denotes the inner product of vectors or tensors (\(\varvec{a} \cdot \varvec{b} = a_i b_i\), \(\varvec{A} \cdot \varvec{B} = A_{ij}B_{ij}\)). This additional condition is known as the Maxwell relation [34, 35] and was introduced by James [36] in 1981. According to Gurtin [35], a consideration of the contributions of the interfacial energy results in the energetic jump condition on singular planes
where \(\kappa \) represents the double mean curvature of the singular plane and \(\gamma _{\alpha \beta }\) represents the interfacial energy between the neighboring phases \(\alpha \) and \(\beta \). Equation (30) is referred to by Gurtin [35] as configurational force balance. Considering chemical configurational forces, Eq. (30) is equivalent to the generalized Gibbs–Thomson equation, which was derived by Johnson [37] in 1986. The Gibbs–Thomson equation balances all acting configurational forces on inhomogeneities in a body. Thus, \(\llbracket W \rrbracket - \llbracket \varvec{S} \varvec{n}_r^s \cdot \varvec{F} \varvec{n}^s_r \rrbracket \) is the elastic configurational force on inhomogeneities.
The Hadamard condition on a singular surface is given by
with \((\otimes )\) as the outer product of two vectors and \(\varvec{a} = \llbracket \varvec{F}\varvec{n}^s \rrbracket \) as the jump of \(\varvec{F}\) in normal direction (see e.g. [38]). Hence, for the jump of the infinitesimal strain, this leads to
With the balance of linear momentum on a singular surface
the balance of configurational forces (30) results in
By using the assumption \(\llbracket \varvec{\nabla }\varvec{u} \rrbracket \varvec{n}^s \cdot \varvec{\sigma }\varvec{n}^s \approx \llbracket \varvec{\varepsilon } \rrbracket \varvec{n}^s \cdot \varvec{\sigma }\varvec{n}^s\) for a geometrically linear case, according to Voorhees and Johnson [39], the configurational force balance (30) can be written as
Thus, Eq. (35) is the balance of the mechanical and surface configurational forces for infinitesimal deformations.
5 Multiphase elasticity model
In our preliminary work [22], a phase-field model for two phases was introduced and validated. Both the Hadamard condition (31) and the balance of linear momentum on a singular surface (33) are fulfilled during the phase transition. In this section, we demonstrate that this model already reflects exactly the balance of the configurational forces (35). This lays the foundation to investigate the influence of the mechanical configurational forces on phase transition and grain growth processes, using the introduced model. The necessary extension of the model to applications in polycrystalline systems is described in the following.
In a region with three phases \(\phi _\alpha \), \(\phi _\beta \) and \(\phi _\delta \), the normals of the respective phases are shown on the left. The three phases coexist in the highlighted region. This is why no unique normal can be defined. On the right, \({\mathcal {M}_E}(\varvec{\phi })\) (36) and the normals \(\varvec{n}\) (37) are presented. Since \(E^\beta =0.5E^\alpha \) and \(E^\delta =0.25E^\alpha \) are chosen, a lopsided normal profile is evident
The knowledge of the normal vector in the transition region is important for the application of the jump conditions (33) and (31), as well as for the calculation of the configurational forces (35). Apart from singularities, such as e.g. quadruple points or triple lines, respectively triple points in two dimensions, the normal vector is uniquely determined in the parametrization of a region with sharp interfaces. If the transition region is diffuse, a volumetric region exists, where several phases can coexist. Despite this coexistence, a normal vector \(\varvec{n}_\alpha = \varvec{\nabla }\phi _\alpha / |\varvec{\nabla }\phi _\alpha |\) for each phase \(\phi _\alpha (\varvec{x}, t)\) and point in the region can be assigned with the help of the existing order parameters. If only two phases coexist in a point, the normal vector is uniquely determinable, as  , and represents the normal vector on a singular surface \(\varvec{n}^s\). If more than two phases coexist, the normal vector can no longer be determined uniquely, as can be seen on the left side of Fig. 3. The three phases coexist in the highlighted area. For this reason, there are three different normals \(\varvec{n}_\alpha , \varvec{n}_\beta \) and \(\varvec{n}_\delta \) in each point of the area.
, and represents the normal vector on a singular surface \(\varvec{n}^s\). If more than two phases coexist, the normal vector can no longer be determined uniquely, as can be seen on the left side of Fig. 3. The three phases coexist in the highlighted area. For this reason, there are three different normals \(\varvec{n}_\alpha , \varvec{n}_\beta \) and \(\varvec{n}_\delta \) in each point of the area.
In the case of sharp interfaces, the singular plane is characterized by the jump of the material parameters \(\llbracket \varvec{\mathcal {C}}\rrbracket \), for both jump conditions (31) and (33) and the Maxwell relation (29). For isotropic materials, the jump of the Lamé constants \(\llbracket \lambda \rrbracket \), \(\llbracket \mu \rrbracket \) or the jump of the Young’s modulus \(\llbracket E \rrbracket \) and the Poisson’s ratio \(\llbracket \nu \rrbracket \) are sufficient for the explicit definition of the singular plane. Each of these material parameters can be employed for the calculation of a scalar field \(\mathcal {M}(\varvec{\phi })\) to calculate a unique normal. Expressed by the interpolated Young’s modulus, this yields
With this scalar field, a normal vector can be calculated as
for each point within the transition region, especially in regions with many overlapping phases. In accordance with the specification when only two phases coexist in a region, \(\varvec{n}({\mathcal {M}_E}(\varvec{\phi }))\) reduces to the formulation of a two-phase model
On the right side of Fig. 3, \({\mathcal {M}_E}(\varvec{\phi })\) and the normal vectors for the considered three-phase region are presented. When comparing both methods, it can be seen that the directions of the normals in the two-phase regions do not differ, as was shown by Eq. (38). If three phases coexist in a region, advantages of the normal calculation through Eq. (37) can be recognized. Since the normal vector is a locally homogenized quantity, the normal \(\varvec{\nabla }\phi _\alpha \) of the phase with the largest Young’s modulus \(E^\alpha \) is preferred. If the jump of the material parameters disappears between two phases, the gradient of \({\mathcal {M}}(\varvec{\phi })\) vanishes as well and the spatial point can be treated as a bulk material for any of the occurring phases. This is another advantage of this method, which can be used to reduce the complex calculation of stresses in transition regions to the calculation rule within a phase.
In general, the singular plane is characterized by the jump of the total stiffness tensor \(\llbracket \varvec{\mathcal {C}}\rrbracket \) and the jumps of the nonelastic strains \(\llbracket \tilde{\varvec{\varepsilon }} \rrbracket \). For this reason, the following general form is suggested for the calculation of the scalar field \({\mathcal {M}}(\varvec{\phi })\)
Only if the jumps of all components of the stiffness tensor \(\llbracket \mathcal {C}_{ijkl} \rrbracket \) and the jumps of all components of the nonelastic strains \(\llbracket \tilde{\varepsilon }_{kl} \rrbracket \) disappear, the singular plane disappears as well.
A formulation for the scalar field \({\mathcal {M}}(\varvec{\phi })\), independent from material parameters, is related to the free energy potential (5). Depending on the chosen potential type, choices can be made for the scalar field \({\mathcal {M}}(\varvec{\phi })\), considering only the local configuration
5.1 Driving force potential for multiphase systems
Equivalent to the procedure in the previously published two-phase model [22], we first define the continuous variables for the formulation of the strain energy density as a function of these variables. The jump conditions (31) and (33) are the basis for the definition of these variables. By incorporating the definition of the normal \(\varvec{n}\) in Eq. (37), the stresses and strains are first transformed into a orthonormal basis \(\varvec{B}=\{\varvec{n},\varvec{t},\varvec{s}\}\). If these transformed stresses and strains for phase \(\alpha \) are represented in the Voigt notation and the order is interchanged, as described in our preliminary work [22], this results in
The continuous contributions of the stresses and strains are summarized in \(\varvec{\sigma }_n := {(\sigma _{nn},\sigma _{nt},\sigma _{ns})}\) and \(\varvec{\varepsilon }_t := {(\varepsilon _{tt},\varepsilon _{ss},2 \varepsilon _{ts})}\), since the jump of these variables vanishes on a singular plane, according to the jump conditions (31) and (33). The variables \(\varvec{\sigma }^\alpha _t := {(\sigma _{tt}^\alpha ,\sigma _{ss}^\alpha ,\sigma _{ts}^\alpha )}\) and \(\varvec{\varepsilon }_n^\alpha := {(\varepsilon _{nn}^\alpha ,2 \varepsilon _{nt}^\alpha ,2 \varepsilon _{ns}^\alpha )}\) correspondingly summarize the discontinuous contributions of the stresses and strains. The superscript \(\alpha \) implies that the variable is discontinuous and therefore phase-dependent. Furthermore, the stiffness tensor, formulated in the basis \(\varvec{B}\), is divided into blocks for further calculations
with \(\varvec{\mathcal {C}}_{nn}\) and \(\varvec{\mathcal {C}}_{tt}\) as symmetrical matrices of dimension \(3 \times 3\). \(\varvec{\mathcal {C}}_{nt}\) and \(\varvec{\mathcal {C}}_{tn}\) are \(3 \times 3\) matrices for which the condition \(\varvec{\mathcal {C}}_{tn} = \varvec{\mathcal {C}}^\mathsf {\!T}_{nt}\) is fulfilled. With these notations, the strain energy density of phase \(\alpha \) can be formulated as follows
According to Eq. (8), the strain energy density in a multiphase system is the linear interpolation of the respective contributions with the interpolation function (10)
Following [22], the variational derivative of the strain energy \(E = \int _V {\bar{W}} \mathrm {d}{V}\) in a two-phase system results in
Here, \(p^\alpha (\varvec{\sigma }_n, \varvec{\varepsilon }_t)\) represents the Legendre transform of \(W^\alpha (\varvec{\varepsilon }_B^\alpha )\) with respect to \(\varvec{\varepsilon }_n^\alpha \)
with \(\varvec{\mathcal {T}}^\alpha \), as implicitly defined in (48) - (50). \(P(\varvec{\phi },\varvec{\sigma }_n, \varvec{\varepsilon }_t) = p^\alpha (\varvec{\sigma }_n, \varvec{\varepsilon }_t) h^\alpha (\varvec{\phi }) + p^\beta (\varvec{\sigma }_n, \varvec{\varepsilon }_t) h^\beta (\varvec{\phi })\) is the locally homogenized mixture of the strain energy and the complementary strain energy density, containing only continuous variables \(\varvec{\sigma }_n\) and \(\varvec{\varepsilon }_t\). \(P(\varvec{\phi },\varvec{\sigma }_n, \varvec{\varepsilon }_t)\) can easily be extended to multiphase systems and becomes
The locally averaged contributions of the proportionality matrix \(\bar{\varvec{\mathcal {T}}}\) are split in the same way as \(\varvec{\mathcal {C}}_B\) in eq. (42) and are defined as follows
The evolution of the order parameters is described by Eq. (12). The local change \(\partial \phi _\alpha / \partial t = 0\) disappears when the system is in equilibrium. The variational derivative of the strain energy density is given by Eq. (45) and can be described directly by means of the potential \(P(\varvec{\phi },\varvec{\sigma }_n, \varvec{\varepsilon }_t)\). For a two-phase system in equilibrium, this leads to
when considering the strain energy and using the obstacle potential \(\omega _{\text {ob}}(\varvec{\phi })\) (5). In the sharp interface context, the right-hand side of Eq. (51) corresponds to \(-\gamma _{\alpha \beta }\kappa \) [41]. The left-hand side of the equation corresponds to the difference of the potentials \(p^\alpha (\varvec{\sigma }_n, \varvec{\varepsilon }_t)\) and \(p^\beta (\varvec{\sigma }_n, \varvec{\varepsilon }_t)\), so that we rewrite Eq. (51) to

The configurational equilibrium condition (51) gives rise to the balance of the configurational forces in a geometrically linear case. Thus, the balance of the configurational forces (35) is exactly reproduced in the phase-field context by using the potential \(P(\varvec{\phi }, \varvec{\sigma }_n, \varvec{\varepsilon }_t)\).
5.2 Calculation of stresses
Equivalent to the calculations in [22], the calculation of the stresses can be derived from the potential P. In a multiphase system, the stress results in
with \(\tilde{\varvec{\chi }}_n\) and \(\tilde{\varvec{\chi }}_t\) as normal and tangential parts of the inelastic strains, which are defined as
With the transformations \(\varvec{\mathcal {K}}(\varvec{\phi }) = \varvec{M}_\varepsilon ^\mathsf {\!T}\varvec{\mathcal {K}}_B (\varvec{\phi }) \varvec{M}_\varepsilon \) and \(\tilde{\varvec{\sigma }}^\text {v}(\varvec{\phi }) = \varvec{M}_\sigma ^\mathsf {\!T}\tilde{\varvec{\sigma }}_{B}(\varvec{\phi })\), where the corresponding transformation matrices are defined in Schneider et al. [22], the following result is derived for the stresses in the Voigt representation and in a Cartesian coordinate system
6 Validation of the model
A detailed validation of the stresses and the driving forces for two-phase systems and a comparison with VT and RS homogenization schemes can be found in Schneider et al. [22]. In this section, we therefore only focus on the validation of the stresses in multiphase regions. We choose a two-dimensional domain with a quadruple point, as shown in Fig. 4, and use \(\varvec{n}=\varvec{n}(\mathcal {M}_E(\varvec{\phi }))\) [see Eqs. (36) and (37)] for the calculation of the normal vector.
For a parametrization of a region with sharp transitions between the order parameters, no homogenization of the material parameters is necessary and the calculation rule for the stresses reduces to Hooke’s law \(\varvec{\bar{\sigma }} = \varvec{\mathcal {C}}[\varvec{\varepsilon }]\). In addition, a cubically symmetric division of the region is chosen to enable an exact parametrization on the used equidistant orthogonal grid. This sharp interface solution is employed for the validation and is referred to as SI solution in the following. Additionally, we compare the results of the proposed model with the solutions of the finite deformation model of Schneider et al. [25], denoted as FD solutions. In order to ensure the comparability, we guaranty that the resulting local strains are below 2%. A macroscopic stress boundary condition is applied on all sides of the two-dimensional region, which guarantees a mean stress of \(\varvec{\hat{\sigma }} = \left( \int \varvec{\bar{\sigma }}(\varvec{x}) \mathrm {d}{V} \right) / V\). The resulting von Mises stress \(\sigma _{\text {mises}}\) of the sharp and diffuse interface solution can be seen in the lower part of Fig. 4. The comparison of both solutions shows a good agreement of the von Mises stress \(\sigma _{\text {mises}}\).
Validation of the stress \(\bar{\sigma }_{\text {mises}}\) and the potentials \(P_{\varvec{n}_1}\) or \(P_{\varvec{n}_2}\) in a quadruple point. The domain contains four phases with \(\varvec{\mathcal {C}}^\alpha = \varvec{\mathcal {C}}^\delta = 2 \varvec{\mathcal {C}}^\beta = 2 \varvec{\mathcal {C}}^\chi \) and is presented in the top-left image. The macroscopic stress boundary condition \(\hat{\sigma }_{xx}= \hat{\sigma }_{yy} = \sigma _0\) and \(\hat{\sigma }_{zz} = \hat{\sigma }_{xy} = \hat{\sigma }_{xz} = \hat{\sigma }_{yz} =0\) is applied on all sides. The solutions of the presented model with diffuse interface parametrization, using \(h^\alpha = \phi _\alpha \) and \(\epsilon = 5 \varDelta x\), (denoted by “new”) are contrasted with the solutions of a parametrization with sharp interfaces (denoted by “SI”) and with the solutions of the finite deformation model of Schneider et al. [25] (denoted by “FD”). A comparison of the von Mises stress \(\bar{\sigma }_{\text {mises}}\) of the whole domain is shown in the lower area of the figure. A detailed comparison of the profiles of \(\bar{\sigma }_{\text {mises}}\) and of the potential \(P_{\varvec{n}_1}\) or \(P_{\varvec{n}_2}\) along the dashed lines, in the direction of \(\varvec{n}_1\), between the points (175, 175, 0) and (225, 225, 0), and respectively, between the points (175, 225, 0) and (225, 175, 0), in the direction of \(\varvec{n}_2\), is shown in the top-right
For a detailed validation of the stresses at the quadruple point, the profiles of the von Mises stress along the diagonals of the domain, which are characterized by the normals \(\varvec{n}_1 = {(1,1,0)}^\mathsf {\!T}/ \sqrt{2}\) and \(\varvec{n}_2 = {(1,-1,0)}^\mathsf {\!T}/ \sqrt{2}\), are shown in the top-right in Fig. 4. Compared to the SI solution, the stress peaks at the quadruple point are neither reproduced by the FD nor by the presented model. However, the interpolation of the material parameters guarantees that the stresses outside the transition region are in excellent agreement. Thus, it can be assumed that the proposed model and the FD model correctly approximate the SI solution, even in the presence of the multiphase region.
Validation of the stress \(\bar{\sigma }_{\text {mises}}\) and the potentials \(P_{\varvec{n}_1}\) and \(P_{\varvec{n}_2}\) in a quadruple point with different material parameters. The domain is initialized with four phases, as displayed in the top-left of Fig. 4, and \(\varvec{\mathcal {C}}^\alpha = 2 \varvec{\mathcal {C}}^\beta = 4 \varvec{\mathcal {C}}^\delta = 4/3 \varvec{\mathcal {C}}^\chi \). A detailed comparison of the profiles of \(\bar{\sigma }_{\text {mises}}\) and the potential \(P_{\varvec{n}_1}\) or \(P_{\varvec{n}_2}\) along the dashed lines, in the direction of \(\varvec{n}_1\) and \(\varvec{n}_2\), is shown on the right. The solutions of the presented model with diffuse interface parametrization (denoted by “new”) are contrasted with the solutions of a parametrization with sharp interfaces (denoted by “SI”) and with the solutions of the finite deformation model of Schneider et al. [25] (denoted by “FD”)
The jump of the configurational forces is described by Eq. (35), and according to Eq. (51), the jump of the potential \(P(\varvec{\phi },\varvec{\sigma }_n, \varvec{\varepsilon }_t)\) reproduces the mechanical configurational forces. For this reason, we investigate the potential \(P(\varvec{\phi },\varvec{\sigma }_n, \varvec{\varepsilon }_t)\) along the diagonals \(\varvec{n}_1\) and \(\varvec{n}_2\) for the validation of our model. For \(P(\varvec{\phi },\varvec{\sigma }_n, \varvec{\varepsilon }_t)\) along the direction of \(\varvec{n}_1\), this leads to
and for the potential \(P(\varvec{\phi },\varvec{\sigma }_n, \varvec{\varepsilon }_t)\) along the domain diagonal \(\varvec{n}_2\), this results in
\(P_{\varvec{n}_1}\) and \(P_{\varvec{n}_2}\) are equivalent to the potential \(P(\varvec{\phi }, \varvec{\sigma }_n, \varvec{\varepsilon }_t)\) of the presented model along the corresponding domain diagonal and result in the mechanical configurational force. Therefore, the profiles of the potentials \(P_{\varvec{n}_1} = \varvec{n}_1 \cdot \varvec{P} \varvec{n}_1\) and \(P_{\varvec{n}_2} = \varvec{n}_2 \cdot \varvec{P} \varvec{n}_2\) along the corresponding diagonals are presented in Fig. 4, for the validation of the driving forces below the stress profiles. Compared to the SI solution, the profiles of the presented model outside the transition region match very closely.
In Fig. 5, a more realistic validation case of the quadruple point is illustrated. Since all material parameters of the corresponding phases are chosen differently, a jump does exist for both the resulting von Mises stress \(\bar{\sigma }_{\text {mises}}\) and the potentials \(P_{\varvec{n}_1}\) and \(P_{\varvec{n}_2}\) along the diagonal at the quadruple point. Compared to the SI solutions, a very good agreement of the corresponding profiles of \(\bar{\sigma }_{\text {mises}}\) outside the transition region can be recognized for the proposed as well as for the FD model, regardless of these jumps. For the profiles of \(P_{\varvec{n}_1}\) and \(P_{\varvec{n}_2}\), the SI, the FD and the diffuse solutions are very close until just before the quadruple point.
This shows that the mechanical configurational forces of a sharp interface description can be very well reproduced with the presented diffuse interface model, even in a multiphase region. Thus, the model can be used to investigate the influence of the mechanical configurational forces on phase transitions and grain growth processes in multiphase systems.
7 Application: martensitic transformation
Martensite plays a key role in increasing the mechanical strength of steel. Due to the fast transformation speed, it is difficult to perform in-situ studies of the displacive formation of martensite. Numerical methods provide a powerful way to obtain a detailed insight into the transformation behavior and to gain a better understanding of the underlying mechanisms. The phase-field approach has emerged as a potent tool to study martensitic transformation [44, 45] using standard interpolation schemes for material parameters. However, as presented in the last sections, standard interpolation schemes, such as the VT or RS interpolation, produce undesirable excess energy, which distorts the mechanical driving force and thus the resulting microstructure. In the next sections, we demonstrate the applicability of the proposed model to describe martensitic phase transformation and show deviations in the resulting microstructure caused only by the used interpolation scheme.
7.1 Model characterization for martensitic phase transformation
Martensite arises from a complex interaction of three principal driving forces [46]. The transformation is caused by a temperature difference that causes a lower chemical energy density \(W_\text {chem}\) of martensite than of austenite. This is counteracted by the strain energy density W, which usually acts against the chemical driving force. In addition, a new interface between martensite and austenite must be built up, which acts against the formation of supercritical martensitic nuclei, with the strength of \(\gamma _{\alpha \beta }\kappa \). Therefore, the total free energy of the system can be expressed as
From a crystallographic point of view, austenite can transform into 24 different martensit variants, which differ in the orientation relationship to their parent phase. For simplicity, they can be grouped into three different main types known as Bain variants. It is experimentally observed that the growth of martensite stops at grain boundaries [47]. This implies that modeling each austenite grain and its resulting variants with its own set of order parameters is appropriate in order to take account of this behavior. For the modeling of martensitic transformation, the N-tuple \(\varvec{\phi }\) is subdivided into blocks consisting of one parent phase and its resulting Bain variants, e.g.
Here, \(\phi _{a1}\) is the order parameter of the first austenitic grain, and \(\phi _{a1_{v1}}\), \(\phi _{a1_{v2}}\) and \(\phi _{a1_{v3}}\) are the order parameters of its martensitic variants. The strain energy density for each phase is calculated according to Sect. 5. For austenite as well as for martensitic variants, we use the stiffness of a cubic material, which reads
The transformation-induced eigenstrains for each variant are given by the Bain strains [48]
where \(\varepsilon _1 = (a-a_c)/a_c\) and \(\varepsilon _3 = (c-a_c)/a_c\) are dependent on the crystal lattice parameters of martensite (a, c) and austenite (\(a_c\)).
It is assumed that the undercooling is constant in terms of time and space, so that the difference in the chemical energy densities between austenite and martensite can be modeled as a phase-dependent constant value. To realize this, the respective chemical driving force \(W^\alpha _{\text {chem}}\) is multiplied with the interpolation function \(h^\alpha (\varvec{\phi })\)
The energetical zero level is set to the chemical energy density of austenite, so that only the difference in the chemical energy densities between austenite and martensite \(\varDelta W^{a-v}_{\text {chem}}\) has to be determined, resulting in \(W^\alpha _{\text {chem}}=0\) if \(\alpha \) is an austenitic phase and in \(W^\alpha _{\text {chem}}=-\varDelta W^{a-v}_{\text {chem}}\) if \(\alpha \) is one of the corresponding martensitic variants. Considering a two-phase system consisting of a martensite phase \(\phi _v\) and an austenite phase \(\phi _a=1-\phi _v\), the interfacial and chemical energy density of the martensite phase is calculated as
and is shown in Fig. 6. It can be seen that an energetical barrier for the martensite phase does exist which has to be overcome in the case of a nucleation event. Depending on the local stresses, the contributions of the elastic driving forces shift the potential curve upwards or downwards, which leads to a respective increase or decrease of the nucleation barrier. The evolution Eq. (12) is extended by a Langevin noise term \(\zeta \) and reads
The noise \(\zeta \), representing thermal fluctuations, is only active in the diffuse interface region and leads to the nucleation of martensite at austenite grain boundaries. This is consistent with experimental findings that martensite nucleates heterogeneously [49]. In addition, autocatalytic nucleation at martensite-austenite interfaces is enabled. The mobility \(M_{\alpha \beta }\) is only nonzero between a parent phase and its related variants.
7.2 Simulation parameters
A 2D grain structure, which was obtained as a result of a grain growth simulation, is utilized as the starting point for the simulation of martensitic transformation. Periodic boundary conditions are applied for all presented simulations and preprocessing steps. In a \((500 \,{\Delta \hbox {x}) \times } (500 \,{\Delta \hbox {y}})\) domain, 150 austenitic grains are filled with a Voronoi tessellation, which is rotated randomly around the z-axis. Using the grid size of \(\varDelta x = \varDelta y = 1.3 \hbox { nm}\), we resolve a domain of size \( 0.65 \times 0.65\, \upmu \hbox {m}^2\). The parameter \(\epsilon \), related to the interface width, is set to \(\epsilon = 2.5 \,{\Delta \hbox {x}}\) to resolve the interface region with approximately six cells. Equation (65) is solved numerically using a finite difference method, without any additional driving forces and without the noise term. The simulation is stopped when 50 grains remain. The grains are numbered in groups of three, so that the newly appearing martensite variants are indexed \(\alpha +1\) and \(\alpha +2\), where \(\alpha \) is the index of the parent austenitic phase. We use the physical parameters listed in Table 1 for an Fe-31at.\(\%\)Ni alloy, according to [50]. The interfacial energy of \(\gamma _{\alpha \beta }=0.1 \hbox { J/m}^2\) is taken to be constant for all occurring interfaces. The third order parameter in the potential (5) is set to \(\gamma _{\alpha \beta \delta } = 15\gamma _{\alpha \beta }\). A detailed discussion for the choice of the \(\gamma _{\alpha \beta \delta }\) values can be found in [29]. The driving force due to the relative undercooling is determined by
where \(Q= 3.5 \times 10^8 \hbox {J/m}^3\) is the latent heat, \(T_0=405 \hbox { K}\) is the stress-free equilibrium temperature and T denotes the undercooling temperature. A quenching temperature of \(T=254 \hbox { K}\) leads to a chemical driving force of \(\varDelta W^{a-v}_{{\text {chem}}} = 1.3 \times 10^8 \hbox { J/m}^3\). We use anisotropic elastic constants, which are calculated according to Schmidt and Gross [51]
where \(\mu =28 \hbox { GPa}\) is the shear modulus and \(\nu =0.375\) is the Poisson ratio. Using an anisotropic case of \(A_z = 2\mathcal {C}_{44}/(\mathcal {C}_{11}-\mathcal {C}_{12}) = 2\), the components of the stiffness tensor are determined to be \(\mathcal {C}_{11} = 130.7 \hbox { GPa}\), \(\mathcal {C}_{12} = 93.3 \hbox { GPa}\) and \(\mathcal {C}_{44} = 37.3 \hbox { GPa}\). Since our model does not include plasticity, we use reduced eigenstrains of \(\varepsilon _1 = 0.07\) and \(\varepsilon _3 = -0.07\) to avoid nonphysically high stresses. Both the eigenstrains and the stiffnesses are rotated depending on the orientation of the parent phase. Since the experimental data for the transformation speed is ambiguous, the mobility \(M_{\alpha \beta }\) between an austenitic phase and its variants is chosen in such a way that the simulation is numerically stable. The noise \(\zeta \) in Eq. (65) is applied every hundredth time step, with a uniform distribution. This leads to a fluctuation of up to 0.2 in the phase-field values. In the first time step, a 2.5 times higher amplitude is used to enable first-time nucleation.
Initial polycrystalline austenitic microstructure a and growth of martensitic variants c–f. Different phases are separated by black lines. The color of a phase correlates with its index position in the N-tuple \(\varvec{\phi }\). Thus, martensitic variants within an austenitic grain have nearly the same color but correspond to separate phases. It should be mentioned that the phases are displayed with a sharp interface profile, although the transition region is diffuse
The simulations are performed with the Pace3D (Parallel Algorithms for Crystal Evolution in 3D) software package, version 2.1.1. For each order parameter, a separate phase-field evolution Eq. (65) is solved on a finite difference grid with an explicit forward Euler scheme. For polycrystalline systems, the approach results in a large number of order parameters to be stored in each cell. To efficiently solve the set of phase-field equations, we use a Locally-Reduced Order Parameter (LROP) optimization [52, 53]. By means of a dynamic list, the LROP algorithm fixes a maximum number of equations solved in each cell of the computational domain. Therefore, the number of phase-field equations does not increase with an increasing total number of phases or grains because only the locally active phase-fields are updated. In the initially purely austenitic polycrystalline microstructure depicted in Fig. 7a, only binary interfaces and triple junctions are present. Thus, we set the LROP algorithm to deal with a maximum of nine phases, without any loss in accuracy. The mechanical equilibrium condition \(\varvec{\nabla }\cdot \varvec{\bar{\sigma }} = \varvec{0}\) is solved in every time step, where \(\mathcal {M}_{\llbracket \rrbracket }(\varvec{\phi })\) [see Eq. (39)] is used for the calculation of the normal vectors in multiphase regions. To reduce simulation time, the domain is decomposed in x- as well as in y-direction utilizing the MPI (Message Parsing Interface) standard.
7.3 Results and discussion
The temporal evolution of the microstructure is shown in Fig. 7. At time \(t=t_0\), no martensite variants exist (Fig. 7a), and thus we avoid any a priori assumptions about the martensitic transformation path. By heterogeneous noise at the austenite grain boundaries, growable martensitic nuclei occur both at triple junctions as well as at grain boundaries (Fig. 7b). This is only possible when two variants meet and grow as twins to reduce the strain energy. This behavior is similar to that reported in [50]. If the nucleation barrier is not overcome, the variations introduced into the system disappear within some time steps. By the growth of one martensite variant, the nucleation barrier for a second variant decreases through the incorporated eigenstrains. The noise enables autocatalytic nucleation. For example, in a two-phase interface between an austenitic phase and a martensitic variant, the second variant does not exist. Hence, the phase-field equation of the second variant is not solved in this region and an autocatalytic nucleation is not possible. This makes the simulation numerically efficient and enables an exact calculation of all interpolated quantities, but requires the incorporation of a separate noise term.
Martensite at an austenitic grain boundary leads to a reduction of the nucleation barrier for martensite in the neighboring grain and thus favors autocatalytic nucleation [47]. This mechanism causes the spread over the austenitic grain structure (Fig. 7c–f). Due to the definition of the eigenstrains, dilatation effects are not present in 2D and a hundred percent martensitic microstructure is achieved. Thereby, the martensitic lamellae are arranged depending on the crystal orientation of its parent phase.
Fig. 8 displays the resulting martensitic microstructure using different interpolation schemes by keeping all other settings. In order to increase comparability, both the simulations with the VT interpolation as well as the simulations with the RS interpolation are started from the microstructure in Fig. 7b. It is clearly evident that the choice of the interpolation scheme relates to different strain energy potentials [see Eqs. (20), (22) and (47)] and different driving forces, correspondingly. The resulting microstructures in Fig. 8a–c clearly show the effect of the interpolation method on the phase arrangement of the martensitic variants.
8 Conclusion
In this work, we present a multiphase-field model to describe phase transformation processes in multiphase / multigrain systems. Regardless of the diffuse transition region, the proposed model satisfies the mechanical jump conditions of the sharp interface and uses configurational forces as driving forces for phase transitions. It should be noted that the approach does not give an exact solution in regions with more than two phases due to the homogenization of the interfacial normal vectors. Nevertheless, the simulation examples show a convincing approximation, in comparison with the sharp interface solution. Additionally, we demonstrate the applicability of the model to martensitic phase transformation processes in multiphase systems. However, the influence of plastic deformations on the martensitic phase transformation processes has not been considered yet. In the last numerical example, we demonstrate the influence of the interpolation scheme on the resulting microstructures for an identical set of material parameters and initial conditions.
The model is defined for an obstacle-type as well as for a well-type potential, but we use only the obstacle-type potential as the energetic potential for all demonstrated validations and simulations. The reason is that the obstacle-type potential has a defined transition region, allowing to reduce the number of locally existing phases in a multiphase system [52, 53]. The numerical advantage of the obstacle potential enables large-scale simulations of multigrain systems, including martensitic phase transformations with the phase-field method, as shown in [54,55,56,57,58,59]. A detailed investigation of martensitic phase formation in 2D and 3D is the objective of forthcoming research work. Another promising application is crack propagation in multiphase or multi-grain systems, as discussed in Schneider et al. [16]. For such problems, a precise calculation of the stress field is indispensable. Therefore, the usage of a model which satisfies the mechanical jump conditions in the transition region, such as the proposed one, is of high importance. By combining the advantages of the crack propagation model [16] with the proposed local homogenization approach, simulations covering phase transformations coupled with crack propagation processes are possible, as discussed in [60]. As outlined in Schneider et al. [22], the model offers the possibility to calculate phase-inherent stresses in the transition region. This property is very useful for the calculation of phase-inherent plastic strains, which will be discussed in forthcoming work.
Change history
07 December 2017
In the original publication, equation 52 was published incorrectly.
References
Chen LQ (2002) Phase-field models for microstructure evolution. Ann Rev Mater Res 32(1):113. https://doi.org/10.1146/annurev.matsci.32.112001.132041
Moelans N, Blanpain B, Wollants P (2008) An introduction to phase-field modeling of microstructure evolution. Calphad 32(2):268. https://doi.org/10.1016/j.calphad.2007.11.003
van der Waals JD (1894) Thermodynamische Theorie der Kapillarität unter voraussetzung stetiger Dichteänderung. Z Phys Chem Leipzig 13:657
Ginzburg VL, Landau LD (1950) On the theory of superconductivity. Zh Eksp Teor Fiz 20:1064
Cahn JW, Hilliard JE (1958) Free energy of a nonuniform system. I. interfacial free energy. The J Chem Phys 28(2):258. https://doi.org/10.1063/1.1744102
Halperin B, Hohenberg P, Ma S (1974) Renormalization-group methods for critical dynamics: I. Recur Relat Eff Energy Conserv Phys Rev B 10(1):139. https://doi.org/10.1103/PhysRevB.10.139
Steinbach I (2013) Phase-field model for microstructure evolution at the mesoscopic scale. Ann Rev Mater Res 43(1):89. https://doi.org/10.1146/annurev-matsci-071312-121703
Nestler B, Choudhury A (2011) Phase-field modeling of multi-component systems. Curr Opin Solid State and Mater Sci 15(3):93. https://doi.org/10.1016/j.cossms.2011.01.003
Ammar K, Appolaire B, Cailletaud G, Forest S (2009) Combining phase field approach and homogenization methods for modelling phase transformation in elastoplastic media. Revue européenne de mécanique numérique 18(5–6):485. https://doi.org/10.3166/ejcm.18.485-523
Khachaturyan AG (1983) Theory of structural transformation in solids. John Wiley & Sons Inc, Hoboken
Voigt W (1889) Über die Beziehung zwischen den beiden Elastizitätskonstanten isotroper Körper. Annalen der Physik 274(12):573
Spatschek R, Müller-Gugenberger C, Brener E, Nestler B (2007) Phase field modeling of fracture and stress-induced phase transitions. Phys Rev E 75(6):066111. https://doi.org/10.1103/PhysRevE.75.066111
Mennerich C, Wendler F, Jainta M, Nestler B (2011) A phase-field model for the magnetic shape memory effect. Arch Mech 63:549
Schneider D, Selzer M, Bette J, Rementeria I, Vondrous A, Hoffmann MJ, Nestler B (2014) Phase-field modeling of diffusion coupled crack propagation processes. Adv Eng Mater 16(2):142. https://doi.org/10.1002/adem.201300073
Schneider D, Schmid S, Selzer M, Böhlke T, Nestler B (2015) Small strain elasto-plastic multiphase-field model. Comput Mech 55(1):27. https://doi.org/10.1007/s00466-014-1080-7
Schneider D, Schoof E, Huang Y, Selzer M, Nestler B (2016) Phase-field modeling of crack propagation in multiphase systems. Comput Methods in Appl Mech Eng 312:186–195. https://doi.org/10.1016/j.cma.2016.04.009
Levitas VI (2013) Thermodynamically consistent phase field approach to phase transformations with interface stresses. Acta Mater 61(12):4305. https://doi.org/10.1016/j.actamat.2013.03.034
Reuss A (1929) Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizittitsbedingung fiir Einkristalle. Z Angew Math Mech 9:49
Steinbach I, Apel M (2006) Multi phase field model for solid state transformation with elastic strain. Phys D 217:153. https://doi.org/10.1016/j.physd.2006.04.001
Apel M, Benke S, Steinbach I (2009) Virtual dilatometer curves and effective Young’s modulus of a 3D multiphase structure calculated by the phase-field method. Comput Mater Sci 45(3):589. https://doi.org/10.1016/j.commatsci.2008.07.007
Durga A, Wollants P, Moelans N (2013) Evaluation of interfacial excess contributions in different phase-field models for elastically inhomogeneous systems. Modell Simul Mater Sci Eng 21(5):055018. https://doi.org/10.1088/0965-0393/21/5/055018
Schneider D, Tschukin O, Choudhury A, Selzer M, Böhlke T, Nestler B (2015) Phase-field elasticity model based on mechanical jump conditions. Comput Mech 55(5):887. https://doi.org/10.1007/s00466-015-1141-6
Schneider D (2017) Phasenfeldmodellierung mechanisch getriebener Grenzflächenbewegungen in mehrphasigen Systemen. Ph.D. thesis
Mosler J, Shchyglo O, Hojjat HM (2014) A novel homogenization method for phase field approaches based on partial rank-one relaxation. J Mech Phys Solids 68:251. https://doi.org/10.1016/j.jmps.2014.04.002
Schneider D, Schwab F, Schoof E, Reiter A, Herrmann C, Selzer M, Böhlke T, Nestler B (2017) On the stress calculation within phase-field approaches: a model for finite deformations. Comput Mech (in press). https://doi.org/10.1007/s00466-017-1401-8
Nestler B, Garcke H, Stinner B (2005) Multicomponent alloy solidification: phase-field modeling and simulations. Phys Rev E 71(4):041609. https://doi.org/10.1103/PhysRevE.71.041609
Provatas N, Elder K (2010) Phase-field methods in materials science and engineering. Wiley-VCH Verlag, Weinheim. https://doi.org/10.1002/9783527631520
Nestler B (2000) Phasenfeldmodellierung mehrphasiger Erstarrung. Ph.D. thesis
Hötzer J, Tschukin O, Ben Said M, Berghoff M, Jainta M, Barthelemy G, Smorchkov N, Schneider D, Selzer M, Nestler B (2016) Calibration of a multi-phase field model with quantitative angle measurement. J Mater Sci 51(4):1788. https://doi.org/10.1007/s10853-015-9542-7
Moelans N (2011) A quantitative and thermodynamically consistent phase-field interpolation function for multi-phase systems. Acta Mater 59(3):1077. https://doi.org/10.1016/j.actamat.2010.038
Steinbach I, Pezzolla F (1999) A generalized field method for multiphase transformations using interface fields. Phys D: Nonlinear Phenom 134(4):385. https://doi.org/10.1016/S0167-2789(99)00129-3
Eshelby JD (1951) The force on an elastic singularity. Philosophical transactions of the royal society. A: Math Phys Eng Sci 244(877):87–112. https://doi.org/10.1098/rsta.1951.0016
Eshelby JD (1975) The elastic energy-momentum tensor. J Elast 5(3–4):321. https://doi.org/10.1007/BF00126994
Gurtin ME (1983) Two-phase deformations of elastic solids. Arch Ration Mech Anal 84(1):1–29. https://doi.org/10.1007/BF00251547
Gurtin ME (1995) The nature of configurational forces. Arch Ration Mech Anal 131(1):67. https://doi.org/10.1007/BF00386071
James RD (1981) Finite deformation by mechanical twinning. Arch Ration Mech Anal 77(2):143–176. https://doi.org/10.1007/BF00250621
Johnson WC (1987) Precipitate shape evolution under applied stress thermodynamics and kinetics. Metall Trans A 18A:233
Silhavy M (1997) The Mechanics and thermodynamics of continuous media. Springer Verlag, Berlin
Voorhees PW, Johnson WC (1986) Interfacial equilibrium during a first-order phase transformation in solids. The J Chem Phys 84(9):5108. https://doi.org/10.1063/1.450664
Gurtin ME (2000) Configurational forces as basic concepts of continuum physics. Springer, Berlin
Garcke H, Stoth B, Nestler B (1999) Anisotropy in multi-phase systems: a phase field approach. Interfaces and Free Bound 1(2):175–198. https://doi.org/10.4171/IFB/8
Johnson WC, Alexander JID (1986) Interfacial conditions for thermomechanical equilibrium in two-phase crystals. J Appl Phys 59(8):2735. https://doi.org/10.1063/1.336982
Mai AK, Singh SJ (1991) Deformation of elastic solids. Prentice-Hall, Upper Saddle River
Wang Y, Khachaturyan AG (2006) Multi-scale phase field approach to martensitic transformations. Mater Sci Eng: A 438–440:55. https://doi.org/10.1016/j.msea.2006.04.123
Mamivand M, Zaeem MA, El Kadiri H (2013) A review on phase field modeling of martensitic phase transformation. Comput Mater Sci 77:304. https://doi.org/10.1016/j.commatsci.2013.04.059
Ueda M, Yasuda HY, Umakoshi Y (2003) Controlling factor for nucleation of martensite at grain boundary in Fe-Ni bicrystals. Acta Mater 51(4):1007. https://doi.org/10.1016/S1359-6454(02)00503-7
Rios PR, Guimarães JRC (2010) Microstructural path analysis of martensite burst. Mater Res 13(1):119. https://doi.org/10.1590/S1516-14392010000100023
Artemev A, Jin Y, Khachaturyan AG (2001) Three-dimensional phase field model of proper martensitic transformation. Acta Mater 49(7):1165. https://doi.org/10.1016/S1359-6454(01)00021-0
Krauss W, Pabi SK, Gleiter H (1989) On the mechanism of martensite nucleation. Acta Metall 37(1):25. https://doi.org/10.1016/0001-6160(89)90262-9
Heo TW, Chen LQ (2014) Phase-field modeling of displacive phase transformations in elastically anisotropic and inhomogeneous polycrystals. Acta Mater 76:68. https://doi.org/10.1016/j.actamat.2014.05.014
Schmidt I, Gross D (1997) The equilibrium shape of an elastically inhomogeneous inclusion. J Mech Phys Solids 45(9):1521. https://doi.org/10.1016/S0022-5096(97)00011-2
Kim SG, Kim DI, Kim WT, Park YB (2006) Computer simulations of two-dimensional and three-dimensional ideal grain growth. Phys Rev E 74:061605
B. Nestler, M. Reichert, M. Selzer (2008) Massive multi-phase-field simulations: methods to compute large grain system. In: proceedings of the 11th international conference on aluminium alloys pp. 1251–1255
Vondrous A, Bienger P, Schreijäg S, Selzer M, Schneider D, Nestler B, Helm D, Mönig R (2015) Combined crystal plasticity and phase-field method for recrystallization in a process chain of sheet metal production. Comput Mech 55(2):439. https://doi.org/10.1007/s00466-014-1115-0
Hötzer J, Jainta M, Steinmetz P, Nestler B, Dennstedt A, Genau A, Bauer M, Köstler H, Rüde U (2015) Large scale phase-field simulations of directional ternary eutectic solidification. Acta Mater 93:194. https://doi.org/10.1016/j.actamat.2015.03.051
Hötzer J, Steinmetz P, Jainta M, Schulz S, Kellner M, Nestler B, Genau A, Dennstedt A, Bauer M, Köstler H, Rüde U (2016) Phase-field simulations of spiral growth during directional ternary eutectic solidification. Acta Mater 106:249. https://doi.org/10.1016/j.actamat.2015.12.052
Steinmetz P, Yabansu YC, Hötzer J, Jainta M, Nestler B, Kalidindi SR (2016) Analytics for microstructure datasets produced by phase-field simulations. Acta Mater 103:192. https://doi.org/10.1016/j.actamat.2015.09.047
Steinmetz P, Hötzer J, Kellner M, Dennstedt A, Nestler B (2016) Large-scale phase-field simulations of ternary eutectic microstructure evolution. Comput Mater Sci 117:205. https://doi.org/10.1016/j.commatsci.2016.02.001
Bauer M, Rüde U, Hötzer J, Jainta M, Steinmetz P, Berghoff M, Schornbaum F, Godenschwager C, Köstler H, Nestler B (2015) Massively parallel phase-field simulations for ternary eutectic directional solidification. In: proceedings of the international conference for high performance computing pp. 1–12. https://doi.org/10.1145/2807591.2807662
Schmitt R, Kuhn C, Skorupski R, Smaga M, Eifler D, Müller R (2015) A combined phase field approach for martensitic transformations and damage. Arch Appl Mech 85(9–10):1459. https://doi.org/10.1007/s00419-014-0945-8
Acknowledgements
We thank the DFG for funding our investigations in the framework of the Research Training Group 1483 and the International Research Training Group 2078. The work was further supported by the state of Baden-Württemberg through the “Mittelbau” program and by the Helmholz program “EMR-Energy efficiency, Materials and Ressources”. The authors gratefully acknowledge the editorial support by Leon Geisen. The authors also thank the referees for their very useful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original version of this article was revised: In the original publication, the equation 52 was published incorrectly and is corrected now.
Rights and permissions
About this article
Cite this article
Schneider, D., Schoof, E., Tschukin, O. et al. Small strain multiphase-field model accounting for configurational forces and mechanical jump conditions. Comput Mech 61, 277–295 (2018). https://doi.org/10.1007/s00466-017-1458-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-017-1458-4