A quartic B-spline based explicit time integration scheme for structural dynamics with controllable numerical dissipation

Abstract

An explicit time integration scheme based on quartic B-splines is presented for solving linear structural dynamics problems. The scheme is of a one-parameter family of schemes where free algorithmic parameter controls stability, accuracy and numerical dispersion. The proposed scheme possesses at least second-order accuracy and at most third-order accuracy. A 2D wave problem is analyzed to demonstrate the effectiveness of the proposed scheme in reducing high-frequency modes and retaining low-frequency modes. Except for general structural dynamics, the proposed scheme can be used effectively for wave propagation problems in which numerical dissipation is needed to reduce spurious oscillations.

1 Introduction

Numerical methods are employed these days for solving structural dynamics problems, as these methods are increasingly powerful in calculation. For these problems, the spatial discretization models are commonly obtained by the Finite Element Methods (FEM). Many time integration schemes have been presented in the literature to describe the history of structures’ transient responses. These schemes can be categorized on the basis of the following characteristics: (i) energy conservation or dissipation; (ii) momentum conservation or dissipation; (iii) implicit or explicit.

When time integration schemes are employed to describe hyperbolical problems, especially for wave propagation problems, numerical spurious oscillation often happens, and thus, numerical dissipation/dispersion property is of great significance for time integration schemes. By use of dispersive implicit or explicit time integration schemes, spurious oscillation can be effectively reduced. There are a large amount of researches on the implicit damping schemes [1,2,3,4,5,6]. As for explicit schemes, few dispersive schemes are available [7,8,9,10,11,12,13]. Another technique to obtain damping schemes is to add a viscous pressure term to the dynamic equilibrium equation [14, 15].

Recently, a new family of time integration schemes involving explicit and implicit schemes have been proposed by use of uniform B-spline functions in terms of the outstanding ability of B-spline functions in interpolation and approximation [16,17,18]. To improve accuracy and numerical dispersion characteristics, an explicit scheme with controllable numerical dispersion is proposed here utilizing uniform quartic B-spline functions. In following section, uniform quartic B-spline is introduced and applied to solve the discretized dynamic equilibrium equations. In Sects. 3 and 4, the stability and accuracy properties are deliberately analyzed and compared with other two representative damping schemes proposed by Noh and Bathe [11] and Tchamwa and Wielgosz [10, 12]. In Sect. 5, numerical dispersion characteristics of the proposed scheme are demonstrated by theoretically considering a two-dimensional wave propagation problem with a uniform 4-node finite element adopted to obtain spatial discretization equations, where wave velocity errors of various schemes are compared to verify the acceptable dispersion property of the proposed quartic B-spline scheme. In Sect. 6, several numerical simulations are considered to verify the effectiveness of the proposed scheme. In Sect. 7, conclusions are made based on the theoretical and numerical results.

2 The proposed scheme

2.1 Initial approximations based on quartic B-spline interpolation

B-spline functions have been employed by Wen et al. in two research papers [16, 17] to develop time integration schemes for structural dynamics. While, quartic B-spline functions are first used to develop non-dispersive time integration scheme by Rostami et al. [18]. However, in this paper, an explicit time integration scheme with controllable dissipation is proposed by applying uniform quartic B-spline interpolation in time integration field. To implement the proposed scheme for linear structural dynamic analysis, the following well-known equation is considered

$$\begin{aligned} {\varvec{M}}{\ddot{{\varvec{u}}}}+{\varvec{D}}{\dot{{\varvec{u}}}}+{\varvec{Ku}}={\varvec{f}} \end{aligned}$$

(1)

where ${\varvec{u}}$, $\dot{{\varvec{u}}}$ and $\ddot{{\varvec{u}}}$ are the nodal physical variables vector and its first and second derivative vectors with respect to time variable t. ${\varvec{M}}$, ${\varvec{D}}$ and ${\varvec{K}}$ are the mass, damping and stiffness matrices, respectively. For nonlinear case, ${\varvec{D}}$ and ${\varvec{K}}$ can be, respectively, obtained by ${\varvec{D}}=\frac{\partial {{\varvec{f}}}_{{\varvec{d}}}}{\partial \dot{{\varvec{u}}}}$ and ${\varvec{K}}=\frac{\partial {{\varvec{f}}}_{s}}{\partial {\varvec{u}}}$, where ${\varvec{f}}_{d}$ and ${\varvec{f}}_{s}$ are the nodal damping force and the elastic force vectors corresponding to the element internal stresses, respectively.

Let the considered time domain [a, b] be divided into subintervals $[t_{i},t_{i+1}]$ by a set of equidistant knots $t_{i}=a+i\Delta t$, $i=0,1,2,3,\cdots ,n-1$, where $\Delta t=\frac{b-a}{n}$. Let N be the number of degree of freedom of vector ${\varvec{u}}$.

For the proposed scheme, the following initial conditions are required

$$\begin{aligned}&{\varvec{u}}\left( t_{0} \right) ={\varvec{u}}_{\mathbf {0}} \end{aligned}$$

(2a)

$$\begin{aligned}&\dot{{\varvec{u}}}\left( t_{0} \right) ={\varvec{v}}_{\mathbf {0}} \end{aligned}$$

(2b)

$$\begin{aligned}&\ddot{{\varvec{u}}}\left( t_{0} \right) ={\varvec{M}}^{-1}({\varvec{f}}\left( t_{0} \right) -{\varvec{D}}\dot{{\varvec{u}}}\left( t_{0} \right) -{\varvec{Ku}}\left( t_{0} \right) ) \end{aligned}$$

(2c)

$$\begin{aligned}&\dddot{{\varvec{u}}}\left( t_{0}^{+} \right) ={\varvec{M}}^{-1}(\dot{{\varvec{f}}}\left( t_{0}^{+} \right) -{\varvec{D}}\ddot{{\varvec{u}}}\left( t_{0} \right) -{\varvec{K}}\dot{{\varvec{u}}}\left( t_{0} \right) ) \end{aligned}$$

(2d)

where the superscript ‘$+$’ in this paper is employed to define the right derivative, and thus $\dddot{{\varvec{u}}}\left( t_{0}^{+} \right)$ denotes the third right derivative of ${\varvec{u}}$ at time $t = t_{0}$. The first right derivative value $\dot{{\varvec{f}}}\left( t_{0}^{+} \right)$ in Eq. (2d) is approximated as

$$\begin{aligned} \dot{{\varvec{f}}}\left( t_{0}^{+} \right) =\frac{-{11}{\varvec{f}}\left( t_{0} \right) +{18}{\varvec{f}}\left( t_{1/3} \right) -{9}{\varvec{f}}\left( t_{2/3} \right) +{2}{\varvec{f}}\left( t_{1} \right) }{2\Delta t}\nonumber \\ \end{aligned}$$

(3)

where the approximation of $\dot{{\varvec{f}}}\left( t_{0}^{+} \right)$ is obtained by conducting some mathematical calculations based on the Taylor series expansion of ${\varvec{f}}\left( t_{1/3} \right)$, ${\varvec{f}}\left( t_{2/3} \right)$ and ${\varvec{f}}\left( t_{1} \right)$ at time $t{=}t_{0}$. Actually, when ${\varvec{f}}\left( t_{0} \right)$, ${\varvec{f}}\left( t_{1/3} \right)$, ${\varvec{f}}\left( t_{2/3} \right)$ and ${\varvec{f}}\left( t_{1} \right)$ are accurate enough, the proposed approximation is of second-order accuracy. For clarity, deliberate mathematical deduction is not presented here.

In the proposed scheme, quartic B-spline is employed to form the numerical expressions of physical variables. With an explicit recursive definition of B-spline [16, 19], the ith and q-degree B-spline function in terms of variable t, briefly denoted by $B_{i,q}(t)$, is expressed as

$$\begin{aligned} B_{i,0}(t)= & {} \left\{ {\begin{array}{ll} 1,&{}\quad t_{i}\le t<t_{i+1}\\ 0,&{}\quad { otherwise}\\ \end{array} } \right. ,\quad \hbox { for }q = 0. \end{aligned}$$

(4a)

$$\begin{aligned} B_{i,q}(t)= & {} \left\{ {\begin{array}{ll} \left( \frac{t-t_{i}}{t_{i+p}-t_{i}} \right) B_{i,q-1}(t)+\left( \frac{t_{i+q+1}-t}{t_{i+q+1}-t_{i+1}} \right) B_{i+1,q-1}(t),&{}\quad t_{i}\le t<t_{i+1} \\ 0 &{}\quad { otherwise} \\ \end{array}} \right. ,\;\hbox { for }q > 0. \end{aligned}$$

(4b)

In Eq.(4b), $\left\{ {\cdots ,}\,t_{i}{,}\,t_{i+1}{,\cdots ,}\,t_{n+q}{,}\,t_{n+q+1}, \right\}$ are a set of increasing time instants, and we adopt the convention $0\big /0=0$.

With Eq.(4), uniform quartic B-spline function $B_{i,4}(t)$, can be expressed in a piecewise form as [19, 20]

$$\begin{aligned} B_{i,4}(t)\mathrm {=}\frac{1}{{4!(\Delta t)}^{4}}\left\{ {\begin{array}{ll} {(t-t_{i})}^{4} &{}\quad t\in [t_{i},t_{i+1}] \\ {(t-t_{i})}^{4}-5\left( t-t_{i+1} \right) ^{4} &{}\quad t\in [t_{i+1},t_{i+2}] \\ {(t-t_{i})}^{4}-5\left( t-t_{i+1} \right) ^{4}+10\left( t-t_{i+2} \right) ^{4}&{}\quad t\in [t_{i+2},t_{i+3}] \\ \left( t_{i+5}-t \right) ^{4}-5\left( t_{i}-t \right) ^{4} &{}\quad t\in [t_{i+3},t_{i+4}] \\ \left( t_{i+5}-t \right) ^{4} &{}\quad t\in [t_{i+4},t_{i+5}] \\ \end{array}} \right. \end{aligned}$$

(5)

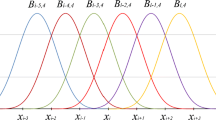
where the uniform time interval $\Delta t=t_{i+1}-t_{i}$. Eq.(5) reveals that $B_{j,4}(t)$ is the shifted instance of $B_{i,4}(t)$, that is, $B_{j,4}(t)=B_{i,4}\left( t-\left( j-i \right) \Delta t \right)$. In Fig. 1, a family of quartic B-splines are illustrated in a piecewise form.

Fig. 1

A family of quartic B-splines curves in a piecewise form

Then, by implementation of uniform quartic B-spline interpolation within any time subinterval $I_{i}\equiv [t_{i},t_{i+1}]$, we have [21]

$$\begin{aligned} {\varvec{u}}^{(l)}(t)=\sum \nolimits _{k=-4}^0 {B_{i+k,4}^{\left( l \right) }(t)} {\varvec{C}}_{k}^{i}, \quad t\in I_{i} \end{aligned}$$

(6)

Here, for the convenience of definition, l in this paper is the order of derivative, ${\varvec{C}}_{k}^{i} (k=-4,-3,-2,-1,0)$ is the kth unknown B-spline coefficients vector corresponding to any time subinterval $I_{i}$. In Fig. 2, the usable piecewise B-spline functions for quartic B-spline interpolation within any time interval $I_{i}$ are displayed.

Fig. 2

Piecewise quartic B-spline functions within any interpolation interval $t\in [t_{i},t_{i+1}]$

By substituting $t=t_{i}$ into Eq.(6), ${\varvec{u}}^{(l)}\left( t_{i} \right)$ $(l=0,1,,2,3)$ (i.e., ${\varvec{u}}\left( t_{i} \right)$, $\dot{{\varvec{u}}}\left( t_{i} \right)$, $\ddot{{\varvec{u}}}\left( t_{i} \right)$ and $\dddot{{\varvec{u}}}\left( t_{i}^{+} \right) )$, can be expressed as

$$\begin{aligned} \left[ {\begin{array}{l} {\varvec{u}}\left( t_{i} \right) \\ (\Delta t)\cdot \dot{{\varvec{u}}}\left( t_{i} \right) \\ {(\Delta t)}^{(2)}\cdot \ddot{{\varvec{u}}}\left( t_{i} \right) \\ {(\Delta t)}^{(3)}\cdot \dddot{{\varvec{u}}}\left( t_{i}^{+} \right) \\ \end{array}} \right] ={\varvec{Q}}\otimes {\varvec{I}}{\cdot }\left[ {\begin{array}{l} {\varvec{C}}_{-4}^{i} \\ {\varvec{C}}_{-3}^{i} \\ {\varvec{C}}_{-2}^{i} \\ {\varvec{C}}_{-1}^{i} \\ \end{array}} \right] \end{aligned}$$

(7)

where $\dddot{{\varvec{u}}}\left( t_{i}^{+} \right)$ is the third right derivative of ${\varvec{u}}$ at ${t=t}_{i}$. ${\varvec{C}}_{-4}^{i}$, ${\varvec{C}}_{-3}^{i}$, ${\varvec{C}}_{-2}^{i}$ and ${\varvec{C}}_{-1}^{i}$ are the unknown B-spline coefficients vector of size $N\times 1$, ${\varvec{I}}$ is the identity matrix of size $N\times N$. The constant matrix ${\varvec{Q}}$ is expressed as

$$\begin{aligned} {\varvec{Q}}=\left[ {\begin{array}{llll} \frac{1}{24} &{}\quad \frac{11}{24} &{}\quad \frac{11}{24} &{}\quad \frac{1}{24}\\ -\frac{1}{6} &{}\quad -\frac{1}{2} &{}\quad \frac{1}{2} &{}\quad \frac{1}{6}\\ \frac{1}{2} &{}\quad -\frac{1}{2} &{}\quad -\frac{1}{2} &{}\quad \frac{1}{2}\\ -1 &{}\quad 3 &{}\quad -3 &{}\quad 1 \\ \end{array} } \right] \end{aligned}$$

(8)

In Eq.(7), the right derivative $\dddot{{\varvec{u}}}\left( t_{i}^{+} \right)$ is determined by

$$\begin{aligned} \dddot{{\varvec{u}}}\left( t_{i}^{+} \right) ={\varvec{M}}^{-1}({\varvec{f}}^{\left( 1 \right) }\left( t_{i}^{+} \right) -{\varvec{D}}\ddot{{\varvec{u}}}\left( t_{i} \right) -{\varvec{K}}\dot{{\varvec{u}}}\left( t_{i} \right) ) \end{aligned}$$

(9)

Similar to Eq.(3), $\dot{{\varvec{f}}}\left( t_{i}^{+} \right)$ is approximated as

$$\begin{aligned} \dot{{\varvec{f}}}\left( t_{i}^{+} \right) =\frac{-{11}{\varvec{f}}\left( t_{i} \right) +{18}{\varvec{f}}\left( t_{i+1/3} \right) -{9}{\varvec{f}}\left( t_{i+2/3} \right) +{2}{\varvec{f}}\left( t_{i+1} \right) }{2\Delta t} \end{aligned}$$

(10)

With Eq. (7), ${\varvec{C}}_{-4}^{i}$, ${\varvec{C}}_{-3}^{i}$, ${\varvec{C}}_{-2}^{i}$ and ${\varvec{C}}_{-1}^{i}$ can be obtained by

$$\begin{aligned} \left[ {\begin{array}{l} {\varvec{C}}_{-4}^{i} \\ {\varvec{C}}_{-3}^{i} \\ {\varvec{C}}_{-2}^{i} \\ {\varvec{C}}_{-1}^{i} \\ \end{array}} \right] ={\varvec{Q}}^{-1}\otimes {\varvec{I}}{\cdot }\left[ {\begin{array}{l} {\varvec{u}}\left( t_{i} \right) \\ (\Delta t)\cdot \dot{{\varvec{u}}}\left( t_{i} \right) \\ {(\Delta t)}^{(2)}\cdot \ddot{{\varvec{u}}}\left( t_{i} \right) \\ {(\Delta t)}^{(3)}\cdot \dddot{{\varvec{u}}}\left( t_{i}^{+} \right) \\ \end{array}} \right] \end{aligned}$$

(11)

Then, substitution of $t=t_{i+1}$ in Eq. (6) leads to the B-spline approximations of ${\varvec{u}}\left( t_{i+1} \right)$, $\dot{{\varvec{u}}}\left( t_{i+1} \right)$, $\ddot{{\varvec{u}}}\left( t_{i+1} \right)$ and $\dddot{{\varvec{u}}}\left( t_{i+1} \right)$ which are denoted with the subscript ‘b’ and expressed in a matrix form as

$$\begin{aligned} \left[ {\begin{array}{l} {\varvec{u}}_{b}\left( t_{i+1} \right) \\ (\Delta t)\cdot \dot{{\varvec{u}}}_{b}\left( t_{i+1} \right) \\ {(\Delta t)}^{(2)}\cdot \ddot{{\varvec{u}}}_{b}\left( t_{i+1} \right) \\ \left( \Delta t \right) ^{\left( 3 \right) }\cdot \dddot{{\varvec{u}}}_{b}\left( t_{i+1} \right) \\ \end{array}} \right] ={\varvec{Q}}\otimes {\varvec{I}}{\cdot } \left[ {\begin{array}{l} {\varvec{C}}_{-3}^{i} \\ {\varvec{C}}_{-2}^{i} \\ {\varvec{C}}_{-1}^{i} \\ {\varvec{C}}_{0}^{i} \\ \end{array}} \right] \end{aligned}$$

(12)

With Taylor series expansion, we first define the initial approximations (briefly denoted with subscript ‘ini’) as

$$\begin{aligned} {\varvec{u}}_{\mathrm{ini}}\left( t_{i+1} \right)= & {} {\varvec{u}}\left( t_{i} \right) +\Delta t\cdot \dot{{\varvec{u}}}\left( t_{i} \right) \nonumber \\&+\,\frac{1}{2}{(\Delta t)}^{2}\cdot \ddot{{\varvec{u}}}\left( t_{i} \right) +\frac{1}{6}{(\Delta t)}^{3}\cdot \dddot{{\varvec{u}}}\left( t_{i}^{+} \right) \end{aligned}$$

(13)

$$\begin{aligned} \Delta t\cdot \dot{{\varvec{u}}}_{\mathrm{ini}}\left( t_{i+1} \right)= & {} \Delta t\cdot \dot{{\varvec{u}}}\left( t_{i} \right) +{(\Delta t)}^{2}\cdot \ddot{{\varvec{u}}}\left( t_{i} \right) \nonumber \\&+\,\frac{1}{2}{(\Delta t)}^{3}\cdot \dddot{{\varvec{u}}}\left( t_{i}^{+} \right) \end{aligned}$$

(14)

Substituting Eq. (7) into Eq. (13) and Eq. (14) gives

$$\begin{aligned}&{\varvec{u}}_{\mathrm{ini}}\left( t_{i+1} \right) =-\frac{1}{24}{\varvec{C}}_{-4}^{i}+\frac{5}{24}{\varvec{C}}_{-3}^{i}+\frac{5}{24}{\varvec{C}}_{-2}^{i}+\frac{5}{8}{\varvec{C}}_{-1}^{i} \nonumber \\\end{aligned}$$

(15)

$$\begin{aligned}&\Delta t\cdot \dot{{\varvec{u}}}_{\mathrm{ini}}\left( t_{i+1} \right) =-\frac{1}{6}{\varvec{C}}_{-4}^{i}+\frac{1}{2}{\varvec{C}}_{-3}^{i}-\frac{3}{2}{\varvec{C}}_{-2}^{i}+\frac{7}{6}{\varvec{C}}_{-1}^{i}\nonumber \\ \end{aligned}$$

(16)

To obtain explicit scheme, the following discretized dynamic equations are used

$$\begin{aligned}&{\varvec{M}}\ddot{{\varvec{u}}}_{b}\left( t_{i+1} \right) +{\varvec{D}}\dot{{\varvec{u}}}_{\mathrm{ini}}\left( t_{i+1} \right) +{\varvec{K}}{\varvec{u}}_{\mathrm{ini}}\left( t_{i+1} \right) ={\varvec{f}}(t_{i+1}),\nonumber \\&\quad i=0,1,2,3,\cdots ,n-1. \end{aligned}$$

(17)

Substituting Eqs. (12), (15) and (16) into Eq. (17) renders

$$\begin{aligned} {\varvec{M}}{\varvec{C}}_{0}^{i}= & {} 2{(\Delta t)}^{2}\cdot {\varvec{f}}\left( t_{i+1} \right) -{\varvec{\alpha }}_{1}\cdot {\varvec{C}}_{-1}^{i}\nonumber \\&-\,{\varvec{\alpha }}_{2}\cdot {\varvec{C}}_{-2}^{i}-{\varvec{\alpha }}_{3}\cdot {\varvec{C}}_{-3}^{i}-{\varvec{\alpha }}_{4}\cdot {\varvec{C}}_{-4}^{i} \end{aligned}$$

(18)

where

$$\begin{aligned} {\varvec{\alpha }}_{1}= & {} \frac{5}{4}{(\Delta t)}^{2}\cdot {\varvec{K}}+\frac{7}{3}\Delta t\cdot {\varvec{D}}-{\varvec{M}} \end{aligned}$$

(19)

$$\begin{aligned} {\varvec{\alpha }}_{2}= & {} \frac{5}{12}{(\Delta t)}^{2}\cdot {\varvec{K}}-3\Delta t\cdot {\varvec{D}}-{\varvec{M}} \end{aligned}$$

(20)

$$\begin{aligned} {\varvec{\alpha }}_{3}= & {} \frac{5}{12}{(\Delta t)}^{2}\cdot {\varvec{K}}+\Delta t\cdot {\varvec{D}}+{\varvec{M}} \end{aligned}$$

(21)

$$\begin{aligned} {\varvec{\alpha }}_{4}= & {} -\frac{1}{12}\left( \Delta t \right) ^{2}\cdot {\varvec{K}}-\frac{1}{3}\Delta t\cdot {\varvec{D}} \end{aligned}$$

(22)

Clearly, with the solved coefficients vectors ${\varvec{C}}_{-4}^{i}$, ${\varvec{C}}_{-3}^{i}$, ${\varvec{C}}_{-2}^{i}$ and ${\varvec{C}}_{-1}^{i}$ in Eq. (11), ${\varvec{C}}_{0}^{i}$ in Eq. (18) can be explicitly solved.

2.2 Final approximations

In this Section, the obtained third derivatives, $\dddot{{\varvec{u}}}\left( t_{i}^{+} \right)$ (in Eq.(9)) and $\dddot{{\varvec{u}}}_{b}\left( t_{i+1} \right)$ (in Eq.(12)) are employed to improve the accuracy of variable $\ddot{{\varvec{u}}}\left( t_{i+1} \right)$. Then, final $\ddot{{\varvec{u}}}\left( t_{i+1} \right)$ is formed as

$$\begin{aligned} \dot{{\varvec{u}}}\left( t_{i+1} \right)= & {} \dot{{\varvec{u}}}\left( t_{i} \right) +\Delta t\cdot \ddot{{\varvec{u}}}\left( t_{i} \right) +\frac{1}{2}\left( \Delta t \right) ^{2}\cdot (p\cdot \dddot{{\varvec{u}}}\left( t_{i}^{+} \right) \nonumber \\&+\,(1-p)\cdot \dddot{{\varvec{u}}}_{b}\left( t_{i+1} \right) ) \end{aligned}$$

(23)

where the free algorithmic parameter p is adopted to control algorithmic accuracy. Eq.(23) shows that, when $p=\frac{2}{3}$, the obtained $\dot{{\varvec{u}}}$ is theoretically of highest accuracy, which is also illustrated in Sect. 4. However, parameter p also shows capability in controlling stability and dissipation properties which are, respectively, elucidated in Sects. 3 and 5.

The final ${{\varvec{u}}}\left( t_{i+1} \right)$ and $\ddot{{\varvec{u}}}\left( t_{i+1} \right)$ are obtained by

$$\begin{aligned} {\varvec{u}}\left( t_{i+1} \right)= & {} {\varvec{u}}_{\mathrm{ini}}\left( t_{i+1} \right) \end{aligned}$$

(24)

$$\begin{aligned} \ddot{{\varvec{u}}}\left( t_{i+1} \right)= & {} \ddot{{\varvec{u}}}_{b}\left( t_{i+1} \right) \end{aligned}$$

(25)

To improve algorithmic accuracy, the final $\dddot{{\varvec{u}}}\left( t_{i+1}^{+} \right)$ (i.e., $\dddot{{\varvec{u}}}\left( t_{i+1} \right)$ ) is modified as

$$\begin{aligned} \dddot{{\varvec{u}}}\left( t_{i+1}^{+} \right) ={\varvec{M}}^{-\mathbf {1}}(\dot{{\varvec{f}}}\left( t_{i+1}^{+} \right) -{\varvec{D}}\ddot{{\varvec{u}}}_{b}\left( t_{i+1} \right) -{\varvec{K}}\dot{{\varvec{u}}}_{b}\left( t_{i+1} \right) ) \end{aligned}$$

(26)

The calculation process in Sects. 2.1 and 2.2 illustrates that the explicit nature of the proposed scheme.

2.3 Calculation procedure for MDOF systems

In Table 1, the calculation procedure for Sects. 2.1 and 2.2 is listed from the perspective of computer programming. Compared with the quartic B-spline scheme by Rostami et.al [18], the proposed scheme only requires triangular factorization of mass matrix, and thus, inherits the advantages of explicit time integration method. For the computation time cost, it can be noted in the table that more time cost than the explicit Bathe scheme is needed to calculate $\dot{{\varvec{f}}}\left( t_{i}^{+} \right)$ in the initial calculation; as for the recurrence calculation process, the proposed scheme costs roughly same magnitude of time for triangular factorization of mass matrix ${\varvec{M}}$ and the solving of linear equations [11], but consumes more time effort for B-spline approximations(i.e., Eq.(11) and Eq.(12)) which, however, are far less than the time effort for linear equations. In general, computation efficiency of the proposed scheme is desirable.

Table 1 Calculation procedure of the proposed scheme for MDOF systems

3 Stability analysis

For the proposed scheme as illustrated in Sect. 2, consider a SDOF system as

$$\begin{aligned} \ddot{u}(t)+2\xi \omega \dot{u}(t)+\omega ^{2}u(t)=f(t) \end{aligned}$$

(27)

where $\xi$, $\omega$ and f(t) are the damping ratio, the undamped angular frequency of the system, and the forcing excitation, respectively.

After temporal discretization, the recurrence formula of the SDOF system can be represented by

$$\begin{aligned} \left\{ {\begin{array}{l} u\left( t_{i+1} \right) \\ (\Delta t)\cdot \dot{u}\left( t_{i+1} \right) \\ {(\Delta t)}^{(2)}\cdot \ddot{u}\left( t_{i+1} \right) \\ {(\Delta t)}^{(3)}\cdot \dddot{u}\left( t_{i+1} \right) \\ \end{array}} \right\}= & {} {\varvec{A}}\left\{ {\begin{array}{l} u\left( t_{i+1} \right) \\ (\Delta t)\cdot \dot{u}\left( t_{i} \right) \\ {(\Delta t)}^{(2)}\cdot \ddot{u}\left( t_{i} \right) \\ {(\Delta t)}^{(3)}\cdot \dddot{u}\left( t_{i} \right) \\ \end{array}} \right\} \nonumber \\&+\,{\varvec{L}}_{\mathbf {1}}f\left( t_{i+1} \right) +{\varvec{L}}_{\mathbf {2}}f^{\left( 1 \right) }\left( t_{i+1}^{+} \right) \nonumber \\ \end{aligned}$$

(28)

where the amplification matrix ${\varvec{A}}$ and the load operators ${\varvec{L}}_{\mathbf {1}}$ and ${\varvec{L}}_{\mathbf {2}}$ are given in Appendix A.

Assigning $\xi =0$ in ${\varvec{A}}$ gives following characteristic polynomial

$$\begin{aligned} \tilde{p}\left( \gamma \right) =\gamma ^{4}+A_{1}\gamma ^{3}+A_{2}\gamma ^{2}+A_{3}\gamma +A_{4} \end{aligned}$$

(29)

where

Table 2 ${(\omega {\Delta }t)}_{b}$, $\rho _{{min}}\left( {\varvec{A}} \right)$ for various p values

$$\begin{aligned} A_{1}= & {} \frac{p-1}{6}{(\omega {\Delta }t)}^{4}{+}{(\omega {\Delta }t)}^{2}{-2},\; \nonumber \\ A_{2}= & {} \frac{4p-3}{12}{(\omega {\Delta }t)}^{4}{+}1, \quad A_{3}=0, \quad A_{4}=0 \end{aligned}$$

(30)

Conducting the Routh-Hurwitz stability criteria on Eq. (29), we obtain three conditions as

$$\begin{aligned} p\ge & {} g_{0}\left( \omega {\Delta }t \right) =\frac{\left( \omega {\Delta }t \right) ^{4}+12\left( \omega {\Delta }t \right) ^{2}-48}{2\left( \omega {\Delta }t \right) ^{4}} \end{aligned}$$

(31a)

$$\begin{aligned} p\le & {} g_{1}\left( \omega {\Delta }t \right) =\frac{{5\left( \omega {\Delta }t \right) }^{4}-12\left( \omega {\Delta }t \right) ^{2}+48}{6\left( \omega {\Delta }t \right) ^{4}} \end{aligned}$$

(31b)

$$\begin{aligned} p\le & {} g_{2}\left( \omega {\Delta }t \right) =\frac{3}{4} \end{aligned}$$

(31c)

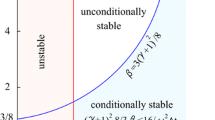
where conditions Eqs. (31a)–(31c) are displayed in Fig. 3 where the proposed scheme can attain conditional stability for $0 \le p\le \frac{3}{4}$. With some arithmetic, the stable region may be expressed as

$$\begin{aligned}&0<\omega {\Delta }t\le \sqrt{\frac{2\sqrt{21-24p} -6}{1-2p}},\quad 0\le p\le \frac{1}{2} \end{aligned}$$

(32a)

$$\begin{aligned}&0<\omega {\Delta }t\le 2,\quad p=\frac{1}{2} \end{aligned}$$

(32b)

$$\begin{aligned}&0<\omega {\Delta }t\le \sqrt{\frac{6-2\sqrt{21-24p} }{2p-1}}\quad \hbox { and}\nonumber \\&\omega {\Delta }t\ge \sqrt{\frac{6+2\sqrt{21-24p} }{2p-1}},\quad \quad \frac{1}{2} \le p\le \frac{3}{4} \end{aligned}$$

(32c)

Fig. 3

The stability property of the proposed scheme with variation of parameter p

As shown in Fig. 3, when $p=\frac{3}{4}$, largest stable region can be obtained. By solving $\tilde{p}\left( \gamma \right) =0$, four eigenvalues $\gamma _{i}$ $(i=1,2,3,4)$ can be obtained as

$$\begin{aligned} \gamma _{1,2}=0,\quad \gamma _{3,4}=\left( -A_{1}\pm \sqrt{A_{1}^{2}-4A_{2}} ) \right) \Bigg /2 \end{aligned}$$

(33)

When $p=\frac{3}{4}$, the absolute eigenvalues $\left\| \gamma _{3,4} \right\|$ is equal to unity (i.e., $\rho \left( {\varvec{A}} \right) =1)$ in the stable region.

In Eq. (32), $\gamma _{3,4}$ are the functions in terms of $\omega {\Delta }t$ and algorithmic parameter p. To obtain numerical dissipation characteristics, the eigenvalues $\gamma _{3,4}$ should be in the complex plane. The bifurcations are the points where the eigenvalues alter between complex values and real values. Thus, $\gamma _{3,4}$ at the bifurcations can be obtained by prescribing $A_{1}^{2}-4A_{2}=0$. Then, with some mathematical operations and numerical calculation, $\rho \left( {\varvec{A}} \right)$ value at the bifurcation, briefly denoted by $\rho _{b}\left( {\varvec{A}} \right)$, as a function of algorithmic parameter p, is plotted in Fig. 2 where $\omega {\Delta }t$ at the bifurcation (briefly denoted by ${(\omega {\Delta }t)}_{b})$ is also delineated. For clarity, ${(\omega {\Delta }t)}_{b}$ and $\rho _{b}\left( {\varvec{A}} \right)$ for various p values are listed in Table 2 where the corresponding stable regions in terms of $\omega {\Delta }t$, briefly denoted by $S_{p}$, are also attached.

In Fig. 3 and Table 2, it is noteworthy that, when $p=0.604$, ${(\omega {\Delta }t)}_{b}$ is equal to 2 which is the same as the Central Difference scheme. Actually, for wave propagation problems in which numerical dispersion is needed, the $p=0.604$ case is desirable in terms of its convenience in selecting time increment ${\Delta }t$.

Fig. 4

Stability variation in terms of algorithmic parameter p

Fig. 5

The spectral radii of the proposed scheme versus $\omega {\Delta }t$ for various p value

Fig. 6

The spectral radii versus $\omega {\Delta }t$ for the proposed scheme and other schemes

Fig. 7

Percentage amplitude decay versus ${{\Delta }t} \big / T$ for the proposed scheme and other schemes

Fig. 8

Percentage period elongation versus ${{\Delta }t} \big / T$ for the proposed scheme and other schemes

Further, the spectral radii curves of different p value cases are illustrated in Fig. 5 where the bifurcation points are in good agreement with the results shown in Table 2 and Fig. 4. Meanwhile, Fig. 5 shows that, with free parameter p, the proposed scheme is flexible in controlling numerical dissipation/dispersion. In Fig. 6, the spectral radii of the proposed scheme are compared with that of the Noh–Bathe scheme, HC and TW schemes [9, 11, 12].

4 Accuracy analysis

For step-by-step schemes, to evaluate accuracy of the proposed scheme, two error norms, that is, amplitude decay (AD) and period elongation (PE) are employed [22, 23]. In Figs. 7 and 8, percentage AD and PE in terms of ${{\Delta }t} {\big /} T$ are respectively plotted, where $T={{2\uppi }} \big /\omega$. In the figures, TW and Noh–Bathe schemes (with excellent dispersion) [11, 12] are employed for comparison. In Fig. 7, for the proposed scheme, all AD results are larger than that of the Noh–Bathe scheme, and the $p=\frac{2}{3}$ case shows smallest AD. As for PE, only the $p=0.604$ and $p=\frac{2}{3}$ cases show same magnitude of PE as the Noh–Bathe scheme. Especially, the $p=\frac{2}{3}$ case illustrates small PE in the low-frequency band, which is in good agreement with accuracy remark in Sect. 2.2. In Fig. 7, the $p=\frac{3}{4}$ case displays no dispersion as the CD scheme. In Fig. 8, it is noteworthy that the $p=0.604$ case shows small PE and large AD in relatively high frequency band. Thus, theoretically, the $p=0.604$ case possesses desirable numerical dispersion properties.

5 A demonstrative dispersion analysis

To quantify the dispersion properties of the proposed scheme, a dispersion analysis for 2D wave propagation is conducted here. As well known, the governing equation for the scalar wave propagation can be represented by

$$\begin{aligned} \frac{\partial ^{2}u}{\partial t^{2}}-c_{0}^{2}{\nabla }^{2}u=0 \end{aligned}$$

(34)

where u is field variable and $c_{0}$ is the wave velocity. Here we focus on the dispersion associated with the propagations of disturbances due to initial conditions, and thus homogeneous boundary conditions and no body force are considered. The initial conditions are given as

$$\begin{aligned} u\left( {\varvec{x}},0 \right) =u_{0}({\varvec{x}}),\quad \; \frac{\partial u}{\partial t}\left( {\varvec{x}},0 \right) =v_{0}({\varvec{x}}) \end{aligned}$$

(35)

where $u_{0}$ and $v_{0}$ are the initial displacement and velocity, respectively. ${\varvec{x}}$ is the coordinate vector.

The corresponding discretized finite element formulation of Eq. (33) is given as

$$\begin{aligned} {\varvec{M}}\ddot{{\varvec{u}}}+c_{0}^{2}{\varvec{Ku}}=\mathbf {0} \end{aligned}$$

(36)

where ${\varvec{u}}$ and $\ddot{{\varvec{u}}}$ are the discretized nodal field variable vector and its second derivative, respectively. Here ${\varvec{M}}$ is the lumped mass matrix.

The general solution of Eq. (34), for a plane wave traveling in the Cartesian coordinate (x, y), can be given by $u=Ae^{i( k_{0}xcos( \theta )+k_{0}ysin( \theta )-\omega _{0}t )}$ and its numerical solution is $u(x,y,t)=Ae^{i( kxcos( \theta )+kysin( \theta )-\omega t )}$, where $\omega _{{0}}$ is the frequency of the wave mode and $k_{{0}}=\omega _{0} \big / c_{\mathrm {0}}$ is the wave number, $\omega$ and $k=\omega \big / c$ are the corresponding numerical ones, $\theta$ is the wave propagation angle from the x axis. Then, for finite element analysis with equidistantly distributed nodes along the x and y axes, that is, ${\Delta }x={\Delta }y=h$, the numerical finite element solution at location $x=n_{x}h$, $y=n_{y}h$ and time $t=n_{t}{\Delta }t$ is

$$\begin{aligned} u\left( x,y,t \right)= & {} u\left( n_{x}h,n_{y}h,n_{t}{\Delta }t \right) \nonumber \\= & {} A_{k}e^{i\left( kn_{x}hcos\left( \theta \right) +kn_{y}hsin\left( \theta \right) -\omega n_{t}{\Delta }t \right) }\nonumber \\= & {} A_{k}e^{ikh\left( n_{x}cos\left( \theta \right) +n_{y}sin\left( \theta \right) -n_{t}(CFL)(c \big / c_{0}) \right) } \end{aligned}$$

(37)

where $CFL=\frac{c_{0}\mathrm {\Delta }t}{h}$.

With Eq. (28), a linear multistep form of the proposed scheme is obtained as

$$\begin{aligned}&u\left( t+{\Delta }t \right) +\left( -2+\left( \omega {\Delta }t \right) ^{2}+\frac{p-1}{6}\left( \omega {\Delta }t \right) ^{4} \right) u(t)\nonumber \\&\quad +\left( 1+\frac{4p-3}{12}\left( \omega {\Delta }t \right) ^{4} \right) u\left( t-{\Delta }t \right) =0 \end{aligned}$$

(38)

For the considered wave propagation system (i.e., Eq. (36)), the corresponding multistep form is

$$\begin{aligned}&{\varvec{u}}\left( t+{\Delta }t \right) +\left( -2+\left( {\Delta }t \right) ^{2}{\varvec{\varLambda }} +\frac{p-1}{6}\left( {\Delta }t \right) ^{4}{\varvec{\varLambda }}^{\mathbf {2}} \right) {\varvec{u}}(t)\nonumber \\&\quad +\left( 1+\frac{4p-3}{12}\left( {\Delta }t \right) ^{4}{\varvec{\varLambda }}^{\mathbf {2}} \right) {\varvec{u}}\left( t-{\Delta }t \right) =0 \end{aligned}$$

(39)

where ${\varvec{\varLambda }}$ is the diagonal matrix which satisfies $c_{0}^{2}{\varvec{K}}{\varvec{\phi }} ={\varvec{M}}{\varvec{\phi }} {\varvec{\varLambda }}$, where ${\varvec{\phi }}$ is the corresponding eigenvectors.

Eq. (39) can be further rewritten as

$$\begin{aligned}&{\varvec{u}}\left( t+{\Delta }t \right) +\left( -2{\varvec{I}}+\left( CFL \right) ^{2}{\varvec{K}}+\frac{p-1}{6}\left( CFL \right) ^{4}{\varvec{K}}^{\mathbf {2}} \right) {\varvec{u}}(t)\nonumber \\&\quad +\left( 1+\frac{4p-3}{12}\left( CFL \right) ^{4}{\varvec{K}}^{\mathbf {2}} \right) {\varvec{u}}\left( t-{\Delta }t \right) =0 \end{aligned}$$

(40)

where ${\varvec{I}}$ is the identity matrix.

For uniform 4-node finite element [11, 22], the effective terms of the matrix ${\varvec{Ku}}(t)$ for the middle node at (x, y) are

$$\begin{aligned}&\frac{1}{3}\left( {8}u\left( x,y,t \right) {-}\left( u\left( x\pm h,y,t \right) +u\left( x,y\pm h,t \right) \right. \right. \nonumber \\&\quad \left. \left. +\,u\left( x\pm h,y\pm h,t \right) \right) \right) \end{aligned}$$

(41)

and the corresponding terms from matrix ${\varvec{K}}^{\mathbf {2}}{\varvec{u}}(t)$ are [11]

$$\begin{aligned}&\frac{1}{9}\left\{ 72u\left( x,y,t \right) \right. \left. -14u\left( x\pm h,y\pm h,t \right) \right. \nonumber \\&\quad \left. +\,u\left( x\pm 2h,y\pm 2h,t \right) \right\} \nonumber \\&\quad +\,u\left( x\pm h,y\pm 2h,t \right) -12\left( u\left( x\pm h,y,t \right) \right. \nonumber \\&\quad \left. +\,u\left( x,y\pm h,t \right) \right) \nonumber \\&\quad \left. +\,3\left( u\left( x\pm 2h,y,t \right) +u\left( x,y\pm 2h,t \right) \right) \right. \nonumber \\&\quad \left. +\,2\left( u\left( x\pm 2h,y\pm h,t \right) \right) \right\} \end{aligned}$$

(42)

Fig. 9

Relative wave velocity errors of various schemes, and the dotted lines define the discarded wave modes

Fig. 10

Relative wave velocity errors of two schemes for different wave propagating angles, the dotted lines denote the discarded wave modes. a The Proposed scheme. b The Noh–Bathe scheme

With Eqs. (36) and (40)–(42), we obtain for the proposed scheme a relation between CFL, ${(c-c_{0})} \big / c_{0}$ and kh. This relation can be represented by

$$\begin{aligned} R\left( CFL,\,kh,\frac{c{-}c_{{0}}}{c_{{0}}} \right) {=0} \end{aligned}$$

(43)

Here instead of obtain the explicit expression of ${(c-c_{0})} \big / c_{0}$, we take the Maclaurin series expansion with respect to ${(c-c_{0})}\big / c_{0}$ and obtain a simplified expression of R as

$$\begin{aligned}&R\left( CFL,\, kh{,}\frac{c{-}c_{{0}}}{c_{{0}}} \right) = R\left( CFL,\, kh{,0} \right) \nonumber \\&{+}\left( \frac{\partial R}{\partial \left( \frac{c{-}c_{{0}}}{c_{{0}}} \right) } \right) _{\frac{c{-}c_{{0}}}{c_{{0}}}{=0}}{\cdot }\left( \frac{c{-}c_{{0}}}{c_{{0}}} \right) {+}\nonumber \\&\quad \cdots +\frac{1}{l!}\left( \frac{\partial ^{l}R}{\partial \left( \frac{c-c_{0}}{c_{0}} \right) ^{l}} \right) _{\frac{c-c_{0}}{c_{0}}=0}\cdot \left( \frac{c-c_{0}}{c_{0}} \right) ^{l}+o\left( \frac{c-c_{0}}{c_{0}} \right) ^{l+1}=0\nonumber \\ \end{aligned}$$

(44)

With given CFL and kh, ${(c-c_{0})}\big / c_{0}$ can be solved using some convergent iteration algorithm. By omitting the high-order infinitesimal term in Eq. (44), a convergent iteration equation is represented as

$$\begin{aligned} \left( \frac{c-c_{0}}{c_{0}} \right) _{J+1}=\tilde{R}\left( \left( \frac{c-c_{0}}{c_{0}} \right) _{J} \right) ,\; \left( \frac{c-c_{0}}{c_{0}} \right) _{0}=0\nonumber \\ \end{aligned}$$

(45)

where J is the iteration number, and is determined by the iteration error $\epsilon$ as

$$\begin{aligned} \left\| \left( \frac{c-c_{0}}{c_{0}} \right) _{J+1}-\left( \frac{c-c_{0}}{c_{0}} \right) _{J} \right\| _{2}<\epsilon \end{aligned}$$

(46)

Fig. 11

Accuracy and convergence rate for the proposed scheme and other schemes, when standard system 6.1 considered. a Displacement. b Velocity. c Acceleration

Fig. 12

Accuracy of the proposed scheme and other scheme for simulation example 6.2. a Displacement. b Velocity. c Acceleration

After solving Eq.(45), the real part of $\frac{c-c_{0}}{c_{0}}$ denotes the relative wave velocity error and is plotted in Fig. 9 in terms of the wavelength $\lambda$ and the element size used. In Fig. 9, for the proposed scheme ($p=0.604)$, three demonstrative CFL values are considered for dispersion errors. It can be noted that the $CFL=1.0$ one gives desirable wave velocity when compared with other two CFL ones, which matches well with the numerical dispersion remarks in Sects. 3 and 4. In the figure, error curves of the TW scheme ($\varphi =1.033$, $CFL=0.9)$ [12] and the Noh–Bathe scheme ($p=0.54$, $CFL=1.85)$ [11] are also plotted with the suggested optimal CFL values considered. Further, in Fig. 10a, the relative wave velocity errors of the proposed scheme along different wave propagating angles are illustrated. For various angles, the proposed scheme shows minimal variations in wave velocity errors, and thus, is desirable for wave propagation problems. Also for comparison, error curves of the Noh–Bathe scheme are displayed in Fig. 10b.

6 Numerical simulations

In this section, several numerical examples are tested to demonstrate the validity of the proposed scheme. In the simulations, TW scheme and Noh–Bathe scheme (with excellent dispersion) are used for comparison. For the proposed scheme, three representative cases including the $p=\frac{2}{3}$ case (with highest accuracy), the $p=0.604$ case (with desirable dispersion properties) and the $p=\frac{3}{4}$ case (with no dispersion) are selected for simulations.

6.1 A standard undamped system

To test the calculation accuracy of the proposed scheme, free vibration of a standard undamped SDOF system is considered. This system is presented as

$$\begin{aligned} \ddot{u}(t)+\omega ^{2}u(t)=0;\quad u\left( 0 \right) =1,\quad \dot{u}\left( 0 \right) =0 \end{aligned}$$

(47)

where $\omega =\pi$, that is, $T=2$.

A time duration of $t=2{\hbox {s}}$ is considered and calculated for accuracy and efficiency tests, and a global error norms $E_{l}(l=0,1,2)$ are employed and defined as

$$\begin{aligned} E_{l}=\sqrt{\sum \nolimits _{i=0}^{n-1} \left( u_{i}^{(l)}-\tilde{u}_{i}^{(l)} \right) ^{2} \big / \sum \nolimits _{i=0}^{n-1} \left( \tilde{u}_{i}^{(l)} \right) ^{2}} {\times 100\% } \end{aligned}$$

(48)

In which l is the order of derivative. $u_{i}^{(l)}$(i.e., $u_{i}$, $\dot{u}_{i}$ and $\ddot{u}_{i})$ are numerical results at time $t_{i}$, and $\tilde{u}_{i}^{(l)}$ are the corresponding exact ones.

In Fig. 11, global errors of various schemes are plotted in a log form. It can be noted that the $p=\frac{2}{3}$ case gives higher accuracy than other cases and other schemes, which is in good agreement with the PE results in Fig. 8. However, Noh–Bathe scheme displays higher accuracy than other cases, and the TW scheme shows lowest accuracy.

Fig. 13

Pre-stress membrane wave propagation problem, wave speed $c_{0}=1$, the initial displacement and velocity are zero

Fig. 14

Displacement variations of two schemes along x- direction at around 6.0s, for $120\times 120$ finite elements considered

Fig. 15

Velocity variations of two schemes along x-direction at around 6.0s, when $120\times 120$ finite elements considered

Fig. 16

Snapshots of displacement at around 6.0s for two schemes, when different elements considered

Fig. 17

Snapshots of velocity at around 6.0s for two schemes, when different elements considered

6.2 A damped system

Here to verify the validity of the proposed scheme for damped system, consider following numerical example,

$$\begin{aligned} \ddot{u}(t)+4\dot{u}(t)+5u(t)=\sin (2t);\quad u\left( 0 \right) =\frac{57}{65},\quad \dot{u}\left( 0 \right) =\frac{2}{65}.\nonumber \\ \end{aligned}$$

(49)

The exact solution is $u(t)=e^{-2t}\left( \cos t+2\sin t \right) {-}\frac{1}{65}(8\cos {2t}-\sin {2t})$.

In Fig. 12, same time increment $\Delta {t=2\times {10}^{-2}{\hbox {s}}}$ is adopted for calculation, and the relative error norms are defined by

$$\begin{aligned} \varepsilon _{l}=\frac{\left| u^{(l)}-\tilde{u}^{(l)} \right| }{\left| \tilde{u}^{(l)} \right| }\times 100\%,\;\quad l=0,1,2. \end{aligned}$$

(50)

where $u^{(l)}$(i.e., u, $\dot{u}$ and $\ddot{u})$ and $\tilde{u}^{(l)}$ are the numerical results and the exact results at discrete times, respectively. In the figures, among all schemes, the $p=\frac{2}{3}$ case of the proposed scheme displays highest accuracy, which matches well with the accuracy remarks in Sect. 2.2. The $p=0.604$ and $p=\frac{3}{4}$ cases also show desirable accuracy when compared with other schemes.

6.3 2D scalar wave propagation

To test the numerical dispersion properties of the proposed scheme, wave propagation problem of a pre-stress membrane (see., Fig. 13) is considered. This problem is governed by [11, 24]

$$\begin{aligned} \frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial y^{2}}+f\left( 0,0,t \right) =\frac{1}{c_{0}^{2}}\frac{\partial ^{2}u}{\partial t^{2}} \end{aligned}$$

(51)

where the impulse load is given by

$$\begin{aligned} f\left( 0,0,t \right) =\left\{ {\begin{array}{ll} 4\left( 1-{(2t-1)}^{2} \right) ,&{}\quad 0<t<1 \\ 0,&{}\quad t\ge 1 \\ \end{array}} \right. \end{aligned}$$

(52)

The analytical solution can be obtained by

$$\begin{aligned} u\left( x,y,t \right) =\int \nolimits _0^t {f(t)G(x,y,t-\bar{t})d\bar{t}} \end{aligned}$$

(53)

where the Green’s function G is given by

$$\begin{aligned} G\left( x,y,t \right) =\frac{H(c_{0}t-\sqrt{x^{2}+y^{2}} )}{2\pi c_{0}\sqrt{{c_{0}^{2}t^{2}-x^{2}-y^{2}}}} \end{aligned}$$

(54)

where H is the Heaviside step function.

In Figs. 14 and 15, displacement and velocity curves along the x-direction at around time 6.0s are plotted, respectively. In the figures, the suggested optimal CFL value 1.85 for the Noh–Bathe scheme ($p=0.54)$ and the suggested desirable CFL value 1.0 for the proposed scheme ($p=0.604)$ are employed for calculation. In Figs. 14 and 15, for wave propagating angles $\theta =0$ and $\theta =\frac{\pi }{4}$, displacement curves of both two considered schemes are desirable when $120\times 120$ finite element number considered. For both displacement and velocity, the numerical results of $\theta =\frac{\pi }{4}$ are less accurate than that of $\theta =0$. However, the proposed scheme begets larger errors than the Noh–Bathe scheme.

In Figs. 16 and 17, the snapshot of displacements and velocities at around time 6.0s are plotted to demonstrate wave propagation morphology of two considered schemes along all propagating angles, respectively. In the figures, two element numbers, $60\times 60$ and $120\times 120$, are considered to test the convergence rate of the two schemes. For $60\times 60$ mesh, $\Delta t=0.4625{\hbox {s}}$ for the Noh–Bathe scheme and $\Delta t=0.25{\hbox {s}}$ for the proposed scheme are adopted; for $120\times 120$ mesh, the corresponding time intervals are $\Delta t=0.23125{\hbox {s}}$ and $\Delta t=0.125{\hbox {s}}$. From Figs. 14–17, it can be noted that the proposed scheme gives reasonable wave propagation morphology, and less accurate results than the Noh–Bathe scheme. However, the proposed scheme is still desirable due to its convenience in selecting time interval $\Delta t \Big (\text {for various meshes, the suggested time interval} \Delta t \text {can} \text {be selected as} \Delta t=\frac{h}{c_{0}}\Big )$.

In Fig. 18, time consumption of three schemes for this wave propagation simulation are compared to demonstrate the computation efficiency of the proposed scheme. In the figure, the proposed scheme costs slightly more time than the Bathe scheme, and needs about 20% more time effort than the CD scheme. The time cost results agree with the time cost remarks in Sect. 2. Conclusively, the proposed scheme is desirable due to its acceptable time cost and high accuracy.

Fig. 18

Time cost comparison of various schemes, when $60\times 60$ mesh for example 6.3 considered

7 Concluding remarks

A quartic B-spline based explicit integration scheme of B-spline family schemes is presented for structural dynamics. With one algorithmic parameter, the proposed scheme can possess at least second-order accuracy and at most third-order accuracy, meanwhile, stability analysis shows that desirable numerical dispersion can be obtained by adjusting parameter value. Theoretical analysis shows that the PE and AD results of the proposed scheme are desirable when appropriate parameter value is selected, which is also confirmed by comparing with other representative explicit schemes when a standard undamped system and a damped system considered. The desirable dispersion characteristics of the proposed scheme is demonstrated by considering a 2D scalar wave propagation problem analytically and numerically. In conclusion, the proposed scheme is desirable for linear structural dynamics due to its high accuracy and desirable numerical dissipation, and thus, is very applicable for wave propagation problems. Given the general explicit form, theoretically, the proposed scheme can be extended for nonlinear problems.

Appendix A

$$\begin{aligned} {\varvec{A}}=\left[ {\begin{array}{*{20}c} A_{11} &{}\quad A_{12} &{}\quad A_{13} &{}\quad A_{14}\\ A_{21} &{}\quad A_{22} &{}\quad A_{23} &{}\quad A_{24}\\ A_{31} &{}\quad A_{32} &{}\quad A_{33} &{}\quad A_{34}\\ A_{41} &{}\quad A_{42} &{}\quad A_{43} &{}\quad A_{44}\\ \end{array} } \right] \end{aligned}$$

(55)

where

$$\begin{aligned} A_{11}= & {} 1,\quad A_{12}=1,\quad A_{13}=\frac{1}{2},\quad A_{14}=\frac{1}{6} \end{aligned}$$

(56)

$$\begin{aligned} A_{21}= & {} (p-1) \left( \omega {\Delta }t \right) ^{2},\nonumber \\ A_{22}= & {} \left( p-1 \right) \left( \omega {\Delta }t \right) ^{2}+2\left( p{-1} \right) \xi \omega {\Delta }t+1 \end{aligned}$$

(57)

$$\begin{aligned} A_{23}= & {} \frac{1}{2}\left( p-1 \right) \left( \omega {\Delta }t \right) ^{2}{+2}\left( p{-1} \right) \xi \omega {\Delta }t+1 \end{aligned}$$

(58)

$$\begin{aligned} A_{24}= & {} \frac{1}{6}\left( p-1 \right) \left( \omega {\Delta }t \right) ^{2}{+}\left( p{-1} \right) \xi \omega {\Delta }t+p-\frac{1}{2} \end{aligned}$$

(59)

$$\begin{aligned} A_{31}= & {} -\left( \omega {\Delta }t \right) ^{2},\quad A_{32}=-\left( \omega {\Delta }t \right) ^{2}-2\xi \omega {\Delta }t \end{aligned}$$

(60)

$$\begin{aligned} A_{33}= & {} -\frac{1}{2}\left( \omega {\Delta }t \right) ^{2}-2\xi \omega {\Delta }t,\nonumber \\ A_{34}= & {} -\frac{1}{6}\left( \omega {\Delta }t \right) ^{2}-\xi \omega {\Delta }t \end{aligned}$$

(61)

$$\begin{aligned} A_{41}= & {} \left( {1-}p \right) \left( \omega {\Delta }t \right) ^{4}+2\xi \left( \omega {\Delta }t \right) ^{3} \end{aligned}$$

(62)

$$\begin{aligned} A_{42}= & {} \left( {1-}p \right) \left( \omega {\Delta }t \right) ^{4}+\left( 4-2p \right) \xi \left( \omega {\Delta }t \right) ^{3}\nonumber \\&+\,{(4\xi ^{2}-1)\left( \omega {\Delta }t \right) }^{2} \end{aligned}$$

(63)

$$\begin{aligned} A_{43}= & {} \frac{1}{2}\left( {1-}p \right) \left( \omega {\Delta }t \right) ^{4}+\left( 3-2p \right) \xi \left( \omega {\Delta }t \right) ^{3}\nonumber \\&+\,{(4\xi ^{2}-p)\left( \omega {\Delta }t \right) }^{2} \end{aligned}$$

(64)

$$\begin{aligned} A_{44}= & {} \frac{1}{6}\left( {1-}p \right) \left( \omega {\Delta }t \right) ^{4}+\left( \frac{4}{3}-p \right) \xi \left( \omega {\Delta }t \right) ^{3}\nonumber \\&+{\left( 2\xi ^{2}-p+\frac{1}{2}\right) \left( \omega {\Delta }t \right) }^{2} \end{aligned}$$

(65)

$$\begin{aligned} {\varvec{L}}_{1}= & {} \left\{ {\begin{array}{l} 0 \\ 1-p \\ 1 \\ \left( p-1 \right) \left( \omega {\Delta }t \right) ^{2}-2\xi \omega \mathrm {\Delta }t \\ \end{array}} \right\} ,\quad {\varvec{L}}_{2}=\left\{ {\begin{array}{l} 0 \\ 0 \\ 0 \\ 1 \\ \end{array}} \right\} .\nonumber \\ \end{aligned}$$

(66)